Spontaneous initiation of premature ventricular complexes and arrhythmias in type 2 long QT syndrome

Under type 2 long QT conditions, cellular phase 2 early afterdepolarizations are suppressed by repolarization gradient, but tissue-scale phase 3 early afterdepolarizations occur spontaneously via dynamical instabilities caused by repolarization gradient and enhanced L-type calcium current, resulting in both the trigger and the vulnerable substrate simultaneously for spontaneous initiation of arrhythmias.

Abstract

The occurrence of early afterdepolarizations (EADs) and increased dispersion of repolarization are two known factors for arrhythmogenesis in long QT syndrome. However, increased dispersion of repolarization tends to suppress EADs due to the source-sink effect, and thus how the two competing factors cause initiation of arrhythmias remains incompletely understood. Here we used optical mapping and computer simulation to investigate the mechanisms underlying spontaneous initiation of arrhythmias in type 2 long QT (LQT2) syndrome. In optical mapping experiments of transgenic LQT2 rabbit hearts under isoproterenol, premature ventricular complexes (PVCs) were observed to originate from the steep spatial repolarization gradient (RG) regions and propagated unidirectionally. The same PVC behaviors were demonstrated in computer simulations of tissue models of rabbits. Depending on the heterogeneities, these PVCs could lead to either repetitive focal excitations or reentry without requiring an additional vulnerable substrate. Systematic simulations showed that cellular phase 2 EADs were either suppressed or confined to the long action potential region due to the source-sink effect. Tissue-scale phase 3 EADs and PVCs occurred due to tissue-scale dynamical instabilities caused by RG and enhanced L-type calcium current (I_Ca,L), occurring under both large and small RG. Presence of cellular EADs was not required but potentiated PVCs when RG was small. We also investigated how other factors affect the dynamical instabilities causing PVCs. Our main conclusion is that tissue-scale dynamical instabilities caused by RG and enhanced I_Ca,L give rise to both the trigger and the vulnerable substrate simultaneously for spontaneous initiation of arrhythmias in LQT2 syndrome.

NEW & NOTEWORTHY

Under type 2 long QT conditions, cellular phase 2 early afterdepolarizations are suppressed by repolarization gradient, but tissue-scale phase 3 early afterdepolarizations occur spontaneously via dynamical instabilities caused by repolarization gradient and enhanced L-type calcium current, resulting in both the trigger and the vulnerable substrate simultaneously for spontaneous initiation of arrhythmias.

prolongation of action potential duration (APD) in long QT syndromes (LQTS) as well as in other cardiac diseases is associated with an increased risk of ventricular arrhythmias, in particular Torsade de Pointes (TdP) (34, 45, 54). Two key factors are closely associated with arrhythmogenesis in LQTS (1, 2, 6, 17, 21, 43, 44, 59, 62, 68): early afterdepolarizations (EADs) and increased dispersion of repolarization. EADs occur during the repolarization phase of the action potential (AP), resulting from increased inward currents and/or decreased outward currents. Dispersion of repolarization exists in the ventricles of normal hearts due to heterogeneous ion channel distributions, which is amplified in LQTS (6, 62). EADs are known to be able to trigger premature ventricular complexes (PVCs) while increased dispersion of repolarization increases the chance of conduction block of a PVC. Therefore, it is natural to assume that an EAD occurring in one region generates a PVC that propagates into another region with a steep repolarization gradient (RG) and is then blocked regionally to initiate arrhythmias in LQTS. However, for an EAD to cause a PVC in tissue, the EAD in the longer APD region must propagate to the adjacent shorter APD region. It is well known that, due to the source-sink effect, increasing RG tends to suppress EADs (22, 66), making it more difficult for EADs to trigger PVCs. Therefore, increased RG and the occurrence of EADs are two competing processes at the tissue scale, but how they interact to promote arrhythmias in LQTS remains unclear.

Whether an EAD can propagate to cause a PVC in structurally normal tissue, such as in LQTS, remains controversial. Damiano and Rosen (13) showed that phase 3 EADs (takeoff potential under −50 mV) can trigger PVCs in Purkinje fibers but phase 2 EADs (takeoff potential over −30 mV) could not. Yan et al. (67) used wedge preparations and intracellular microelectrode recordings to show that phase 2 EADs might propagate from the endocardial layer to the epicardial layer to initiate PVCs and finally lead to TdP, but an increased RG was needed for the phase 2 EADs to induce arrhythmias in rabbit hearts. Supporting the observation that increased RG was required for phase 2 EADs to induce PVCs, Maruyama et al. (32), who used optical mapping of rabbit hearts under E4031 and hypokalemia, observed that when the phase 2 EADs were confined to the center of the long APD region, they could not generate PVCs, but when they occurred near or transmitted to the steep RG region, phase 3 EADs and PVCs were induced and resulted in ectopic excitations or reentry. Other optical mapping studies (23, 27) also showed that PVCs originated spontaneously from the steep RG regions. These experiments seemed to show that increased RG potentiated propagation of phase 2 EADs into PVCs to initiate arrhythmias in LQTS. This contradicts the commonly held belief that raising the RG increases the sink effect, which suppresses EADs.

In this study, we systematically investigated the roles of EADs and RG in the genesis of PVCs and ventricular arrhythmias in LQT2 syndrome. We hypothesized that PVCs are consequences of a tissue-scale dynamical instability caused by RG and enhanced L-type calcium (Ca) current (I_Ca,L), not a result of propagation of cellular phase 2 EADs. RG-induced PVCs propagate unidirectionally, which can result in reentrant arrhythmias without requiring an additional tissue substrate. To test this hypothesis, we carried out optical mapping experiments in transgenic LQT2 rabbit hearts and computer simulations of one-dimensional (1D) cable and two-dimensional (2D) tissue using a rabbit ventricular myocyte model. Optical mapping experiments showed that PVCs tended to initiate spontaneously in the steep RG region and propagate unidirectionally. Systematic computer simulations showed that cellular phase 2 EADs (i.e., EADs that occur in isolated single cells) were mostly suppressed or confined to the long APD region due to the source-sink effect. On the other hand, tissue-scale phase 3 EADs (i.e., EADs in tissue but not in isolated cells) could occur in the RG region due to tissue-scale dynamical instabilities, resulting in unidirectionally propagating PVCs. PVCs could occur under either large or small RG depending on the magnitude of I_Ca,L, while requiring a two- to threefold increase in I_Ca,L, which is much higher than that required for the occurrence of cellular EADs, but within the physiological range induced by sympathetic stimulation. The presence of cellular phase 2 EADs potentiated RG-mediated tissue-scale phase 3 EAD and PVC formation when the RG was small. Because the PVCs propagated unidirectionally, reentry could form in tissue in the same location where the PVCs were initiated, i.e., the triggers and tissue substrate for arrhythmia initiation originated from the same source: a tissue-scale dynamical instability caused by RG and enhanced I_Ca,L.

MATERIALS AND METHODS

Optical Mapping Experiments

Transgenic LQT2 rabbits (6) were killed with buprenorphene (0.03 mg/kg im), acepromazine (0.5 mg/kg im), xylazene (15 mg/kg im), ketamine (60 mg/kg im), pentothal (35 mg/kg iv), and heparin (200 U/kg). This investigation conformed to the current Guide for the Care and Use of Laboratory Animals published by the National Institutes of Health (NIH Publication No. 85-23, revised 2011) and approved by the Lifespan Animal Welfare Committee at Rhode Island Hospital. Hearts were excised, retrogradely perfused through the aorta with (in mmol/l) 130 NaCl, 24 NaHCO₃, 1.0 MgCl₂, 4.0 KCl, 1.2 NaH₂PO₄, 5 dextrose, 25 mannitol, and 1.25 CaCl₂, at pH 7.4, gassed with 95% O₂ and 5% CO₂, and stained with the voltage-sensitive dye di-4-ANEPPS (Invitrogen). Hearts were placed in a water-heated chamber to maintain temperature at 37.0 ± 0.2°C, and 5 μmol/l blebbistatin were added to reduce movement artifact. Perfusion rate was set to 20 ml/min. Twelve LQT2 rabbits were used in this project. The atrioventricular (AV) node was ablated to control heart rate using a cautery unit (World Precision Instruments). After ablation, the rabbits exhibited a slower heart rate, with the cycle length typically ranging from 700 to 2,000 ms. If the cycle length was longer than 2,000 ms, the base of the right ventricle (RV) was paced at a cycle length of 2,000 ms. Isoproterenol was delivered as a bolus injection via the bubble trap (5 ml, 140 nM) to hearts to trigger ectopic excitations and polymorphic ventricular tachycardia (pVT). Fluorescence images of APs were recorded from the anterior surface of the heart using a CMOS camera (100 × 100 pixels, 1,000 frames/s, 2.0 × 2.0 cm² field of view, Ultima-L; SciMedia). Activation maps and APD maps were generated using dF/dt and dF²/dt² using digital image analysis routines as previously described (24).

Computer Simulation

Tissue models.

Computer simulations were carried out in single cell model, one-dimensional (1D) and two-dimensional (2D) isotropic monodomain tissue models. The governing partial differential equation for voltage is

$$\frac{\partial V}{\partial t}=-\left(I_{\text{ion}}+I_{\text{sti}}\right)/C_{\text{m}}+D{\nabla }^{2}V$$ (1)

where C_m is the membrane capacitance, which was set as C_m = 1 μF/cm², and D is the diffusion coefficient, which was set as D = 0.0005 cm²/ms. This resulted in a conduction velocity of 0.036 cm/ms in the 1D cable. I_ion is the total ionic current density described by the rabbit ventricular AP model by Mahajan et al. (31) with a modified I_Ca,L detailed below. I_sti is the stimulus current density of amplitude 50 μA/cm² and duration 2 ms.

Ionic current and AP models.

In the rabbit ventricular AP model by Mahajan et al. (31), I_Ca,L was formulated using Markov transitions. Although it can exhibit phase 2 EADs (52, 53), it involves a number of parameter changes, and the EAD amplitude is relatively small. Moreover, it is inconvenient to change the window I_Ca,L alone without changing other properties due to the Markov scheme. To promote EADs and change the window I_Ca,L, we substituted the Markov formulation of I_Ca,L by a Hodgkin-Huxley formulation by Luo and Rudy (28) and Zeng et al. (70). The I_Ca,L formulation in the original Mahajan et al. model (31) is

$$I_{\text{Ca},\text{L}}=G_{\text{Ca},\text{L}}\hspace{0.17em}{P}_{\text{o}}{i}_{\text{Ca},\text{L}}$$ (2)

where G_Ca,L is the maximum conductance of I_Ca,L, P_o is the open probability of the channel, and i_Ca,L is the unitary current of the channel. We substituted P_o by

$$P_{\text{o}}=d\cdot f\cdot f_{\text{Ca}}$$ (3)

where d is the voltage-gated activation gating variable and f is the voltage-dependent inactivation gating variable taken from the Luo and Rudy model (28), and f_Ca is the Ca-dependent inactivation gating variable taken from Zeng et al. (70). We substituted the intracellular Ca concentration with submembrane Ca concentration (c_s) in the f_Ca formulation, i.e.,

$$f_{\text{Ca}}=\frac{1}{1+\frac{{\text{c}}_{\text{s}}}{0.6}}$$ (4)

Figure 1A shows the current-voltage (I–V) curves of peak I_Ca,L for different G_Ca,L.

Fig. 1.

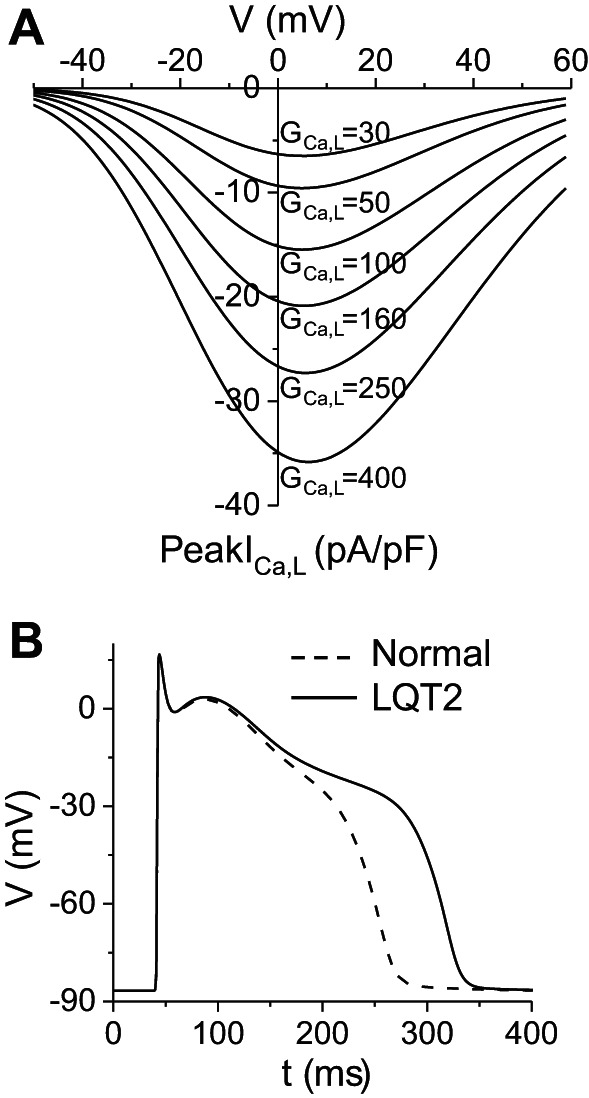
L-type calcium current (I_Ca,L) and action potentials (APs) of the modified rabbit ventricular cell model. A: peak I_Ca,L vs. holding voltage under voltage clamp for different maximum conductance values of I_Ca,L [G_Ca,L, mmol/(cm,C)]. Note that a 5-fold increase in G_Ca,L (from 50 to 250) resulted in roughly a 3-fold increase in peak I_Ca,L. B: AP under normal control condition (dashed), G_Ca,L = 40 mmol/(cm,C), and AP under LQT2 condition (solid), in which we set G_Kr = 0 from the normal control condition. Pacing cycle length was 1 s.

A wide range of peak I_Ca,L has been reported in normal rabbit ventricular myocytes (6, 26, 31, 38, 57), ranging from 5 to 18 pA/pF. According to Fig. 1A, this range roughly corresponds to G_Ca,L 30–150 mmol/(cm,C) in our model. We chose G_Ca,L = 40 mmol/(cm,C) for our normal control model, which gives rise to a peak I_Ca,L ∼6 pA/pF during an AP. The maximum conductance of the slow component of the delayed-rectifier potassium current (G_Ks) was set as G_Ks = 0.5 mS/cm² for control, which gives rise to a peak slow component delayed-rectifier potassium current (I_Ks) of 0.4 pA/pF during an AP, roughly the same as the measurements in rabbit experiments (6, 26, 38). We also set the Na/Ca exchange pump strength as g_NaCa = 1.0 μM/s and clamped intracellular Na concentration = 8 mM. Other parameters were the same as in the original Mahajan et al. model. This gives rise to an APD around 210 ms for the normal control (Fig. 1B). We completely blocked the rapid component of the delayed-rectifier potassium current [I_Kr, by setting the maximum conductance of I_Kr to 0, i.e., maximum conductance of the rapid component of the delayed-rectifier potassium current (G_Kr) = 0] from the normal control to simulate LQT2 since I_Kr was almost undetectable in the transgenic LQT2 rabbit hearts (6). This resulted in an APD around 280 ms for LQT2 control (Fig. 1C). These APD values agree with experimental measurements in normal and transgenic LQT2 rabbit hearts (6).

Modeling the Effects of Isoproterenol

We simulated the effects of isoproterenol by increasing the conductance of I_Ca,L and I_Ks. As shown by Liu et al. (26), the time courses of activation of the two currents caused by isoproterenol are different, with I_Ca,L being activated earlier. Therefore, infusion of isoproterenol first increases APD and APD dispersion and then decreases APD and APD dispersion, which was demonstrated in previous experimental studies (26, 56). For simplicity, we used different combinations of I_Ca,L and I_Ks to model the isoproterenol effects. Based on Liu et al. (26), isoproterenol can double I_Ca,L and triple I_Ks in rabbit ventricular myocytes, and thus the maximum peak I_Ca,L can reach 30–40 pA/pF after isoproterenol. This corresponds to a G_Ca,L >300 mmol/(cm,C) in our model. Therefore, in this study, we explored the G_Ca,L range 30–400 mmol/(cm,C) in our simulations.

Modeling Repolarization Heterogeneities in Tissue

In the real hearts, repolarization heterogeneity or gradient is a result of heterogeneous distributions of the ionic current as well as Ca cycling properties. For the sake of simplicity, in most of the tissue simulations, we used heterogeneous I_Ks conductance to simulate APD dispersion or RG while keeping other currents uniform except for the population-based simulations. Twofold regional difference of I_Ks in rabbit hearts was reported (25). Data from other species also showed a 1.5- to 2-fold regional difference (18, 36). In the 2D tissue model, we used G_Ks = 0.43 mS/cm² in the long APD region and 0.7 mS/cm² in the short APD region for normal control, which is within the twofold range. However, to generate larger APD gradients and systematically investigate the mechanisms of PVCs, we explored a range of regional difference of I_Ks conductance much larger than the twofold differences in our simulations of the 1D cable model.

Population-Based Simulations

To systematically investigate the diversity of heterogeneities in the real hearts, we carried out a large number of 1D cable simulations to cover a wide range of heterogeneities. In these simulations, APD heterogeneities were simulated using heterogeneous I_Ca,L, I_Ks, and transient outward K current (I_to) distributions, and parameter combinations were selected to simulate different APD gradients. The detailed settings for these simulations are presented in results.

Simulation Methods

An explicit Euler method and the Rush-Larsen method (48) were used to integrate the differential equations with a fixed time step Δt = 0.01 ms. For the simulations of 1D and 2D tissue, a space step Δx = Δy = 0.015 cm was used. I_sti was delivered to the first five cells from one end of the 1D cable or from the left side of the 2D tissue with a duration of 2 ms and magnitude of 50 μA/μF. The 1D cable length was 200 cells (corresponding to 3 cm) unless otherwise specified. The 2D tissue size was 300 × 300 cells (corresponding to 4.5 × 4.5 cm²). The heterogeneous region in 2D tissue was a circular area in the center with a radius r = 0.9 cm. No-flux boundary conditions were used. Except for the simulations of pause-induced PVCs, for all other simulations, a single pacing simulation was applied after the cells reached their steady-state resting states. Simulations were carried out using Graphic Processor Units (Nvidia Tesla K20) and C programing language.

RESULTS

RG Induced PVCs and Arrhythmias in Transgenic LQT2 Rabbit Hearts

Our previous study (6) has shown that, under the normal condition, 60% of the transgenic LQT2 rabbits die suddenly at the age of one year. ECG monitoring from these rabbits showed pause-induced pVTs, agreeing with the well-known clinical observation that pVTs or TdPs are pause dependent in LQT2 patients (14, 44, 54, 63). Ideally, one should capture the pVT events under normal conditions to investigate the mechanisms underlying spontaneous initiation of ventricular arrhythmias. However, it is almost impossible to capture these episodes using optical mapping experiments under normal conditions since the arrhythmia events are very rare. To increase the arrhythmia events so that one can optically map the incidence of spontaneous initiation of ventricular arrhythmias, we used AV ablation to slow the heart rate. After the AV node was ablated in these rabbits, the heart rates were slowed, exhibiting cycle lengths typically longer than 700 ms. To avoid the heart rate to be too slow, a pacing stimulus was delivered to the base of RV to excite the heart if the cycle length was longer than 2,000 ms. Because the heart was paced either by spontaneous firings from the Purkinje fiber or by external stimuli from the RV base, we call these beats non-PVC beats or excitations to distinguish them from the PVC beats.

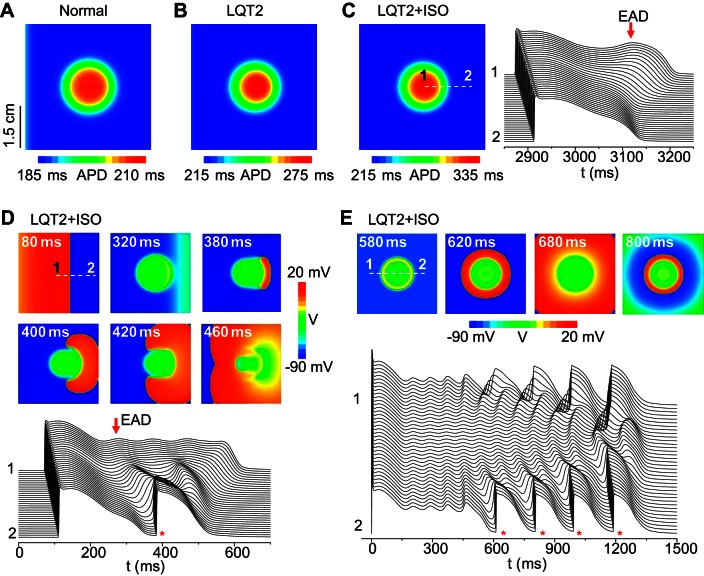
We mapped 12 LQT2 rabbit hearts from the anterior with a field view of 2 × 2 cm², which partially covers both the RV and the left ventricle (LV), as indicated in Fig. 2A. After isoproterenol infusion, PVCs and arrhythmias occurred in these hearts. Figure 2B shows an example of APD distribution (left) and a space-time plot of APs (right) under isoproterenol for a non-PVC beat in a LQT2 rabbit heart. A phase 2 EAD (arrow) occurred in the long APD region. Ten seconds later in the same heart, an ectopic beat occurred (Fig. 2C). A phase 2 EAD (arrow) was still seen in the long APD region, and a focal excitation (*) originated from the APD gradient region propagated around the long APD region, forming a short-lived reentry [Supplemental Movie S1 (Supplemental material for this article is available on the Journal website.)]. Figure 2D shows another scenario of a focal excitation originating from the APD gradient region and propagating around the long APD region, as indicated by the APD map of a normal beat and the activation map of the PVC. Figure 2E shows a case in which the repetitive focal excitations propagated in all directions without local block. These ectopic events either manifested as single or multiple PVCs or eventually led to polymorphic ventricular arrhythmias in the LQT2 rabbit hearts.

Fig. 2.

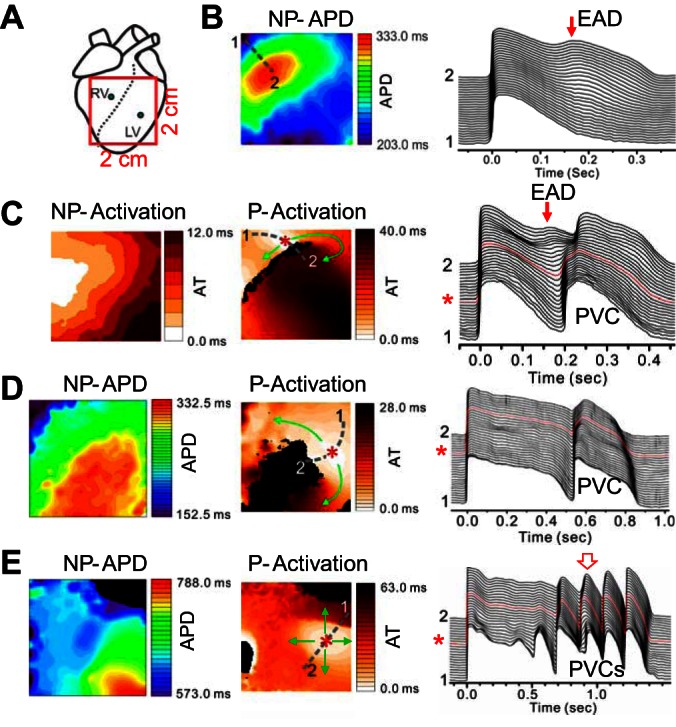
Repolarization gradient-induced premature ventricular complexes (PVCs) in transgenic LQT2 rabbit hearts. A: schematic plot of the optical mapping field on the anterior surface. B: action potential duration (APD) distribution (left) and space-time plot of voltage (right, along the broken line from position 1 to position 2 marked on left) for a non-PVC beat after infusion of isoproterenol. C: 10 s later in the same heart as in B, a PVC was triggered following a non-PVC excitation (see right). Left, activation map of the normal excitation. Middle, activation map of the focal excitation. Arrows indicate the directions of propagations, and * marks the initiation site. Right, space-time plot of voltage showing the non-PVC and the focal excitation (marked as PVC) beats. D: a PVC following a non-PVC excitation in a different rabbit heart. Left, APD map of a non-PVC excitation beat. Middle, activation map of the PVC beat. Right, space-time plot of voltage showing the non-PVC and the focal excitation (marked as PVC) beats. E: repetitive PVCs originating from the same site propagate in all directions in a different rabbit heart. Left, APD map of a non-PVC excitation beat. Middle, activation maps of the second PVC beat as marked by the open arrow on the right. Right, space-time plot of voltage showing the non-PVC and the PVC beats. The abbreviated labels above the maps are: NP-APD-APD map of a non-PVC beat; NP-Activation-Activation map of a non-PVC beat; and P-Activation-Activation map of a PVC beat.

In 12 rabbit hearts, we examined 127 pVT events, 42 of which (33.0%) had PVCs that can be categorized into the type shown in Fig. 2, C and D, i.e., PVCs originated from the RG region and propagated toward the short APD region only, forming a short-lived reentry, whereas 10 pVT events (7.9%) had PVCs that can be categorized into the type shown in Fig. 2E, where PVCs propagated in all directions. The remaining 75 pVT events cannot be categorized because the initiation sites of PVCs were outside the mapping field.

RG induced PVCs and Reentry in a 2D LQT2 Rabbit Tissue Model

To recapitulate the experimental observations, we carried out simulations of 2D heterogeneous tissue. For simplicity, we created a circular region in the center of the tissue and paced from the left edge. Heterogeneity was simulated by a lower I_Ks in the circular area to prolong APD. Figure 3A shows the APD distribution for normal control, in which APD varied from 185 to 210 ms. After removing I_Kr to simulate LQT2, APD varied from 215 to 275 ms (Fig. 3B). These data correspond to our published experimental measurements of APD and dispersion in control and transgenic LQT2 rabbit hearts (6, 72). We then increased I_Ca,L and I_Ks to simulate the effects of isoproterenol (26). At a low isoproterenol level, APD was prolonged, and dispersion was increased, with an EAD occurring in the long APD region (Fig. 3C), similar to the experimental data shown in Fig. 2B. As the isoproterenol effect was enhanced (Fig. 3D and Supplemental Movie S2), APD increased further, and a focal excitation originated from the RG region at the right side of the long APD region and propagated around the long APD region. The two wavefronts collided in the other side of the long APD region without forming a reentrant circuit, resulting in an ectopic beat. This scenario is the same as that shown in the LQT2 hearts in Fig. 2, C and D. Whether a true reentry can form depends on the size of the long APD region, and, when we increased the size of that region, reentry formed (Supplemental Movie S3). On the other hand, when we lengthened the APD further in the long APD region, multiple ectopic beats occurred (e.g., Supplemental Movie 4). In our computer model, the heterogeneity was symmetrical, but, due to the conduction delay, the focal excitation occurred in one side of the long APD region. For asymmetric or irregular heterogeneities as in real tissue, the location of the focal site will depend on the specific structure of the heterogeneity and the conduction direction. In this simplified tissue model, when we paced the whole tissue simultaneously, the spontaneous excitations occurred in all sides, resulting in target patterns (Fig. 3E and Supplemental Movie S5) similar to the experimental patterns shown in Fig. 2E.

Fig. 3.

Repolarization gradient-induced PVCs in a 2D tissue model. A: APD distribution under normal control. G_Ca,L = 40 mmol/(cm,C), maximum conductance of the slow component of the delayed-rectifier potassium current (G_Ks1) = 0.7 mS/μF; G_Ks2 = 0.43 mS/μF; and G_Kr = 0.01 mS/μF. B: APD distribution under simulated LQT2 (G_Kr = 0). The parameters are the same as in A except G_Kr = 0. C: APD distribution (left) and space-time plot of voltage (right) under simulated LQT2 conditions with a low isoproterenol effect. G_Ca,L = 60 mmol/(cm,C), G_Ks1 = 0.9 mS/μF, and G_Ks2 = 0.56 mS/μF. Note the difference in color scales in A–C. D: voltage snapshots (marked by timing) and space-time plot (bottom) under simulated LQT2 with a higher isoproterenol effect. G_Ca,L = 176 mmol/(cm,C), G_Ks1 = 1.1 mS/μF, and G_Ks2 = 0.7 mS/μF. E: voltage snapshots (marked by timing) and space-time plot (bottom) under simulated LQT2 with a high I_Ca,L. G_Ca,L = 276 mmol/(cm,C), G_Ks1 = 0.7 mS/μF, and G_Ks2 = 0.6 mS/μF. The white broken lines in C, D, and E mark the locations (from 1 to 2) for the corresponding space-time plots of voltage. Red arrows in C and D mark early afterdepolarizations (EADs). * in D and E marks the PVC beats. Tissue size is 4.5 cm × 4.5 cm. APD gradient was modeled by a smaller G_Ks (G_Ks2) in the circular region (r = 0.9 cm) in the center, and all other parameters in the tissue are uniform. A stimulus was given at the left side of the tissue in all cases except E in which the stimulus was given to all cells at time (t) = 0.

Mechanisms of RG-Induced Unidirectionally Propagating PVCs

To investigate the underlying mechanisms and the roles of EADs and RG in the spontaneous genesis of PVCs, we carried out simulations using 1D heterogeneous cable models, systematically exploring the parameters detailed in the sections below.

Cellular phase 2 EADs, RG-induced tissue-scale phase 3 EADs, and PVCs.

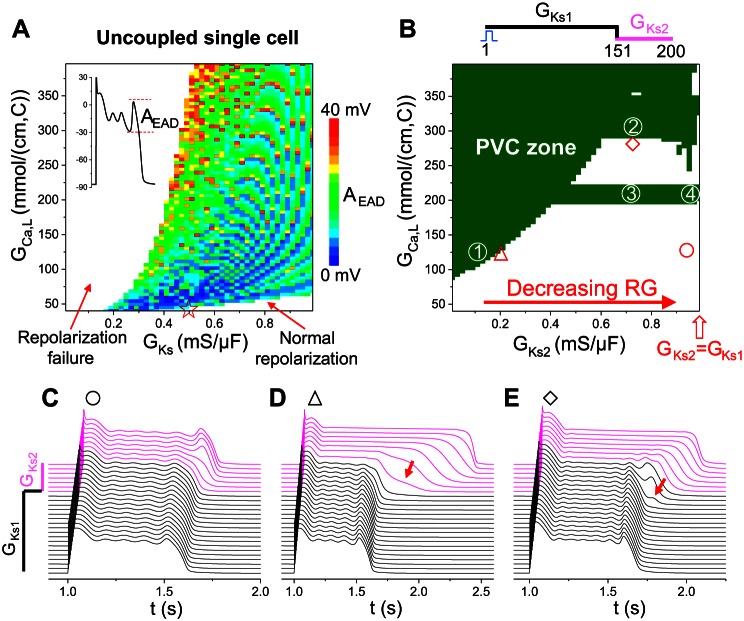
To investigate the roles of cellular phase 2 EADs in PVC formation in tissue, we first carried out simulations of an uncoupled single cell to explore the AP behaviors under the condition of simulated LQT2 (G_Kr = 0) for different G_Ca,L and G_Ks. We scanned G_Ca,L from 40 to 400 mmol/(cm,C) and G_Ks from 0.01 to 1 mS/cm². Figure 4A shows the observed AP behaviors: 1) normal repolarization, occurring at large G_Ks and small G_Ca,L; 2) repolarization failure, occurring at small G_Ks and large G_Ca,L; and 3) EADs. In the EAD zone, we plotted the EAD amplitude (defined in the inset of Fig. 4A) in color scales. We recorded the largest EAD in an AP. The maximum EAD amplitude in the scanned parameter ranges was ∼40 mV. The EAD amplitude tended to be larger for a larger I_Ca,L in general. However, note that the EAD amplitude color map is discretized, and large-amplitude EADs could occur for small I_Ca,L. All EADs were phase 2 EADs with takeoff potentials above −40 mV (data not shown); −40 mV is close to the I_Ca,L activation threshold, indicating that these EADs were the result of reactivation of I_Ca,L.

Fig. 4.

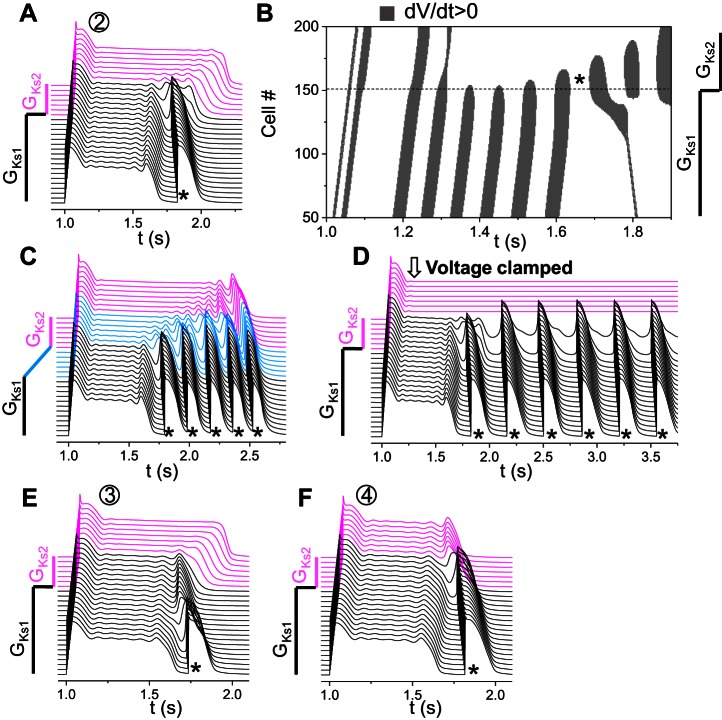
Tissue-scale EADs and PVCs in a heterogeneous 1D cable. A: EAD amplitude (A_EAD) distribution from an isolated single cell by scanning G_Ca,L and G_Ks. G_Kr = 0. A_EAD (indicated by color) was defined as in the inset, which was the largest of the EADs in an AP. The red star on the x-axis indicates the control condition of LQT2 whose AP was shown in Fig. 1C. B: PVC zones (olive) for different combinations of G_Ca,L of the whole cable and G_Ks (G_Ks2) in the long APD region. Simulations were carried out in a 200-cell cable with G_Ks1 being used for the first 150 cells and G_Ks2 for the remaining 50 cells. All other currents are uniform in the whole cable. G_Ks1 = 1 mS/μF and G_Kr = 0. C–E: space-time plots of voltage for three different combinations of G_Ca,L and G_Ks2 as marked by symbols in B. G_Ca,L = 125 mmol/(cm,C) and G_Ks2 = 0.942 mS/μF for C, G_Ca,L = 120 mmol/(cm,C) and G_Ks2 = 0.19 mS/μF for D, and G_Ca,L = 287 mmol/(cm,C) and G_Ks2 = 0.71 mS/μF for E. Arrows in D and E indicate phase 3 EADs. The magenta traces in C–E are voltage traces from the cells with the small G_Ks (G_Ks2), and the black ones are from the cells with the large G_Ks (G_Ks1).

We then carried out simulations in a heterogeneous 1D cable for PVC formation. The 1D cable was composed of two types of cells distinguished by different G_Ks (G_Ks1 and G_Ks2 as shown in the inset of Fig. 4B). We fixed G_Ks1 = 1 mS/cm² and varied G_Ks2 to alter RG. The cable length was 200 cells, and the length of the G_Ks2 (long APD) region was 50 cells. A single stimulus was applied from the short APD side to induce AP conduction. We scanned G_Ks2 from 0.01 to 1 mS/cm² and G_Ca,L of the whole cable from 40 to 400 mmol/(cm,C); therefore, the G_Ks and G_Ca,L ranges in the long APD region were the same as those for the single cell in Fig. 4A. Figure 4B shows the parameters that exhibit PVCs (olive) and no PVCs (white). Compared with the occurrence of EADs in the uncoupled single cell (Fig. 4A), the occurrence of PVCs in the heterogeneous 1D cable (Fig. 4B) required a two- to threefold increase in I_Ca,L (see Fig. 1A for the relationship between peak I_Ca,L and G_Ca,L). Note that, in the uncoupled single cell, repolarization failure occurred when G_Ks was relatively small, but, when the cells were coupled in the 1D heterogeneous cable, they repolarized with long APDs (such as the examples shown in Figs. 4D and 6A).

Fig. 6.

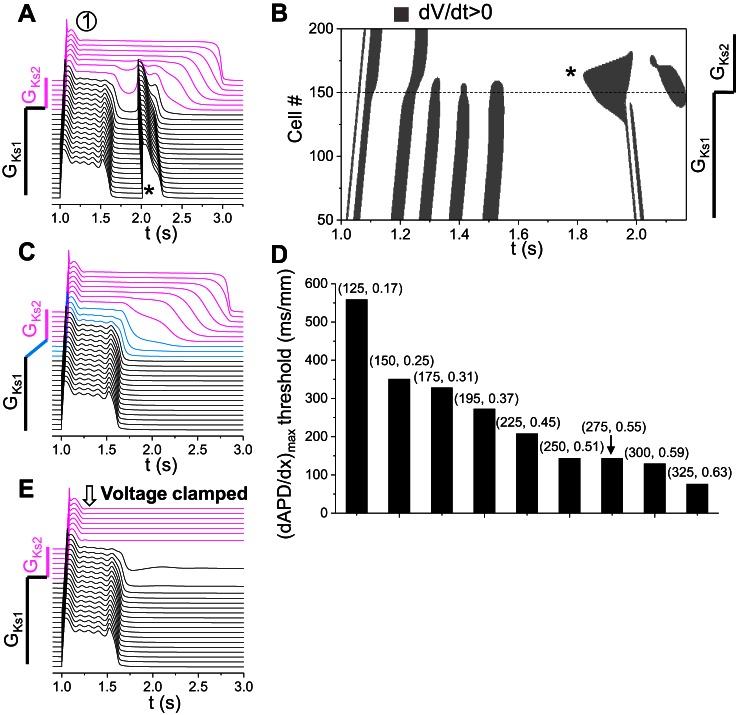
Large RG-induced PVCs. A: space-time plot of voltage showing a PVC (*) generated due to RG via the first mechanism (location “1” in Fig. 4B). G_Ca,L = 120 mmol/(cm,C) and G_Ks2 = 0.15 mS/μF. B: space-time plot of dV/dt > 0 for the voltage shown in A. C: same as A, but the change of G_Ks1 to G_Ks2 occurred across 20 cells, and the PVC disappeared. D: critical APD gradient (maximum APD gradient in the cable) for PVC genesis for the parameter set (G_Ca,L, G_Ks2) as marked. E: same as A, but the cells in the long APD region are voltage clamped at their value at t = 1,160 ms.

In the no-PVC zones, the cellular phase 2 EADs were either suppressed or confined to the long APD region (see Fig. 4C). At the border near the PVC zone, tissue-scale EADs were generated when RG was large (Fig. 4D) and/or I_Ca,L was large (Fig. 4E). When RG was large, the phase 3 repolarization was markedly slowed in the RG region (arrow in Fig. 4D). These slow phase 3 repolarizations were previously called phase 3 EADs (16) and were very similar to those observed in experiments by Maruyama et al. (32). A further increase in RG (from “△” to “1” in Fig. 4B) resulted in PVCs. When I_Ca,L was large, small depolarizations could occur in phase 3 of the APs in the cells in the RG region (arrow in Fig. 4E). Because no EADs were present in the long APD region, and the takeoff potential of EADs in uncoupled single cells was above −40 mV, these are tissue-scale EADs caused by the RG, not a single cell property. If I_Ca,L was increased further (from “◇” to “2” in Fig. 4B), these EADs then grew toward the short APD region and successfully propagated into PVCs.

Note that the APD in the long APD region in Fig. 4D is very long (>1 s), which is much longer than that under the normal condition. However, it is not uncommon to see very long APDs in rabbit hearts under experimental conditions with slow pacing. For example, in the optical mapping by Maruyama et al. (32) and the microelectrode recordings by Yan et al. (67) in drug-induced LQT2 rabbits, very long APDs were demonstrated at slow heart rates.

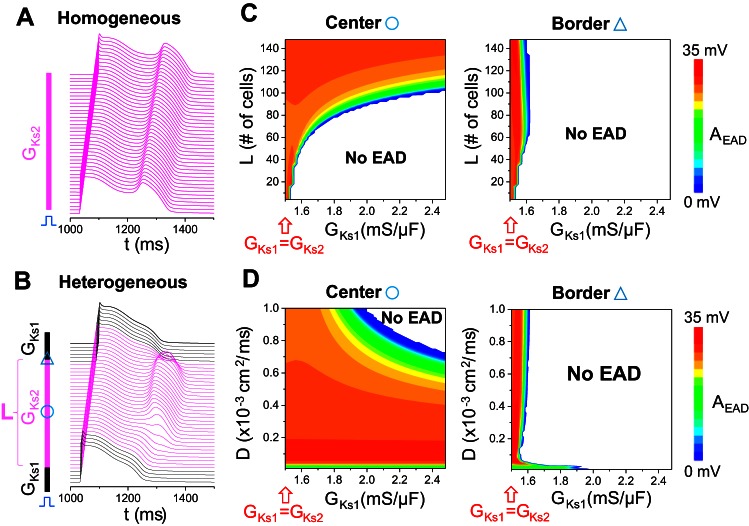
By comparing Fig. 4, A and B, one can see that a large parameter region that gave rise to EADs in uncoupled single cell did not exhibit PVCs in the 1D cable although large-amplitude cellular phase 2 EADs occurred in this parameter region. To systematically investigate the effects of RG on cellular phase 2 EADs, we performed additional simulations in a 1D cable by altering RG, the size of the EAD region, and gap junction coupling (Fig. 5). We first simulated a homogeneous cable in which a cellular EAD occurred in every cell with an amplitude of ∼35 mV (Fig. 5A). We then gradually increased G_Ks (G_Ks1) in the two ends of the cable (see inset in Fig. 5B) to investigate the EAD behaviors. Figure 5B shows an example in which the EAD still occurred in the center region but was suppressed in the border regions, and thus the EAD cannot propagate out the center region to generate a PVC in the short APD regions. We systematically scanned the size of the center region (L) and the G_Ks1 value for the control diffusion constant (D = 0.0005 cm²/ms) and measured the corresponding EAD amplitude in the center of the cable (Fig. 5C, left) and in one of the border regions (Fig. 5C, right). When L was short, the EAD was completely suppressed unless the cable was almost homogeneous (G_Ks1∼G_Ks2). When L was large, the EAD was suppressed in the RG regions but remained intact in the center region (compare Fig. 5C, left and right). Therefore, as RG was increased, the EAD was confined to the long APD region, which could not transmit to the RG region to induce a PVC. Similarly, we scanned D and G_Ks1 for a fixed center region (L = 120 cells) and measured the corresponding EAD amplitude in the center of the cable (Fig. 5D, left) and in one of the border regions (Fig. 5D, right). The EAD was completely suppressed when both D and G_Ks1 are large (Fig. 5D, left). No EAD could be detected in the RG region, even after D is reduced by several fold (Fig. 5D, right).

Fig. 5.

Suppression of cellular phase 2 EADs by repolarization gradient (RG) in a 1D cable. A: space-time plot of voltage from a homogeneous cable showing a cellular EAD in every cell. G_Ca,L = 120 mmol/(cm,C), G_Kr = 0, and G_Ks1 = G_Ks2 = 1.5 mS/μF. A large cellular EAD (∼35 mV in magnitude) occurs in the AP. B: same as A, but the cable is heterogeneous. The inset shows the distribution of the slow component of the delayed-rectifier potassium current (I_Ks). The cable length is 320 cells, the middle 120 cells (magenta) of which exhibit EADs when uncoupled (G_Ks2 = 1.5 mS/μF as in the homogeneous cable in A), and the cells on both sides have a shorter APD (G_Ks1 = 1.7 mS/μF). For visualization purpose, not all G_Ks1 cells in the cable are plotted in this panel. C: left, EAD A_EAD (defined as in Fig. 4A and plotted in color scale as indicated by the color bar) from a cell in the middle of the cable vs. G_Ks1 and length of the middle segment (L, defined in B). Right, A_EAD from a cell in the gradient region marked by the triangle in B vs. G_Ks1 and L. Diffusion constant D = 0.0005 cm²/ms. D: left, A_EAD from a cell in the middle of the cable vs. G_Ks1 and diffusion constant D. L = 120. Right, A_EAD from a cell in the gradient region marked by the circle in B vs. G_Ks1 and diffusion constant D.

Our simulation results in Figs. 4 and 5 suggest that PVCs may not be a direct consequence of phase 2 EAD propagation since cellular phase 2 EADs tend to be suppressed or confined by RG. However, we note that, whether a cellular phase 2 EAD can propagate into a PVC or not, or under what condition it can propagate into a PVC, cannot be concluded merely by simulations of a specific model. More rigorous theoretical or systematic analyses are still needed. On the other hand, our simulations demonstrated that new mechanisms occurred at the tissue scale to generate PVCs, which are tissue-scale dynamical instabilities and are different from the traditional thinking of PVC as a consequence of phase 2 EAD propagation. We identified two different mechanisms of PVC genesis in the 1D cable, as described in detail in the following sections.

Large RG-induced PVCs.

In this mechanism, PVCs occur when the RG is larger than a critical value and strongly depends on the properties of the cells in the long APD region. Figure 6A shows a PVC (*) caused by this mechanism (from location 1 in Fig. 4B). Figure 6B is the corresponding space-time plot of dV/dt > 0 showing that the leading site of depolarization initiating the PVC occurred in the RG region. To demonstrate that a critical APD gradient is needed, rather than a sudden change from G_Ks1 to G_Ks2, we changed G_Ks1 to G_Ks2 linearly cross a region (as in the inset of Fig. 6C) to reduce the APD gradient. When this linear region exceeded the length that reduces the maximum APD gradient below a critical value, PVCs no longer occurred (Fig. 6C). Note that the APD in the long APD region became slightly longer, and the APD in the short APD region remained unchanged (compare Fig. 6, C and A), but the APD gradient was reduced in the RG region due to the gradual transition from G_Ks1 to G_Ks2. This indicates that a critical RG is needed for PVCs to occur. Using this gradual G_Ks1-to-G_Ks2 transition, we obtained the APD gradient thresholds for a couple of G_Ca,L and G_Ks2 combinations along the left border between the PVC and no-PVC zones in Fig. 4B, which were plotted in Fig. 6D in a bar graph. The APD gradient threshold decreased as I_Ca,L conductance increased. However, we found that a large APD gradient per se was not sufficient for causing PVCs; other conditions were required. To show this, we clamped the cells in the long APD region at their plateau voltages, which greatly increased the voltage or APD gradient, but surprisingly PVCs no longer occurred (Fig. 6E). This indicates that, in addition to a large APD gradient, the cells in the long APD region have to be free of oscillation for PVC formation. This also demonstrates that the PVC is not simply “prolonged repolarization-dependent reexcitation” proposed previously (5). As shown in Figs. 4D and 6B, before the transition to PVCs, the cells in the short APD region pulled down the voltage of the cells in the long APD region, which resulted in a very slow phase 3 repolarization [or phase 3 EADs (16)] of the cells in the long APD region. As the RG increased further, spontaneous depolarizations suddenly occurred in the long APD side of the RG region to result in PVCs. No cellular EADs were involved in the PVC genesis, and thus the PVCs were not originated from propagation of EADs. The occurrence of PVCs was caused by a tissue-scale dynamical instability that depends on not only the properties of tissue heterogeneities but also the cellular properties.

Small RG or boundary effect-induced PVCs.

This mechanism of PVC formation does not require a critical RG but strongly depends on the properties of the cells in the short APD region. Figure 7A shows a PVC (*) of this mechanism (from location 2 in Fig. 4B). Figure 7B is the corresponding space-time plot of dV/dt > 0 showing that the leading site of depolarization initiating the PVC occurred in the RG region. Following the same method to reduce APD gradient by changing G_Ks1 to G_Ks2 gradually as in Fig. 6C, we could not eliminate the PVC but created more PVCs (Fig. 7C). This indicates that a critical RG is unnecessary, which is opposite to the mechanism of large RG-induced PVCs. When we clamped the voltages of the cells in the long APD region the same way as we did in Fig. 6E, the oscillations became sustained (Fig. 7D). This indicates that the oscillations were generated in the short APD side in the RG region. Therefore, in this mechanism, cells in the long APD region provide an electrical source to cells in the short APD region to cause tissue-scale phase 3 EADs in the RG region. When I_Ca,L is strong enough, these EADs can then grow in the short APD region to result in PVCs. This mechanism requires that the cells in the short APD region are prone to cellular EADs or oscillations in the repolarizing phase. Note that, in this mechanism, a PVC is also not a result of EAD propagation but a tissue-scale dynamical instability dependent on both cellular properties and RG.

Fig. 7.

Small or intermediate RG-induced PVCs. A: space-time plot of voltage shown in a PVC (*) generated due to RG via the second mechanism (location “2” in Fig. 4B). G_Ca,L = 292 mmol/(cm,C) and G_Ks2 = 0.71 mS/μF. B: space-time plot of dV/dt > 0 for the voltage shown in A. C: same as A, but the change of G_Ks1 to G_Ks2 occurred across 50 cells. D: same as A, but the cells in the long APD region were voltage clamped at their values at t = 1,160 ms. E: space-time plot of voltage showing a PVC (*) at the boundary (“3” in Fig. 4B ). G_Ca,L = 211 mmol/(cm,C) and G_Ks2 = 0.71 mS/μF. F: space-time plot of voltage showing a PVC (*) when RG is small (“4” in Fig. 4B). G_Ca,L = 196.75 mmol/(cm,C) and G_Ks2 = 0.97 mS/μF.

We observed two special cases of this mechanism: a PVC occurred at the tissue boundary (Fig. 7E) or started from the RG region when the RG was very small (Fig. 7F). In both cases, a cellular EAD was present in the long APD region, which provided an additional electrical source for PVC formation. However, only when the RG was very small could an EAD survive at the RG region (see Fig. 5) and become the source of a PVC. At the tissue boundary, the no-flux boundary condition caused a slightly shorter APD at the boundary region, resulting in a small RG to facilitate this mechanism. Because it was a boundary effect, region 3 in Fig. 4B was a horizontal bar that did not depend on the RG caused by the G_Ks heterogeneity in our model. Because phase 2 EADs and RG compete with each other, this type of PVC occurs only at certain I_Ca,L ranges in which the EAD amplitude and RG are properly matched.

Modulation of RG-Induced PVCs by Other Factors

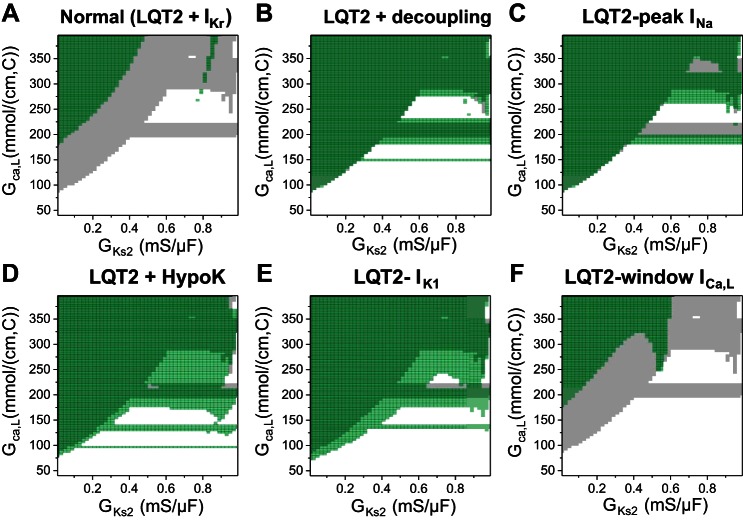
We also investigated the effects of other factors on modulating PVC genesis by carrying out simulations that scanned the same parameter space as in Fig. 4B under different conditions, and the results are summarized in Fig. 8.

Fig. 8.

PVC genesis modulated by other factors. In each panel, the PVC zone in Fig. 4B was taken as control and colored gray. The PVC zone after a parameter change was colored green. Because the green was set to be semitransparent, the color became darker when the PVC zone overlapped with that of the control. A: normal [LQT2 + the rapid component of the delayed-rectifier potassium current (I_Kr)]. B: reduced gap junction coupling (from 0.0005 to 0.0001 ms/cm²). C: reduced peak Na current (I_Na) by reducing the maximum conductance (from 12 to 8 mS/μF). D: hypokalemia [extracellular K concentration ([K]_o) changed from 5.4 to 2.7 mM]. E: reduction of inward-rectifier K current (I_K1) by 30% (approximately the same reduction of I_K1 as in D). F: 10-mV shift to more negative voltages of the steady-state inactivation curve [f_∞ in the L-type Ca channel (LCC) model] to suppress window I_Ca,L.

Figure 8A shows the case in which we added normal I_Kr back into the model (and thus it became the normal control model). The PVC zone was suppressed as expected. It required a much larger I_Ca,L or I_Ks heterogeneity for PVCs to occur except in some small regions in the upper right quadrant.

Figure 8B shows the case in which we reduced gap junction coupling by 50%. This reduction of gap junction coupling had almost no effect on the large RG-induced PVCs but slightly potentiated the boundary effect-induced PVCs (see the changes in the horizontal bar in Fig. 8B). This indicates that PVC formation caused by the tissue-scale dynamical instabilities does not depend on cell coupling. This is different from PVCs originating from cellular EAD propagation, whose formation depends sensitively on cell coupling (66).

Because PVC propagation depends on Na current (I_Na), we then reduced I_Na to investigate its effects on PVC formation in our model. Figure 8C shows a case in which we reduced peak I_Na by reducing its maximum conductance from 12 to 8 mS/cm². This reduction in peak I_Na did not reduce PVC formation but instead caused the boundary effect-induced PVCs to occur at a lower I_Ca,L.

It is well known that hypokalemia potentiates arrhythmia risk in LQTS (12, 46). We lowered the extracellular K concentration ([K]_o) from 5.4 (normal) to 2.7 mM to simulate hypokalemia (Fig. 8D). This change increased PVCs from both mechanisms but had a much larger effect on small RG- or boundary effect-induced PVCs. Note that more horizontal PVC zones occurred at lower I_Ca,L. Because our current model lacks Ca/calmodulin-dependent protein kinase II signaling (39), the major effect of lowering [K]_o in our model was inward-rectifier K current (I_K1) reduction. Reducing I_K1 causes a slower phase 3 repolarization and thus promotes phase 3 EAD formation. Therefore, based on our observations shown in Fig. 4, D and E, these phase 3 EADs can result in PVCs under large RG or I_Ca,L. When we reduced I_K1 by the same extent as that (∼30%) by lowering [K]_o, it had a very similar effect on PVC formation (Fig. 8E).

Previous studies have shown that reducing window I_Ca,L can eliminate EADs and shorten APD at slow heart rates (29, 30, 40). Figure 8F shows the effects of reducing window I_Ca,L (by shifting the steady-state inactivation curve to more negative voltages) on PVC formation. Reducing the window I_Ca,L could also effectively suppress PVCs of all mechanisms. Note that, in the cases shown in Figs. 8, B–D, and 4B, PVCs could occur at very small RG (G_Ks1∼G_Ks2). After reducing the window I_Ca,L, a certain RG was required for PVCs to occur (the PVC zone shifted to the left).

Population-Based Modeling Simulating the Effects of Heterogeneity Diversity

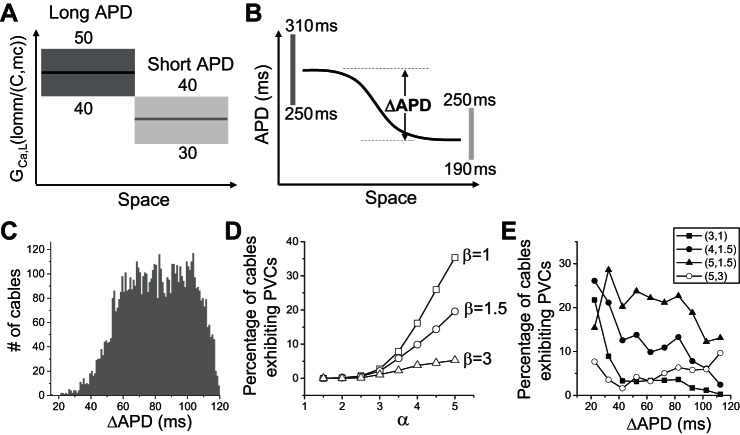
In all the simulations above, the repolarization heterogeneity was simulated by heterogeneous I_Ks distributions alone. In real tissue, other ionic currents are also heterogeneously distributed. Moreover, their distributions may vary from cell to cell in the same heart or from heart to heart. To take into account this diversity, population-based models are needed (4, 33, 49, 51). We simulated a population of 1D cables that exhibit a diversity of parameter combinations and APD gradients. The parameters were randomly selected from preassigned ranges (see the legend for Fig. 9). The maximum conductances of I_Ks, I_Ca,L, and I_to were heterogeneous in the cable, and those of other currents were homogeneous throughout the cable. The cable length was 200 cells, and the long and short APD regions each contained 100 cells. In each cable, two different conductances of I_Ks, I_Ca,L, or I_to were randomly drawn from certain intervals and assigned to the long and short APD regions, respectively. For example, the G_Ca,L range is 40–50 mmol/(cm,C) in the long APD region and 30–40 mmol/(cm,C) in the short APD region (Fig. 9A). This gives rise to an ∼30% difference in average I_Ca,L, agreeing with the experimental data by Sims et al. (57). We also applied another constraint based on experimental data from rabbits (6, 26) showing that the maximum APD in the long APD region is 250–310 ms and in the short APD region 190–250 ms (Fig. 9B). If the resulting APD of a parameter set fell outside the assigned APD ranges, the case was discarded. Using this filtering method, we generated ∼6,000 1D cables that satisfied the APD requirements. Figure 9C shows the histogram of ΔAPD as defined in Fig. 9B. No PVCs were seen under the control conditions. To induce PVCs and simulate the effects of isoproterenol, we multiplied I_Ca,L by a factor α and I_Ks by a factor β. Figure 9D shows the percentage of the cables exhibiting PVCs under isoproterenol simulated by different combinations of α and β. No PVCs occurred when α was increased less than twofold in the ∼6,000 cables for different β. The probability of PVC increased with α after α was increased by twofold or more and became smaller for a larger β. We did not observe a clear correlation between the PVC probability and the ΔAPD at control (Fig. 9E), agreeing with our observation that PVCs can occur at both large and small RG.

Fig. 9.

Population-based analysis of PVC genesis. A: schematic plot of the assigned G_Ca,L ranges and heterogeneity in the 1D cable model in which two G_Ca,L values randomly drawn from the assigned ranges were used for each cable. The cable length was 200 cells, and the long and short APD regions were each 100 cells. We assigned the G_Ca,L range from 40 to 50 mmol/(cm,C) in the long APD region and 30 to 40 mmol/(cm,C) in the short APD region. The same two-region heterogeneity was used for the slow transient outward K current (I_to,s), the fast transient outward K current (I_to,f), and I_Ks with the following assigned maximum conductance ranges (in the same units as in the original model): slow transient outward conductance (G_to,s, 0.01, 0.04), fast transient outward conductance (G_to,f, 0.01, 0.11), and G_Ks (0.3, 0.7) in the long APD region; and G_to,s (0.04, 0.08), G_to,f (0.11, 0.22), and G_Ks (0.7, 1.3) in the short APD region. I_K1, Na/Ca exchange current (I_NCX), and I_NaK are uniform in space with the following assigned maximum conductance ranges: G_K1 (0.1, 0.5), Na/Ca exchange conductance (G_NCX, 0.5, 1), and maximum conductance of I_Ks (G_NaK, 1.0, 2.0). B: schematic plot of the assigned APD ranges in the 1D cable model. The solid line represents an APD distribution of a specific cable, and ΔAPD was defined as the maximum APD less the minimum APD in this cable. The two vertical bars indicate the allowed APD ranges for the maximum APD and minimum APD, respectively. C: histogram of ΔAPD from the 6,000 cables satisfying the APD requirements described in B. D: percentage of cables exhibiting spontaneous PVCs at different levels of the isoproterenol effects described by α and β. α is the multiplier of I_Ca,L, and β is the multiplier of I_Ks. E: percentage of cables exhibiting spontaneous PVCs vs. the initial ΔAPD before isoproterenol (α = β = 1, the same ΔAPD data presented in C) for different combinations of α and β as indicated by different symbols.

Pause-Induced Arrhythmias in LQT2

It is widely known that arrhythmias in LQT2 patients tend to occur after a pause (or so-called short-long-short cycle) or under bradycardia (14, 44, 54, 63). It was also demonstrated in transgenic LQT2 rabbits (38). A pause can have two consequences: causing EADs (64) and increasing RG due to different regional rate dependence of APD (43). To demonstrate whether the above mechanisms of PVC genesis are applicable to arrhythmogenesis clinically, we carried out simulations to mimic pause-induced arrhythmias. We paced the 1D cable periodically at 600-ms intervals for many beats and then applied a last pacing stimulation with a coupling interval of 1,500 ms to simulate the pause. Figure 10A shows a case in which the RG was large (the same parameters as for Fig. 6A), EADs occurred in the long APD region during regular pacing, but no PVCs were induced. After the pause, the APD was increased in both the long and short APD regions, but to a much greater extent in the long APD region. Moreover, EADs in the APD region disappeared after the pause. For the intermediate RG (the same parameters as for Fig. 7A), similar behaviors were observed (Fig. 10B). For small RG (the same parameters as for Fig. 7F), no EADs occurred during the regular pacing but did occur after the pause, and the last EAD in the long APD region elicited the PVC (Fig. 10C).

Fig. 10.

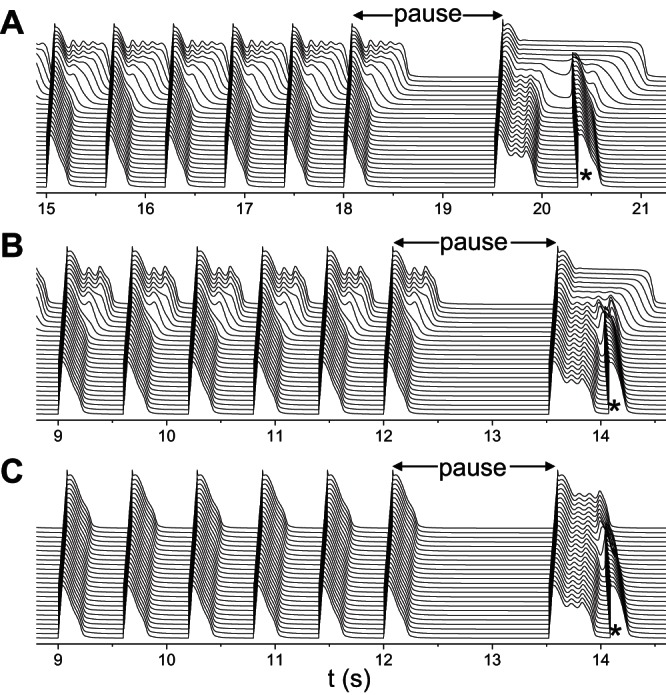
Pause-induced arrhythmias. Space-time plots of voltage showing pause-induced PVCs (*). The same heterogeneous cable as in Fig. 4B was used with G_Ks1 = 1 mS/μF. A: large RG. G_Ca,L = 152 mmol/(cm,C) and G_Ks2 = 0.27 mS/μF. B: intermediate RG. G_Ca,L = 176 mmol/(cm,C) and G_Ks2 = 0.45 mS/μF. C: small RG. G_Ca,L = 176 mmol/(cm,C) and G_Ks2 = 0.93 mS/μF. The cable was paced at 600 ms for 30 beats in A and 20 beats in B and C followed by a last pacing stimulation that was applied at a coupling interval of 1,500 ms.

DISCUSSION

Here we systematically investigated the mechanisms of spontaneous arrhythmia initiation by RG and the role of phase 2 EADs in LQTS. In transgenic rabbit experiments, we showed that focal excitations tended to occur at spatially steep repolarization gradient regions and propagate unidirectionally. In computer simulation, we showed that cellular phase 2 EADs were mostly suppressed or confined regionally by RG, while tissue-scale phase 3 EADs were induced by RG and I_Ca,L to initiate unidirectionally propagating PVCs. Two mechanisms of PVC genesis were identified: 1) large RG-induced PVCs, in which a critical RG is necessary (Fig. 6); and 2) small RG-induced PVCs, in which a critical RG is not needed, but the cells in the short APD region need to be prone to cellular EADs, and the presence of phase 2 EADs in the long APD region provides an additional electrical source for PVC formation (Fig. 7). For both mechanisms, I_Ca,L plays a critical role, which required severalfold higher I_Ca,L than that needed for EADs to occur in a single cell. Because the PVCs are generated from the APD gradient region, propagating unidirectionally, they can initiate reentry without an additional vulnerable substrate, i.e., the triggers and vulnerable substrates of arrhythmias originate from the same source: tissue-scale dynamical instabilities caused by RG and I_Ca,L. The computer simulations dissected out the roles of EADs and RG in arrhythmogenesis in LQTS and provided mechanistic insights into experimental and clinical observations, as well as potential antiarrhythmic targets for LQTS, as discussed below.

Roles of EADs and RG in Arrhythmogenesis in LQTS

EADs, as a hallmark of LQTS, are widely considered triggers of TdP. As shown in many experimental (20, 26, 59) and computational (10, 11, 35) studies in isolated ventricular myocytes, ionic current defects in LQTS cause mainly phase 2 EADs. Computer simulation studies demonstrated that phase 3 EADs can propagate to generate PVCs when there is a sufficient electrical source (66), and phase 2 EADs might produce PVCs in heterogeneous tissue when the cells are very weakly coupled to simulate ischemia (15, 50). However, no studies have shown that phase 2 EADs can induce PVCs in LQTS in which gap junction coupling is normal. Our simulations showed that the cellular phase 2 EADs were suppressed or confined regionally by RG, no matter how large the EAD area was, which was not affected by severalfold reduction of gap junction coupling (see Fig. 5). Moreover, the comparison of parameter regions of cellular phase 2 EADs and PVCs in tissue showed little correlations (Fig. 4, A and B). Although cellular phase 2 EADs may not directly initiate PVCs, they still play important roles in arrhythmogenesis in LQTS. First, when the RG is very small or at the tissue boundary, a phase 2 EAD can survive in the APD gradient region and provide an additional electrical source for PVC formation. Second, for PVCs initiated by small or intermediate RGs, the cells in the short APD region must be prone to cellular EADs, and thus a small electrical source from their neighbors can cause tissue-scale phase 2 and phase 3 EADs to induce PVCs.

RG exists in normal hearts and is increased in LQTS (6, 62). It is widely assumed that EADs are the sources of PVCs and that increased RG promotes a vulnerable substrate for conduction block to cause reentry. However, this picture of arrhythmogenesis in LQTS may not be true. First, increased RG tends to suppress EADs due to the source-sink effect as also shown in our simulations (Fig. 5), while spontaneous arrhythmias required a critical RG (67, 68). Second, in both previous optical mapping studies in drug-induced LQTS (23, 27, 32) and the current study of transgenic LQT2, ectopic excitations tend to occur in the steep RG region and propagate unidirectionally. If a cellular phase 2 EAD were the cause of an ectopic beat, the earliest activation site would be in the long APD region instead of the RG region, since phase 2 EADs are more suppressed in the RG region. Our simulations show that tissue-scale phase 3 EADs and PVCs are caused by RG, which originate from the steep RG region and propagate unidirectionally. The presence of the cellular EADs is not required but can potentiate PVC formation. The tissue-scale EADs and PVCs are the result of a tissue-scale dynamical instability that relies on both RG and the properties of the ionic currents, while the instability causing cellular EADs relies solely on the properties of the ionic currents (42). The cellular factors promoting cellular EADs also promote tissue-scale EADs and PVCs under increased RG, but the tissue-scale EAD and PVC formation requires a much larger I_Ca,L. This explains why both cellular EADs and tissue RG are important for arrhythmogenesis in LQTS. Because RG-induced PVCs propagate unidirectionally, promoting both a trigger and a vulnerable substrate at the same location, reentry occurs spontaneously without requiring an additional RG region for conduction block. This is different from the traditional concept that arrhythmia triggers and substrates are due to different causes, which interact to induce arrhythmias (41, 47).

Mechanisms of Focal Excitation in Transgenic Rabbit Hearts

As shown in our experiments in transgenic LQT2 hearts (Fig. 2), focal excitations tend to occur in the steep-RG region and propagate unidiretionally. We observed different focal excitation patterns, which are similar to those in our simulations (Fig. 3). EADs were present in the long APD region, consistent with the previous findings that single cells isolated from the LV of LQT2 rabbit hearts often exhibited EADs (6, 26). According to our computer simulations, PVCs can occur in tissue with small to very large RG, propagating unidirectionally or in all directions in either the presence or absence of cellular phase 2 EADs. We postulate that both mechanisms of PVC genesis identified in computer simulations may occur in LQT2 rabbits. RG-induced ectopic excitations may also be responsible for arrhythmogenesis in transgenic LQT1 rabbits, as shown in our previous experiments (24), which found that the APD is longer in LV than in RV, and ectopic excitations frequently originated from the border region between RV and LV and propagated toward RV but not LV [see Fig. 4 in Kim et al. (24)]. In both transgenic LQT1 and LQT2 hearts, isoproterenol was needed to induce ectopic excitations, indicating that greater I_Ca,L was required, which agrees with the computer simulation results.

Role of I_Ca,L in Arrhythmogenesis in LQTS

An important observation from our simulations in this study is that the magnitude of I_Ca,L needed to initiate PVCs or focal excitations in tissue is much larger than either its control value or the magnitude required for the occurrence of EADs in a single cell. Moreover, a smaller RG is needed for a larger I_Ca,L to induce PVCs. In our transgenic rabbit experiments, spontaneous arrhythmias were always initiated under isoproterenol. As shown in our computer simulations (Figs. 4B and 10C), PVCs could occur when RG is relatively small, as long as I_Ca,L is strong enough. Isoproterenol can increase I_Ca,L by twofold in rabbit myocytes (26), which may be strong enough to promote arrhythmias in LQT2 rabbit hearts. Other studies have shown that progesterone (which decreases I_Ca,L) is protective while estrogen (which increases I_Ca,L) is proarrhythmic in LQT2 (37, 57, 69). Clinically, β-blockers, although they slow heart rates, are still the most effective treatment for arrhythmia prevention in LQTS (19, 55). The current experimental and clinical observations agree with the observation that a large I_Ca,L is needed for spontaneous arrhythmias in LQTS. Moreover, recent studies have shown that enhanced I_Ca,L can mediate conduction in cardiac tissue under reduced repolarization reserve without activation of I_Na or in absence of I_Na (7, 8, 24, 61).

Although I_Ca,L plays a key role in arrhythmogenesis in LQTS, the traditional L-type Ca channel (LCC) blockade cannot be used as an antiarrhythmic therapy, since it also has the negative ionotropic effect of suppressing contraction. Our previous studies showed that reducing window I_Ca,L by modifying LCC properties could effectively shorten ultralong APD and suppress EADs (30, 40, 42). Unlike the traditional LCC blockers, reducing window I_Ca,L has almost no effect on Ca cycling under normal conditions and thus will have almost no effect on contraction. As shown in our simulations in Fig. 8F, suppressing the window I_Ca,L without reducing its peak value can still effectively suppress the PVCs caused by the tissue-scale dynamical instabilities. This indicates that modifying the LCC properties that suppress the window I_Ca,L could be an effective candidate therapeutic target for suppressing arrhythmias in LQTS.

Limitations

Because the optical mapping only recorded signals from epicardial or subepicardial cells, it cannot be sure that the foci shown in our recordings (Fig. 2) were the true origins of the focal excitations. They could be breakthroughs originating from somewhere underneath the surface. As shown by Yan et al. (67), ectopic beats can be caused by transmural RG, and we believe that the same mechanisms identified in this study are likely responsible. The unidirectional propagation of PVCs observed in our experiments could also be caused or potentiated by other tissue-scale heterogeneity factors, such as the LV-to-RV thickness gradient (3). Another limitation of the experimental study is that, under the normal condition, the cycle lengths of sinus rhythm for the rabbit hearts range from 180 to 350 ms. Under these heart rates, we were not able to observe EADs and PVCs. We ablated the AV node to slow the heart rate to promote EADs and PVCs. However, after the AV ablation, the APD and the patterns of RG may be very different from those under normal conditions, and thus the mechanisms of arrhythmogenesis may not be the same for the two conditions. Nevertheless, our goal is to understand the mechanisms of spontaneous initiation of arrhythmias caused by RG, and the mechanistic insights obtained under the slow heart rates may still provide important insights into spontaneous initiation of ventricular arrhythmias in human.

In the present study, the simulations were carried out in single-cell, 1D cable, and 2D tissue, but real hearts are three-dimensional (3D) with specific geometries. Due to the source-sink and curvature effects, the conditions for PVC formation and reentry induction in 3D tissue may differ from 1D and 2D tissue. In a recent study (60), Vandersickel et al. showed that TdP could be induced spontaneously by RG in 2D tissue, similar to the mechanisms identified in the current study, and they demonstrated that the same mechanism was also responsible for TdP in the anatomically based 3D human ventricle model. Similar 3D human heart simulations were carried out in another recent study by Dutta et al. (15) who showed that spontaneous ectopic excitations and reentrant arrhythmias could be caused by dispersion of repolarization in ischemic tissue with reduced repolarization reserve. However, as shown in this study, PVC formation was caused by tissue-scale dynamical instabilities; the source-sink or curvature effects may not be the same as the traditional source-sink or curvature effects as in the propagation of EADs or delayed afterdepolarizations (66). More rigorous analyses are needed to dissect this out. In all the models we simulated, none generated Ca oscillation-mediated EADs (58, 65, 71), while experimental studies have shown that Ca oscillations may also play an important role in formation of focal excitations in LQTS (9, 23); these may be responsible for the focal exactions observed in our experiments. Additionally, we investigated only the effects of RG caused by preexisting heterogeneities. As we showed previously, in the presence of EADs, chaotic AP dynamics can give rise to dynamical RG (53), which can also promote PVCs via the same mechanisms as shown in this study.

In conclusion, in LQT2 rabbit hearts, cellular phase 2 EADs, which may be either suppressed or regionally confined in heterogeneous tissue, cannot propagate into PVCs. PVCs are a result of tissue-scale dynamical instabilities caused by RG and enhanced I_Ca,L, differing from that PVCs are a consequence of EAD propagation. Two mechanisms of PVCs can exist. In the first mechanism, occurrence of PVCs requires a critical RG without requiring cellular EADs. In the second mechanism, PVCs can occur in an intermediate or small RG that is potentiated when the cells in the long APD region exhibit EADs or the cells in the short APD region are prone to EADs. Both mechanisms require the presence of a large I_Ca,L. Because PVC formation requires the occurrence of tissue-scale phase 3 EADs, it sensitively depends on I_K1 conductance, i.e., reducing I_K1 conductance or hypokalemia promotes PVCs, agreeing with the knowledge that hypokalemia is a severe risk factor of arrhythmogenesis in LQTS patients. Unlike the case of PVCs originating from EAD propagation (66), gap junction coupling has a small effect on the PVC formation caused by the tissue-scale dynamical instabilities. Because the PVCs induced by the tissue-scale dynamical instabilities propagate unidirectionally, an additional tissue substrate is not required for initiation of reentrant arrhythmias. In other words, the arrhythmia trigger (i.e., PVCs) and vulnerable tissue substrate originate from the same source. The mechanistic insights into PVC formation and arrhythmogenesis from the present study may shed light on identifying novel therapeutic targets for preventing arrhythmias in LQTS.

GRANTS

This work is supported by National Heart, Lung, and Blood Institute Grants R01-HL-110791 and R01-HL-096669 (to B.-R. Choi).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

X.H., B.-R.C., and Z.Q. conception and design of research; X.H. and T.Y.K. performed experiments; X.H., T.Y.K., B.-R.C., and Z.Q. analyzed data; X.H., T.Y.K., G.K., B.-R.C., and Z.Q. interpreted results of experiments; X.H., T.Y.K., and Z.Q. prepared figures; X.H., T.Y.K., B.-R.C., and Z.Q. drafted manuscript; X.H., T.Y.K., G.K., B.-R.C., and Z.Q. edited and revised manuscript; X.H., T.Y.K., G.K., B.-R.C., and Z.Q. approved final version of manuscript.