Foraging in an unsteady world: bumblebee flight performance in field-realistic turbulence

Abstract

Natural environments are characterized by variable wind that can pose significant challenges for flying animals and robots. However, our understanding of the flow conditions that animals experience outdoors and how these impact flight performance remains limited. Here, we combine laboratory and field experiments to characterize wind conditions encountered by foraging bumblebees in outdoor environments and test the effects of these conditions on flight. We used radio-frequency tags to track foraging activity of uniquely identified bumblebee (Bombus impatiens) workers, while simultaneously recording local wind flows. Despite being subjected to a wide range of speeds and turbulence intensities, we find that bees do not avoid foraging in windy conditions. We then examined the impacts of turbulence on bumblebee flight in a wind tunnel. Rolling instabilities increased in turbulence, but only at higher wind speeds. Bees displayed higher mean wingbeat frequency and stroke amplitude in these conditions, as well as increased asymmetry in stroke amplitude—suggesting that bees employ an array of active responses to enable flight in turbulence, which may increase the energetic cost of flight. Our results provide the first direct evidence that moderate, environmentally relevant turbulence affects insect flight performance, and suggest that flying insects use diverse mechanisms to cope with these instabilities.

1. Introduction

Natural environments are highly complex. In addition to structural and visual complexity [1,2], outdoor environments vary substantially over time, with abiotic conditions (e.g. wind [3], temperature [4] and light, among others) varying over timescales ranging from seconds to seasons. Such environmental complexity can pose significant challenges to flying animals that must move through natural habitats to forage for food [5], capture prey or escape from predators [6], and find mates [7], potentially restricting when and where they can fly, or increasing the energetic cost of flight. Variation in the cost of locomotion can impact key aspects of animal ecology by affecting movement at the landscape scale [8]. The challenges associated with manoeuvring through complex environments have likely played a key role in shaping the evolutionary and ecological pressures on flying animals [9,10]. Understanding how animals contend with the complexities of natural environments—whether this involves active or passive coping mechanisms, or avoidance of certain conditions—is thus key for understanding their evolution and ecology, as well as for providing guiding principles for the design of micro-aerial vehicles (MAVs) capable of traversing outdoor environments.

Wind variability represents one of the most important, and potentially most challenging, components of environmental complexity for flying animals and MAVs. Wind carries substantial kinetic energy [3], and varies locally over timescales that are typically much faster (i.e. sub-second scale) than other abiotic conditions, such as temperature and light. Air flows in natural environments are highly variable across a range of spatio-temporal scales [3,11], and can affect the performance, energetics, and behaviour of flying animals [12–14]. Instabilities imposed by high-frequency variation in wind flow may also pose a significant control challenge for both flying insects and MAVs [15].

Environmental air flows can be characterized as a combination of mean flow, and fluctuations around this flow (often quantified as ‘turbulence intensity’, or standard deviation of flow speed divided by the mean) [3]. While we have a relatively strong understanding of how mean flows affect the locomotion and ecology of flying animals, we know comparatively little about how turbulence impacts animal flight performance [16]. Recently, a number of wind tunnel studies have helped elucidate the effects of variable, but structured flows such as von Kármán vortex trails that form behind cylinders, on flight in both hummingbirds [13,17] and insects [18–20]. While such flows may be locally dominant (e.g. immediately downstream of physical objects in the environment such as tree branches), aerial environments are more often characterized by turbulent flow consisting of a chaotic mix of eddies of many sizes and frequencies [3]. Previous work has shown that turbulence limits top flight speed and increases drag (and presumably associated energetic costs) in orchid bees [12]. A single previous indoor wind tunnel study has shown that hummingbirds display flight instabilities in freestream turbulence at a relatively high flow speed (5 m s⁻¹), and that birds alter several aspects of their wing kinematics in response [18]. In addition, recent computational work [21] has suggested that turbulence may have only minimal effects on the mean aerodynamic properties of flying insects, despite leading to increased fluctuations of instantaneous aerodynamic forces. It thus remains unclear whether turbulence has a significant impact on insect flight performance at environmentally relevant levels.

A key limitation to our current understanding of this issue is the dearth of information available on turbulent flow conditions experienced by flying insects in nature. While wind flows in natural environments have been characterized extensively [3,11]—albeit often at timescales that are of little relevance for flying insects—to our knowledge no previous studies have simultaneously recorded local flow variability and the activity of flying animals, which would provide direct information about the wind environments actually experienced.

Here, we use a combination of field studies and wind tunnel tests to answer the questions: (i) what range of wind speeds and turbulence intensities do foraging bumblebees (Bombus impatiens) typically experience and (ii) how do environmentally relevant flow conditions affect body stability and wing kinematics?

2. Material and methods

2.1. Field study

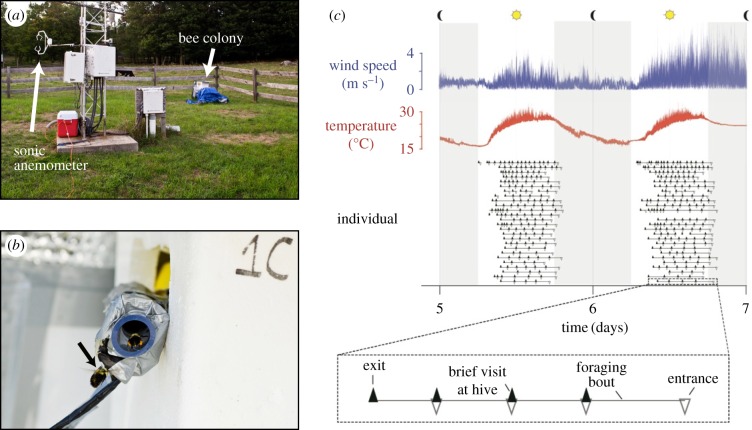
Eighty-seven bumblebee workers (B. impatiens) were removed from a commercial colony (BioBest) located in an open field at the Harvard Forest in Petersham, MA, over the course of 2 days (15–16 August 2012). Each bee was cold-anaesthetized and outfitted with a unique radio-frequency identification (RFID) tag (1.4 × 8 mm, 32 mg, Freevision Technologies). Intertegular span (IT span, a common proxy for body size in bees [22,23]) was measured with calipers to the nearest 0.1 mm, and bees were returned to the colony. After a 5-day acclimation period, two custom RFID readers placed in series at the hive's only opening recorded all forager transits to and from the colony over a two-week period (21 August–4 September 2012; figure 1b). The two adjacent RFID readers allowed us to distinguish entrances and exits from the colony, from which we determined the timing and duration of foraging bouts undertaken by uniquely identified bees. Simultaneously, we recorded three-dimensional instantaneous wind speeds at 5 Hz using a sonic anemometer (CSAT3, Campbell-Scientific^®), located approximately 3 m from the hive, and approximately 2 m off the ground (figure 1a). While such stationary recording does not provide direct data on the wind environment experienced by individual, mobile bees in flight, bumblebees typically forage over relatively short distances (approx. 275 m, [24]), and the colony was situated within a homogeneous, grassy landscape. The static measurements presented here are thus likely to be representative of average conditions experienced by these bees during local foraging flights.

Figure 1.

Simultaneous sampling of environmental wind and bumblebee foraging behaviour. (a) Field experimental set-up, showing location of the experimental bumblebee colony and adjacent sonic anemometer for recording wind speed and turbulence. (b) RFID-tagged bumblebee forager (black arrow) approaching the nest entrance. (c) Sample data collected over 2 days, showing environmental wind (blue, top), temperature (red, middle), and foraging behaviour of individual bumblebee workers (black, bottom). For each worker, nest exits and entrances are indicated by filled and open triangles, respectively, arranged along a single row.

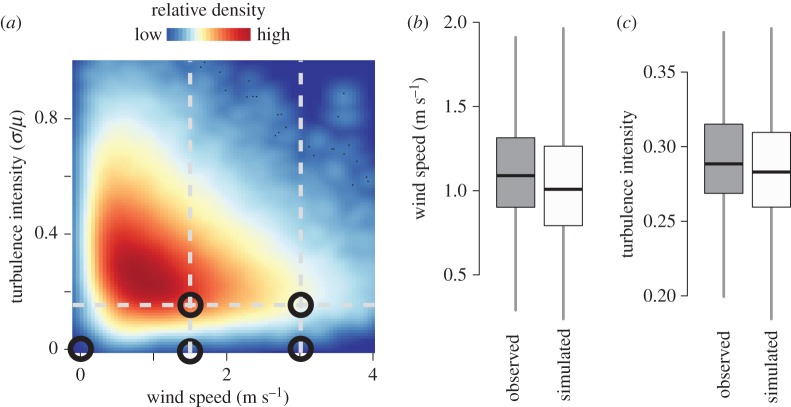
We combined these two datasets to investigate the natural distribution of wind conditions experienced by bumblebee foragers, using the bees' foraging activity to sample the wind environment. For each foraging bout, we measured the mean wind speed and turbulence intensity (σ_wind/μ_wind, where σ is standard deviation, and μ is the mean of instantaneous wind speeds, respectively) for each 10-s interval over the duration of the foraging bout (figure 2a). These brief measurement intervals were intended to capture higher frequency wind fluctuations (which would be more likely to cause rotational instabilities of the body), rather than lower frequency changes in mean wind speed (which would be experienced as linear perturbations or changes in overall flow direction). Standard deviation of wind speed was calculated by averaging the standard deviations of instantaneous flow speed in each of the three directions (u, v and w) measured independently, and this was divided by mean flow speed in the primary wind direction. Mean wind speeds and turbulence intensities for all such 10-s time intervals were then pooled to determine the distribution of flows experienced by foraging bees.

Figure 2.

Foraging bumblebees experience highly variable wind environments. (a) Heat map of instantaneous wind speeds and turbulence intensities observed over 10-s intervals during all bumblebee foraging bouts. Dashed grey lines and open black circles show combinations of wind speeds and turbulence intensity used in subsequent wind tunnel experiments. (b,c) Mean wind speed (b) and turbulence intensity (c) of observed (grey) versus simulated (white) foraging bouts. Boxes show the median and inter-quartile range (IQR), and whiskers indicate data range (75th and 25th ± 1.5 × IQR, respectively).

To test whether bees were less likely to forage during periods of high wind speed or turbulence, we then calculated the mean wind speed and turbulence intensity for each foraging bout, and compared this to the mean wind speed and turbulence intensity during a simulated foraging bout of the same length and on the same day, but starting at a randomly sampled time between 6.00 and 17.00 (figure 2b,c), when the majority of foraging activity occurred (figure 1c).

2.2. Wind tunnel experiments

2.2.1. Study organisms and experimental design

Mature bumblebee (B. impatiens) colonies were acquired from BioBest^® and maintained in a temperature-controlled laboratory environment from June to August 2014 at the Concord Field Station, Bedford, MA. Bees were given ad libitum access to artificial nectar (BioGluc^®) and fresh pollen in a foraging chamber.

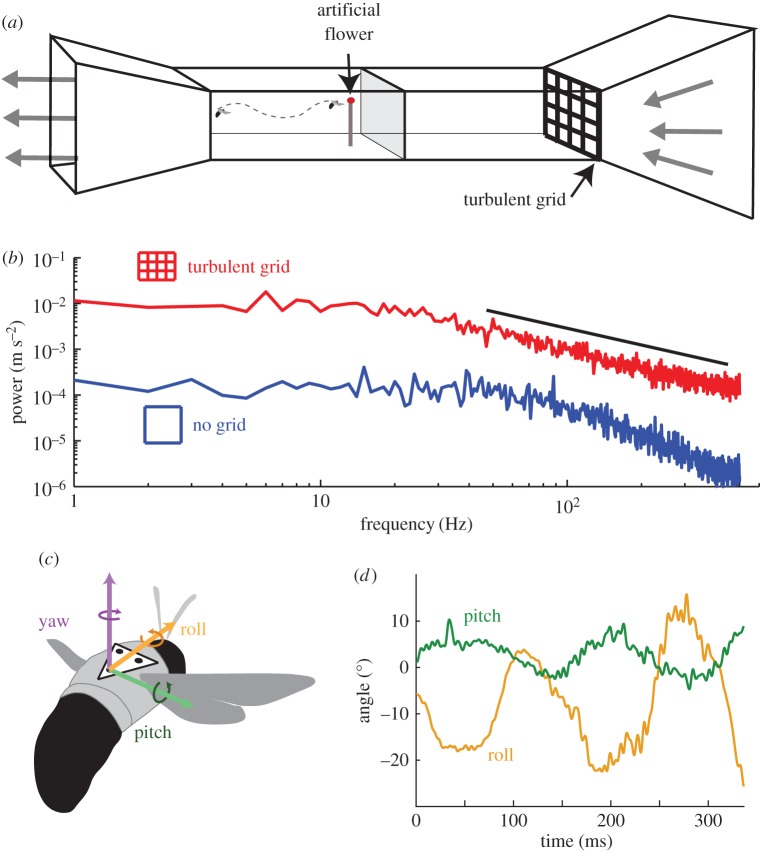
Prior to experimental trials, individual foragers (i.e. bees actively foraging outside the nest chamber) were removed from the colony, cold-anaesthetized and outfitted with a triangular marker (as in [25]), attached to the dorsal part of their thorax with cyanocrylate glue. After tag attachment, individual bees were isolated for at least 1 h to increase feeding motivation, then introduced to the downstream end of the working section (0.9 × 0.5 × 0.5 m) of a wind tunnel with low-speed, laminar flow (less than 0.5 m s⁻¹). On the upstream end of the wind tunnel, we placed an artificial flower (purple, approx. 2 cm diameter) with a pipette tip in the middle containing a few drops of artificial nectar, attached to a thin metal rod (figure 3a). Each bee was allowed to explore the wind tunnel until it found the artificial flower and began feeding. After this, the purple artificial flower was removed, leaving only the pipette tip (to minimize flow disturbance), and the bee was again released from the downstream end of the wind tunnel. This procedure was repeated under one of five experimental flow conditions, presented in a randomized order: 0 m s⁻¹ flow, 1.5 m s⁻¹ laminar flow, 1.5 m s⁻¹ turbulent flow, 3.0 m s⁻¹ laminar flow and 3.0 m s⁻¹ turbulent flow.

Figure 3.

Wind tunnel experiments to test the effect of turbulent flow on bumblebee flight. (a) Schematic diagram of wind tunnel design. (b) Turbulent power spectra for laminar (blue) and turbulent (red) flow conditions in the wind tunnel. Black line indicates the expected −5/3 decay characteristic of freestream turbulence in natural environments. (c) Schematic drawing of a bumblebee showing the three axes of body angular orientation. (d) Sample trace of pitch and roll over a single trial with turbulent flow at 1.5 m s⁻².

Turbulence was introduced into the working section of the wind tunnel via a grid located upstream of the working section (figure 3a). This grid introduced near-isotropic turbulence with a turbulence intensity of approximately 15% (compared to less than 2% in laminar flow [18]). The power spectrum of experimental turbulence displayed a −5/3 slope, characteristic of fully mixed turbulence (figure 3b, [26]). For a more detailed description of flow conditions and turbulence spectra, see [18].

2.2.2. Kinematic reconstruction

Flights were recorded within an interrogation volume of approximately 200 cm³ just downstream of the artificial flower at 5000 frames per second using three Photron SA3 cameras, calibrated via direct linear transformation [27]. The three markers on the triangular tags of the bees' thorax (figure 3c) were tracked automatically using DLTdv5 [27] under manual supervision (electronic supplementary material, movie S1). For a subset of bees, wingtip positions of both wings at each stroke reversal were manually digitized (electronic supplementary material, movie S1), and the positions of the wing bases were recorded at five evenly spaced frames throughout the video sequence. Three-dimensional kinematics of these points were then calculated via DLTdv5 [27]. To reduce digitization noise, three-dimensional coordinates were smoothed using a fifth-order Butterworth filter with a low-pass cut-off frequency of 1000 Hz, and the first and last 30 frames of each trial sequence were removed from subsequent analyses to reduce filtering artefacts.

Roll, pitch and yaw orientations of the body were calculated from the three triangular markers on the bee's thorax, following [25] (figure 3c,d). Standard deviations of body orientations were calculated after filtering the roll, pitch and yaw data using a fifth-order Butterworth filter with a high-pass frequency cut-off of 10 Hz, to remove low-frequency casting motions [25]. For each wing stroke digitized, amplitude was calculated separately for each wing, by rotating data into the body frame using the body's instantaneous roll, pitch and yaw orientations (x′–y′–z′), then calculating the minimum angle between the wingtip location at pronation, the wing base, and the wingtip location at supination. Asymmetry in left–right amplitude was calculated for each wing stroke, and the maximum value and variance of stroke asymmetry were calculated for each trial. Correlations between stroke-by-stroke amplitude asymmetry and body roll angle were assessed.

To estimate variation in the position of pronation and supination, we calculated the wing sweep angle at pronation and supination independently, with respect to the sagittal plane of the bee body, projected into the x′–y′ plane. Wingbeat frequency was calculated manually by counting wing strokes in the camera view where the bee was visible for the longest time period.

2.2.3. Statistical models for effects of flow

To investigate the effects of flow speed and turbulence on body and wing kinematics, we constructed a series of linear mixed effects models using the ‘lmer’ function [28] in R. These models allowed us to test for effects of experimental conditions, while accounting for variation across individuals. First, we tested the effects of wind speed (independent of flow condition) on body and wing kinematics by building models with flow speed as a fixed effect and individual as a random effect, using only laminar flow trials. To test the effects of turbulence, we then constructed separate models for each of the non-zero flow speeds (1.5 and 3.0 m s⁻¹) with flow condition as a fixed effect and individual as a random effect. P-values for fixed effects (i.e. flow speed and condition) were calculated in the ‘lmerTest’ package [29], using Satterthwaite approximations for denominator degrees of freedom.

3. Results

3.1. Field study

We recorded a total of 1934 foraging bouts from 33 unique bees over 14 days (figure 1c). Across all foraging bouts, the median wind speed was 1.00 m s⁻¹, and the median turbulence intensity was 0.28 (figure 2a). However, there was substantial variation in both wind metrics, with wind speed ranging from 0.22 to 3.06 m s⁻¹ (1st and 99th percentile, respectively), and turbulence intensity ranging from 0.10 to 0.57 (1st and 99th percentile, respectively). Mean within-bout wind speeds and turbulence intensities during individual foraging bouts were not lower than that expected under random simulation (figure 2b,c; wind speed, one-sided paired t-test, d.f. = 1933, t = 9.22, p > 0.99; turbulence intensity, one-sided paired t-test, d.f. = 1933, t = 8.72, p > 0.99), supporting the hypothesis that bees do not adjust the timing of their foraging to avoid windy conditions.

3.2. Wind tunnel experiments

In the wind tunnel, we recorded a total of 96 flight trials from 21 unique bumblebee foragers, and analysed body and wing kinematics for a subset of 65 trials from 13 bees (figure 3d). Standard deviation of roll orientation increased significantly in turbulent flow when compared with laminar flow at 3.0 m s⁻¹ (figure 4a and table 1), but not at 1.5 m s⁻¹ (table 1). Standard deviation of roll in laminar flow was significantly higher at 3.0 m s⁻¹ than in still air (figure 4a and table 1) but there was no significant difference between still air and 1.5 m s⁻¹ laminar flow or between 1.5 and 3.0 m s⁻¹ laminar flow (figure 4a and table 1). In a separate model including body mass and [flow condition × speed] as fixed effects, we found no effect of body mass (dry mass, range = 35.3–68.1 mg across experimental individuals) on standard deviation of roll position (t = −0.885, d.f. = 9.9, p = 0.397). Standard deviation of pitch orientation did not differ significantly with flow or speed (table 1).

Figure 4.

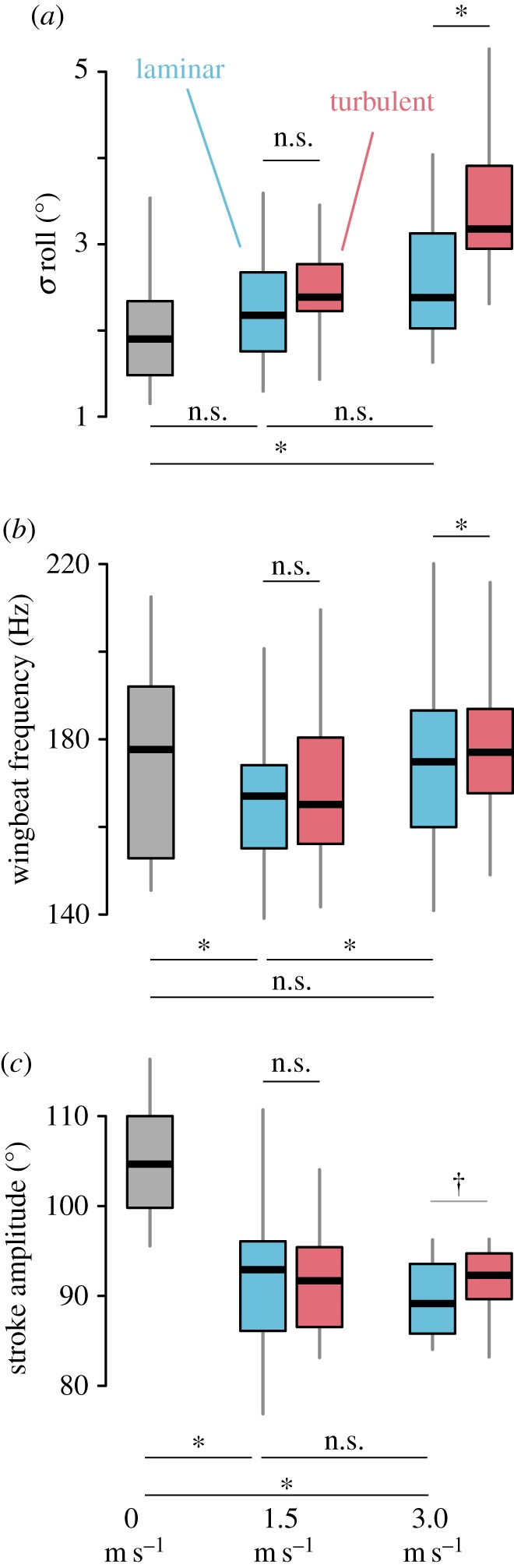
Body stability and mean wing kinematics across flow conditions. (a) Standard deviation of roll orientation, (b) mean wingbeat frequency and (c) mean stroke amplitude by speed and flow condition, with laminar trials in blue and turbulent trials in red. Bars above show comparisons between laminar and turbulent flow trials, at 1.5 and 3.0 m s⁻¹, and bars below show comparisons between laminar flow trials across speeds. Asterisks indicate significant differences between groups at the α = 0.05 level, and daggers indicate marginal significance (0.05 < p < 0.10). Boxplots show the median and IQR, and whiskers depict the data range (75th and 25th ± 1.5 × IQR, respectively).

Table 1.

Summary of linear mixed effects models examining the effects of wind speed and turbulence on body and wing kinematics in bumblebee (Bombus impatiens) foragers. Significant effects (p < 0.05) are highlighted in bold, while marginally significant effects (0.05 < p < 0.10) are highlighted in italics. See text for details of model specification.

variable	comparison (m s−1)	effect	d.f.	t	p-value
standard deviation of roll (high frequency, °)	1.5 (lam) versus 0	0.28	21.7	1.02	0.31
	3.0 (lam) versus 0	0.57	21.7	2.1	0.048
	3.0 (lam) versus 1.5 (tur)	0.29	22	1.01	0.33
	1.5 (tur) versus 1.5 (lam)	0.25	10.1	1.3	0.22
	3.0 (tur) versus 3.0 (lam)	0.88	21	2.62	0.016
standard deviation of pitch (high frequency, °)	1.5 (lam) versus 0	0.042	20.91	0.39	0.7
	3.0 (lam) versus 0	0.049	20.91	0.46	0.65
	3.0 (lam) versus 1.5 (tur)	6.8 × 10−3	11	0.064	0.95
	1.5 (tur) versus 1.5 (lam)	0.12	10.99	1.11	0.292
	3.0 (tur) versus 3.0 (lam)	0.12	9.99	1.24	0.243
wingbeat frequency (Hz)	1.5 (lam) versus 0	−7.91	33.4	−3.3	2.3 × 10−3
	3.0 (lam) versus 0	−1.42	33.3	−0.59	0.56
	3.0 (lam) versus 1.5 (tur)	6.45	19.1	4.12	5.7 × 10−4
	1.5 (tur) versus 1.5 (lam)	1.31	20	0.78	0.44
	3.0 (tur) versus 3.0 (lam)	4.52	1.62	2.79	0.012
stroke amplitude (°)	1.5 (lam) versus 0	−13.84	24.72	−6.24	1.65 × 10−6
	3.0 (lam) versus 0	−15.66	23.22	−6.93	4.41 × 10−7
	3.0 (lam) versus 1.5 (tur)	−1.84	13.08	−0.82	0.43
	1.5 (tur) versus 1.5 (lam)	0.165	12.38	0.099	0.92
	3.0 (tur) versus 3.0 (lam)	3.98	12.64	2.13	0.054
variance in L-R amplitude asymmetry (°)	1.5 (lam) versus 0	30.87	31	2.23	0.033
	3.0 (lam) versus 0	20.96	31	1.48	0.15
	3.0 (lam) versus 1.5 (tur)	−9.91	21	−0.62	0.54
	1.5 (tur) versus 1.5 (lam)	−11.43	15.09	−0.76	0.46
	3.0 (tur) versus 3.0 (lam)	25.37	23	1.96	0.062
maximum L-R amplitude asymmetry (°)	1.5 (lam) versus 0	2.46	24.3	0.98	0.34
	3.0 (lam) versus 0	−1.43	22.56	−0.56	0.58
	3.0 (lam) versus 1.5 (tur)	−4.38	24	−1.61	0.12
	1.5 (tur) versus 1.5 (lam)	−0.67	24	−0.28	0.78
	3.0 (tur) versus 3.0 (lam)	7.15	12.75	3.15	7.8 × 10−3

Mean wingbeat frequency displayed a small but statistically significant increase of approximately 4.5 Hz in turbulence at 3.0 m s⁻¹ compared to laminar flow (figure 4b and table 1), while there was no significant difference at 1.5 m s⁻¹ (table 1). Wingbeat frequency was significantly lower in 1.5 m s⁻¹ laminar flow than in either still air (figure 4b and table 1) or 3.0 m s⁻¹ laminar flow (figure 4b and table 1).

Mean stroke amplitude showed a marginally significant increase of approximately 4° in turbulence at 3.0 m s⁻¹ compared with laminar flow (figure 4c and table 1), while there was no significant difference at 1.5 m s⁻¹ (table 1). Stroke amplitude was significantly lower in both 1.5 m s⁻¹ laminar flow (figure 4c and table 1) and 3.0 m s⁻¹ laminar flow (figure 4c and table 1) than in still air, but showed no difference between 1.5 and 3.0 m s⁻¹ laminar flow (figure 4c and table 1).

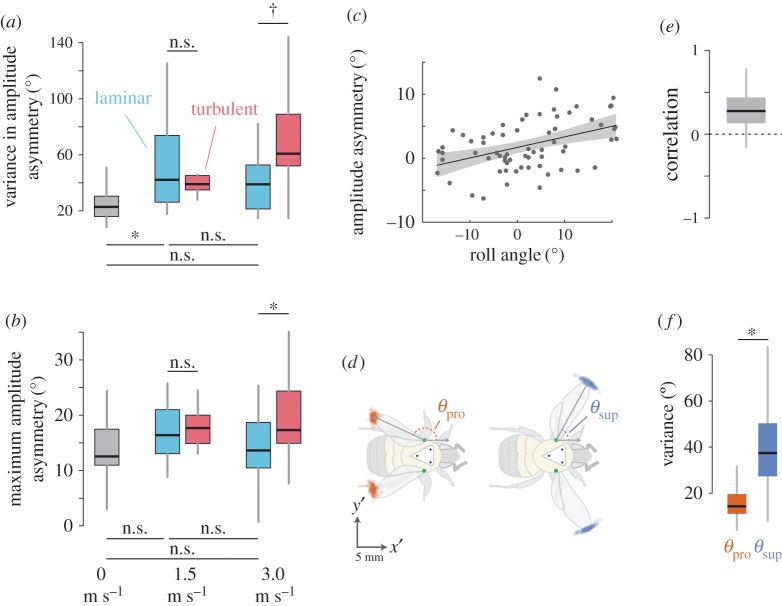
Within-trial variance in stroke amplitude asymmetry showed a marginally significant increase in turbulence when compared with laminar flow at 3.0 m s⁻¹ (figure 5a and table 1), but not at 1.5 m s⁻¹ (figure 5a and table 1). Variance in stroke amplitude asymmetry was significantly higher in 1.5 m s⁻¹ laminar flow than in either still air (figure 5a and table 1) or 3.0 m s⁻¹ laminar flow (figure 5a and table 1), but there was no difference between 1.5 and 3.0 m s⁻¹ laminar flow (figure 5a and table 1).

Figure 5.

Variability in wing kinematics during flight in turbulence. (a) Within-trial variance in left–right amplitude asymmetry and (b) maximum left–right amplitude asymmetry, with laminar trials in blue and turbulent trials in red. Bars above show comparisons between laminar and turbulent flow trials, at 1.5 and 3.0 m s⁻¹, and bars below show comparisons between laminar flow trials across speeds. (c,e) Correlations between absolute roll angle of the body and asymmetry in stroke amplitude between the left and right wings, shown (c) for each stroke during one trial and (e) stroke-averaged correlations across all trials. (d) Locations of wingtips at pronation (orange) and supination (blue) during a single trial, rotated into the body frame. (f) Variance of pronation angle (orange) and supination angle (blue) across trials. Boxplots show the median and IQR, while whiskers depict the data range (75th and 25th ± 1.5 × IQR, respectively). Asterisks indicate significant differences between groups at the α = 0.05 level, and daggers indicate marginal significance (0.05 < p < 0.10).

Maximum within-trial stroke amplitude asymmetry increased significantly in turbulence when compared with laminar flow at 3.0 m s⁻¹ (figure 5b and table 1), but not at 1.5 m s⁻¹ (figure 5b and table 1). Maximum stroke amplitude asymmetry showed no significant difference across flow speeds in laminar wind (figure 5b and table 1).

Roll orientation of the body and left–right stroke amplitude asymmetry were positively correlated across trials (figure 5c,e, one-sample t-test, d.f. = 58, t = 9.28, p = 4.5 × 10⁻¹³) and experimental flow conditions (electronic supplementary material, figure S1). Within-trial variance in the angle of supination was significantly higher than within-trial variance in the angle of pronation (figure 5d,f, paired t-test, d.f. = 58, t = −8.00, p = 6.13 × 10⁻¹¹).

4. Discussion

The results of our field study clearly demonstrate that turbulence is a common challenge for insects flying in natural environments (figures 1 and 2). Wind speed and turbulence intensity vary substantially in the environments where bees forage (figures 1 and 2) and bees do not avoid foraging during periods of higher flow speeds or turbulence intensities (figure 2b,c). This indicates that bees are subjected to substantial turbulence and variable wind speeds during their daily foraging activities. It is important to note that the measurements of environmental flow presented here were collected at a single location in space over a relatively short time window, and so likely do not represent the full range of flow conditions that foraging bees experience. Our data show that bees do not alter their foraging patterns within the range of flow speeds and turbulence intensities measured, but the question of whether their foraging activity is curtailed by more severe wind conditions remains unanswered.

We were able to reproduce some aspects of environmentally realistic turbulence in our wind tunnel, although the turbulence intensities generated were on the lower end of what bees experience in outdoor environments (figure 2a). The wind tunnel experiments revealed that both body stability and wing kinematics were affected by turbulent flow, but only at the higher end of environmentally relevant speeds (i.e. 3.0 m s⁻¹, figures 2 and 4). While previous work has demonstrated that the flight performance of orchid bees and hummingbirds is affected by turbulence at higher wind speeds (approx. 4 m s⁻¹ and above, [12,18]), our results provide the first direct evidence that turbulence affects animal flight performance at lower, environmentally relevant wind speeds and turbulence intensities (figures 2 and 4). Further work is needed to generate wind tunnel flows that mimic what bees most commonly experience in the environment—low mean speeds but high turbulence intensities (e.g. speeds approx. 1 m s⁻¹ and turbulence intensities of 0.25–0.30; figure 2a), so that the effects of these common flow conditions on flight performance can be assessed.

Bumblebees in our study responded to the increased body instability introduced by turbulence at higher flow speeds with a variety of active changes in wing kinematics. Bees displayed a small but statistically significant increase in wingbeat frequency in turbulence (figure 4b), consistent with results from hawkmoths flying in von Kármán vortex flows [19] and hummingbirds flying in turbulence [18]. This increase in wingbeat frequency may increase the energetic cost of flight due to an associated increase in the inertial power requirements for accelerating and decelerating the wings [30]. However, this increase in wingbeat frequency may represent an important strategy for increasing control authority, by reducing the time between wing strokes and thus decreasing the delay in updating control input to wing kinematics, a key factor in insect flight control [31]. Recent physical modelling studies also suggest that wings flapping more rapidly experience more consistent flow fields that are driven by kinematic forcing, and less subject to the random fluctuations of external, turbulent flows [32]. Bumblebees in our study also displayed a trend towards increased mean stroke amplitude in turbulent flow at higher speeds (figure 4c), suggesting a potential demand for higher aerodynamic power output during flight in turbulence [33–35].

In addition to shifts in mean wing kinematics, we found that bumblebees flying in turbulence displayed more variable and extreme wing kinematics (figure 5), suggesting that they respond actively to at least some of the high-frequency body instabilities induced by turbulent flow [21]. The significant correlation between roll angle of the body and left–right asymmetry in wing stroke amplitude (figure 5c) is consistent with the hypothesis that bees employ stroke amplitude asymmetry to help control body orientation during flight [36]. Asymmetric stroke amplitude could lead to both asymmetric lift generation and asymmetric stroke-averaged drag between the wing pairs, thus generating a net torque on the body [37].

Interestingly, bees appear to primarily adjust the angle of supination, rather than pronation, when modulating stroke amplitude (figure 5d,f). This could represent a strategy of simplifying control by reducing the number of free kinematics parameters. However, such simplification may also create coupling between kinematic parameters (in this case, between stroke amplitude and mean stroke position, potentially inducing pitching moments on the body [9]). Strategies for simplifying control mechanisms while avoiding disadvantageous coupling of kinematic parameters represent a potentially fruitful area of future research for both biological studies and bio-robotic applications. While in the current study we examined only the wingtip kinematics at stroke reversals, bumblebees may use a variety of other kinematic strategies to control body attitude in addition to asymmetric stroke amplitude. Future work investigating time-varying wing kinematics in turbulence could be highly informative for revealing the full suite of kinematic control mechanisms available to insects flying in variable wind flows [36].

Overall, our results suggest that even relatively low levels of environmental turbulence, typical of those encountered on a daily basis by insects flying through natural aerial environments, can impact flight stability. We found that bumblebees respond to the instabilities resulting from turbulence with both static (e.g. altered mean values) and dynamic (stroke by stroke) changes in wing kinematics.

However, this study of one animal species in a single wind environment by necessity represents only a small fraction of variation in natural wind environments. Mean wind speeds and turbulence intensities vary substantially within habitats (e.g. higher turbulence and wind speed in forest canopies than in understories [11]), as well as across habitats [3]. In addition, while we focused here on exploring the effects of relatively small-scale, higher frequency turbulence (with an integral length scale—the size of the largest eddy—in our wind tunnel of approx. 4 cm [18]), wind flows in natural environments are characterized by integral length scales that typically range up to metre or kilometre scales. Our wind tunnel experiment recreated a naturalistic turbulence spectrum at higher frequencies [18], but was missing low-frequency components of turbulence, which are characteristic of natural environments but challenging to recreate in all but the largest laboratory wind tunnels. Future work linking flight behaviour to environmental flow characteristics, particularly studies exploring the effects of eddy size and more extreme wind conditions on insect flight, will be helpful in understanding the role of turbulence in the behaviour and ecology of flying insects.

Our results most probably represent only a subset of the strategies for coping with turbulence among animal fliers. Indeed, our findings suggest that bumblebees may use a set of mechanisms for increasing stability in turbulence that are distinct even from closely related orchid bees [38], suggesting the possibility of a wide range of turbulence-mitigation strategies among biological fliers. Exploring such strategies is of particular interest given recent advances in biologically inspired flying robots [39]. While there is growing demand and interest in small, autonomous flying robots for use in urban, agricultural and natural environments, navigating such complex physical environments remains a significant challenge for MAVs [40,41].

Future work exploring a broader range of animal species that must cope with environmental turbulence in diverse natural environments is of crucial importance for understanding the ecology and evolution of flight in animals. Such work may also reveal diverse flight stability mechanisms among flying animals applicable to the promising, but challenging development of autonomous robots operating at the scale of flying animals. In addition to these biological studies inspiring robotic design, the recent development of insect-scale, flapping-wing robots [39] provides an unprecedented opportunity for experimental exploration of basic questions regarding the control and stability of flying animals that are difficult or impossible to explore in real animals, or by using established modelling approaches such as dynamic scaling [42]. Future work that takes advantage of these synergies has the potential to shed light on how flying animals cope with the wide range of complex, natural environments they encounter, and reveal principles that could aid in the design of robust, bioinspired flying robots capable of meeting these same challenges.

Data accessibility

Associated data and custom scripts are deposited on zenodo.org.

Competing interests

We declare we have no competing interests.

Funding

This research was supported by an NSF Graduate Research Fellowship to J.D.C., a Robert K. Enders Field Biology Award of Swarthmore College to J.J.C., and NSF grant no. CCF-0926158 and IOS-1253677 to S.A.C.