A Probabilistic Analysis of Muscle Force Uncertainty for Control

Abstract

Background

We control the movements of our body and limbs through our muscles. However, the forces produced by our muscles depend unpredictably on the commands sent to them. This uncertainty has two sources: irreducible noise in the motor system's processes (i.e. motor noise) and variability in the relationship between muscle commands and muscle outputs (i.e. model uncertainty). Any controller, neural or artificial, benefits from estimating these uncertainties when choosing commands.

Methods

To examine these benefits we used an experimental preparation of the rat hindlimb to electrically stimulate muscles and measure the resulting isometric forces. We compare a functional electric stimulation (FES) controller that represents and compensates for uncertainty in muscle forces with a standard FES controller that neglects uncertainty.

Results

Accounting for uncertainty substantially increased the precision of force control.

Conclusion

Our work demonstrates the theoretical and practical benefits of representing muscle uncertainty when computing muscle commands.

Significance

The findings are relevant beyond FES as they highlight the benefits of estimating statistical properties of muscles for both artificial controllers and the nervous system.

I. Introduction

Muscle forces can be difficult to predict. For a given command, the force produced by a muscle depends on a large number of variables distributed across many spatial and temporal scales [1]. While the nervous system clearly has knowledge of some of these variables (e.g. muscle length, velocity and force), other aspects of muscle dynamics may be much more difficult to measure and estimate (e.g. the detailed dynamics of molecules at the level of individual myofibrils and sarcomeres). With knowledge of those variables the nervous system has access to, the relationship between commands and muscle forces can be estimated and used to predict, or model, force generation. This relationship itself cannot be estimated exactly, hence the presence of model uncertainty. The remaining unaccounted aspects of muscle dynamics will result in what appears to be random fluctuations in force, which can be attributed to motor noise. The effects of model uncertainty and motor noise on muscle force can be mitigated but never altogether eliminated. Thus a central problem for the nervous system, or any artificial controller, is how to command muscles effectively in the presence of uncertainty.

Many studies use computational models to understand how the nervous system commands muscles when executing behavior. These studies investigate issues ranging from how groups of muscles are coordinated [2-6], to the adaptation of muscle coordination after injury or altered dynamics [7, 8], to the optimality of muscle commands [9-11]. However, most of these studies neglect noise and uncertainty and rely on deterministic descriptions of control. While some studies do model noise in the command, they rely on assumed accurate models of muscles, neglecting model uncertainty [10, 12-15]. Thus the implications of these two aspects of uncertainty on neural control remain poorly understood.

These two aspects of uncertainty in muscle force production are also potentially important in studies that directly stimulate muscle. The chief clinical application is functional electrical stimulation (FES). Here the goal is to replace weak or absent muscle commands with artificial stimulations that restore impaired behaviors, e.g. toe drag in stroke/multiple sclerosis [16, 17], or command paralyzed limbs with brain-machine interfaces [18-23]. In this application, as in the previous studies, some aspects of muscle force dynamics can usually be estimated. However, the force expected from stimulating a muscle often remains very inaccurate, both because models are imperfectly estimated and because of unaccounted muscle dynamics. Yet these uncertainties are usually neglected when designing FES controllers.

In this study, we examine the issues of uncertainty in muscle force production in the context of control. We present a data-driven, probabilistic model of force production, explicitly representing both motor noise and model uncertainty. We validate these ideas using a clinically relevant animal FES model. We find that the forces produced using our feedforward probabilistic controller are substantially more accurate than standard deterministic FES controllers. The results of this study demonstrate the benefits of estimating muscle uncertainty to enable precise control.

II. Materials and Methods

We first present a toy model analysis illustrating the methods and concepts we used in our approach. We then apply these same methods to an experimental situation, validating their applicability to the clinical application of FES.

A. Muscle Models

For our simulated experiments as well as the experimental modeling, we consider steady state, isometric force production. We assume each muscle's force production varies with activation level as described by the conventional sigmoidal recruitment curve,

$$f\left(u\right)=\alpha +\beta \left(\frac{1}{1+e^{\gamma (u-\delta )}}\right)+n$$ (1)

where u is the activation level, α, β, δ, γ are model parameters that describe the recruitment curve's overall shape and n is a noise term (a random variable drawn from some distribution). The noise term accounts for errors in capturing the true functional relationship and any unmodeled dynamics that result in trial-to-trial variability. Data pairs consisting of activation levels and the measured forces, {u_i, f_i} are used to fit these model parameters.

Typically, data is used to find point estimates for the model parameters such that some “best” fit is achieved. For instance, α, β, δ, and γ may be chosen to minimize the sum of squared errors between the model predictions and the data, the so-called least-squares solution. The residuals of this fit can be used to approximate the noise term (motor noise), or as is often done, neglected all together. Using these point estimates, and neglecting the motor noise, the muscle model is deterministic and models the average muscle force for a given value of activation, u.

Under a full statistical treatment of the model, we recognize that many model parameter values may be equally likely given a particular set of observations. Therefore, rather than find point estimates for α, β, δ, and γ, we seek the distributions over their values induced by our data, i.e. P(α, β, δ, γ|{u_i, f_i}). This distribution characterizes our confidence in the model parameters, i.e. the model uncertainty. Similarly, we can characterize the motor noise, the remaining variability in the data that the model parameters cannot account for. Then, rather than find a deterministic function for the force value, we now describe the probability of forces by integrating out over all the model parameters. The end result is a posterior distribution of possible muscle forces given the activation level and our experimental data.

Since our model is nonlinear in its parameters, a closed form representation for these posterior distributions is intractable. We approximate these distributions by implementing a Markov Chain Monte Carlo (MCMC) sampling technique using software written for this purpose [24]. Briefly, for each muscle's data, “samples” are drawn, where each sample is a set of muscle parameters described in equation 1. 10,000 samples were drawn for a burn-in period, effectively settling to a location in parameter space where the values accurately describe the data. Thereafter each 50^th sample was stored, collecting 5,000 samples in total (see e.g., [25, 26] for a review of this approach). From these samples the median values and standard deviations were computed for all parameter values.

The MCMC algorithm returns many sample recruitment curves representative of the posterior distribution (given our data), similar to a boot-strapping technique. With these samples we can then compute the mode, or most probable recruitment curve, which also serves as a deterministic model. In addition we computed the standard deviation of the curve as a function of the level. This process was repeated for each individual muscle, yielding approximations to the posterior distribution of forces conditioned on the activation level and the data.

The above procedures were used to compute both deterministic and probabilistic muscle models of force (for both the toy models and the experimental models). In the animal experiments isometric muscle forces were modeled as vectors in a plane. Therefore, for each muscle, the direction of its force vector was assumed constant across stimulation levels and obtained by averaging over that muscle's data [27]. The total force output of the limb was then modeled as the vector sum of the individual muscles.

B. Controllers

To compute activation levels for our deterministic models we minimized the error between the desired force and our model-predicted force, while penalizing large activations. Since many activations can produce the same desired force, penalizing unnecessarily large values sidesteps this redundancy. This approach also has the practical advantage of minimizing metabolic costs and muscle fatigue. We note that the relationship between a muscle's command and its metabolic cost, or any other number of characteristics such as fatigue and noise, are difficult to describe. Thus we take an agnostic approach, and merely assume that commands that produce the same output with less activation are desirable. As is standard, we quantified this trade-off with a quadratic cost function and used the minimizing commands as our activations.

$$u^o=\arg \min \{{(F\left(u\right)-F_d)}^T\Phi (F\left(u\right)-F_d)+u^{T}Ru\}$$ (2)

where u^o is the optimal command, F(u) is the force produced by command u, F_d is the desired force, and Φ and R are weights penalizing errors from the desired force and size of command, respectively. In this general form all the terms are matrices appropriate for deriving multi-dimensional activations.

To compute activations for our probabilistic models we minimized the same cost function, but, since we consider the distribution of forces that might be produced by an activation pattern, now we must instead minimize its expected value. That is, we found activations according to the rule,

$$u^o=\arg \min \left\{E\{{(F\left(u\right)-F_d)}^T\Phi (F\left(u\right)-F_d)+u^{T}Ru\}\right\}$$ (3)

Which, after rearranging terms is,

$$u^o=\arg \min \{{(E\left[F\left(u\right)\right]-F_d)}^T\Phi (E\left[F\left(u\right)\right]-F_d)+Tr\left[\Phi \Sigma \left(\mathrm{u}\right)\right]+u^{T}Ru\}$$ (4)

where Σ is the covariance of the force vector, which is a function of the motor noise, model uncertainty and activation. The distribution of forces produced by an activation pattern was determined using the posterior distributions estimated by the MCMC described above.

To compute activations for the controllers that maximized and minimized uncertainty, we used the following cost,

$$u=\arg \max ∕\min \left\{Tr[\Phi \Sigma \left(\mathrm{u}\right)+{\mathrm{u}}^T\mathrm{Ru}]\right\}$$

subject to the constraint, F(u)=F_d.

For our simulated muscles, F(u) is the scalar sum of the individual muscle outputs, Φ = 100, and R is the identity matrix. For the experiments, Φ = 1e10, and R = 10 in all cost functions described above. To find optimal activations, these cost functions were minimized using software written for Matlab.

To quantify uncertainty we operationally define it as the mean squared expected error in force, which in close approximation is equal to the trace of the covariance.

$$E\left[{(F\left(u\right)-F_d)}^T(F\left(u\right)-F_d)\right]=Tr\left(\Sigma \left(\mathrm{u}\right)\right)+{(\widehat{F}-F_d)}^T(\widehat{F}-F_d)\approx Tr\left(\Sigma \left(\mathrm{u}\right)\right)$$

F̂ = E[F(u)] is the mean force value, (F̂ – F_d) and is the bias error, which in practice was several orders of magnitude smaller than the trace of the covariance.

Finally, we note that for multivariate Gaussian variables, the principle axes of the confidence ellipse are the eigenvectors of the covariance matrix. Their size is found by scaling the eigenvalues by according to a Chi-squared distribution. If the variance in both F_x and F_y is equivalent and σ², the 95% confidence ellipse is a circle with radius (χ₂²(0.95)* σ²)^1/2.

C. Experimental Methods

An experimental test bed designed specifically for examining FES systems was used to analyze different controllers on a rat model. All procedures were conducted under protocols approved by Northwestern University's Animal Care and Use Committee. Details of the experimental preparation can be found elsewhere [27]. Briefly, seven female, Sprague Dawley rats were anesthetized (80mg/kg ketamine and 10mg/kg Xylazine) and implanted with stimulating electrodes (stainless steel, 1-3mm exposure) in 9-13 muscles in their left hindlimb. Subcutaneously implanted plates at the back and belly served as return electrodes. We have shown in our previous work that this configuration of electrodes minimizes current spread and allows for isolated stimulation of implanted muscles. The muscles used for stimulation typically included biceps femoris anterior (BFa) and posterior (BFp), semitendinosus (ST), semimembranosus (SM), adductor magnus (AM) and longus (AL; activated together), vastus medialis (VM), vastus lateralis (VL), rectus femoris (RF), iliopsoas (IP), gracilis (anterior and posterior heads activated together), and caudofemoralis (CF). Each animal's hip was immobilized and ankle fixed to a 6-axis force transducer with the use of bone screws and surgical posts. In this orientation the hip joint, knee and ankle were approximately in the same, sagittal plane and remained isometric throughout the experiment. Using custom software written in Matlab, stimulations were systematically delivered to the limb's implanted muscles (FNS-16 Multi-Channel Stimulator, CWE, Inc.) to gather data necessary for estimating recruitment curves. Muscles were stimulated with a 75Hz, 0.1msec biphasic pulse train of varying current, typically between 0.05mA and 4mA for 1.5 seconds. We waited at least 1 minute between stimulation of the same muscle in order to minimize effects of fatigue. Experiments were conducted until the health of the animal degraded, typically after about 6 hours. The animal was then euthanized using a 1ml intraperitoneal injection of Euthasol followed by a bilateral thoracotomy.

For each implanted muscle, force data was recorded at a series of stimulation levels. Forces elicited from each muscle generally increased monotonically with the stimulus level and had a consistent direction. Due to the animal's posture, as well as the muscles chosen, elicited forces were strongest within the sagittal plane of the limb, although the same analyses described here can be readily extended to handle three-dimensional forces. Forces elicited during co-stimulation of multiple muscles were approximately equivalent to the vector sum of their individual forces (see [27]). As a result, we could model the ankle forces as the vector sum of the individual muscle models.

To gather the data necessary to build models of force production, the maximum isometric forces and corresponding plateau stimulation values were determined for each muscle. Then for each muscle, we swept through a series of 5 activation levels, starting at baseline levels and moving through plateau levels, measuring the resulting isometric forces. In order to minimize muscle fatigue, we cycled through all muscles at their first stimulation level waiting one minute between each muscle before moving to the next stimulation for each muscle. With 9-13 muscles implanted for each animal, this allowed for adequate recovery time between stimulations of the same muscle. When this process was complete, we had a data set appropriate for building our force production models (see Fig 3 for an example animal's data). For each activation level, we used the steady-state forces to compute all muscle recruitment parameters (see Methods and [27]).

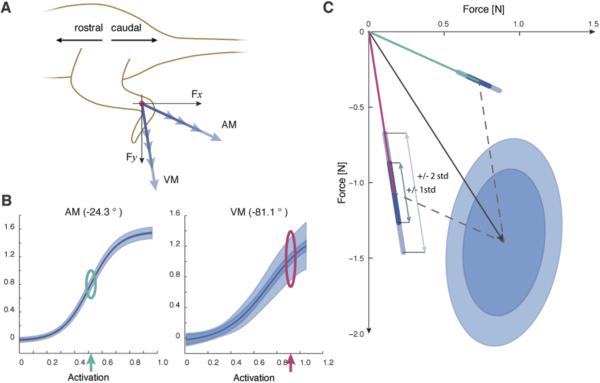
Fig. 3.

A) Depiction of experimental setup and force vector orientations. All forces were measured in the animal's sagittal plane. For illustrative purposes hypothetical force vectors are shown for adductor magnus (AM) and vastus medialis (VM). The orientation of each muscle's force vector is an angle measured relative to horizontal. B) Experimentally obtained recruitment curves for rectus adductor magnus and vastus medialis illustrate the variability in predicted forces. Displayed are the maximum likelihood values (solid lines), model uncertainty (+/−1 standard deviation) and motor noise (+/−1 standard deviation). C) An example force vector, demonstrating how individual muscle forces and uncertainty (depicted at the activation levels marked with the green and magenta arrows from B) are used to make predictions for forces resultant force prediction.

We repeated this data collection approximately every 2 hours to redefine each muscle's recruitment curve. As the number of samples increases, the amount of model uncertainty could decrease. However, a large number of stimulations is often impractical in clinical scenarios such as FES and, therefore, we restricted ourselves to 5 samples for each muscle. Each experiment was terminated when we noticed a significant reduction in force from the majority of muscles.

III. Results

A. Model Study

Two distinct factors contribute to uncertainty in muscle force production. Model uncertainty accounts for the uncertainty in the explicitly modeled relationship between muscle commands and muscle outputs. Motor noise refers to muscle properties that are not accounted for by our model and that therefore appear as random “noise” in muscle forces. Neglecting either of these inherent uncertainties a controller eliminates the means to actively reduce them and in turn accepts potentially degraded performance. To illustrate this point, we begin by presenting results from a toy model system.

Suppose we wish to characterize the force output of a muscle whose individual properties we initially do not know. To estimate these properties we collect data pairs consisting of commands (stimulation to the muscle) and the resulting forces (Fig 1A, black dots). For each stimulation level we measure the resulting force output multiple times. Further suppose that both the average force and its variability increases with increasing stimulation levels -- a common phenomenon classified as signal-dependent noise.

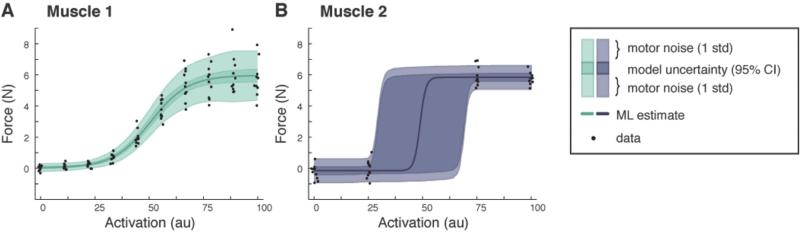
Fig. 1.

Two fundamental sources of noise in muscle force. A) Data collected for Muscle 1 is used to find a maximum likelihood estimate of the recruitment curve along with a distribution of possible forces. Note how the signal-dependent noise induces greater uncertainty with increasing activation. B) Data collected for Muscle 2 and its distribution. Due to the limited data, there is a large amount of uncertainty in the intermediate force values.

Based on the collected data we can build a statistical representation of the unknown model parameters and the overall force output (see Materials and Methods). This representation characterizes a probabilistic relationship between stimulation levels and evoked forces, whereby each stimulation induces a distribution over possible forces. With this distribution we can identify the most likely (ML) forces for each stimulation level (Fig 1A solid line); a curve that is equivalent to what we would obtain with a conventional deterministic approach (e.g. least squares regression). However, unlike the deterministic approach, we also characterize two sources of uncertainty: our uncertainty in the model and the additional uncertainty due to motor noise (dark and lightly shaded regions, respectively).

To illustrate the dependence of model uncertainty on data collection, consider what happens if we used stimulation levels that provide poor information about the recruitment curve (sampling responses around baseline and plateau portions of the recruitment curve, Fig 1B). We find that our uncertainty in both baseline and plateau force levels is relatively low and constant, while our uncertainty in intermediate force levels (and the corresponding model parameters) is high. We could ignore this uncertainty and merely rely on our ML estimates (as is conventionally done), but the forces we predict are likely to be inaccurate.

Neglecting these sources of uncertainty can lead to degraded motor control. Suppose we wish to produce a force using two new muscles, characterized by recruitment curves illustrated in Figure 2A,B. With Muscle 1, the recorded forces are very consistent at each stimulation level, and as the stimulation level increases the force output gradually climbs and then plateaus (Fig 2A, block dots). Muscle 2 produces larger forces than Muscle 1, but the recorded forces are more variable (Fig 2B, black dots), this variability increases with stimulation, and data is not available at intermediate force levels.

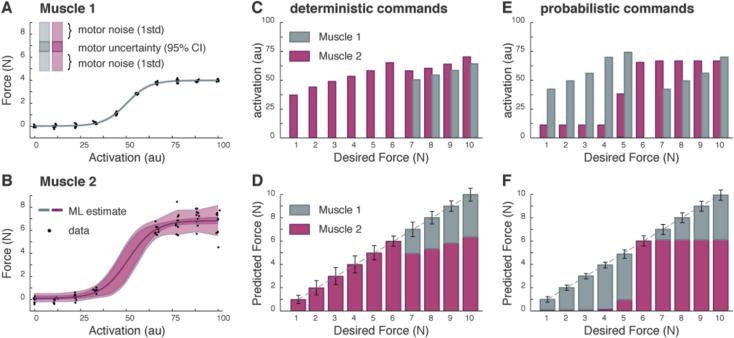
Fig. 2.

Control of two simulated muscles. In all panels, Muscle 1 is denoted in grey, Muscle 2 in magenta. A) Data collected for Muscle 1 is used to find a maximum likelihood estimate of the recruitment curve along with a distribution of possible forces. B) Data collected for Muscle 2 is used to find the same distribution, though the signal-dependent noise induces greater uncertainty. C) A deterministic controller finds commands for the two muscles that achieve desired forces while minimizing the command cost. D) Using these commands we compute the expected forces and the uncertainty associated with them. E), F) A probabilistic controller solves the same problem but uses different commands to achieve reduced uncertainty.

Consider first a deterministic controller that neglects muscle uncertainty (see Materials and Methods). The result is a set of commands that have small magnitude and produce a negligibly small average force error (i.e. a small bias force error). Since Muscle 2 produces larger forces for the same level of stimulation, it is preferentially used. Note in particular that Muscle 1 is only used when the force output of Muscle 2 has plateaued (Fig 2C, D). Although this example only considers control of force magnitude, this same approach can be used with minor variations to compute commands for multiple muscles acting in multiple dimensions.

Consider now the performance of a controller that relies on our probabilistic model of muscle force production (see Materials and Methods). Unlike the approach above, stimulations that produce uncertain forces are penalized since they decrease performance accuracy. Again the controller produces negligibly small average force errors but uses a very different pattern of commands (Fig 2E). Now Muscle 1, with its relatively small uncertainty, is preferentially used. Muscle 2, with its relatively large uncertainty at intermediate and plateau force values, is used in what is essentially “bang-bang” control: at low stimulation levels where its forces are relatively certain, or at large levels when Muscle 1 can no longer produce increasing forces (Fig 2F).

The deterministic and probabilistic treatments of our data lead to different motor commands for the same desired motor output. The deterministic controller finds commands that use little motor effort, but produces forces whose accuracy is unknown and unreliable. The probabilistic controller produces forces that are more accurate and less uncertain (Fig 2, compare error bars in D & F), but relies on a relative increase in motor effort. This toy problem illustrates how, by incorporating information about the uncertainty in motor output, a probabilistic controller can improve motor performance.

B. Experimental evaluation of a probabilistic controller

To evaluate the performance of a probabilistic controller, we utilized an FES test bed using the rat hindlimb as a model system (see Materials and Methods and [27]). We use the same approach presented above with the simulated system. First we use experimental data to build probabilistic models of individual muscles. Then we evaluate the expected performance of deterministic and probabilistic controllers side-by-side, focusing on the uncertainty in the resulting forces and the accompanying command effort. We then directly test whether these analyses improve FES controller performance by controlling forces in arbitrary directions and magnitudes in the rat hindlimb.

Just as with the simulated muscles, the experimentally measured forces were noisy and varied from one stimulation to the next. Combining data from many stimulation trials, we built a probabilistic model of each muscle, whereby arbitrary activation values evoke a planar force vector with a known orientation but a distribution of possible magnitudes (see Fig 3A). Using these models we could then compute the expected distributions of force vectors for any combination of muscle commands (Fig 3B). This force data also determined the range of possible forces for each animal; i.e. the feasible force space (FFS) describing the two-dimensional bounding region of all possible force vectors [28]. Each animal's FFS served as a workspace for eliciting forces and comparing controllers.

As with our toy model system, we compared the expected performance of the two different controllers by examining their commands and force distributions. For each animal, the controllers were used to find a set of commands (9-13 for each animal) for a grid of target force vectors covering the entire FFS (Fig 4A). These commands determined a distribution of forces, which we characterized with a mean error, or bias, and a covariance matrix, describing the spread or uncertainty in forces. Just as with the toy system, both controllers predict forces with small biases. Averaging these biases across each animal's FFS and then across animals, the mean bias for the probabilistic controller was 0.015N and that of the deterministic controller was 0.004N (a significant difference, paired t-test, p < 0.001). These biases were small relative to the range of desired forces and their expected uncertainty (see below). Thus both controllers predict accurate forces with small average errors relative to the range of force values available.

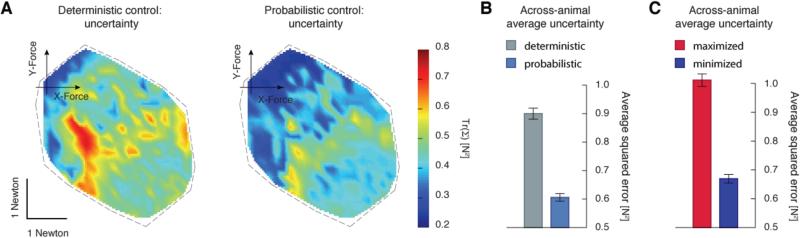
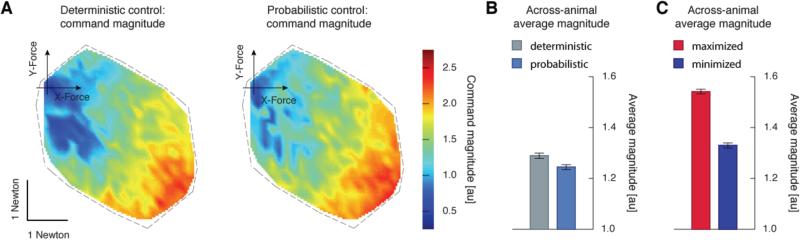
Fig. 4.

Comparison of the controller's expected force uncertainty. A) The uncertainty in force production across an example animal's FFS using deterministic and probabilistic controllers. This uncertainty is quantified via the trace of a force's covariance matrix. B) Uncertainty is averaged across each animal's FFS and then averaged across animals for the deterministic (grey) and probabilistic (light blue) controllers. C) The across-animal averages for controllers that maximize (red) and minimize (blue) uncertainty, respectively.

Since both controllers predicted accurate forces on average, our next goal was to quantify the uncertainty expected in each controller's force production; this describes how broad the spread of possible force errors were. We defined the uncertainty of a force vector by the trace of its covariance matrix. This very closely approximates the mean squared expected force error (see Materials and Methods). The uncertainty varied across the workspace of the hindlimb differently for each animal (see Fig 4A for a typical animal), likely due to details of that animal's muscles and the stimulating electrode placement. However, across most animals the uncertainty associated with small forces was relatively small (the region around the depicted axis in Fig 4A) since weak muscles, and small commands, often resulted in consistent and predictable forces. Note too that this variation in uncertainty across an animal's FFS verifies the need to treat motor noise as signal-dependent [10, 11, 29].

To compare the controllers in terms of their uncertainty, we computed the average uncertainty across the entire FFS. Across 7 animals there was a statistically significant reduction in this average uncertainty when using the probabilistic controller (0.29N², paired t-test, p < 0.001, Fig 4B). This demonstrated that the probabilistic approach, taking into account muscle uncertainties in the form of motor noise and model uncertainty, could generate more reliable forces.

We then examined whether the benefits of the probabilistic controller came at the expense of increased motor commands. For example, the probabilistic controller may have used a large number of weak but precise muscles, relying on a large net command signal to reduce uncertainty. For each force value in the FFS, the magnitude of the corresponding command was computed (Fig 5A). As might be expected, for small force values (near the axis) the commands were relatively small, and progressively increased with increasingly large forces. Interestingly, we found that the decreased uncertainty of the probabilistic controller was not the result of an increased amount of control effort. Averaging across each animal's FFS there was actually a small but significant reduction in command strength using the probabilistic controller (paired t-test, p < 0.001, Fig 5B).

Fig. 5.

Comparison of the controller's commands. A) The command magnitudes across an example animal's FFS using deterministic and probabilistic controllers. The color coding depicts the Euclidean norm of each force's command. B) Command magnitudes are averaged across each animal's FFS and then averaged across animals for the deterministic (grey) and probabilistic (light blue) controllers. C) The across-animal averages for controllers that maximize (red) and minimize (blue) uncertainty, respectively.

The fact that the probabilistic controllers used slightly lower control effort might seem counterintuitive. The deterministic controller balances two terms, the effort of a command and that command's resulting force error. Thus a small but non-zero bias error in the commanded force can be accepted if the command effort is reduced. The probabilistic controller balances not only these two terms, but also the force's uncertainty. This controller therefore accepts a relatively larger non-zero bias error if both the command effort and uncertainty in the forces are reduced; precisely what was found. However, these biases in forces were small relative to their uncertainty. For example, for the deterministic controller the across-animal average uncertainty was ~0.9 N², (see Fig 4B) suggesting that if the variance in Fx and Fy was on average 0.45 N² (assuming the x and y forces contribute equally to the uncertainty), then the 95% confidence interval for force errors is contained within a radius of 1.64 Newtons (see Materials and Methods). Yet the across-animal average bias was only 0.004 Newtons.

The specific results thus far are based on controllers that optimize a particular choice of controller gains for balancing effort and accuracy. To demonstrate that these reductions in uncertainty were not the serendipitous outcome of our specific cost function, we performed an additional analysis. We constrained the probabilistic controller to be perfectly accurate, with zero bias error in target forces, while maximizing or minimizing uncertainty (see Materials and Methods). Not surprisingly, the deterministic controller's uncertainty (and in turn mean squared expected error) was between these two extremes (Fig 4C). The command strength however, was lower than either extreme (Fig 5C). Again, as mentioned above this is an outcome of balancing biases (mean errors) in the target force with the command effort. Finding this same balance, our probabilistic controller found forces with less than the minimal uncertainty, with less command effort (Fig 4B, 5B). Regardless, these two extreme controllers demonstrated that an average reduction in uncertainty of 0.34 N² was available. This serves as further evidence that reducing muscle force uncertainty can be achieved by cleverly exploiting the redundancies of the muscles rather than relying on large activations.

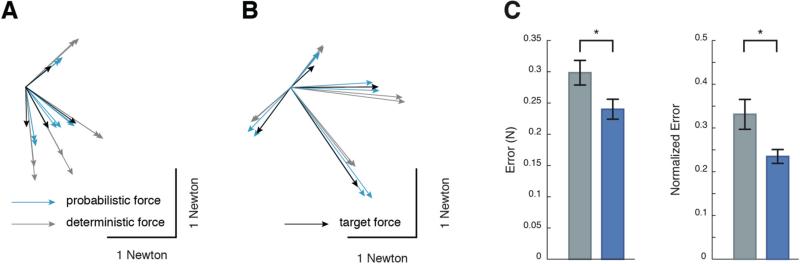
The results presented above demonstrate that a probabilistic controller is expected to produce more accurate forces than standard deterministic controllers. To test this possibility directly, we performed a series of FES experiments. For each animal a series of target forces were arbitrarily chosen throughout its FFS. The corresponding commands were then obtained from our probabilistic and deterministic controllers. For each target force, we stimulated the hindlimb muscles multiple times with each of the two controllers’ commands in a randomized order (see Fig 6A, B for examples). The forces obtained using the probabilistic commands were on average closer to the target values, both within each animal (data not shown) and across animals (Fig 6C). Across animals the average reduction in error was 0.06N (paired t-test, p < 0.001). As shown previously [27], we found that noise in forces was strongly correlated with command size. Therefore we also computed a normalized error to control for this effect, but the results were similar (Fig 6C, paired t-test, p < 0.001). The results demonstrate that a probabilistic controller that models both motor noise and model uncertainty outperforms a controller that ignores it.

Fig. 6.

Experimental validation of controllers. A), B) Example force vectors created with deterministic (grey) and probabilistic (light blue) controllers. Target force vectors are displayed in black. C) Across animal results in terms of Euclidean error (left) and normalized Euclidean error (right).

IV. Discussion

There are two categories of uncertainty in muscle force production, model uncertainty and motor noise. Ignoring either of these uncertainties can harm controller performance and is generally suboptimal. Explicitly representing both we built probabilistic models using experimentally gathered force data. A model-based comparison across each animal's feasible force space revealed the degree to which the probabilistic approach could reduce uncertainty compared with a standard deterministic controller, and that this reduction would not come at the cost of larger commands. Finally, we found that experimentally produced forces using our probabilistic controller were more accurate. The results emphasize the benefits of representing both kinds of uncertainty, information that may be crucial for artificial controllers and the nervous system to effectively produce motor commands.

Our experimental results in force production constitute a proof of concept for FES systems. In contrast with our approach, many recent FES studies use deterministic controllers and rely heavily on feedback commands to achieve good performance [30-32]. Some FES studies attempt to improve performance by incorporating knowledge about motor noise and designing robust or adaptive controllers [33-36]. Still others have attempted to optimize stimulation parameters for improved performance [37]. However, with a fully probabilistic treatment that characterizes motor noise and model uncertainty a controller can achieve its maximum potential. Our approach has characterized this potential mathematically and validated it experimentally in the context of an application that approximates the relevant clinical problem.

Analyzing muscles in terms of the uncertainty they produce in forces, and ultimately behaviors, is potentially a valuable new tool. For example, recent studies examining the contribution of muscles to behavior rank muscles in terms of their robustness, defined by how their absence would reduce the limb's possible forces, and the feasible force space [2, 38]. Other factors such as the metabolic cost of individual muscles should also play a factor in recruitment. Our work complements these studies by providing a new functional measure for quantifying muscles contributions to behavior in terms of the resulting uncertainty. Future work could pursue this topic further, illuminating how muscle uncertainty may influence their recruitment.

In this study we focused on how to optimally generate commands when relying only on a model; that is, how to compute feedforward commands. Of course information about on-going performance, i.e. feedback information, can be used to improve commands. Many studies on motor behavior search for the relative contributions and importance of feedforward and feedback commands [39, 40]. For example, an important question is how accurate the motor system is in the absence of feedback [41, 42] and how accurately behaviors can be planned [34, 43, 44]. In this regard the analysis we present here defines the upper bounds on motor performance when the nervous system relies on strictly feedforward commands, and how important feedback control must be when further increases in performance are needed.

A related matter is whether the performance benefits of this approach warrant the increased computational demands. For example, in our experimental comparison of FES controllers we found a modest reduction in error as compared to the analyses illustrated in Figures 4 and 5. Those analyses used data pooled over multiple sessions of recruitment curve measurements. Owing to the fact that recruitment curves varied over time, this data set predicted relatively large variability in muscle responses and there was a correspondingly large benefit to using the probabilistic controller. In the experimental control evaluation, however, we used the most recent recruitment curve for each muscle, so that the muscle responses produced during control more closely matched the predicted responses. Thus in situations where recruitment curves can be measured quickly and frequently relative to how quickly recruitment curves vary, this probabilistic approach may not offer significant improvements.

As a first step, we have examined a controller for generating isometric forces; an obvious FES application where motor uncertainty can play a key role. This approach, by design, bypassed the muscle's dynamical properties and the inertial mechanics of the limb. To examine more sophisticated controllers, for either clinical applications or neuroscience, future work could include additional independent variables (e.g., initial limb configuration, muscle length and velocity) to describe the muscle force distributions. Additionally, while we choose to penalize command strength and target force error, alternative tasks or controller designs might require altogether different objectives to be optimized. All these changes, though computationally intensive, are conceptually equivalent to the approach we have presented here.

Finally, it is worth noting that there are many hurdles that must be overcome before making the transition from a successful FES application in a rat model, to a human clinical population. As with the many other studies that examine FES our hope is that the continued work on animal models, along with new preliminary work in humans [45] will ultimately justify these new approaches in patients.

V. Conclusion

We have demonstrated the theoretical benefits of representing muscle uncertainty when computing muscle commands. These benefits were then verified experimentally in an FES application. We propose that the nervous system, when producing commands, may solve the same fundamental problem: how to build probabilistic representations of muscle output and choose commands that maximize the probability of a successful outcome. Future studies can examine the extent to which this uncertainty is represented and how it is used when producing commands. How this information is encoded may be found via imaging techniques [46], electrophysiology [47] or perhaps in the muscle commands themselves. Regardless, if the nervous system is acting rationally [48] these uncertainties will influence its behavior.