Impacts and shortcomings of genetic clustering methods for infectious disease outbreaks

Abstract

For infectious diseases, a genetic cluster is a group of closely related infections that is usually interpreted as representing a recent outbreak of transmission. Genetic clustering methods are becoming increasingly popular for molecular epidemiology, especially in the context of HIV where there is now considerable interest in applying these methods to prioritize groups for public health resources such as pre-exposure prophylaxis. To date, genetic clustering has generally been performed with ad hoc algorithms, only some of which have since been encoded and distributed as free software. These algorithms have seldom been validated on simulated data where clusters are known, and their interpretation and similarities are not transparent to users outside of the field. Here, I provide a brief overview on the development and inter-relationships of genetic clustering methods, and an evaluation of six methods on data simulated under an epidemic model in a risk-structured population. The simulation analysis demonstrates that the majority of clustering methods are systematically biased to detect variation in sampling rates among subpopulations, not variation in transmission rates. I discuss these results in the context of previous work and the implications for public health applications of genetic clustering.

1. Introduction

Whether or not we intend to, we are naturally inclined to perceive patterns in everything we encounter. A major aspect of recognizing patterns is clustering, the act of assigning objects into groups so that objects in the same group are more similar than objects in different groups. A clustering method or algorithm codifies this process into a set of rules that confers transparency and reproducibility (Everitt et al. 2011); even so, clustering remains an inherently subjective process. Nevertheless, clustering methods play an important role in studying the extensive genetic diversity that accumulates in viruses (Foxman and Riley 2001; Van Regenmortel 2007).

Genetic clustering methods operate on variation that is typically measured by nucleotide sequencing or nucleic acid profiling of conspicuous genetic features, such as restriction fragment length polymorphisms (RFLPs). Historically, genetic clustering has often been used to partition the sequence diversity of a virus into clades or subtypes, so that different investigators can refer to similar variants using a common nomenclature (Van Regenmortel 2007). For example, Simmonds et al. (1993) proposed an early nomenclature system for hepatitis C virus based on a genetic clustering analysis of the nucleotide sequence variation in the NS5B gene. More recently, there has been a surge of interest in the use of genetic clustering to identify and characterize localized outbreaks of an infectious disease. By detecting subpopulations exposed to high rates of transmission, clustering may potentially facilitate a more impactful and cost-effective deployment of public health resources (Little et al. 2014; Novitsky et al. 2015; Poon et al. 2016), such as point-of-care testing or pre-exposure prophylaxis (Pillay et al. 2015). There are now many different genetic clustering methods that have been developed for this purpose, predominantly in the field of HIV (e.g. Balfe et al. 1990; Yerly et al. 2001; Hué et al. 2004). Furthermore, software implementations for several of these methods have since been released into the public domain (Prosperi et al. 2011; Ragonnet-Cronin et al. 2013; Vrbik et al. 2015). However, these methods have seldom been validated on simulated data where actual clusters are known (but see Villandre et al. 2016), and few studies have evaluated different clustering methods on the same empirical datasets.

In this article, I will first briefly review the evolution of genetic clustering methods in the context of infectious diseases, and show how different categories of clustering methods are related. Next, I will apply six genetic clustering methods to trees and sequence alignments simulated under a compartmental epidemic model. This model is designed to mimic the spread of an infectious disease through a structured population, which allows one to evaluate the ability of different clustering methods to capture heterogeneity in rates of transmission and sampling. The principal result of this simulation analysis is that most methods are systematically biased to detect subpopulations with higher rates of sampling, for example, becoming diagnosed following infection. However, the majority of methods are less effective, and in some cases incapable, of detecting differences among subpopulations in rates of transmission. Finally, I discuss the implications of this finding for the utility of clustering for public health.

2. Genetic Clustering

A cluster of genetically similar infections may represent an outbreak related through a succession of recent transmission events (Brenner et al. 2007; Fisher et al. 2010; Volz et al. 2012). Furthermore, clusters can be used to characterize the structure of an epidemic driven by repeated introductions (Hué et al. 2005). Using genetic data instead of phenotypic assays provides a faster and potentially cost-effective means to detect outbreaks from what might otherwise appear to be a number of unrelated cases, to determine risk factors associated with recent transmissions, and to track the spread of clinically significant variants (Foxman and Riley 2001). One of the earliest examples of genetic clustering to detect an outbreak of infectious disease was the use of RFLPs to characterize isolates from a nosocomial outbreak of herpes simplex virus type 1 (HSV-1) in a pediatric intensive care unit in 1978 (Buchman et al. 1978). Based on these data, the investigators were able to distinguish between the cases in the outbreak from control samples, and to extrapolate that there had been two separate introductions of HSV-1 into the unit. Similar “genetic fingerprinting” methods have also been used extensively to characterize outbreaks of Mycobacterium tuberculosis (e.g. Daley et al. 1992). One of the first uses of nucleotide sequences for genetic clustering was a study of a common source outbreak of HIV infection among hemophiliacs who had received transfusions from a contaminated batch of a blood clotting factor (Balfe et al. 1990). Six out of eight hemophiliacs who had been exposed to this source comprised a cluster of closely related HIV nucleotide sequences with short pairwise genetic distances between subjects. The use of genetic clustering to characterize regional epidemics of HIV has since come to predominate this field. Consequently, most of the clustering methods referenced in this article were originally developed for the study of HIV and may not be directly translatable to other viruses and infectious diseases, where the extent of sampling and levels of genetic diversity vary substantially; I will expand on this issue in Section 4.

To date, every genetic clustering method that has been applied to virus sequences has been nonparametric, in that clusters are defined on the basis of criteria that are not informed by a model. Instead, these decisions are based on the genetic or evolutionary distances between the sequences. However, the specific criteria used to derive clusters from this information tend to vary from one study to the next (Grabowski and Redd 2014). Figure 1 displays a dendrogram generated from a hierarchical clustering analysis of a binary character state matrix for nine categories of nonparametric clustering methods (Supplementary Table S1). This dendrogram indicates that nonparametric methods can be split into two broad categories: methods that cluster directly on sequence variation via pairwise distance measures, and methods that interpret this variation in the context of subtrees in a phylogeny.

Figure 1.

A hierarchical clustering dendrogram of nonparametric genetic clustering methods. This dendrogram was generated from a binary character state matrix that encodes ten different features for nine categories of nonparametric methods. Internal nodes of the dendrogram are labeled with features that distinguish the categories below the node. Each category is annotated with a small number of citations to publications that either describe the method or provide examples of its usage; these are not meant to be exhaustive lists.

2.1. Distance-Based Methods

A genetic distance is a function that maps two genetic sequences to a non-negative number that roughly corresponds to the extent they have diverged from a common ancestor (Nei and Kumar 2000). A key advantage of genetic distances is that they can be computed rapidly. For some basic models of molecular evolution, the corresponding distance can be computed exactly using a finite number of mathematical operations; in other words, the distance exists as a closed form expression. Pairwise genetic distances have played an important role in the development of virus nomenclature systems (Simmonds et al. 1993; Van Regenmortel 2007) and early applications of clustering to infectious disease outbreaks (Balfe et al. 1990). Clusters can be obtained from the pairwise distance matrix by specifying a cutoff distance below which individuals are assigned to the same cluster (Aldous et al. 2012). Under this criterion, one assumes that individuals within a cluster are related through one or more recent transmission events, such that there has been limited time for their respective virus populations to diverge in sequence from their common ancestors. More sophisticated clustering algorithms that operate on pairwise genetic distances have since been proposed by Prosperi et al. (2010) and Vrbik et al. (2015, Gap Procedure; see below).

A distance between pairs of sequences can also be derived from a phylogenetic tree that represents how the sequences are related by their common ancestors. Each tip of the tree corresponds to an observed sequence, and each branch represents the descent of the respective lineage from an ancestor it shares with another lineage. If the phylogeny is reconstructed by maximum likelihood for a given substitution model, then the branch lengths are measured in the expected number of substitutions (evolutionary distance; Felsenstein 1981). Without additional information, it is not possible to express branch lengths in units of real time. The length of path from one tip of the tree to another is known as the patristic distance (Farris 1967). Similar to pairwise genetic distances, clusters can be assembled from pairs of sequences whose patristic distance is below a cutoff value (Pommier et al. 2009; Poon et al. 2015). Although the joint reconstruction of branch lengths in the tree by maximum likelihood is a more computationally demanding task, it also utilizes more of the information content of the sequence alignment. For instance, genetic distances are unable to differentiate between rapidly and slowly evolving sites in a pairwise comparison of sequences, which can cause this approach to underestimate their divergence time (Gillespie 1986). However, it may be sufficient for the purpose of clustering that the genetic distances are significantly correlated with the underlying evolutionary distances (Wertheim et al. 2014).

2.2. Subtree-Based Methods

Distance-based methods assemble clusters from pairwise comparisons of sequences without consideration for how these sequences related through common ancestors. For instance, one may want to include a sequence in a cluster despite its genetic or patristic distance from the others because it shares a recent common ancestor. These relationships can be evaluated by examining the subtrees of a phylogeny. A subtree is a portion of the tree that contains all descendants of a given ancestor that is represented by an internal node of the tree. Clusters have been defined on the basis of the characteristics of individuals represented by the tips of a particular subtree, such as the country of sample collection. For example, Hué et al. (2005) identified clusters in an HIV-1 pol phylogeny from subtrees relating over twenty-five sequences, of which at least 90% were collected in the UK. In general, clusters generated by this approach have been based on geographical labels, but labels can potentially be clustered on other characteristics such as risk factors or demographic groups. As a result, I propose to refer to this approach as label-based subtree clustering (Fig. 1).

The bootstrap support value is another criterion for classifying subtrees as clusters (Yerly et al. 2001; Hué et al. 2004). One of the earliest examples of using bootstrap support to define clusters was published by Yerly et al. (2001), who used this method to identify clusters of HIV-infected individuals that they subsequently compared with documented epidemiological linkages. Bootstrapping refers to the non-parametric technique of randomly resampling new datasets from the original dataset; thus, “pulling oneself up by one’s bootstraps”. It is used when it is not feasible to estimate the confidence interval by collecting a large number of true replicates. The application of bootstrapping to assess confidence in phylogenies was first proposed by Felsenstein (1985). Trees are generated from replicate alignments with the same dimensions as the original alignment by sampling columns from the latter at random with replacement (such that the same column may be sampled more than once). The support value of an internal node is the proportion of replicate trees that contain an internal node ancestral to a particular group of sequences to the exclusion of all others, that is, a monophyletic group. Note that the node support value does not correspond to any particular subtree out of all possible subtrees relating sequences in the group. There is no guarantee that the true tree is represented in the bootstrap set. Hence, one’s confidence in the monophyletic group is specific to the dataset and method of phylogenetic reconstruction (Hillis and Bull 1993).

Nonparametric bootstrapping scales linearly with the number of replicates. Since a phylogeny needs to be reconstructed for each replicate, it can become too computationally demanding to perform bootstrapping when the original dataset is large. Consequently, studies employing this clustering method (e.g. Yerly et al. 2001; Hué et al. 2004) have tended to use faster distance-based methods for phylogenetic reconstruction, such as neighbor-joining (Saitou and Nei 1987). In addition, several groups have developed methods to approximate support values in the framework of maximum likelihood phylogenetic reconstruction (Hasegawa and Kishino 1994). Thus, in cases where bootstrap support is used as a clustering criterion, it is important for the authors to specify which method was used to generate the support values.

Node support values have also been used to filter subtrees for further evaluation on the basis of pairwise distances or branch lengths within each subtree. One of the earliest examples of this “bootstrap and branch lengths” approach was implemented by Hué et al. (2004), who extracted clusters from a neighbor-joining tree constructed from HKY85 distances among HIV-1 pol sequences, given a support value exceeding 99% and a mean branch length within the subtree below 0.015. A large number of genetic clustering studies have employed a similar approach with variations on the evaluation of the composition of subtrees with high node support values. For example, the software Cluster Picker calculates the maximum pairwise genetic distance between sequences within a subtree (Ragonnet-Cronin et al. 2013). Alternatively, the patristic distances can be used to evaluate subtrees with high support values (Prosperi et al. 2011).

A side effect of subtree-based clustering methods is that the cluster must include every sequence in the subtree; for instance, one cannot exclude a descendant sequence that is highly divergent from the others. In addition, subtree-based methods do not provide a representation scheme for the individual-level structure of a cluster (Wertheim et al. 2014).

3. Evaluation of Clustering Methods

3.1. Methods

I used MASTER 5.0.0 (Vaughan and Drummond 2013) for the forward-time simulation of transmission trees under a structured susceptible-infected-removed (SIR) model in which the susceptible and infected populations were partitioned into two subpopulations indexed by i. Epidemics were seeded by a single individual in the majority subpopulation (i = 0), such that the initial population sizes were $S_0=8999,S_1=1000,I_0=1$ and $I_1=0$. Transmission dynamics were described by the following system of ordinary differential equations:

$$\begin{array}{c}\frac{d{S}_0}{dt}=-{\beta }_0{S}_0{I}_0+m(S_1-S_0)\\ \frac{d{S}_1}{dt}=-{\beta }_1{S}_1{I}_1+m(S_0-S_1),\end{array}$$

$$\begin{array}{c}\frac{d{I}_0}{dt}={\beta }_0{S}_0{I}_0+m(I_1-I_0)-(\mu +\psi )I_0\\ \frac{d{I}_1}{dt}={\beta }_1{S}_1{I}_1+m(I_0-I_1)-(\mu +\psi )I_1,\end{array}$$

$$\frac{d{I}_0^{*}}{dt}={\psi }_0{I}_0\frac{d{I}_1^{*}}{dt}={\psi }_1{I}_1,$$

where $I_i^{*}$ are infected individuals in the i^th subpopulation who have been sampled at a constant rate ψ_i, m is the migration rate between subpopulations, μ is the mortality rate of infected individuals, and β_i is the transmission rate in the i^th subpopulation. Note that transmission occurs exclusively between individuals in the same subpopulation. This model assumes that sampled infections are not transmissible to susceptible individuals; hence, individuals are removed by either mortality or sampling.

I generated ten replicate trees under four different scenarios to evaluate the impacts of transmission and sampling rates on clustering: (1) control, ${\beta }_1=0.045,\hspace{0.17em}{\psi }_1=0.5$; (2) faster sampling, ${\beta }_1=0.045,\hspace{0.17em}{\psi }_1=2.5$; (3) faster transmission, ${\beta }_1=0.135,\hspace{0.17em}{\psi }_1=0.5$; (4) both faster, ${\beta }_1=0.135,\hspace{0.17em}{\psi }_1=2.5$. All other parameters were held constant as follows: m = 0.05, $\mu =0.01,\hspace{0.17em}{\beta }_0=0.005$, and ${\psi }_0=0.5$. Note that β₁ was always rescaled by a factor of nine to compensate for the smaller size of the minority subpopulation. One of the shortcomings of compartmental models is that an individual is equally likely to transmit to any susceptible member of their subpopulation, and the transmission rate is cumulative with this number. As a result, setting ${\beta }_1={\beta }_0$ resulted in significantly longer internal branches in the subtrees of the phylogeny mapping to the minority subpopulation. Each simulation terminated once 1000 infections had been sampled from either subpopulation.

Given limited migration between subpopulations, we expect that subtrees will be “compartmentalized” by subpopulation such that adjacent branches will tend to represent infections sampled from the same subpopulation. By chance, trees may contain shapes that are recognized as clusters. We expect clusters to be associated with the minority subpopulation in the presence of substantial variation in model rates among subpopulations. If the transmission rate in the minority subpopulation (β₁) is substantially higher than the majority, then less time elapses between transmission events in that subpopulation and the internal branch lengths should be shorter in the respective subtrees. Similarly, if the sampling rate in the minority subpopulation (ψ₁) is substantially higher, then less time elapses between a transmission event and sampling of the descendant lineage and the terminal branch lengths should be shorter.

To confirm that the model parameters had the expected effect on tree shapes, I plotted the average lengths of internal and terminal branches for replicate trees under the different scenarios. Increasing β₁ (“faster transmission”) resulted in markedly shorter internal branch lengths in lineages sampled from the minority subpopulation (Fig. 2A). Similarly, increasing ψ₁ (“faster sampling”) resulted in significantly shorter terminal branch lengths in the minority subpopulation. Further, I manually examined the simulated trees to confirm that clusters associated with the minority subpopulation were visually recognizable to the casual observer when β₁ and ψ₁ were both increased (Fig. 2B).

Figure 2.

Forward simulation of trees from SIR model. Branch lengths are in units of the simulation processes. (A) Distribution of mean internal and terminal branch lengths from the two subpopulations under four different transmission and sampling scenarios. Upper and lower case symbols correspond to the majority and minority subpopulations, respectively, where the latter has the potential to form clusters in the tree. Lower numbers of sampled lineages from minority subpopulations under “control” and faster “transmission” scenarios resulted in greater dispersion in estimates of mean branch lengths. (B) An example tree simulated under a scenario where both transmission and sampling rates are elevated in the minority subpopulation (cyan).

Next, I simulated multiple sequence alignments along each tree using INDELIBLE version 1.03 (Fletcher and Yang 2009). Each simulation was seeded with a sequence of 1197 bases spanning the region of HIV-1 pol gene from the reference variant HXB2 (GenBank accession number K03455) encoding protease and the first 300 codons of reverse transcriptase. Variation in the nonsynonymous/synonymous rate ratio (ω) across sites was modeled by a gamma distribution with shape parameter $\alpha =1.5$ and rate parameter β = 3, discretized into fifty classes at regular intervals along ω. The transition bias parameter was set to $\kappa =8.0$. Input trees were rescaled such that the pairwise Tamura-Nei distances had a mean and interquartile range that was similar to those observed between baseline HIV-1 subtype B pol sequences from different individuals in the British Columbia Drug Treatment Database (0.055, IQR 0.047–0.062; Poon et al. 2015).

Phylogenies were reconstructed from these alignments by approximate maximum likelihood using FastTree2 version 2.1.9 with double precision (Price et al. 2010) or by neighbor-joining using MEGA version 7.0.15 (Kumar et al. 2016). Bootstrap support values at internal nodes were approximated by the implementation of the (SH; Shimodaira and Hasegawa 1999) test in FastTree2, or by nonparametric sampling with 1000 replicates in MEGA for neighbor-joining trees.

I evaluated a number of clustering methods on these simulations, by generating the true and false positive rates under varying settings, as follows:

• Tamura-Nei (TN93) pairwise genetic distance: TN93 distances were calculated using an open source implementation in C ++  (http://github.com/spond/TN93, commit number 284f093), which is also used by the clustering software HIV-TRACE for defining clusters based on pairs of individuals whose distance falls below a user-defined cutoff (Wertheim et al. 2014). In this evaluation, any sequence with at least one pairwise distance below the cutoff was classified as being clustered.

• Patristic distance: A patristic distance is the sum of branch lengths on the path from one tip to another in the tree (Farris 1967). The use of patristic distances for genetic clustering is essentially an extension of clustering by pairwise genetic distances (Pommier et al. 2009; Poon et al. 2015). I extracted patristic distances extracted from 100 replicate trees reconstructed from bootstrap alignments using FastTree2. A Python script for rapidly extracting these distances from a tree is publicly available at http://git.io/vrcmz. A sequence was classified as clustered if its shortest patristic distance to another sequence was below the cutoff in 80% or more of the bootstrap trees. This is the same clustering method being used for near real-time monitoring of HIV hotspots in British Columbia, Canada (Poon et al. 2016).

• Gap Procedure: This program partitions sequences based on the largest gaps between adjacent pairwise genetic distances in a sorted vector for the ith sequence: $\max \left\{{\delta }_{i,j}\right\}$ where the range of j is truncated to omit the n largest gaps as outliers (Vrbik et al. 2015). Each simulated alignment was used as the input matrix for the GapProcedure function in R, which was computed using its default implementation of the Kimura 2-parameter model (“aK80”) and an outlier adjustment value of 0.9. Sequences uniquely assigned to singleton clusters by the GapProcedure function were classified as not clustered.

• Bootstrap and branch-lengths: This method emulates the approach taken by Hué et al. (2004) where subtrees in a neighbor-joining tree were classified as clusters if the support value exceeded a cutoff, and the mean branch length within the cluster was below a second cutoff distance. All sequences within subtrees meeting both criteria were classified as clustered.

• Cluster Picker: This program performs a depth-first search of the tree starting at the root (Ragonnet-Cronin et al. 2013). For this evaluation, I used version 1.2.4 of the program. For each subtree with a support value that exceeds a user-defined cutoff, it computes the maximum pairwise genetic distance within the subtree; if this distance is below the second user-defined cutoff, then the subtree is classified as a cluster. An alignment and its corresponding tree, reconstructed by FastTree2 with support values based on the SH test, were used as inputs for this program. Following the author recommendations, the initial threshold was set to the same value. Sequences assigned a cluster number greater than −1 in the “clusterPicks_list.txt” output were classified as clustered.

• PhyloPart: Similar to Cluster Picker, PhyloPart performs a depth-first search of the tree starting at the root to evaluate subtrees with a support value exceeding a fixed cutoff of 0.9 (Prosperi et al. 2011). The program computes the distribution of patristic distances for the entire tree. Next, it evaluates the patristic distances within a given subtree and classifies the subtree as a cluster if the median falls below a user-defined percentile threshold in the full distribution. Based on the initial application of this program by the authors, I used trees generated by FastTree2 with SH test-based support values. For this evaluation, I used the original version of the program associated with Prosperi et al. (2011). Although a second version has since been released, the batch command-line functionality appears to have been disabled in the newer version. Sequences assigned a cluster number greater than 0 in the output were classified as clustered.

Each method was evaluated by their assignment of individual sequences into clusters of two or more. Sequences assigned to clusters were counted as “true positives” if they were sampled from the minority subpopulation, and “false positives” otherwise. Sequences that were not assigned to clusters were counted as “true negatives” if they were sampled from the majority subpopulation, and “false negatives” otherwise.

3.2. Results

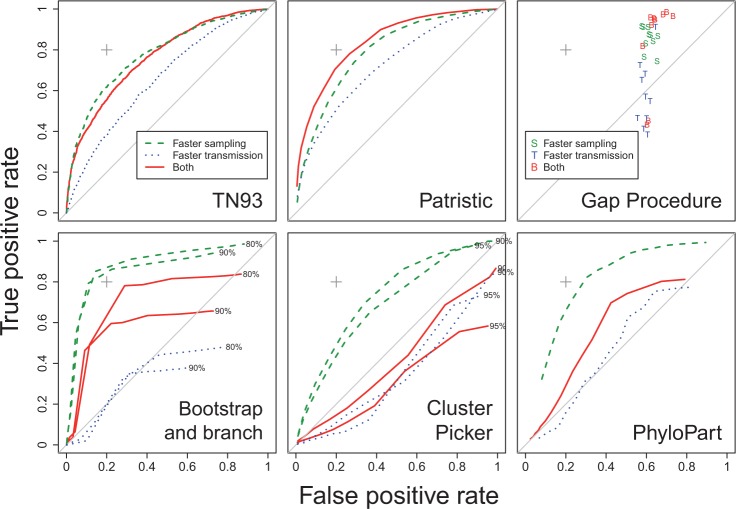
Results from this simulation analysis are summarized in Figure 3. Each receiver operator characteristic curve illustrates the trade-off between the true and false positive rates (TPR and FPR) in classifying individuals into the minority and majority subpopulations. These rates varied in response to varying the threshold on a continuous parameter; in most cases, this parameter was a genetic distance measure. Similar results were obtained for both pairwise distance methods (TN93 and patristic distances). The patristic method achieved a slightly higher TPR than TN93 owing to the additional robustness conferred by evaluating replicate patristic distance estimates across 100 bootstrap trees. For example, given a 20% FPR, TN93 obtained a 55% TPR whereas the patristic method obtained 71% under the “both faster” scenario. Both pairwise methods were comparably robust to varying simulation scenarios. Moreover, patristic distance was the only method overall that was more sensitive to the combination of both faster rates of sampling and transmission.

Figure 3.

Receiver operator characteristic (ROC) curves summarizing the performance of six clustering methods on simulated data. An ideal method would reach the extreme upper-left of a plot region, with a zero false positive rate (FPR) and 100% true positive rate (TPR). The FPR = TPR line indicates the expected performance of a random classifier. A reference point (cross) at FPR = 20% and TPR = 80% is drawn in each plot to facilitate comparisons across methods. The methods were evaluated on ten replicate phylogenies generated under three scenarios in which the minority population exhibited: faster sampling rates (dashed, green); faster transmission rates (dotted, blue); or both (solid, red). For methods that use bootstrap support values, ROC curves are displayed for two different support cutoffs (labeled by percentiles to the right of each curve). Results obtained using Cluster Picker with a bootstrap support cutoff of 99% were not qualitatively different from the results under a cutoff of 95%. There was no tuning parameter used for the Gap Procedure method, so the results for each replicate tree were plotted directly on the graph.

Results obtained by Gap Procedure under the “both faster” scenario were similar to those obtained under “faster sampling”, indicating a lack of sensitivity to faster transmission rates. This method did not have a continuous parameter to vary with useful effect; for example, the same results were obtained under a broad range of outlier cutoff values. In all cases, this method suffered from a high FPR (about 60%). Under the “faster transmission” scenario, the method did not perform measurably better than a random classifier.

The “bootstrap and branch length” clustering method using neighbor-joining trees obtained the best performance for simulations under the “faster sampling” scenario. However, this performance was highly sensitive to the threshold value used for the mean branch length within subtrees. The best results under this scenario with a 80% bootstrap support cutoff, for example, were obtained with a branch length cutoff of 0.007 (TPR 78%, FPR 29%) but the FPR rose to 52% when this cutoff was increased to 0.008; similarly, the TPR fell to 50% when the cutoff was decreased to 0.006. This sensitivity may be a side-effect of defining clusters at the level of subtrees rather than pairs of individuals, resulting in “all-or-nothing” outcomes. This method did not perform as well in the presence of faster transmission in the minority subpopulation, and was as bad as random in the absence of variation in sampling rates.

Cluster Picker and PhyloPart yielded mutually similar results; for instance, both methods performed poorly with variation in transmission rates. This result is surprising because both methods use criteria similar to the “bootstrap and branch length” method. I verified that this difference was not due to the use of maximum likelihood versus neighbor-joining trees (Supplementary Fig. S1). Cluster Picker computes the maximum pairwise genetic distance separating sequences in a subtree with strong support. It is possible that its poor performance is due to the inherent stochasticity in using the maximum branch length as opposed to a measure of central tendency. On the other hand, PhyloPart compares the median patristic distance within well-supported subtrees to an empirical distribution from the entire tree. The best results were obtained when subtrees with medians below the 1st percentile of this distribution were classified as clusters. Given the size of the trees used in this study, there should have been an adequate number of pairwise comparisons to obtain a reliable estimate of this percentile threshold.

Despite no variation in transmission or sampling rates under the “control” scenario, all six clustering methods detected a residual association between clusters and the minority subpopulation (Supplementary Fig. S2). This result implies that population structure in the simulations contributed to the formation of clusters in resulting trees. Next, I evaluated the extent that these methods identified clusters in the absence of any variation among individuals (unstructured populations). I compared the proportion of sequences assigned to clusters across treatments by summing true and false positive rates. The “bootstrap and branch” and Gap Procedure methods demonstrated the greatest separation in these outcomes, with a strong tendency for fewer sequences from unstructured populations to be clustered (Supplementary Fig. S3). The TN93 and patristic methods exhibited a similar trend with less separation between the control and unstructured scenarios, whereas Cluster Picker and PhyloPart could only differentiate the “fast sampling” from other scenarios.

4. Discussion

When a study employs a genetic clustering method to characterize outbreaks of an infectious disease, there is an implicit assumption that the resulting clusters represent actual subpopulations affected by high transmission rates. The alarming overall result of this simulation study is that the majority of clustering methods evaluated here were unable to detect heterogeneity among the subpopulations in rates of transmission. When applied to simulations where both transmission and sampling rates were elevated in the minority subpopulation, the methods performed no better—in some cases, substantially worse—than on simulations where only sampling rates were elevated (Fig. 3). In other words, faster transmission rates in the minority subpopulation had little impact on the rate that sequences from this subpopulation were assigned to clusters. This overall result is consistent with previous work. For example, Volz et al. (2012) used a mathematical model to determine that excess clustering of acute infections (quantified by the times to their most recent common ancestors) was more likely to be caused by the relative recency of sampling than by an elevated transmission rate at this stage of infection. Villandre et al. (2016) also recently published a similar simulation-based evaluation of genetic clustering methods. To generate transmission trees, they simulated epidemics that percolated over the nodes of an “interconnected islands” contact network, which provided an explicit graphical representation of clusters. As a result, their study emphasized the effect of contact network structures on variation in transmission rates. The simulated trees presented in Villandre et al. (2016) do not exhibit the features that would generally be recognized as genetic clusters. Long terminal branches in these trees imply a low rate of lineage removal by sampling, although this rate was not reported. A low sampling rate may have been necessary for the epidemic to spread to the entire network; for instance, to prevent sampling from prematurely terminating the spread of lineages between islands.

Taken together, these results highlight a critical ambiguity in how genetic clusters are interpreted. To reiterate, a genetic cluster is generally a group of sequences that are more similar to each other than to the other sequences in the data set. In the context of a phylogenetic tree, similar sequences may be related by short internal branches that imply a cluster of transmission events, or short terminal branches that imply a cluster of sampling soon after transmission, or both. The approach taken by Villandre et al. (2016) focused on clusters of transmission irrespective of whether the observed sequences remained genetically similar by the time they were sampled. Our results indicate that most genetic clustering methods are systematically biased to detect variation among subpopulation in sampling rates, that is, the waiting time until diagnosis of a new HIV infection. In other words, genetic clusters will tend to collect individuals sampled soon after infection, irrespective of (in some cases, in spite of) whether those infections resulted from higher rates of transmission. This is at odds with the conventional interpretation of a genetic cluster has representing a group of infections related by a rapid succession of transmission events (Volz et al. 2012), which is reflected by the widespread use of the term “transmission cluster” (e.g. Leitner et al. 1996; Hué et al. 2004; Wertheim et al. 2014). This discrepancy has significant implications for the public health interpretation of clusters as potential foci for prevention services. By focusing our attention on subpopulations indicated by certain genetic clustering methods, we may be diverting public health resources towards those who are already highly engaged in accessing primary care, and thereby diagnosed earlier in infection, and away from the subpopulations with less access to primary care who are also burdened by higher rates of transmission.

There are several limitations with this simulation study that need to be recognized while interpreting its results. First, it is unlikely that the structured SIR model yielded trees that are highly representative of a typical HIV phylogeny. This model assumes that individuals are unable to transmit once they have been sampled from the population (Kühnert et al. 2014). It also assumes that individuals are sampled at a uniform rate with respect to the time since infection. In real scenarios, the waiting time to diagnosis of a new infection is unlikely to be exponentially distributed. At the level of the population, sampling rates tend to increase over time as resources for routine genotyping become increasingly available. Second, the structured SIR model was not parameterized using empirical data, which would have required fitting the model to an observed phylogeny in which the partition of the sample population into clusters was known without ambiguity. Simulation of sequence evolution along the trees, on the other hand, was informed by empirical data. Third, this model was used to generate transmission trees, which are not equivalent to phylogenetic trees that would be reconstructed from real data. Unlike the transmission tree, splits in a phylogenetic tree do not correspond to transmission events; the discordance between these splits can be exacerbated by incomplete lineage sorting within hosts (Romero-Severson et al. 2014). In addition, the branch length distribution in the simulated trees does not incorporate the well-documented reduced rate of evolution among hosts (Alizon and Fraser 2013), which may be caused by the preferential transmission of early variants (Vrancken et al. 2014). Since the objective of this study was to validate a comprehensive set of clustering methods on known clusters, I put forward that it was sufficient for the simulated tree shapes to be a rough approximation of virus phylogenies; it is more important that the trees clearly articulate differences between subpopulations that should be detected by clustering methods.

The limitations of clustering methods identified by the present study and previous work do not preclude their application to public health. First, the pairwise distance methods evaluated here (TN93 and patristic) did yield clusters that were informative about variation in transmission rates. Second, the fixed 3-fold increase in the rate of transmission within the simulated minority populations may be modest relative to the magnitude of rate change that may arise in priority subpopulations for a public health response. There are also new areas of research that may significantly improve the utility of genetic clusters for public health. Nearly all uses of genetic clustering to infectious diseases have occurred in the context of retrospective studies, in which clusters are identified at a fixed point in time and seldom revisited in subsequent studies. In settings where there is widespread access to routine HIV genotyping, however, it is possible to prospectively track the appearance of new infections in clusters in real time (Little et al. 2014; Poon et al. 2016). Regardless of the inherent biases of genetic clustering methods, observing a rapid succession of new infections in a predefined cluster may represent an important source of evidence of a localized outbreak. In addition, new methods are constantly being developed in the area of phylodynamics, the study of the relationship between the epidemiology of an infectious disease and the shape of its phylogeny (Volz et al. 2013)—genetic clustering is essentially a simple non-parametric phylodynamic method. For example, the recent development of methods to fit structured epidemic models to phylogenies (Stadler and Bonhoeffer 2013; Rasmussen et al. 2014; Poon 2015) represents an emerging opportunity to develop parametric or “model-based” methods for genetic clustering. Within such frameworks, clusters could be identified by mapping discrete state transitions to branches of the phylogeny.

The use of genetic clustering for identifying outbreaks has focused primarily on HIV. Can these methods be used for other infectious diseases? A key prerequisite for the effective use of clustering is that measurable sequence evolution has occurred on the time scale of transmission. Although this criterion could potentially exclude bacterial pathogens from consideration, advances in whole-genome sequencing can compensate for the relatively lower substitution rates per site (e.g. Harris et al. 2013; Walker et al. 2013). The establishment of persistent chronic infections may also be a requisite feature of the pathogen, because this results in greater internal structure in the phylogeny for clusters to appear. For instance, methods developed for HIV have also been applied to study hepatitis C virus epidemics (Sacks-Davis et al. 2012; Jacka et al. 2014), sometimes for both viruses in the same population (de Oliveira et al. 2006; Pilon et al. 2011). On the other hand, Plotkin et al. (2002) used a pairwise Hamming distance to identify clusters in an influenza A virus phylogeny; phylogenies of this virus tend to be “comb-like” with a high rate of lineage extinction. The literature also provides several other examples in different viruses including hepatitis E virus (Takahashi et al. 2003), hepatitis B virus (Dumpis et al. 2001), and human herpesvirus (Lamers et al. 2015). However, investigators studying different pathogens tend to develop own clustering methodologies, and the details of these methods are not consistently provided. With the impending prospect of genetic clustering being used to inform public health decisions, and the methodological issues identified in this paper and previous work, the research community needs to have greater skepticism about clustering methods and, ultimately, to reach a consensus on best practices for generating and interpreting clusters.

Supplementary data

Supplementary data are available at Virus Evolution online.

Funding

This study was supported in part by the Government of Canada through Genome Canada and the Ontario Genomics Institute (OGI-131).

Conflict of interest: None declared.