Multivariate Bayesian Variable Selection Exploiting Dependence Structure Among Outcomes: Application to Air Pollution Effects on DNA Methylation

Summary

The analysis of multiple outcomes is becoming increasingly common in modern biomedical studies. It is well-known that joint statistical models for multiple outcomes are more flexible and more powerful than fitting a separate model for each outcome; they yield more powerful tests of exposure or treatment effects by taking into account the dependence among outcomes and pooling evidence across outcomes. It is, however, unlikely that all outcomes are related to the same subset of covariates. Therefore, there is interest in identifying exposures or treatments associated with particular outcomes, which we term outcome-specific variable selection. In this work we propose a variable selection approach for multivariate normal responses that incorporates not only information on the mean model, but also information on the variance-covariance structure of the outcomes. The approach effectively leverages evidence from all correlated outcomes to estimate the effect of a particular covariate on a given outcome. To implement this strategy, we develop a Bayesian method that builds a multivariate prior for the variable selection indicators based on the variance-covariance of the outcomes. We show via simulation that the proposed variable selection strategy can boost power to detect subtle effects without increasing the probability of false discoveries. We apply the approach to the Normative Aging Study (NAS) epigenetic data and identify a subset of five genes in the asthma pathway for which gene-specific DNA methylations are associated with exposures to either black carbon, a marker of traffic pollution, or sulfate, a marker of particles generated by power plants.

1. Introduction

The identification of environmental determinants of asthma is a major priority in environmental health research. A number of studies have reported evidence suggesting that air pollution not only exacerbates existing asthma but also elevates the incidence of asthma (von Mutius, 2000; Trasande and Thurston, 2005). Recent work has focused on possible epigenetic mechanisms underlying these observed effects. Such work is important because changes in DNA methylation, a common epigenetic outcome, may persist over time even after exposure to a given environmental factor has ceased, and represent a mechanism through which interventions to counteract exposure, such as administration of methyl donors, might be possible.

In this article, we analyze data from the Normative Aging Study (NAS) (Bell et al., 1972), a Boston-area longitudinal study of the elderly veterans conducted by the Veteran’s Administration (VA) since 1963, to identify genes within the asthma pathway for which gene-specific DNA methylation is associated with air pollution levels in the Boston area. The study enrolled 2,280 male volunteers from the greater Boston metropolitan area. The participants, who have an average age of 42 at entry, were screened and determined to be free of major chronic medical health conditions to be admitted to NAS. Recently, Sofer et al. (2013) conducted a pilot study of particulate exposures on 141 individuals in the NAS and analyzed pathway-specific associations with methylation markers assessed in a genome-wide scan of gene promoter regions. We consider the same data and focus on (i) the identification of specific genes in the asthma pathway that are associated with exposure to black carbon (BC), a marker of traffic pollution, and sulfate, a marker of particles from power plants, and (ii) estimation and inference of the effect sizes for the genes identified in (i). For our analysis, we exclude 9 individuals who had been diagnosed with asthma at the time of the examination and 40 individuals for whom black carbon and sulfate measures are not available. These are missing because NAS started measuring BC in 1995 and did not start measuring sulfate until 2000, and can thus be considered to be missing completely at random. Therefore the data considered for analysis consist of DNA methylation in 27 genes within the asthma pathway from 92 subjects in the NAS.

Statistically the goals of the study equate to identifying and estimating the association between each of the 27 gene-specific methylation outcomes and the environmental exposures, black carbon and sulfate concentrations, while controlling for potential confounders. An increasingly common approach to analyzing data on multiple outcomes is the development of a joint model that relates the mean vector of outcomes to a set of covariates of interest. This approach provides multiple advantages over the simpler strategy of analyzing each outcome separately, including the opportunity to pool evidence across outcomes which can lead to more powerful tests on effects of interest (Breiman and Friedman, 1997).

In this work we propose a new Bayesian variable selection model that identifies outcomes associated with a set of covariates incorporating not only information on the mean model, but also information on the variance-covariance structure of the outcomes. The approach effectively leverages the dependence across outcomes in order to assess the effect of a particular covariate on a given outcome. To accomplish this, we utilize the covariance model, which is estimated in the model fitting process, to specify a multivariate prior on the latent binary selection indicators. The prior has the appearance of a Markov random field (MRF) prior with edge potentials specified in terms of the model covariance, which is updated and re-evaluated at each Markov chain Monte Carlo (MCMC) step. Hereafter, we refer to this prior as an MRF prior.

There has been a considerable amount of research on Bayesian variable selection methods. Spike and slab approaches have been widely adopted for variable selection problems (George and McCulloch, 1993, 1997; Hernández-Lobato et al., 2013; Narisetty and He, 2014) and the idea has been extended to multivariate regression problems (Brown et al., 1998). In this approach, the regression coefficients are assumed to arise from a scale mixture of a point mass at 0 and a normal density.

In our case, the approach of Brown et al. (1998) is suboptimal because the method selects the same covariates for all responses. Several priors based on an MRF have been proposed to incorporate biological information on the structured dependence between covariates in variable selection for univariate regression models (Li and Zhang, 2010; Vannucci and Stingo, 2010; Stingo et al., 2011). Our approach differs from these existing MRF models in that we leverage the dependence among multiple outcomes in our prior specification for the variable selection indicators, as opposed to specifying it based on the network structure known a priori among covariates.

The remainder of this paper is organized as follows. Section 2 describes the proposed Bayesian framework, including model formulation and specification of prior distributions, as well as the MCMC algorithm to sample from the posterior distribution. Section 3 presents results from simulation studies that evaluate the operating performance of the proposed approach and compare it to that obtained using existing Bayesian variable selection methods based on independent Bernoulli priors. Section 4 presents results from the analysis of the NAS data. Section 5 concludes the paper with a discussion.

2. A Bayesian Framework for Multivariate Data

In this section, following a description of a general multivariate normal regression model, we present prior distributions including the proposed MRF prior for the latent binary selection indicators. We provide general guidelines for specifying the hyperparameters and covariance structures considered in this paper. Details of the computational algorithm are provided in Web Appendix A.

2.1 Model Formulations

Suppose that outcomes y_i = (y_i,1,…, y_i,q)^⊤ are observed for subject i = 1,…, n. We consider a linear regression model with multivariate response y_i and p candidate predictors x_i = (x_i,1,…, x_i,p)^⊤. Specifically, we assume y_i follows a multivariate Normal distribution:

$${\mathit{y}}_i|{\mathit{\beta }}_0,{\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_q,\sum ~{\mathcal{N}}_q\left({\mathit{\beta }}_0+B^{\top }{\mathit{x}}_i,\sum \right),$$ (1)

where β₀ = (β_0,1,…, β_0,q)^⊤ are the intercepts, β_j = (β_j,1,…, β_j,p)^⊤, for j = 1,…, q, are the regression parameters. B is the p × q matrix whose columns are β₁,…, β_q, and Σ is the variance-covariance matrix.

2.2 Prior Distributions

A Bayesian framework requires the specification of prior distributions for model parameters. In the context of Bayesian stochastic search variable selection, a mixture of two normal distributions has been widely used for the regression parameter prior (George and McCulloch, 1993, 1997):

$${\beta }_{j,k}|{\gamma }_{j,k},\sum ~{\gamma }_{j,k}\mathcal{N}\left(0,{\nu }_{1j}^2{\sum }_{(j,j)}\right)+(1-{\gamma }_{j,k})\mathcal{N}\left(0,{\nu }_{0j}^2{\sum }_{(j,j)}\right)$$

where Σ_(i,j) is the (i,j)-th element of Σ and γ_k=(γ_1,k,…,γ_q,k)^⊤, for k=1,…, p, is a vector of binary latent variables indicating the membership of each regression parameter to one of the components. In general, v_0j and v_1j are set to small and large values, respectively. If the data support γ_j,k = 1 over γ_j,k = 0 then the covariate k is deemed to be an important covariate for the j-th outcome. An alternative to the mixture of normal distributions is to specify a spike-and-slab prior distribution, by letting ${\nu }_{1j}^2={\nu }_j^2$ and ${\nu }_{0j}^2=0$ , as follows:

$${\beta }_{j,k}|{\gamma }_{j,k},\sum ~{\gamma }_{j,k}\mathcal{N}\left(0,{\nu }_j^2{\sum }_{(j,j)}\right)+(1-{\gamma }_{j,k}){ℐ}_0,$$ (2)

where ${ℐ}_0$ is the point mass distribution at 0. The spike-and-slab prior has several advantages over a mixture of two normal priors including: i) a clear separation for variable selection by setting β_j,k = 0 when γ_j,k = 0; ii) ease of performing sensitivity analyses as there is only one hyperparameter ${\nu }_j^2$ to specify. Therefore, we take the prior (2) for β_j,k in our proposed framework.

The latent binary variables γ_j,k, for j = 1,…, q, k = 1,…, p, are typically assumed to be independent Bernoulli random variables with inclusion probabilities π_k, which can be viewed as the initial guess for the proportion of outcomes associated with the k-th covariate. However, the independent prior for variable selection does not exploit information in the data on the within-subject correlations among outcomes. Indeed, one would expect that highly correlated outcomes might be associated with the same covariates. Therefore, we propose a prior that can incorporate the underlying dependence between outcomes into the inclusion probabilities. Following Li and Zhang (2010), we model the relations among the variable selection indicators γ_k, using an MRF. Letting c_i,j denote the correlation between the i-th and j-th outcomes, we specify the following MRF prior distribution for γ_k:

$$P\left({\mathbf{\gamma }}_k|{\omega }_k,\eta ,\sum \right)\propto \exp \left\{{\omega }_k{\mathbf{1}}_q^{\top }{\mathbf{\gamma }}_k+\eta {\mathbf{\gamma }}_k^{\top }(C_{\text{abs}}-I){\mathbf{\gamma }}_k\right\},$$ (3)

where 1_q is a q-vector of ones and C_abs is a q×q matrix whose (i,j)-th element is given by $|c_{i,j}|=|{\sum }_{ij}|/\sqrt{{\sum }_{ii}{\sum }_{jj}}$ . While the hyperparameter ω_k dictates the shrinkage of the model together with ${\nu }_j^2$ in (2), the hyperparameter η determines the extent to which other outcomes impact the probability of including a given covariate in the model for a given outcome. It can be shown that the joint prior (3) corresponds to a set of conditional Bernoulli distributions given by

$$\pi \left({\gamma }_{j,k}|{\mathbf{\gamma }}_{(-j),k},{\omega }_k,\eta ,\sum \right)=p{\left({\mathbf{\gamma }}_{(-j),k},\sum \right)}^{{\gamma }_{j,k}}{\left\{1-p\left({\mathbf{\gamma }}_{(-j),k},\sum \right)\right\}}^{1-{\gamma }_{j,k}},$$

where

$$p\left({\mathbf{\gamma }}_{(-j),k},\sum \right)={\left\{1+\exp \left(-{\omega }_k-\eta {\displaystyle \sum _{r\ne j}|c_{r,k}|{\gamma }_{r,k}}\right)\right\}}^{-1},$$

and γ_(−j),k is the vector γ_k with the j-th element removed. Note that setting η=0 is the conditional prior being equivalent to the conventional independent Bernoulli prior distribution. Lastly, we assign a conjugate normal distribution for the intercept ${\mathit{\beta }}_0,{\mathcal{N}}_q({\mathit{\mu }}_0,h_0{I}_q)$, where (μ₀, h₀) are hyperparameters to be specified and I_q is the q × q identity matrix.

2.3 Specification of Hyperparameters and Phase Transition

Since the prior distributions for β_j,k and γ_j,k play an important role in the proposed variable selection framework, the corresponding hyperparameters should be carefully selected. A realistic value can be chosen for ${\nu }_j^2$ based on the expected magnitude of effects for relevant covariates. When there is not sufficient information in the data, an unreasonably large value of ${\nu }_j^2$ may lead the prior to support a large value for β_j,k as if the corresponding covariate were important, while too small a value for ${\nu }_j^2$ may result in the prior being highly concentrated around 0 (Liang et al., 2008). In practice, one could fit a univariate regression model for each of the outcomes to obtain estimates of β_j,k then ${\nu }_j^2$ can be chosen based on the variance of the estimates of β_j,k (Li and Zhang, 2010). Logistic transformation of the hyperparameter ω_k, denoted by logit⁻¹(ω_k), can be interpreted as the prior proportion of responses that are associated with the k-th covariate when the underlying dependence between outcomes is ignored (i.e., η = 0).

As mentioned in Section 2.2, the hyperparameter η controls the extent to which the dependence between outcomes is taken into account for variable selection. A greater value of η encourages the selection of a covariate for an outcome when the covariate is selected for other outcomes correlated to the one under consideration. It is important to note that the specification of η requires special attention because of the phase transition behavior (Li and Zhang, 2010; Stingo et al., 2011). The phase transition problem commonly occurs in models that use an MRF parametrization as in (3). One crucial issue is that, for a given value of $\left({\nu }_j^2,{\omega }_k\right)$ , the model size in terms of the number of selected predictors increases with a small change of η value. Several guidelines have been suggested to preclude this problem by detecting the phase transition boundary for η in the Bayesian variable selection context although no theoretical results have been obtained. Li and Zhang (2010) derived an approximate prior-based estimate of the phase transition boundary in the hyperparameter space given that the MRF prior is exchangeable and provided a heuristic method for choosing hyperparameters to avoid the phase transition: first choose realistic values for ${\nu }_j^2$ and η under the assumption of a sparse model then choose the value of ω_k based on the approximate prior-based estimates of the phase transition boundary. For a given choice of ω_k and ${\nu }_j^2$, Stingo et al. (2011) simulated from the prior distribution in (3) over a grid of η values to detect the phase transition boundary η_pt (the smallest value that leads to the selection of all covariates) and specified a Beta hyperprior on η/η_pt. Our approach is close to how Stingo et al. (2011) found η_pt except that we perform the grid search strategy on the posterior distribution. Specifically, we implement the following strategy to detect η_pt over the posterior distribution:

1. Simulate M₀ posterior samples for model parameters over a grid of η values, {η^g :g = 0,…,G, η⁰=0}.

2. For the k-th covariate (k=1,…, p), let ${{\gamma }_k}_{,\left({\eta }^g\right)}$ denote the 10th percentile of posterior mean estimates of γ_k (across the outcomes) for the model with η = η^g. Calculate ${{\gamma }_k}_{,\left({\eta }^g\right)}$ for g = 0,…, G.

3. Declare the phase transition point η_pt to be η^g if ${{\gamma }_k}_{,\left({\eta }^g\right)}-{{\gamma }_k}_{,\left({\eta }^0\right)}>0.05$ for any k=1,…,p.

4. Set η=η^g−1.

The logic behind the strategy is that the phase transition can typically be detected prior to convergence of an MCMC chain and at least 10% of outcomes are assumed not to be associated with a particular covariate. Given ${\nu }_j^2=100$ and logit⁻¹(ω_k)=0.1 or 0.5, Figure 1 illustrates the phase transition boundaries of η based on a prior simulation approach and our posterior simulation approach for the analysis of the Normative Aging Study data. Both methods detect the phase transition with smaller value of η as ω_k gets larger. This is also consistent with the investigation of Li and Zhang (2010) based on their approximate prior-based estimates. However, we can see that the phase transition boundary detected from the posterior distribution (2.1 in Figure 1 (a) and 1.1 in Figure 1 (b)) provides a better guideline to specify η than that suggested by the prior distribution because the phase transition point would have been underestimated by the approach relying solely on the prior (1.0 in Figure 1 (a) and <0.1 in Figure 1 (b)).

Figure 1.

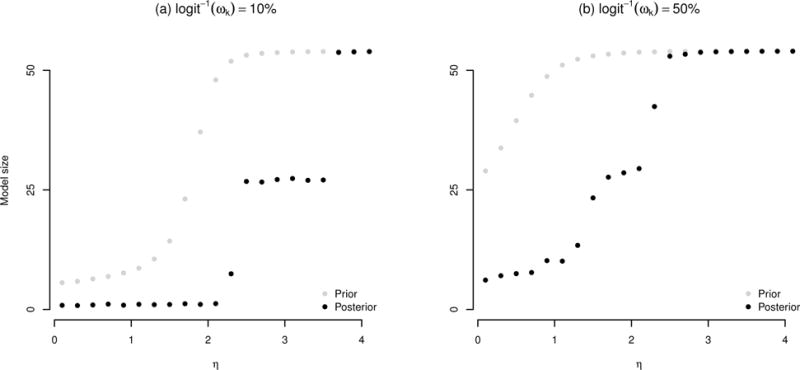
Detection of phase transition boundary for η in the analysis of Normative Aging Study data. The estimated model sizes, ${\sum }_{j,k}{\overline{\gamma }}_{j,k}$, where ${\overline{\gamma }}_{j,k}$ is the average of prior/posterior simulations for γ_j,k, are provided over a grid of η values based on the prior simulation approach and our posterior simulation approach given that ${\nu }_j^2=100$ and logit⁻¹(ω_k)=0.1 (panel (a)) or 0.5 (panel (b)).

2.4 Covariance Structure

The proposed MRF structure is flexible in that it can incorporate either an unstructured matrix or structured covariance pattern, such as compound symmetry or factor-analytic structure for the variance-covariance matrix Σ. One question that arises is how the proposed variable selection approach performs when this matrix is misspecified. In order to examine this issue here, we consider two models for Σ, a factor-analytic covariance structure assuming a single latent factor and the unstructured model.

In a factor-analytic model (Hogan and Tchernis, 2004), we assume that each subject has a latent variable b_i that captures unobserved characteristics that are associated with y_i. Then ${\mathit{y}}_i|{\mathit{\beta }}_0,{\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_q,{\sigma }^2,b_i~{\mathcal{N}}_q\left({\mathit{\beta }}_0+B^{\top }{\mathit{x}}_i+\mathbf{\lambda }{b}_i,{\sigma }^{2}I\right)$, where λ=(λ₁,…,λ_q)^⊤ is a q × 1 vector of factor loadings and σ² measures the residual variation in y_i. The model assumes independence between responses conditionally on b_i. In order to ensure identifiability of λ (Bartholomew et al., 2011) and to exploit prior-posterior conjugacy for σ², we take $b_i~\mathcal{N}\left(0,{\sigma }^2\right)$. Marginalizing over the latent variable b_i, the factor-analytic model corresponds to (1) with Σ = σ²(λλ^⊤ + I), implying the correlation between the j-th and j′-th responses is ${\lambda }_j{\lambda }_{j^{\prime }}/\sqrt{({\lambda }_j^2+1)({\lambda }_{j^{\prime }}^2+1)}$. For the factor-analytic model, we specify a normal distribution, ${\mathcal{N}}_q\left({\mathit{\mu }}_{\lambda },h_{\lambda }{\sigma }^2{I}_q\right)$, for λ and a conjugate inverse-gamma distribution, $ℐ\mathcal{G}\left({\nu }_0/2,{\nu }_0{\sigma }_0^2/2\right)$, for σ².

The unstructured covariance structure imposes no specific pattern on Σ in (1). Therefore, q(q + 1)/2 parameters need to be estimated for Σ under the unstructured model. For the unstructured model, an inverse-Wishart prior distribution, $ℐ\mathcal{W}\left({\mathrm{\Psi }}_0,{\rho }_0\right)$, is specified for the variance-covariance matrix Σ.

2.5 Markov Chain Monte Carlo

In order to perform posterior inference, we use an MCMC algorithm to obtain samples from the joint posterior distribution by either exploiting prior-posterior conjugacies or using a Metropolis-Hastings algorithm to update model parameters. A detailed description of the proposed computational scheme is provided in Web Appendix A. In order to improve the computation speed, we developed a series of core functions in C and provide the algorithm in the mBvs package for R. The software is available from the Comprehensive R Archive Network (http://cran.r-project.org/web/packages/mBvs/). To provide a sense of computational time, for the unstructured model, which is the more complex covariance structure requiring the estimation of a larger number of parameters, it takes 12 minutes to generate 10,000 MCMC scans on a 2.5 GHz Intel Core i7 MacBook Pro for the analysis of the NAS data.

3. Simulation Studies

We assess the performance of the proposed multivariate Bayesian variable selection model on simulated data. Data sets are generated under several scenarios with different correlation structures between outcomes as well as different association patterns between two covariates and the vector of outcomes.

3.1 Setting

We design four different simulation scenarios where various correlation structures are considered between outcomes: in Scenario I the outcomes associated with covariate x₁ are highly correlated but others are moderately correlated; in Scenario II the outcomes have the same correlation as in Scenario I but none of them are associated with any of the covariates (the null model); in Scenario III the outcomes associated with covariate x₁ are moderately correlated to each other and the remaining outcomes are weakly correlated; in Scenario IV the outcomes related to covariate x₁ are weakly correlated while those not associated to covariate x₁ are highly correlated. Samples of size n=100 with q=10 responses and p=2 covariates are generated under the model (1). Two continuous covariates are generated from $\mathcal{N}(0,4)$ assuming Cor(x₁, x₂)=0.3 and 0.6, and the intercepts β₀ are randomly set to values in the range of (−1, 1). In Scenarios I, III and IV, the effects of the covariates on the responses are assumed to be

$$B=\left(\begin{array}{cccccccccc}\hfill 0.05\hfill & \hfill 0.15\hfill & \hfill 0.15\hfill & \hfill 0.20\hfill & \hfill 0.25\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0.05\hfill & \hfill 0\hfill & \hfill 0.15\hfill & \hfill 0\hfill & \hfill 0.25\hfill & \hfill 0.10\hfill & \hfill 0.20\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$$

while Scenario II considers the null case by setting all elements of B to zero. The variance-covariance matrix Σ is set to an exchangeable correlation structure with correlation c₁ within the block of the first five variables, an exchangeable structure with correlation c₂ within the block of the second five outcomes, and a common cross-block correlation of c₃ for pairs of outcomes from different blocks. The pairwise correlations (c₁, c₂, c₃) are set to (0.70, 0.20, 0.30) in Scenario I and Scenario II, while they are set to (0.40, 0.05, 0.10) and (0.20, 0.70, 0.30) in Scenario III and Scenario IV, respectively. We consider 100 simulated replications for each scenario. In Web Appendix B, we provide the results from additional simulation studies (Scenarios I′-IV′) where data are generated under a factor-analytic covariance structure.

3.2 Analyses and Specification of Hyperparameters

In order to assess the performance of the model when the variance-covariance structure is both correctly specified and misspecified, we fit both unstructured and factor-analytic models with MRF prior to 100 simulated data sets under each scenario. For the intercept β₀, we assign a non-informative prior distribution: (μ₀, h₀)=(0, 10⁶). The hyperparameter ${\nu }_j^2$, set to 100, is chosen to be fairly non-informative and ω_k is set to 0, which corresponds to a 0.5 prior probability of being selected when ignoring the dependence between outcomes. For the factor-analytic model, a non-informative prior distribution is assigned for λ with (μ_λ, h_λ)=(0, 10⁶). We set $\left({\nu }_0,{\sigma }_0^2\right)=(2,1)$ so that the induced prior for σ² has a median of 1.44 and 95% central mass between 0.27 and 39.81. Finally, for the unstructured model, (Ψ₀, ρ₀) are set to (δI, q+δ+1) with δ = 3. This choice corresponds to a prior distribution centered at I and having a variance equal to 2.0 for the diagonal elements of Σ. For the analysis of each simulated data set, the hyperparameter η is specified based on the posterior simulation approach described in Section 2.3, with a grid of η values {η^g=0.1(2g-1): g=1,…,G=50, η⁰=0} and M₀=5,000 iterations. The average chosen values of η for the unstructured model are 1.26, 1.94, 1.44, and 1.26 in the four simulation scenarios, respectively, when Cor(x₁, x₂)=0.3. We ran each MCMC chain for 40,000 iterations with the first half taken as burn-in. We note that, in order to make a fair comparison with the existing independent Bernoulli prior, we keep the overall prior inclusion probability logit⁻¹(ω_k) equal to 0.5 for both the independent Bernoulli prior and our proposed MRF prior. Therefore, differences in performance between the two prior choices can be attributed to the proposed MRF prior for γ_k.

3.3 Results

Table 1 provides the results for the proposed Bayesian method under Scenarios I and II. In order to facilitate a comparison with the conventional approach, we also implemented the unstructured covariance model with an independent Bernoulli (IB) prior (equivalent to η=0) for γ_j,k. In addition, we assessed the effect of model misspecification by fitting the model using a factor-analytic covariance structure and present the results in Table 2. While, in the main paper, we only present the results that are associated with the first covariate (x₁) for scenarios I and II when Cor(x₁, x₂)=0.3, results related to the second covariate (x₂) as well as all results for Scenarios III and IV both with Cor(x₁, x₂)=0.3 and 0.6, are presented in Web Appendix B.

Table 1.

Results from simulation studies with 100 replications using unstructured models with a conventional independent Bernoulli (IB) prior and with our proposed MRF prior for γ_k under Scenarios I and II where the correlation between x₁ and x₂ equals 0.3. The medians of the posterior means (PM) and posterior standard deviations (SD) of β_j,1 (conditioning on γ_j,1=1), the medians of the posterior means of γ_j,1 (marginal posterior probabilities of inclusion) are provided. We also present the average width (WI) of the 95% highest posterior density (HPD) intervals for β_j,1 and the coverage probability (CP) of the HPD intervals.

Scenario	j	True	Unstructured with IB prior				Unstructured with MRF prior
		βj,1	βj,1|γj,1=1	γj,1	βj,1		βj,1|γj,1=1	γj,1	βj,1
			PM (SD)	PM	WI	CP	PM (SD)	PM	WI	CP
	1	0.05	−0.03 (0.04)	0.03	0.04	0.06	0.03 (0.04)	0.28	0.11	0.51
	2	0.10	0.02 (0.04)	0.02	0.04	0.15	0.08 (0.04)	0.36	0.12	0.61
	3	0.15	0.10 (0.04)	0.08	0.09	0.37	0.13 (0.04)	0.71	0.14	0.61
	4	0.20	0.13 (0.03)	0.86	0.13	0.38	0.16 (0.04)	0.99	0.17	0.70
I	5	0.25	0.18 (0.04)	0.99	0.16	0.50	0.21 (0.04)	1.00	0.18	0.71
	6	0.00	0.01 (0.05)	0.02	0.01	1.00	0.02 (0.05)	0.06	0.03	1.00
	7	0.00	−0.02 (0.05)	0.01	0.01	1.00	−0.01 (0.05)	0.02	0.02	1.00
	8	0.00	−0.03 (0.05)	0.02	0.02	1.00	−0.01 (0.05)	0.06	0.05	1.00
	9	0.00	−0.03 (0.05)	0.02	0.02	1.00	−0.01 (0.05)	0.06	0.04	1.00
	10	0.00	−0.04 (0.05)	0.02	0.02	1.00	−0.02 (0.05)	0.07	0.05	1.00
	1	0.00	0.00 (0.03)	0.01	0.01	1.00	0.00 (0.04)	0.07	0.04	1.00
	2	0.00	0.00 (0.03)	0.01	0.01	1.00	0.01 (0.04)	0.07	0.04	1.00
	3	0.00	0.00 (0.03)	0.01	0.01	1.00	0.00 (0.04)	0.07	0.04	1.00
	4	0.00	−0.00 (0.03)	0.01	0.01	1.00	0.00 (0.04)	0.07	0.04	1.00
II	5	0.00	0.01 (0.03)	0.01	0.00	1.00	0.00 (0.04)	0.07	0.04	1.00
	6	0.00	0.01 (0.04)	0.02	0.01	1.00	0.00 (0.04)	0.04	0.02	1.00
	7	0.00	−0.01 (0.04)	0.02	0.02	1.00	−0.00 (0.04)	0.05	0.03	1.00
	8	0.00	0.01 (0.04)	0.02	0.01	1.00	0.02 (0.05)	0.05	0.03	1.00
	9	0.00	0.00 (0.05)	0.02	0.01	1.00	0.00 (0.05)	0.04	0.02	1.00
	10	0.00	−0.01 (0.05)	0.02	0.01	1.00	−0.01 (0.05)	0.04	0.02	1.00

Table 2.

Results from simulation studies with 100 replications using factor-analytic models with a conventional independent Bernoulli (IB) prior and with our proposed MRF prior for γ_k under Scenarios I and II where the correlation between x₁ and x₂ equals 0.3. The medians of the posterior means (PM) and posterior standard deviations (SD) of β_j,1 (conditioning on γ_j,1=1), the medians of the posterior means of γ_j,1 (marginal posterior probabilities of inclusion) are provided. We also present the average width (WI) of the 95% highest posterior density (HPD) intervals for β_j,1 and the coverage probability (CP) of the HPD intervals.

Scenario	j	True	Factor-analytic with IB prior				Factor-analytic with MRF prior
		βj,1	βj,1|γj,1=1	γj,1	βj,1		βj,1|γj,1=1	γj,1	βj,1
			PM (SD)	PM	WI	CP	PM (SD)	PM	WI	CP
	1	0.05	0.00 (0.05)	0.03	0.02	0.13	0.04 (0.05)	0.16	0.09	0.55
	2	0.10	0.04 (0.05)	0.03	0.05	0.24	0.07 (0.05)	0.18	0.11	0.56
	3	0.15	0.14 (0.05)	0.20	0.13	0.53	0.15 (0.05)	0.36	0.16	0.64
	4	0.20	0.15 (0.05)	0.72	0.18	0.57	0.16 (0.05)	0.90	0.20	0.70
I	5	0.25	0.20 (0.05)	0.92	0.22	0.73	0.22 (0.05)	0.98	0.22	0.78
	6	0.00	−0.01 (0.04)	0.02	0.02	1.00	−0.00 (0.04)	0.06	0.04	1.00
	7	0.00	−0.03 (0.04)	0.01	0.02	1.00	−0.02 (0.04)	0.02	0.03	1.00
	8	0.00	−0.03 (0.04)	0.02	0.03	1.00	−0.02 (0.04)	0.07	0.06	1.00
	9	0.00	−0.04 (0.04)	0.03	0.03	1.00	−0.02 (0.04)	0.08	0.06	1.00
	10	0.00	−0.04 (0.04)	0.03	0.03	1.00	−0.03 (0.04)	0.07	0.05	1.00
	1	0.00	0.00 (0.04)	0.02	0.00	1.00	0.00 (0.05)	0.06	0.03	1.00
	2	0.00	0.00 (0.04)	0.02	0.00	1.00	0.01 (0.05)	0.07	0.04	1.00
	3	0.00	0.00 (0.04)	0.02	0.00	1.00	0.00 (0.05)	0.07	0.04	1.00
	4	0.00	0.00 (0.04)	0.02	0.00	1.00	−0.00 (0.05)	0.06	0.04	1.00
II	5	0.00	0.00 (0.04)	0.02	0.00	1.00	0.01 (0.05)	0.06	0.04	1.00
	6	0.00	0.01 (0.04)	0.02	0.02	1.00	0.00 (0.04)	0.05	0.03	1.00
	7	0.00	−0.00 (0.04)	0.02	0.02	1.00	−0.00 (0.04)	0.06	0.04	1.00
	8	0.00	0.01 (0.04)	0.02	0.02	1.00	0.01 (0.04)	0.06	0.03	1.00
	9	0.00	−0.00 (0.04)	0.02	0.02	1.00	0.00 (0.04)	0.05	0.03	1.00
	10	0.00	−0.01 (0.04)	0.02	0.01	1.00	−0.01 (0.04)	0.05	0.02	1.00

We first evaluate the performance of the proposed MRF prior when the model is correctly specified. We do this by comparing the unstructured model with IB prior to the unstructured model with MRF prior in Table 1. Inference for variable selection can be done through the marginal posterior distribution of γ_j,1. In Scenario I, we can see that the posterior inclusion probabilities for the outcomes associated with the covariate using the MRF prior are uniformly, significantly larger than their IB prior counterparts. Applying a marginal posterior probability cutoff of 0.5, both the conventional and our proposed framework successfully identify the association with the covariate for the two outcomes with largest effect sizes (β_j,1⩾0.20, j=4,5). However, the estimated inclusion probabilities for the outcomes with smaller effect sizes (β_j,k≤0.15, j=1,2,3) are less than 0.08 with the IB prior while they are substantially increased and large enough for one more relevant variable to be selected using the MRF prior (0.28, 0.36, 0.71, respectively). In Scenario I, we can see that the estimates of β_j,1, conditioning on γ_j,1=1, are less biased when using our proposed MRF prior. Furthermore, the associated posterior uncertainties, measured by the width of the 95% highest posterior density (HPD) intervals, appear to be larger for the proposed MRF prior. Therefore, the model with MRF prior has significantly higher coverage probabilities for the relevant outcomes. In the null case (Scenario II), both models successfully exclude the covariate for all of the outcomes despite the presence of a group of strongly correlated outcomes.

In order to investigate how much the performance of the proposed prior deteriorates when the model is misspecified, we fitted a factor-analytic model with the MRF prior (Table 2). The misspecified factor-analytic model shows similar results for the estimates of β_j,1 compared to the unstructured model and the two models have comparable coverage probabilities. However, the estimated inclusion probabilities for the outcomes with smaller effect sizes (β_j,k≤0.15, j=1,2,3) are generally smaller for the misspecified factor-analytic model compared to the unstructured model. For example, for the outcome j=3, the inclusion probability is 0.36 when the model is misspecified (factor-analytic in Table 2) while it is 0.71 when the model is correctly specified (unstructured in Table 1). The reduced posterior inclusion probability from the factor analytic model needs to be understood based on an important characteristic of the proposed MRF prior: the prior has the ability to increase the power to detect a subtle effect for an outcome when there exist other outcomes for which the effects are clearly strong. That is, since the factor-analytic model less successfully detects the strong effects $\left({\widehat{\gamma }}_{4,1}=0.90,{\widehat{\gamma }}_{5,1}=0.98\text{in}\text{Table}2\right)$ compared to the unstructured model $\left({\widehat{\gamma }}_{4,1}=0.99,{\widehat{\gamma }}_{5,1}=1.00\text{in}\text{Table}1\right)$, primarily due to its more restrictive covariance structure, the MRF prior utilizes less information from the model covariance to improve the power to detect smaller, more subtle effects. However, even when misspecified, the factor analytic model still performs better than the standard practice of using an IB prior that ignores the dependence structure among the outcomes in the variable selection prior.

In conclusion, compared to the conventional prior, our proposed MRF prior provides more power to detect real effects by yielding higher inclusion probabilities when there is a true association. Furthermore, the MRF prior avoids the inclusion of non-relevant associations. The estimates of effect sizes and their associated uncertainties are relatively similar for both priors.

4. Application to DNA Methylation Data

The proposed Bayesian method described in Section 2 is motivated by an ongoing research investigating epigenetic variations induced by air pollution in the asthma pathway. Specific goals of the research include the identification of genes in the asthma pathway that are influenced by airborne pollutants and the estimation of their effects.

4.1 Normative Aging Study Data

As outlined in the Introduction, our proposed variable selection method is applied to data from 92 participants in the NAS study focusing on q=27 genes in the asthma pathway. The algorithm for calculating the gene-specific methylation scores has been described previously (Sofer et al., 2013). We consider two prominent components of particulate matter (p=2): BC as a marker of traffic particles and sulfate as a marker of particles from power plants. The measurements on the components are averaged for the month before the blood draw. Since DNA methylation varies depending on age, we adjust for participants’ age, but do not perform variable selection on it.

4.2 Results

We fit the model with the proposed MRF prior and the model with the independent Bernoulli prior to the NAS data. We set the hyperparameters $({\mathit{\mu }}_0,h_0,v_j^2,{\omega }_k)$ to the same values as in Section 3.2. Based on the posterior simulation approach with a grid of η values {η^g=0.1(2g-1): g=1,…,G=50, η⁰=0} and M₀=50,000 iterations, we set the hyperparameter η to 1.1 (see Figure 1 (b)). For the prior of Σ, we set (Ψ₀, ρ₀) to (δI, q+δ+1) with δ = 3 so that the prior is centered at I and has variance equal to 2.0 for the diagonal elements of Σ. We ran two MCMC chains for 300,000 iterations each with the first half taken as burn-in. In order to assess convergence of the MCMC sampler, we plotted traces of the MCMC scans for each parameter. Overlaid plots for the two MCMC chains provide a visual assessment of convergence to the stationary distribution. The plots suggest that the chains are mixing well and do not show evidence of non-convergence. We provide the trace plots for illustrative parameters in Web Appendix C.

We apply a marginal posterior probability cutoff of 0.5 for variable selection. Estimated inclusion probabilities for BC and sulfate for each of the 27 genes are presented in Figure 2. A conventional Bayesian variable selection approach with IB prior identifies 2 genes (HLA-DRA, IL9) associated with BC and no genes associated with sulfate. In contrast, our proposed method identifies 3 genes (HLA-DRA, FCER1G, IL9) associated with BC and 2 genes (IL5, CCL11) associated with sulfate. As noted in Section 3, the proposed MRF prior improves the ability to identify subtle effects of exposure on a gene methylation score when there exist other correlated gene methylation sites for which exposure effects are present. For example, the exposure to BC is associated with methylation score in HLA-DRA based on the estimated inclusion probability (0.64 from model with IB prior; 0.79 from the proposed MRF prior); the 0.12 correlation between methylation scores in HLA-DRA and FCER1G helps the proposed model identify the effect of exposure to BC on FCER1G, which is not detected by the IB prior. A similar explanation holds for the substantial increase in inclusion probabilities using our approach for sulfate in association to CCL11 and IL5, which have a correlation of 0.37. In Table 3, we provide the estimated effects of exposure to BC and sulfate on genes selected based on our method and using the IB prior. Associated uncertainties in the form of posterior standard deviation conditioning on γ_j,k=1 and 95% HPD intervals are also provided. It appears that the estimated effects and uncertainties are relatively similar for both choices of prior.

Figure 2.

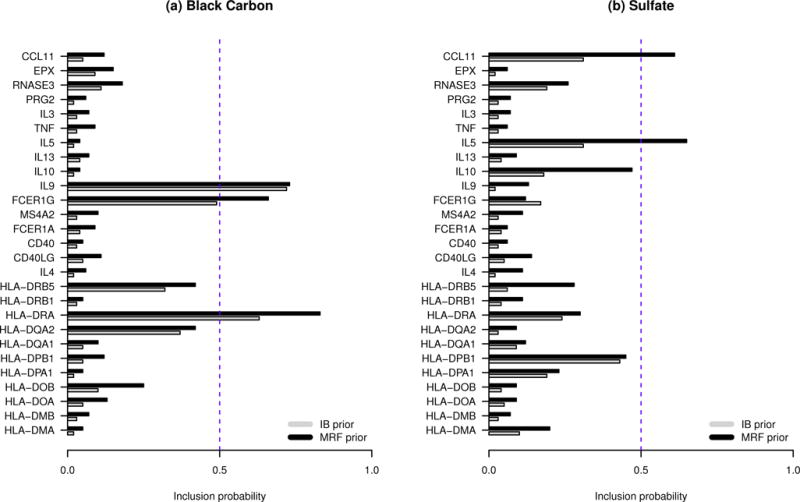
Analysis of Normative Aging Study data. Unstructured models are fitted using IB or MRF prior for γ_j,k. Marginal posterior probabilities of inclusion for black carbon or sulfate in relation to the 27 genes in the asthma pathway are presented.

Table 3.

Estimated covariate effects on methylation outcomes identified for association using a marginal posterior probability cutoff of 0.5. Posterior mean (PM) and posterior standard deviation (SD) of β_j,k (conditioning on γ_j,k=1), 95% highest posterior density (HPD) intervals for β_j,k are provided.

		IB prior		MRF prior
		βj,k|γj,k=1	βj,k	βj,k|γj,k=1	βj,k
		PM (SD)	95% HPD	PM (SD)	95% HPD
Black carbon (k=1)	HLA-DRA	−0.26 (0.09)	(−0.39, 0.00)	−0.27 (0.09)	(−0.41, 0.00)
	FCER1G	–	–	−0.27 (0.09)	(−0.40, 0.00)
	IL9	−0.22 (0.07)	(−0.32, 0.00)	−0.23 (0.08)	(−0.35, 0.00)
Sulfate (k=2)	IL5	–	–	0.29 (0.11)	(0.00, 0.44)
	CCL11	–	–	0.29 (0.11)	(0.00, 0.46)

Table 4 provides a summary of genes whose methylation scores are identified to be associated with exposures by our proposed approach. Supplementary information on the results of the analysis, such as estimated effects of exposures on all 27 gene methylation sites and the correlations between methylation markers, is given in Web Appendix C.

Table 4.

Summary of genes in asthma pathway identified to be associated with black carbon and/or sulfate using the proposed Bayesian framework. Official full names and related biological processes are provided (NCBI, 2015).

Gene symbol	Official full name	Recognized biological process
HLA-DRA	major histocompatibility complex, class II, DR alpha	Immune system
FCER1G	Fc fragment of IgE, high affinity I, receptor for; gamma polypeptide	Allergic reactions
IL5	interleukin 5	Eosinophilic inflammatory disease†
IL9	interleukin 9	Asthma
CCL11	chemokine (C-C motif) ligand 11	Eosinophilic inflammatory diseases†

^†These include atopic dermatitis, allergic rhinitis, asthma and parasitic infections

5. Discussion

In this paper, we have developed a Bayesian variable selection method for multivariate data that accounts for the correlation structure between outcomes in the selection prior. A special MRF prior is devised to increase the power to detect subtle associations between multiple outcomes and one or more exposures. This has allowed us to address two important scientific questions from an ongoing epigenetic research: a) identify genes in the asthma pathway that are associated with particular environmental exposures; b) investigate effects of exposures on the identified gene methylation responses. Our proposed Bayesian framework determined a subset of genes associated with fine particulate levels that were not found using standard Bayesian variable selection approaches.

It should be noted that the use of an unstructured covariance matrix in the proposed Bayesian framework is not exactly the same as that in a frequentist mixed model analysis. While the latter approach would involve a very large number of covariance parameters, which could yield unstable coefficient estimates or convergence problems during model fitting, the former assumes a prior structure using an inverse-Wishart distribution and therefore shrinks the estimated variance-covariance matrix back towards the mean of the prior inverse-Wishart distribution. This shrinkage yields a more parsimonious fit than a frequentist fit based on an unstructured matrix.

In general, one could choose the covariance structure by conducting exploratory analyses comparing fitted and observed variances and correlations, along with information criteria such as BIC or DIC. In the NAS application, there was a demonstrated lack of fit with the factor-analytic structure. Therefore, we used an unstructured model.

It is noted that our proposed method can be implemented for data with multiple covariates (large p). Like any other Bayesian variable selection approach, application of the proposed method to data with p > n would require the specification of an informative prior to compensate for the lack of information in the likelihood. Otherwise, with a general prior, the MCMC algorithm stochastically searches through a lower-dimensional subspace, so that the number of covariates in the proposed models at each MCMC iteration is always less than n (Zhang et al., 2008). In order to provide more details on computation time and how realistically our proposed approach could scale up with p for other applications, we ran simulation studies with n=100 subjects and q=10 outcomes to check how the computation time grows as the number of covariates p increases, using a 2.5 GHz Intel Core i7 MacBook Pro. We monitored the time to generate 10,000 MCMC scans for the unstructured model, which is the more complex covariance structure requiring the estimation of a larger number of parameters. Using the mBvs R package we built, it took 2, 8, and 42 minutes for data with p=10, 100, and 1,000 covariates, respectively. However, a longer chain may be needed for data with high-dimensional covariates to make sure the right model subspace is being sampled with sufficient frequency.

While our analysis focused on a pre-selected pathway, it is often of interest in epigenetics to study the entire epigenome. Applying our method to the entire epigenome will raise computational issues, especially with the unstructured covariance model, as the number of outcomes q will be very large. One possibility would be to extend the method to multivariate mixture models, where groups of methylation sites with similar profiles will be identified and group-specific regression would be fit, thus requiring the estimation of component-specific covariance matrices which will have smaller dimensions. Our proposed MRF prior could also be adopted for models with different types of outcomes. However, the computation could be more challenging as generalized linear models will need to be considered for non-Gaussian response variables. In these cases, one possibility would be to consider approximate Bayes methods for computationally efficient strategies. Adapting the beta-binomial priors on γ and scaled priors on v² (Celeux et al., 2012) for our proposed multivariate prior formulation is another promising area for future development. Finally, while we chose the model covariance as a dependence measure between outcomes, one might be interested in considering a different distance/correlation matrix in equation (3). The proposed methodology is fairly general and can be applied with different choices of correlation/dissimilarity matrix.