Abstract
Many studies in the social and behavioral sciences involve multivariate discrete measurements, which are often characterized by the presence of an underlying individual trait, the existence of clusters such as domains of measurements, and the availability of multiple waves of cohort data. Motivated by an application in child development, we propose a class of extended multivariate discrete hidden Markov models for analyzing domain-based measurements of cognition and behavior. A random effects model is used to capture the long-term trait. Additionally, we develop a model selection criterion based on the Bayes factor for the extended hidden Markov model. The National Longitudinal Survey of Youth (NLSY) is used to illustrate the methods. Supplementary technical details and computer codes are available online.
Keywords: Junction tree, Mixed effects, National Longitudinal Survey of Youth
1. INTRODUCTION
Empirical studies in social and behavioral research often involve multivariate discrete data. Dichotomized responses from multiple items on a survey, which are indicators of the presence of a multitude of behaviors (or the lack thereof), are routinely included in such studies. The past decade has also witnessed, for good reasons, a tremendous growth of cohort data in the social sciences (Frees 2004, p. 4; Singer and Willet 2003). Unlike cross-sectional data, longitudinal data collected from a cohort are valuable for informing the researcher about the dynamics of behavior and changing attitudes and perceptions in a population. As an example, the field of child development traditionally has sought to describe universals of development and to investigate mechanisms of development through the use of small-scale, cross-sectional experiments. However, emphasis has recently been shifting from this kind of so-called variable-centered study to person-centered longitudinal studies, which include large-scale, long-term projects such as the National Longitudinal Survey of Youth (NLSY, Chase-Lansdale et al. 1991). These studies often aim to identify subgroups of differential risks, and to delineate risk and protective factors that explain how development proceeds differently in different subgroups (Laursen and Hoff 2006). Indeed, in the NLSY, extensive cognitive and linguistic outcome measures on a national sample of children are being collected over an extended period of time, and these measures can be related to external variables such as socioeconomic status (SES) and maternal health, both mental and physical.
The discrete hidden Markov model (HMM, Rabiner 1989; MacDonald and Zucchini 1997) is a natural way for modeling discrete multiple outcomes (also referred to interchangeably as “responses” in this article) collected on individuals or social units over time. The HMM assumes the presence of two parallel stochastic processes: an observed sequence of outcomes and a Markovian sequence of underlying latent states that drives the observed stochastic changes. Observed outcome variables over time are assumed to be conditionally independent given latent state. Furthermore, when more than one outcome variable is involved, conditional independence between multiple outcomes given latent state is also assumed.
Although the multivariate HMM has many features necessary for successful person-centered longitudinal studies, several modeling and computational limitations exist. First, while the conditional independence assumption greatly simplifies computation, the assumption may not be realistic in many social science applications. In the NLSY dataset, a child-developmental profile may contain clearly identifiable domains such as problematic behaviors and cognitive development. It is unlikely that measurements within the same domain (e.g., oral reading and reading comprehension within the domain of cognitive development) would satisfy the conditionally independent assumption given latent state.
Second, in person-centered longitudinal studies, there often exist discernible individual stable traits that “drive” an individual’s responses both across domains and across time points. In a longitudinal study of domestic violence, Snow Jones et al. (2010) found evidence that a relatively stable individual trait of violent behavior exists among batterers, despite the fact that their behaviors may cycle back and forth from overtly violent behavioral states to relatively nonabusive behavioral states. Statistically, the stable trait can be modeled as an individual-specific random effect that induces a level of conditional correlation across outcomes and time points given latent state. In other words, the conditional independence assumption in HMM is relaxed to allow for heterogeneity among individuals within a specific latent state.
A third challenge in person-centered longitudinal studies is that conventional indexes for model selection in HMM, such as the AIC and BIC, may be invalid because observations across time points are generally not independent. For example, in BIC, the sample size needs to be adjusted to account for the correlation between observations across time.
This article describes our effort to resolve the aforementioned limitations of the HMM, especially in the context of social and behavioral data. We discuss (1) a domain-based model for handling the existence of domains of items within the data, (2) a random effects model for capturing the individual-specific stable trait, and (3) a Bayes factor-based goodness-of-fit index, which we call the modified BIC, that takes into account the correlation between observations across time points. Related computational methods for implementing the three solutions will be discussed.
Several works in the literature of HMM are especially pertinent to this article. In an application of the HMM to rainfall data, Zucchini and Guttorp (1991) suggested modifications to relax the conditional independence assumption across their multisite precipitation model because sites in close proximity may exhibit similar rainfall patterns. Hughes, Guttorp, and Charles (1999) described a nonhomogeneous HMM for precipitation. Scott, James, and Sugar (2005) described an HMM for multiple, continuous observed data that are assumed to follow a multivariate t-distribution. Altman (2007) proposed mixed-effects HMMs and applied the model to lesion-count data in a two-state Poisson model. The author also proposed using a quasi-Newton method for HMM and either numerical integration or Monte Carlo methods for handling the random effects. Rijmen, Vansteelandt, and De Boeck (2008) proposed, from an item-response theory (IRT, Lord and Novick 1968) perspective, HMMs for analyzing psychological data. Rijmen et al. (2008) applied the HMM to biomedical data collected from patients with brain tumor. A structurally identical family of models—the latent Markov models—has also been extensively studied in the social science literature. Some recent applications in social and economic sciences include the work of Bartolucci, Pennoni, and Francis (2007), Paas, Bijmolt, and Vermunt (2007), and Ip et al. (2010). Dias and Vermunt (2007) discussed model selection issues in latent Markov and mixture models. For a history of development of latent Markov models, see the works by Wiggins (1973), Humphreys (1998), Vermunt, Langeheine, and Bockenholt (1999), and the references therein.
The remainder of this article is organized as follows. We first describe the basic multivariate discrete HMM model and methods of estimating the models. Then we describe the aforementioned methods (1)–(3) for solving the several limitations of the HMM. Subsequently, we describe an application using NLSY data to illustrate the proposed methods.
2. MODEL
2.1 The Basic Discrete Hidden Markov Model
Let yitj denote the discrete response of subject i at occasion t on outcome j, i = 1, …, N; j = 1, …, J; t = 1, …, T. We assume that each outcome indicates the level of response k, k = 1, …, Kj, from an individual as measured by an “item,” such as a survey question. Specifically, yit = (yit1, …, yitJ)′ denotes the response vector of subject i at occasion t, and represents the complete response pattern of subject i. Additionally, zit = 1, …, S denotes the categorical (unobserved) latent state of subject i at occasion t. Thus, zi = (zi1, …, ziT)′ is the state sequence of subject i through the latent space over time. A first-order Markov chain for the latent variable assumes that the latent state at occasion t + 1 depends only upon the latent state at occasion t; that is, for any i, p (zit|zi1, …, ziT) = p (zit|zit−1). Accordingly, the basic hidden Markov model contains the following three sets of parameters:
τ = (τrs), the S × S matrix of time-homogeneous transition probabilities between latent states, where for any i, τrs = p (zit = s|zit−1 = r), t = 2, …, T.
α1 = (α11, …, α1S)′, the S × 1 vector of marginal probabilities of the states at occasion 1, α1s = p (zi1 = s). The vector αt = (αt1, …, αtS)′, t = 2, …, T, can be recursively derived by the formula .
π = (πjsk), the J × S × Kj array of state-conditional response probabilities, where k is the index of outcome category, k = 1, …, Kj, and for any i, t, πjsk = Pr(yitj = k|zit = s), where .
Assuming conditional independence between responses given the latent state, the marginal probability of a response pattern yi is given by
| (2.1) |
with the summation over the entire latent state space 𝒵 of size ST, and
| (2.2) |
Furthermore, we write out the likelihood equation using the local independence assumption given a latent state:
| (2.3) |
where δ (yitj, k) = 1 if yitj = k, and 0 otherwise.
2.2 Estimation of the Basic HMM
The EM algorithm (Dempster, Laird, and Rubin 1977) is used to evaluate parameters for the basic HMM. For historical reasons, a version of the EM algorithm used to estimate HMM is also known as the Baum–Welch algorithm (Baum and Petrie 1966). Briefly, in the EM terminology, the latent state is treated as “missing data.” The objective here is to maximize the conditional expected log-likelihood of the complete data, which include the observed data y and the latent states z, given y and some provisional estimates for the parameters, where y and z, respectively, denote the vector of the collection of data (yi) and (zi).
Denote the entire parameter set defined in (2.1)–(2.2) by β, and let β(n) be defined as the estimate at the nth iteration of the EM algorithm. Furthermore, let
where Q is the conditional expected value of the complete data log-likelihood function given observed data y:
| (2.4) |
With discrete latent state variables z, we have
| (2.5) |
Assuming that observations between individuals are independent, it follows that
| (2.6) |
The posterior probabilities, p (zi|yi, β(n)), can be derived via the Bayes theorem in the so-called E-step, which we shall describe in Section 3.2. Updating parameter values can be accomplished through the maximization of (2.6) with respect to β in the so-called M-step of the EM algorithm. The algorithm alternates between the E-step and the M-step until the absolute change in the objective function is smaller than a predetermined threshold value.
Specifically, the joint distribution of the complete data of subject i in (2.6) is
| (2.7) |
One appealing feature about (2.7) is the separability of three sets of parameters, which can be optimized individually. By taking the logarithm on (2.7), we rewrite the objective function in (2.6):
| (2.8) |
We further define two sets of subject-specific HMM “pseudo-counts” as follows:
- , where is an S ×S matrix and for each i, the (r − s)th entry is
(2.9) , and . The vector , can be recursively derived by the formula .
Using the notation above, each of the three terms over the right side of (2.8) can be expressed as a multinomial log-likelihood of the form
| (2.10) |
where I is a vector of summation indices, 𝒴iI are the “pseudo-counts,” which may take non-integer values, and ψI are the model-based estimated probabilities. Specifically, in the first row of (2.8), I = {s|s = 1, …, S}, , and ψiI = α1s; in the second row of (2.8), I = {(r, s)|r = 1, …, S, s = 1, …, S}, , and ψI = τrs; and in the third row of (2.8), I = {(j, s, k)| j = 1, …, J, s = 1, …, S, k = 1, …, Kj }, , and ψI = πjsk.
In (2.10), the pseudo-counts , and can be treated as observed responses in a cell of a multinomial distribution, and α1s, τrs, and πjsk as the cell probability parameters to be estimated. The following two conditions are satisfied for each of the three components: (1) the expected value of the pseudo-count equals the corresponding parameter, (2) the probability parameter entries sum to 1. For example, for the marginal component, for any i, , and . The M-step thus involves applying the sum-to-1 constraints to each of α1s, τrs, and πsjk, adding a Lagrange multiplier to each term in (2.8), and taking the derivative of each term. The updating equation for maximum likelihood estimates (MLEs) of α1s, τrs, and πjsk are the solutions of the re-estimation formulas of the basic HMM (Rabiner 1989):
| (2.11) |
| (2.12) |
| (2.13) |
Stated in various forms, the above expression of the conditional expected complete log-likelihood function as multinomial log-likelihood and the estimation formula for the parameters are not new and well known in the literature (e.g., Cowell et al. 1999, p. 202). Our point of stating the result in the above form is to provide the formalism for the subsequent inference procedure when the HMM is extended.
3. EXTENDED MULTIVARIATE DISCRETE HMM
To fix notation, we denote item j within domain d by d (j), d = 1, …, D, and the predictive p-vector of the individual long-term trait by xi. For example, the second item (j = 2) measuring anxiety in the domain of problematic behavior (d = 1) is subscripted as 1(2). On the other hand, xi may contain predictors such as family background. We denote the individual-specific conditional probability Pr(yitj = k|zit = s) by πijsk. Note that an index i has been added to the subscript for π. As we shall see, by extending the HMM to include individual-specific effects, the conditional probabilities given latent states would be functions of i. For discrete data, we use an appropriate link function for transforming the state-conditional response probabilities π. For the sake of illustration, we only describe the model for ordinal outcomes, although models for binary and unordered categorical responses can be constructed in a similar way. A modified cumulative logit transform (Fahrmeir and Tutz 1994) for the response solicited from item j can be written as
| (3.1) |
where the cumulative probability ζijsk is given by
| (3.2) |
with i = 1, …, N, j = 1, …, J, s = 1, …, S, and k = 1, …, Kj, and subject to the constraint . By requiring that the difference in logits in (3.1) be positive, the log–log transform enforces the order of the responses such that the cumulative logit of a higher category is always larger than that of a lower category. We shall refer to the collection of link functions (h1, …, hKj−1) simply as h(·).
We study the following ordinal cumulative logistic models:
(A) Domain-based HMM:
| (3.3) |
where k = 2, …, Kj − 1; s = 1, …, S − 1. No coefficients ϕ, ξ are defined for the last category Kj, and . To parameterize (3.3) into a full-rank model, no coefficient is estimated for ξd(j)sk at the last state S. See also the example of a design matrix discussed in the Appendix Estimation of GLM.
The simplest domain-based model is to constrain all of the items within the same domain to have identical logit: h1 (ζijs1) = ξd(j)s1, and hk (ζijsk, ζijs(k−1)) = ξd(j)sk, s = 1, …, S. Including the parameter ϕjk allows deviation of the logit of a specific item from the common logit of the domain. The domain-based model generally has fewer parameters than the model (3.1). The saving in the number of parameters can be substantial when there are many states. Other special cases of (3.3) are possible (e.g., ϕjk ≡ ϕj), but they will not be pursued further here.
(B) Person-specific HMM:
| (3.4) |
where k = 2, …, Kj − 1, θi is the individual random effect, and θi ~ N (0, σ2), where σ2 is the variance of the normal distribution. Model B represents a basic HMM with an additional random effect. The random effect θi can be interpreted as a relatively stable trait that consistently affects all of the measured outcomes of an individual.
Clearly, a unifying model can be constructed by combining the domain-based and the person-specific HMMs, and also including person-specific predictors xi for the latent trait:
(C) Unified HMM:
| (3.5) |
where k = 2, …, Kj − 1, and , where γ is a p-vector of regression coefficients.
3.1 Parameter Estimation and the M-Step
We first describe the estimating algorithm for the HMM with random effects (Model B). Subsequently, we discuss the estimation of the unified HMM. The EM algorithm continues to be the workhorse for parameter estimation in both cases. Following the notation in the section for the basic HMM estimation, the conditional expected log-likelihood of the complete data Q (β, β(n)) for Model B is given by
| (3.6) |
where θ = (θ1, …, θN). Assuming that θ and z are independent, we have p (zi, θi|yi, β(n)) = p (zi|yi, β(n)) fβ(n)(θi|yi), where fβ(n)(θi|yi) is the posterior density of θ.
Thus, the objective function is
| (3.7) |
in which the joint distribution of the complete data of subject i within (3.7) is given by
| (3.8) |
By taking the logarithm on (3.8) and substituting (3.7), we rewrite the objective function:
| (3.9) |
In the M-step of the EM algorithm, one needs to evaluate the integrals in (3.9). There is generally no closed-form solution for the integral of the random effects θi. Various numerical procedures, including the Gauss–Hermite quadrature (Hinde 1982), Monte Carlo techniques (McCulloch 1997), and Taylor expansions (Wolfinger and O’Connell 1993) have been proposed. Our choice is the Gauss–Hermite quadrature for integration. Denote the vector of q quadrature points by v = (υl). The corresponding collection of weights , which depend upon the current estimate of the variance structure, σ(n), are used to approximate fβ(n) (θi). At a quadrature point υl, denote the conditional probability by πijksl = [πijsk (θi)]θi=υl. The integration notwithstanding, computationally the conditional expected log-likelihood still retains the multinomial form. We summarize this observation as a lemma.
Lemma 1
Equation (3.9), which is a generalized form of log-likelihood functions in (2.8) but with an additional dimension of quadrature points for random effects, simplifies to four separate multinomial expressions (2.10). In particular, the first two terms on the right side remain in the same form as the basic HMM. Additionally,
in the third term of (3.9), I = {s, j, k, l}, , and ψiI = πijskl, where , of which the conditional density is evaluated at θi = υl; and
- the fourth term of (3.9) can be simplified into the log-likelihood function of multinomial responses as follows:
(3.10)
where , and wl = fβ(υl).
Proof
Comparing the third row of (3.9) with that of (2.8), we only need to add in and add an extra dimension l to α̃(n), and thus the proof of the first part is straightforward.
For the second part, because θi’s are independent of the latent states, the fourth row of (3.9) simplifies to .
Lemma 1 implies that the computational methods for the basic HMM can still be applied to the random effects model (Model B), but with an additional dimension of quadrature points. For the unified HMM in Model C, there is no closed-form solution for solving the regression coefficients in the conditional probability model. Following the setup in Lemma 1, we can include a generalized linear model (GLM) for the unified HMM. Technical details for estimation of the GLM are provided in an Appendix.
3.2 Computation of the E-Step
The E-step involves the computation of posterior probabilities of the latent states given observed data. Accordingly, the joint distribution and selected marginal distributions have to be evaluated. In HMM, the E-step involves the evaluation of p (yi) and p (zi). It is well known that brute force summation is not efficient for obtaining marginal probabilities. Various techniques, including approximating algorithms such as Monte Carlo methods, have been proposed (Korb and Nicholson 2003, p. 61). The computations of p (yi) and p (zi), for example, both require the summation of ST terms. In our implementation, we adopted the junction-tree method developed from graphical model theory (Jensen, Lauritzen, and Olesen 1990; Lauritzen 1995). The essence of this implementation is a decomposition of a high-dimensional joint probability distribution into self-contained modules of lower dimensions called cliques (to be defined later) and the subsequent local computation of clique probability distribution. In order to do this, the first step is to create a Directed Acyclic Graph (DAG) for the associated statistical model. The directed graph, consisting of nodes (variables) and arcs, is a pictorial representation of the conditional dependence relations of the statistical model. Figure 1(a) shows the DAG of the extended HMM with random effects θ. The second step is to “moralize” the graph, that is, remove arrows and connect (marry) parents, if they are not already connected. A third step is to triangulate the moral graph; edges are added so that chordless cycles contain no more than three nodes. For the basic HMM, the moral and triangulated graphs are topologically identical to the DAG, but for the HMM with random effects, the graphs are not identical. We show the triangulated graph in Figure 1(b). The fourth step is to identify cliques (maximal subsets of nodes that are all interconnected) from the triangulated graph and form compound nodes by fusing nodes of the same clique into a single node. The fifth step is to create separator nodes, which consist of intersections of adjacent compound nodes (Figure 1(c)). The final tree structure is known as a junction tree, an important property of which is that the joint probability function can be factorized into the product of clique marginals over separator marginals (e.g., Jensen, Lauritzen, and Olesen 1990):
| (3.11) |
where 𝒞 and 𝒮, respectively, denote the set of cliques and the set of separators. Cowell et al. (1999, pp. 28–35) provided a simple example to illustrate the process. The junction tree forms the basis of efficient local computation of clique marginals in the E-step and the global computation of the joint density through so-called message-passing schemes (Pearl 1988; Jensen, Lauritzen, and Olesen 1990), which essentially consists of repeated applications of the Bayes theorem.
Figure 1.
(a) Directed Acyclic Graph (DAG) for HMM with random effects. Shaded ovals indicate observed variables (two are shown here at each time point), and unshaded ovals indicate latent variables. (b) Moral and triangulated graphs for DAG in (a). The parents of the observed variables are joined in a moral graph (e.g., arc from θ to Zi1). (c) Junction tree for DAG in (a). Ovals indicate clique nodes and variables between clique nodes are separators.
Implementation through the junction-tree method has several advantages. First, it has proved to be a highly efficient and scalable algorithm for inference in graphical models, and has been implemented in commercial software such as Hugin (Hugin Expert, Aalborg, Demark). As a special form of the graphical model, the HMM described in this article can be efficiently implemented using junction tree. More importantly, the graphical model framework permits the extension of the basic HMM to include model refinements in highly flexible ways. For example, in the unified model with random effects, nodes representing the stable latent trait can be added to the graphical representation, and the modified junction tree can then be implemented through the aforementioned general algorithm.
The above algorithm was built upon a Matlab toolbox called BNL (Rijmen 2006), which combines the toolbox of Kevin Murphy (Murphy 2001) for constructing the junction tree with a GLM estimation framework for parameterizing the conditional probabilities. The entire program can be downloaded from http://www.phs.wfubmc.edu/public/downloads/MHMM.zip.
3.3 Model Selection
In the fitting of HMM models, the number of hidden states is usually not known a priori. An approach suggested by Huang and Bandeen-Roche (2004) in a context of latent class analysis is to employ the Bayesian Information Criterion (BIC; Schwarz 1978) to determine the optimal number of states that gives the lowest BIC value by fitting a range of basic HMMs, without covariates, to the data. While BIC is simple and easy to use, it is a function of the sample size N and has the potential problem of not being able to specify the appropriate “effective sample size” in a longitudinal context because observations of the same subject at different time points are correlated. Generally, if observations from across all T time points are used to determine the number of latent states, the correct sample size should be somewhere between N and NT.
Following the work on the Bayes factor (Kass and Raftery 1995), we derive a criterion that can be used for model selection in the HMM context. Specifically, the criterion is an approximation of the probability density of observations given a specific Model H.
Denote the observed data by Y and the model parameter by β = (βi) = (α1, τ, π), i = 1, …, d. The marginal probability density of observing the data under Model H can then be written in an integral form:
| (3.12) |
where f (β|H) is the prior distribution of parameters of Model H. By assuming that the integrand is highly peaked about its maximum at the maximum likelihood estimate β̂, we can approximate the integral by Laplace’s method (De Bruijn 1970), that is,
| (3.13) |
where Σ̂ is the covariance matrix, that is, [−D2l(β̂)]−1, and l(β) = log(p (Y|β, H) × f (β|H)) is the log-likelihood of observed data and the parameter priors.
In HMM, we can explicitly derive from the likelihood functions (2.8) an analytical form of (3.13). Recently, Bayarri et al. (2007) provided a similar derivation for a Bayes factor-based BIC using the multivariate ANOVA model. Visser et al. (2006) derived another Bayes factor under a multivariate autocorrelation model. In the latter work, through simulation experiments, it was also shown that Bayes factor-based criteria perform better than BIC. For the basic HMM (2.8), we follow the notation in Section 2.1 and assume that Kj ≡ K. The Laplace approximation leads to the following results.
Lemma 2
The (−2) times log probability of observing the data, given a discrete hidden Markov model with parameters that follow a Dirichlet prior distribution with a count vector of 1, can be approximated with Laplace’s method as follows:
| (3.14) |
where d = S2 − 1 + SJ (K − 1) is the number of parameters of an S-state HMM, Σ̂ = [−D2l̃(β̂)]−1, and l̃ = log(p (Y|β, H).
Notice that compared to l, l̃ is only the log-likelihood of observed data without the prior parameters. The exact covariance matrix Σ̂ can be computed using Lystig and Hughes’s method (2002) for HMM. A proof is provided in an Appendix. We call the model selection index in (3.14) the modified BIC (mBIC).
To compare the performance of mBIC with BIC, a simulation study was undertaken with the following conditions and levels within each condition: number of states S = 3, 4; sample size N = 100, 200, 400; number of outcomes J = 2, 8, 19; and number of time points T = 3, 5, 10. Both 3-state and a 4-state HMMs were used to generate 100 datasets under each condition. The parameters used to generate the data were based on the structure of a 19-item dataset reported by Rijmen et al. (2008). We modified the parameters so that the states are relatively well separated. Table 1 shows the proportion of correct models selected among 100 datasets within each condition. The mBIC tends to perform better than the BIC when any one of the three conditions: sample size N, number of outcomes J, or the number of time points T, is small. For example, for 3-state models, when N = 100, J = 8, and T = 3, mBIC correctly selected the 3-state model 68% of the time versus 49% for BIC. Both models tended to select the 2-state model when they did not select the correct model. Both the mBIC and BIC perform consistently well when the levels of sample size, number of outcomes, and number of time points become higher.
Table 1.
Model selection simulation results: Proportion of correct models selected for combinations of S states, J outcomes, T time points, with sample size N.
| S | N | J | T | BIC | mBIC | N | J | T | BIC | mBIC |
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 100 | 2 | 3 | 0 | 0.07 | 400 | 2 | 3 | 0.01 | 0.08 |
| 100 | 2 | 5 | 0.23 | 0.36 | 400 | 2 | 5 | 1 | 1 | |
| 100 | 2 | 10 | 0.96 | 0.97 | 400 | 2 | 10 | 1 | 0.97 | |
| 3 | 100 | 8 | 3 | 0.49 | 0.68 | 400 | 8 | 3 | 1 | 1 |
| 100 | 8 | 5 | 0.9 | 0.9 | 400 | 8 | 5 | 1 | 1 | |
| 100 | 8 | 10 | 0.98 | 0.92 | 400 | 8 | 10 | 1 | 0.99 | |
| 3 | 100 | 19 | 3 | 1 | 1 | 400 | 19 | 3 | 1 | 1 |
| 100 | 19 | 5 | 0.98 | 0.98 | 400 | 19 | 5 | 1 | 1 | |
| 100 | 19 | 10 | 0.92 | 0.9 | 400 | 19 | 10 | 1 | 1 | |
| 4 | 200 | 2 | 3 | 0 | 0.02 | 400 | 2 | 3 | 0.01 | 0.12 |
| 200 | 2 | 5 | 0.12 | 0.11 | 400 | 2 | 5 | 0.62 | 0.65 | |
| 200 | 2 | 10 | 0.66 | 0.61 | 400 | 2 | 10 | 0.87 | 0.85 | |
| 4 | 200 | 8 | 3 | 0.9 | 0.87 | 400 | 8 | 3 | 1 | 1 |
| 200 | 8 | 5 | 1 | 1 | 400 | 8 | 5 | 0.99 | 0.99 | |
| 200 | 8 | 10 | 1 | 1 | 400 | 8 | 10 | 1 | 1 |
4. DATA ANALYSIS EXAMPLE
The dataset contains three waves of biennial data collected from 1989 to 1994 in the National Longitudinal Survey of Youth (NLSY79), and the 1990–1994 Children of the NLSY (CoNLSY). Because of missing value problems, which are rather extensive within this NLSY subsample, we only selected those children who had at most two missing values out of a total of 24 measurements taken over the three-year period. This resulted in a sample of 367 children (52% female, 29% African–American, and 20% Hispanic; age range approximately 5–9). There are partially missing values within this final sample, but the percentage is less than 3%. We used multiple imputation (Rubin 1987; Schafer 1997) for handling missing item responses. Before conducting HMM analysis, the dataset was preprocessed—a set of m = 5 values were imputed for missing values using PROC MI (SAS Institute Inc.).
Our analysis focuses on cognitive and social development in children five to nine years old. The goal is to identify homogeneous groups of children in terms of their behavioral and cognitive outcomes and to examine how various risk factors, including maternal alcoholism, may affect development. While previous studies (e.g., Snow Jones 2007) have found a positive association between parents’ or maternal alcohol consumption and children’s behavioral and cognitive problems, many of these studies only assume a linear trend in social or cognitive outcomes as a function of risk factors.
Five outcome variables were selected from the Behavior Problem Index (BPI): anti-social, anxious, peer conflict, headstrong, and hyperactive behaviors. Three variables that measure academic achievement were selected from Peabody Individual Achievement Test (PIAT) scores: math, oral reading, and reading comprehension. We respectively refer to these two sets of variables as representatives of Domains 1 and 2. The BPI and PIAT outcomes were trichotomized into three categories (0, 1, 2) based on nationally normed percentiles with cutpoints at 15% and 85%. Diagnostic groups determined by cutoff points have been commonly used in school reporting systems and research studies to categorize at-risk status. Shepard, Smith, and Vojir (1983), for example, used a cutoff at the 12th percentile in PIAT math to define “below-grade performance” in fifth graders. In a personality study, Hart, Atkins, and Fegley (2003) used the 80th percentiles as cutoff scores on the BPI scales for forming diagnostic groups. We also observe that many school systems use the 15th, 50th, and 85th percentile for reporting purposes, and our choice of cutoffs at 15% and 85% reflects these considerations. To further facilitate model interpretation, BPI categories were then reordered so that movement from 0 to 2 represented increasingly better behavior and conformed to the direction of the PIAT classification.
An important variable that may significantly contribute to a child’s development trajectory is home environment. In our analysis, we include home environment variables in the conditional distributions using the Home Observation for Measurement of the Environment (HOME) inventory. Two HOME scores were available that measured cognitive stimulation and emotional support. Demographic variables such as gender were found not to be significant in this sample, and the analysis results reported here do not include such variables. We report regression models using maternal drinking, and the other HOME variables.
4.1 Results of HMM Analyses
Table 2 shows the BIC and mBIC values for models with two to five hidden states. Both BIC and mBIC values suggest the 5-state model, but both values for the 5-state model are very close to those of the 4-state model. One of the states in the 5-state has low prevalence and was not seen to offer significant information when further consultation with content experts was solicited. We therefore selected the 4-state model for all subsequent analyses. To illustrate the several proposed features of HMM described in Section 2.2, we report results from analyzing the NLSY data using several different HMM models:
Model 0: Basic HMM. No covariate was used, and a saturated conditional probability model was fitted to the data.
Model I: Domain-based HMM. Items that belong to the same domain d = 1, 2 (for behavioral and cognitive, respectively) are assumed to follow (3.3).
Model II: HMM with person-specific random effects θi to account for dependency given state but without covariate.
- Model III: HMM with only fixed effects on conditional probabilities:
where xi1, xi2, and xi3 are the two HOME scores and the maternal pregnancy drinking score, and β1 to β3 are the corresponding fixed effects.(4.1) Model IV: Unified HMM with both fixed and random effects on conditional probabilities that follows (3.5).
Table 2.
Number of parameters, deviance, and BIC for the estimated models.
| States | Parameters | Deviance | BIC | mBIC | |
|---|---|---|---|---|---|
| Basic HMM | 2 | 35 | 16758 | 16964 | 16999 |
| 3 | 56 | 16215 | 16543 | 16576 | |
| 4 | 79 | 15819 | 16284 | 16324 | |
| 5 | 104 | 15702 | 16255 | 16293 | |
| 6 | 131 | 15520 | 16294 | 16361 |
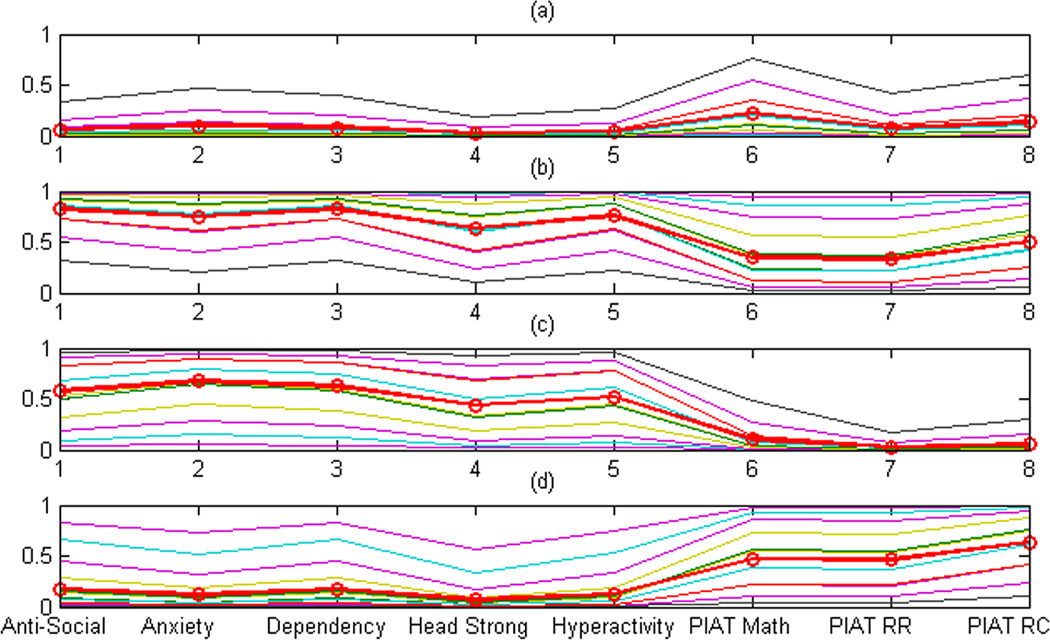
Table 3 contains the prior probabilities of five states and the transition probabilities table under Model 0, whereas Figure 2 displays the profile of each of the four states, also estimated from Model 0. Each stacked bar in Figure 2 shows the conditional probability distribution of the response categories for a specific item within each state. State 1 can be interpreted as the “no problem or a minor problem” state, State 2 as the “bad behavior (Domain 1) but good academics (Domain 2)” state, State 3 as the “good behavior but poor academics” state, and State 4 as the “bad behavior and poor academics” state. While different models fitted to the data produce different conditional probabilities, the profiles of the four states remain relatively stable (for Models II and IV, the profiles are obtained from averaging over individual profiles). Table 4 reports parameter estimates of Models I–IV and their respective standard errors. The random effects in both Models II and IV are significant. To investigate the heterogeneity of the individuals within a given state, we graphically display the probabilities of the N = 367 individual responses over all the items in Figure 3. The heterogeneity among individuals within a given state appears to be substantial, and the significant variance of θi in Models II and IV also reflects the potential conditional dependence among item responses within a given latent state.
Table 3.
Estimated prior state probabilities and transition probabilities.
| State 1 | State 2 | State 3 | State 4 | |
|---|---|---|---|---|
| Prior probabilities α | 0.21 | 0.31 | 0.28 | 0.20 |
| Transition probabilities τ | 0.89 | 0.06 | 0.03 | 0.01 |
| 0.07 | 0.80 | 0.04 | 0.09 | |
| 0.07 | 0.11 | 0.69 | 0.13 | |
| 0.00 | 0.05 | 0.13 | 0.82 |
Figure 2.
Conditional probability profile for the 4-state model. Each column represents the distribution of expected responses to an item. The bar at the bottom represents the worst response category (0) and the second bar the next worst category (1).
Table 4.
Parameter estimates (standard error) of Model I to Model IV on conditional probabilities. Significant effects at α = 0.05 level are highlighted in bold.
| Model I | Model II | Model III | Model IV | |||
|---|---|---|---|---|---|---|
| Anti-social | Response 1 | −1.45 (0.10) | −1.42 (0.17) | −2.08 (0.11) | −1.04 (0.10) | |
| Response 2 | −3.47 (0.21) | −3.80 (0.32) | −3.87 (0.16) | −2.72 (0.11) | ||
| Anxiety | Response 1 | −1.99 (0.10) | −1.97 (0.17) | −2.60 (0.11) | −1.60 (0.10) | |
| Response 2 | −3.96 (0.21) | −4.36 (0.33) | −4.37 (0.17) | −3.29 (0.12) | ||
| Dependency | Response 1 | −1.73 (0.10) | −1.70 (0.17) | −2.34 (0.11) | −1.32 (0.10) | |
| Response 2 | −3.45 (0.21) | −3.81 (0.32) | −3.86 (0.16) | −2.73 (0.11) | ||
| Head strong | Response 1 | −0.72 (0.10) | −0.66 (0.17) | −1.37 (0.11) | −0.26 (0.10) | |
| Response 2 | −4.64 (0.22) | −5.11 (0.33) | −5.07 (0.18) | −4.06 (0.13) | ||
| Hyperactivity | Response 1 | −1.16 (0.10) | −1.12 (0.17) | −1.79 (0.11) | −0.73 (0.10) | |
| Response 2 | −3.90 (0.21) | −4.29 (0.32) | −4.30 (0.17) | −3.22 (0.12) | ||
| Math | Response 1 | −0.29 (0.10) | 0.25 (0.21) | −1.18 (0.12) | 2.34 (0.16) | |
| Response 2 | −3.02 (0.17) | −3.13 (0.28) | −3.87 (0.17) | −0.71 (0.11) | ||
| Oral reading | Response 1 | 1.01 (0.12) | 1.79 (0.22) | 0.16 (0.13) | 3.85 (0.18) | |
| Response 2 | −3.09 (0.17) | −3.19 (0.28) | −3.92 (0.17) | −0.78 (0.11) | ||
| Reading comprehension | Response 1 | 0.37 (0.11) | 1.02 (0.21) | −0.51 (0.12) | 3.10 (0.17) | |
| Response 2 | −2.15 (0.16) | −2.18 (0.27) | −2.98 (0.15) | 0.23 (0.11) | ||
| State 1 | Domain 1 | Response 1 | 3.70 (0.12) | 3.37 (0.17) | 3.51 (0.13) | 3.72 (0.25) |
| Response 2 | 4.00 (0.21) | 3.96 (0.32) | 3.46 (0.16) | 3.70 (0.19) | ||
| Domain 2 | Response 1 | 3.92 (0.30) | −0.22 (0.22) | 3.42 (0.28) | −0.84 (0.31) | |
| Response 2 | 3.54 (0.18) | −0.23 (0.28) | 3.19 (0.16) | −0.38 (0.23) | ||
| State 2 | Domain 1 | Response 1 | 1.31 (0.09) | 1.46 (0.17) | 1.05 (0.08) | 1.03 (0.08) |
| Response 2 | 1.65 (0.22) | 2.19 (0.32) | 1.25 (0.16) | 0.87 (0.09) | ||
| Domain 2 | Response 1 | 3.18 (0.20) | 3.28 (0.25) | 3.29 (0.20) | −1.73 (0.16) | |
| Response 2 | 2.81 (0.17) | 3.55 (0.28) | 2.76 (0.15) | −1.93 (0.11) | ||
| State 3 | Domain 1 | Response 1 | 2.90 (0.10) | 2.56 (0.18) | 2.76 (0.10) | 2.36 (0.10) |
| Response 2 | 3.32 (0.21) | 3.18 (0.32) | 2.91 (0.15) | 2.28 (0.10) | ||
| Domain 2 | Response 1 | 0.50 (0.11) | 1.49 (0.22) | 0.57 (0.11) | −2.92 (0.17) | |
| Response 2 | −0.04 (0.21) | 1.79 (0.30) | −0.10 (0.19) | −3.00 (0.16) | ||
| Home cognitive stimulation | 0.83 (0.05) | 0.57 (0.05) | ||||
| Home emotional support | 0.12 (0.05) | 0.35 (0.05) | ||||
| Maternal pregnancy drinking | 0.52 (0.20) | 0.07 (0.22) | ||||
| Standard deviation of θi | 0.78 (0.02) | 0.70 (0.02) |
Figure 3.
Comparison of sample average conditional probabilities, πjsk, in circles, with fitted individual conditional probabilities, πijsk, in lines, under Model II. (a) State 1, response category 0; (b) State 1, response category 2; (c) State 2, response category 0; (d) State 2, response category 2. A color version of this figure is available in the electronic version of this article.
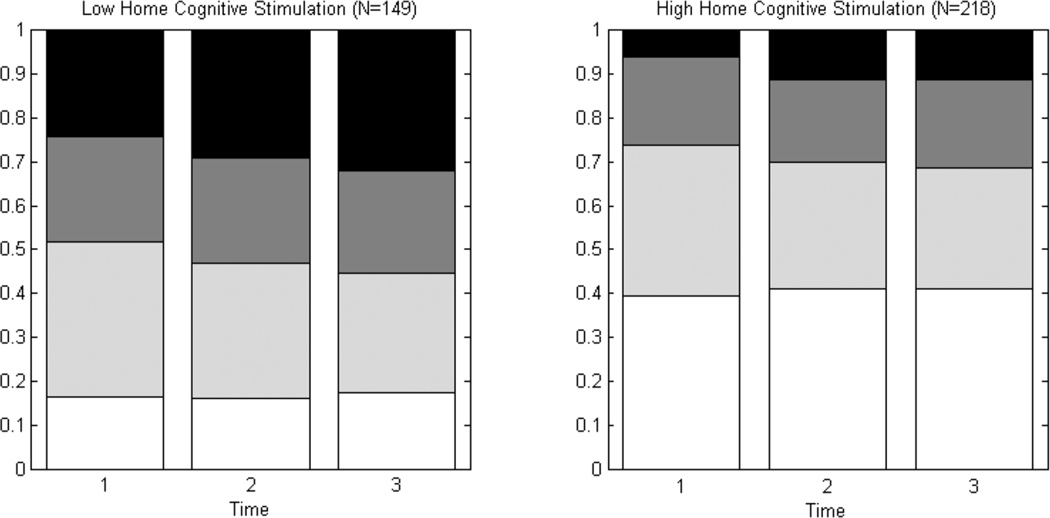
From Table 4, the domain-based model suggests that the domain effect—that is, the domain (behavior or academic) to which an item belongs—is highly significant. The domain estimates for the states are consistent across the several models and agree with the findings in Figure 2. For example, the values of domain estimates are higher in State 1 for both academic and behavior, showing that children in State 1 perform better in both domains. State 2 generally has low values in academic and moderately high values in behavior, whereas the values in State 3 are reversed. Models III and IV each contain a regression component for the conditional probabilities using HOME scores and maternal drinking status. Both cognitive stimulation and emotional support at home show strong positive impacts on the conditional response probabilities (p < 0.001), indicating that more supportive home environments are associated with better behavior and academic performance. Figure 4 shows that although both high and low Home Cognitive Stimulation groups have increases in State 4 children over time, the percentage of State 1 students is indeed higher in the high Home Cognitive Stimulation group than in the low Home Cognitive Stimulation group. Maternal drinking was not statistically significant. In other words, the long-term stable trait underlying individual behavior and cognition is associated more with home environmental variables and not so much with maternal drinking status. However, it is worth noting that there are only 12 high-risk-pregnancy drinkers in this sample, which may contribute to low power that is not sufficient to detect a difference.
Figure 4.
State prevalence over time for two Home Cognitive Stimulation groups. States 1 to 4 are ordered from bottom up.
Supplementary Material
Acknowledgments
This research was made possible by grants R01 AA11071 (Snow Jones (PI)) from the National Institute of Alcohol Abuse and Alcoholism and the Office of Research on Women’s Health, and 0532185 from the National Science Foundation (Ip (PI), Snow Jones (co-PI)).
Footnotes
SUPPLEMENTAL MATERIALS
Appendix: Technical details on GLM estimation, the proof of Lemma 2, and instructions to use the computer codes. (appendix.pdf)
Computer codes: MATLAB-package containing codes to fit Models I to IV in Section 4.1 with instructions appearing in the online Appendix. The package also contains a subset of the NLSY dataset used in this article. (MHMM.zip)
Contributor Information
Qiang Zhang, Department of Biostatistical Sciences, Wake Forest University School of Medicine, Winston-Salem, NC 27159..
Alison Snow Jones, Business and Public Health Partnerships, Drexel University School of Public Health, Philadelphia, PA 19102..
Frank Rijmen, Educational Testing Service, Princeton, NJ 08541..
Edward H. Ip, Department of Biostatistical Sciences and Department of Social Sciences and Health Policy, Wake Forest University School of Medicine, Winston-Salem, NC 27159 (eip@wfubmc.edu)..
REFERENCES
- Altman RM. Mixed Hidden Markov Models: An Extension of the Hidden Markov Model to the Longitudinal Data Setting. Journal of the American Statistical Association. 2007;102:201–210. [Google Scholar]
- Bartolucci F, Pennoni F, Francis B. A Latent Markov Model for Detecting Patterns of Criminal Activity. Journal of the Royal Statistical Society, Ser. A. 2007;170:115–132. [Google Scholar]
- Baum LE, Petrie T. Statistical Inference for Probabilistic Functions of Finite State Markov Chains. The Annals of Mathematical Statistics. 1966;37:1554–1563. [Google Scholar]
- Bayarri S, Berger J, Jang W, Pericchi L, Ray S, Rueda R, Visser I. 6th Workshop on Objective Bayesian Methodology. Roma, Italy: 2007. Extension and Generalization of BIC. [Google Scholar]
- Chase-Lansdale PL, Mott FL, Brooks-Gunn J, Phillips DA. Children of the National Longitudinal Survey of Youth: A Unique Research Opportunity. Developmental Psychology. 1991;27:918–931. [Google Scholar]
- Cowell RG, Dawid AP, Lauritzen SL, Spiegelhalter DJ. Probabilistic Networks and Expert Systems. New York: Springer; 1999. [Google Scholar]
- de Bruijn NG. Asymptotic Methods in Analysis. Amsterdam: North-Holland; 1970. [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum Likelihood From Incomplete Data via EM Algorithm. Journal of the Royal Statistical Society, Ser. B. 1977;39:1–38. [Google Scholar]
- Dias JG, Vermunt JK. Latent Class Modeling of Website Users’ Search Patterns: Implications for Online Market Segmentation. Journal of Retailing and Consumer Services. 2007;14:359–368. [Google Scholar]
- Fahrmeir L, Tutz G. Multivariate Statistical Modeling Based on Generalized Linear Models. New York: Springer; 1994. [Google Scholar]
- Frees EW. Longitudinal and Panel Data Analysis and Applications in the Social Sciences. Cambridge, U.K.: Cambridge University Press; 2004. [Google Scholar]
- Hart D, Atkins R, Fegley SG. Personality Types of 6-Year-Olds and Their Associations With Academic Achievement and Behavior. Monographs of the Society for Research in Child Development. 2003;68(1):19–34. [PubMed] [Google Scholar]
- Hinde JP. Compound Regression Models. In: Gilchrist R, editor. GLIM 82: International Conference for Generalized Linear Models. New York: Springer; 1982. pp. 109–121. [Google Scholar]
- Huang GH, Bandeen-Roche K. Building an Identifiable Latent Variable Model With Covariate Effects on Underlying and Measured Variables. Psychometrika. 2004;69:5–32. [Google Scholar]
- Hughes JP, Guttorp P, Charles SP. A Nonhomogeneous Hidden Markov Model for Precipitation. Applied Statistics. 1999;48:15–30. [Google Scholar]
- Humphrey K. The Latent Markov Chain With Multivariate Random Effects: An Evaluation of Instruments Measuring Labor Market Status in the British Household Panel Study. Sociological Methods and Research. 1998;26:269–299. [Google Scholar]
- Ip EH, Snow Jones A, Heckert DA, Zhang Q, Gondolf E. Latent Markov Model for Analyzing Temporal Configuration for Violence Profiles and Trajectories in a Sample of Batterers. Sociological Methods and Research. 2010 to appear. [Google Scholar]
- Kass RE, Raftery AE. Bayes Factors. Journal of the American Statistical Association. 1995;90(430):773–795. [Google Scholar]
- Korb KB, Nicholson AE. Bayesian Artificial Intelligence. London: Chapman & Hall; 2003. [Google Scholar]
- Jensen FV, Lauritzen SL, Olesen KG. Bayesian Updating in Causal Probabilistic Networks by Local Computation. Computational Statistics Quarterly. 1990;4:269–282. [Google Scholar]
- Lauritzen SL. The EM Algorithm for Graphical Association Models With Missing Data. Computational Statistics and Data Analysis. 1995;19:191–201. [Google Scholar]
- Laursen B, Hoff E. Person-Centered and Variable-Centered Approaches to Longitudinal Data. Merrill–Palmer Quarterly. 2006;52:377–389. [Google Scholar]
- Lord FM, Novick MR. Statistical Theories of Mental Tests Scores. Readings, MA: Addison-Wesley; 1968. [Google Scholar]
- Lystig TC, Hughes JP. Exact Computation of the Observed Information Matrix for Hidden Markov Models. Journal of Computational and Graphical Statistics. 2002;11:678–689. [Google Scholar]
- MacDonald IL, Zucchini W. Hidden Markov and Other Models for Discrete Valued Time Series. Boca Raton, FL: Chapman & Hall; 1997. [Google Scholar]
- McCulloch CE. Maximum Likelihood Algorithms for Generalized Linear Mixed Models. Journal of the American Statistical Association. 1997;92:162–170. [Google Scholar]
- Murphy K. Computing Sciences and Statistics: Proceedings of the 33rd Symposium on the Interface. Costa Mesa, CA: 2001. The Bayesian Net Toolbox for Matlab. [Google Scholar]
- Paas LJ, Bijmolt TH, Vermunt JK. Acquisition Patterns of Financial Products: A Longitudinal Investigation. Journal of Economic Psychology. 2007;28:229–241. [Google Scholar]
- Pearl J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. San Mateo, CA: Kaufman; 1988. [Google Scholar]
- Rabiner LR. A Tutorial on Hidden Markov-Models and Selected Applications in Speech Recognition. Proceedings of the IEEE. 1989;77:257–286. [Google Scholar]
- Rijmen F. BNL: A Matlab Toolbox for Bayesian Networks With Logistic Regression Nodes. technical report. 2006 available at http://www.mathworks.com/matlabcentral/fileexchange/loadFile.do?objectId=13136&objectType=file.
- Rijmen F, Ip E, Rapp S, Shaw E. Qualitative Longitudinal Analysis of Symptoms in Patients With Primary or Metastatic Brain Tumors. Journal of Royal Statistical Society, Ser. A. 2008;171:739–753. doi: 10.1111/j.1467-985x.2008.00529.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rijmen F, Vansteelandt K, De Boeck P. Latent Class Models for Diary Method Data: Parameter Estimation by Local Computations. Psychometrika. 2008;73:163–182. doi: 10.1007/s11336-007-9001-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin DB. Multiple Imputation for Nonresponse in Surveys. New York: Wiley; 1987. [Google Scholar]
- Schafer JL. Analysis of Incomplete Multivariate Data. London: Chapman & Hall; 1997. [Google Scholar]
- Schwarz G. Estimating the Dimension of a Model. The Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Scott SL, James GM, Sugar CA. Hidden Markov Models for Longitudinal Comparisons. Journal of the American Statistical Association. 2005;100:359–369. [Google Scholar]
- Shepard LA, Smith ML, Vojir CP. Characteristics of Pupils Identified as Learning Disabled. American Educational Research Journal. 1983;20:309–331. [Google Scholar]
- Singer JD, Willet JB. Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence. New York: Oxford University Press; 2003. [Google Scholar]
- Snow Jones A. Maternal Alcohol Abuse/Dependence, Children’s Behavior Problems and Home Environment: Estimates From the NLSY Using Propensity Score Matching. Journal of Studies on Alcohol and Drugs. 2007;68(2):266–275. doi: 10.15288/jsad.2007.68.266. [DOI] [PubMed] [Google Scholar]
- Snow Jones A, Heckert DA, Gondolf ED, Zhang Q, Ip EH. Complex Behavioral Patterns and Trajectories of Domestic Violence Offenders. Violence and Victims. 2010;25:3–17. doi: 10.1891/0886-6708.25.1.3. [DOI] [PubMed] [Google Scholar]
- Vermunt JK, Langeheine R, Böckenholt U. Discrete-Time Discrete-State Latent Markov Models With Timeconstant and Time-Varying Covariates. Journal of Educational and Behavioral Statistics. 1999;24:178–205. [Google Scholar]
- Visser I, Ray S, Jang W, Berger J. Workshop on Latent Variable Modeling in Social Sciences. Research Triangle Park, NC: SAMSI; 2006. Effective Sample Size and the Bayes Factor. [Google Scholar]
- Wiggins LM. Panel Analysis: Latent Probability Models for Attitude and Behavior Processes. San Francisco, CA: Jossey-Bass; 1973. [Google Scholar]
- Wolfinger R, O’Connell M. Generalized Linear Mixed Models: A Pseudo-Likelihood Approach. Journal of Statistical Computation and Simulation. 1993;48:233–243. [Google Scholar]
- Zucchini W, Guttorp P. A Hidden Markov Model for Space Time Precipitation. Water Resources Research. 1991;27:1917–1923. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.