QUANTILE REGRESSION FOR MIXED MODELS WITH AN APPLICATION TO EXAMINE BLOOD PRESSURE TRENDS IN CHINA

Abstract

Cardiometabolic diseases have substantially increased in China in the past 20 years and blood pressure is a primary modifiable risk factor. Using data from the China Health and Nutrition Survey we examine blood pressure trends in China from 1991 to 2009, with a concentration on age cohorts and urbanicity. Very large values of blood pressure are of interest, so we model the conditional quantile functions of systolic and diastolic blood pressure. This allows the covariate effects in the middle of the distribution to vary from those in the upper tail, the focal point of our analysis. We join the distributions of systolic and diastolic blood pressure using a copula, which permits the relationships between the covariates and the two responses to share information and enables probabilistic statements about systolic and diastolic blood pressure jointly. Our copula maintains the marginal distributions of the group quantile effects while accounting for within-subject dependence, enabling inference at the population and subject levels. Our population level regression effects change across quantile level, year, and blood pressure type, providing a rich environment for inference. To our knowledge, this is the first quantile function model to explicitly model within-subject autocorrelation and is the first quantile function approach that simultaneously models multivariate conditional response. We find that the association between high blood pressure and living in an urban area has evolved from positive to negative, with the strongest changes occurring in the upper tail. The increase in urbanization over the last twenty years coupled with the transition from the positive association between urbanization and blood pressure in earlier years to a more uniform association with urbanization suggests increasing blood pressure over time throughout China, even in less urbanized areas. Our methods are available in the R package BSquare.

1. Introduction

Globally, cardiovascular disease accounts for approximately 17 million deaths a year, and nearly one third of the total causes of death in 2008 (World Health Organization and others, 2011). Of these, complications of hypertension account for 9.4 million deaths worldwide every year (Lim et al., 2013). Maximum (systolic) blood pressure and minimum (diastolic) blood pressure are physiologically correlated outcomes but are differentially affected by environmental factors (Benetos et al., 2001; Chobanian et al., 2003; Choh et al., 2011; Egan, Zhao and Axon, 2010; Franklin et al., 2009; Luepker et al., 2012; Sesso et al., 2000). Most studies construct a combined measure using hypertension cutpoints rather than looking across the distribution. Systolic blood pressure (SBP) and diastolic blood pressure (DBP) have differential effects on cardiovascular disease events (Benetos et al., 2001; Franklin et al., 2009; Sesso et al., 2000; Stokes et al., 1989), so we model the conditional quantile functions of SBP and DBP. In linear quantile regression the quantiles of the response (e.g. the 90^th percentile) change linearly with the predictors, and the regression effects are contingent upon on the percentile chosen. This allows the effects of urbanization to change along the distribution of blood pressure, enabling sharper insight into the relationship between urbanization and hypertension. By conducting inference in the upper tails of SBP and DBP, we are able to examine how urbanization affects individuals most at risk for hypertension. Quantile regression also allows comparisons of conditional 90^th percentiles at different levels of a covariate. We use longitudinal data from the China Health and Nutrition Survey (Popkin et al., 2010) to study the impact of urbanicity on those trends. China provides an outstanding case study given recent and rapid modernization and substantial concomitant environmental change.

In developed countries that experienced slow rates of modernization, studies have suggested declines or leveling off in mean blood pressure over the last century, potentially due to increased hypertension treatment (Burt et al., 1995; Luepker et al., 2012; Egan, Zhao and Axon, 2010; McCarron et al., 2001). However, in China during a period of rapid modernization, we observed a substantial increase in mean SBP and DBP over time, particularly in low urbanicity areas (Attard et al., 2015). Understanding the association with urbanization across the full distribution of blood pressure will allow researchers and policymakers to understand the points along the distribution that may be most amenable to environmental change, allowing more tailored intervention targeting in China and in other low to middle income countries undergoing similar urbanization.

The purpose of our paper is to address two important gaps in the hypertension literature: 1) lack of attention to continuous SBP and DBP as correlated outcomes; and 2) attention to the tails of their distribution to examine how an environment-related exposure, in this case urbanization, is associated with the distribution of SBP and DBP. We utilize quantile regression to permit tail inference of SBP and DBP. However, the China Health and Nutrition Survey (CHNS) data are longitudinal in nature and we are interested in a multivariate outcome, and current quantile regression methods would not permit satisfactory exploration of our scientific aims.

Several previous approaches in the longitudinal literature simply ignore the within-subject dependence when estimating the marginal quantile effects. Wang and Zhu (2011) constructed an empirical likelihood under the GEE framework, then adjusted for the dependence in the confidence intervals. For censored data, Wang and Fygenson (2009) ignored the within-subject dependence when estimating the marginal effects and controlled for the within-subject dependence when conducting inference via a rank score test. While these estimators are consistent, ignoring the within-subject dependence for estimation can result in a loss of efficiency and undercoverage. Another avenue is to introduce dependence via random intercepts, as in Koenker (2004). Waldmann et al. (2013) and Yue and Rue (2011) assumed asymmetric Laplace errors and included a random subject effect in the location parameter. Presenting separate methodology for marginal and conditional inference, Reich, Bondell and Wang (2010) accounted for within-cluster dependence via random intercepts and flexibly modeled the density using an infinite mixture of normals. Jung (1996) preserved marginal effects by incorporating correlated errors in a quasi-likelihood model. These models account for within-subject dependence via a location adjustment for each cluster, which may not be sufficiently flexible. Models that incorporate random slopes include Geraci and Bottai (2013), who used numerical integration to average out random effects for marginal inference, and the empirical likelihood of Kim and Yang (2011). The marginal effects of Geraci and Bottai (2013) do not neccesarily maintain their original interpretation after integrating over the random effects. Kim and Yang (2011) permit subject-specific inference for clustered data. While these methods account for dependence, we are interested in inference at the population level of temporally correlated data. Jung (1996) incorporates temporally correlated errors within a subject, at the cost of assuming the response is distributed Gaussian. Collectively these models lack attributes needed for our research question, which relates to understanding the effects of urbanization on SBP and DBP as correlated outcomes. First, we want to conduct inference at multiple quantile levels without assuming our response is distributed Gaussian. The approaches above model one quantile level at a time and can result in “crossing quantiles” (Bondell, Reich and Wang, 2010), where for certain values of the predictors the quantile function is decreasing in quantile level. Second, we need to model the autocorrelation within a subject to maintain nominal coverage probabilities. Third, for our application we anticipate that the effect of a covariate on SBP may be similar to its effect on DBP, so we want a bivariate model to facilitate communication across blood pressure type.

In this paper we introduce a mixed modeling framework for quantile regression with these necessary attributes. We accomplish these methodological innovations by extending the model of Reich and Smith (2013) to accommodate autocorrelation and multiple responses. In the random component we account for the dependence across time and response via a copula (Nelsen, 1999). This permits the relationships between the covariates and the two responses to share information and enables probabilistic statements about SBP and DBP jointly. Our copula approach maintains the marginal distributions of the population-level quantile effects while accounting for within-subject dependence, enabling inference at the population and subject levels. Copulas previously utilized in the longitudinal literature (Smith et al., 2010; Sun, Frees and Rosenberg, 2008) focused on mean inference and do not account for predictors. Chen, Koenker and Xiao (2009) uses a copula to account for serial dependence in quantile estimation, without predictors. Copulas have a straightforward connection to quantile function modeling, as both rely on connecting the response to a latent uniformly distributed random variable. Our copula model resembles the usual mixed model (Diggle et al., 2002) in that covariates affect both the marginal population distribution via fixed effects and subject specific distributions via random slopes. In the fixed component we allow for different predictor effects across quantile level, response, and year. Our model is centered on the usual Gaussian mixed model, and contains it as a special case.

We present a multilevel framework that extends the current Gaussian mixed model to the quantile regression domain. Our model permits examination of how urbanization has affected the distributional tails of SBP and DBP, while controlling for the dependence within CHNS subjects. This allows us to draw new inferences in a more flexible manner than mixed models where only the mean is affected by covariates. For example, we can examine how regression effects in the lower tail, middle of the distribution, and upper tail change over time, and we can examine how the quantiles of multiple responses adapt to changes in a predictor. To our knowledge, this is the first quantile function model for temporally-correlated responses within a subject and the first quantile function model that accommodates a multivariate response with covariates. We describe the data in Section 2. In Section 3 we describe the mixed effect quantile model in the univariate and multivariate cases. In Section 4 we show the results of a simulation study that illustrates the need to account for within-subject dependence in a quantile framework. In Section 5 we analyze hypertension and we conclude in Section 6.

2. Data

The CHNS was designed in 1986 to gauge a range of economic, sociological, demographic and health questions (Popkin et al., 2010). The CHNS is a large scale household-based survey drawing from 228 communities which were cluster sampled from 9 provinces. Community structures include villages, townships, urban neighborhoods, and suburban neighborhoods. The communities sampled are designed to be economically and demographically representative of China. Procedures for collecting the data are described in Adair et al. (2014). We use data collected in 7 waves, starting in 1991 and ending in 2009. We focus on the Shandong province, located in central China, where hypertension rates are elevated (Batis et al., 2013). We utilize the urbanicity index of Jones-Smith and Popkin (2010). Rather than dichotomizing communities into urban/rural groups, for each wave Jones-Smith and Popkin (2010) assigned 0–10 scores for each of 12 factors, including population density, economic activity, traditional markets, modern markets, transportation, infrastructure, sanitation, communications, housing, education, diversity, health infrastructure, and social services. Jones-Smith and Popkin (2010) used factor analysis to confirm these factors represent one latent construct.

We have two scientific goals for these data. First, we want to estimate the role of urbanicity in these trends. Second, we want to examine blood pressure trends over time across different age cohorts. We bin individuals into six age groups: age < 18, 18 ≤ age < 30, 30 ≤ age < 40, 40 ≤ age < 50, 50 ≤ age < 60 and age ≥ 60. For individuals with age < 18, blood pressure is very correlated with height and age, rendering uninterpretable comparisons across children and adults. For this reason, most studies focus on children or adults, and we focus on adults in this paper. The plots in Figure 1 show slight increases over time in blood pressure across both genders and large increases over time in urbanicity. We construct an urbanicity by age interaction effect to look for associations between urbanicity and different age cohorts. As in Attard et al. (2015) we stratify our analyses by gender. Other covariates include current smoking status (men only due to low female rates) and current pregnancy status (female only). To look for changes across time we include temporal linear trends for all predictors.

Fig 1.

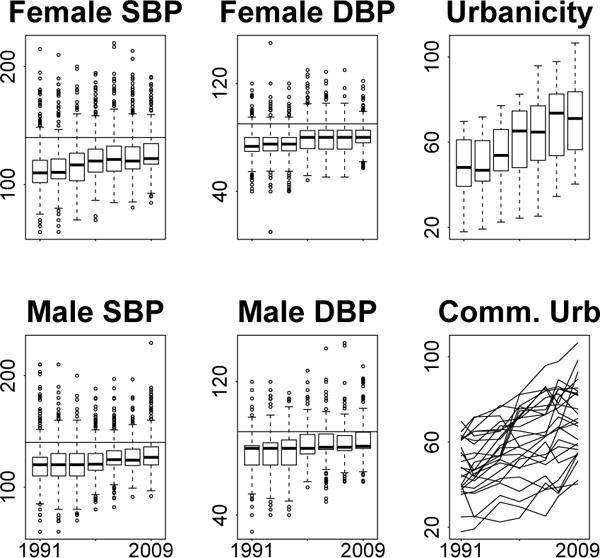
Systolic blood pressure (SBP) and diastolic blood pressure (DBP) by gender and urbanicity scores across time. Blood pressure measurements are in millimeters of mercury (mmHg). Urbanicity is a composite score measuring 12 features of the community environment (Jones-Smith and Popkin, 2010). Horizontal lines represent thresholds for high blood pressure, located at 140 mmHg and 90 mmHg for systolic and diastolic blood pressure respectively.

3. Methods

In this section we present our methods for mixed model quantile regression. We first specify the marginal quantile functions in Section 3.1. In Section 3.2 and Section 3.3 we describe different approaches to accommodate within-subject dependence.

3.1. Marginal Quantile Model

Denote Y_ij as the measurement of SBP on individual i = 1, 2, …, N at visit j = 1, 2, …, J indexing the years 1991, 1993,…, 2009. While in general J can vary by individual, in our application J is constant across subjects. This section describes a model for SBP that allows urbanization effects to change along the distribution, with the extension to SBP and DBP in Section 3.3. Let X_ij be a covariate vector of length P containing the variables such as age and urbanization for individual i at visit j. Denote the conditional distribution function of Y_ij as F(y|X_ij) = P(Y_ij ≤ y|X_ij). We specify the distribution of absolutely continuous Y_ij via its quantile function, defined as Q(τ|X_ij) = F⁻¹(τ|X_ij), where τ ε (0, 1) is known as the quantile level. For each response Y_ij there exists a latent U_ij ~ U(0,1) such that Y_ij = Q(U_ij|X_ij).

We assume the quantile function of SBP Q(τ|X) is a linear combination of covariates, that is,

$$Q(\tau |\mathbf{X})={\displaystyle \sum _{p=1}^P{X}_p{\beta }_p(\tau )}.$$

The regression parameter β_p(τ) is the effect of the p^th covariate on Q(τ|X). A one-unit increase in X_p is associated with a β(τ) increase in the τ^th population quantile. We refer to β(τ) as a “fixed effect”, since this effect applies to the full population.

Similar to Reich and Smith (2013) we project β_p onto a space of M ≥ 2 parametric basis functions I₁(τ), …, I_M(τ) defined by a sequence of knots 0 = κ₀ < κ₁ < … < κ_M < κ_M+1 = 1. Let q₀(τ) be the quantile function of a random variable from a parametric location/scale family with location parameter 0 and scale parameter 1. The basis functions are defined as I₁(τ) ≡ 1, $I_2(\tau )=q_0(\tau ){\mathrm{𝟙}}_{\tau \le {\kappa }_1}+q_0({\kappa }_1){\mathrm{𝟙}}_{\tau >{\kappa }_1}$, and

$$I_m(\tau )=\{\begin{array}{ll}0\hfill & \tau \le {\kappa }_{m-1}\hfill \\ q_0(\tau )-q_0({\kappa }_{m-1})\hfill & {\kappa }_{m-1}\le \tau \le {\kappa }_m\hfill \\ q_0({\kappa }_m)-q_0({\kappa }_{m-1})\hfill & \tau >{\kappa }_m\hfill \end{array}$$

for m > 2. Our model is of the form ${\beta }_p(\tau )={\displaystyle {\sum }_{m=1}^M{I}_m(\tau ){\theta }_{mp}}$ and thus

$$Q(\tau |X_{\mathit{ij}})={\displaystyle \sum _{p=1}^P{X}_{\mathit{ijp}}{\beta }_p(\tau )}={\displaystyle \sum _{p=1}^P{X}_{\mathit{ijp}}{\displaystyle \sum _{m=1}^M{I}_m(\tau )}{\theta }_{mp}}$$ (3.1)

where θ_mp are the regression weights. By partitioning our distribution by the knots, we only assume our distribution is locally parametric, so our method is semi-parametric. We set X_ij1 ≡ 1 for all i and j for the intercept.

An example of our model is displayed in Figure 2. The left panel shows an example of Gaussian basis functions, where q₀(τ) = Φ⁻¹(τ), Φ(z) is the distribution function of the standard normal distribution, with knots at (0.25, 0.5, 0.75). Only one basis function changes at each quantile of the distribution. The middle panel illustrates the projection of these basis functions for θ.1 = (0, 3, 3, 3, 3) corresponding to basis coefficients for the intercept and θ.2 = (0, 0, 2, −2, −2) corresponding to basis coefficients for lone covariate x (e.g. urbanization score). The middle panel shows the quantile function when x = 0 (β₁(τ)) and how the covariate effects on the quantile function change across the distribution (β₂(τ)). The final panel displays the conditional quantile function, which is (β₁(τ)) + x(β₂(τ)), for x ε (−1, 0, 1). The effect of x is 0 in the first quartile, positive in the second quartile, and negative in the third and fourth quartiles.

Fig 2.

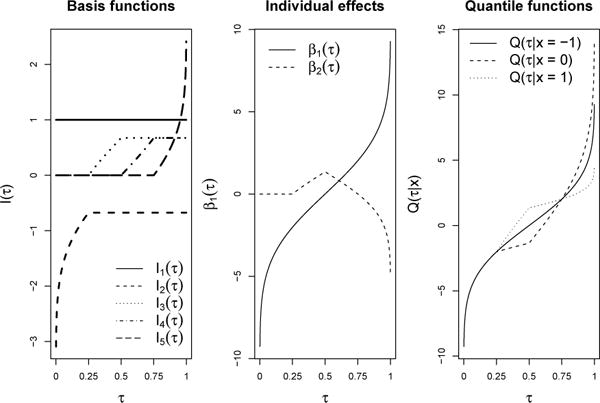
Plots of the quantile model with M = 5 basis functions with knots at (0.25, 0.5, 0.75) and one covariate x, with θ_.1 = (0, 3, 3, 3, 3) corresponding to basis coefficients for the intercept and θ_.2 = (0, 0, 2, −2, −2) corresponding to basis coefficients for x. The left plot displays the constant basis function (m = 1) and 4 Gaussian basis functions that each correspond to a different quartile of the distribution. The middle plot displays the intercept process β₁(τ), which is the distribution when all covariates are 0, and the covariate effect β₂(τ), defined as the deviation in the intercept process due to a one unit change in x. The final panel displays the conditional quantile function Q(τ|x) = β₁(τ) + xβ₂(τ) for x = −1, x = 0, and x = 1.

To achieve a valid quantile function (i.e. increasing in τ) we map all predictors into the interval [−1, 1], and constrain the regression parameters such that ${\theta }_{m1}>{\displaystyle {\sum }_{p=2}^P|{\theta }_{mp}|}$ for m > 1. We model θ_mp as a function of a Gaussian random variable ${\theta }_{\mathit{mp}}^{\star }$. The regression parameter θ_mp is set to ${\theta }_{\mathit{mp}}^{\ast }$ if the constraint is satisfied and set to

$${\theta }_{mp}=\{\begin{array}{ll}0.001& p=1\\ 0& \text{otherwise}\end{array}$$

if θ^⋆ is outside of the constraint space. Details are outlined in Reich and Smith (2013). The latent regression variables ${\theta }_{\mathit{mp}}^{\star }$ are given Gaussian priors with means μ_mp and precisions ${\iota }_{\mathit{mp}}^2$.

Let θ_m. be the collection of regression parameters associated with basis function m. When the base quantile function is Gaussian (i.e. q₀(τ) = Φ⁻¹(τ)), if M = 2 or θ_2. = … = θ_M. this model simplifies to a Gaussian heteroskedastic regression model, where $Q(\tau )={\mathbf{X}}_{\mathit{ij}}^{\prime }{\mathit{\theta }}_{m1}+{\mathbf{X}}_{\mathit{ij}}^{\prime }{\mathit{\theta }}_{m2}{\mathrm{\Phi }}^{-1}(\tau )$ and thus $Y_{\mathit{ij}}|{\mathbf{X}}_{\mathit{ij}}~\mathrm{N}({\mathbf{X}}_{\mathit{ij}}^{\prime }{\mathit{\theta }}_{m1},{({\mathbf{X}}_{\mathit{ij}}^{\prime }{\mathit{\theta }}_{m2})}^2)$. Standard Gaussian linear regression is a special case of the heteroskedastic regression model where M = 2 and θ_mp ≡ 0 for m > 1 and p > 1 and $Y_{\mathit{ij}}|{\mathbf{X}}_{\mathit{ij}}~\mathrm{N}({\mathbf{X}}_{\mathit{ij}}^{\prime }{\mathit{\theta }}_{m1},{\theta }_{12}^2)$.

3.2. Mixed Effects Quantile Model

In this section we introduce a semi-parametric model that extends the standard Gaussian mixed effects model to the quantile regression domain. This enables us to examine the effects of urbanization across the full distribution while accounting for the longitudinal structure of CHNS data through random effects. We utilize Gaussian basis functions (q₀(τ) = Φ⁻¹(τ)) for connections to standard mixed models. Recall the canonical Gaussian random effects model (Fitzmaurice, Laird and Ware, 2012)

$${\mathbf{Y}}_i={\mathbf{X}}_i\mathit{\beta }+{\mathbf{Z}}_i{\gamma }_i+{\mathbf{E}}_i$$ (3.2)

where β is a vector of fixed effects, Z_i is a J by R matrix of random effect covariates, ${\gamma }_i\stackrel{\text{iid}}{~}N(\mathbf{0},\mathbf{\Delta })$ is a vector of length R of random effects specific to unit i, and ${\mathbf{E}}_i\stackrel{\text{iid}}{~}N(\mathbf{0},\mathbf{\Lambda })$ are random errors.

We can rewrite (3.2) in three forms. Conditional on the random effects, ${\mathbf{Y}}_i|{\mathbf{X}}_i,{\mathbf{Z}}_i~N({\mathbf{X}}_i\mathit{\beta }+{\mathbf{Z}}_i{\gamma }_i,{\sigma }^2\mathbf{I})$. Marginally over the random effects, Y_i|X_i ~ N(X_iβ, Ψ_i), where ${\mathbf{\Psi }}_i={\mathbf{Z}}_i\mathbf{\Delta }{\mathbf{Z}}_i^{\prime }+\mathbf{\Lambda }$. Finally, the marginal quantile function form is $Q(\tau |{\mathbf{X}}_{\mathit{ij}})={\mathbf{X}}_{\mathit{ij}}^{\prime }\mathit{\beta }+{\psi }_{\mathit{ij}}{\mathrm{\Phi }}^{-1}(\tau )$, where ψ_ij is the j^th diagonal element of Ψ_i. Therefore, $Y_{\mathit{ij}}|{\mathbf{X}}_{\mathit{ij}}={\mathbf{X}}_{\mathit{ij}}^{\prime }\beta +{\psi }_{\mathit{ij}}{\mathrm{\Phi }}^{-1}(U_{\mathit{ij}})$, where U_ij ~ U(0,1) marginally, with dependence between the U_ij within the same subject.

We use the third representation to extend mixed models to the quantile domain by viewing the transformed response as a realization from a potentially correlated Gaussian process. To account for the within-subject dependence, we hierarchically model the latent U_ij through a Gaussian copula. Our model is

$$\begin{array}{l}{Y}_{\mathit{ij}}={\displaystyle \sum _{p=1}^P{X}_{\mathit{ijp}}{\beta }_p(U_{\mathit{ij}})}\\ U_{\mathit{ij}}=\mathrm{\Phi }(W_{\mathit{ij}}/\sqrt{{\psi }_{\mathit{ij}}})\\ {\mathbf{W}}_i={\mathbf{Z}}_i^{\prime }{\gamma }_i+{\mathbf{E}}_i.\end{array}$$ (3.3)

The fixed regression effects β(τ) are modeled as in Section 3.1. As in (3.2) the random effects ${\gamma }_i\stackrel{\text{iid}}{~}N(\mathbf{0},\mathbf{\Delta })$ and random errors ${\mathbf{E}}_i\stackrel{\text{iid}}{~}N(\mathbf{0},\mathbf{\Lambda })$.

The copula in (3.3) permits structured dependence in the U_ij. This preserves the interpretability of population level quantile effects β_p and accounts for within-subject dependence, enabling simultaneous inference at the population and subject levels. This formulation allows predictors to have a complex relationship with the response. A covariate can have a different effect in the middle of the distribution relative to the tails. This is represented by the fixed component X′β(τ), the conditional τ^th population quantile, with the same interpretation of covariate effects as in Section 3.1. Further, individuals in a population are allowed to respond differently to the same covariate. This is represented by the random component ${\mathbf{Z}}_i^{\prime }\gamma$. A one unit increase in Z_ijr is associated with a ${\gamma }_{\mathit{ir}}/\sqrt{{\psi }_{\mathit{ij}}}$ increase in the Z-score of individual Y_ij.

For the CHNS data we anticipate that between-individual variability is strong, which can be estimated through a random intercept inside the copula. Covariates that change across time (e.g. urbanicity) can be used to further capture within-subject variability. For longitudinal data we anticipate serial within-subject correlation, so we model Λ = I + λΞ(α) as the sum of an identity matrix and a scaled (by positive λ) autoregressive order-1 (AR-1) correlation matrix Ξ(α), where Ξ(α)[u, v] = α^−|u−v| with correlation parameter α. The scaling factor λ determines the proportion of variability determined by the temporal signal.

While we have thus far defined our model in terms of Gaussian basis functions, any of the parametric bases described in Reich and Smith (2013) can be utilized to model effects at the population level. Finally, the standard Gaussian mixed model is a special case of (3.3) where q₀(τ) = Φ⁻¹(τ), M = 2 and θ_mp ≡ 0 for m > 1 and p > 1. This allows us to center our flexible model on the popular model.

We assume the distribution of SBP can be partitioned into M − 1 components such that within each partition the distribution of SBP behaves parametrically. This partitioning enables the error distribution to adapt across components. For example, the error term can be different in the lower tail, the middle of the distribution, and the upper tail. Our error distribution is dependent on the covariates, so even in the least flexible fit (M = 2) our model permits more flexibility than standard mixed models.

We assume the within-subject dependence can be characterized through a multivariate normal distribution for several reasons. Using Gaussian basis functions and a Gaussian copula enables us to center our prior distribution on the canonical Gaussian mixed model. The Gaussian copula allow us to account for within-subject serial correlation, a potential issue with CHNS data, and correlation structures that are affected by covariates (e.g. urbanicity). The Gaussian copula easily imputes missing values, which was necessary for our application and its high rate of missing values. Finally, the Gaussian copula is computationally cheap. However, the price of the Gaussian copula is a lack of flexibility, as we discuss in Section 6. Nonparametric copulas (Fuentes, Henry and Reich, 2013) could be a useful extension in other applications.

3.3. Multivariate Mixed Effects Quantile Model

Here we extend (3.3) to the multivariate domain. We are not concerned with trying to define a multivariate quantile (Chakraborty, 2003), which imposes order on a collection of objects of multivariate dimension. The most common example of a multivariate quantile is a multivariate median, which is a common alternative to the multivariate mean for defining the center of a multivariate distribution. Instead, we want to conduct simultaneous inference on observations with multiple responses. We anticipate SBP and DBP may have similar distributions, so by jointly modeling them we can borrow information across responses. Further, SBP and DBP are correlated within an individual, so we must account for this dependence. Otherwise, our estimates of uncertainty will be too small. In summary, we are interested in conducting simultaneous inference at the marginal medians (and other quantile levels) of SBP and DBP, rather than defining a central point for both distributions. A forerunner of our approach is (Gilchrist, 2000), who constructed ordered quantile surfaces by reducing the dimension of a multivariate random variable to one. Our multivariate quantile regression approach allows us to simultaneously analyze both responses and include covariates. This allows us to draw inferences about how urbanization and other covariates affect SBP and DBP, while preserving flexibility in how changes in urbanization affect these distributions. The approach in Gilchrist (2000) does not permit covariates or preserve the marginal distributions.

Denote Y_1ij and Y_2ij as the measurements of SBP and DBP on individual i at time j. We specify different quantile effects for each response (i.e. β_1p(τ₁) and β_2p(τ₂) for covariate p). Our bivariate model then accounts for dependence between the parameters in these quantile processes, and in the residual copula model.

Our multivariate mixed quantile model is

$$\begin{array}{l}{Y}_{\mathit{hij}}={\displaystyle \sum _{p=1}^P{X}_{\mathit{ijp}}{\displaystyle \sum _{m=1}^M{I}_m(U_{\mathit{hij}}){\theta }_{\mathit{hmp}}}}\\ U_{\mathit{hij}}=\mathrm{\Phi }(W_{\mathit{hij}}/\sqrt{{\psi }_{\mathit{hij}}})\\ {\mathbf{W}}_i={\mathbf{Z}}_i{\gamma }_i+{\mathbf{E}}_i,\end{array}$$ (3.4)

where now h = 1, 2 indexes the response of dimension H, W_i is of length JH, and the covariance of E_i is Ξ(α) ⊗ Λ + I where Ξ(α)[u, v] = α^−|u−v| with correlation parameter α and Λ is an unstructured H × H correlation matrix.

This formulation allows the uniform random variables U_ij to be interpreted as the individual’s percentile relative to the population. That is, an individual may be at the conditional 70^th percentile (U_1ij = 0.70) for SBP and the 75^th percentile (U_2ij = 0.75) for DBP, and the similarity in these percentiles can be exploited.

To borrow strength across the responses we model $({\theta }_{1mp},{\theta }_{2mp})\prime ~BVN({\mu }_{mp}\mathbf{1},{\iota }_{mp}^2{\mathbf{I}}_2)$. By shrinking regression effects to a common location, we are able to borrow information across SBP/DBP to estimate covariate effects. This multivariate framework enables statements about joint effects of a predictor, and allows for probabilistic estimates regarding both responses (e.g. the conditional probability an individual has blood pressure higher than 140/90).

We assign μ_mp independent normal priors with mean μ_0mp and precision ${\iota }_{0mp}^2$. We give ι_mp independent Gamma (a_mp, b_mp) priors. We designate Λ an inverse Wishart prior with scale matrix Λ₀ and ν₀ degrees of freedom. For our application we assign Δ a diagonal matrix structure with diagonal elements ${\delta }_{hr}\stackrel{\text{iid}}{~}\text{Gamma}(1,1)$, h = 1, 2, …, H, r = 1, 2, …, R. In applications with more observations per subject and correlation on the within-subject regression coefficients is easier to detect, more complicated structures for Δ could be useful. We use the Metropolis within Gibbs algorithm to sample from the posterior, with details in Smith et al. (2015).

4. Simulation Study

We conducted a simulation study to examine the effect of within-subject dependence on parameter estimation. To construct univariate, auto-correlated responses we generated dependent J-dimensional realizations W_i ~ N(0, Ψ_i), where ${\mathbf{\Psi }}_i={\mathbf{Z}}_i\mathit{\Delta }{\mathbf{Z}}_i^{\prime }+\mathbf{\Xi }(\alpha )+\mathbf{I}$ with j^th diagonal element ψ_ij. The design matrix Z_i contains an intercept and one continuous predictor $X_{1ij}\stackrel{\text{iid}}{~}\mathrm{U}(-1,1)$.

The first factor we examine in the simulation study is the strength of the within-subject dependence. We look at three levels, 0.0,0.5,0.9, of the temporal correlation parameter α, which correspond to no, moderate and strong within-subject dependence, respectively. Our second factor is the strength of the dependence determined by the covariance of the within-subject random effects, Δ = ΔI₂. In one setting the variance Δ = 0, corresponding to the coefficients having no effect on the dependence. In the other Δ is a diagonal matrix with nonzero values of Δ = 3, corresponding to roughly 60% of the variance within a subject being explained by covariates.

Given these correlated responses we perform the probability integral transform $U_{\mathit{ij}}=\mathrm{\Phi }(W_{\mathit{ij}}/\sqrt{{\psi }_{\mathit{ij}}})$. The third factor in our study is the marginal distribution given these uniform random variables. The response data are

$$Y_{\mathit{ij}}=3{\mathrm{\Phi }}^{-1}(U_{\mathit{ij}})+(X_{1ij}+X_{2ij})(0.5-U_{\mathit{ij}})\ast {\mathrm{𝟙}}_{U_{\mathit{ij}}<0.5}$$ (1)

$$Y_{\mathit{ij}}=(3+X_{1ij}+X_{2ij})Q_t(U_{\mathit{ij}})$$ (2)

where Q_t is the quantile function of Student’s t-distribution with 5 degrees of freedom, i = 1, 2, …, N individuals, and j = 1, 2, …, J visits. The covariate X_2i is binary with equal probability of −1 and 1 and is constant over time. Design (2) is a heteroskedastic linear model, but design (1) is more challenging to fit, with nonzero effects for only half of the distribution. We generated data at J = 7 timepoints for N = 50 and N = 100 individuals. For each level of our design we ran 100 Monte Carlo replications.

We examine three competitors for our simulation study. The first is the marginal quantile model of Section 3.1. This model assumes independent replications within an individual. The second model is the mixed effects quantile model of Section 3.2. This model can account for serial correlation and subject specific effects. For both of these two models we fit 2,3 and 5 basis functions for two different parametric bases (Gaussian and Student’s t). For each Monte Carlo replication the final model is selected by having the highest log psuedo marginal likelihood (Ibrahim, Chen and Sinha, 2005) across number of basis functions and parametric bases. For data type (1) log pseudo marginal likelihood (LPML) most commonly selected 5 Gaussian basis functions for the independent model without a copula and 5 Student’s t-distributed basis functions for the copula model. For data type (2) LPML most commonly selected 2 Student’s t-distribution basis functions for both models. The third competitor is the model of Reich, Bondell and Wang (2010) using 25 approximation terms, denoted “RBW”. RBW is able to fit marginal effects while accounting for a random intercept, but ignores temporal correlation covariate effects within a subject.

Prior means for ${\theta }_{\mathit{mp}}^{\ast }$ were 1 for p = 1 and 0 otherwise, and prior variances were 10. For the copula model we set (scalar) Λ₀ = 1 and ν₀ = 3, corresponding to a prior mean of 4 and infinite variance for Λ. For the Student’s t-distribution basis functions we gave the shape parameter a normal prior on the log scale with mean log(10) and variance log(10)/2. Averages of coverage probability (CP) of 95% intervals and mean squared error (MSE) of each model evaluated at the quantile levels τ = .1, .3, .5, .7, .9 for the N = 50 case are shown in Table 1. All of the conclusions listed below similarly held for the N = 100 case, shown in Smith et al. (2015).

Table 1.

Coverage probability (CP) and mean squared error (MSE) for the N = 50 arm of the simulation study. Nominal coverage probability is 95%. We compare treating the data as independent within a subject (“Ind”), fitting with a copula (“Cop”), and the random effects model of (Reich, Bondell and Wang, 2010) (“RBW”). Coverage and MSE were evaluated at and averaged over the quantile levels {0.1, 0.3, 0.5, 0.7, 0.9}. For datatype = 1, MSE values are less than depicted values by a factor of 10. Estimators whose MSE were statistically significantly different than the copula model are indicated by*.

Δ = 0, Datatype = 1
	Coverage						MSE
	α = 0.0		α = 0.5		α = 0.9		α = 0.0		α = 0.5		α = 0.9
	X1	X2	X1	X2	X1	X2	X1	X2	X1	X2	X1	X2
Ind	0.91	0.95	0.88	0.94	0.73	0.94	0.05	0.09	0.07	0.10	0.11	0.11
Cop	0.95	0.96	0.95	0.97	0.94	0.96	0.05	0.10	0.06	0.10	0.09	0.10
RBW	0.83	0.90	0.86	0.89	0.88	0.87	0.11*	0.16*	0.13*	0.15*	0.16*	0.14*
Δ = 0, Datatype = 2
	Coverage						MSE
	α = 0.0		α = 0.5		α = 0.9		α = 0.0		α = 0.5		α = 0.9
	X1	X2	X1	X2	X1	X2	X1	X2	X1	X2	X1	X2
Ind	0.94	0.97	0.89	0.94	0.76	0.95	0.06	0.09	0.09	0.11	0.15	0.13
Cop	0.98	0.98	0.95	0.98	0.93	0.97	0.07	0.11	0.10	0.13	0.16	0.13
RBW	0.96	0.98	0.95	0.96	0.93	0.95	0.07	0.10	0.10	0.11	0.14	0.10
Δ = 3, Datatype = 1
	Coverage						MSE
	α = 0.0		α = 0.5		α = 0.9		α = 0.0		α = 0.5		α = 0.9
	X1	X2	X1	X2	X1	X2	X1	X2	X1	X2	X1	X2
Ind	0.61	0.76	0.58	0.78	0.56	0.72	0.17	0.24	0.19	0.25*	0.23	0.24*
Cop	0.92	0.91	0.91	0.90	0.89	0.91	0.14	0.18	0.15	0.17	0.18	0.17
RBW	0.85	0.70	0.85	0.69	0.86	0.67	0.23*	0.26*	0.24	0.26*	0.25	0.24*
Δ = 3, Datatype = 2
	Coverage						MSE
	α = 0.0		α = 0.5		α = 0.9		α = 0.0		α = 0.5		α = 0.9
	X1	X2	X1	X2	X1	X2	X1	X2	X1	X2	X1	X2
Ind	0.64	0.76	0.60	0.78	0.57	0.74	0.26	0.26	0.28	0.25	0.32*	0.29*
Cop	0.90	0.90	0.89	0.89	0.91	0.92	0.21	0.21	0.20	0.21	0.19	0.17
RBW	0.86	0.80	0.84	0.79	0.83	0.77	0.26	0.21	0.26	0.22	0.31*	0.24

When observations within a subject are independent (Δ = 0, α = 0 case), all models attain the nominal 95% coverage probability for both predictors and data types, except RBW for data type (1). Fitting a copula to independent data seems to have little effect on marginal inference. Increasing α causes undercoverage in the independent model for the continuous predictor X₁. In contrast, the copula and RBW models maintain proper coverage. As within-subject dependence increases, each observation contributes less information about the marginal distribution. This can be seen by the increases in MSE due to increases in α. We compare MSE across the estimators when the covariates do not affect within-subject dependence (i.e. Δ = 0). The copula model is better than RBW with respect to MSE for data type (1). RBW assumes the heteroskedastic model, as in data type (2), yet none of the three models are statistically significantly better with respect to MSE.

The results change when the subject-level regression coefficients affect dependence (i.e. Δ = 3). RBW and the independent model suffer from poor coverage when the predictors account for dependence in the response. In contrast, the copula model maintains close to nominal coverage. Further, the copula model dominates RBW and the independent model with respect to MSE. The copula model has a statistically significantly lower MSE in roughly half of the cases and is lowest in all cases. In summary, accounting for covariates in the dependence can reduce MSE and preserve coverage.

5. CHNS Analysis

In this section we analyze the CHNS data. Our final sample consisted of 1421 females missing 56% of blood pressure measurements and 1248 males missing 55% of blood pressure measurements. Missing household income in year j was imputed using the community average for year j. Missing smoking status was imputed using the value from the previous sampling wave, and assumed to be a nonsmoker in the first wave if missing. Missing pregnancy status was assumed to be not pregnant.

With a large number of predictors and so many missing observations, allowing all 14 predictors to change with quantile level is not feasible. In our analysis we have urbanicity change with quantile level and all other effects be constant with quantile level, that is, we fix β_p(τ) ≡ β_p = θ₁ for all τ by setting θ₂ = … = θ_m = 0. The interpretations for these effects are equivalent to those in mean regression in that they are allowed to affect the location but not the shape of the response distribution.

Another challenge presented by these data is confounding due to blood pressure medication. Medication artificially supresses blood pressure values. For individuals on medication we ignore the measured values and assume only that they have high blood pressure. Using the method of Reich and Smith (2013) we treat these values as right-censored above the thresholds for high blood pressure, located at 140 for SBP and 90 for DBP. For individuals on blood pressure medication the censored likelihood is p₁ = P (Y1_i|X_i > 140) = 1 − F_Y1(140|X_i)) for SBP and p₂ = P(Y2_i|X_i > 90) = 1 − F_Y2(90|X_i)) for DBP. We use these censored probabilities in the likelihood for these individuals.

We linearly transformed the responses to have mean 0 and standard deviation 1. We assigned ${\mu }_{m1}\stackrel{\text{iid}}{~}\mathrm{N}(1,1)$ priors for the intercept process and m > 1 and ${\mu }_{mp}\stackrel{\text{iid}}{~}\mathrm{N}(0,1)$ priors for all other regression parameters. We set Λ ~ IW(10, 7Λ₀) where Λ₀ is an H × H correlation matrix with off-diagonal elements of 0. This corresponds to a prior mean of 1 and variance of 0.4 for the diagonal elements of Λ. This centers the prior distributions of SBP and DBP on a mean zero, unit variance normal distribution that is independent across SBP and DBP. We assigned ${\iota }_{mp}^2\stackrel{\text{iid}}{~}\mathrm{G}(1,1)$ priors. We assigned α a uniform prior on the unit interval. We ran our models for 40,000 MCMC iterations, the first half of which we discarded.

5.1. Analysis

We fit 3 different models to compare dependence structures. In model 1 we fit our model without a copula, assuming independence across sampling wave and response. We also fit two copula models. In model 2 the covariance of W_i is Ξ(α)⊗Λ+I_JH, where the non-diagonal component is the Kronecker product of an AR-1 correlation matrix and an unstructured 2 × 2 covariance matrix Λ. In model 3 we fit a mean component consisting of a random intercept and an urbanicity effect with the same covariance as model 2, that is, ${\mathbf{W}}_i={\mathbf{Z}}_i{\gamma }_i+{\mathbf{E}}_i$. Finally, we fit SBP and DBP jointly and singly for all copula models. For each model we fit M = 2 and M = 4 basis functions. The runs with 4 basis functions had convergence issues, probably due to the large number of missing observations, so we present results for the M = 2 case.

LPML values were −32060, −17681, and −34282 for females for models 1,2, and 3 (−27683, −15576, and −29310 for males). The large values for model 2 indicate strong within-subject correlation that is captured in the covariance. The small LPML value for model 3 indicates that including subject-specific slopes for urbanization leads to overfitting. Figure 3 illustrates the urbanicity random effect γ_i2 on systolic blood pressure across female subjects. These effects are not statistically significant. Nonzero slope effects combined with missing observations can lead to estimating many extreme quantile levels for the first and last sampling waves. In applications with fewer missing observations or more timepoints, random slope effects could be useful.

Fig 3.

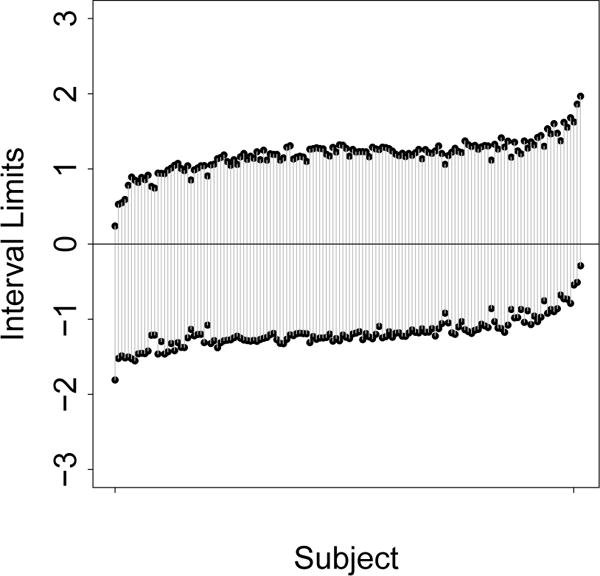
Plots of posterior credible sets of urbanicity random effects on females for systolic blood pressure. For visual clarity posterior credible sets are ordered by posterior median and every 10th subject is shown.

The posterior means of the off-diagonal elements of the correlation between responses were 0.94 and 0.95 for females and males respectively, with posterior standard deviations around 0.01. Therefore, SBP and DBP at one timepoint within an individual are very strongly correlated, and the posterior distribution of the correlation effects is dominated by the data. The posterior means of the temporal correlation parameter α were 0.12 and 0.10 for females and males respectively, with posterior standard deviations around 0.02. For the univariate fits of blood pressure the posterior means of α ranged from 0.70 to 0.82 with posterior standard deviations around 0.02. The multivariate and temporal correlation seem to be fighting for the same signal. This strong correlation within an individual across response and time is useful when imputing missing values.

For females, the average of the posterior variance of the regression effects at the median β_p(0.5) was 3.59 for the multivariate copula model and 4.24 for the multivariate independent model. This 13% increase in posterior variance (5% for males) suggests the independent model may be susceptible to undercoverage. For females, the mean of the posterior variance of the regression effects at the median was 3.62 for the univariate copula model. This 2% decrease in posterior variance for the multivariate model (1% for males) suggests that covariate effects are similar across SBP and DBP. In applications where multivariate observations within an individual were less correlated, we would expect a larger reduction in posterior variance of the effects. In summary, the copula models account for the within-subject dependence and are less susceptible to undercoverage than models that assume independent replications within an individual. The multivariate quantile approach reduces posterior variance by modeling SBP and DBP jointly.

Posterior plots of the intercept process β₁(τ) for the age 40–50 cohort and population urbanicity effects are shown in Figure 4. The intercept process represents the values of our baseline age 40–50 cohort when all predictors are zero, which is a central value after transformation to [−1, 1] for all covariates. For the intercept process, the light 2009 regions differ statistically from the dark 1991 regions for males in the lower tails of SBP and DBP. In contrast to the intercept process, the urbanicity effects change qualitatively from the first to the last sampling wave. In 1991 urban areas had higher blood pressure in the upper tail and lower blood pressure in the lower tail. In 2009 the urbanicity effect is negative or zero for SBP for all quantile levels. In contrast, urban areas are now associated with lower DBP in the upper tail of the distribution. Figure 1 illustrates that both blood pressure values and urbanization have increased over time, while Figure 4 shows that urban areas now have similar or lower quantiles of SBP and DBP than their rural counterparts. This indicates that rural areas are driving the increases in the upper tails of the distributions of SBP and DBP.

Fig 4.

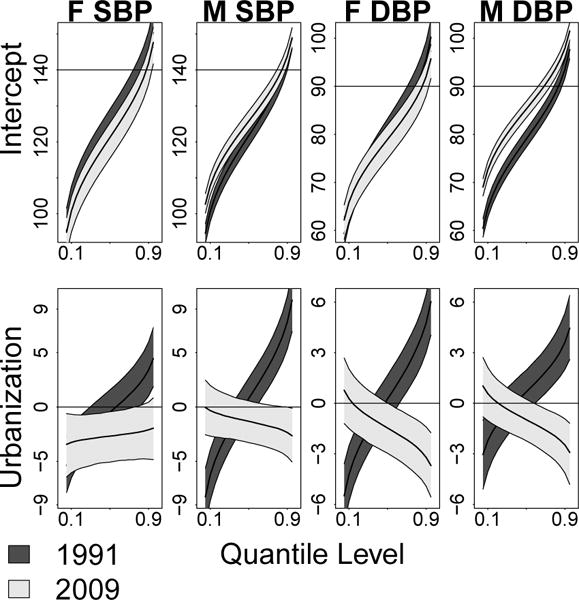
Plots of the intercept process for the age 40–50 cohort and population urbanicity effects by gender and blood pressure type. The intercept process is the distribution of the response when all covariates are 0. The urbanicity plots are the effects of a one standard deviation increase in urbanicity on the τ^th quantile of blood pressure. Dark regions correspond to 1991 estimates, while light regions correspond to 2009 estimates.

Estimated location effects are presented in Table 2, where several general associations are apparent. Blood pressure increases with age, as expected a priori. The interaction effects between urbanization and age represent the differences in urbanization effects across different age groups. Other than the cohort older than 60 years of age, 0 is in or very near the limits of the credible sets of interaction effects for both males and females for all years. This indicates there is little evidence that the urbanization effect changes much with age for individuals aged 60 and below, indicating that rural Chinese youth may be more at risk for hypertension. However, there are very few young individuals measured in later waves (only 91 in 2006, 0 in 2009), so estimates for this cohort are less stable and have larger variances. For Chinese aged 60 and above the urbanization interaction effect is positive for 2009. This tends to bring the effect in the upper tails closer to 0, and reduces the discrepancy in urbanization effect for older Chinese. The covariates household income, pregnancy and smoking status have little effect. To examine the robustness of assuming a male was a nonsmoker if smoking status was missing, we reran our final model assuming the individual was a smoker instead of a nonsmoker if the first wave was missing. The smoking effect was unchanged.

Table 2.

Posterior parameter estimates and 95% credible intervals for location effects. Mean effects include age cohort (with baseline group aged 40–50), urbanicity by age cohort interaction (indicated by U *), household income (HHI), current pregnancy status, and smoking.

Female Effects
Predictor	SBP 1991		SBP 2009		DBP 1991		DBP 2009
18 < Age < 30	−5.5	(−6.9, −3.9)	−4.2	(−5.9, −2.7)	−2.8	(−3.7, −2.0)	−3.2	(−4.3, −2.2)
30 < Age < 40	−4.5	(−5.9, −3.3)	−1.5	(−2.8, −0.0)	−2.6	(−3.5, −1.8)	−0.2	(−1.1,0.7)
50 < Age < 60	2.7	(1.0,4.3)	3.2	(1.8,4.6)	1.3	(0.1,2.3)	1.4	(0.5,2.3)
60 < Age	7.7	(6.0,9.6)	5.5	(4.1,6.9)	3.1	(2.0,4.4)	1.9	(0.9,2.7)
U * (18 < Age < 30)	−0.9	(−5.7,3.6)	1.1	(−4.1,7.1)	1.2	(−2.0,4.2)	3.6	(0.3,7.4)
U * (30 < Age < 40)	−4.5	(−10.1,1.5)	0.8	(−4.1,6.2)	−0.8	(−4.4,3.1)	−0.0	(−3.0,3.1)
U * (50 < Age < 60)	4.2	(−2.8,10.9)	0.4	(−4.9,5.5)	2.2	(−2.5,7.0)	2.0	(−1.2,5.1)
U * (60 < Age)	2.7	(−3.2,8.2)	6.6	(1.6,11.4)	1.9	(−2.1,5.6)	1.3	(−1.7,4.7)
HHI	4.0	(−0.7,8.2)	−2.0	(−3.6, −0.1)	2.2	(−0.6,4.8)	−0.8	(−1.9,0.4)
Pregnant	−1.1	(−4.5,2.9)	2.0	(−1.8,4.8)	−1.0	(−2.8,1.6)	−0.3	(−3.2,1.9)
Male Effects
Predictor	SBP	1991	SBP	2009	DBP	1991	DBP	2009
18 < Age < 30	−1.9	(−3.6, −0.5)	−4.0	(−5.7, −2.5)	−1.6	(−2.5, −0.5)	−3.3	(−4.2, −2.4)
30 < Age < 40	−1.3	(−3.0,0.0)	−2.1	(−3.3, −0.7)	−1.0	(−2.0,0.1)	−1.2	(−2.1, −0.4)
50 < Age < 60	4.7	(3.4,6.5)	0.8	(−0.4,2.1)	2.1	(1.1,3.3)	0.1	(−0.7,0.9)
60 < Age	8.3	(6.2,10.1)	3.2	(1.9,4.5)	3.6	(2.4,4.8)	0.3	(−0.5,1.2)
U * (18 < Age < 30)	−0.2	(−5.8,4.7)	−0.5	(−5.8,4.9)	−1.6	(−5.2,1.8)	3.1	(−0.4,6.6)
U * (30 < Age < 40)	−5.2	(−10.1, −0.6)	−1.2	(−6.1,3.5)	−4.0	(−7.6, −0.5)	1.5	(−1.7,4.4)
U * (50 < Age < 60)	5.7	(−0.1,11.5)	0.6	(−4.5,6.4)	0.9	(−2.9,5.3)	0.9	(−2.6,4.4)
U * (60 < Age)	7.0	(1.6,13.6)	2.4	(−2.5,7.4)	1.0	(−2.9,5.1)	−0.0	(−3.2,3.1)
HHI	2.6	(−0.5,5.3)	−1.8	(−3.4, −0.2)	0.9	(−1.0,3.0)	−0.7	(−1.8,0.3)
Smoke	−0.1	(−0.9,0.9)	0.5	(−0.2,1.4)	−0.1	(−0.7,0.5)	0.0	(−0.5,0.5)

6. Discussion

In this paper we have presented novel methods for analysis using mixed models in a quantile regression framework to address a major limitation in the hypertension literature: the inability to consider continuous SBP and DBP as correlated outcomes. Most hypertension literature either considers the discrete hypertension outcome or continuous SBP or DBP outcomes in separate models. Our quantile regression model enabled the exposure effect of urbanization to vary smoothly along the distributions of SBP and DBP, offering much more flexibility than mean regression models or models that specify cutpoints. We conducted a simulation study that illustrates the utility of estimating dependence in SBP and DBP for quantile regresssion in a longitudinal setting. We found strong evidence of dependence of SBP and DBP and serial correlation within an individual. We found that the effects of the covariates are similar across SBP and DBP, and inference can be enhanced by borrowing information across outcomes. There are many biostatistical and epidemiological applications where cutpoints are currently utilized to enable separate inference at different parts of the distribution, including analyses of air pollution, nutrients, and apolipoprotiens, to name a few. Our model obviates the choice of cutpoints. This is a key advantage, as inference is often nonrobust to cutpoint selection.

We found that urbanicity is now associated with lower rather than higher blood pressure, especially in the upper tails of the distribution, potentially illuminating the segment of the population at highest risk relative to dietary or physical activity changes occurring with modernization. It is possible that modernization-related changes of urbanization lead to more protective lifestyle habits for individuals at the highest levels of urbanization. Perhaps these individuals have greatest access to health care and environmental supports for healthy diet and physical activity, which leads to some degree of protection at the upper tail of the distribution. Our findings suggest that attention be paid to the center of the urbanization distribution to address individuals who might be in urbanizing areas, but without access to supports for healthy lifestyle behaviors. Given that urbanization has increased over the last twenty years and the urbanization effect in the upper tail has diminished, blood pressure appears to be increasing in China even in less urbanized areas.

We flexibly model the population level regression effects using a linear combination of parametric basis functions. We model the within-subject level dependence using a Gaussian copula. We chose a Gaussian copula to facilitate centering of the prior distribution, to accommodate within-subject serial correlation and covariates affecting the within-subject dependence, and for simplicity in computation and imputation of missing values. However, these advantages may not be worth the restrictive behavior of the Gaussian copula in other applications, and this is an area of future research. Gaussian copulas assume independence in the deep tails and assume the same dependence in the lower tail as the upper tail. In this paper we focus on the quantile levels from 0.1 to 0.9. In practice if inference at more extreme quantile levels is of interest, other copulas should be considered. Another useful extension is a fully nonparametric approach to the quantile function.