Synaptic homeostasis and input selectivity follow from a calcium-dependent plasticity model

Abstract

Modifications in the strengths of synapses are thought to underlie memory, learning, and development of cortical circuits. Many cellular mechanisms of synaptic plasticity have been investigated in which differential elevations of postsynaptic calcium concentrations play a key role in determining the direction and magnitude of synaptic changes. We have previously described a model of plasticity that uses calcium currents mediated by N-methyl-d-aspartate receptors as the associative signal for Hebbian learning. However, this model is not completely stable. Here, we propose a mechanism of stabilization through homeostatic regulation of intracellular calcium levels. With this model, synapses are stable and exhibit properties such as those observed in metaplasticity and synaptic scaling. In addition, the model displays synaptic competition, allowing structures to emerge in the synaptic space that reflect the statistical properties of the inputs. Therefore, the combination of a fast calcium-dependent learning and a slow stabilization mechanism can account for both the formation of selective receptive fields and the maintenance of neural circuits in a state of equilibrium.

Synaptic plasticity as a physiological basis for learning and memory storage has been extensively investigated. Induction of bidirectional synaptic plasticity has been shown to depend on calcium influx into the postsynaptic cell (1, 2). In a previous paper, we proposed a model of bidirectional activity-dependent synaptic plasticity that depends on the calcium currents mediated by N-methyl-D-aspartate receptors (NMDARs) (3). In this model, which we henceforth denote calcium-dependent plasticity (CaDP), the direction and magnitude of synaptic changes are determined by a function of the intracellular calcium concentration: basal levels of calcium generate no plasticity, moderate ones induce depression, and higher elevations lead to potentiation (4). At a synapse, the amount of neurotransmitter bound to NMDARs provides information on the local, presynaptic activities, whereas back-propagating action potentials signal the global, postsynaptic activities. This association between pre- and postsynaptic activities thus forms the basis for Hebbian learning. Analysis and simulations have shown that this model can explain the rate-, voltage-, and spike timing-dependent plasticity as consequences of, respectively, the temporal integration of calcium transients, the voltage-dependence of NMDAR conductances, and the coincidence-detection property of these receptors (3, 5). In addition, numerous experimental results support the idea that NMDARs play key roles in activity-dependent development and refinement of synapses because of their permeability to calcium ions (6-11).

However, typical of associative forms of plasticity rules, CaDP is not completely stable. Excessive neural excitation generates high levels of depolarization, favoring calcium entry into the dendrites and thus promoting synaptic potentiation. Such potentiation further enhances the excitability of the cell. In this paper, we complement CaDP with a biologically motivated method of synaptic stabilization. We propose an activity-dependent regulation of calcium levels that counteracts sustained increases or decreases of neuronal excitability. Calcium mediates a myriad of cellular processes in addition to synaptic plasticity, and under certain conditions, it can be deleterious (12). Mechanisms exist that control the flux of calcium in the various compartments of the cell and through its various sources. There are a variety of calcium sources including voltage- and receptor-dependent channels, as well as release from the intracellular stores. Therefore, many possible pathways of control coexist. We have previously shown that modifications of the NMDAR intrinsic properties can modify the CaDP learning curves (3, 13). In the interest of presenting a concrete and relatively simple model, we implement calcium homeostasis through an activity-driven regulation of NMDARs. If other pathways prove to be important, they can easily be incorporated into our model.

We show that such a regulation results in a learning dynamics comparable to those observed in homeostatic forms of synaptic modifications, such as synaptic scaling (14, 15) and metaplasticity (16, 17). In scaling, chronic increase (decrease) in the global levels of cellular activity weakens (strengthens) the synaptic weights. In metaplasticity, sustained increase (decrease) in neural activities makes further potentiation (depression) more difficult to be elicited. At first sight, these properties seem in contradiction to classical results from experience-dependent synaptic modifications, such as long-term depression (LTD) and long-term potentiation (LTP). These types of plasticity require that synaptic strengths increase with high, and decrease with low, levels of neural excitation. Through our implementation, we propose that LTP and LTD share the same pathways as the homeostatic forms of plasticity, with the latter occurring in a time scale longer than the former. In addition, our results suggest that scaling and metaplasticity could be alternative manifestations of similar processes, recruited to maintain a working level of dendritic calcium.

We also investigate the implications of a slow stabilizing mechanism on the collective dynamics of the synapses. A familiar property of single neurons is their input selectivity: their response is typically tuned to a particular subset of the stimuli that they receive. This can arise from selectively strengthening some synapses, whereas depressing others in other words, through synaptic competition. The emergence of structure in the synaptic space should reflect the nature of the input statistics. Here, we show that our model neuron is sensitive to temporal correlations among the input spike-trains in a manner similar to spike timing-dependent plasticity (STDP) (18). Furthermore, after sequential, random presentations of a set of input rate patterns, the neuron develops selectivity to only one of these patterns. This is comparable to traditional rate-based learning models such as the Bienenstock-Cooper-Munro (BCM) rule (19). This finding suggests that synaptic homeostasis could be an essential aspect of learning that participates not only in synaptic growth control, but also in the emergence of time- and rate-sensitive structures in the synaptic space.

Methods

Learning Rule. According to CaDP (3), calcium currents through NMDARs I_i depend both on a function f_i of the glutamate binding, and on a function H of the postsynaptic depolarization level

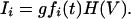1

Upon the arrival of a presynaptic spike at synapse i, f_i reaches its maximum value. Part of it decays exponentially with a fast time constant; the remainder decays slowly. Analogously, upon the triggering of a postsynaptic spike, the back-propagating action potentials reaches its peak value and decays as a sum of two exponentials. The voltage dependence of the H function describes the magnesium blockage of the NMDARs (20). Intracellular calcium [Ca]_i is integrated locally, and decays passively with a time constant τ,

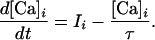2

The synaptic weights are updated as

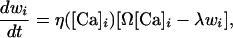3

where η([Ca]_i) is a calcium-dependent learning rate, Ω is a U-shaped function of calcium, and λ is a decay term. The detailed implementation has been presented (3), and the parameter values can be found in the supporting information, which is published on the PNAS web site.

Model of Stabilization. In this paper, the control of dendritic calcium concentrations is implemented through a slow, activity-dependent regulation of the NMDAR permeability, which depends on the time-integrated membrane voltage. If the postsynaptic voltage is chronically low, NMDAR conductance increases to allow more potentiation; if it is persistently high, the conductance decreases.

The specific dynamic equation

4

can be derived from a kinetic model of NMDAR insertion and removal, with parameter g_t and transition rates k₊ and k_-(V - V_rest)², respectively. For simulation details and parameter values, see supporting information.

Simulation Methods. Following the methodology detailed in ref. 18, we simulate an integrate-and-fire point neuron, with 100 excitatory and 20 inhibitory synapses. Only excitatory synapses are plastic. Each synapse receives a Poisson spike-train whose parameter is the mean input rate of that synapse (see supporting information).

To introduce correlation into a subset of spike trains, we adopt the model described in ref. 21. Let the number of correlated inputs be N_c. Given a correlation parameter c (0 ≤ c ≤ 1), and an input frequency r, we pregenerate N₀ Poisson events with rate r, where 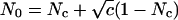. At each time step, these events are randomly distributed among the N_c synapses. Redundancy results from the fact that N₀ ≤ N_c. Thus, coincident spikes will occur with a higher-than-chance probability without affecting the mean rate within each spike train. We also simulate two independently correlated groups (or channels), each consisting of N_c = 50 synapses. The same procedure described above is applied to each channel, using two different sets of N₀ Poisson events. Only excitatory synapses receive correlated inputs.

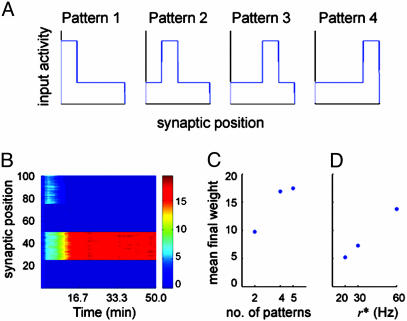
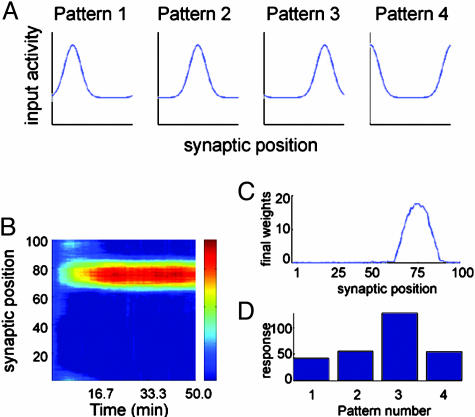
Spatial patterns of rate distribution are presented to the cell as follows. For square patterns (where the rates are piecewise constant functions of the synaptic position), the synaptic vector with 100 synapses is divided into N_p nonoverlapping channels with 100/N_p synapses each. Every 500 ms, one of these channels is randomly chosen to receive stimulus rate r^*; the remaining groups receive rate r < r^* (see Fig. 5A). For bell-shaped patterns (where the rates are Gaussian functions of the synaptic position), Gaussian functional forms with amplitude A and width σ are added to a constant, “background” rate r (see Fig. 6A). For each pattern, the peak rate r^* = r + A is at a different synapse position. If there are N_p patterns, the peak positions are the synapses 100/N_p, 200/N_p,... 100. For example, a pattern with peak rate at synapse 50 is described by

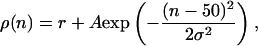5

Fig. 5.

Selectivity to nonstatic square patterns of input rate distribution. (A) An example with four patterns, each pattern consists of 75 inputs at a lower rate r, and 25 inputs at a higher rate r^*. Inhibitory inputs are at 10 Hz. Every 500 ms, one of these patterns is randomly chosen and presented to the cell. (B) Each of the 100 rows represents the temporal evolution of a synapse over the 50 min of simulated time. The color bar indicates the synaptic strength. In this case, four patterns are presented, and the neuron develops selectivity to pattern 2. (C) The averaged final weight of the potentiated channel after training with two, four, and five patterns (r = 10 Hz and r^* = 40 Hz). When only one channel is potentiated, the remainder collapses to zero. (D) The averaged final weight of the potentiated channel, with higher rate r^* = 20, 30, and 60 Hz (lower rate r = 10 Hz, using two patterns). Selectivity is robust for different pattern dimensions and amplitudes.

Fig. 6.

Selectivity to nonstatic Gaussian patterns of input rate distribution. (A) In this example with four patterns, each pattern has a width of 10 synapses, a baseline amplitude of 10 Hz, and a peak amplitude of 40 Hz, but the peaks are at different positions for each of them. (B) Temporal evolution of the synaptic weights; the color bar scale is the same as in Fig. 5B. (C and D) The final weight distribution (C) and the test stimulus (D) indicate that the neuron becomes selective to pattern 3.

where ρ(n) is the input rate at synapse n. Every 500 ms, one of these patterns is randomly chosen and presented to the cell. It should be noted that these are the instantaneous rates of the inhomogeneous Poisson spike trains and not the frequencies of regularly firing stimuli.

All of our simulations were performed by using the same set of parameters. However, to speed up some of the simulations, both the learning and the stabilization rates were made 100 times faster in the simulations involving different input statistics because we are mostly interested in the final state. We have verified that the fixed point of the system does not change if both rates are multiplied by the same factor. We run all simulations with time steps of 1 ms, until the fixed points (or the saturation limits, if these are present) are reached.

Results

Homeostasis. It has previously been shown that CaDP alone is unstable (13). For low and high input rates, the synapses depress and potentiate until the saturation limits are reached. Complementing the model with a mechanism of calcium-level homeostasis introduces a stable fixed point to the synaptic weight dynamics. To illustrate this, we simulate a neuron receiving homogeneous Poisson spike trains at a given rate until the fixed point is reached, and repeat the procedure for rates spanning the interval (5 and 60 Hz).

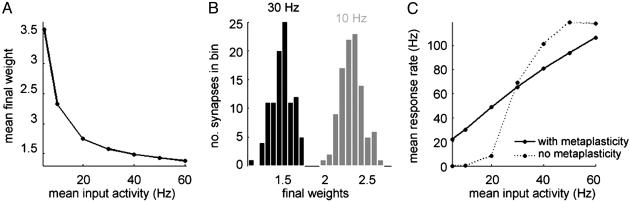
The final weight distribution is stable and finite for all input rates in the range presented (Fig. 1A). In addition, the values of the fixed points decrease for increasing rates. This property is reminiscent of the results observed in synaptic scaling experiments (15). In fact, the distribution of the synaptic weights is unimodal (Fig. 1B), similar to the results obtained from the theoretical formulations of scaling (22). Although the weights scale down, the output rates still increase monotonically with increasing input rates (Fig. 1C; for comparison, we also show the input-output relation in the absence of the stabilization mechanism). This differs from previously proposed models proposed to stabilize spiking neurons, where roughly the same output levels are achieved regardless of the input rate (22-24). If the input rate holds information about the stimulus, maintaining the input-output relationship could be important for the propagation of such information across the different layers of processing in the brain.

Fig. 1.

Stabilizing effects caused by calcium homeostasis. (A) The averaged final weights scale down with increasing input activity. (B) The final weight distribution is unimodal when the input consists of structureless Poisson spike trains. Black, 30-Hz input activity; gray, 10-Hz input activity. (C) The final response rate is an increasing function of the input rate whether there is homeostatic regulation (solid line) or there is not (dotted line). However, the gain is smaller in the presence of a stabilization mechanism. Results are shown after 2 h and 46.7 min of simulated time in the presence of homeostasis, and after 1,000 stimulating pulses in its absence.

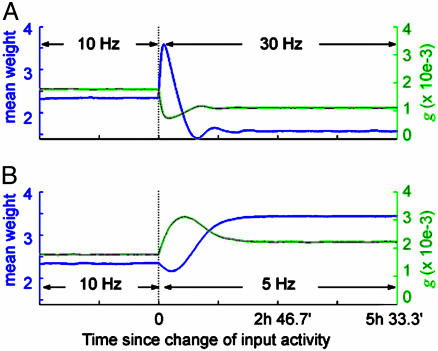
Depression of the weights with increasing input rate is in apparent contradiction with the well known results of experiments using rate-based LTD- and LTP-inducing protocols (7, 8, 25). To address this issue, we investigate the full temporal dynamics of the synaptic weights when the input rates are switched from a reference level (10 Hz) to a higher (30 Hz) or a lower value (5 Hz). The temporal evolutions of the synaptic weights are shown in Fig. 2. In a short time scale, switching input rates from 10 to 30 Hz results in LTP (Fig. 2 A), and changing the rates from 10 to 5 Hz produces LTD (Fig. 2B).

Fig. 2.

Different time scales of synaptic modification. (A) When the input activity increases from a reference value (10 Hz) to a higher rate (30 Hz), the synapses are transiently potentiated (blue line). The effects of homeostasis manifests on a much longer time scale. The evolution of the NMDAR conductance is also shown (green line). (B) Similarly, when the input decreases from the reference to a lower rate (5 Hz), the synapses first undergo depression, then potentiation.

The effects of homeostasis are only manifested in a longer time scale, leading to a 33% down-scaling of the weights in the former case, and a 46% up-scaling in the latter. This finding is in agreement with observations that the time scale for LTD and LTP induction is on the order of seconds or minutes, whereas the induction of metaplasticity and scaling takes hours to days. Our results suggest that long-term plasticity (LTD and LTP) and neuronal homeostasis (metaplasticity and scaling) could both share the same biological pathways of synaptic modifications, differing only in the respective time scales.

Selectivity to Temporally Correlated Spike Trains. The unimodal synaptic distribution presented previously resulted from an input environment that contained no structure. To demonstrate that patterned distribution can arise under stabilized CaDP, we present spike trains with different statistical structures to the simulated neuron. We first divide the synaptic vector into two channels: one has synapses receiving spikes with a higher-than-chance probability of arriving together; the other receives uncorrelated Poisson spike trains.

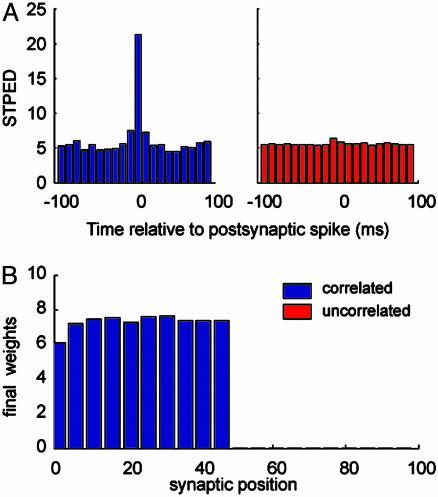
The effects of correlation can be observed through the spike-triggered presynaptic event density (STPED), which measures the average number of presynaptic spikes arriving with a lag Δt before or after a postsynaptic spike. In Fig. 3A, we plot the STPED for an input rate of 10 Hz and in the absence of plasticity. The STPED peaks immediately before Δt = 0 for the correlated group (blue). For the uncorrelated group (red), the STPED is flat. This finding indicates that coincident spikes have a greater chance of eliciting a postsynaptic spike. Therefore, due to the spike timing-dependent property of CaDP, presynaptic spikes that precede postsynaptic spikes are selectively potentiated. Excessive potentiation subsequently triggers homeostastic regulation, which in turn depresses the uncorrelated channel. The final weight distribution is thus segregated into strong, correlated synapses and weak, uncorrelated ones, as depicted in Fig. 3B.

Fig. 3.

Selectivity to correlated inputs. (A) The STPED shows the number of presynaptic events that occur at different time lags with respect to a postsynaptic event. The STPED peaks immediately before a postsynaptic spike for the correlated (blue) channel but is flat for the uncorrelated (red) channel. Results are for a input rate of 10 Hz, and intervals were binned at every 10 ms. (B) The final weight distribution is bimodal, and the correlated group is selectively potentiated (synapses 50-100 are zero, and thus hardly visible in the figure). The segregation is only possible with the implementation of a homeostatic calcium control.

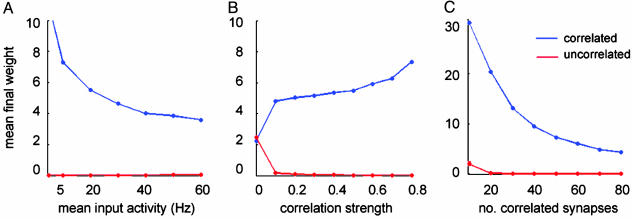
Such segregation is robust across a wide range of spike train parameters, such as the spike rate r, correlation strength c, and number of correlated units N_c (Fig. 4). The weights of the correlated synapses decrease as the input rate increases, showing again the effects of homeostasis (Fig. 4A). Furthermore, strengthening the correlation increases segregation (Fig. 4B). Finally, if more synapses are correlated, their average weight is weaker, suggesting that, when many inputs arrive together, less potentiation is needed to control the neuronal response (Fig. 4C).

Fig. 4.

Robustness of input selectivity. (A) The correlated group is selectively potentiated for a wide range of input rates; shown are the averaged final weights for the correlated (blue) and the uncorrelated (red) groups. The weights of the potentiated group decay with increasing rate in a manner similar to Fig. 1. (B) Strengthening the correlation parameter c increases the segregation between the two channels. (C) Increasing the number of correlated synapses decreases the final weights of the correlated channel, indicating that less potentiation is needed for this channel to control the postsynaptic firing.

This model differs in an important aspect from existing learning rules where STDP potentiates synapses that receive temporally correlated spike trains. Here, patterned weight distribution only emerges if the input is structured. In the some formulations of STDP, bimodal distribution of weights arises even when the stimuli are nonstructured Poisson spike trains (18). One also should notice that robust segregation between the correlated and the uncorrelated channels is only possible with the stabilization mechanism we introduced here. Previous simulations have shown that, without stabilization, such segregation is only achieved within a narrow range of input rates: the weights are all potentiated or all depressed for rates slightly above or below this range (26).

Independently Correlated Channels. We have extended the temporally correlated environment from one correlated and one uncorrelated channel to two independent correlated channels. Under this condition, the two groups compete with each other until one of them gains control over the postsynaptic firing. The final states are similar to the ones presented above (see supporting information). However, because the correlation parameter c is the same for both groups, the winning group is random at each run. In addition, the time course can be significantly different across runs. These properties illustrate that this system undergoes spontaneous symmetry breaking. Bias, which can break this symmetry, can be introduced by changing the correlation strength or the number of synapses of a group.

Selectivity to Patterns of Input Rate. The results we presented so far use stationary input patterns: the synapses within a channel are either correlated or uncorrelated throughout the simulation. In addition, the mean input rate is the same across all inputs. However, sensory receptive fields typically develop in natural, nonstationary environments where different groups of synapses are transiently excited at different times. To explore whether, in addition to temporal correlations, our model neuron also develops selectivity to nonstationary patterns of input rate, we deliver inhomogeneous Poisson spike trains with instantaneous rates defined as a function of synaptic position and of time. Because the patterns change rapidly, compared with the rate of learning, the mean input is statistically homogenous across synapses. Nonetheless, in each case, the neuron develops selectivity to only one of the patterns presented.

Fig. 5B shows an example of the temporal evolution of the weights when four square patterns with the lower rate r = 10 Hz and the higher r^* = 40 Hz are presented to the cell. Symmetry breaking occurs and the synapses evolve to a state such that the neuron responds most strongly to pattern 2. Because the patterns switch randomly during training and all of the weights start with the same initial condition, the selected pattern is random at each run.

The results hold for different numbers of patterns, as well as for different rate intensities. Fig. 5C compares the final weights after simulations using two, four, and five patterns, with r = 10 Hz and r^* = 40 Hz. Fig. 5D shows the final weights for two patterns where r = 10 Hz, but with r^* = 20, 30, and 60 Hz. All simulations reach a final state where a single channel is potentiated; the remainder depresses to zero. The precise values of the synaptic weights are consistent with the ongoing homeostatic regulation. Because only a subset of the synapses becomes nonzero, their final weights are stronger than those presented above. Similarly, the fewer synapses are present in the potentiated subset, or the lower the input rate, the more these synapses are strengthened.

An alternative environment is one where the input rates are distributed as mutually overlapping bell-shaped patterns. Fig. 6A shows an example using four Gaussian patterns with background rate r = 10 Hz, peak rate r^* = 40 Hz (Gaussian amplitude A = 30 Hz), and width σ = 10 synapses. The evolution of the synaptic weights can be seen in Fig. 6B, where the neuron develops selectivity to pattern 3. Fig. 6C shows the final weight distribution. In this case, it does not have the same width as the input patterns, but the selected input is unambiguous, as can be seen by the responses to test stimuli shown in Fig. 6D.

Discussion

Here, we extend our previous work on CaDP and show how two important cell properties, stability and input selectivity, emerge from a common framework based on a fast calcium-dependent synaptic plasticity combined with a slow calcium regulation mechanism.

Stability is introduced through a slow, activity-dependent regulation of the dendritic calcium levels. This extends the “sliding threshold” of rate-based Bienenstock-Cooper-Munro (BCM) to spiking neurons and may serve as a biological basis for neuronal homeostasis. Our results can be related to observations in synaptic scaling experiments (Fig. 1). A key conclusion is that neuronal stabilization processes detected in different types of experimental protocols (namely, metaplasticity and synaptic scaling) can rely on similar underlying processes that are involved in the fine control of intracellular calcium concentrations. Moreover, these slow homeostatic processes can coexist with LTD and LTP within the same formalism (Fig. 2). Plasticity at different time scales might be due to different cellular mechanisms. However, our results show that the rapid long-term plasticity and the slow homeostatic processes can share the same substrate or substrates for synaptic modification. One prediction of our model is that transient LTP-inducing stimulation should lead to high elevations of calcium as shown in the literature (4, 27, 28), but sustained stimulation should subsequently produce calcium levels that are similar to baseline levels.

In many spike timing-dependent learning rules, stability and competition are conflicting properties. Some learning rules (18) exhibit strong synaptic competition, giving rise to patterned synaptic weight distribution even in the absence of structure in the stimulus. However, these rules are typically unstable and require saturation limits for the synaptic growth. Other models (22, 24) are highly stable, but competition needs to be enforced through an additional mechanism. In these models, stabilization regulates the output rate in such a way that this is roughly maintained, regardless of the input rate. In our model, stimuli without structure produce unimodal weight distributions (Fig. 1). At the same time, patterned inputs produce a selective potentiation of a subset of synapses (Figs. 3, 4, 5, 6). In addition, the input-output relation of the neuron is positively correlated; this could be important to preserve the information contained in the input activity. It is important that stability and competition are consequences of a single mechanism.

In addition to reproducing the STDP results, our model is responsive to input rates. We are thus able to achieve selectivity to rate patterns in a spiking neuron in a manner comparable to the selectivity obtained in rate-based models (7, 8, 25). Both rate- and spike-based forms of plasticity have been observed experimentally in the same preparation (29), and the relationships between the models have been proposed at a phenomenological level (30, 31). Here, we show that the interplay between these two mechanisms, previously shown in a one-dimensional neuron (3, 13), also is present in a multiinput environment and could involve subcellular mechanisms of coincidence detection and temporal integration of metabolites.

In this paper, calcium homeostasis is implemented, for convenience and clarity, through a dynamic regulation of NMDAR permeability. However, evidence for the role of NMDAR in synaptic stabilization remains conflicting. Many studies reveal activity-dependent modification of the NMDAR function. These may involve receptor trafficking (32-34) or modification of its subunit composition (35-37). However, other experiments indicate that synaptic homeostasis can still be detected when NMDARs are blocked (38). Calcium can be recruited into the synapse through numerous cellular pathways that may act in parallel. The results presented here do not depend on the particular choice of calcium regulation mechanism but rely on the assumption that calcium is the signal for triggering both long-term and homeostatic bidirectional plasticity. The involvement of additional calcium sources can be readily incorporated into our model.