Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2016 Nov 7;27(22):3574–3582. doi: 10.1091/mbc.E16-06-0414

T-lymphocyte passive deformation is controlled by unfolding of membrane surface reservoirs

Lionel Guillou a, Avin Babataheri a, Michael Saitakis b, Armelle Bohineust b,c, Stéphanie Dogniaux b, Claire Hivroz b, Abdul I Barakat a, Julien Husson a,*
Editor: Patricía Bassereaud
PMCID: PMC5221589  PMID: 27605708

T-lymphocyte passive deformation when squeezing through narrow capillaries is limited by the excess membrane contained in microvilli and membrane folds. During active processes such as transendothelial migration, larger deformations are made possible by an increase in membrane area, possibly through recruitment of internal membrane reservoirs.

Abstract

T-lymphocytes in the human body routinely undergo large deformations, both passively, when going through narrow capillaries, and actively, when transmigrating across endothelial cells or squeezing through tissue. We investigate physical factors that enable and limit such deformations and explore how passive and active deformations may differ. Employing micropipette aspiration to mimic squeezing through narrow capillaries, we find that T-lymphocytes maintain a constant volume while they increase their apparent membrane surface area upon aspiration. Human resting T-lymphocytes, T-lymphoblasts, and the leukemic Jurkat T-cells all exhibit membrane rupture above a critical membrane area expansion that is independent of either micropipette size or aspiration pressure. The unfolded membrane matches the excess membrane contained in microvilli and membrane folds, as determined using scanning electron microscopy. In contrast, during transendothelial migration, a form of active deformation, we find that the membrane surface exceeds by a factor of two the amount of membrane stored in microvilli and folds. These results suggest that internal membrane reservoirs need to be recruited, possibly through exocytosis, for large active deformations to occur.

INTRODUCTION

The ability of T-lymphocytes to patrol both the vasculature and extravasate into surrounding tissue is a central feature of the human adaptive immune response (von Andrian and Mempel, 2003; Valignat et al., 2013; Crotty, 2015; DuPage and Bluestone, 2016). Accomplishing these tasks requires T-lymphocytes to undergo large deformations, both passively, as they move through narrow capillaries during their patrols (Fung, 2013), and actively, upon extravasation at a site of inflammation or injury (Carman and Springer, 2004; Carman, 2009; Carman and Martinelli, 2015). In certain cell types—for instance, neural cells during brain trauma—excessive strain can cause membrane damage both in vitro (Geddes et al., 2003) and in vivo (Pettus et al., 1994; Pettus and Povlishock, 1996). To our knowledge, however, there have been no reports of T-lymphocyte membrane damage in vivo despite the large deformations that these cells undergo. In the present study, we sought to understand how T-lymphocytes respond to large, passive deformations. We asked specifically whether there was a physical criterion for these deformations to trigger membrane rupture and whether this criterion changed during the life of a T-lymphocyte (when the resting T-lymphocyte becomes a lymphoblast). Finally, we investigated whether such a criterion would also apply to large active deformations as occurs during cell spreading and extravasation.

RESULTS

A T-lymphocyte increases its surface area at constant volume when entering into a narrow capillary

To mimic the partial or complete passage of T-lymphocytes through a narrow capillary in vivo, we aspirated T-lymphocytes into glass micropipettes of a few micrometers in diameter. Indeed, the relevant length scale here is the micrometer, given that human capillary diameters are in the range of 5–10 μm (Fung, 2013) and that, based on our measurements, resting T-lymphocytes have a diameter of 6.7 ± 0.4 μm (mean ± SD). Active migrations of T-lymphocytes also occur at the same length scale, as previous studies measured pore sizes from transendothelial migration of T-lymphocytes to be close to 5 μm (Carman and Springer, 2004; Shulman et al., 2011).

After grabbing T-lymphocytes using a small aspiration pressure (10–20 Pa), we applied a constant aspiration pressure ΔP (Figure 1A) and observed the entry of the aspirated cell for 5 min. Measuring the cell dimensions before and after this aspiration period, we found that cell volume was constant regardless of the T-lymphocyte activation state, the aspiration pressure, or the capillary size (Figure 1B and Supplemental Figure S1). The volumes seen here for T-lymphocytes are consistent with what we find using fluorescence staining and confocal microscopy (Supplemental Figure S2). The preservation of the volume during aspiration is consistent with the fact that applied aspiration pressures on the order of ∼10–1000 Pa are much lower than the cellular osmotic pressure of ∼106 Pa acting to maintain the cell volume constant. The value for osmotic pressure was derived using the van’t Hoff law, assuming a cell osmolality of ∼300 mOsm for white blood cells, as measured by Schmid-Schönbein et al. (1980). To accommodate the constant-volume constraint during aspiration, cells depart from their initial relatively spherical shape, which is the geometric shape that minimizes surface area for a given volume. As a result, their surface area increases, so that the membrane of a T-lymphocyte is stretched when it passes through a capillary.

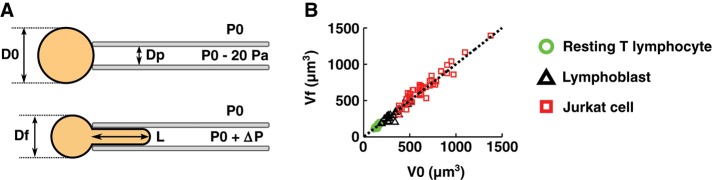
FIGURE 1:

FIGURE 1:

Open in a new tab

T-lymphocyte volume is conserved during micropipette aspiration. (A) Diagram of a micropipette aspiration experiment. We impose an aspiration pressure P0 + ΔP (ΔP assumes only negative values) and measure the initial cell diameter, D0, the final cell diameter, Df, the micropipette diameter, Dp, and the final entry length, L. (B) Plot of the final cell volume, Vf (see Supplemental Figure S1 for details on volume measurement), as a function of initial cell volume, V0. Data points fall on the dotted line of slope 1 (Vf = V0), showing that cell volume is conserved.

Surface area expansion of T-lymphocytes is accompanied by an increase in cell stiffness

To determine whether resting T-lymphocytes respond mechanically to passive deformations undergone during their aspiration into a micropipette, we measured the evolution of their effective stiffness as determined by microindentation. Microindentation consists in applying a known compressive force to a T-lymphocyte while measuring the resulting indentation (Figure 2 and Supplemental Movie S1). Using a model linking the applied force to the measured deformation allows the extraction of the mechanical parameters of the cell, such as its elastic properties (Guillou et al., 2016).

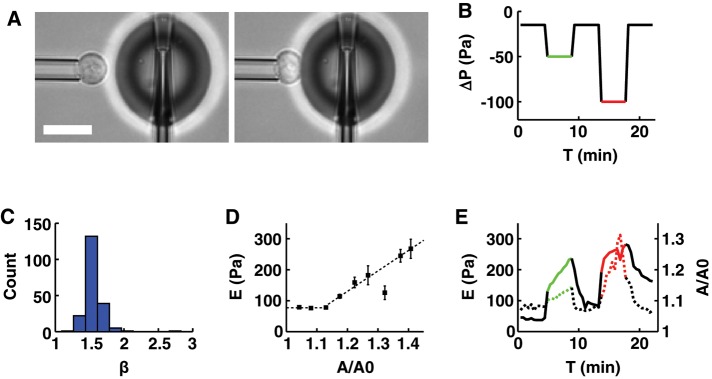
FIGURE 2:

FIGURE 2:

Open in a new tab

The apparent stiffness of a resting T-lymphocyte increases with apparent membrane surface area. (A) Example of a resting T-lymphocyte being aspirated into a micropipette while its apparent stiffness is measured using profile microindentation. Scale bar, 10 μm. (B) Plot of the aspiration pressure, ΔP, used to hold the resting T-lymphocytes during profile microindentation as a function of time. Each resting T-lymphocyte is indented ∼50 times, once every 30 s. Black, aspiration pressure is −15 Pa; green, −50 Pa; red, −100 Pa. (C) Histogram of the indentation scaling exponent β found during the profile microindentations. We fit the force–indentation curve using the relation F = α δβ, with F the force, δ the indentation, and α and β two fitting parameters. (D) Plot of the apparent stiffness, E, as a function of the normalized apparent membrane surface area, A/A0, where A0 is the initial membrane surface area and A is the membrane surface area at the time when E is measured. Bars represent SD. Five cells and 201 microindentations. The number of cells decreases for large values of A/A0. The three last points to the right correspond to only 5, 7, and 2 microindentations, respectively, compared with >30 on average for the six points to the left. Dotted line represents the best fit using the phenomenological relation E = E0 for A/A0 < 1 + ε and E = E0 + k[A/A0 − (1 + ε)] for A/A0 > 1 + ε. (E) Plot of E (left axis, dotted line) and A/A0 (right axis, continuous line) averaged over five cells, as a function of time.

First, we find that resting T-lymphocyte behavior upon indentation is consistent with an elastic solid model. Indeed, the force-indentation curves we obtain are well described by the classical Hertz model, which is a standard model used to describe the indentation of an elastic solid (Johnson, 1985) and is often used to analyze atomic force microscopy experiments (Dimitriadis et al., 2002; Krause et al., 2013). In this model, the indentation force, F, applied to an incompressible elastic substrate is related to the resulting indentation of this medium, δ, through the relationship F = (16/9)Eδ3/2. Thus the force is directly proportional to the Young’s modulus of the material, E, which measures the elasticity of the medium (expressed in pascals), and to the indentation raised to the power 3/2. Because other types of elastic behavior exist that are described by an exponent of the indentation other than 3/2 (Lomakina et al., 2004), we fit our data using a more general relationship, F = αδβ, where α and β are adjustable fitting parameters. We find that β = 1.55 ± 0.14 (mean ± SD) for a set of 201 cell indentations (Figure 2C), in excellent agreement with the prediction of the Hertz model of β = 3/2 (see example curve in Supplemental Figure S3). From the fitted value of α = (16/9)E, we deduce that E = 77 ± 8 Pa (mean ± SE of the mean) when the cell membrane is not stretched.

Second, we find that the effective cell stiffness increases with the apparent membrane surface area (Figure 2D). The increase in apparent membrane surface area is evaluated by tracking the ratio A/A0, where A is the apparent membrane surface area at the time of indentation and A0 is the initial apparent membrane surface area. To test whether this increase in cell stiffness depends on the applied aspiration pressure, we submitted cells to a constant pressure while monitoring both the effective stiffness and the ratio A/A0. We find that both increase continuously under a constant aspiration pressure (Figure 2E). When different aspiration pressures are applied, the relationship between the effective stiffness and the apparent membrane surface area remains the same, that is, the data points lie on the same E = f(A/A0) curve. Furthermore, the relationship is reversible, in the sense that when aspiration pressure is reset to a low level (typically 10–20 Pa), both effective stiffness and apparent membrane surface decrease, following the same conserved relationship (see Figure 2E and Supplemental Figure S4 for details). Of interest, we note that this reversibility appears to depend on the activity of myosin-II. Indeed, disrupting myosin-II activity with blebbistatin prevents the apparent stiffness from returning to its baseline value (Supplemental Figure S5). This shows that, consistent with previous work (Spinler et al., 2015), myosin-II activity influences the cell behavior in reaction to micropipette aspiration. In any case, we find that, similar to the approaches of Herant et al. (2005) and Lam et al. (2009), the relationship E = f(A/A0) is well described by the following phenomenological law:

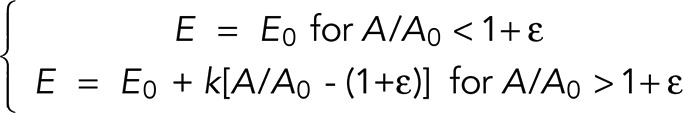graphic file with name 3574uequ1.jpg

(fit in Figure 2D), where E0 is the initial effective stiffness, k is an elastic expansion modulus, and ε is a measure of membrane slack, corresponding to the fraction of initial apparent membrane surface area that can be taken before it is necessary to unfurl folds or microvilli. Fitting our data with this relation, we find E0 = 77 ± 8 Pa (mean ± SE of the mean; see Supplemental Table T1 for details on the other two fitting parameters). This finding is consistent with a previous estimate of human primary CD4+ T-lymphocyte stiffness of 85 ± 5 Pa using a parallel-plate technique (Bufi et al., 2015). Note that the same study measured a very similar stiffness of 90 ± 10 Pa for Jurkat cells, which means that any difference in behavior that might be seen during micropipette aspiration between the two cell types is not attributable to differences in cell stiffness.

Previous micropipette aspiration experiments showed that membrane expansion is directly associated with an increase in cell tension γ for both neutrophils (Herant et al., 2005) and macrophages (Lam et al., 2009). In fact, the dependence of cell tension on membrane expansion takes the same form as we found for effective stiffness (Lam et al., 2009):

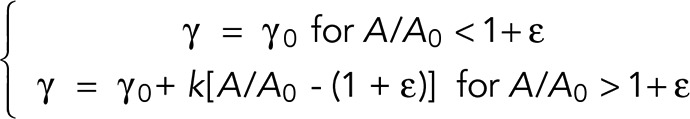graphic file with name 3574uequ2.jpg

Hence the increase in effective stiffness we measure here is a direct indication that cell tension also increases. The connection between these two mechanical properties is further supported by recent experiments that show that the effective stiffness of a nonadherent cell, as measured by microindentation, is directly related to its cortical tension via the relation E = γ2(πD0)/(4hF) (Cartagena-Rivera et al., 2016), where E is the apparent stiffness of the cell, γ is its cortical tension, D0 is the cell diameter, h is the cell’s cortical thickness, and F is the indentation force. Taken together, these results show that apparent membrane surface area is a good predictor of cell mechanical properties.

T-lymphocyte membrane ruptures at a well-defined entry length for a given capillary size

Beyond measuring how effective stiffness is reversibly linked to an increase of cell apparent area, we sought to see whether it is possible to induce permanent damage to a T-lymphocyte by forcing it through a narrow capillary. To do so, we again used micropipette aspiration as a proxy for passage into capillaries and used propidium iodide as a reporter of membrane rupture (Figure 3, A–C, and Supplemental Movies S2–S4).

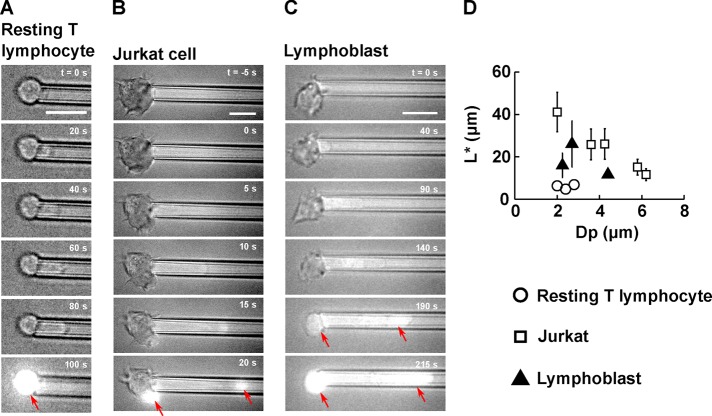
FIGURE 3:

FIGURE 3:

Open in a new tab

T-lymphocyte membrane ruptures at a well-defined entry length L* during micropipette aspiration. (A–C) Example of membrane rupture triggered using micropipette aspiration for (A) a resting T-lymphocyte, (B) a Jurkat cell, and (C) a lymphoblast. Scale bar, 10 μm. The time is indicated in the top right-hand corner, with t = 0 s chosen as the time at which the aspiration pressure goes from −20 Pa to ΔP. A background of bright-field light is kept to visualize the cell throughout the experiment. On membrane rupture, propidium iodide enters the cell and binds to DNA, emitting a bright fluorescent signal (red arrows). (D) Plot of the entry length at rupture, L*, vs. micropipette diameter, Dp, for three cell types: resting T-lymphocytes (14 cells), Jurkat cells (27 cells), and lymphoblasts (14 cells). Bars represent SD.

We observe that the membrane of resting T-lymphocytes ruptures at a well-defined entry length L* = 6.3 ± 1.1 μm (mean ± SD) for micropipette diameter Dp between 2.0 and 2.8 μm (Figure 3D). For larger micropipette diameters, the membrane of resting T-lymphocytes does not rupture, as cells are entirely aspirated into the pipette, provided that a sufficient aspiration pressure is applied. Because of the experimental difficulties associated with performing micropipette aspiration with micropipettes <2.0 μm in diameter, the range of micropipette diameters explored for resting T-lymphocytes is de facto limited to values between 2.0 and 3.0 μm. As mentioned previously, physiological pore sizes are typically slightly larger than that, with capillary diameters usually >5 μm (Fung, 2013) and pore sizes from transendothelial migration close to 5 μm (Carman and Springer, 2004; Shulman et al., 2011). The implications of that observation are examined in the Discussion.

To further explore the effect of micropipette diameter on membrane rupture, we performed micropipette aspirations on Jurkat cells, a leukemic T-cell line commonly used as a model for T-lymphocytes. Jurkat cells are larger than resting T-lymphocytes, with an average diameter D0 = 10.6 ± 1.0 μm (mean ± SD) compared with D0 = 6.7 ± 0.4 μm (mean ± SD) for resting T-lymphocytes, and therefore allow a wider range of micropipette diameters. We find that whereas the entry length at rupture L* is still a well-defined quantity for a given micropipette diameter Dp, L* decreases as Dp increases (Figure 3D). We also note that for a given micropipette diameter, the entry length at rupture is much greater for Jurkat cells than for resting T-lymphocytes.

Activated T-lymphocytes, also referred to as lymphoblasts, are much more effective at extravasating than resting T-lymphocytes (Springer, 1994). This is due to the increased expression of receptors to certain chemokines and adhesion molecules. In addition, mechanical and morphological properties of these activated T-lymphocytes might also contribute to these functions. Thus, to understand how activating T-lymphocytes affects their ability to deform, we performed micropipette aspirations on lymphoblasts. We found that lymphoblasts are slightly larger than resting T-lymphocytes, with an initial diameter D0 of 8.1 ± 0.7 μm (mean ± SD), and that their entry length at rupture L* = 19.0 ± 9.2 μm (mean ± SD) is three times as large as that of resting T-lymphocytes (Figure 3D). Activation therefore considerably increases a T-lymphocyte’s ability to deform its membrane.

Maximum deformation of T-lymphocytes at rupture does not depend on aspiration pressure

To test whether the value of aspiration pressure affects the maximal entry length at rupture, L*, we varied aspiration pressure while holding the micropipette diameter constant. We found that, for a given micropipette diameter Dp, L* does not depend on the aspiration pressure for both resting T-lymphocytes and Jurkat cells (Figure 4A). This shows that neither the level of aspiration pressure nor the duration of aspiration is an intrinsic parameter to describe membrane rupture of T-lymphocytes. Nonetheless, higher aspiration pressures lead to shorter rupture times, as the cell entry into the micropipette occurs faster (Figure 4B). Consistent with this notion, a previous study also found that higher aspiration led to faster lysis of red blood cells (Hategan et al., 2003). Strain rates in those experiments were comparable to ours, albeit somewhat smaller. Indeed, for T-lymphocytes, our strain rates were on the order of ∼1–10 μm2/s, whereas Hategan et al. (2003) reported strain rates for red blood cells on the order of ∼0.1–1 μm2/s.

FIGURE 4:

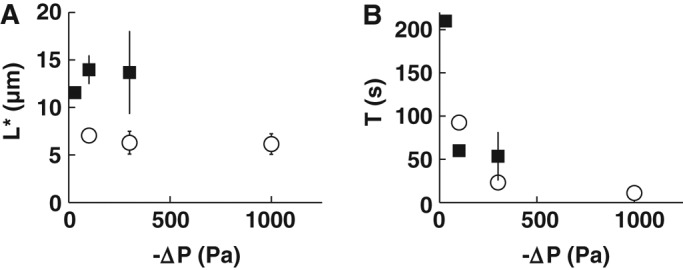
FIGURE 4:

Open in a new tab

Effect of the aspiration pressure on T-lymphocyte membrane rupture. (A) Plot of the entry length at rupture, L*, as a function of the absolute value of the aspiration pressure, ΔP, for resting T-lymphocytes (white circles) and Jurkat cells (black squares). (B) Plot of the duration of micropipette aspiration time, T, to rupture as a function of the absolute value of ΔP for resting T-lymphocytes (white circles) and Jurkat cells (black squares). Bars indicate SD. For resting T-lymphocytes, micropipette diameters between 2.0 and 2.8 μm were included (14 ruptured cells). For Jurkat cells, micropipette diameters between 5.8 and 6.2 μm were included (10 ruptured cells).

Moreover, we found that cell rupture can be located anywhere along the cell circumference, that is, either in the distal or proximal portions of the cell, with no particular preference. Therefore any mechanism of cell rupture that tends to favor a rupture location, such as the nucleus acting as a piston that would create a pressure accumulation in the distal part of the cell, as discussed by Petrie et al. (2014), seems unlikely with respect to our experimental observations.

T-lymphocyte membrane rupture occurs at a critical apparent membrane expansion

To elucidate the factor limiting passive deformations of T-lymphocytes, we sought a criterion that is predictive of T-lymphocyte membrane rupture. As noted, cell volume is conserved during micropipette aspiration, so that the apparent membrane surface area increases as soon as the cell departs from a spherical shape that minimizes its surface area. Membrane expansion is again defined as the ratio between the apparent membrane surface area, A, divided by the initial apparent membrane surface area, A0. Computing this membrane expansion across all the capillary sizes tested, we found that a critical membrane expansion defining a threshold beyond which membrane rupture is a criterion that predicts our data for both resting T-lymphocytes and Jurkat cells fairly accurately (Figure 5). We found a critical membrane expansion A*/A0 = 1.22 ± 0.09 and 1.48 ± 0.15 (mean ± SD) for resting T-lymphocytes and Jurkat cells, respectively, where A* is the apparent membrane surface area at rupture. Lymphoblasts, on the other hand, show more variability, with A*/A0 = 1.36 ± 0.27 (mean ± SD). In the case of Jurkat cells, we also observed that for larger micropipette diameters, the critical membrane expansion decreased slightly, a possible bias being that large micropipette diameters are associated with lower aspiration pressures and shorter rupture times (Supplemental Figure S6). It is therefore possible that in Jurkat cells, membrane expansion is favored by a longer squeezing time.

FIGURE 5:

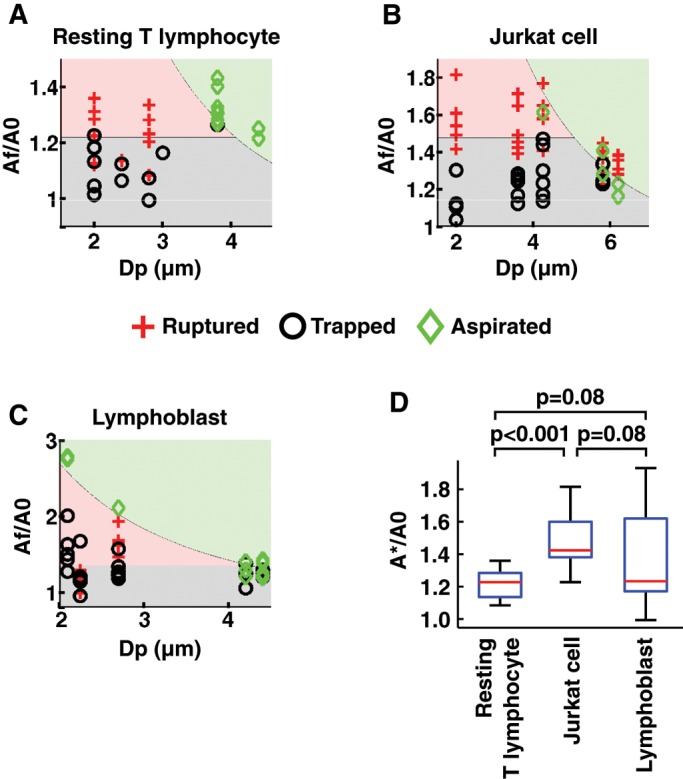
FIGURE 5:

Open in a new tab

T-lymphocyte membrane rupture occurs at a critical increase in apparent membrane surface area, A*/A0. (A–C) “Phase diagram” of cell state after micropipette aspiration, depending on the micropipette diameter, Dp, and the membrane expansion, defined as the final apparent membrane surface area, Af, divided by the initial apparent membrane surface area, A0. The phase diagrams are given for various cell types and conditions: (A) resting T-lymphocytes, (B) Jurkat cells, and (C) lymphoblasts. A red cross indicates a cell whose membrane ruptured, a black circle a cell that stayed trapped after 5 min of aspiration, and a green diamond a cell that was entirely aspirated inside the micropipette. The red filling indicates that in this zone, cell membranes are expected to rupture. The gray filling indicates that in this zone, a cell is expected to stay trapped inside the micropipette without rupturing or being entirely aspirated. The cutoff on the vertical axis between the rad and gray zones is chosen as the mean increase in apparent membrane surface area. The green filling indicates that in this zone, cells are expected to be entirely aspirated, based on geometrical considerations and volume conservation (Supplemental Movie S6). (D) Boxplot of the normalized apparent membrane surface area at rupture, A*/A0, for the cell types and conditions in A–C.

We also investigated how the state of the cytoskeleton might affect this membrane expansion at rupture. To do so, we incubated cells in 1 μM latrunculin B for at least 60 min to disrupt cortical actin polymerization (Wakatsuki et al., 2001). We found that the membrane expansion at rupture A*/A0 for resting T-lymphocytes increased from 1.22 ± 0.09 (mean ± SD, 14 cells) in the control case to 1.41 ± 0.15 (9 cells) for cells treated with latrunculin B and from 1.36 ± 0.27 (14 cells) to 1.42 ± 0.16 (23 cells) for lymphoblasts. Hence, in both cases, depolymerizing actin increased the membrane expansion at rupture, up to a maximum value of ∼40%.

Although our rupture criterion relates to membrane expansion, it is still consistent with a criterion based on a threshold in cell tension as used by others to describe the rupture of the membrane of fibroblasts (Tan et al., 2011) or lipid vesicles (Evans et al., 2003). In fact, as mentioned before, previous investigators found that cell tension and membrane expansion are directly related in neutrophils (Herant et al., 2005) and macrophages (Lam et al., 2009). In our experiments, Laplace’s law, although imprecise outside equilibrium, allows us to roughly estimate the cell tension at rupture, γ*. We find that γ* = 0.5 ± 0.4 mN/m (mean ± SD) for resting T-lymphocytes, 1.2 ± 0.9 mN/m for lymphoblasts, and 1.3 ± 0.8 mN/m for Jurkat cells. These values are close for all cell types, suggesting that this critical tension is an intrinsic mechanical parameter shared by different cell types. However, this critical value might be different for adherent cells: Tan et al. (2011), who used micropipette aspiration to rupture the membranes of fibroblasts, found a higher—although consistent—value of γ* ≈ 3 mN/m at rupture.

The amount of membrane deployed by T-lymphocytes before rupture matches the stock of membrane contained in microvilli and membrane folds

Although T-lymphocytes might appear smooth (with some ruffles in the case of lymphoblasts and Jurkat cells) under optical microscopy, observations at the submicrometer scale under scanning electron microscopy reveal that the surface of T-lymphocytes is covered with microvilli and membrane folds (Figure 6). For resting T-lymphocytes and lymphoblasts, we mainly see microvilli, whereas for Jurkat cells, most of the excess membrane is found in the form of membrane folds.

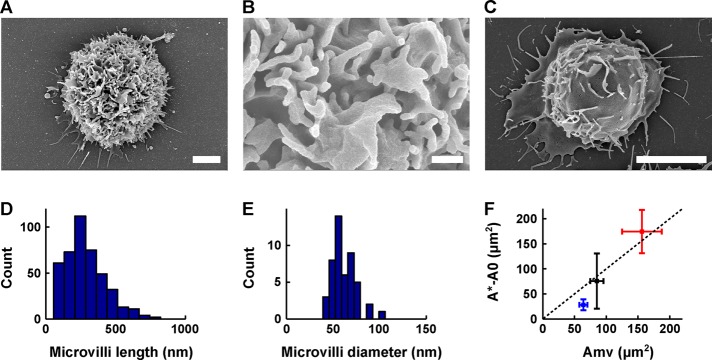
FIGURE 6:

FIGURE 6:

Open in a new tab

Maximum membrane surface area increase during micropipette aspiration is of the same order of magnitude as the excess membrane contained in microvilli and membrane folds. (A–C) Scanning electron microscopy images of a lymphoblast (A, B) and a Jurkat cell (C). Scale bars, 2 μm (A), 400 nm (B), 5 μm (C). (D) Histogram of lymphoblast microvilli length (432 measurements, 10 cells). The length is 284 ± 140 nm (mean ± SD). (E) Histogram of lymphoblast microvilli diameter (48 measurements, one cell, as we observed that the diameter was well conserved across cells). The diameter is 62 ± 13 nm (mean ± SD). (F) Plot of the maximum increase in apparent membrane surface area during micropipette aspiration experiments (defined as the apparent membrane surface area at rupture, A*, minus the initial apparent membrane surface area, A0) as a function of the estimated excess membrane contained in microvilli and membrane folds, Amv, for resting T-lymphocytes (blue), Jurkat cells (red), and lymphoblasts (black). Squares represent the mean; bars represent the SD. Dotted line represents the A* − A0 = Amv (slope equal to 1) line.

The excess membrane contained in the microvilli of resting T-lymphocytes was previously estimated using scanning electron microscopy (Majstoravich et al., 2004). Majstoravich et al. (2004) assumed a cylindrical shape for microvilli and measured the microvilli density (4.1 per μm2), average length (380 nm), and average diameter (100 nm). This led them to estimate a relative excess membrane of ∼49% for resting T-lymphocytes. Work in the 1980s that used a combination of transmission electron microscopy and stereology found values ranging from 21% (Boesen and Hokland, 1982) to ∼130% (Schmid-Schönbein et al., 1980).

We follow the same approach as Majstoravich et al. (2004) using scanning electron microscopy. We preferred this method to alternatives—transmission electron microscopy combined with stereology (Schmid-Schönbein et al., 1980; Boesen and Hokland, 1982) and a capacitance-based method (Ross et al., 1994)—for two reasons: 1) it is a direct and hence essentially model-independent measurement, and 2) it appears to lead to less variable results. For lymphoblasts, we find microvilli density of 6.9 per μm2, length of 284 ± 140 nm (mean ± SD), and diameter of 62 ± 13 nm (mean ± SD; Figure 6, D and E). This translates into a relative excess membrane of ∼40% for lymphoblasts.

For Jurkat cells, we took a slightly different approach. Indeed, we did not see as many microvilli on the surface of Jurkat cells, but we did see many more membrane folds (Figure 6, A and C). Therefore, instead of assuming that the excess membrane is contained in cylindrical microvilli, we assumed that most of the excess membrane is in the form of infinitesimally fine membrane folds whose height can be estimated for a given cell using the folds seen in profile. Using this approach, we found a relative excess membrane of ∼41% for Jurkat cells. Consistent with this estimate, an earlier study that used capacitance, as measured by patch clamping, as an indirect method to estimate surface area found that Jurkat cell had an external membrane reservoir of ∼40–70% of their apparent membrane surface area (Ross et al., 1994).

To assess whether the membrane stored in ruffles and microvilli is sufficient to explain the deformation of T-lymphocytes in micropipettes, we compared the maximum membrane surface area deployed, using micropipette aspiration (defined as the apparent membrane surface area at rupture, A*, minus the initial apparent membrane surface area, A0) with the excess membrane surface area contained in microvilli and folds and found that they are in good qualitative agreement for resting T-lymphocytes, lymphoblasts, and Jurkat cells (Figure 6F). Consistent with this picture, others showed that, upon osmotic swelling, Jurkat cell membrane ruptures if the surface area increases beyond what is contained in their external membrane reservoir (Ross et al., 1994).

T-lymphocyte membrane expansion during active deformation can greatly exceed the limit observed in passive deformation

To determine how our criterion of maximum membrane expansion for passive deformations applies to active deformations, we reproduced in vitro two situations in which the T-lymphocyte is activated: one in which a T-lymphoblast migrates across an endothelial monolayer (Figure 7 and Supplemental Movie S5), and one in which it spreads on an activating surface (Figure 7). We chose both because we expect the apparent membrane surface area to increase substantially and because they occur on time scales comparable to the micropipette aspiration experiments (∼3 min for transendothelial migration and ∼20 min for cell spreading).

FIGURE 7:

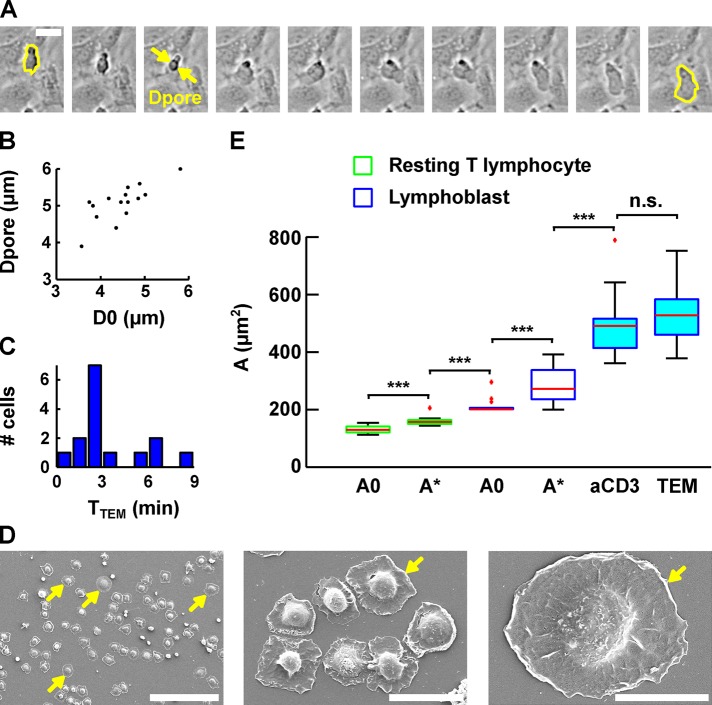
FIGURE 7:

Open in a new tab

Evolution of lymphoblast membrane surface area during transendothelial migration and cell spreading. (A) Time lapse of a lymphoblast transmigrating between human aortic endothelial cells. Scale bar, 20 μm. Images were taken every 15 s. The projected surface area Sproj is represented in yellow before (leftmost image) and after (rightmost image) transendothelial migration. The pore diameter, Dpore, is estimated by taking the image in which the lymphoblast width is identical above and below the pore (yellow arrows). (B) Dpore during transendothelial migration as a function of the lymphoblast’s projected diameter before transendothelial migration (computed using D0 = Sproj/2π, and D0 is an equivalent diameter for a sphere whose projected area is Sproj). (C) Histogram of the duration of transmigration. The mean duration is 3 ± 2 min (mean ± SD). (D) Scanning electron microscopy images of lymphoblasts spreading on a substrate coated with anti-CD3 plus anti-CD28 activating antibodies. Scale bars, 100 μm, 20 μm, 10 μm (left to right). Yellow arrows indicate spread cells. (E) Boxplots of the apparent membrane surface area of T-lymphocytes under both passive (white-filled box) and active (blue-filled box) deformations. The bottom and top of the box indicate the 25th and 75th percentiles, respectively. Red plus signs indicate outliers. From left to right, resting T-lymphocytes initially (column 1, A0, n = 14) and at rupture (column 2, A*, n = 14) aspirated using a micropipette, lymphoblasts at rest (column 3, A0, n = 14) and at rupture (column 4, A*, n = 14) aspirated using a micropipette, lymphoblasts spread on anti-CD3 plus anti-CD28 monoclonal antibodies (column 5, aCD3, n = 17), and lymphoblasts after transendothelial migration (column 6, TEM, n = 15). ***p < 0.001. n.s., p > 0.05.

In both cases, the apparent membrane surface area reaches values that are much larger than the limit found in passive deformations, with an area of 526 ± 98 μm2 (mean ± SD) after transendothelial migration and 489 ± 103 μm2 (mean ± SD) after cell spreading. These values are similar to each other, and both are statistically significantly higher than the initial apparent membrane surface area of lymphoblasts, 213 ± 26 μm2 (mean ± SD), and their apparent membrane surface area at rupture upon micropipette aspiration, 288 ± 64 μm2 (mean ± SD).

DISCUSSION

The amount of membrane surface reservoir predicts T-lymphocyte membrane rupture

We showed that the amount of membrane area expansion predicts membrane rupture of T-lymphocytes passing through narrow capillaries and that the limiting factor is the amount of excess membrane contained in microvilli and membrane folds. This result holds regardless of whether the T-lymphocyte is activated or not (resting T-lymphocyte and T-lymphoblast) and regardless of whether it is a primary cell or a leukemic cell (primary T-lymphocytes and Jurkat T-cell). We therefore speculate that there could be a degree of generality to these results and that they may also be valid for other types of leukocytes. This is supported by the observation made by Evans and Kukan (1984) that the excess membrane area of granulocytes is what enables them to pass through capillaries as small as 2.6 μm in diameter.

Membrane surface reservoirs allow T-lymphocytes to pass unharmed through the microvasculature

We showed that T-lymphocytes, when aspirated into a micropipette, retain a constant volume and that beyond a critical membrane expansion of ∼20 to ∼50% (depending on the cell type), the T-lymphocyte membrane ruptures. T-lymphocytes passing through a capillary assume a sausage-like shape (a cylinder with two hemispherical caps; see Supplemental Movie S6), similar to what has been reported for chondrocytes and neutrophils (Hochmuth, 2000). Given that their volume is also known (because it remains unchanged), we are able to compute mathematically the apparent membrane surface area, A, of a T-lymphocyte passing through a capillary of a given size (following the method detailed in Supplemental Figure S1). Because we also have access to the initial apparent membrane surface area, A0 (by measuring the initial T-lymphocyte diameter), we can compute the membrane expansion A/A0, associated with a given capillary size (this is shown, for a T-lymphocyte of average size, by the line separating the green zone from the red and black zones in Figure 5, A–C). We see that the smaller the capillary, the greater does the T-lymphocyte membrane expansion need to be to pass through it. Further, because we showed previously that T-lymphocytes rupture at a critical membrane expansion (shown by the line separating the red and black zone in Figure 5, A–C), this means that for each type of T-lymphocyte, there exists a critical capillary size under which the T-lymphocyte will either be trapped or rupture depending on the pressure exerted on it. This critical diameter is given by the intersection of the two lines in the “phase diagrams” (by analogy with physical phase diagrams) in Figure 5, A–C. We deduce a minimum capillary size of 4.1 μm for resting T-lymphocytes, 4.2 μm for lymphoblasts, and 5.1 μm for Jurkat cells.

Human capillaries are in the range of 5–10 μm (Fung, 2013), which is in some cases smaller than the typical size of a T-lymphocyte but always sufficiently large for the T-lymphocyte to pass through without risking membrane rupture or getting trapped, according to our results. Therefore, we suggest that the excess membrane contained in the microvilli and membrane folds of T-lymphocytes is tightly regulated to enable them to pass unharmed through the microcirculation.

Pore size during extravasation is determined by the T-lymphocyte, not the endothelial cell

Our in vitro transmigration assay allows for the quantification of the endothelial pore size during T-lymphocyte transmigration. We find a diameter of 5.1 ± 0.5 μm. Consistent with this value, images from previous studies indicate pore sizes from transmigrating T-lymphocytes of 5.3 (Carman and Springer, 2004) and 5.4 μm (Shulman et al., 2011). Of importance, we observe that the pore size increases with cell size (Figure 7B), which suggests that leukocytes and not endothelial cells determine the size of this pore. Furthermore, the pore size is comparable to the size of the smallest capillaries that a T-lymphocyte may find itself going through without rupture. Hence the pore size might be an optimum that minimizes the mechanical effort needed to create it while also minimizing the risk of leukocyte membrane damage during transmigration.

Active deformations of T-lymphocytes require more membrane than is available in surface reservoirs

We showed that the membrane surface area of lymphoblasts during cell spreading and transendothelial migration is ∼200–250 μm2 higher than the external membrane surface area of lymphoblasts, even when accounting for microvilli and membrane folds. This means that additional membrane must be recruited during active deformations. We propose that this is enabled by internal membrane reservoirs, possibly through exocytosis.

Indeed, there are numerous examples in which cells recruit additional membrane through exocytosis to enable large active deformations. For cell spreading, there is direct evidence in fibroblasts that the increase in membrane surface area is enabled by exocytosis (Gauthier et al., 2011). Similarly, during phagocytosis, the dramatic increase in macrophage membrane surface area is enabled by exocytosis (Hackam et al., 1998; Bajno et al., 2000; Niedergang et al., 2003; Braun et al., 2004). Drosophila cellularization provides yet another example. Indeed, exocytosis has been shown to add membrane to the cell surface to enable the furrow ingression needed for cellularization (Figard et al., 2013). Finally, multiple cell types (AS49, 16HBE 140, CHO, and NIH 3T3 cells) have been observed to use exocytosis to enable volume expansion during hyposmotic swelling (Groulx et al., 2006). Of interest, Groulx et al. (2006) remarked that the membrane surface area can increase 3.6-fold under normal conditions but only 1.7-fold when exocytosis is blocked. This difference in membrane surface area is consistent with the difference we observed between passive and active deformations. Indeed, during passive deformations, we saw a 1.2- to 1.5-fold increase in membrane surface area, whereas during active deformations, we saw ∼2.5-fold increase in membrane surface area for lymphoblasts. The difference between the two cases would presumably be made up by exocytosis, as in hyposmotic swelling. Hence we speculate that numerous active cell processes involving large deformations, including cell spreading and transendothelial migration, but also phagocytosis and even embryonic development for some species, could be dependent on exocytosis.

MATERIALS AND METHODS

Cell purification and culture

All cells used in this study were human cells. This study was conducted according to the Helsinki Declaration, with informed consent obtained from the blood donors, as requested by the Etablissement Français du Sang.

Human primary CD4+ T-lymphocytes were negatively selected from peripheral blood mononuclear cells isolated from blood of healthy donors with the CD4 T-cell isolation kit (130-096-533; Miltenyi Biotec, Auburn, CA) as described previously (Chemin et al., 2012).

To obtain CD4+ T-lymphoblasts, six-well plastic plates were coated with anti-CD3 (OKT3 clone; 16-0037-85, eBioscience, San Diego, CA; 2.5 μg/ml in 1.3 ml final) overnight at 4°C. Wells were washed, and 5.4 × 106 purified primary human CD4+ T-cells were plated per well in the presence of soluble anti-CD28 (LEAF purified anti-human CD28; BLE302923; Biolegend, San Diego, CA; 2.5 μg/ml) and recombinant interleukin-2 (IL-2; 20 U/ml). Fresh medium containing IL-2 (20 U/ml) was added every 3 d, and lymphoblasts were used from day 6.

Jurkat cells (clone 20; obtained from A. Alcover, Pasteur Institute, Paris, France) were grown in GlutaMAX-containing RPMI 1640 (Invitrogen Life Technologies, Carlsbad, CA) supplemented with 10% fetal calf serum as described previously (Blanchard et al., 2002).

Primary human aortic endothelial cells (HAECs) were purchased from ThermoFisher Scientific and cultured in medium 200 (M200500; ThermoFisher Scientific, Waltham, MA) supplemented with low serum growth supplement (S00310; ThermoFisher Scientific). They were passaged three times a week using trypsin, followed by resuspension in fresh medium.

Optical microscopy

In all micropipette aspirations, profile microindentation, and transendothelial migration experiments, the Petri dish containing cells was mounted on a TE300 inverted microscope (Nikon Instruments, Tokyo, Japan) placed on an air suspension table (CVI Melles Griot, Didam, Netherlands). The microscope was equipped with a 100× oil immersion, 1.3 numerical aperture objective (Nikon Instruments) for experiment monitoring and lower-magnification objectives (40, 20, 10, and 4×; Nikon) for micropipette positioning. Images were acquired using a Flash 4.0 complementary metal–oxide–semiconductor camera (Hamamatsu Photonics, Hamamatsu City, Japan).

Micropipette aspiration

Micropipette aspiration experiments were performed using a micropipette connected to a water reservoir, as described previously (Guillou et al., 2016). We left the micropipettes in complete medium for at least 5 min before starting experiments to avoid cell adhesion to the micropipette wall. Propidium iodide (Sigma-Aldrich, St. Louis, MO) at a concentration of 40 μg/ml was used as a reporter of membrane rupture. For membrane rupture experiments, we left a background of bright-field light to visualize the cell before rupture. The fluorescent signal from the propidium iodide was sufficiently intense to be visible despite this light. Image sequences were acquired using Micro-Manager (Edelstein et al., 2010).

Profile microindentation

To perform microindentations, cells were held using a micropipette and indented using a thin glass capillary, as described previously (Guillou et al., 2016). Briefly, we imposed a displacement to the base of the glass capillary using a piezoelectric controller (TPZ001; Thorlabs, Newton, NJ) and monitored the position of the capillary tip by using optical microscopy combined with cross-correlation image analysis. We used a microindenter of stiffness 0.54 nN/μm and radius 11 μm, the base of which we displaced at a speed of 0.5 μm/s. For the profile microindentation experiments with blebbistatin, the cells were incubated for 1 h before the experiment in 50 μM blebbistatin (B0560-1MG; Sigma-Aldrich). Blebbistatin at the same concentration was then left in the medium for the duration of the microindentation experiments.

Transendothelial migration

For transendothelial migration experiments, HAECs were grown to confluence in thin-bottom Petri dishes (FluoroDish, 35 mm; World Precision Instruments, Sarasota, FL) and inflamed overnight in tumor necrosis factor α (TNF-α; CYT-252-5 μg; Biovalley, Nanterre, France) at a concentration of 50 ng/ml. The next morning, the TNF-α was washed twice with HAEC medium. The Petri dish was then placed in a custom-made Plexiglas chamber to maintain the temperature at 37°C. The chamber was heated by heating pads (Radiospare, Corby, United Kingdom) connected to an electrical generator (ALR3002M; ELC, Annecy, France) via a proportional–integral–derivative controller (PID) controller. The target temperature of the PID was set to 40°C, with the input temperature to the PID given by a thermocouple placed inside the chamber at a fixed location. The chamber was also sealed at the top to minimize air flow and temperature gradients. Further, the objective was heated at a target temperature of 40°C using an objective heater (Okolab, Naples, Italy). Both target temperatures were chosen after control experiments revealed that the actual temperature of the medium inside the Petri dish was 37°C (as measured by a thermocouple inside the medium) when the target temperatures were both set to 40°C. After waiting 20 min for the temperature to equilibrate inside the HAEC medium, we injected 500 ml of lymphoblasts at a concentration of ∼106 cells/ml using a 1-ml pipette. Bright-field images were then acquired every 15 s for a period of 60 min under 10× magnification.

Data analysis

Images were analyzed using ImageJ (National Institutes of Health, Bethesda, MD), and data were analyzed using a custom-written Matlab (MathWorks, Natick, MA) code. Data are reported as mean ± SD, both in the text and in plots, unless specified otherwise. Samples were deemed statistically significantly different (*p < 0.05) using Student’s unpaired t test. ***p < 0.001.

Scanning electron microscopy

Scanning electron microscopy was performed on T-lymphocytes (1.50 × 105) incubated for 20 min at room temperature on slides precoated with 0.02% poly-l-lysine alone or followed by incubation with anti-CD3 (OKT3 clone; 16-0037-85, eBioscience) and anti-CD28 (LEAF purified anti-human CD28; BLE302923, Biolegend) at 10 μg/ml overnight at 4°C. The cells were then washed in phosphate buffer, pH 7.4 (PB), fixed overnight at 4°C in PB plus 2% glutaraldehyde, and finally washed in PB. Samples were then dehydrated by passage through a graded series of ethanol solutions, dried by the CO2 critical-point method (CPD75; Quorum Technologies, Sacramento, CA), and coated by sputtering with a 20- to 40-nm gold thin layer using a Scancoat Six (Edwards, Crawley, England). Acquisitions were performed using a GeminiSEM 500 (Zeiss, Oberkochen, Germany), except for the cell spreading experiments, for which acquisitions were performed using a Cambridge Stereoscan 260.

Fluorescence staining and confocal microscopy for cell volume measurement

Cells were fluorescently stained and their volume measured using a confocal microscope as detailed previously (Bufi et al., 2015). Briefly, cells were plated on fibronectin (10 μg/ml; Sigma-Aldrich)–coated glass coverslips, fixed, permeabilized, and stained for 4′,6-diamidino-2-phenylindole (Life Technologies, Waltham, MA) and phalloidin–Alexa 546 (Life Technologies). The samples were observed on an inverted spinning-disk confocal microscope Nikon TiE (Nikon, Tokyo, Japan) equipped with a piezo-stage NanoScanZ mounted on a Marzhauser XYZ motorized scanning stage. Three-dimensional stacks of images were acquired with a step of 0.2 mm using a 100× immersion oil objective and an electron-multiplying charge-coupled device iXon 897 Andor camera (Andor, Belfast, United Kingdom). Images were analyzed using the ImageJ software.

Supplementary Material

Supplemental Materials
supp_27_22_3574__index.html (2.8KB, html)

Acknowledgments

We acknowledge Caroline Frot, Antoine Garcia, Daniel Guy, Delphine L’Huillier, Magali Tutou, and Do Chi Toai Vu at the Laboratoire d’Hydrodynamique for technical support. We also acknowledge Virginie Bazin from the Electron Microscopy platform at Université Pierre et Marie Curie. This work benefited from financial support of the LabeX LaSIPS (ANR-10-LABX-0040-LaSIPS), managed by the French National Research Agency under the Investissements d’Avenir program (ANR-11-IDEX-0003-02). This work was also supported by an endowment in cardiovascular cellular engineering from the AXA Research Fund. L.G. was supported by a Gaspard Monge doctoral fellowship from the Ecole Polytechnique. This research received funding from the National Institute of Health and Medical Research, the Agence Nationale de la Recherche (ANR-12-BSV5-0007-01, ImmunoMeca), and the Fondation pour la Recherche Médicale (DEQ20140329513). M.S. was financed by the Fondation pour la Recherche Médicale and A.B. by la Ligue contre le Cancer and l’Association de Recherche contre le Cancer.

Footnotes

This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E16-06-0414) on September 7, 2016.

REFERENCES

  1. Bajno L, Peng XR, Schreiber AD, Moore HP, Trimble WS, Grinstein S. Focal exocytosis of VAMP3-containing vesicles at sites of phagosome formation. J Cell Biol. 2000;149:697–705. doi: 10.1083/jcb.149.3.697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Blanchard N, Lankar D, Faure F, Regnault A, Dumont C, Raposo G, Hivroz C. TCR activation of human T cells induces the production of exosomes bearing the TCR/CD3/ complex. J Immunol. 2002;168:3235–3241. doi: 10.4049/jimmunol.168.7.3235. [DOI] [PubMed] [Google Scholar]
  3. Boesen AM, Hokland P. Stereological analysis of the ultrastructure in isolated human T and non-T lymphoid cells. Cell Pathol. 1982;39:273–284. doi: 10.1007/BF02892854. [DOI] [PubMed] [Google Scholar]
  4. Braun V, Fraisier V, Raposo G, Hurbain I, Sibarita J-B, Chavrier P, Galli T, Niedergang F. TI-VAMP/VAMP7 is required for optimal phagocytosis of opsonised particles in macrophages. EMBO J. 2004;23:4166–4176. doi: 10.1038/sj.emboj.7600427. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bufi N, Saitakis M, Dogniaux S, Buschinger O, Bohineust A, Richert A, Maurin M, Hivroz C, Asnacios A. Human primary immune cells exhibit distinct mechanical properties that are modified by inflammation. Biophys J. 2015;108:2181–2190. doi: 10.1016/j.bpj.2015.03.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Carman CV. Mechanisms for transcellular diapedesis: probing and pathfinding by “invadosome-like protrusions.”. J Cell Sci. 2009;122:3025–3035. doi: 10.1242/jcs.047522. [DOI] [PubMed] [Google Scholar]
  7. Carman CV, Martinelli R. T lymphocyte-endothelial interactions: emerging understanding of trafficking and antigen-specific immunity. Front Immunol. 2015;6:603. doi: 10.3389/fimmu.2015.00603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Carman CV, Springer TA. A transmigratory cup in leukocyte diapedesis both through individual vascular endothelial cells and between them. J Cell Biol. 2004;167:377–388. doi: 10.1083/jcb.200404129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cartagena-Rivera AX, Logue JS, Waterman CM, Chadwick RS. Actomyosin cortical mechanical properties in nonadherent cells determined by atomic force microscopy. Biophys J. 2016;110:2528–2539. doi: 10.1016/j.bpj.2016.04.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chemin K, Bohineust A, Dogniaux S, Tourret M, Guégan S, Miro F, Hivroz C. Cytokine secretion by CD4+ T cells at the immunological synapse requires Cdc42-dependent local actin remodeling but not microtubule organizing center polarity. J Immunol. 2012;189:2159–2168. doi: 10.4049/jimmunol.1200156. [DOI] [PubMed] [Google Scholar]
  11. Crotty S. A brief history of T cell help to B cells. Nat Rev Immunol. 2015;15:185–189. doi: 10.1038/nri3803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dimitriadis EK, Horkay F, Maresca J, Kachar B, Chadwick RS. Determination of elastic moduli of thin layers of soft material using the atomic force microscope. Biophys J. 2002;82:2798–2810. doi: 10.1016/S0006-3495(02)75620-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. DuPage M, Bluestone JA. Harnessing the plasticity of CD4(+) T cells to treat immune-mediated disease. Nat Rev Immunol. 2016;16:149–163. doi: 10.1038/nri.2015.18. [DOI] [PubMed] [Google Scholar]
  14. Edelstein A, Amodaj N, Hoover K, Vale R, Stuurman N. Computer control of microscopes using manager. Curr Protoc Mol Biol. 2010:1–17. doi: 10.1002/0471142727.mb1420s92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Evans E, Heinrich V, Ludwig F, Rawicz W. Dynamic tension spectroscopy and strength of biomembranes. Biophys J. 2003;85:2342–2350. doi: 10.1016/s0006-3495(03)74658-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Evans E, Kukan B. Passive material behavior of granulocytes based on large deformation and recovery after deformation tests. Blood. 1984;64:1028–1035. [PubMed] [Google Scholar]
  17. Figard L, Xu H, Garcia H, Golding I, Sokac A. The plasma membrane flattens out to fuel cell-surface growth during drosophila cellularization. Dev Cell. 2013;27:648–655. doi: 10.1016/j.devcel.2013.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Fung Y. Biomechanics: Circulation. New York: Springer; 2013. [Google Scholar]
  19. Gauthier NC, Fardin MA, Roca-Cusachs P, Sheetz MP. Temporary increase in plasma membrane tension coordinates the activation of exocytosis and contraction during cell spreading. Proc Natl Acad Sci USA. 2011;108:14467–14472. doi: 10.1073/pnas.1105845108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Geddes DM, Cargill RS, LaPlaca MC. Mechanical stretch to neurons results in a strain rate and magnitude-dependent increase in plasma membrane permeability. J Neurotrauma. 2003;20:1039–1049. doi: 10.1089/089771503770195885. [DOI] [PubMed] [Google Scholar]
  21. Groulx N, Boudreault F, Orlov SN, Grygorczyk R. Membrane reserves and hypotonic cell swelling. J Membr Biol. 2006;214:43–56. doi: 10.1007/s00232-006-0080-8. [DOI] [PubMed] [Google Scholar]
  22. Guillou L, Babataheri A, Puech P-H, Barakat AI, Husson J. Dynamic monitoring of cell mechanical properties using profile microindentation. Sci Rep. 2016;6:21529. doi: 10.1038/srep21529. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hackam DJ, Rotstein OD, Sjolin C, Schreiber AD, Trimble WS, Grinstein S. v-SNARE-dependent secretion is required for phagocytosis. Proc Natl Acad Sci USA. 1998;95:11691–11696. doi: 10.1073/pnas.95.20.11691. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hategan A, Law R, Kahn S, Discher DE. Adhesively-tensed cell membranes: lysis kinetics and atomic force microscopy probing. Biophys J. 2003;85:2746–2759. doi: 10.1016/s0006-3495(03)74697-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Herant M, Heinrich V, Dembo M. Mechanics of neutrophil phagocytosis: behavior of the cortical tension. J Cell Sci. 2005;118:1789–1797. doi: 10.1242/jcs.02275. [DOI] [PubMed] [Google Scholar]
  26. Hochmuth RM. Micropipette aspiration of living cells. J Biomech. 2000;33:15–22. doi: 10.1016/s0021-9290(99)00175-x. [DOI] [PubMed] [Google Scholar]
  27. Johnson KL. Contact mechanics. J Am Chem Soc. 1985;37:1–17. [Google Scholar]
  28. Krause M, te Riet J, Wolf K. Probing the compressibility of tumor cell nuclei by combined atomic force–confocal microscopy. Phys Biol. 2013;10:065002. doi: 10.1088/1478-3975/10/6/065002. [DOI] [PubMed] [Google Scholar]
  29. Lam J, Herant M, Dembo M, Heinrich V. Baseline mechanical characterization of J774 macrophages. Biophys J. 2009;96:248–254. doi: 10.1529/biophysj.108.139154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lomakina EB, Spillmann CM, King MR, Waugh RE. Rheological analysis and measurement of neutrophil indentation. Biophys J. 2004;87:4246–4258. doi: 10.1529/biophysj.103.031765. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Majstoravich S, Zhang J, Nicholson-Dykstra S, Linder S, Friedrich W, Siminovitch KA, Higgs HN. Lymphocyte microvilli are dynamic, actin-dependent structures that do not require Wiskott-Aldrich syndrome protein (WASp) for their morphology. Blood. 2004;104:1396–1403. doi: 10.1182/blood-2004-02-0437. [DOI] [PubMed] [Google Scholar]
  32. Niedergang F, Colucci-Guyon E, Dubois T, Raposo G, Chavrier P. ADP ribosylation factor 6 is activated and controls membrane delivery during phagocytosis in macrophages. J Cell Biol. 2003;161:1143–1150. doi: 10.1083/jcb.200210069. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Petrie RJ, Koo H, Yamada KM. Generation of compartmentalized pressure by a nuclear piston governs cell motility in a 3D matrix. Science. 2014;345:1062–1065. doi: 10.1126/science.1256965. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Pettus EH, Christman CW, Giebel ML, Povlishock JT. Traumatically induced altered membrane permeability: its relationship to traumatically induced reactive axonal change. J Neurotrauma. 1994;11:507–522. doi: 10.1089/neu.1994.11.507. [DOI] [PubMed] [Google Scholar]
  35. Pettus EH, Povlishock JT. Characterization of a distinct set of intra-axonal ultrastructural changes associated with traumatically induced alteration in axolemmal permeability. Brain Res. 1996;722:1–11. doi: 10.1016/0006-8993(96)00113-8. [DOI] [PubMed] [Google Scholar]
  36. Ross PE, Garber SS, Cahalan MD. Membrane chloride conductance and capacitance in Jurkat T lymphocytes during osmotic swelling. Biophys J. 1994;66:169–178. doi: 10.1016/S0006-3495(94)80754-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Schmid-Schönbein GW, Shih YY, Chien S. Morphometry of human leukocytes. Blood. 1980;56:866–875. [PubMed] [Google Scholar]
  38. Shulman Z, Cohen SJ, Roediger B, Kalchenko V, Jain R, Grabovsky V, Klein E, Shinder V, Stoler-Barak L, Feigelson SW, et al. Transendothelial migration of lymphocytes mediated by intraendothelial vesicle stores rather than by extracellular chemokine depots. Nat Immunol. 2011;13:67–76. doi: 10.1038/ni.2173. [DOI] [PubMed] [Google Scholar]
  39. Spinler KR, Shin JW, Lambert MP, Discher DE. Myosin-II repression favors pre/proplatelets but shear activation generates platelets and fails in macrothrombocytopenia. Blood. 2015;125:525–533. doi: 10.1182/blood-2014-05-576462. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Springer TA. Traffic signals for lymphocyte recirculation and leukocyte emigration: the multistep paradigm. Cell. 1994;76:301–314. doi: 10.1016/0092-8674(94)90337-9. [DOI] [PubMed] [Google Scholar]
  41. Tan SCW, Yang T, Gong Y, Liao K. Rupture of plasma membrane under tension. J Biomech. 2011;44:1361–1366. doi: 10.1016/j.jbiomech.2011.01.010. [DOI] [PubMed] [Google Scholar]
  42. Valignat MP, Theodoly O, Gucciardi A, Hogg N, Lellouch AC. T lymphocytes orient against the direction of fluid flow during LFA-1-mediated migration. Biophys J. 2013;104:322–331. doi: 10.1016/j.bpj.2012.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. von Andrian UH, Mempel TR. Homing and cellular traffic in lymph nodes. Nat Rev Immunol. 2003;3:867–878. doi: 10.1038/nri1222. [DOI] [PubMed] [Google Scholar]
  44. Wakatsuki T, Schwab B, Thompson NC, Elson EL. Effects of cytochalasin D and latrunculin B on mechanical properties of cells. J Cell Sci. 2001;114:1025–1036. doi: 10.1242/jcs.114.5.1025. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Materials
supp_27_22_3574__index.html (2.8KB, html)
supp_E16-06-0414v1_CombinedSupMats.pdf (323KB, pdf)
Download video file (378.4KB, mov)
Download video file (501.7KB, mov)
Download video file (124.8KB, mov)
Download video file (349.9KB, mov)
Download video file (183.3KB, mov)
Download video file (118.5KB, mov)

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES