AFM study shows prominent physical changes in elasticity and pericellular layer in human acute leukemic cells due to inadequate cell-cell communication

Abstract

Biomechanical properties of single cells in-vitro or ex-vivo and its pericellular interface have recently attracted a lot of attention as a potential biophysical (and possibly prognostic) marker of various diseases and cell abnormalities. At the same time, the influence of the cell environment on the biomechanical properties of cells is not well studied. Here we use atomic force microscopy (AFM) to demonstrate that cell-cell communication can have a profound effect on both cell elasticity and its pericellular coat. A human pre-B p190^BCR/ABL acute lymphoblastic leukemia cell line (ALL3) was used in this study. Assuming that cell-cell communication is inversely proportional to the distance between cells, we study ALL3 cells in-vitro growing at different cell densities. ALL3 cells demonstrate a clear density dependent behavior. These cells grow very well if started at a relatively high cell density (HD, >2×10⁵ cells/ml)) and are poised to grow at low cell density (LD, <1×10⁴ cells/ml). Here we observe ~6x increase in the elastic (Young's) modulus of the cell body and ~3.6x decrease in the pericellular brush length of LD cells compared to HD ALL3 cells. The difference observed in the elastic modulus is much larger than typically reported for pathologically transformed cells. Thus, cell-cell communication must be taken into account when studying biomechanics of cells, in particular, correlating cell phenotype and its biophysical properties.

1. Introduction

The majority of cell types like muscle, skin, blood cells, neurons, and others live in environments of constantly changing mechanical stresses. Mechanical properties of cells define their physical response to the external stresses. During organismal growth and regeneration, cell mechanics are expected to play a substantial role as well. Therefore, the study of biomechanical properties of cells is of fundamental interest. Furthermore, biomechanical properties of single cells in vitro or ex vivo and its pericellular interface have recently attracted a lot of attention as a potential physical biomarker of various diseases, and even might be used for prognostics [1-4].

Atomic force microscopy (AFM) [5] is one of the most versatile methods to study physical properties of soft materials, in particular, biophysical properties of single cells [6, 7]. AFM allows high accuracy measurements of forces and deformations in a very broad range of strains [8]. Using the AFM technique, correlation between elasticity of cells and different human diseases or abnormalities has been reported. Specifically, it has been implicated in the pathogenesis of many progressive diseases, including vascular diseases, cancer, malaria, kidney disease, cataracts, Alzheimer's Dementia, complications of diabetes, cardiomyopathies [9],[10],[11]. In some cases, it is believed that the loss of tissue elasticity arises from the changes in the extracellular matrix [12], not the cells themselves. However, it has recently been shown that the cells themselves can also change their rigidity quite considerably due to cancer [4, 13-17], malaria [18-21], ischemia [22], arthritis [23], and even aging [24-26]. For instance, the stiffening of red blood cells infected with malaria [18-21] was found to be responsible for fatal outcomes of this disease. It was also discovered that the mobility and spreading of cancer cells might be controlled by the application of external forces, which may alter the rigidity of a tumor. Recently, the reported low rigidity of cancer cells was suggested to be useful for cancer diagnosis [4, 13-17].

It has recently been shown that cell substrate influences the development of specific phenotype of stem cells. However, the influence of cell-cell communication on biomechanical properties of cells has not been systematically studied. At the same time, it is known that the collective behavior is an important feature and it is involved in regulating many biological processes such as cell migration, stem-cell maintenance, growth of proper organ size, immune system regulation, hematopoiesis, homeostasis and regeneration [27-34]. Individual cells utilize ‘autocrine’ and/or ‘paracrine’ factors to coordinate these beneficial collective behaviors. Even prokaryotic cells utilize these quorum-sensing (QS) molecules to ‘count’ their population numbers to determine whether the conditions are suitable to perform specific tasks including complex behaviors, such as formation of complex biofilms, antibiotic production, motility, sporulation, virulence, competence, conjugation and symbiosis [30, 34-38]. Cancer cell populations also function collectively to initiate and maintain abnormal cell proliferation, permit invasion and metastasis, avoid inhibition by the immune system, develop therapeutic resistance, and metabolic reprogramming [39, 40]. The underlying biochemical and biological QS mechanisms responsible for the deviant behavior of cancer cell populations are still poorly understood [30, 34, 41-43].

In the present work we investigate the influence of cell-cell communication (aka the QS effect) on the biophysical properties of leukemia blood cells. Assuming that cell-cell communication depends inversely on the distance between cells, we studied by mechanical properties of the same cell type but grown in different densities. A newly established cell line freshly obtained from the leukemic cells growing as ascitic cells in the pleural effusion of a terminally ill patient with Ph+ acute lymphoblastic leukemia (ALL3) is used in this work. ALL3 is a clonal proliferation of p190^BCR-ABL transformed pre B cells that arise in the bone marrow[30, 34]. We observed that there is a significant difference in the growth rate of ALL3 cells at low (LD) and high starting cell densities (HD). ALL3 cells do not grow except very transiently sometimes dividing once at cell densities at 5-10 × 10³ cells/ml or less, but grow progressively faster at increasing cell densities (~2 × 10⁴ – 4 × 10⁵ cells/ml). At each cell density they grow much better if packed closely together in a small growing area at the bottom of the culture plate than if more dispersed. Thus, cell proximity as well as overall cell density are important. Labeling studies with proliferation markers Ki67, BrdU or EdU showed that the LD ALL3 cells were poised to begin proliferating but could not do so without being triggered by supernate (HDSN) from ALL3 cells or some other normal or leukemic cells growing at HD [30, 34].

To study the effect of the cell-cell communication mentioned above, we use AFM, a technique that has been extensively used for high-resolution imaging of biological surfaces [44-46]. However, here we use this technique working not in imaging but in an indenting (force-volume) mode. The data obtained in this mode allows measuring the elastic modulus of the cell body and the characteristics of the pericellular brush layer using the methods described in [6, 47, 48]. Specifically, the elastic modulus (aka the effective Young's modulus) and the parameters of the pericellular coat (aka the pericellular brush layer) can be experimentally measured with the help of AFM. The term pericellular brush was introduced to describe a specific mechanical property of this layer, which demonstrates elastic behaviour similar to the classical polymer brush. The pericellular brush can be parameterized via its equilibrium size (or length), and its grafting density (an effective number of the brush constituents or “molecules” per unit area). Thus, mechanical properties of cells can be characterized with three physical parameters, the elastic modulus of a cell body, the equilibrium length, and the grafting density of the pericellular brush layer. Using the above approach, here we report on statistically significant differences between ALL3 cells caused by the different cell densities, and consequently, different (inadequate) cell-cell communication.

2. Methods

2.1. ALL3 Cells

The human p190^BCR-ABL driven ALL cells line (ALL3) was derived from the rapidly growing Ph+ ALL leukemic cells growing in ascitic form in the pleural fluid of a patient with widely disseminated Ph+ ALL who died shortly thereafter [30]. Multiple aliquots of ALL3 cells were frozen to preserve the cells’ condition as closely as possible to their status in the pleural fluid. When experiments were planned, an aliquot was thawed about a month ahead of time as it took a few weeks or months for the majority of cells surviving the freeze/thaw procedures to resume growing in vitro at about their original rate with doubling time of ~24-30 hr in the pleural fluid and immediately after the thoracentesis. The low density (LD) cells were obtained simply by dilution of the proliferating HD ALL3 cells, but do not continue growing at low densities below ~ <10⁴ cells/ml although the majority of LD ALL3 cells remain viable for a day or so and some for several days. The majority are dead or dying by ~ 8-10 days without additional stimulus to divide [30]. A portion of the thawed cells was refrozen for future use. During the course of a series of experiments the cells were passaged serially for about 4-6 months during which they usually maintained their original growth characteristics, but with longer passage they sometimes began to adapt to the liquid culture conditions and started to grow at lower cell densities at which they would not grow originally. During the experimental period the cells were maintained in Iscove's modified Dulbecco's medium (IMDM) supplemented with 10% heat-inactivated fetal bovine serum (FBS) (Hyclone Laboratories, Logan, Utah, USA), 1% penicillin-streptomycin solution (PSN; 10,000 I.U. penicillin and 10,000 μg/ml streptomycin) (Corning # 30-001-CI, Fisher Scientific, Pittsburgh, PA, USA), 1% sodium pyruvate (Mediatech Inc, Manassas, VA, USA # 25-000-CI), 1% HEPES buffer (N-2-hydroxyethylpiperazine-N’-2-ethanesulphonic acid) (Mediatech # 25-060-CI), 1% non-essential amino acids (NEAA; Mediatech #25-025) and 0.1% β-mercaptoethanol (BME) (Life Technologies, Grand Island, NY, USA # 21985-023). The media including supplements hereafter is called ALL3 media. To determine the cell number and cell viability, hemocytometer counts and the trypan blue exclusion method were used [49]. Cells stained with trypan blue were considered as dead cells. We used a 0.4% solution of trypan blue (Sigma Aldrich, St. Louis, MO, USA #T8154) in buffered isotonic salt solution, pH 7.2 to 7.3 (i.e., phosphate-buffered saline, PBS).

2.2. Ki67 labeling

ALL3 cells were cultured at LD and HD, and collected and processed to stain with MIB-1 Ki67 antibody and nuclei were stained with DAPI (4’,6-Diamidino-2-phenylindole dihydrochloride) (Sigma, St.Loius, MO, USA # D9542). The Ki67 positive cells were counted and imaged using immunofluorescence microscope with help from Molecular Cytology Core Facility at Memorial Sloan-Kettering Cancer Center (MSKCC), NY.

2.3. Atomic force microscopy

Bioscope Catalyst (Bruker/Veeco, Inc., CA) AFM installed on Nikon U2000 confocal Eclipse C1 microscope and Dimension 3100 (Bruker Nano/Veeco, Inc.) AFM with Nanoscope V controller and nPoint close-loop scanner (200 μm×200 μm×30 μm, XYZ) were used. Standard cantilever holders for operation in liquids were employed. To obtain the distribution of the properties over the cell surface and simultaneously record cell topography, the force-volume mode of operation was utilized. The force curves were collected with the vertical ramp size of 12 μm. To minimize viscoelastic effects, the force-indentation curves were recorded with the constant vertical speed of 20μm/sec (the frequency of ~0.8Hz). This speed was a compromise between desire to minimize viscoelastic contributions and disturbance of the cells by the AFM probe. It is conceivable that the obtained parameters still contain viscoelastic contribution. This is one of the reasons of why this modulus is frequently not called the Young's modulus (which strictly speaking is the static modulus) but rather an effective one. Thus, it is important to keep this speed the same in all measurements. It has to be noted that the speed used in this work is quite ordinary when studying cell mechanics [50]. Furthermore, as was demonstrated for neurons, the mechanics of the cell body is virtually speed independent within 1-10μm/sec [51] (whereas the parameters of the brush do depend on the ramp speed).

The force-volume images of cells were collected with the resolution of 16×16 pixels (typically within 35×35 μm² area). The maximum load force was in the range of 8 – 10 nN. Before the AFM imaging cells were placed in cell culture dishes with ALL3 Medium (Quality Biological Inc Cat#160-204-101) at 37°С with 5% CO₂ for 5-8 hours. ALL3 cells were allowed to attach to bottom of the uncoated plastic 10 cm² culture dish. The measurements were performed in ALL3 culture medium at room temperature (23°C).

AFM measurements were done as soon as we received the cells and plant them relax in the incubator for several hour. It is important because prior experiments have shown that some LD ALL3 cells without HDSN (supernatant of high density cells) stimulation may divide once within the first day or two, but then no more, and all the cells are usually dead after ~ 2 weeks [30,34]. There is a low incidence of spontaneous apoptosis in both HD and LD fresh new cultures (~5-10%). The percentage of live cells in HD cultures starting ~ 200,000 cells/ml as determined by cytoflurometric Annexin V-FITC/Propidium Iodine assays is usually ~ 70-80% during the first few days and remains about the same until they approach saturation density about a week later, depending on the exact starting cell density. The percentage of live cells in LD cultures starting ~ 5000 cells/ml is lower during the first few days ~ 40-50% and gradually declines as more cells and eventually all undergo apoptosis during the following 2 weeks unless they are rescued by HDSN. Therefore the AFM measurements of both LD and HD cells in the experiments discussed in this paper were all made during the first two days.

2.4. AFM probe: spherical indenter

The use of a large spherical AFM probe allows us to study relatively small and loosely attached ALL3 cells without the need of their special attachment to a solid substrate (and consequently, their potential alteration). As was demonstrated in [48], a sufficiently weak attachment of cells to a rigid substrate is sufficient to study them with the AFM method and the appropriate model.

A standard V-shaped arrow 200 μm AFM tipless cantilevers (Veeco, Santa Barbara, CA) were used throughout the study. Silica balls (5μm, Bangs Labs, Inc.) were glued to the cantilevers as described in [24]. The radius of the probe was measured by imaging the inverse grid (TGT1 by NT-MDT, Russia). The cantilever spring constant was measured using the thermal tuning method (~0.06N/m).

It should be noted that we have previously demonstrated the superiority of a spherical indenter rather than a sharp commercial one. This is justified by: a) the need to work in the linear stress-strain regime to derive the Young's modulus [6], b) less disturbing action of the indenting probe (stresses acting on the cell is orders of magnitude less compared to the sharp probe), c) weak adherence of hematopoietic cells including leukemic cells to the culture dish; it is rather easy to dislodge the cell when using the sharp probe.

2.5. Model used to characterize cells

As was shown in [52], it is critically important to take into account the pericellular coat for proper determination of biophysical properties of cells in the AFM indentation experiments. While the presence of the pericellular layer is well known, its nontrivial contribution to cell mechanics has only recently been confirmed [6, 47, 48, 53]. Moreover, it was shown that the self-consistent mechanical model of cells can only be developed when the pericellular brush layer is taken into account [6]. A model for a spherical loosely attached cell covered with pericellular brush deformed by a spherical AFM probe was developed in [48]. The presence of the pericellular coat/brush can easily be seen in the AFM force-deformation curves by its specific exponential force-distance dependence. The pericellular brush layer cannot physically be described with the elastic modulus in a consistent way (a major part of the pericellular coat is the entropic molecule brush which is essentially not an elastic material). Therefore, it has to be considered as a separate layer.

Here we briefly describe this model to explain how the analysis of the collected data was done. It should be noted that there are three primary static moduli of elasticity that can be used to describe the cell: the Young's modulus (tensile), shear, and bulk modulus. Assuming a cell is a homogeneous and isotropic material (at least for relatively small strains), the cell can be characterized by two parameters, for example, by the elastic modulus and the Poisson ratio [54]. It should be noted that the term 'elastic modulus' exclusively refers to the Young's modulus in this work. It is done for consistency with our previous works and to address the existing concern that the Young's modulus might require redefinition at the nanoscale. Since the Poisson ratio of soft materials typically ranges within 0.3-0.5 [55, 56], the maximum error in the definition of the elastic modulus due to the unknown Poisson ratio is expected to be less than 10% [8]. Therefore, it makes sense to characterize mechanics of cells with just one parameter, the elastic modulus.

The analysis of force indentation curves recorded with AFM is performed in two steps. First, the part of the force curve that corresponds to the highest load force is analyzed. This part of the curve should correspond to almost fully compressed pericellular brush layer (if it is not fully compressed at the maximum load force it should be increased). Thus, it corresponds to the deformation of the cell body, which is considered to be elastic material. The elastic modulus of the cell body is derived from that part of the curve. The knowledge of the elastic modulus allows one to extrapolate the cell body deformation to smaller deformation forces. This is the second step of the brush model. The force due to pericellular brush layer is now derived as the difference between the extrapolated and measured forces. Our previous studies have shown that this force is well fitted with the exponential function, and can be well characterized in terms of polymeric brush model [6, 47, 48].

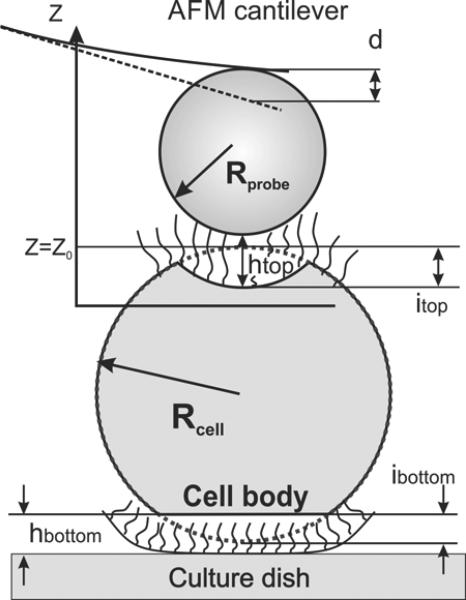
It should be noted that ALL3 cells are loosely attached to the dish surface and dislodge easily upon moving the cell substrate (it can easily be seen under optical microscope). Since this model was described previously [48], it is summarized below just briefly. Figure 1 shows a scheme of the interaction of a spherical AFM probe with a cell represented as a (double) two-layer structure. Geometry presented in Figure 1 implies the following equation: h_top + h_bottom = Z – Z₀ + i_top + i_bottom + d, where Z is the relative vertical scanner position. The position Z=0 was chosen for Z corresponded to the maximum cantilever deflection d. Z₀ is the scanner position for the non-deformed state of the cell body, h_top is the separation distance between the cell body and the spherical probe, h_bottom is the distance between cell body and the substrate, i_top and i_bottom are the top and bottom deformation of the cell body, respectively.

Figure 1.

A scheme of the AFM probe deforming a cell loosely attached to the bottom of the culture dish. An elastic cell body is surrounded by the pericellular brush layer.

It was assumed that the cell's pericellular brush is completely squeezed (h= h_bottom + h_top =0) near the maximum indentation force. Certainly, in reality the brush is not squeezed to zero. But as we demonstrated previously [6, 47] the model is self-consistent if we treat the brush as “completely squeezed” when the AFM probe-surface distance (h) is 10% of the brush length. For cells considered in this work, this corresponds to the load force exceeding ~2nN.

If the model is self-consistent, then the increase of the load force above 2nN should not result in the substantial change of the elastic modulus [6]. However, one has to be careful not to deform the cell too much to start measuring the influence of the substrate (strain becomes more than ~10%). As a reasonable compromise, we found that one can use the maximum load force of ~4nN. (see the verification of self-consistency of the Hertz model in the supplementary materials, Fig.S3).

When the pericellular brush is squeezed, one can find the elastic modulus E of the cell body from the observed deformation i by using the Hertz model:

$$i=Z_0-d-Z=d^{2∕3}\cdot {\left[\frac{3}{4}\frac{k(1-v^2)}{E}\sqrt{\frac{R_{probe}+R_{cell}}{R_{probe}{R}_{cell}}}\right]}^{2∕3},$$ (1)

where i=i_top+i_bottom, k is the AFM cantilever spring constant, and R_probe and R_cell are the radii of the AFM probe and cell body, respectively. The Poisson ratio of a cell v was chosen to be 0.5. (the specific choice of this parameter doesn't change the conclusions of this work, neither changes the elastic modulus beyond the accuracy of the measurements).

Radius of each cell was determined from the topography images collected within the force volume mode which were corrected for deformation (the height of each pixel was increased by the value of i); see the Supplementary material for detail. With known cell deformation, the force-separation dependence F(h) can be reconstructed using the following formula:

$$F\left(h\right)=kd=k(h-Z+Z_0-i)$$ (2)

To describe the brush layer parameters quantitatively, the following steric interaction equation can be used [6, 47, 48]:

$$F\left(h\right)\approx 50k_{B}T{R}^{\ast }{N}^{3∕2}\exp \left(-2\pi \frac{h}{L}\right)L,$$ (3)

where k_B is the Boltzmann constant, T is temperature, $R^{\ast }=1∕2\sqrt{R_1{R}_2}$ is the effective radius, R₁ = R_probe · R_cell/(R_probe + R_cell), R₂ = R_cell is the radius of the cell body, N is the surface density of the brush constituents, i.e., the effective number of molecules per unit area (aka the grafting density), and L is the equilibrium thickness of the pericellular brush layer surrounding the cell body. Here we assumed that N is a geometrical average of the top and bottom densities ($N=\sqrt{N_{top}{N}_{bottom}}$) and L is equal to the top and bottom brush length (L = L_top + L_bottom = L/2 + L/2). This formula is valid for 0.1<h/L<0.8.

2.6. Statistical analysis

Statistical analyses were done by using one-side ANOVA test and the confidence level p<0.05.

3. Results

3.1. ALL3 Cell growth at different starting cell densities

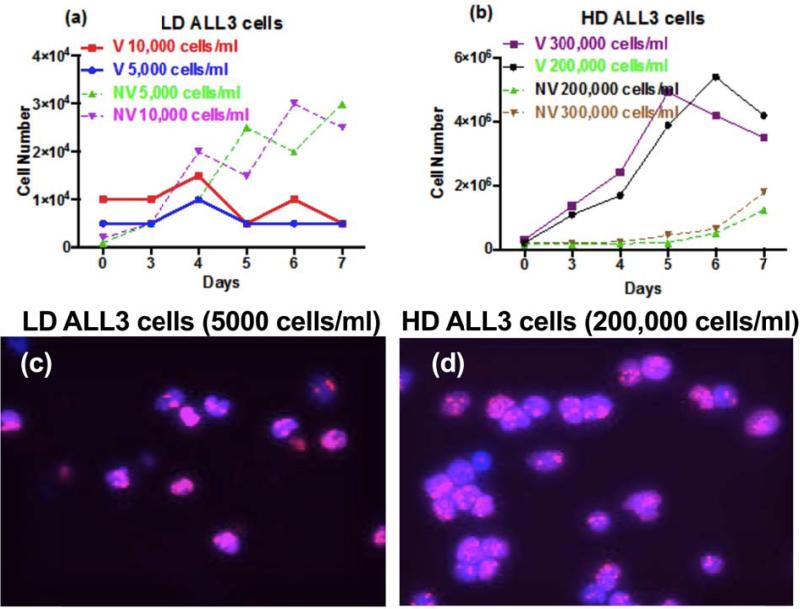
To study biomechanical properties of the ALL3 cells at low and high starting cell densities, we need to define the terms “low’ and “high” as below. It refers to the initial number of cell concentrations per unit volume used to culture cells in in vitro studies. Figure 2 shows the comparison of the growth rates of the ALL3 cells at different starting cell densities (time zero). The ALL3 cells cultured at densities of 5,000-10,000 cell/ml (Figure 2a) show minimal transient growth for the first few days but this was not sustained and there is a rapid increase in non-viable cells as estimated by trypan-blue staining and apoptotic assays [30]. These cell densities are called low cell density (LD). Fig.2b shows the growth of the ALL3 cells cultured at densities of 200,000-300,000 cell/ml. These cells grew excellently with doubling times of ~24 hours and there was only a slow increase in non-viable cells beginning about the 5^th day. These cell densities are called high cell density (HD). For AFM measurement, ALL3 cells were grown in 10cm² uncoated plastic dishes at starting density of LD and HD for 24 hours.

Figure 2.

Growth and proliferation profile of the ALL3 cells at different starting cell densities. ALL3 cells were grown in ALL3 medium as described in ‘Methods’. Comparative growth of the ALL3 cells at starting cell density of a) LD of 5,000 and 10,000 cells/ml and b) 200,000 and 300,000 cells/ml. Y-axis represents total number of viable (V) and non-viable (NV) cells on different days as determined using the trypan-blue exclusion method. Note: In both cases, a) and b) Y-axis are of different scale. Images of LD (c) and HD (d) cells on Day 2 that were stained with the MIB-1 Ki67 antibody.

As shown in figure 2 (c and d), LD and HD ALL3 cells were tested for their proliferation states using Ki67 antigen. Expression of Ki67 occurs preferentially during late G1, S, G2 and M phases of the cell cycle and is absent in the G0 phase [57]. After two days both LD and HD cells were stained with MIB-1 Ki67 antibody to determine their proliferation states. LD and HD ALL3 cells were found to be ~90% and 100% Ki67+, respectively (Figure 2 c and d).

In addition, labeling studies with BrdU or EdU which measures the fraction of cells synthesizing DNA (S phase of cell cycle) showed that the LD ALL3 cells were poised to begin proliferating but could not do so without being triggered by supernate (HDSN) obtained from ALL3 cells or some other normal or leukemic cells growing at HD (data not shown). The fraction of LD ALL3 cells incorporating EdU (i.e. in S-phase) was higher than that of the HD ALL3 cells for the first 2 days indicating some LD ALL3 cells were continuing to begin synthesizing DNA, but were not able to complete it and become arrested in S phase in which they died within a few more days without additional stimulation by HDSN; almost all of the LD ALL3 cells were dead or dying by 8-10 days [30].

3.2. Mechanical properties of cells grown in different densities

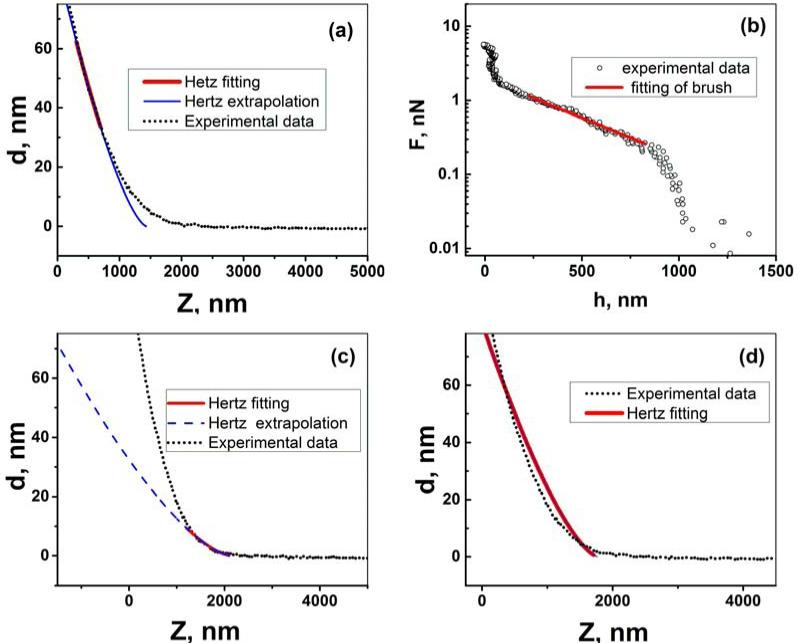
The AFM data obtained in the force-volume mode without any processing are the graphs of cantilever deviation (d) versus the vertical position of the AFM scanner (Z) (aka “raw data”). Processing of such data is shown in Figure 3 for HD ALL3 cells as an example. The data are processed with the help of the model described in the Model section. Figure 3a shows the use of the first part of the brush model, the Hertz fitting of the part of the force curve corresponding to the load force when the brush is squeezed, equation (1). The brush model fits well for higher forces. This good fitting results in the independence of the elastic modulus on the indentation depth (or cell deformation), which verifies self-consistency of the model, see the Supplementary materials (Fig.S3) for detail. The deviation of the Hertz fitting from the experimental data seen for small forces (small deflection d) is expected because the presence of an undeformed pericellular brush layer. It is attributed to the steric repulsion between the AFM probe and pericellular layer. This force dependence (found by using equation (2)) is presented in Figure 3b. Exponential behavior is typical for the pericellular brush (straight line in the logarithmic scale). This fit is further processed with equation (3) to calculate the grafting density and the length (thickness) of the pericellular brush layer.

Figure 3.

An example of processing of the AFM curve recorded on the surface of the ALL3 cell through the brush model. (a, c and d) fitting of the different regions of raw Z-d curve with the eq.(1) (points represent the raw AFM Z-d curve, solid (red) lines show region of data used for fitting and solid (dashed) (blue) lines are the calculated Hertz curve). (b) Forces of interaction between the AFM probe and the brush layer obtained by processing raw Z-d curve for the d=85-100 nm (here open circles correspond to the force-separation data, solid line is the model fitting eq.(3)).

Figures 3 (c and d) demonstrate a typical inconsistency when the presence of pericellular brush is ignored. Figure 3(c) shows a substantial deviation of the Hertz model from the experimental data when fitted for small forces. Figure 3d shows also a poor Hertz fitting when trying to fit the entire force range.

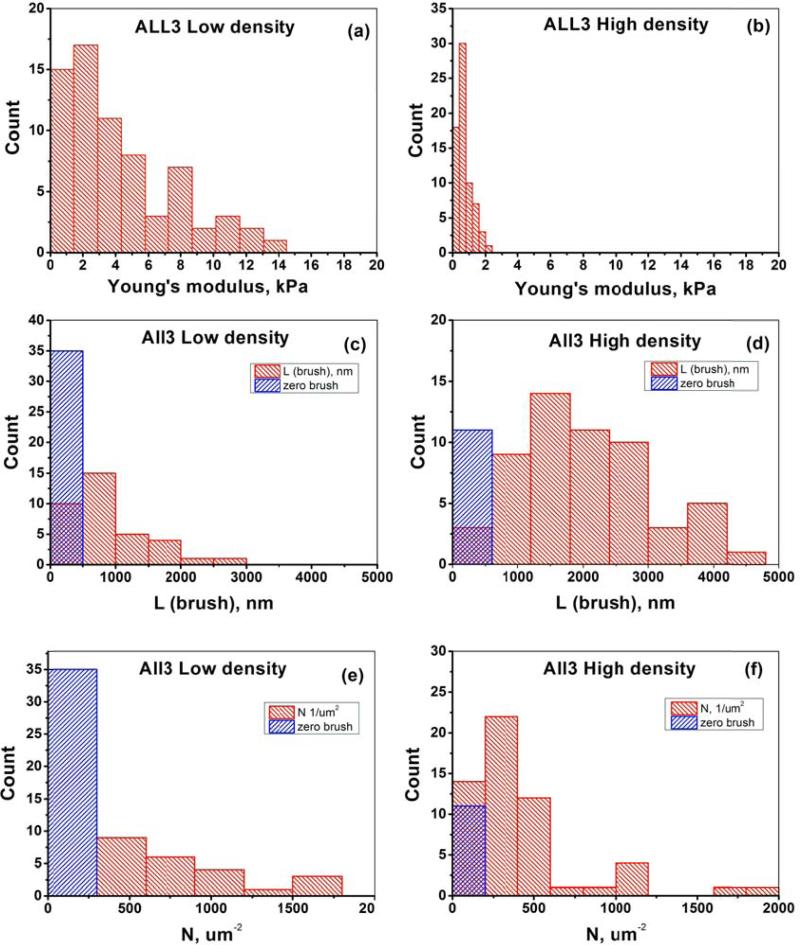
To study the influence of cell-cell communication on the biomechanical properties of cells, we measured low- and high- density ALL3 cells. Nine LD ALL3 cells (69 force curves total, 5-10 force curves per cell) and eight HD ALL3 cells (69 force curves total, 7-11 force curves per cell) were analyzed. Only the force curves from the top area of the cell were processed. Specifically, we take the force curves in the surface points around the top when the incline of the surface is <10-15 degrees. To identify such curves, the AFM image of cell heights was used (the height image was collected as a part of the force-volume data set; the effective radius of the cell was derived from these images after taking into account the cell deformation, see the Supplementary Information for detail). The relatively modest number of cells analyzed is explained by the fact that many cells were not sufficiently well attached to the dish surface. As a result, such cells sled sideway when the AFM probe approached them (it can be seen through the optical microscope attached to AFM). The results of the data analysis are presented in Fig.4 as histograms. Although the distributions of the modulus values are not Gaussian, it is instructive to characterize it by a formal average and standard error. The results are presented in Table 1. It should be noted that some of the force curves did not demonstrate the presence of the pericellular brush (no deviation from the Hertz model extrapolation seen in Figures 3 a,c,d). We consider this as a real absence of the brush at that particular point of the cell surface because it cannot be explained by the errors of measurements (which are relatively small [48]), neither by assumptions of the model (the force-deformation behavior is substantially different for the brush and cell body). Therefore, we assign L=N=0 to the cases of when pericellular brush was absent. An example of the distribution of parameters of the pericellular coat is shown in Fig.S2 (supplementary materials).

Figure 4.

Results for biomechanical properties of ALL3 cells at low and high starting cell densities. The elastic modulus (a,b), equilibrium pericellular brush length (c,d), and grafting density (e,f).

Table 1.

	Low density average±SEM	High density average±SEM	Low density Lower/Upper 95% CI of mean	High density Lower/Upper 95% CI of mean
Elastic modulus [kPa]	4.3±0.4	0.72±0.05	3.5/5.1	0.61/0.83
Brush Length L [58]	500±90	1800±160	310/680	1500/2100
Grafting density N [um−2]	370±71	360±45	230/510	270/450
Effective size of the brush L*N [k°um−1]	230±35	563±44	160/300	480/650

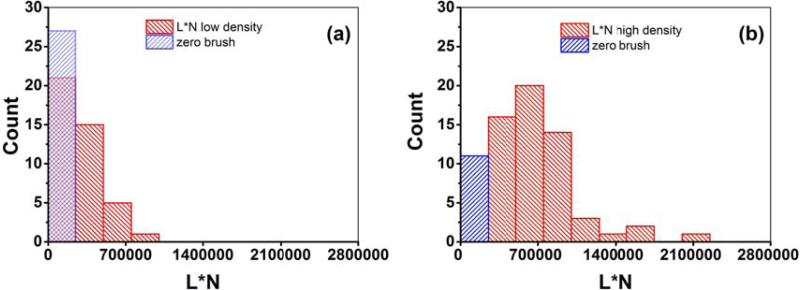
It is also interesting to compare the “amount” of pericellular brush, which can be roughly approximated as a multiplication of L and N. This multiplication (L*N) can be interpreted as an estimation of the brush “amount” per unit area. In the case of a fully stretched classical polymeric brush, L*N would be the total length of the brush molecules per unit area. These parameters are shown in Figure 5 and also included in Table 1. Lower and upper boundary of 95% of confidence interval of mean for all parameters and cell densities are also shown in Table 1 to help to estimate the statistical significance of the observed difference. One can now see that the elastic moduli, brush length, and the brush effective size are significantly different for LD and HD cells. The grafting density of the pericellular brush are not significantly different for LD and HD cells.

Figure 5.

Comparison of the effective brush size (N*L parameters) for (a) low and (b) high density ALL3 cells.

4. Discussion

The cell density refers to the initial number of cells per unit volume used to culture cells in-vitro. The higher the cell density, the smaller the distances between individual cells, and consequently, the stronger the (biochemical) cell-cell communication. Thus, to study the effect of cell-cell communication on biomechanical properties of cells, we studied ALL3 cells grown at different cell densities.

To find the appropriate cell densities in which cell-cell communication (the quorum effect) can be seen, we monitored the cell growth, which was found to be significantly different for these cells at different cell densities [30, 59]. We observed a significant difference in the cell growth when the starting cell densities change from 10,000- 200,000 cell/ml. HD ALL3 cells grow very well with great viability and a doubling times of ~24 hr while LD cells (which originate from dilution of other fast growing HD cells, and start at over 90% viable LD cells) may double once or not at all. Thus, the LD cells are still poised to proliferate, but cannot do so without additional stimulation. The proliferating Ki67 marker shows that both LD and HD ALL3 cells are still poised to continue proliferating. LD cells continue to begin DNA synthesis for the first day or so after being prepared by dilution of HD cells (the cell density is drastically reduced (usually from ~2-3×10⁵ cells/ml to 5×10³-10⁴ cells/ml). However, the LD cells are unable to complete synthesizing DNA and die arrested in S phase, whereas the HD cells continue DNA synthesis and the subsequent mitosis.

A substantial difference between LD and HD ALL3 cells was found in both the elastic modulus of the cell body and the parameters of the pericellular brush layer (brush length, and the brush effective size). At the same time, the difference in the grafting density of the pericellular layer is not significantly different for HD vs LD ALL3 cells. The average size of the brush layer per unit area (multiplication of the grafting density and equilibrium length) increased for HD cells by a factor of 2.5. The average equilibrium length of the pericellular brush is higher for HD cells by a factor of 3.6x. The most profound effect was found for the elastic modulus of the cell body. LD cells showed ~6x increase in the elastic modulus of the cell body compared to HD cells. This result is quite significant because the elastic modulus of cells has been considered as a potential physical marker of pathologically transformed cells, [13-17], [18-21], [22], [23], [24-26, 60, 61]. The difference in the elastic modulus observed in the present work is substantially larger than typically reported for pathologically transformed cells. For example, the difference between the modulus of normal and cancerous human lung epithelial cells reported in [60, 61] was only about 70%. Those cells were extracted ex-vivo and analyzed without taking into account the cell-cell communication, and proliferating ability of cells. Therefore, the cell-cell communication effect is certainly has to be taken into account when studying cell mechanics.

As explained in the Methods Section, without rescue by HDSN, some LD ALL3 cells started at ~5000/ml may divide once during the first few days but not thereafter and the cell viability then gradually declines until all the cells are dead by ~ 2 weeks. Both the HD and LD AFM measurements reported here were only made during the first two days on live cells which are the only ones that adhere even lightly to glass, making it possible to virtually exclude contamination of the data by measuring dead cells (dying or dead cells do not adhere well to the culture dish). Thus, while the impending apoptosis of LD cells cannot be entirely excluded as a contributory cause of the observed differences, at most it probably only has a minor role since both the LD and HD cells measured by AFM appeared quite viable.

From a biochemical point of view, the change of stiffness (elastic modulus) of cell is typically explained by the alteration of the cytoskeleton. There is considerable evidence that cell stiffness is defined by the cellular cytoskeleton [7, 53], mostly by F-actin and its organization at the mesh layer of cytoskeletal [7, 24, 62, 63]. Thus, the ALL3 cells may be undergoing considerable F-actin reorganization in non-growing LD and growing HD ALL3 cells. In particular, it was shown that this cross-linking is increasing with aging (or the number of cell population doublings). Therefore, it is quite plausible to expect that fast growing cells do not have enough time to develop sufficient cytoskeletal cross-linking, and consequently, become softer.

It is worth noting that the results reported here are rather different from the known increase of the Young's modulus during cell mitosis [64]. This is because the substantial increase of the Young's modulus of cells was found only at the end of anaphase and when cells started to separate during the cytokinesis. In addition, those results were obtained well before the correct models of cell mechanics were developed. Here the cell brush model [6, 47, 48] was used here to derive the elastic modulus of the cell body and the parameters of the pericellular coat (brush layer) to measure the biomechanical properties of cells. Self-consistency of the model was examined. Specifically, a reasonable independence of the elastic modulus of the indentation depth was demonstrated in the range between 100-900nm (<10% cell strain). Figure S3 (supplementary materials) shows virtually the independence of the elastic modulus of the indentation depth. It implies that our assumption that treating the cell body as a homogeneous isotropic medium is correct. If we assume that only the cell nucleus increases its stiffness substantially, the assumption of homogeneity of the cell body would be incorrect (unless one assumes that the measured modulus comes entirely from the nucleus; this would contradict the previously cited results on correlation between the cell stiffness and cytoskeleton).

As to the observed change of the pericellular coat, this area is much less studied. While the physical presence of brush-behaving nanoscale structure on the cell surface can be measured with AFM, this technique does not distinguish biochemical compositions of these structures. The detailed molecular composition and biological functions of this pericellular brush are still not understood well [65, 66]. The pericellular coat is involved in various processes such as physical cell-cell repulsion cell adhesion, differentiation, and proliferation [67-70] [69, 71]. For example, it was found that more aggressive metastatic tumor areas demonstrated substantially higher content of the hyaluronic acid (HA), the major component of the pericellular coat [72]. Recently it was confirmed that the larger pericellular brush (glycocalyx) promotes cell growth [73]. Specifically, it was shown that expression of large tumor associated pericellular coat in non-transformed mammary cells promoted focal adhesion assembly and facilitated integrin-dependent growth factor signaling to support cell growth and survival. Furthermore, shorter molecules in the pericellular coat demonstrated reduction proliferation and migration of human aortic smooth muscle cells in vitro [74]. All the above seems to be in agreement with the observed size of the pericellular brush and proliferation ability of HD ALL3 cells. Nevertheless, the opposite behavior was observed for epidermal proliferation of nonmalignant human keratinocytes [70]. It should be noted that in all previous reports, the study were focused on a particular biochemical component of the pericellular coat. In contrast to those methods, the AFM approach detects the undisturbed (no labeling needed) physical presence of all components of the pericellular coat. Thus, this method can be treated as a complementary to the biochemical and immunostaining methods.

The molecular part of the pericellular brush layer consists mostly of negatively charged polysaccharides [65, 66]. While such a layer does not seem to have a well-defined specific biological function, its presence definitely alters the interaction of the cell body with the surrounding. Because of electrostatic and steric interactions of all biochemical moieties with the pericellular layer, this layer might serve as a protective shell preventing entry of (negatively charged) anticancer drugs into the cell body, or oppositely, the brush molecules can attract and accumulate the positively charged drugs, enhancing its efficacy. This recently was demonstrated for nanoparticles [51, 75].

Let us discuss briefly a biochemical reason for the cell-cell communication. One can note that the observed data suggest that ALL3 cells at low starting cell density are poised to grow. It is plausible to expect that cells secrete additional stimulatory factor(s) to support their growth, but at low density they are either not secreted or not present in enough amounts to stimulate LD ALL3 cells to grow, i.e., the cell-cell communication is inadequate [30]. This phenomenon is termed quorum sensing; it has been observed and studied extensively for prokaryotic cells [76, 77]. In a cancer as an example, the CD40 ligand (also known as CD40L/CD154) is one of such quorum-sensing molecule’ that has shown to sustain CD40-dependent survival behavior when Burkitt lymphoma cells fall below a certain suicidal threshold cell number [41]. The CD40 pathways are dysregulated in several cancers such as renal cancers, melanoma, multiple myeloma, non-Hodgkin's lymphoma, chronic lymphocytic leukemia, B cell lymphoma and many more [58, 78]. However, the LD ALL3 cells fail to sustain their growth and require supply of external stimulatory factors such as from the same ALL3 cells growing at high density (though the biochemical nature of these stimulatory factors is yet unknown) [30, 34].

5. Conclusions

Atomic force microscopy was used to study biophysical properties of cells, the rigidity of the cell body and the parameters of its pericellular coat. The cell brush model was used here to derive the biophysical parameters of cells. Self-consistency of the model was demonstrated by demonstrating a reasonable independence of the elastic modulus over the cell body of the indentation depth. The biophysical properties of cell at the single cell level are interesting from both fundamental and applied points of view. One of the most promising aspects of application of such parameters is their use for diagnostics and possibly prognostics of diseases and abnormalities. Here, to the best of our knowledge, we show the first demonstration of profound importance of the effect of cell-cell communication on the key biophysical parameters of cells, its modulus of elasticity and pericellular coat. Using the model of human pre-B p190^BCR/ABL acute lymphoblastic leukemia (ALL3) cells, we demonstrate that the biophysical properties of cells can significantly change depending on the cell-cell distance (the cell density) in the culture dish even if cells are well sub confluent. For example, the observed increase in the elastic (Young's) modulus of the cell body seems to be substantially larger than the difference between cancer and normal cells reported in some papers. This implies the importance of taking into account the cell-cell communication when measuring biophysical properties of cells.