Wolbachia in the Drosophila yakuba Complex: Pervasive Frequency Variation and Weak Cytoplasmic Incompatibility, but No Apparent Effect on Reproductive Isolation

Abstract

Three hybridizing species—the clade [(Drosophila yakuba, D. santomea), D. teissieri]—comprise the yakuba complex in the D. melanogaster subgroup. Their ranges overlap on Bioko and São Tomé, islands off west Africa. All three species are infected with Wolbachia—maternally inherited, endosymbiotic bacteria, best known for manipulating host reproduction to favor infected females. Previous analyses reported no cytoplasmic incompatibility (CI) in these species. However, we discovered that Wolbachia from each species cause intraspecific and interspecific CI. In D. teissieri, analyses of F₁ and backcross genotypes show that both host genotype and Wolbachia variation modulate CI intensity. Wolbachia-infected females seem largely protected from intraspecific and interspecific CI, irrespective of Wolbachia and host genotypes. Wolbachia do not affect host mating behavior or female fecundity, within or between species. The latter suggests little apparent effect of Wolbachia on premating or gametic reproductive isolation (RI) between host species. In nature, Wolbachia frequencies varied spatially for D. yakuba in 2009, with 76% (N = 155) infected on São Tomé, and only 3% (N = 36) infected on Bioko; frequencies also varied temporally in D. yakuba and D. santomea on São Tomé between 2009 and 2015. These temporal frequency fluctuations could generate asymmetries in interspecific mating success, and contribute to postzygotic RI. However, the fluctuations in Wolbachia frequencies that we observe also suggest that asymmetries are unlikely to persist. Finally, we address theoretical questions that our empirical findings raise about Wolbachia persistence when conditions fluctuate, and about the stable coexistence of Wolbachia and host variants that modulate Wolbachia effects.

ENDOSYMBIOTIC Wolbachia bacteria infect about half of all insect species (Werren and Windsor 2000; Zug and Hammerstein 2012), as well as many other arthropods (Bouchon et al. 1998; Jeyaprakash and Hoy 2000; Hilgenboecker et al. 2008; Weinert et al. 2015). Hosts can acquire Wolbachia horizontally from distantly related taxa, cladogenically from common ancestors, or through introgression (O’Neill et al. 1992; Lachaise et al. 2000; Raychoudhury et al. 2009; Hamm et al. 2014). Wolbachia gained attention for their effects on host reproduction (Laven 1951; Yen and Barr 1971; Rousset et al. 1992; O’Neill et al. 1997), which, in Drosophila, includes cytoplasmic incompatibility (CI) and male killing (Hoffmann et al. 1986; Hoffmann and Turelli 1997; Hurst and Jiggins 2000). Because host females vertically transmit Wolbachia, natural selection favors Wolbachia variants that enhance host fitness (Prout 1994; Turelli 1994; Haygood and Turelli 2009). Many Wolbachia infections do not appreciably manipulate host reproduction—wAu in D. simulans, wSuz in D. suzukii, and wMel in D. melanogaster (Hoffmann 1988; Hoffmann et al. 1996; Kriesner et al. 2013; Hamm et al. 2014). These infections presumably persist through positive effects on host fitness (Hoffmann and Turelli 1997) that are mostly not understood, although viral protection and nutritional supplementation have been documented (Hedges et al. 2008; Teixeira et al. 2008; Brownlie et al. 2009; Martinez et al. 2014; Cattel et al. 2016a). Similarly, even for the best understood CI systems, it is unknown how Wolbachia increase host fitness so that infections tend to spread from low frequencies. For example, the spread of wRi in D. simulans has been studied for decades, and was thought to have “bistable” dynamics, in which strong CI counteracted the effects of imperfect maternal transmission and negative fitness effects, such that infection frequencies tended to rise only once a threshold frequency was passed (Turelli and Hoffmann 1991, 1995). However, more recent data suggest that wRi must have a net positive effect on D. simulans fitness, allowing it to systematically increase from low frequencies (Kriesner et al. 2013).

Simple models describe Wolbachia infection frequency dynamics. The spread and maintenance of CI-inducing Wolbachia depend primarily on the proportion of uninfected ova produced by infected females (μ), the relative hatch rate of uninfected eggs fertilized by infected males (H), and the relative fecundity—or any factors that affect host fitness—of infected females relative to uninfected females (F) (Caspari and Watson 1959; Hoffmann et al. 1990). When Wolbachia produce F(1−μ) < 1, infections tend to decrease in frequency when rare, and require stochastic effects for initial establishment (Jansen et al. 2008). If F(1−μ) < 1, but F(1−μ) > H, Wolbachia frequencies will tend to increase once the infection is sufficiently common, such that infected males lower the effective fecundity of uninfected females below that of infected females. CI-causing infections that generate H < F(1−μ) < 1 lead to “bistable” dynamics with stable equilibria at 0, and at a higher frequency denoted p_s, where 0.50 < p_s ≤ 1 (Barton and Turelli 2011). Bistability applies to Aedes aegypti mosquitoes transinfected with wMel Wolbachia from D. melanogaster that are being released as a biocontrol of the dengue virus (McMeniman et al. 2009; Hoffmann et al. 2011; Walker et al. 2011; M. Turelli and N. H. Barton, unpublished results), but seems not to apply to natural Wolbachia infections (Fenton et al. 2011; Kriesner et al. 2013; Hamm et al. 2014; Kriesner et al. 2016).

The fitness effects of Wolbachia on their hosts depend on environmental conditions, and on interactions with hosts. For example, the fidelity of maternal transmission of wRi by D. simulans increases under laboratory conditions (Turelli and Hoffmann 1995). In very low and in very high iron environments, wMel-infected D. melanogaster have higher fecundity than do uninfected females (Brownlie et al. 2009). wMel also increases D. melanogaster fitness in the presence of some environmental pathogens (Hedges et al. 2008; Teixeira et al. 2008), and similar pathogen protection is produced by many Wolbachia variants placed in a common D. simulans nuclear background (Martinez et al. 2014). Interactions with the environment also underlie stable clines in wMel infection frequencies in eastern Australia. Across 20 years, wMel infection frequencies in D. melanogaster have remained higher at low latitudes, due partly to fitness costs of wMel in colder environments (Kriesner et al. 2016). Many studies document interactions between Wolbachia and their hosts. Wolbachia that cause CI in D. recens become male killers when introgressed into certain strains of the sister species D. subquinaria (Jaenike 2007). Wolbachia from D. melanogaster that cause limited CI in their natural host induce nearly complete CI in D. simulans (Poinsot et al. 1998), and complete CI in Ae. aegypti (Walker et al. 2011). Thus, the fitness effects of Wolbachia may fluctuate across abiotic and genetic environments, altering predictions about the spread and maintenance of Wolbachia infections.

Three hybridizing species—D. yakuba, D. santomea, and D. teissieri—comprise the yakuba complex within the D. melanogaster subgroup (Lachaise et al. 2000). The human commensal D. yakuba is widely distributed throughout sub-Saharan Africa and on the islands of Bioko and São Tomé in west Africa. D. yakuba’s sister species, D. santomea, is endemic to the volcanic island São Tomé. On São Tomé, D. yakuba occurs at low elevations (below 1450 m), and D. santomea occurs in higher altitude mist forests (between 1153 and 1800 m), but D. yakuba and D. santomea occasionally hybridize in the midlands of the extinct volcano of Pico de São Tomé (Llopart et al. 2005a,b)—hybrids represent about 3% of flies sampled between 1000 and 1600 m (Comeault et al. 2016). The third species of this clade, D. teissieri [sister to the pair (D. yakuba, D. santomea)], has a fragmented distribution throughout tropical Africa produced by the loss of rain forests. D. teissieri occurs on Bioko, but is absent from São Tomé (Lachaise et al. 1981; Devaux and Lachaise 1988; Joly et al. 2010). Crosses between D. yakuba and D. santomea produce fertile F₁ females; and, despite diverging from this species pair at least 1 MYA (Monnerot et al. 1990; Long and Langley 1993; Bachtrog et al. 2006; Obbard et al. 2012), D. teissieri also produces fertile F₁ females with both species in the laboratory (Turissini et al. 2015). Hence, hybridization with D. teissieri is possible, but its frequency in nature remains unclear. Mitochondrial genetic and genomic analysis suggest that pervasive introgression has led to shared cytoplasms in the yakuba complex (Lachaise et al. 2000; Llopart et al. 2005b; Bachtrog et al. 2006; Llopart et al. 2014). However, the most recent analyses of introgression using whole genome data rely substantially on IMa2 analyses (Llopart et al. 2014), known to produce false positives for migration when there are few loci, or when there is little genomic variation (Becquet and Przeworski 2009; Cruickshank and Hahn 2014; Hey et al. 2015); both limitations apply to these mitochondrial comparisons. Indeed, our analyses of whole mitochondrial and Wolbachia genomes reveal some differentiation of yakuba complex cytoplasms, despite historic and current introgression (M. Turelli, W. R. Conner, D. R. Matute, D. A. Turissini, and B. S. Cooper, unpublished results).

Previous analyses suggest that the yakuba complex Wolbachia infections resemble wAu (Hoffmann et al. 1996; Zabalou et al. 2004), one of five variants from D. simulans (Ballard 2004). Like wAu, the yakuba complex variants seemed not to cause CI, yet they did provide protection from CI in crosses between naturally infected D. yakuba and D. yakuba transinfected with wRi (Charlat et al. 2004; Zabalou et al. 2004). Wolbachia from D. teissieri caused strong CI when transinfected into D. simulans, while Wolbachia from D. yakuba and D. santomea did not (Martinez et al. 2014). This suggests differences among the Wolbachia in these species, and host dependence of CI, at least for the D. teissieri strain. Limited surveys also indicated different Wolbachia infection frequencies among yakuba complex species, with ∼10–30% of D. yakuba infected, 30% of D. santomea, and 95% of D. teissieri (Lachaise et al. 2000; Charlat et al. 2004). CI-causing Wolbachia are known to have high equilibrium frequencies (Turelli 1994; Jaenike 2009; Kriesner et al. 2016), further suggesting that D. teissieri Wolbachia may cause CI.

Here, we use collections of yakuba complex species sampled from Bioko and São Tomé over 15 years to assess frequency variation, phenotypic effects of Wolbachia on hosts, reproductive manipulation within hosts, and influence on reproductive isolation (RI) between host species. Wolbachia contribute to RI between co-occurring D. paulistorum semispecies (Miller et al. 2010), and seem to have contributed to reinforcement between Wolbachia-uninfected D. subquinaria and Wolbachia-infected D. recens (Shoemaker et al. 1999; Jaenike et al. 2006). The yakuba complex has become a model for understanding the evolution of RI (Coyne et al. 2002; Moehring et al. 2006; Matute 2010, 2015; Turissini et al. 2015); but the role, if any, of Wolbachia on RI in this clade has not previously been investigated. We characterize the effect of Wolbachia on premating, gametic, and postzygotic RI. We also describe Wolbachia frequencies through time (15 years) and space (between islands). Finally, we address theoretical questions our results raise about the maintenance of variation in Wolbachia and their hosts.

Materials and Methods

Prevalence and typing of Wolbachia infections in natural populations

We estimated Wolbachia frequencies in populations of D. yakuba, D. santomea, and D. teissieri sampled from Bioko and São Tomé over 15 years (Table 1). DNA was extracted using a standard “squish” buffer protocol (Gloor et al. 1993), and infection status was determined using a polymerase chain reaction (PCR) assay. DNA was extracted for multiple genotypes in 96-well extraction plates—lines of known infection status were included throughout each plate as positive and negative controls. Infection status was determined using primers for the Wolbachia-specific wsp gene (Braig et al. 1998; Baldo et al. 2006). The lines that we phenotyped were screened individually a second time using wsp, and a second reaction for the arthropod-specific 28S rDNA (Nice et al. 2009), which serves as a positive control (primers are listed in Supplemental Material, Table S1). No discrepancies in infection status were found between our initial population screens using plates, and our subsequent screens of individual lines used for phenotyping. Our PCR thermal profile began with 3 min at 94°, followed by 34 rounds of 30 sec at 94°, 30 sec at 55°, and 1 min and 15 sec at 72°. The profile finished with one round of 8 min at 72°. We visualized PCR products using 1% agarose gels that included a molecular-weight ladder. Assuming a binomial distribution, we estimated exact 95% binomial confidence intervals for the infection frequencies identified for each collection.

Table 1. Wolbachia infection frequencies in Bioko and São Tomé populations of D. yakuba, D. santomea, and D. teissieri.

Species	Location	Yr	N	Infected	p (Confidence Interval)
D. yakuba	São Tomé	2001	35	14	0.40 (0.24, 0.58)
		2009	155	118	0.76 (0.69, 0.83)
		2015	41	31	0.76 (0.60, 0.88)
	Bioko	2009	36	1	0.03 (0.001, 0.15)
		2013	21	4	0.19 (0.06, 0.42)
D. santomea	São Tomé	2005	39	25	0.64 (0.47, 0.79)
		2009	57	44	0.77 (0.64, 0.87)
		2015	38	14	0.37 (0.22, 0.54)
D. teissieri	Bioko	2009	27	13	0.48 (0.29, 0.68)
		2013	30	20	0.67 (0.47, 0.83)

Sample sizes (N), infection frequencies (p), and exact 95% binomial confidence intervals for each collection.

Two Wolbachia-infected isofemale lines from each population of each species were selected for multilocus sequence typing (MLST) (Baldo et al. 2006). The five MLST protein-coding genes (gatB, coxA, hcpA, ftsZ, and fbpA) were sequenced in both directions using an ABI 3730 DNA Analyzer (Applied Biosystems) at the University of California, Davis, DNA Sequencing Facility. We assembled the chromatograms into contigs, and generated a consensus sequence using a custom script. We visually inspected each sequence for quality and for ambiguities. We verified that orthologous genes were amplified using a BLASTn search and the NCBI “nr” database (Altschul et al. 1990). To categorize each Wolbachia, we used the “multiple locus query” function of the Wolbachia MLST database (http://pubmlst.org/wolbachia/).

Screening for CI

When Wolbachia cause incomplete CI, crosses between uninfected females and infected males (denoted UI) produce lower egg hatch, and thus lower egg-to-adult viability, than do the other crosses (IU, II, and UU). We assessed CI in two ways: Wolbachia effects on egg hatch and Wolbachia effects on egg-to-adult viability, both using single-pair matings. The sample sizes for all CI experiments are listed in Table 2, Table 3, and Table 8. We first screened a single population collection within each host species for intraspecific variation in the strength of CI by measuring the egg hatch of UI and IU crosses between N independent pairs of infected and uninfected isofemale lines. Reciprocal crosses examine Wolbachia effects in mostly controlled genetic backgrounds. In contrast, curing Wolbachia-infected lines with tetracycline may affect mitochondrial density and function (Ballard and Melvin 2007). We report data only from the pairs in which both reciprocal crosses produced at least eight eggs—our analyses are not sensitive to this threshold. Because Wolbachia that cause CI generally have relatively high equilibrium frequencies (Jaenike 2009; Kriesner et al. 2016), we screened the population collection for each species with the highest infection frequency (Table 1). Virgins were collected from each line, and placed into holding vials for 48 hr. We then set up each UI and IU cross in a vial containing a small spoon with cornmeal medium and yeast paste for 24 hr—both males and females were 2 days old at the beginning of these experiments. Because CI decreases with age in other Drosophila (Reynolds and Hoffmann 2002), we used very young males. Each pair was transferred every 24 hr for 3 days. The proportion of eggs that hatched on each spoon was scored 24 hr after the adults were transferred. During preliminary trials, we confirmed that 24 hr sufficed for all eggs to hatch. For D. teissieri, we replicated UI and IU crosses for pairs that indicated CI during the initial 3-day screen. To isolate D. teissieri and Wolbachia effects, we also generated F₁ genotypes—and four-generation backcrosses—with different combinations of Wolbachia and host backgrounds. These infected lines were reciprocally crossed to uninfected lines to quantify CI. We also reciprocally crossed infected D. teissieri lines to assess whether Wolbachia infections in females provide protection from CI. For all D. teissieri experiments that followed the initial population screen, we assessed egg hatch over 5 days, rather than 3 days.

Table 2. Wolbachia in the yakuba complex cause CI.

		N	Mean	SD	♀I × ♂I	♀U × ♂I	♀I × ♂U	♀U × ♂U
D. teissieri	♀I × ♂I	44	0.94	0.05		623.64	1.307	23.08
	♀U × ♂I	44	0.75	0.09	376.10		624.94	646.72
	♀I × ♂U	44	0.94	0.04	376.10	376.10		21.77
	♀U × ♂U	44	0.95	0.05	376.10	376.10	376.10
D. yakuba	♀I × ♂I	44	0.93	0.08		494.72	29.14	59.74
	♀U × ♂I	44	0.79	0.11	376.10		523.85	554.45
	♀I × ♂U	44	0.95	0.06	376.10	376.10		30.60
	♀U × ♂U	44	0.96	0.04	376.10	376.10	376.10
D. santomea	♀I × ♂I	44	0.95	0.04		580.80	261.70	89.56
	♀U × ♂I	55	0.79	0.10	356.80		320.10	491.24
	♀I × ♂U	44	0.88	0.08	376.10	356.80		172.15
	♀U × ♂U	44	0.93	0.05	376.10	356.80	376.10

UI crosses generally have reduced egg-to-adult viability. N is the number of single-pair matings that produced the mean and standard deviation (SD). The last four columns show our statistical analyses as 4 × 4 matrices for each species. The upper triangular matrix shows the observed Kruskal-Wallis difference. The lower triangular matrix shows the critical value required to achieve statistical significance at P < 0.05 after correcting for multiple comparisons. For example, the mean egg-to-adult viability of ♀U × ♂I D. teissieri crosses (0.75) is significantly different from the mean egg-to-adult viability of the ♀I × ♂U crosses (0.94) as evidenced by the observed Kruskal-Wallis difference (624.94) surpassing the critical value (376.10). Statistically significant differences (P < 0.05) are indicated in boldface.

Table 3. Cytoplasmic incompatibility assays for D. teissieri lines.

Cross	Infection Status		Mean Hatch Rate (± SD)	N	P Value
	Female	Male
1. L18(I) × L3(U)	U	I	0.61 ± 0.40	29	0.028
	I	U	0.84 ± 0.22	28
2. L11(I) × L3(U)	U	I	0.84 ± 0.08	17	<0.0001
	I	U	0.96 ± 0.06	17
3. L13(I) × L3(U)	U	I	0.79 ± 0.26	20	0.071
	I	U	0.88 ± 0.13	18
4. F1(L18 × L3) × L3	U	I	0.86 ± 0.18	17	0.260
	I	U	0.92 ± 0.08	15
5. F1(L18 × L3) × L4	U	I	0.81 ± 0.20	20	<0.0001
	I	U	0.97 ± 0.02	19
6. F1(L11 × L18) × L3	U	I	0.84 ± 0.31	18	0.12
	I	U	0.89 ± 0.24	18
7. F1(L13 × L18) × L3	U	I	0.93 ± 0.07	14	0.002a
	I	U	0.91 ± 0.25	14
8. L18L11 × L3(U)	U	I	0.83 ± 0.19	18	0.002b
	I	U	0.85 ± 0.29	23
9. L18L13 × L3(U)	U	I	0.71 ± 0.34	20	0.003
	I	U	0.92 ± 0.08	17
10. L5L18(I) × L3(U)	U	I	0.66 ± 0.35	19	0.105
	I	U	0.79 ± 0.28	19
11. L4L18(I) × L3(U)	U	I	0.69 ± 0.35	16	0.279
	I	U	0.73 ± 0.32	16
12. L18 × L13	I (L13)	I (L18)	0.86 ± 0.30	19	0.556
	I (L18)	I (L13)	0.80 ± 0.33	24
13. L18 × L11	I (L11)	I (L18)	0.76 ± 0.40	27	0.820
	I (L18)	I (L11)	0.89 ± 0.23	20

Data are mean hatch rates of eggs laid over 5 days. For backcross experiments, superscripts denote source isofemale line for the Wolbachia. For crosses that used F₁, parental lines are listed in parentheses, female first. P values are for one-tailed Wilcoxon tests, with the exception of II crosses (12 and 13), which are two tailed. Statistically significant differences between reciprocal crosses at P < 0.05 are highlighted in bold.

^aThe one-sided MWU indicates that UI tend to produce lower egg hatch than do IU crosses despite UI having lower mean egg hatch than IU. This result is driven by the larger variance in egg hatch for UI (0.25 SD) vs. IU (0.07 SD)—one IU replicate produced 0% egg hatch (0/27). The lower median egg hatch of UI (0.94) vs. IU (0.99) supports this conclusion (Figure 4).

^bThis difference is highly statistically significant despite similar means as indicated by the lower median egg hatch rate of UI (0.89) vs. IU (0.98) crosses. Two replicates within the IU class produced 0% eggs hatch (0/34 and 0/36) (Figure 4).

Table 8. Wolbachia cause CI in the majority of interspecific pairings.

		N	Mean	SD	♀I × ♂I	♀I × ♂U	♀U × ♂I	♀U × ♂U
♀san × ♂tei	♀I × ♂I	44	0.81	0.20		114.67	458.83	406.43
	♀I × ♂U	44	0.77	0.21	382.70		344.16	291.76
	♀U × ♂I	44	0.54	0.29	394.95	392.76		52.40
	♀U × ♂U	44	0.61	0.23	384.95	382.70	394.95
♀tei × ♂san	♀I × ♂I	44	0.77	0.23		40.59	470.63	14.63
	♀I × ♂U	44	0.81	0.17	382.92		511.21	55.22
	♀U × ♂I	44	0.46	0.29	378.28	385.06		456.0
	♀U × ♂U	44	0.66	0.37	382.92	389.61	385.06
♀yak × ♂san	♀I × ♂I	44	0.82	0.10		65.45	240.58	32.70
	♀I × ♂U	44	0.80	0.10	376.10		175.13	98.16
	♀U × ♂I	44	0.74	0.11	376.10	376.10		273.28
	♀U × ♂U	44	0.83	0.12	376.10	376.10	376.10
♀san × ♂yak	♀I × ♂I	44	0.88	0.08		18.70	388.60	379.77
	♀I × ♂U	44	0.88	0.10	376.10		407.31	398.47
	♀U × ♂I	44	0.70	0.24	376.10	376.10		8.83
	♀U × ♂U	44	0.71	0.21	378.28	378.28	378.28
♀tei × ♂yak	♀I × ♂I	44	0.78	0.17		46.63	470.10	68.54
	♀I × ♂U	44	0.71	0.29	382.70		423.47	115.16
	♀U × ♂I	44	0.48	0.24	387.29	385.06		538.63
	♀U × ♂U	44	0.75	0.30	382.70	380.45	385.06
♀yak × ♂tei	♀I × ♂I	44	0.72	0.22		150.82	314.62	82.56
	♀I × ♂U	44	0.78	0.23	392.28		465.43	233.37
	♀U × ♂I	44	0.51	0.26	400.67	407.72		232.06
	♀U × ♂U	43	0.64	0.26	394.95	402.10	410.28

Hybrid viability of interspecific crosses are represented as the proportion of eggs that survived to adulthood. N is the number of single-pair matings that produced the mean and SD. The last four columns show our statistical analyses as 4 × 4 matrices for each species. The upper triangular matrix shows the observed Kruskal-Wallis difference. The lower triangular matrix shows the critical value required to achieve significance at P < 0.05 after correcting for multiple comparisons. For example, the mean egg-to-adult viability of ♀U × ♂I ♀tei × ♂san crosses (0.46) is significantly different from the mean egg-to-adult viability of the ♀I × ♂U ♀tei × ♂san crosses (0.81) as evidenced by the observed difference (511.21) surpassing the critical value (385.06). Statistically significant differences (P < 0.05) are indicated in boldface.

We next assessed Wolbachia effects on progeny viability, and determined whether Wolbachia infections in females generally provide protection from CI. This experiment assayed egg-to-adult viability for eggs produced by females following a single mating to a 4-day-old male. Egg-to-adult viability serves as a proxy for CI assayed by egg hatch alone. For these assays, two infected and two uninfected isofemale lines were selected from each species for a total of 12 (Table S2). We paired these isofemales lines in all possible ways, within and between species, such that any particular line was crossed to itself and the other 11 lines—this design includes one putatively incompatible (UI), and three putatively compatible crosses (II, IU, and UU). For each cross, virgin females and males were collected and maintained in isolation for 4 days. Four-day-old females were paired individually with a 4-day-old conspecific or heterospecific male in a standard fly vial containing cornmeal food. All fly transfers were performed by aspiration with no anesthesia. To ensure that mating took place, we observed all pairs for up to 8 hr until we obtained at least 10 mated pairs per line combination for intraspecific and interspecific experiments. After mating, we removed the male from the vial and allowed each mated female to oviposit for 24 hr. After 24 hr, the females were aspirated into new vials and their eggs counted. This was repeated every 24 hr for 10 days. The number of eggs laid serves as a measure of fecundity (see below). After counting the eggs in each vial, we added 1 ml of propionic acid (0.5% v/v solution) and provided a pupation substrate (Kimberly Clark, Kimwipes Delicate Task, Irving, TX). We counted the adults that emerged from each vial and calculated egg-to-adult viability as the ratio of adults to eggs laid in each vial. This viability ratio was treated as the response variable for the statistical analyses described below. We used the interspecific data to evaluate whether asymmetries in Wolbachia-associated egg-to-adult viability might contribute to postzygotic RI.

Wolbachia effects on mating behavior within and between species

To determine whether Wolbachia influence mating behavior, we conducted no-choice mating experiments en masse (Coyne et al. 2002, 2005; Matute 2010). For these experiments, we used the same 12 lines (two infected and two uninfected) used in our assays of egg-to-adult viability, and, again, we completed all possible pairings within and between species. We collected virgin males and females within 8 hr of eclosion from each of the 12 lines, and maintained each sex in isolation. After 4 days, we paired groups of ∼100 virgin females with ∼100 males in vials with cornmeal food, so that each vial contained about 200 flies. These males and females were kept together for 24 hr. After 24 hr, females from the intraspecific and interspecific experiments were dissected and their reproductive tracts were mounted in Ringer’s solution. The seminal receptacle and both spermathecae were checked for sperm. The number of mated females per vial was treated as the response variable for statistical analyses. Sample sizes are listed in Table 4 and Table 6.

Table 4. Wolbachia do not affect intraspecific mating defined as the proportion of mated females in 24 hr.

		N	Mean (%)	SD (%)	♀I × ♂I	♀U × ♂I	♀I × ♂U	♀U × ♂U
D. teissieri	♀I × ♂I	60	89.78	9.36		14.33	44.80	8.01
	♀U × ♂I	40	90.43	6.77	381.48		30.48	22.33
	♀I × ♂U	40	86.83	14.48	381.48	417.89		52.81
	♀U × ♂U	50	91.74	4.95	357.86	396.45	396.45
D. yakuba	♀I × ♂I	50	89.22	11.06		20.40	29.36	22.59
	♀U × ♂I	40	91.52	6.40	396.45		8.96	2.20
	♀I × ♂U	40	90.75	9.85	396.45	417.89		6.77
	♀U × ♂U	50	91.94	6.00	373.77	396.45	396.45
D. santomea	♀I × ♂I	50	88.70	8.68		8.50	2.03	10.69
	♀U × ♂I	40	88.80	7.90	396.45		10.53	2.19
	♀I × ♂U	40	89.65	6.30	396.45	417.89		12.71
	♀U × ♂U	40	88.83	7.65	396.45	417.89	417.89

N is the number of mass matings between sets of 100 females and 100 males that produced the mean (percentage of females mated) and SD. The last four columns show our statistical analyses as 4 × 4 matrices for each species. The upper triangular matrix shows the observed Kruskal-Wallis difference. The lower triangular matrix shows the critical value required to achieve significance at P < 0.05 after correcting for multiple comparisons. No pairwise comparison showed a statistically significant difference. Each replicate was composed of 100 females.

Table 6. Wolbachia do not affect interspecific mating defined as the proportion of mated females in 24 hr.

		N	Mean (%)	SD (%)	♀I × ♂I	♀I × ♂U	♀U × ♂I	♀U × ♂U
♀san × ♂tei	♀I × ♂I	50	1.92	6.35		68.73	46.41	39.15
	♀I × ♂U	40	0.63	1.61	396.45		22.33	29.58
	♀U × ♂I	40	1	2.53	396.45	417.89		7.26
	♀U × ♂U	50	0.80	1.81	373.77	396.45	396.45
♀tei × ♂san	♀I × ♂I	50	0.66	1.41		4.24	4.55	8.95
	♀I × ♂U	40	0.70	1.94	396.45		8.79	4.71
	♀U × ♂I	40	0.60	1.17	396.45	417.89		13.5
	♀U × ♂U	50	0.54	1.22	373.77	396.45	396.45
♀yak × ♂san	♀I × ♂I	50	33.10	14.63		17.50	9.80	7.61
	♀I × ♂U	40	31.43	15.57	396.45		7.70	25.11
	♀U × ♂I	40	30.85	11.41	396.45	417.89		17.41
	♀U × ♂U	50	33.16	10.55	373.77	396.45	396.45
♀san × ♂yak	♀I × ♂I	50	19.07	9.66		0.78	9.61	40.03
	♀I × ♂U	40	20.35	11.69	396.45		8.84	39.26
	♀U × ♂I	40	22.20	12.45	396.45	417.89		30.42
	♀U × ♂U	50	23.96	12.31	373.77	396.45	396.45
♀tei × ♂yak	♀I × ♂I	60	0	0		0	8.51	13.62
	♀I × ♂U	50	0	0	357.86		8.51	13.62
	♀U × ♂I	40	0.03	0.16	381.48	396.45		5.11
	♀U × ♂U	50	0.04	0.20	357.86	373.77	396.45
♀yak × ♂tei	♀I × ♂I	50	0.04	0.20		5.11	5.11	13.62
	♀I × ♂U	40	0.03	0.16	396.45		0	8.51
	♀U × ♂I	40	0.03	0.16	396.45	417.89		8.51
	♀U × ♂U	50	0	0	373.77	396.45	396.45

N is the number of mass matings between sets of 100 females and 100 males that produced the mean (percentage of females mated) and SD. The last four columns show our statistical analyses as 4 × 4 matrices for each species pair. The upper triangular matrix shows the observed Kruskal-Wallis difference. The lower triangular matrix shows the critical value required to achieve significance at P < 0.05 after correcting for multiple comparisons. No pairwise comparison showed a statistically significant difference. Each replicate was composed of 100 females.

Wolbachia effects on fecundity within and between species

We completed two separate experiments to evaluate Wolbachia effects on host fecundity. We first performed an intraspecific fecundity experiment where we screened N pairs of infected and uninfected isofemale lines from the same population collections described above for our initial CI screen (to avoid artifacts associated with unmated females, we report data only from the pairs in which both reciprocal crosses produced at least eight eggs over 5 days). We hypothesized that populations with the highest Wolbachia frequencies would be most likely to show Wolbachia-induced fecundity increases. To control the nuclear background, we reciprocally crossed each pair. The F₁ females were collected as virgins and placed in holding vials for 3 days. Each female was then paired with a male from the associated uninfected line to stimulate oviposition. Individual pairs were placed in vials containing a spoon with cornmeal medium and yeast paste, and allowed to lay eggs for 24 hr. Each pair was transferred to new vials every 24 hr for 5 days. The eggs laid were counted 24 hr after mating pairs were removed from each vial. We also scored egg hatch to assess viability. Sample sizes are listed in Table S3.

The second fecundity experiment evaluated the number of eggs laid by mated females in our intraspecific and interspecific egg-to-adult viability experiments, described above. The intraspecific crosses provide a measure of female fecundity following an observed single mating with a conspecific male. For the interspecific crosses, the number of eggs produced over 10 days serves as an estimate of gametic RI (Chang 2004; Matute 2010). The number of eggs laid in both intraspecific and interspecific crosses was treated as the response variable for statistical analyses. Sample sizes are listed in Table 5 and Table 7.

Table 5. Wolbachia do not affect intraspecific fecundity defined as the number of eggs laid by females following an observed mating.

		N	Mean	SD	♀I × ♂I	♀U × ♂I	♀I × ♂U	♀U × ♂U
D. teissieri	♀I × ♂I	44	71.14	11.41		52.09	35.58	57.91
	♀U × ♂I	44	75.18	12.19	387.27		16.51	5.82
	♀I × ♂U	44	73.30	9.99	387.27	387.27		22.33
	♀U × ♂U	44	74.91	11.21	387.27	387.27	387.27
D. yakuba	♀I × ♂I	44	70.05	11.76		141.77	42.39	228.73
	♀U × ♂I	44	79.55	15.39	387.27		99.39	86.95
	♀I × ♂U	44	72.91	12.51	387.27	387.27		186.34
	♀U × ♂U	44	84.14	8.75	387.27	387.27	387.27
D. santomea	♀I × ♂I	44	75.32	11.12		6.09	35.58	64.68
	♀U × ♂I	44	76.38	12.22	367.40		41.67	58.59
	♀I × ♂U	55	73.73	12.57	387.27	367.40		100.26
	♀U × ♂U	44	80.05	14.16	387.27	367.40	387.27

N is the number of single-pair matings that produced the mean and SD. The last four columns show our statistical analyses as 4 × 4 matrices for each species. The upper triangular matrix shows the observed Kruskal-Wallis difference. The lower triangular matrix shows the critical value required to achieve significance at P < 0.05 after correcting for multiple comparisons. No pairwise comparison showed a statistically significant difference.

Table 7. Wolbachia do not affect patterns of gametic isolation defined as the number of eggs laid by a single female over 10 days, following an observed interspecific mating.

		N	Mean	SD	♀I × ♂I	♀I × ♂U	♀U × ♂I	♀U × ♂U
♀san × ♂tei	♀I × ♂I	44	9.89	8.74		2.16	47.53	7.28
	♀I × ♂U	44	9.39	7.22	387.27		45.38	9.44
	♀U × ♂I	44	8.30	8.18	387.27	387.27		54.82
	♀U × ♂U	44	9.0	5.37	387.27	387.27	387.27
♀tei × ♂san	♀I × ♂I	44	9.64	7.41		39.85	38.08	70.11
	♀I × ♂U	44	11.0	8.31	387.27		77.93	109.97
	♀U × ♂I	44	8.32	6.61	387.27	387.27		32.03
	♀U × ♂U	44	7.34	6.31	387.27	387.27	387.27
♀yak × ♂san	♀I × ♂I	44	56.32	12.68		79.05	129.28	101.24
	♀I × ♂U	44	62.75	9.01	387.27		50.24	22.19
	♀U × ♂I	44	64.91	14.36	387.27	387.27		28.05
	♀U × ♂U	44	63.68	12.26	387.27	387.27	387.27
♀san × ♂yak	♀I × ♂I	44	37.77	13.11		16.77	110.59	49.23
	♀I × ♂U	44	36.57	16.38	387.27		93.82	32.45
	♀U × ♂I	44	29.55	15.68	387.27	387.27		61.36
	♀U × ♂U	44	35.05	16.07	387.27	387.27	387.27
♀tei × ♂yak	♀I × ♂I	44	10.52	6.91		39.32	16.69	4.33
	♀I × ♂U	44	9.16	6.09	387.27		56.01	43.65
	♀U × ♂I	44	11.0	6.86	387.27	387.27		12.36
	♀U × ♂U	44	11.11	7.95	387.27	387.27	387.27
♀yak × ♂tei	♀I × ♂I	44	12.02	9.62		11.06	78.94	71.12
	♀I × ♂U	44	10.98	8.47	387.27		67.89	60.06
	♀U × ♂I	44	8.48	6.94	387.27	387.27		7.83
	♀U × ♂U	43	8.65	6.62	389.51	389.51	389.51

N is the number of females that produced the mean and SD. The last four columns show our statistical analyses as 4 × 4 matrices for each species pair. The upper triangular matrix shows the observed Kruskal-Wallis difference. The lower triangular matrix shows the critical value required to achieve significance at P < 0.05 after correcting for multiple comparisons. No pairwise comparison showed a statistically significant difference.

Statistical analyses

We used parametric and nonparametric tests implemented in R version 3.1.3 (R Development Core Team 2015). Nonparametric tests were used when the data remained non-Gaussian following log and square root transformations. We used Fisher’s exact test to assess differences in Wolbachia infection frequencies among collections. For our initial egg-hatch CI experiments, we used one-sided Wilcoxon tests to assess whether UI crosses have lower egg hatch than do IU crosses, and we used two-sided Wilcoxon tests to determine whether infected D. teissieri females receive protection from Wolbachia-infected D. teissieri males. For our population screen of fecundity, we also used Wilcoxon tests to assess differences in the number of eggs laid by infected and uninfected females and their hatch rates.

To test for variation in CI intensity within the Bioko population of D. teissieri, we fit a linear model to evaluate the fixed effects of D. teissieri line and day—and their interaction—on the difference in mean daily egg hatch between IU and UI crosses. We took a similar approach to evaluate variation in CI intensity among D. teissieri-Wolbachia combinations in two backcross experiments. The first experiment compared lines that share nuclear backgrounds but carry different Wolbachia; the second experiment compared lines that carry the same Wolbachia but have different nuclear backgrounds. For each experiment, we fit a linear model to evaluate the fixed effects of line and day, and their interaction, on the difference in mean daily egg hatch between IU and UI crosses.

Finally, we used a Kruskal-Wallis rank-sum test with multiple post hoc comparisons to test several hypotheses: (1) that within host species, Wolbachia affect mating behavior, the number of eggs laid by females following an observed mating, and egg-to-adult viability; and (2) that between species, Wolbachia affect the magnitude of behavioral, gametic, and postzygotic RI. For these analyses, line data were first pooled based on infection status (I and U), which resulted in 36 levels of “cross type”; P values were adjusted for multiple comparisons (630 possible pairwise comparisons) using the kruskalmc function [R package “pgirmess,” (Siegel and Castellan 1988, pp. 213–214; Giraudoux 2013)]. In total, 18 intraspecific pairwise comparisons (six per species), and 36 interspecific pairwise comparisons (six per type of interspecific cross) were conducted. All analyses were completed using the kruskalmc function (R package “pgirmess,” Giraudoux 2013).

Data availability

Sequences for the Wolbachia genes gatB, coxA, hcpA, ftsZ and fbpA have been deposited in GenBank (http://www.ncbi.nlm.nih.gov/Genbank) under accession numbers KX584056–KX584095. All data are archived in Dryad (http://datadryad.org/resource/doi:10.5061/dryad.vh396).

Results

Wolbachia identity and frequency variation in nature

Sequencing five MLST protein-coding genes (gatB, coxA, hcpA, ftsZ, and fbpA)—from two Wolbachia-infected flies from each population of each species—revealed no nucleotide variation among populations or species, consistent with previous assertions of shared cytoplasms. In contrast, genomic analyses (M. Turelli, W. R. Conner, D. R. Matute, D. A. Turissini, and B. S. Cooper, unpublished results) show distinct Wolbachia in each species with variation largely concordant with host phylogenies. Our data suggest that relatively recent introgression or horizontal transmission renders the MLST loci uninformative for classifying yakuba complex Wolbachia.

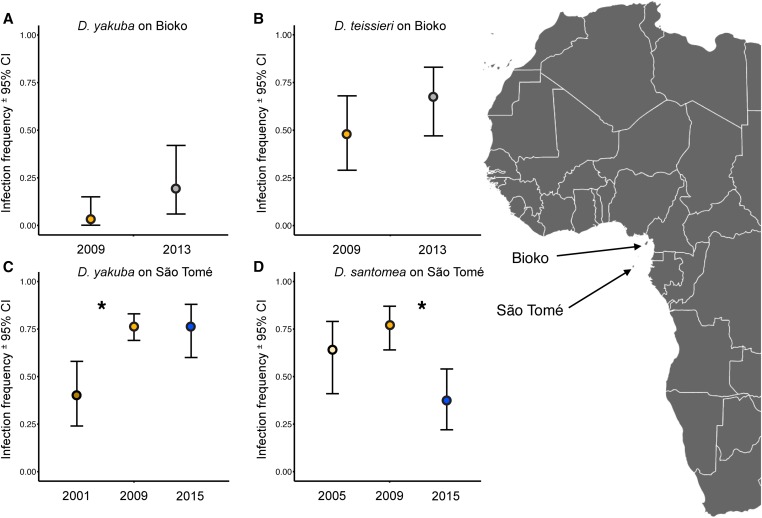
We estimated Wolbachia frequencies in collections of D. yakuba from Bioko and São Tomé, D. santomea from São Tomé, and D. teissieri from Bioko (Figure 1 and Table 1). In D. yakuba on São Tomé, Wolbachia frequencies changed from 0.4 (N = 35) in 2001 to 0.76 (N = 155) in 2009 (Fisher’s exact test, P < 0.001). In 2015, the infection frequency was still 0.76 (N = 41) for D. yakuba in São Tomé. In contrast, for D. santomea, the frequency increase between 2005 and 2009 was not statistically significant; but this was followed by a statistically significant decrease from 0.77 (N = 57) in 2009 to 0.37 (N = 38) in 2015 (Fisher’s exact test, P = 0.0001). On Bioko between 2009 and 2013, the differences in infection frequencies for D. yakuba and D. teissieri were not statistically significant (D. yakuba: Fisher’s exact test, P = 0.06; D. teissieri: Fisher’s exact test, P = 0.19). For D. yakuba in 2009, we found large infection-frequency differences between islands—0.03 on Bioko (N = 36) vs. 0.76 on São Tomé (N = 155) (Fisher’s exact test, P < 0.0001). Finally, Wolbachia frequencies (denoted p) within D. yakuba or D. santomea did not differ appreciably between low and high altitudes on Pico de São Tomé in 2015. For D. yakuba at low elevations (∼450 m), we found p = 0.80 (N = 20); whereas at the highest elevation of its range (∼1150 m) in the midlands of Pico de São Tomé, p = 0.71 (N = 21) (Fisher’s exact test, P = 0.72). Similarly, for D. santomea, p = 0.22 (N = 18) from the lowest elevations (∼1150 m) of their range, in the midlands of Pico de São Tomé, whereas p = 0.50 (N = 20) at our highest sampled elevations (∼1420 m) (Fisher’s exact test, P = 0.10). Thus, while infection frequencies vary through time and among islands, more extensive sampling will be required to determine whether Wolbachia frequencies covary with altitude or its correlates such as temperature and humidity (Keller et al. 2013; Adrion et al. 2015).

Figure 1.

Wolbachia infection frequencies in west Africa. On Bioko, Wolbachia infection frequencies did not differ statistically through time for (A) D. yakuba or (B) D. teissieri. Infection frequencies did differ statistically significantly through time on São Tomé for (C) D. yakuba between 2001 (0.4) and 2009 (0.76) (P < 0.001), and for (D) D. santomea between 2009 (0.77) and 2015 (0.37) (P < 0.0001). In. D. yakuba, Wolbachia frequencies differed spatially in 2009 between Bioko (0.03) and São Tomé (0.76) (P < 0.0001). Data are infection frequencies ± exact 95% binomial confidence intervals. An asterisk denotes a statistically significant difference between years.

Fitness effects of Wolbachia on hosts

Wolbachia cause weak CI in all three yakuba complex species:

To assess Wolbachia effects on egg hatch, we screened N = 16 isofemale pairs from the 2013 Bioko collection of D. teissieri, N = 19 from the 2009 São Tomé collection of D. santomea, and N = 17 from the 2009 São Tomé collection of D. yakuba. The screen of the 2013 collection of Bioko D. teissieri found marginally statistically significant differences in egg hatch between UI (0.70 ± 0.30 SD, N = 16) and IU (0.81 ± 0.31 SD, N = 16) crosses (Figure 2). However, our analogous screens of 2009 São Tomé collections of D. santomea and D. yakuba found no statistically significant differences in egg hatch rates between UI and IU crosses (D. santomea: one-tailed MWU test, W = 242.5, P = 0.97; D. yakuba: one-tailed MWU test, W = 124.5, P = 0.50).

Figure 2.

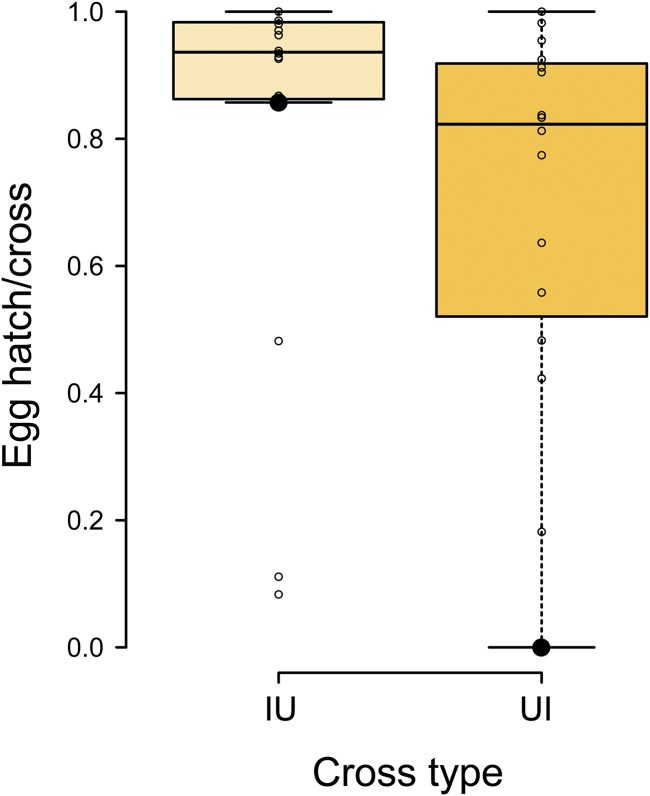
Variation in egg hatch over 3 days among unreplicated matings between pairs of infected and uninfected D. teissieri isofemale lines. IU crosses produce moderately higher egg hatch (0.81 ± 0.31 SD, N = 16) than do UI (0.70 ± 0.30 SD, N = 16; one-tailed MWU test, W = 75.5, P = 0.048). Lines within boxplots denote medians and boxes span the first and third quartiles. The large bold sample points within each cross type represent the egg hatch of the L18 (infected) by L3 (uninfected) cross, initially identified as a CI candidate.

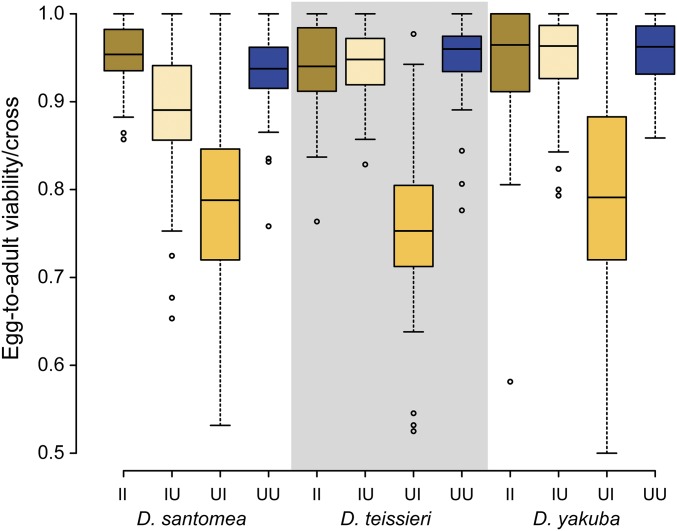
In contrast to these unreplicated reciprocal crosses between many pairs of U and I isofemale lines, our second CI experiment assayed egg-to-adult viability, rather than egg hatch, and replicated all four infection-status crosses (II, IU, UI, and UU) between two infected and two uninfected isofemale lines within each species (N = 539 total females). These experiments confirm statistically significant CI in D. teissieri with UI having an ∼19% reduction in egg-to-adult viability (0.75 ± 0.09 SD, N = 44) relative to IU (0.94 ± 0.04 SD, N = 44), see Table 2 for the statistical analyses. As expected, the egg-to-adult viability from the incompatible UI cross is significantly lower than the egg-to-adult viability from all three crosses expected to be compatible: IU, UU, and II. We also find statistically significant CI in D. yakuba. The UI crosses have statistically significant reductions in egg-to-adult viability (0.79 ± 0.11 SD, N = 44) relative to IU (0.95 ± 0.06 SD, N = 44) and the II and UU crosses (Figure 3 and Table 2). The D. santomea results are more complex, but also indicate statistically significant CI. Although UI crosses generated significantly lower egg-to-adult viability (0.79 ± 0.10 SD, N = 55) than II (0.95 ± 0.04 SD, N = 44) and UU (0.93 ± 0.05 SD, N = 44) crosses, the reduction of about 9% in egg-to-adult viability of UI relative to IU (0.88 ± 0.08 SD, N = 55) was not statistically significant (Table 2). The UI vs. IU comparison is nonsignificant because of lower than expected egg-to-adult viability in IU (Figure 3). Finally, infected females are protected from infected males, as indicated by the statistically significantly higher egg-to-adult viability of the II vs. UI cross classes within each host species (Figure 3 and Table 2).

Figure 3.

Wolbachia cause CI in D. santomea, D. teissieri, and D. yakuba. Of the four cross types, egg-to-adult viability is lowest for UI crosses in all species. For all three species, II crosses are statistically indistinguishable from UU crosses, indicating that Wolbachia infected females are protected from CI. Lines within boxplots denote medians and boxes span the first and third quartiles. The gray shaded boxes only serve to increase the clarity of the comparisons. Means, SD, sample sizes, and statistics are reported in Table 2.

Taken together, our experiments indicate that Wolbachia cause CI in all three species, with D. teissieri showing the largest effect size, and the smallest variance, for UI and IU crosses. The incompatibility parameter H in the standard discrete-generation model of CI (Hoffmann et al. 1990; Turelli 1994) can be estimated from either hatch rate or egg-to-adult viability (cf. Turelli 2010). If we take the ratio of the egg-to-adult viability observed for the incompatible UI cross to the (unweighted) average egg-to-adult viability from the three crosses expected to be compatible (IU, II, and UU), we get H = 0.80 (95% BC_a interval: 0.77, 0.83) for D. teissieri, H = 0.84 (95% BC_a interval: 0.80, 0.87) for D. yakuba, and H = 0.85 (95% BC_a interval: 0.82, 0.88) for D. santomea. [BC_a confidence intervals were calculated using the two-sample acceleration constant given by equation 15.36 of Efron and Tibshirani (1993)]. Although similar, the relative magnitude of the H estimates reflects the ease with which CI was detected in each species. We consider below the possible consequences of IU crosses producing lower egg-to-adult viability than II and UU.

In D. teissieri from Bioko, only some paired lines show statistically significant CI:

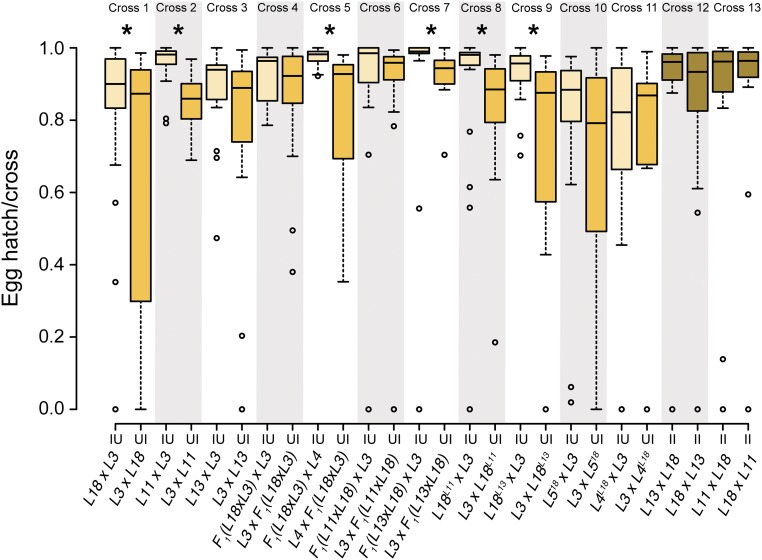
Our initial screen of D. teissieri on Bioko detected a reduction of about 11% in egg hatch of UI (0.70 ± 0.30 SD) relative to IU (0.81 ± 0.31 SD) and suggested significant variation in CI among randomly paired lines (Figure 2). To explore D. teissieri CI further, we replicated the IU (N = 29) and UI (N = 28) crosses for the pair of Bioko isofemale lines—infected line L18 and uninfected line L3—that showed the strongest indication of CI in our initial screen (large black points in Figure 2). The UI crosses showed significantly reduced egg hatch relative to the IU crosses (0.61 ± 0.40 SD vs. 0.84 ± 0.22 SD; one-tailed MWU test, W = 285, P = 0.028; Figure 4 and Table 3, cross 1).

Figure 4.

Egg hatch over 5 days for D. teissieri experiments exploring host-genotype and Wolbachia effects. Cross designation at the top of the plot corresponds to cross number in Table 3. Lines within boxplots denote medians and boxes span the first and third quartiles. Asterisks denote statistical significance at P < 0.05. The alternating gray-shaded boxes indicate the pairwise comparisons. Means, SD, sample sizes, and statistics are reported in Table 3.

To determine whether CI intensity varies significantly among lines, we randomly selected two other infected genotypes (L11 and L13), and reciprocally crossed each with uninfected line L3. Both lines produced lower average egg hatch from UI vs. IU crosses, and the difference was statistically significant for L11 (Figure 4 and Table 3, cross 2, 0.84 ± 0.08 SD vs. 0.96 ± 0.06; one-tailed MWU test, W = 32, P < 0.0001), but not L13 (Figure 4 and Table 3, cross 3, 0.79 ± 0.26 SD vs. 0.88 ± 0.13; one-tailed MWU test, W = 129, P = 0.07). These results are difficult to interpret because the results from the compatible cross IU differ more than do the results from the UI crosses. Hence, we sought a direct test of statistical heterogeneity. Because egg hatch is not normally distributed, we calculated the difference between the mean IU and UI egg hatch for each day. Because very few eggs were laid on day 1, we included only egg hatch data from days 2–5. This egg-hatch difference was approximately normally distributed (Shapiro-Wilk test, W = 0.966, P = 0.867), which enabled us to construct a linear model to evaluate the fixed effects of D. teissieri line and egg-lay day on CI intensity. We found no significant effects, and, specifically, the fixed effect of D. teissieri line did not significantly affect egg hatch reduction (F_2,6 = 4.26, P = 0.07). Thus, the apparent heterogeneity in crosses 1–3 of Figure 4 and Table 3 may not be real. To look more carefully for heterogeneity, additional tests were performed.

In D. teissieri, Wolbachia and host effects modulate CI intensity:

We completed several additional experiments addressing the control of CI intensity in D. teissieri. We first generated F₁ hybrids using females from infected line L18, and males from uninfected line L3. These F₁ genotypes carrying the L18 Wolbachia were reciprocally crossed to L3 and to another uninfected line (L4) to test for CI. These crosses sought to determine whether the relatively intense CI that we observed in the natural L18 genotype persists in an F₁ nuclear background carrying the L18 Wolbachia. We found statistically significant CI when the (L18 × L3) F₁ were crossed to L4 but not L3 (Figure 4 and Table 3, crosses 4 and 5). This heterogeneity seems to depend on the relatively low egg hatch observed in the IU cross involving uninfected L3 males and infected (L18 × L3) F₁ females. We next crossed males from L18 to L11 and L13 females to generate F₁ hybrids for the L18 host genotype, containing Wolbachia from lines that either did (L11), or did not (L13), produce statistically significant CI in our original tests (crosses 6 and 7, Figure 4 and Table 3). When reciprocally crossed to uninfected line L3, F₁ offspring carrying the L11 cytoplasm do not produce statistically significant CI (Figure 4 and Table 3; one-tailed MWU test, W = 117, P = 0.12); whereas F₁ offspring carrying the L13 cytoplasm did cause statistically significant CI, although cross replicates varied greatly (Figure 4 and Table 3; one-tailed MWU test, W = 49, P = 0.002). These results suggest that both Wolbachia and host variation may modulate CI intensity.

To explore possible variation in Wolbachia effects on CI intensity more carefully, we backcrossed Wolbachia from L11 and L13 into the L18 isofemale line for four generations. These backcross composites, denoted L18^L11 and L18^L13 were reciprocally crossed to uninfected line L3 to assess CI (crosses 8 and 9, Figure 4 and Table 3). When placed in the L18 nuclear background, the Wolbachia from L13 now show strong CI with a 21.4% reduction in egg hatch of UI crosses (0.71 ± 0.34 SD, N = 20) relative to IU crosses (0.92 ± 0.08 SD, N = 17) (Figure 4 and Table 3; one-tailed MWU test, W = 79, P = 0.003). In contrast, Wolbachia from L11 cause only a 2.5% reduction when paired with the L18 nuclear background, although this difference between UI (0.83 ± 0.19 SD, N = 18) and IU (0.85 ± 0.29 SD, N = 23) remains statistically significant (Figure 4 and Table 3; one-tailed MWU test, W = 96, P = 0.002). To determine if these differences in CI intensity are statistically significant, we calculated mean daily egg hatch for IU and UI using L3 as the uninfected line and L18^L13, L18^L11, and naturally infected line L18 (denoted L18^L18) as the infected lines. The three infected lines share essentially the same nuclear backgrounds, but carry different Wolbachia. Because egg hatch is not normally distributed, we took the difference between the mean IU and UI egg hatch for each day (omitting day 1 because relatively few eggs were laid). This egg hatch difference was approximately normally distributed (Shapiro-Wilk test, W = 0.953, P = 0.676), which enabled us to construct a linear model to evaluate the fixed effects of line (L18^L13, L18^L11, and L18^L18) and egg-lay day—and their interactions—on CI intensity (i.e., comparing crosses 1, 8, and 9 in Figure 4 and Table 3). Only line had a statistically significant effect on egg hatch reduction (F_2,6 = 17.99, P = 0.003). These data confirm that Wolbachia variation modulates CI intensity in D. teissieri.

We complemented this first backcross experiment with a second experiment to assess whether nuclear genotype also modulates CI intensity. For these experiments, we introgressed the L18 cytoplasm into two uninfected D. teissieri nuclear backgrounds, L4 and L5, for four generations. We then reciprocally crossed these backcross lines with uninfected line L3, which was susceptible to CI caused by L18^L18. The reduced egg hatch observed for UI relative to IU crosses was no longer statistically significant for either L4^L18 or L5^L18 (Figure 4 and Table 3; one-tailed MWU test, W = 137, P = 0.11 for L5^L18; one-tailed MWU test, W = 112, P = 0.28 for L4^L18). To determine if these differences in CI intensity are statistically significant among our reciprocal crosses, we took the same approach as above and calculated mean daily egg hatch for IU and UI with L3 as U and L4^L18, L5^L18, and L18^L18 as I. Again, the differences in egg hatch were approximately normally distributed (Shapiro-Wilk test, W = 0.959, P = 0.772), and we constructed a linear model to evaluate the fixed effects of line (now focused on differences in host backgrounds) and egg-lay day—and their interactions—on CI intensity (i.e., comparing crosses 1, 10, and 11 in Figure 4 and Table 3). As in our backcrosses focused on Wolbachia variation, only line had a statistically significant effect on egg hatch reduction (F_2,6 = 6.38, P = 0.03), confirming that nuclear genotype also modulates CI intensity in D. teissieri.

We can use egg hatch data to estimate the incompatibility parameter H in the standard discrete-generation model of CI (Hoffman et al. 1990; Turelli 1994). Taking the ratio of the egg hatch observed for all of the incompatible UI crosses to the compatible IU and II crosses presented in Table 3, we get H = 0.88 (95% BC_a interval: 0.85, 0.90). Our confidence interval for this H estimate is nonoverlapping with our estimate of H from the egg-to-adult viability experiment in D. teissieri, H = 0.80 (95% BC_a interval: 0.77, 0.83). Thus, we cannot rule out effects of Wolbachia on larval or pupal viability. We can also estimate H for each of the 5 days of these experiments to evaluate any effect of male age on CI as observed in D. melanogaster (Reynolds and Hoffmann 2002). Estimates of H were remarkably similar across days (day 1, H = 0.85, 95% BC_a intervals: 0.70, 1.03; day 2, H = 0.89, 95% BC_a intervals: 0.83, 0.95; day 3, H = 0.89, 95% BC_a intervals: 0.84, 0.94; day 4, H = 0.86, 95% BC_a intervals: 0.81, 0.92; day 5, H = 0.90, 95% BC_a intervals: 0.84, 0.96). These data suggest that male age has little effect on CI in D. teissieri.

In D. teissieri, Wolbachia infection seems to generally protect from CI:

Given that Wolbachia and host genotypes seem to differ in the levels of CI produced, we asked whether Wolbachia infection generally confers resistance to CI. Our egg-to-adult viability CI experiments indicated that the II cross classes have higher egg-to-adult viability than do the UI cross classes, which suggests that infected females receive protection from CI (Figure 3 and Table 2). We reciprocally crossed L18 with L13 and L11, then measured egg hatch (Figure 4 and Table 3, crosses 12 and 13). Neither comparison indicated CI (Figure 4 and Table 3; two-tailed MWU test, W = 252.5, P = 0.56 for L13; two-tailed MWU test, W = 259, P = 0.82 for L11).

Wolbachia do not generate assortative mating in any yakuba host species:

To evaluate Wolbachia effects on intraspecific mating behavior, we paired males and females from the 12 lines used in our earlier experiments (Table S2), in all possible ways within species, and estimated the proportion of females mated after 24 hr (N = 540 vials; 54,000 individual females). We tested whether Wolbachia status leads to assortative mating within species (e.g., discrimination against infected males by uninfected females). We found no statistically significant differences among cross types (Table 4), indicating that Wolbachia did not affect the proportion of mated females within 24 hr in our no-choice mating experiments.

Wolbachia do not enhance female fecundity in any yakuba host species:

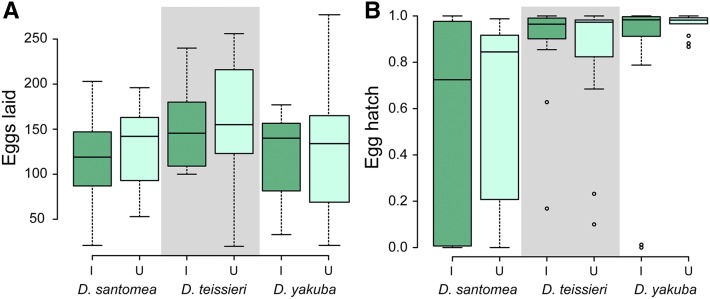
Effects of Wolbachia on host fecundity have been observed in D. simulans (Weeks et al. 2007), and also in D. mauritiana—for the latter, infected females laid four times as many eggs as uninfected females (Fast et al. 2011). Such fecundity effects could generate F(1−μ) > 1 and explain increases in Wolbachia from low frequencies. To test for Wolbachia effects on fecundity, host fecundity was assayed in two ways. We first considered unreplicated single-pair reciprocal crosses between infected and uninfected isofemale lines sampled from the individual populations of D. teissieri (N = 18 pairs), D. santomea (N = 21 pairs), and D. yakuba (N = 14 pairs) described above for our initial CI population screens. For all three species, we found no statistically significant differences in either number of eggs laid or egg hatch from I and U females generated from independent reciprocal crosses (Figure 5 and Table S3). We then replicated all possible crosses between the 12 genotypes used in previous experiments, and measured the number of eggs laid by mated females over 10 days (Table S2). As with our initial fecundity experiments, we found no statistically significant intraspecific effects of Wolbachia on the number of eggs laid (N = 40,732 counted eggs) in our experiments (Table 5).

Figure 5.

Wolbachia do not affect components of fecundity of unreplicated single-pairs in any of the three D. yakuba complex hosts. (A) Wolbachia do not affect the number of eggs laid by yakuba complex species over 5 days. (B) Wolbachia do not affect the hatch rates of eggs laid by infected and uninfected females over 5 days. I denotes infected and U denotes uninfected host females. Lines within boxplots denote medians and boxes span the first and third quartiles. The gray boxes only serve to increase the clarity of the comparisons.

Despite the lack of statistical significance for individual comparisons, it is notable that, for all three species in our second experiment, both sets of crosses that used uninfected females (UU and UI) yielded higher mean egg numbers than either of the crosses using infected females (II and IU). The probability of this pattern arising by chance for all three species is [(1/2)(1/3)]³ = 1/216, which suggests that Wolbachia infections may lower fecundity slightly, but significantly.

Little contribution of Wolbachia to the reproductive isolation of hosts

Wolbachia have little apparent effect on premating isolation:

To evaluate Wolbachia effects on interspecific mating behavior, we paired males and females from the 12 lines used in our earlier experiments (Table S2), in all possible ways between species, and estimated the proportion of females mated after 24 hr (N = 1100 vials; 110,000 individual females). We tested whether Wolbachia affect the magnitude of behavioral RI in any of the interspecific crosses. Behavioral isolation is the main source of RI in the yakuba species group, and is accountable for stopping 50% of the possible gene flow between species (Matute and Coyne 2010). Neither the Wolbachia infection status of females, nor that of males, influenced the proportion of females mated after 24 hr (Table 6). These data suggest that Wolbachia infections do not contribute to behavioral RI between species.

Wolbachia do not contribute to gametic isolation:

We evaluated whether Wolbachia contribute to gametic RI by completing all of the possible interspecific crosses between our 12 exemplar lines (Table S2). We evaluated the number of eggs laid by females over 10 days following an observed mating (N = 23,812 counted eggs), which serves as a proxy of noncompetitive gametic isolation (Chang 2004). We found that the infection status of neither the male nor the female influenced the magnitude of gametic RI in any of the possible comparisons (Table 7). Thus, while gametic isolation is an important barrier to gene flow between species in the yakuba complex (Matute 2010), Wolbachia do not influence the magnitude of this RI.

Wolbachia cause interspecific CI, but contribute little to postzygotic isolation:

Finally, we evaluated whether Wolbachia cause CI in interspecific pairings; and, if so, whether CI generates asymmetries in egg-to-adult viability that could contribute to postzygotic RI. Again, these experiments paired the same 12 lines in all possible ways (Table S2). We see a general pattern of interspecific CI in that the UI crosses show the lowest egg-to-adult viability within the four classes of crosses done for each comparison (N = 1055 total females) (Table 8). The probability that this pattern arises by chance is (1/4)⁶ = 1/4096. We identified statistically significant reductions in the egg-to-adult viability of UI relative to IU for four of the six interspecific comparisons: the UI crosses (0.46 ± 0.29 SD, N = 44) vs. IU crosses (0.81 ± 0.17 SD, N = 44) of ♀tei × ♂san, the UI (0.70 ± 0.24, N = 44) vs. IU crosses (0.88 ± 0.10 SD, N = 44) of ♀san × ♂yak, the UI crosses (0.48 ± 0.24 SD, N = 44) vs. IU crosses (0.71 ± 0.29 SD, N = 44) of ♀tei × ♂yak, and the UI crosses (0.51 ± 0.26 SD, N = 44) vs. IU crosses (0.78 ± 0.23 SD, N = 44) of ♀yak × ♂tei all differed significantly in the direction expected under CI. For ♀san × ♂tei, the egg-to-adult viability of UI (0.54 ± 0.29, N = 44) was not statistically significantly lower than IU (0.77 ± 0.21, N = 44), but was statistically significantly lower than the II crosses (0.81 ± 0.20, N = 44), indicating apparent CI. While the ♀yak × ♂san UI had the lowest egg-to-adult viability of the four cross types, this reduction was not statistically significant (Table 8). For all cases with statistically significant CI, the mean egg-to-adult viability from II crosses is equal to or higher than that from UU crosses, indicating that infected females are generally protected from interspecific CI (Table 8). Although expected to be equivalent, we find that the mean egg-to-adult viabilities differ erratically among the three “compatible” crosses (II, IU, and UU; Table 8). Finally, when we observed statistically significant CI in the intraspecific and interspecific experiments, the reduction in egg-to-adult viability is similar for intraspecific (ranging from 15 to 19%) and interspecific (ranging from 18 to 35%) crosses, with ♀tei × ♂san having the greatest reduction (35%) of all reciprocal crosses (Table 2 and Table 8).

Our results indicate that Wolbachia-infected D. yakuba complex females are protected from the pervasive intraspecific and interspecific CI experienced by uninfected females (Table 2, Table 3, and Table 8). An obvious question is whether CI contributes to postzygotic RI, and especially between the sister species D. yakuba and D. santomea on São Tomé. UI crosses between ♀san × ♂yak have an ∼18% reduction in egg-to-adult viability relative to the IU crosses (Table 8). In contrast, the UI crosses between ♀yak × ♂san produce a statistically nonsignificant reduction in egg-to-adult viability of 6% relative to the IU crosses. While not statistically significant, this reduction of D. yakuba egg-to-adult viability may be biologically significant. The ♀san × ♂yak UU crosses had particularly low egg-to-adult viability (0.71 ± 0.21), which more closely resembled UI (0.70 ± 0.24) than IU (0.88 ± 0.10) or II (0.88 ± 0.08). Thus, it is unclear whether asymmetries exist for CI intensity. Irrespective of CI asymmetry, CI could contribute to RI asymmetry through interspecific differences in infection frequencies. In 2015, Wolbachia frequencies in São Tomé populations of D. yakuba and D. santomea were 0.76 [with 95% confidence interval (0.60, 0.88)] and 0.37 [with 95% confidence interval (0.22, 0.54)], respectively. Thus ♀san × ♂yak crosses were more likely to suffer from CI than are ♀yak × ♂san crosses, because of both differences in CI intensity and infection frequencies. However, the significant temporal fluctuations in infection frequencies we document also suggest that this asymmetry will not persist.

Discussion

How Wolbachia affect host fitness, and the extent to which Wolbachia influence RI between host species is not well understood. Our analysis of Wolbachia effects on yakuba complex hosts found pervasive weak CI, both within and between host species. In D. teissieri, CI intensity seems to depend on both host and Wolbachia variation. Wolbachia infections in females provide protection from both intraspecific and interspecific CI. Male age seems to have no effect on CI intensity, at least for D. teissieri. Lower estimates of relative hatch rate, H, determined from egg-to-adult viability experiments vs. egg hatch alone suggest that Wolbachia may affect larval or pupal viability. Additional data are needed to test this hypothesis.

Our large-scale intraspecific and interspecific experiments reveal that Wolbachia have seemingly no effect on mating behavior or fecundity, within or between species. Hence, Wolbachia do not seem to contribute to premating or gametic RI between yakuba complex hosts. We observe statistically significant temporal and spatial variation in Wolbachia infections. For example, infection frequencies increased significantly in D. yakuba, and decreased significantly in D. santomea on São Tomé between 2009 and 2015. These frequency fluctuations could generate asymmetries in the proportion of females protected from interspecific CI, and influence postzygotic RI. However, these same fluctuations suggest that asymmetries in protection from CI will not persist; and thus, it seems unlikely that Wolbachia influence patterns of postzygotic RI. Below we discuss the consequences of our discoveries and observations.

Wolbachia in the yakuba complex cause CI, but do not affect mating behavior or fecundity

Based on relatively few crosses, the yakuba complex Wolbachia were previously characterized as not causing CI (Charlat et al. 2004; Zabalou et al. 2004). Yet, the Wolbachia from D. teissieri caused significant CI when introgressed into D. simulans, whereas the Wolbachia from D. santomea or D. yakuba did not (Martinez et al. 2014). This anomaly led us to screen many independent reciprocal crosses between Wolbachia-infected and uninfected isofemale lines for CI. While these initial screens of unreplicated single-pair reciprocal crosses failed to identify detectable CI in D. santomea or D. yakuba, we did find statistically significant CI in D. teissieri that seems to vary with Wolbachia and host genotype. Future analysis of many additional lines will be required to assess the extent of this variation. Our egg-to-adult viability experiments confirmed CI in D. teissieri and found CI in D. yakuba. For D. santomea, the UI crosses had lower egg-to-adult viability than did the II and UU crosses, but the UI crosses did not differ statistically from the IU crosses. These results demonstrate the challenge of characterizing weak CI that may occur only with certain host-Wolbachia combinations. For our initial screens, we reciprocally mated many paired lines without replication, while our egg-to-adult viability experiments highly replicated crosses between a few lines, giving us more power to detect relatively weak CI. Another possibility is that egg-to-adult viability experiments reveal more CI because Wolbachia decrease larval or pupal viability in F₁ from UI crosses. We know of no direct evidence for such effects, but the lower H value we estimated from egg-to-adult viability is consistent with them. Wolbachia can impact larval and pupal viability, but the effects seem purely maternal (Hoffmann et al. 1990; Olsen et al. 2001).

Our interspecific crosses revealed a general pattern of CI, although not all reductions in egg-to-adult viability were statistically significant. For all pairings that produced statistically significant CI, we also observed that Wolbachia in females (II crosses) rescued the egg-to-adult viability of UI crosses with the exception of one—the ♀yak × ♂tei pairing—where the 21% recovery of egg-to-adult viability was statistically nonsignificant. Additional replication is needed to determine whether this statistically nonsignificant difference between II and UI crosses is biologically relevant.

Wolbachia have been found to affect host fitness in other ways, for example, through nutritional supplementation, viral protection, and fecundity effects (Weeks et al. 2007; Teixeira et al. 2008; Brownlie et al. 2009; Fast et al. 2011; Martinez et al. 2014; Cattel et al. 2016a). Our large crossing experiments found no apparent support for Wolbachia effects on mating behavior, which is in line with results for D. simulans and D. melanogaster (de Crespigny and Wedell 2007; Arbuthnott et al. 2016), although some evidence exists that Wolbachia influence male mating rates in both of these species (de Crespigny et al. 2006). Similarly, we found no effect of Wolbachia on the fecundity of host females in either our screen of independent pairs, or in our analysis of female fecundity following an observed mating. Thus, while Wolbachia clearly manipulate host reproduction, the factors that may produce F(1–μ) > 1, and enable spread from low frequencies, remain unknown in the yakuba complex.

Host and Wolbachia variation modulates CI

The statistically significant variation in CI intensity observed in our 2013 sample of the Bioko population of D. teissieri after introgression (cross 1 vs. 8–11 in Figure 4 and Table 3) indicates that both Wolbachia and host modulate CI. Interspecific modulation of Wolbachia reproductive manipulations is well documented; for example, wMel causes limited CI in very young males, but induces strong CI in D. simulans backgrounds (Poinsot et al. 1998) and complete CI in Ae. aegypti backgrounds (Walker et al. 2011). Introgression of D. recens Wolbachia into D. subquinaria turns a CI-causing variant into a male killer (Jaenike 2007). In the yakuba complex, Wolbachia from D. teissieri introgressed into D. simulans caused CI (Martinez et al. 2014), which led us to hypothesize that introgressing D. teissieri Wolbachia into different D. teissieri backgrounds might reveal intraspecific host modulation of CI. Our data support this hypothesis and also reveal that Wolbachia variants affect CI intensity, as shown in D. simulans by Hoffmann and Turelli (1988) and Carrington et al. (2011). Using reciprocal introgressions, Cattel et al. (2016a) demonstrate that interactions between host and Wolbachia variants modulate virus protection in D. suzukii. Our data suggest that host–Wolbachia interactions are also likely to affect CI intensity. Although our experiments suggest that Wolbachia and nuclear effects may interact to determine CI intensity, a formal demonstration requires reciprocal introgressions, which are now underway.

We also found suggestive evidence for variation in susceptibility of uninfected lines in our analysis of (L18 × L3) F₁ genotypes. When reciprocally crossed to uninfected line L3, we did not detect CI, but, when reciprocally crossed to L4, we detected statistically significant CI. Further experiments are needed to document variation in susceptibility of uninfected females. To our knowledge, no such intraspecific variation has yet been found (Hoffmann and Turelli 1988; Carrington et al. 2011). In strong-CI systems, with imperfect maternal transmission, such as wRi in D. simulans, there is persistent selection for reduced susceptibility to CI (Turelli 1994). Yet, there is no evidence for reduced susceptibility to CI in California D. simulans after > 30 years––and probably more than 300 generations––of selection in very large natural populations (Carrington et al. 2011). Similarly, Jaenike and Dyer (2008) argue that D. innubila has not evolved resistance to Wolbachia-induced male killing after thousands of years. Understanding the constraints that govern whether Wolbachia-induced reproductive manipulations can be suppressed by host evolution is clearly important for disease-control applications of Wolbachia (Bull and Turelli 2013).

Wolbachia frequency variation in the yakuba complex

Extensive sampling of the yakuba complex revealed Wolbachia frequency variation through space and time. Wolbachia frequencies increased in D. yakuba, and decreased in D. santomea between 2009 and 2015 on São Tomé, although within each species infection frequencies did not differ between low and high altitudes on Pico de São Tomé in 2015. Additional sampling will be required to determine whether Wolbachia frequencies vary within years. In 2009, Wolbachia frequencies in D. yakuba also varied spatially with 76% of the individuals on São Tomé, but only 3% on Bioko having Wolbachia. Temporal frequency fluctuations have also been observed in D. simulans where in an Ivanhoe, CA population, wRi frequency dropped from an apparent equilibrium of 93% in 1992 to 80% in 1993 (Turelli and Hoffmann 1995). Nevertheless, wRi frequencies have remained at about 93% for over a decade in California (Carrington et al. 2011), and now seem to be near the same equilibrium frequency in Eastern Australia (Kriesner et al. 2013). Rapid frequency variation has been seen for wSuz in D. suzukii, with frequencies increasing from 18 to 58% in <1 year in a Winters, CA—wSuz frequencies also varied spatially with frequencies significantly lower in Rochester, NY, than in Winters, CA (Hamm et al. 2014). Extensive spatial variation has also been documented for wSuz in European populations (Cattel et al. 2016b). In contrast to the anomalous variation of wRi in Ivanhoe, CA and wSuz in Winters, CA, and Europe, wMel shows a systematic frequency cline with latitude in eastern Australian populations of D. melanogaster that has persisted for 15 years. The cline is due in part to fitness costs of Wolbachia on D. melanogaster in colder environments (Kriesner et al. 2016). This pattern is partially replicated in North and Central America, but the spatial distributions are much more erratic in Eurasia and Africa. Clearly, Wolbachia frequency estimates of one or a few collections provide a snapshot of Wolbachia frequencies that may or may not be relatively constant.

The relative constancy of wRi frequencies in California and eastern Australia seems attributable to an equilibrium between relatively strong CI driving frequencies toward one vs. imperfect maternal transmission, which continually introduces uninfected individuals (Hoffmann et al. 1990; Turelli and Hoffmann 1995; Carrington et al. 2011; Kriesner et al. 2013). When CI reduces hatch rates from UI crosses to ≤ 0.5 relative to the three compatible crosses, the CI-imperfect-transmission equilibrium frequencies are relatively insensitive to variation in CI intensity, imperfect transmission rates, and relative fecundity of infected females (cf. Jaenike 2009; Kriesner et al. 2013, 2016). In contrast, when CI reduces hatch rates by only about 20% or less, as expected in nature for the yakuba complex species, equilibria are much more sensitive to variation in these parameters (Kriesner et al. 2016).

Thus, the temporal infection-frequency fluctuations we observe may be caused by variation in the fitness effects of Wolbachia on hosts, variation in the fidelity of maternal transmission of Wolbachia, or variation in CI intensity. Laboratory experiments that evaluate fitness components of Wolbachia infected and uninfected yakuba complex hosts, across a range of environmental conditions, may reveal context-dependent phenotypes that impact Wolbachia equilibrium frequencies. Similarly, assays of maternal transmission of Wolbachia using field-caught females from each species and sampling location will provide critical information for understanding frequency variation. Because Wolbachia frequencies increased in D. yakuba, and decreased in D. santomea on São Tomé, over the same time interval (2009–2015), the cause of these fluctuations must be species-specific.

Wolbachia and reproductive isolation in the yakuba complex

We see little apparent effect of Wolbachia on premating and postmating RI. Unlike the Wolbachia-induced assortative mating observed in the D. paulistorum species complex (Miller et al. 2010), we found no evidence for an influence of Wolbachia on the RI of yakuba species in our 24 hr no-choice mating experiments. Analysis of other behaviors (e.g., mate choice, courtship latency, and courtship time) could reveal subtleties that our no-choice experiments did not detect (Coyne et al. 2005). We also assessed whether Wolbachia affect the number of eggs laid by females over 10 days after an observed mating. Again we found no statistically significant differences between our reciprocal crosses. Thus, Wolbachia do not serve as a mechanism of gametic isolation. Finally, we assessed egg-to-adult viability in interspecific crosses. We found that UI ♀san × ♂yak crosses have a statistically significant reduction of ∼18% in egg-to-adult viability relative to the IU crosses, while the UI crosses of ♀yak × ♂san produce a statistically nonsignificant 6% reduction. This asymmetry may contribute to asymmetric postzygotic RI between D. santomea and D. yakuba on São Tomé. This asymmetry may be enhanced by differences in infection frequencies between these species. Our 2015 samples of D. yakuba and D. santomea revealed a relatively low Wolbachia frequency in D. santomea and relatively high Wolbachia frequency in D. yakuba (Figure 1). However, our data from 2009, 2005, and 2001 suggest that these infection-frequency differences may not persist (Table 1).

In contrast, Wolbachia seem to contribute to postzygotic RI between other co-occurring species. For example, Drosophila paulistorum semispecies have obligate relationships with their Wolbachia such that exposure to antibiotics leads to host death. Moreover, in hybrids, Wolbachia over-replicate and generate hybrid inviability and male sterility (Miller et al. 2010). Wolbachia also appear to have contributed to reinforcement between Wolbachia-infected D. recens and uninfected D. subquinaria (Shoemaker et al. 1999; Jaenike et al. 2006). If temporally fluctuating Wolbachia frequencies approach 1 in D. yakuba and 0 in D. santomea, this pair approaches the complete asymmetry observed for interspecific crosses between uninfected D. subquinaria and infected D. recens. However, even under this hypothetical frequency scenario, the level of CI seen in ♀san × ♂yak is much less intense than in ♀subquinaria × ♂recens, which results in ∼98% embryo mortality. We suspect that the contributions of Wolbachia to RI observed in Drosophila may be the exception rather than the rule (Turelli et al. 2014).

Maintenance of variation for Wolbachia and host

Our results raise theoretical questions about the persistence of Wolbachia infections when conditions fluctuate, and about the stable coexistence of Wolbachia and host variants that modulate Wolbachia effects. First, we consider the conditions for the maintenance of Wolbachia infections when the parameters governing their dynamics fluctuate. We use the standard discrete-generation Wolbachia-Drosophila model proposed by Hoffmann et al. (1990), which assumes only a single Wolbachia type, and that host genotypes do not alter its effects. The model incorporates imperfect maternal transmission, CI, and effects on host fitness, modeled as fecundity differences (Hoffmann and Turelli 1997). It assumes that on average a fraction μ of the ova produced by an infected female are uninfected, and that all uninfected ova are equally susceptible to CI (cf. Carrington et al. 2011). Embryos produced from fertilizations of uninfected ova by sperm from infected males hatch with frequency H = 1−s_h relative to the three compatible fertilizations, all of which are assumed to produce equal hatch frequencies. The relative fecundity of infected females is F. These assumptions imply that adult infection frequencies, denoted p_t, change between generations as

$$p_{t+1}=\frac{p_{t}F\left(1-\mu \right)}{1+p_t\left(F-1-s_h\right)+p_t^2{s}_h\left(1-\mu F\right)}\approx p_{t}F\left(1-\mu \right)\hspace{0.17em}\text{for}\hspace{0.17em}{p}_t\approx 0.$$ (1)

To stably maintain intermediate infection frequencies in an isolated population, we want to satisfy the conditions for a “protected polymorphism”—namely, the monomorphism frequencies 0 and 1 must be unstable (Prout 1968). If μ > 0 and s_h < 1, uninfected adults continuously enter the population, and p = 1 is not an equilibrium. Hence, we need only assure that Wolbachia frequency does not converge to 0. If F and μ fluctuate, Equation (1) implies that Wolbachia will persist whenever the geometric mean of F_t(1−μ_t) is >1 (Dempster 1955). We have not estimated μ nor determined that these low-CI Wolbachia infections enhance fitness. Our ignorance of the factors maintaining these Wolbachia is hardly surprising, given that we do not fully understand the benefits associated with any Wolbachia infections in nature, including the most intensively studied, wRi in D. simulans and wMel in D. melanogaster (cf. Kriesner et al. 2016).

It is even more challenging to understand whether host and Wolbachia-mediated variation in CI intensity represent stable polymorphisms maintained by balancing selection associated with Wolbachia effects, or some form of mutation-selection balance. We consider in turn the maintenance of Wolbachia variants, then host variants that alter Wolbachia effects. When host genotypes do not alter Wolbachia effects, and the Wolbachia variants are fully compatible (i.e., each protects from the CI effects of the others), the Turelli (1994) generalization of model (1) implies that Wolbachia variants experience haploid selection dynamics with the relative fitnesses given by F(1−μ). If these parameters fluctuate, the variant with the largest geometric mean of F_t(1−μ_t) is expected to displace all others. Even if the Wolbachia variants are partially incompatible, we do not expect stable coexistence of Wolbachia variants (Rousset et al. 1991). In contrast, spatial variation of haploid fitness, even with complete spatial mixing, can stably maintain multiple genotypes (Gliddon and Strobeck 1975). Hence, it is possible that if Wolbachia effects depend on host genotypes, coadapted combinations of Wolbachia and host genotypes might stably persist as balanced polymorphisms, even though each Wolbachia would regularly find itself in unfavorable host backgrounds. The relevant analyses require that host genotypes alter the parameters in Equation (1), and Turelli (1994) illustrated some possible consequences. The conditions for stable host–Wolbachia polymorphisms, if they exist, are likely to be quite complex. For instance, by considering host variants that alter only one of μ, F, and H = 1−s_h in (1), Turelli (1994) showed that selection would favor lower μ, higher F, and higher H. Hence, if there are pleiotropic tradeoffs between these effects [e.g., one variant raises F(1−μ) but lowers H], variation may be maintained. However, the invasion conditions [e.g., Equation 12 in Turelli (1994)] demonstrate that such tradeoffs are not likely to produce stable host polymorphisms (calculations not shown). As in much of evolutionary genetics, it is likely to be far easier to document Wolbachia-related genetic polymorphisms than to explain their persistence.

Conclusions

Although we find little evidence that Wolbachia contribute significantly to reproductive isolation in the yakuba complex species, we have found evidence of pervasive, but relatively weak CI. Moreover, CI seems modulated by both host and Wolbachia variation in at least D. teissieri. We also document markedly fluctuating infection frequencies that are apparently governed by different factors in different hosts. We find that Wolbachia do not affect host mating behavior or fecundity. Given the close relationship between the Wolbachia infections in this host clade (Lachaise et al. 2000), the yakuba complex provides a promising model system for understanding the forces responsible for maintaining Wolbachia polymorphisms in nature, and understanding how host and Wolbachia variation determine those frequencies.