Abstract
Automated pancreas segmentation in medical images is a prerequisite for many clinical applications, such as diabetes inspection, pancreatic cancer diagnosis, and surgical planing. In this paper, we formulate pancreas segmentation in magnetic resonance imaging (MRI) scans as a graph based decision fusion process combined with deep convolutional neural networks (CNN). Our approach conducts pancreatic detection and boundary segmentation with two types of CNN models respectively: 1) the tissue detection step to differentiate pancreas and non-pancreas tissue with spatial intensity context; 2) the boundary detection step to allocate the semantic boundaries of pancreas. Both detection results of the two networks are fused together as the initialization of a conditional random field (CRF) framework to obtain the final segmentation output. Our approach achieves the mean dice similarity coefficient (DSC) 76.1% with the standard deviation of 8.7% in a dataset containing 78 abdominal MRI scans. The proposed algorithm achieves the best results compared with other state of the arts.
1 Introduction
Automated organ localization and segmentation in medical images, e.g., computed tomography (CT) and magnetic resonance imaging (MRI), is a prerequisite step for many clinical applications. Although good performance in heart, liver, kidney and spleen segmentation has been reported in the literature, automated segmentation of pancreas remains a challenging problem due to the following: 1) there exist large appearance variations in both shape and size of pancreas; 2) the pancreas is a highly deformable because it is relatively soft and can be pushed by its surrounding organs; and 3) the boundaries of pancreas often collapse with intestine, vessels, abdomen fat and other neighboring soft tissues, which causes a significant amount of ambiguities along the boundaries of pancreatic and non-pancreatic tissues. Given all the difficulties listed the accurate measurement of pancreatic volume is still an urgent need in clinical practice.
One of the most popular organ segmentation frameworks is multi-atlas and label fusion (MALF) that segments the target image by transferring combined labels from atlas images. Wolz et al. [8] propose an atlas selection process to improve MALF. They apply a weighted combination of atlas labels as the initial segmentation and refine the segmentation results with markov random field (MRF). Wang et al. [7] utilize image patches instead of pixels for context similar matching and adopt geodesic distance metric for searching the K-nearest atlas patches of the target image patch. Finally the target patch is labeled by the majority voting of the K-nearest atlas. All these methods achieve ∼ 90% dice coefficients on liver, kidney and spleen, but only ∼ 70% on pancreas, using the leave-one-patient-out (LOO) protocol. For MALF, pancreas shape and position in the target image are often not completely covered by the atlas images, which might lead to the low performance of its following intensity context based pixel/patch matching.
Recent work have used convolutional neural networks (CNN) for pixel-wise predictions [1] that gain superior performance in computer vision tasks because of the highly representative learned deep image features using CNN. Roth et al. [4] apply multi-level deep CNN models for dense image pixel labeling, conducting pancreas segmentation gradually from coarse to fine representation. However, pixel or superpixel-wise prediction of deep networks is very inefficient since it requires thousands of inferences for a testing image.
In this paper, we propose to segment pancreas by performing decision fusion within a conditional random field (CRF) framework where we assign the CNN predicted semantic object and boundary probabilistic outputs as its energy terms. Due to the complex nature of pancreas MRI images, we would argue that conducting pancreas segmentation by integrating and fusing separate tissue allocation and boundary detection CNN models is a promising approach. An overview of our segmentation framework is illustrated in Fig. 1.
Fig.1.
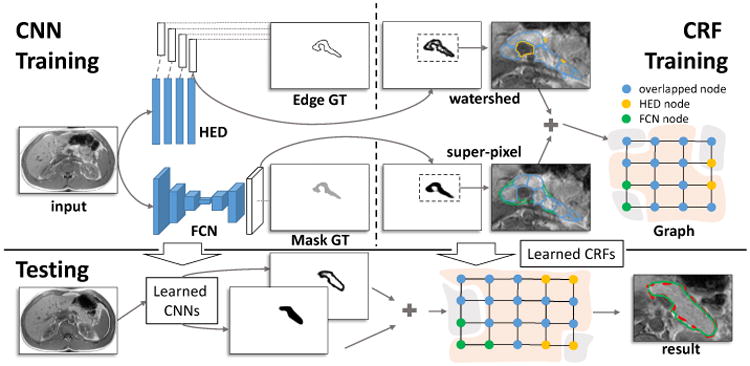
The framework of our approach. CNN Training: CNN models are trained for pancreatic tissue allocation (the FCN model) and boundary detection (the HED model); CRF Training: A CRF model is learned based on the candidate regions that detected by CNN models. Testing: The segmentation begins with CNN models, and then will be further refined by the CRF model. The result of testing and the corresponding human annotation are displayed with the green and red dashed curves, respectively.
2 Methods
Different from CT, MRI imaging modality presents more details in soft tissues, while preventing patients from exposing to harmful radiations. However, slow imaging speed and low resolution of MRI often introduce more boundary artifacts than CT for pancreas. As we show in Fig. 2, some parts of the pancreas collapse with abdomen fat exhibit weak boundaries, which bring a lot of difficulties for automated segmentation. Within the weak boundary area, texture context features would perform better and complement the edge gradient information. On the other hand, other regions of the pancreas present strong boundaries that can be accurately delineated by semantic edge detection methods. Since both weak and strong pancreas boundaries are generally co-existing in MRI, results of the tissue classification and the boundary detection would be complementary to each other. The intrinsic idea of our method is to combine pancreas tissue classification and boundary detection to lead to a better overall segmentation performance. Two separate CNN models are trained for the two tasks, respectively. The CNN results are then combined with a graph based data fustion model to obtain the refined segmentation outputs.
Fig. 2.

Sub-regions with weak and strong boundaries displayed in the first and third column, respectively. The corresponding manual annotations are displayed with red dashed curves.
2.1 The Design of Convolutional Neural Networks
Instead of designing and training a new CNN architecture from scratch [1,4], we prefer to fine-tune two currently existing CNN models due to the following reasons: 1) a very deep CNN architecture needs a large amount of labeled training data to converge, which is often unavailable or difficult to obtain; 2) many CNN architectures have been proved to be highly discriminative with a stable training convergence; 3) a recent work [2] indicates the learned kernels in the bottom layers of the CNN can be successfully transferred from one application domain to the others. Therefore we propose to fine-tune our CNNs from the VGG-16 network [5], which is already pre-trained using a huge amount of natural images.
In traditional CNN, the pixel or superpixel-wise classification strategy [4,2] significantly slows its inference procedure. To address this problem, fully convolutional network (FCN) [3] replaces the pixel-wise prediction with an end-to-end scheme, which is implemented by adding upsampling layers to a regular CNN architecture. The upsampling layers increase the output activation map resolution to the same level of the input image. Since the end-to-end training process calculates loss and updates the network in an image-wise manner, FCN is very computationally efficient. When running on GPU, FCN with VGG-16 network operates at the speed of 5 frames (256 × 256) per second.
The within-class variations of the pancreas shape and size require robust object-level boundary detection. Instead of detecting generic image edges, the boundary detection method should aim at precisely delineating the pancreatic boundaries. Holistically-nested edge detection (HED) [9] improves a regular FCN by adding deep supervision at all convolutional layers against down-sampled maps of the final desirable labeling output. In this way, the training losses are calculated and propagated back per layer. HED is also an end-to-end CNN and it can process 2.5 frames per second.
2.2 Data Fusion
FCN [3] localizes the pancreas position robustly, but it is not effective on precisely delineating pancreatic boundaries due to its upsampling convolutional operations. Nevertheless HED [9] can be fine-tuned to detect strong semantic pancreatic boundaries accurately, but it might fail to capture all weak boundaries. We treat both FCN and HED outputs as priors and conduct decision fusion using a principled CRF model. By minimizing the CRF energy function, our decision fusion method can remove most false positive segments from the original pancreas segmentation areas (initialized by the FCN and HED maps).
Graphical Model
we propose an undirected graphical model with weighted edges for decision fusion. The graphical model node represents its corresponding candidate image region. There are two groups of candidate regions, which are delineated inside the FCN and HED maps in Fig. 3. The first group is generated from watershed transformation of the semantic pancreas gradient maps through HED outputs. These regions align well to the HED detected pancreas boundaries. The second group is produced by superpixel segmentation on the detected FCN regions. As shown in Fig. 3, the node feature extraction will begin with the HED map so as to preserve as many the detected boundaries as possible. Features from the FCN map and MRI image will then be extracted correspondently. The adjacent nodes are linked with weighted edges, which will reflect the likelihood that the two nodes are belonging to the same category (pancreas or non-pancreas). In other words, edges with low similarity will encourage the connected two nodes to take different categories, which is illustrated in Fig. 3.
Fig. 3.
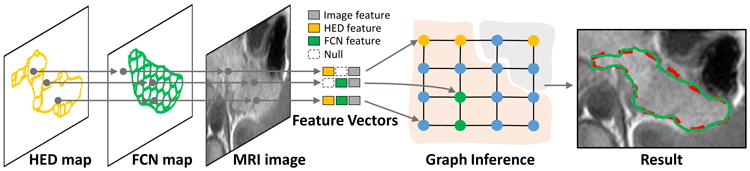
The overview of our graphical model for decision fusion. The feature vector of each node is extracted from its corresponding candidate region of the HED map, the FCN map, and the MRI image. The null feature is defined to refer to the non-detected region in the FCN/HED maps. The graph nodes are then partitioned by graph inference. The result of decision fusion is displayed with the same color notation in Fig. 1.
Conditional Random Field
in the graphical model, nodes contain both FCN and HED features should be assigned with higher likelihood of being the pancreas region than those contain only one of them. Furthermore, the intensity context difference between any connected nodes should be taken into consideration. Hence, the node feature vector contains three parts: the learned FCN and HED features, and hand-crafted image features. Typically, for a CRF node, its corresponding FCN (HED) features would be set to all zeros if it has no detected regions in the FCN (HED) map. We then assign edges between adjacent nodes with weights that reflect the similarity of the corresponding node feature vectors. For a graph 𝒢 with N nodes, we define the CRF model objective function as
| (1) |
where υ = [υ1, …, υn] is the vector containing the labels of all nodes in 𝒢, and υi ∈ {0, 1} presenting the states of nodes (pancreas or non-pancreas). 𝒩 contains index of all the connected node pairs. We apply the stochastic gradient decent algorithm [6] to conduct the CRF learning. The unary and pairwise potentials are defined as
| (2a) |
| (2b) |
where uij = 1[υi = υj], and (α0, …, αK, β0, …, βk) are the parameters of the CRF model we learned. As the node vector fi can be flexibly represented by learned and hand-crafted features, we define the feature vector of i-th node as
| (3) |
where S[FCN,HED,i] denotes to the area of the FCN map, the HED map and the i-th node, respectively. Ii and hi are the mean intensity value and the histogram (4 bins) computed from the pixels inside the region. From what our results indicate, this simple node feature setting is sufficient to obtain satisfying performance. Finally in the testing stage, we follow the iterated conditional modes (ICM) algorithm to perform the graph inference [6].
3 Experimental Results & Discussion
We evaluate our approach with abdominal MRI scans captured from 78 subjects using a 1.5T Semens Avanto scanner. These MRI scans have an in-plane resolution of [152, 232] × 256 voxels with voxel size ranging [1.09, 1.68mm] and contain between 23 to 35 slices with spacing ranging [6.90, 7.20mm] depending on the field of view and the slice thickness. For each scan, manual annotation of the pancreas is given by a board-certified radiologist. The dice similarity coefficient (DSC) is used to evaluate the proposed method. We use L1 and L2 to represent the manual annotation and the automated segmentation results, respectively, and define DSC = 2|L1 ∩ L2|/(|L1| + |L2|).
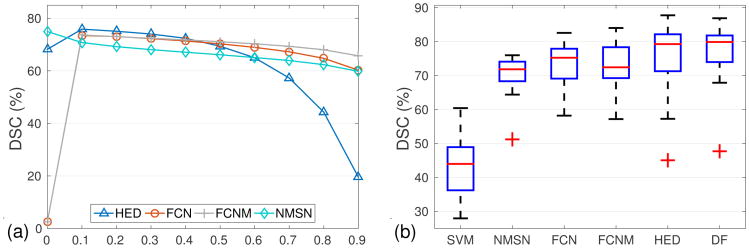
We fine-tune CNN models from pre-trained VGG-16 [5]. For the FCN model, the initial learning rate is set to 1.0 × 10−2 and scaled by 0.1 with every 5.0 × 104 iterations. The maximum iteration is 1.5 × 105. The HED model is trained similarly, with the learning rate as 1.0 × 10−6 and the weight decay equivalents to 0.1 for every 1.0 × 104 iterations. The maximum iteration number is 4.0 × 104. For FCN or HED, we define the output as a probability likelihood map where each location belongs to pancreas. Fig. 4(a) shows the DSC of CNN models as a function of thresholds on the output probability. The plateau in the range of [0.2, 0.6] reveals that segmentation performance is stable within this range.
Fig. 4.
(a) mean DSC with respect to probability threshold, which is applied to the output of CNN models; (b) comparison of segmentation accuracy between different approaches. The red lines and crosses are represent to the means and outliers, respectively. (the thresholds are set to the optimal in (a), DF is the acronym for decision fusion)
To set up a segmentation baseline on our MRI dataset, we extract HoG features from 64 × 64 pixel sized image patches, and conduct superpixel-wise prediction with support vector machine (SVM). To compare with CNN model that trained from scratch, we train a 11-layer neuronal membranes segmentation network (NMSN) model in [1]. The NMSN makes pixel-wise prediction on 95×95 pixel sized image patches. Also to compare with very deep CNN models, we train a FCN model (FCNM) with three classes of pancreatic tissue, pancreatic boundary and the background. To generate the graphical model for decision fusion, we assign graph nodes that have more than 50% overlaps with human annotation as positive, and the rest as negative. All the 78 MRI scans have been randomly separated to 52 for training and 26 for validation. Fig. 4(b) shows the results of all the segmentation methods mentioned above. Our approach achieves the highest accuracy with respect to the mean DSC while remains to be the method with the second minimal standard deviation. It is also worth noting that NMSN, which has been trained from scratch, has the smallest standard variance. However, its overall performance is largely limited by its shallow architecture.
To validate the segmentation stability, we implement three-fold cross validation (CV-3) as our evaluation protocol. Three-fold cross validation (rather than the leave-one-out (LOO) metric [8,7]) is adopted because patient cases from a single clinical site are hardly independent and identically distributed. In this scenario, N-fold CV (where N is small, e.g., 2 4) is a statistically more reliable segmentation criterion as discussed in [4]. The optimal performance of training and testing is upper bounded by the detected FCN and HED regions. We show those optimal values and actual training, testing segmentation accuracy results in Table 1 where we obtain around 4% loss in training and roughly 9% loss in testing. For the total dataset, our maximum test performance is 87.1% DSC with 10%, 30%, 50%, 70%, 80% and 90% of the cases being above 84.8%, 81.1%, 78.4%, 74.7%, 71.5%, and 66.6%, respectively. Finally, we report our overall mean DSC in Table 2, comparing to other recent work reported in the literature. To the best of our knowledge, our approach has reported the best quantitative pancreas segmentation performance with a mean DSC 76.1% (although the results are not strictly comparable due to the lack of common evaluation datasets). In Fig. 5, we present some qualitative pancreas segmentation results.
Table 1.
Results of decision fusion on 3-fold CV: Opt. is the optimally achievable DSC and Acc. is the actual DSC that training and testing achieve.
| Validation | Train Opt. | Train Acc. | Test Opt. | Test Acc. |
|---|---|---|---|---|
| 1st fold | 92.8% | 89.6% | 83.5% | 75.0% |
| 2nd fold | 91.7% | 87.6% | 85.2% | 75.7% |
| 3rd fold | 92.2% | 88.6% | 86.1% | 77.4% |
Table 2.
Overall DSC shown as mean ± standard dev. [worst, best].
Fig.5.
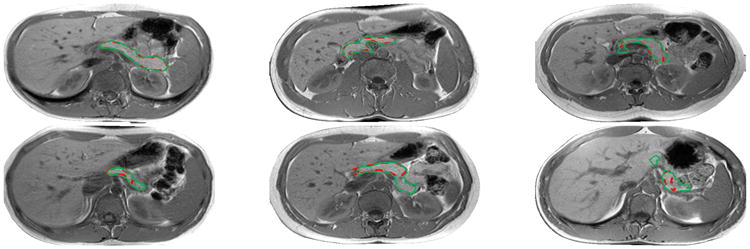
From left to right and top to bottom: Segmentation results with DSC from 95% to 51% using the same color notation in Fig. 1.
4 Conclusion
In this paper, we propose to segment pancreas leveraging both appearance and boundary detection via CNN models that are supplement with each other. A graph based CRF model is used to fuse the deep CNN outputs in a principled manner. With decision fusion, the overall mean DSC boosts from 73.8% to 76.1% while lowering the standard deviation from 12.0% to 8.7%. Our decision fusion model is straightforward to be extended to handle other segmentation tasks.
References
- 1.Ciresan D, Giusti A, Gambardella LM, Schmidhuber J. Deep neural networks segment neuronal membranes in electron microscopy images. In: Pereira F, Burges CJC, Bottou L, Weinberger KQ, editors. Advances in Neural Information Processing Systems. Vol. 25. Curran Associates, Inc; 2012. pp. 2843–2851. [Google Scholar]
- 2.Girshick R, Donahue J, Darrell T, Malik J. Rich feature hierarchies for accurate object detection and semantic segmentation. 2014 IEEE Conference on Computer Vision and Pattern Recognition. 2014 Jun;:580–587. [Google Scholar]
- 3.Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2015 Jun;:3431–3440. doi: 10.1109/TPAMI.2016.2572683. [DOI] [PubMed] [Google Scholar]
- 4.Roth HR, Lu L, Farag A, Shin HC, Liu J, Turkbey EB, Summers RM. DeepOrgan: Multi-level Deep Convolutional Networks for Automated Pancreas Segmentation. Springer International Publishing; Cham: 2015. pp. 556–564. [Google Scholar]
- 5.Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. CoRR abs/1409.1556. 2014 [Google Scholar]
- 6.Vishwanathan SVN, Schraudolph NN, Schmidt MW, Murphy KP. Proceedings of the 23rd International Conference on Machine Learning. ACM; New York, NY, USA: 2006. Accelerated training of conditional random fields with stochastic gradient methods; pp. 969–976. ICML '06, [Google Scholar]
- 7.Wang Z, Bhatia KK, Glocker B, Marvao A, Dawes T, Misawa K, Mori K, Rueckert D. Geodesic Patch-Based Segmentation. Springer International Publishing; Cham: 2014. pp. 666–673. [DOI] [PubMed] [Google Scholar]
- 8.Wolz R, Chu C, Misawa K, Fujiwara M, Mori K, Rueckert D. Automated abdominal multi-organ segmentation with subject-specific atlas generation. IEEE Transactions on Medical Imaging. 2013 Sep;32(9):1723–1730. doi: 10.1109/TMI.2013.2265805. [DOI] [PubMed] [Google Scholar]
- 9.Xie S, Tu Z. Holistically-nested edge detection; 2015 IEEE International Conference on Computer Vision (ICCV); Dec, 2015. pp. 1395–1403. [Google Scholar]