A Bayesian Diagnostic System to Differentiate Glioblastomas from Solitary Brain Metastases

Abstract

This paper aimed to construct a Bayesian network-based decision support system to differentiate glioblastomas from solitary metastases, based on multimodality MR examination. We enrolled 51 patients with solitary brain tumors (26 with glioblastomas and 25 with solitary brain metastases). These patients underwent contrast-enhanced T1-weighted magnetic resonance (MR) examination, diffusion tensor imaging (DTI), dynamic susceptibility contrast (DSC) MRI, and fluid-attenuated inversion recovery (FLAIR). We generated a set of MR biomarkers, including relative cerebral blood volume in the enhancing region, and fractional anisotropy measured in the immediate peritumoral area. We then generated a Bayesian network model to represent associations among these imaging-derived predictors, and the group membership variable, (glioblastoma or solitary metastasis). This Bayesian network can be used to classify new patients' tumors based on their MR appearance. The Bayesian network model accurately differentiated glioblastomas from solitary metastases. Prediction accuracy was 0.94 (sensitivity = 0.96, specificity = 0.92) based on leave-one-out cross-validation. The area under the receiver operating characteristic curve was 0.90. A Bayesian network-based decision support system accurately differentiates glioblastomas from solitary metastases, based on MR-derived biomarkers.

Introduction

Glioblastomas (GBM) and brain metastases, the two most common brain neoplasms in adults, are associated with significant morbidity and mortality. Management strategies and clinical outcomes differ for these two entities¹. Differentiation of these two neoplasms is critical for choosing care plans; in addition, preoperative diagnosis may affect the surgical approach.

To this end, researchers have sought to find a set of biomarkers that differentiate glioblastomas from brain metastases. Some investigators have used clinical history and the presence of more than one enhancing mass to differentiate these two neoplasms². However, differentiation between glioblastoma and solitary brain metastasis is challenging because both display similar signal intensity characteristics and contrast enhancement patterns on conventional magnetic resonance (MR) examination³.

Given these similarities on conventional MR, investigators have applied advanced MR sequences to differentiate metastases from glioblastoma^4,5,6,7,8. Some of these techniques arose from the observation that high-grade gliomas tend to infiltrate the peritumoral region, whereas metastases are often better circumscribed. Law et al. found that relative cerebral blood volume (rCBV) measurements (as measured by perfusion MR) in the peritumoral region of high-grade gliomas to be different from those in solitary metastases⁶. Ishimaru et al. used single-voxel proton MR spectroscopy to differentiate these two neoplasms⁵. Lu et al. used diffusion tensor imaging (DTI) to analyze high-grade gliomas and metastases⁷; they found the peritumoral mean diffusivity of metastatic lesions was significantly greater than that of gliomas.

It is well recognized that combining information from several imaging modalities may improve diagnostic accuracy⁹. However, selecting the optimal diagnostic combination from among the plethora of potential biomarkers is a difficult problem. Statistical and/or data-mining techniques have the potential to select the combination of biomarkers that yield optimal differentiation. A typical process for constructing a classification model consists of three steps: first, we extract (potential) predictor variables, such as peritumoral mean diffusivity; we then build a classification model, or classifier, using data mining algorithms or statistical approaches; finally, we evaluate and validate the resulting diagnostic model.

However, there are several obstacles we must overcome. First, when we aggregate predictor variables obtained from different imaging modalities, the number of predictor variables in the diagnostic model increases rapidly. In this case, we have a limited number of samples (i.e., brain tumors) and a large number of predictor variables (i.e., MR sequences and other information for each patient), leading to severe undersampling. The resulting classification model may not generalize beyond the patients used to create the model if we don't take additional steps, such as regularization, to prevent over-fitting. Second, some sophisticated data-mining methods, such as support vector machines, can achieve high accuracy, but the classification models generated by these approaches are hard for people to understand. Third, some machine-learning methods generate classification models with limited inference capability. Were investigators to use these methods to generate a classification model for differentiating glioblastomas from solitary metastases based on age, perfusion MR and DTI, they could use the resulting classifier only in its original form: if the DTI biomarkers were not available, the investigators could not use the model.

This study aimed to build a Bayesian Network (BN)-based system to differentiate glioblastomas from solitary metastases, based on multimodality imaging. Imaging techniques include T1-weighted MR, DTI, dynamic susceptibility contrast (DSC) MRI, and fluid attenuation inversion recovery (FLAIR). A BN-based decision support system offers five advantages over alternative modeling approaches. 1) BNs are declarative, and tend to be simple for people to comprehend; 2) BNs have very powerful inference capabilities; 3) BNs rest upon a formal mathematical foundation for generating models under uncertainty; 4) expert domain knowledge can be easily incorporated; and 5) since they are based on probability theory, BNs may still be applied when some data are missing.

Materials

This study included 51 patients with solitary brain tumors. Based on pathologic examination, 26 patients had glioblastomas (mean age (standard deviation) 57 (SD 15), 14 males and 12 females), and 25 patients had solitary brain metastases (mean age 59 (SD 12), 14 males and 11 females). Exclusion criteria included more than one mass, non-enhancing tumor, or clinical history of any prior therapy to the brain. The study was approved by our institutional review board.

These patients underwent contrast-enhanced T1-weighted MR, DTI, DSC MRI, and FLAIR. MR examination was performed on a Siemens Tim Trio 3.0T whole-body scanner (Siemens, Erlangen, Germany). The imaging parameters of T1-weighted 3D magnetization prepared rapid acquisition gradient-echo (MPRAGE) were Time to Repetition (TR)/ Time Delay between excitation and Echo Maximum (TE) = 1760/3.1 ms, 192 × 256 matrix size, 1 mm slice thickness. Post-contrast T1-weighted MPRAGE images were obtained after administration of a standard dose (0.1 mmol/kg) of gadodiamide (Omniscan, GE Healthcare, Oslo, Norway) with a power injector. The DTI sequence parameters were TR/TE=4900/83 ms, number of excitations = 6, field of view (FOV) = 22 × 22 cm², 3 mm slice thickness, 128 × 128 matrix, b = 0 and 1000 s/mm² and 40 slices covering the entire brain. To reduce the effect of contrast-agent leakage on rCBV measurements, DSC MR was performed five minutes after a 3 ml preloading dose of intravenous gadodiamide. DSC sequence parameters included TR/TE 2000/45 ms, FOV 22 × 22 cm², in-plane resolution 1.72 × 1.72 × 3 mm³, and 20 slices. FLAIR sequence parameters were TR/TE/TI 9420/141/2500 ms, 3 mm slice thickness.

Methods

Constructing a decision support system involves three steps: biomarker selection, model generation, and model evaluation. In the biomarker selection step, we process the source raw data and extract potential predictor variables. Then, we build a classification model using machine-learning algorithms or statistical models. In the model evaluation step, for a new subject, we predict the subject's group membership (glioblastomas or solitary metastases) using the generated classification model.

Bayesian networks

Let V={X1, …, X_p} denote the variables (nodes) in the problem domain. A BN model B consists of two components: a structure G and parameters Θ. B=(G, Θ). The structure, G, is a directed acyclic graph and encodes a set of conditional-independence statements about variables. A directed edge in G is a link from a parent node to a child node, and corresponds to a probabilistic association between two variables. An advantage of BNs, in contrast to certain other approaches such as support vector machines, is that BNs are declarative; that is, statistical dependence and independence are explicitly represented, and are interpretable by people.

Each variable in a BN is associated with a conditional-probability distribution. Let pa(X_i) represent the parent set of node X_i; The conditional probability Θ_ijk=P(X_i = k | pa(X_i)=j) is the probability that variable X_i assumes state k when the parents of X_i , pa(X_i), assume their j combination of states. If X_i has no parents, then Θijk corresponds to the marginal probability of X_i. Θ is the collection of Θ_ijk; Θ specifies the conditional probabilities that quantify the associations among the variables Figure 1 depicts a hypothetical BN that represents the probabilistic associations among four variables: factional anisotropy (FA) from the enhancing region, linear anisotropy coefficients (CL) from the enhancing region, spherical anisotropy coefficients (CS) from the enhancing region, and the group membership variable C (glioblastoma or brain metastasis). In this BN, C is independent of FA, given CL and CS. The conditional probability P(C = GBM | CL = low, CS = low) = 0.9 indicates that probability of a subject's having glioblastoma when CL is low and CS is high is 0.9.

Figure 1.

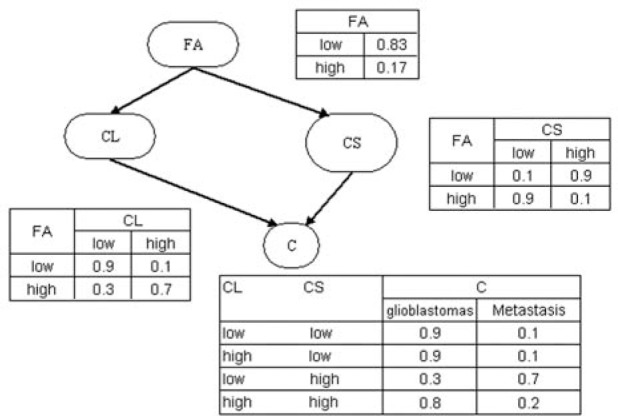
An example of a Bayesian network. FA: factional anisotropy in the enhancing region; CL: the linear anisotropy coefficients in the enhancing region; CS: the spherical anisotropy coefficients in the enhancing region.

The concept of a Markov blanket is central to the BN representation: the Markov blanket of a variable X, mb(X), is defined as the minimum set of variables that render that variable conditionally independent of the other variables in the network¹⁰. For example, in Figure 1, the Markov blanket of C is CL and CS. That is, given knowledge of the status of CL and CS, the status of FA gives us no additional information about the probability of that subject's having glioblastoma or brain metastasis. Formally, mb(X) is defined as the union of X's parents, its children, and the parents of its children.

One of the advantages of the BN representation is its powerful inference capability¹⁰. The inference task is to find the posterior distribution of a set of outcome variables given values for evidence variables. A BN can be used to compute any such probability. For example, in Figure 1, we may be interested in the posterior probability of a subject's having glioblastoma, given that this subject's FA is high. In this query, the outcome variable is C, and the evidence variable is FA. To compute this probability, we apply a standard BN-inference algorithm to the network in Figure 1, obtaining the value 0.42.

Because of this powerful inference capability, BN-based decision support systems can easily accommodate missing data, without having to modify the underlying BN model or inference algorithm. If we construct a BN that predicts C based on FA, CL, and CS (Figure 1), for a new subject, even in the case that CL and CS are missing, we can still predict C, albeit with less certainty than if we had all the information. This feature is of great importance in clinical applications, in which some predictor variables are often missing (e.g., a particular MR sequence could not be acquired, or the patient's weight was not obtained).

Biomarker extraction

To select biomarkers, we first generated a set of scalar maps (FA, apparent diffusion coefficient (ADC), CL, planar anisotropy coefficients (CP)) from DTI images, and rCBV values from DSC images. For each subject, we registered the FLAIR, FA, ADC, CL, CP, and rCBV maps to that subject's T1-weighted image volume using a mutual information-based registration algorithm¹¹.

Based on T1-weighted MR and FLAIR images, we divided each lesion into four sub-regions: central, enhancing, immediate peritu-moral, and distant peritumoral. We delineated an ROI over the FLAIR abnormality to create a 3D mask. We created another mask on the T1-weighted MR volume to indicate contralateral normal WM. We defined the enhancing region to include enhancement greater than three standard deviations (SD) above the mean of WM post-contrast T1 signal intensity. We defined the central region to include those voxels within the enhancing region with enhancement less than the mean + three SD post-contrast T1 signal intensity. We defined the immediate peritumoral region as a 4 mm band around the enhancing region. Finally, we defined the remaining region of FLAIR abnormality, outside the peritumoral region, as the distant peritumoral region.

For each of the four sub-regions, we calculated the average intensity for T1, FLAIR, ADC, FA, CL, CP, CS, rCBV, and maximal rCBV. This process yielded 36 potential predictor variables (Table 1).

Table 1.

MR-derived predictor variables; * = p-value < 0.1.

Name	Modality	Name	Modality
T1 enhancing part	T1	T1 immediate peritumoral area	T1
FLAIR enhancing part *	FLAIR	FLAIR immediate peritumoral area	FLAIR
ADC enhancing part	DTI	ADC immediate peritumoral area	DTI
FA enhancing part *	DTI	FA immediate peritumoral area *	DTI
CL enhancing part *	DTI	CL immediate peritumoral area *	DTI
CP enhancing part *	DTI	CP immediate peritumoral area *	DTI
CS enhancing part *	DTI	CS immediate peritumoral area *	DTI
rCBV enhancing part	DSC	rCBV immediate peritumoral area *	DSC
Maximum rCBV enhancing part	DSC	Maximum rCBV immediate peritumoral area *	DSC
T1 central part	T1	T1 distant peritumoral area	T1
FLAIR central part *	FLAIR	FLAIR distant peritumoral area	FLAIR
ADC central part	DTI	ADC distant peritumoral area	DTI
FA central part *	DTI	FA distant peritumoral area	DTI
CL central part *	DTI	CL distant peritumoral area	DTI
CP central part *	DTI	CP distant peritumoral area *	DTI
CS central part *	DTI	CS distant peritumoral area	DTI
rCBV central part	DSC	rCBV distant peritumoral area	DSC
Maximum rCBV central part	DSC	Maximum rCBV distant peritumoral area *	DSC

Classifier generation

To generate a classifier based on multimodality imaging, for the 36 imaging-derived variables, we used the Wilcoxon rank-sum test to identify variables demonstrating differences between patients with glioblastomas and those with solitary metastases, and set the p-value cutoff to 0.1. Thus, if the p-value of a variable was below 0.1, we considered this variable to be predictive of C, and included it in the classification model. We did not set a stringent p-value cutoff value, such as 0.05 with multiple-comparison correction, because our goal was to detect variables that are predictive of C to some degree, not to detect variables demonstrating significant differences. Let Fdenote this set of variables.

The next step is to construct a BN model to represent probabilistic associations among F and C. We used a standard BN data-mining algorithm, based on the Markov Chain Monte Carlo (MCMC) method¹² and the Bayesian Dirichlet equivalent (BDe) score¹³, to generate the BN classifier.

Classifier evaluation

After generating the classification model for a new case, we apply the classification model to this new case and obtain the probability that this new case belongs to a specific group. This step is referred to as the model evaluation stage.

We used leave-one-out cross validation (LOOCV) to evaluate the BN classifier that we generated in the previous step. In LOOCV, we partition the data set D into N_total data sets. For each data set, we generate a BN model based on N_total minus; 1 subjects, and we determine whether the model can correctly classify the remaining subject's tumor. The overall performance is the average across all N_total data sets.

To assess predictive power, we computed prediction accuracy, defined as N_corr/N_total, where N_corr and N_total represent the number of correctly labeled subjects and the total number of subjects, respectively. Sensitivity is the fraction of subjects who had glioblastoma and were labeled as having glioblastoma by the classification model. Specificity is the fraction of subjects who had solitary metastases and were labeled as solitary metastases by the BN model. We also calculated the area under the receiver operating characteristic (ROC) curve (AUC), using STATA (StataCorp LP, College Station, TX, USA). We tested the equality of two or more AUCs, obtained from applying two or more test modalities to the same sample or to independent samples, using the roccomp procedure in STATA¹⁴.

Results

Histopathologic analysis

Histopathologic analysis of the study population defined tumors for 26 patients to be glioblastomas and those for an additional 25 patients to be solitary brain metastases. For patients with solitary brain metastases, the primary sites of cancer were: lung (17 patients), breast (5 patients), colon (1 patient), melanoma (1 patient), and sarcoma (1 patient).

Variables included in the classification model

The set of variables with p-values below 0.1 included 18 variables (Table 1). Those variables, of which F is comprised, were: FLAIR, FA, CL, CP, and CS in the enhancing region; FLAIR, FA, CL, CP, and CS in the central region, FA, CL, CP, CS, rCBV, and maximum rCBV in the immediate peritumoral region, CP and maximum rCBV in the distant peritumoral region.

The BN-based classification model

Figure 2 shows the structure of the resulting BN classifier. The Markov blanket of C (the tumor-type variable) included eight biomarkers: FLAIR, FA, and CS from the enhancing region, FA from the central region, and CP, CS, rCBV, and maximum rCBV from the immediate peritumoral region. Classification accuracy based on LOOCV was 0.94 (sensitivity = 0.96 and specificity = 0.92), and AUC was 0.90.

Figure 2.

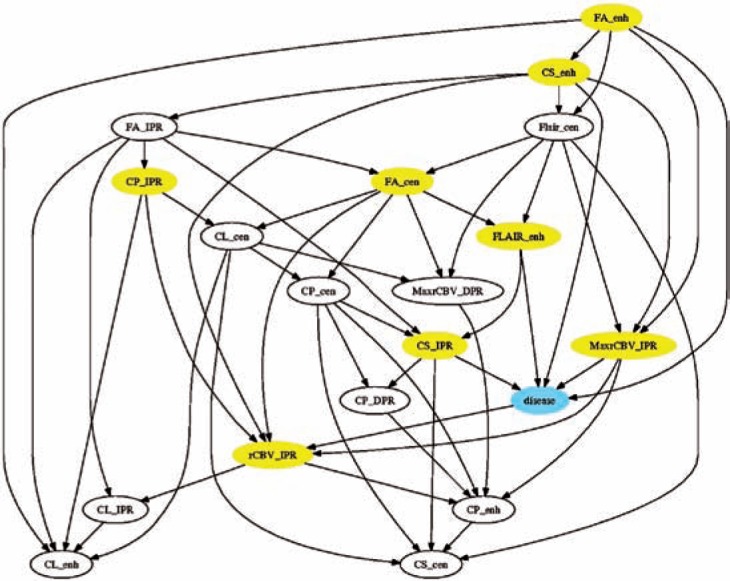
Structure of the Bayesian network generated by our data-mining algorithm. Yellow nodes constitute the Markov blanket of the outcome variable. ENH: enhancing region; CEN: central region; IPR: immediate peritumoral region; DPR: distant peritumoral region.

As we noted in the Introduction section, one of the advantages of the BN representation is its ability to classify new subjects based on partially available data. There are two scenarios in which this feature is critical:

Data are often missing for patients, possibly due to operator error (e.g., failure to record patient's weight or symptoms), hardware (e.g., MR scanner) error, or a patient's inability to submit to a lengthy MR examination, among other causes.

Different imaging sequences or hardware. Our model in Figure 2 is constructed based on T1-weighted MR, DTI, DSC, and FLAIR, yet other medical centers may employ different imaging sequences. These physicians can still use our model, as long as their imaging sequences include a subset of those we used to generate the model.

For a subset A of F, we can evaluate its predictive power as follows. In the LOOCV step, we generate a BN model based on F, and then apply that classifier to those cases that are not in the training set, using only variables in A. Note that we do not have to follow this procedure to use the model generated from F for patients with missing data; this evaluation gives us a basis on which we can compare the relative predictive power of various subsets of available biomarkers.

Table 2 lists the predictive powers of different combinations of sub-regions. Figure 3 shows the corresponding ROC curves. In Table 2, ENH is the enhancing region, CEN is the central region, IPR is the immediate peritumoral region, and DPR is the distant peritumoral region. In the LOOCV stage, we only used a subset of variables. For example, for the second row (ENH), when we applied the BN classifier to those cases that were not used to generate the model, we used only variables from the enhancing region to evaluate classification accuracy.

Table 2.

Predictive power of different combinations of sub-regions. * = no significant difference between AUC of this variable set and that of the full set.

Variable set	Accuracy	Sensitivity	Specificity	AUC
All	0.94	0.96	0.92	0.9031
ENH	0.82	1	0.64	0.8754 *
CEN	0.73	0.62	0.84	0.5831
IPR	0.75	0.92	0.56	0.6169
DPR	0.47	0.23	0.72	0.3446
ENH + CEN	0.82	0.96	0.68	0.8769 *
ENH + IPR	0.92	0.92	0.92	0.8846 *
CEN + IPR	0.75	0.69	0.80	0.7985
ENH + CEN + IPR	0.94	0.96	0.92	0.9031 *

Figure 3.

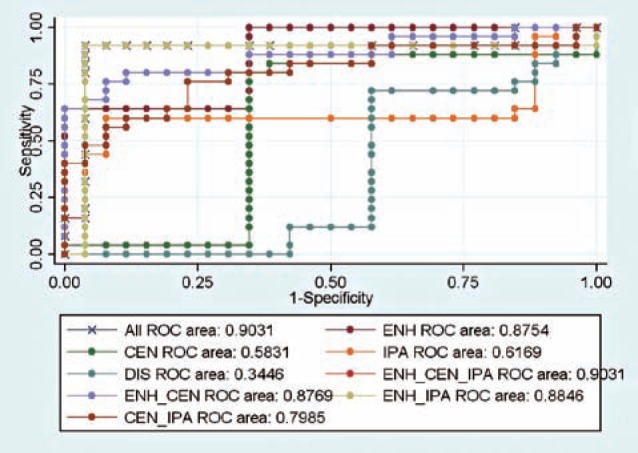
ROC curves of different combinations of sub-regions.

We found that the AUC of variables from the enhancing region, the central region, and the immediate peritumoral region, was identical to that from all sub-regions. We found that there was no significant difference for AUCs between these combinations (p-value > 0.05): 1) all sub-regions versus ENH, 2) all sub-re-gions versus the union of ENH and the CEN, and 3) all sub-regions versus the union of ENH and the IPR.

Table 3 lists the predictive powers of different combinations of imaging sequences; Figure 4 shows the corresponding ROC curves. We found that each individual imaging sequence (FLAIR, DTI, or DSC) had poor predictive power if used in isolation in the testing stage. We found that there was no significant difference between AUCs for these combinations (p-value > 0.05): 1) all imaging sequences versus the union of FLAIR and DTI, 2) all imaging sequences versus the union of DTI and DSC. In other words, the combination of DTI and either FLAIR or DSC was statistically indistinguishable from all sequences, with respect to AUC obtained via cross validation.

Table 3.

Predictive power of different combinations of MR sequences. * = no significant difference between AUC of this variable set and that of the full set.

Variable set	Accuracy	Sensitivity	Specificity	AUC
All	0.94	0.96	0.92	0.9031
FLAIR	0.73	0.81	0.64	0.5908
DTI	0.61	0.46	0.76	0.7692
DSC	0.63	0.42	0.84	0.4338
FLAIR + DTI	0.88	0.84	0.92	0.9015 *
FLAIR + DSC	0.71	0.77	0.64	0.7031
DTI + DSC	0.67	0.62	0.72	0.8277 *

Figure 4.

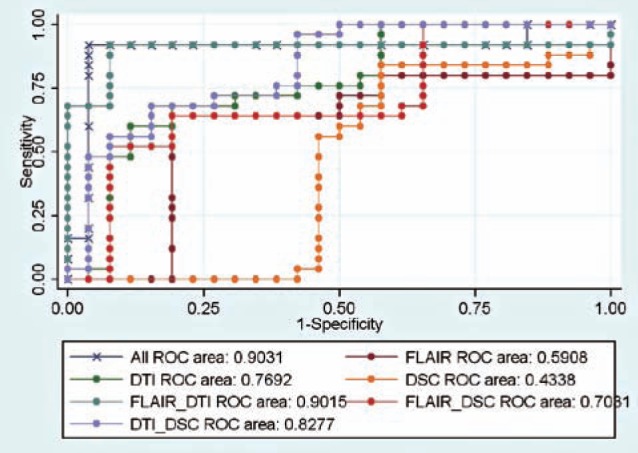
ROC curves of different combinations of MR sequences.

Discussion and Conclusions

We demonstrated that a Bayesian network model (shown in Figure 2) accurately differentiates glioblastomas from solitary metastases. Prediction accuracy was 0.94 (sensitivity = 0.96, specificity = 0.92) and AUC was 0.90, based on leave-one-out cross-validation.

The generated Bayesian network model is declarative. As shown in Figure 2, interpreting this model is relatively straightforward as there are eight variables that directly distinguish glioblastoma from metastasis. This feature is invaluable for understanding associations among imaging biomarkers and the diagnosis variable C. Given knowledge of the states of these eight variables, the states of other variables give us no additional information on the probability that a particular subject has glioblastoma or brain metastasis. Of these eight variables, six of them are derived from DTI, two from DSC, and one from FLAIR. This finding suggests that DTI is critical to the differentiation between glioblastoma and brain metastasis, and is consistent with other results in the literature⁷,⁸.

The generated BN classifier can predict C even under the condition that only a subset of imaging biomarkers is observable. For example, we can predict C when only DTI data are available, or when only the FLAIR sequence has been acquired. In general, we can estimate the predictive power of any subset of variables, assuming that the other variables are unobservable (i.e., unavailable) when using the model for evaluation. Tables 2 and 3 list the predictive power metrics of different combinations of sub-regions and imaging sequences.

Based on Table 2, variables from the enhancing part provided a significant amount of information on the state of C. The AUC for variables from the enhancing region was 0.88, which is not statistically different from the AUC for all 36 variables. For most glioblastomas and brain metastases, the enhancing region corresponds to the solid portion of the tumor. Glioblastomas usually have high cellularity compared to brain metastases¹⁵, which should cause diffusion restriction in the enhancing region relative to metastases. The importance of the enhancing region was also reported in⁸. We found that variables from the immediate peritumoral area provided additional predictive power. The specificity of models based on variables from the enhancing region and those from the immediate peritumoral region was the same as the specificity for the model based on all variables. However, the sensitivity of this set of variables was only slightly less than that for the model based on all variables (0.92 versus 0.96). Glioblastomas are biologically aggressive tumors; they tend to grow in an infiltrative manner, invading the surrounding tissues, especially the white-matter tracts. Brain metastases, in contrast, tend to grow into brain parenchyma in a non-infiltrating, advancing pattern. Therefore, the immediate peritumoral region may have a higher degree of tumor infiltration in glioblastomas⁷. It is noteworthy that no measurements of the DPR contributed significantly to differentiation between glioblastoma and solitary metastasis.

Based on Table 3, variables from a single MR sequence (DTI, FLAIR, or DSC) did not have enough information to accurately predict C; when we combined different imaging sequences, predictive power improved significantly. We found that there was no significant AUC difference between the following combinations: 1) all MR sequences versus the union of DTI and FLAIR, and 2) all MR sequences versus the union of DTI and DSC. This finding suggests the importance of multi-modality MR in the differentiation between glioblastoma and solitary brain metastasis.