Shape control through molecular segregation in giant surfactant aggregates

Abstract

Mixtures of cationic and anionic surfactants crystallized at various ratios in the absence of added salt form micrometer-sized colloids. Here, we propose and test a general mechanism explaining how this ratio controls the shape of the resulting colloidal structure, which can vary from nanodiscs to punctured planes; during cocrystallization, excess (nonstoichiometric) surfactant accumulates on edges or pores rather than being incorporated into crystalline bilayers. Molecular segregation then produces a sequence of shapes controlled by the initial mole ratio only. Using freeze-fracture electron microscopy, we identified three of these states and their corresponding coexistence regimes. Fluorescence confocal microscopy directly showed the segregation of anionic and cationic components within the aggregate. The observed shapes are consistently reproduced upon thermal cycling, demonstrating that the icosahedral shape corresponds to the existence of a local minimum of bending energy for facetted icosahedra when the optimal amount of excess segregated material is present.

Controlling both size and shape of colloidal particles is a major challenge to the predictable formulation of mixed systems consisting of surfactants, polymers, and inorganic solids. Successful control of size and shape requires simultaneous knowledge of the mixture's equilibrium phase behavior and the mechanism of formation. The aim of this article is to describe and test hypotheses based on bending energy to control a general sequence of colloidal shapes, from large discs to punctured planes.

If the elemental building blocks of a complex colloidal aggregate are amphiphilic molecules, the basic concept used to rationalize self-assembly is the concept of spontaneous curvature originating from the surface-to-volume ratio of the surfactant film (1). Common single-chain ionic amphiphiles have a spontaneous radius of curvature equivalent to one surfactant length (2) and therefore form globular micelles. Decreasing monolayer curvature obtained by mixing surfactants first produces giant cylindrical and finally locally flat bilayers.

When the elementary building block is a fragment of a bilayer, line tension of pores, or rims of discs, and elastic energy associated to dihedral angles on the contact line between adjacent facets need to be considered (3). The crystallization/segregation should be consistent with the sequence of shapes observed with strongly interacting charged colloids in the absence of salt. Molecular segregation is demonstrated by specificity of labeling with a dye and direct observation, and we show finally that the resulting shapes correspond to local minima of energy of formation.

Mechanism of Shape Control Through Molecular Segregation

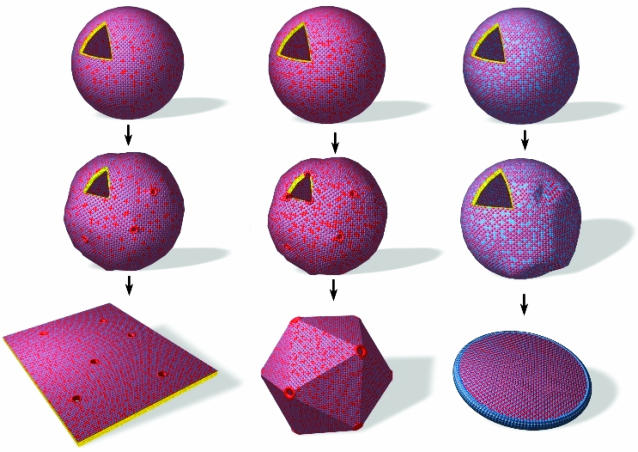
Consider an initial state of the dispersion with unilamellar vesicles in the fluid state. In the fluid state of mixed vesicles, the two components exhibit in-plane miscibility.

• Upon cooling, nucleation and growth of planar crystals occur in the form of polygonal frozen bilayers, which can only form at a fixed mole fraction r (nonnecessary stoichiometric, i.e., different from r = 0.5).

• During growth of cocrystallized material, excess component is expelled and accumulates at the edges of the growing crystal in a manner similar to zone fusion/recrystallization as described for 3D crystals by Czochralski (4).

• Excess material, such as any short-chain ionic surfactant, forms a monolayer with high spontaneous curvature, i.e., readily forms cylindrical sections with one surfactant length as radius. These half-cylinders can form half-toroids without energetic cost.

• These toroids embed the crystallized bilayers, either externally as the outer rims of the discs or “internally” as semitoroidal pores, depending on the preferred Gaussian curvature and the volume ratio of excess material and crystallized bilayers.

• The presence of rims stabilizes the flat discs without any additional cost in bilayer bending energy. The presence of pores results in instability with respect to punctured planes when present in large numbers. The bilayer bending energy is the dominant term and, hence, maximum resistance to breakage is obtained in the facetted objects.

Bending Energy of Facetted Polyhedra

We evaluate now the total free energy change involved when spheres of radius R transform into icosahedra with open pores at vertices.

The energy of formation of a facetted object from a sphere is

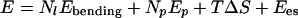[1]

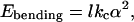[2]

where α is the dihedral angle along each edge of length l.

The first term is the bending energy of dihedral angles along the N_l edges of the polyhedron. The second term is due to the pores formed by excess surfactant. The third term is the mixing entropy cost of segregation between two pseudophases (edges and planar faces), and the last term is the electrostatic term, which does not change during freezing. Mixing entropy is 1 order of magnitude lower than electrostatic energy, which must be lower than 1 k_BT per pore, because the distance between pores is at least 10 times the Debye length.

So, assuming the two first terms dominate and using the energy E_p of formation of a pore (see Evaluation of the Bending Energy Involved in Forming One Pore in Supporting Text, which is published as supporting information on the PNAS web site), we obtain (at 30 k_BT per pore)

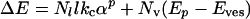[3]

where the last term, E_ves, is the bending energy of the initial vesicle. The first term is the bending energy associated with the dihedral angles on edges. This bending energy of edges can be considered within the harmonic approximation, as in canonic expressions proposed by Helfrich (5): p = 2, i.e., one considers the square of α, the dihedral angle along each edge of length l (6). In solid thin films, the bending energy scales as a^7/3 (7), which does not change qualitatively the shape of the free energy of the possible polyhedra formed as a function of the number of vertices per polyhedra N_n and energy of pore formation.

Model Mixed Molecular System Investigated

True “catanionic” colloids, formed by association of anionic and cationic amphiphiles in the absence of salt, as pioneered by Jokela et al. (8–10), are versatile ternary (i.e., three-component) supramolecular systems for which the equilibrium phase diagram can be determined due to large repulsive forces [i.e., relatively large osmotic pressure (11)] between micrometer-sized charged colloids. The molar ratio r of the anionic to cationic components controls the structural surface charge and, hence, controls the long-range repulsive interaction independently from the weight volume fraction (φ), which in turn controls the average colloid–colloid distance. In a given domain of mole ratio r, anionic–cationic single–chain ion pairs share with uncharged common lipids the property of preferring to form bilayers (spontaneous radius of curvature much larger than molecular length). Spontaneous curvature radius of unpaired “excess” surfactant is of the order of chain length, a crucial feature needed to obtain shape control by cocrystallization and segregation mechanism.

Above the chain-melting temperature, with or without excess salt, diluted unilamellar vesicles are the most stable state, and in-plane mixing of the anionic and cationic components is ensured (12–14). In this molten state, rigidity of the bilayer is low (≈1–10 k_BT); and, thus, small unilamellar vesicles ≈50 nm in diameter can be formed without too much bending energy (15). Stability of micelles (at low temperature, when chains are crystallized) was discussed a long time ago by Fromherz (16). The bending rigidity k_c of frozen bilayers is at least two orders of magnitude larger: hence the in-plane coherence length ξ easily reaches microns (17) because

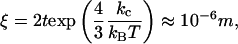[4]

where 2t is the bilayer thickness.

Both nanodiscs (18) and facetted objects, such as icosahedra (19), assemble from catanionic frozen aggregates (see Supporting Text). For brevity, we here use the word “icosahedra” to include all closely related facetted objects similar to true icosahedra, i.e., facetted objects with ≈20 faces of similar area and with an estimated number of vertices between 10 and 15. Facetted objects are preferentially either icosahedral when the cationic soluble component is in slight excess or discs when the water-insoluble anionic component is in excess. The possibility of size control in crystallized nanodiscs has been demonstrated at thermodynamic equilibrium in the dilute corner of the phase diagram when the cationic component is in excess: The equilibrium size decreases from 3 μm to 30 nm when the molar ratio r varies only between 0.45 and 0.40 (20). Therefore, partial miscibility in the edges of nanodiscs of ion pairs preferentially located on bilayers is concomitant with partial miscibility of unpaired excess cationic component on the face. This observation allowed an unambiguous determination of edge and face molar ratios: crystalline faces have a molar ratio r = 0.45, whereas edges have a molar ratio r = 0.3. At this molar ratio, the ternary phase diagram shows a giant worm-like microstructure (21).

Materials and Methods

All samples investigated here are salt-free catanionics. Salt-free catanionics are prepared by slow dissolution of a fatty acid in a solution of cationic surfactant. This solution of cationic surfactant with a hydroxide as counterion is made by using ion exchange from commercial halide forms. Preparation procedure of all salt-free catanionic samples described here is as follows. (i) Recrystallize the myristic acid from acetonitryl. (ii) Ion-exchange the bromide or chloride into hydroxide using resins. (iii) Lyophilize the cationic surfactant in hydroxide form. (iv) Weigh in the desired quantity of fatty acid and cationic surfactant at the desired mole fraction (r). (v) Add high-purity water using gentle stirring with a magnetic bar over the course of several days. (vi) Cycle temperature: heat until above chain-melting temperature of 60°C for a few minutes, and let the solution cool down. Steps iv–vi have to be made in the absence of contact with atmospheric CO₂. A detailed procedure of the preparation of salt-free catanionics is given in refs. 18 and 21.

Results

Sequence of Shapes Versus Variation of Mole Fraction. Dilute (<0.1–0.5%) catanionic solutions present single-phase domains. At higher concentrations and below the chain-melting temperature, a miscibility gap is present between a swollen lamellar phase with in-plane order (L_β) and a diluted dispersion of crystallites. Without salt, the two phases do not separate for synthetic (22) or natural charged lipids (23), but remain optically clear, single fluid microphase-separated samples. These can be partially separated by centrifugation (5,000 rpm, typically 1 h). Coexistence of two different microstructures is most easily identified by neutron scattering or freeze-fracture electron microscopy (FFEM).

Fig. 1 shows the consistent series of microstructures that are encountered when increasing progressively the amount of anionic component (molar ratio varies from 0.416 to 0.75), i.e., on both sides from equimolarity (see preparation procedure in Supporting Text, which is published as supporting information on the PNAS web site). The average structural charge per unit area may be calculated: +17 to –53 μC/cm², taking into account the area per chain of 0.38 nm² per frozen chain pair as deduced from wide-angle x-ray scattering experiments.

Fig. 1.

FFEM of the three states and the coexistence regimes after crystallization. (Bar, 1 μm.) (A) Small discs, r = 0.41; Φ= 3%. (B) Larger discs, r = 0.43; Φ= 3%. (C) Coexistence of discs and icosahedra, r = 0.55; Φ= 0.4%. (D) Icosahedra, r = 0.569; Φ= 0.9%. (E) Coexistence of icosahedra and punctuated planes, r = 0.649; Φ = 2%. (F) Punctured planes, r = 0.75; Φ = 2.65%.

When the excess cationic component is expelled during cocrystallization (0.7 < r < 35), one observes first a dispersion of nanodiscs in an isotropic distribution (Fig. 1 A). With even larger excesses of cationic amphiphiles (r < 0.35), all ion pairs are dissolved into cylindrical micelles of ≈2-nm diameter: no objects can be seen by FFEM, but the typical small-angle neutron-scattering pattern for giant worm-like micelles is obtained.

For r = 0.43, a dispersion of micrometric rigid nanodiscs results (Fig. 1B). Presumably, increasing slightly the molar ratio reduces the amount of cationic component expelled during ion-pair formation. This excess material forms edges in the shape of a half-toroid.

Close to equimolarity (r = 0.55), FFEM microscopy shows a coexistence of discs and closed facetted objects, with disc size comparable with that of opened facetted aggregates (Fig. 1C). Instead of edges, vertices with visible holes are formed when anionic excess material (carboxylate, the anionic insoluble component, with a smaller head group) is excluded during cocrystallization. We find coexistence of flat bits of bilayers (corresponding to broken-up objects) with hollow colloids due to an instability of facetted objects when the number of vertices is too low to form a stable closed facetted aggregate (i.e., a icosahedron). At r = 0.569, only icosahedra are observed, as shown on Fig. 1D. The diameters of all facetted objects ranged from 0.5 to 4 μm. When smaller objects are observed, they remain spherical, reminiscent of a buckling transition. The typical number of vertices is close to 12 and, judging from FFEM pictures, is neither <10 nor >14.

When surface charge is increased above this ideal ratio, one observes the coexistence of punctured bilayers with large objects appearing as crumpled bilayers in the micrometer-size range as shown on Fig. 1E, obtained for r = 0.649. Here, the excess material also forms pores, which act as defects allowing crumpling. Evident on Fig. 1E is that pores are not distributed at random in the plane but repel each other.

At the highest negative surface charge investigated (r = 0.75, Fig. 1F), large (>1 μm) open bilayers punctured with pores are formed. The pore distribution was not randomly distributed but distributed to maximize the nearest-neighbor distance.

Above the chain-melting temperature, large unilamellar vesicles are the stable microstructure. The mechanism of formation of this pore-punctured membrane implies that cocrystallization first creates pores in vesicles. These open bilayers coexist with a swollen L_β phase (“tactoids”), especially if concentration is increased: birefringence and a scattering signature of the lamellar phase appears.

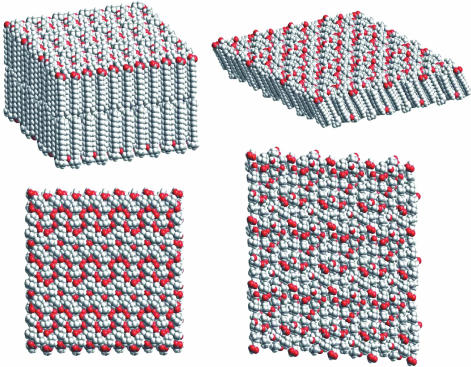
All surfactant aggregates are in the frozen “crystalline” or “gel” state, well known for phospholipids. The 2D lattice of hydrocarbon chains resulting from ion pairing has an in-plane coherence length estimated (≈20 nm resolution) by using profiles obtained for 11 reflections on a Guinier–Mering camera (24). The first-order sharp peak corresponding to an in-plane chain–chain distance of 0.40 nm is not deformed and corresponds to a typical L_β packing without deformation of the hexagonal network (25). A scaled 3D crystalline model of the packing of alternating positive and negative charged amphiphiles in the mole ratios r = 0.66 is shown in Fig. 2 (similar to an antiferromagnetic planar structure). Interdigitated or separated layer lattices of frozen linear hydrophobic chains are possible solutions maximizing packing and minimizing electrostatic interaction energy. [Modeling was performed with cerius² release 4.2 software (Accelrys, Cambridge, U.K.) in the absence of water by using the universal force field. Charges were calculated with the charge-equilibration method.]

Fig. 2.

Packing of myristic acid and cetyltrimethylammonium with straight interdigitated chains at 1:2 relative ratio (Right) and with independent bilayers of 1:1 relative ratio (Left) with thicknesses of 2.2 and 4.5 nm, respectively.

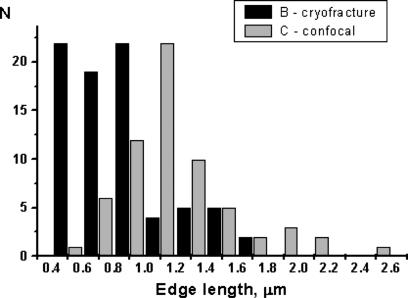
During freezing, an enthalpy of 10 kJ/mol is released, corresponding to 4 k_BT per molecule (26). For the ideal ratio of anionic component (0.56), the distribution of the edge length of icosahedra is centered around 1 μm by confocal microscopy (averaged over 28 objects) and freeze-fracture microscopy (averaged over 79 objects) (Fig. 3). The average size of edges of the facetted objects imaged by microscopy is always 59% of the apparent diameter, as could be deduced from the statistics considering 79 icosahedra imaged by FFEM. This value is characteristic of icosahedra. The mechanism of formation here involves ≈12 pores and 20 edges between adjacent crystallized bilayers per icosahedra, formed during freezing of ion pairs forming the bilayer. Thus, the mechanism of icosahedra formation quenches the smaller part of the distribution of facetted objects, because spontaneous vesiculation of charged surfactants produces significant amounts of vesicles 10 times smaller than the size distribution reported here (5).

Fig. 3.

Statistics of edge lengths of facetted icosahedra as derived from confocal microscopy and FFEM are shown.

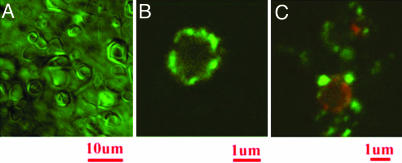
Molecular Segregation at Vertices and Edges. In both, nanodisc and icosahedra formation, we have postulated that excess material forms either edges or pores, so excess charge accumulates on edges and pores. To directly test this hypothesis, we formed complexes between icosahedra and fluorescent charged beads (Fig. 4). The distribution of positively charged 40-nm beads as detected with a scanning confocal fluorescent microscope on the surface of icosahedra lies preferentially on the vertices. Prior incubation with cationic polyelectrolyte (poly-l-lysine) prevented the adsorption of positively charged beads on the icosahedra. To probe whether electrostatic interactions were dominant for bead adsorption on catanionic objects, another bead with negatively charged surface groups was shown by simultaneous confocal fluorescence and differential interference contrast not to be attracted to the surface of icosahedra. When the same experiment is done with a catanionic sample first preincubated with 0.1 μM poly-l-lysine, a polycation, then negatively charged beads are seen on the accumulation sites of poly-l-lysine (Fig. 4C). With increasing concentration and time of incubation beads are also seen at edges. This demonstrates that vertices and, to a smaller degree edges of the icosahedra are negatively charged. Introducing together a very low concentration of positively (20 nm) and negatively (40 nm) charged latex beads, the efficiency of molecular segregation in adsorption is evidenced experimentally: positively charged beads (green) are attracted toward edges and vertices because of excess anionic material, whereas negatively charged beads (red) have more affinity for faces (Fig. 4C).

Fig. 4.

Charge segregation on icosahedra demonstrated by optical microscopy of bead-labeled bilayers. (A) Differential interference contrast image obtained for molar ratio r = 0.56, volume fraction Φ = 0.5%. Shown is the dispersion of icosahedra of a typical 2-μm diameter. (Bar, 10 μm.) (B) Icosahedra as in A were diluted to allow imaging of individual icosahedra with a scanning confocal fluorescence microscope. Fluorescent polystyrene beads (slightly positive latex, 0.1-μm diameter) were found to be specifically adsorbed on vertices and edges of the same sample: r = 0.57, Φ= 0.06%. (Bar, 1 μm.) (C) Same sample as in B labeled with both positive and negative fluorescent beads; 40-nm diameter modified carboxylate (TransFluospheres) beads (red, negative) stain the faces of icosahedra. Aldehyde-sulfate 20-nm beads (green, positive) stain the vertex. The different location of adsorption sites of positive and negative colloids demonstrates heterogeneity of surface charge in icosahedra. (Bar, 1 μm.)

In summary, the three single structures obtained after crystallization are observed in the sequence expected: (i) planes punctured with pores, (ii) facetted objects quasi-equivalent to icosahedra, and (iii) nanodiscs. Because these three microstructures can coexist, five combinations are possible, appearing as a systematic sequence (Fig. 1), because discs can coexist with icosahedra, and these can coexist with planes.

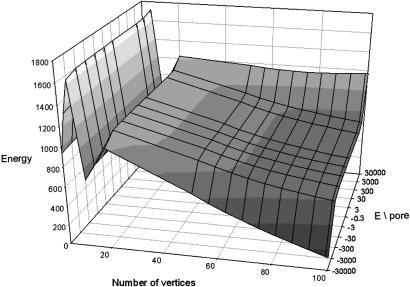
Prevalent Occurrence of Icosahedra Versus Other Polyhedra. We proceed to evaluation of the free energy versus number of vertices, which is shown for a typical diameter of 2 μm. Assuming a bending constant of 200 k_BT, typical for frozen bilayers and an area per molecule of 0.38 nm² per pair in the frozen state, the energy of formation of the five regular polygons and polyhedra made from a large number of adjacent triangles are calculated versus the energy per pore and the number of vertices of facetted polygon.

Polyhedra with N faces have minima in their energy of formation that can range between –3 × 10⁴ and +3 × 10⁴ k_BT per pore (Fig. 5), i.e., 100 times the value estimated from known parameters [i.e., radii of curvature, position of neutral planes and monolayer stiffness (see Evaluation of the Bending Energy Involved in Forming One Pore in Supporting Text)]. The enthalpy gain upon vesicle freezing is 50 kJ/mol (for 2 × 10⁷ amphiphilic ion pairs), 2 orders of magnitude larger than the bending energy associated to faceting of the frozen vesicle shown on Fig. 5 (26). The icosahedron is the local minimum in bending energy, compared with the five platonic solids, and the limiting solid having many triangular faces.

Fig. 5.

Energy per mole of formation of facetted polyhedra embedding N_ν vertices and energy of pore formation. The five platonic polyhedra are compared with discs with a large number of slightly deformed triangles. Icosahedra (12 vertices) correspond to a local minimum of energy of formation as long as the elements needed for forming a large number of pores are not present. Large objects would facet easier than small ones, the mechanism at the origin of narrowing of size distribution.

In principle, a solution exists with lower energy of formation corresponding to a number of elementary triangles exceeding 100. Presumably the formation of this sort of facetted object is not present when crystallizing ion-paired surfactants because it requires fast nucleation and slow growth of each face.

Large excesses of pore-forming molecules preferred to form large punctured planes, as is observed when the pore-forming component (myristic acid) is in excess. A similar preference for some shapes has been obtained as the result of a free energy calculation established by Bruinsma et al. (3). However, in the latter case, an arbitrary local minimum of the bending energy associated with a preferred dihedral angle is required to get shape specificity. The same assumption of a preferred dihedral angle led also to the generation of facetted vesicles in a Brownian dynamics simulation (27). In our case, no such preferred dihedral angle exists.

The first minimum corresponding to 12 pores is an icosahedron, and a large number of pores to vertex decreases total bending energy. In practice, punctured planes are also seen when a thin film superconductor is constrained to a sphere. The evolution of bending energy derived by Dodgson (28) is homothetic to the variation of bending free energy we obtained for facetted catanionic bilayers.

The third term corresponding to the electrostatic internal energy of pores is lower because of the length scales involved: Bjerrum length = 0.7 nm, Debye screening length = 50–100 nm, and edge length = 1 μm, but this term would also facilitate formation of icosahedra (29). (See Thermodynamic Considerations in Supporting Text.)

Seeding-In Pores to Control Shape. As suggested by D. Caspar (personal communication), we tested another consequence of the general mechanism proposed: the possibility of size control through seeding-in defects. Before cooling down the catanionic vesicle solution, we added an amphiphilic molecule with a very large head group to “seed-in” pores and obtain the optimal number of 12 pores per freezing vesicle and hence smaller icosahedra. Indeed, addition of a low mole ratio of amphiphilic cyclodextrins did decrease the average size of facetted objects, as has been established by using the only direct technique combining resolution and absence of preparation protocol, soft x-ray microscopy (see Seeding-In Pores to Form Smaller Icosahedra in Supporting Text).

Discussion

By temperature cycling of catanionic solutions, one may discriminate between thermodynamic and kinetic control. Reversibility can be checked by comparing light scattering before and after heating above the chain-melting temperature, because a sample containing only surfactants in the molten state scatters light several orders of magnitude less than when chains are in the frozen state (30). For the amphiphilic ion pair chosen here, chains melt well above room temperature (60°C), ensuring easy melting into the liquid state and thus reversibility of self-assembly (17). For nanodiscs and icosahedra, temperature cycling allows us to switch back and forth between molten and frozen states (see details in Comparison with Bicelles in Supporting Text).

Although a general theory for shape generation of tapes, ribbons, fibrils, and fibers is available (31), no theory exists for the formation of facetted closed objects (32). A slight misfit within local hexagonal symmetry between adjacent subunits produces helical growth (33), cages, or filaments (34). We have encountered in this study a self-assembling system reminiscent of the shape of some families of virus. However, our aggregates are typically 10 times larger and contain 10⁷ molecules. Viruses are complex self-assembling colloids, where constraints of self-assembly, kinetics, and dynamics produce highly ordered icosahedral capsids. Icosahedral structure is understood by the classic quasi-equivalence principle of Caspar and Klug (35). Typical viral capsids contain 4–5 orders of magnitude fewer molecules per icosahedra than the one described here; hence, the quasi-equivalence principle is not dominant in the catanionics (see Comparison with Quasi-Equivalence in Supporting Text).

The cocrystallization and segregation mechanism proposed here can account for several disparate observations reported in the literature. By using a combination of short-chain and long-chain neutral lipids, such that the short chain accumulates at edges, one expects planar discs, named “bicelles” (36). Comparison with previous observations made with bicelles is given in Comparison with Bicelles in Supporting Text.

The transition from ordered stacks to disordered discs reported with surfactants made from two polar heads at the extremity of one single hydrocarbon chain (“bolaforms”) when temperature is decreased (37) can also be explained by cocrystallization followed by segregation. The bolaform amphipiles can exist in two conformers: straight and hairpin-like, the latter favored at high temperature. The two conformations have only partial miscibility and the hairpin conformation accumulates at edges, so we can simply explain the counterintuitive sequence of shapes of aggregates reported.

Conclusion

All these experiments and observations are consistent with the hypothesis explained above and summarized here: a crystallization and segregation mechanism predicting a general sequence of shapes going from punctured planes to closed aggregates with pores on vertices and finally toward planar nanodiscs, with coexistence between them, as the general route for crystallized charged aggregates (Fig. 6). When the number of holes coming from segregated molecules is ≈12 per initial unilamellar vesicle, a dispersion of icosahedra stabilized by vertices is formed. The amount of the nonstoichiometric component distributes between the lattice, edges, or pores and thus controls the shape of crystallized colloids. (See Generation of Shapes by Crystallization/Segregation Mechanism Using Other Catanionic Ion Pairs in Supporting Text.)

Fig. 6.

The general sequence of morphologies produced upon freezing a two-component vesicle. “Excess” molecules form pores or edges. (Left) With a large number of pores, one obtains punctuated planes. (Center) With 12 pores per vesicle, one obtains icosahedra. (Right) With <12 pores, one obtains fragments and facetted objects. When edges (in blue) are produced, one obtains discs.

One consequence of this study is that segregation after crystallization appears as a general route toward the heterogeneity of lipid domains in the scale of nanometers to microns.