Evolution of Antibody-Drug Conjugate Tumor Disposition Model to Predict Preclinical Tumor Pharmacokinetics of Trastuzumab-Emtansine (T-DM1)

Abstract

A mathematical model capable of accurately characterizing intracellular disposition of ADCs is essential for a priori predicting unconjugated drug concentrations inside the tumor. Towards this goal, the objectives of this manuscript were to: (1) evolve previously published cellular disposition model of ADC with more intracellular details to characterize the disposition of T-DM1 in different HER2 expressing cell lines, (2) integrate the improved cellular model with the ADC tumor disposition model to a priori predict DM1 concentrations in a preclinical tumor model, and (3) identify prominent pathways and sensitive parameters associated with intracellular activation of ADCs. The cellular disposition model was augmented by incorporating intracellular ADC degradation and passive diffusion of unconjugated drug across tumor cells. Different biomeasures and chemomeasures for T-DM1, quantified in the companion manuscript, were incorporated into the modified model of ADC to characterize in vitro pharmacokinetics of T-DM1 in three HER2+ cell lines. When the cellular model was integrated with the tumor disposition model, the model was able to a priori predict tumor DM1 concentrations in xenograft mice. Pathway analysis suggested different contribution of antigen-mediated and passive diffusion pathways for intracellular unconjugated drug exposure between in vitro and in vivo systems. Global and local sensitivity analyses revealed that non-specific deconjugation and passive diffusion of the drug across tumor cell membrane are key parameters for drug exposure inside a cell. Finally, a systems pharmacokinetic model for intracellular processing of ADCs has been proposed to highlight our current understanding about the determinants of ADC activation inside a cell.

INTRODUCTION

The past decade has seen an expeditious emergence of antibody-drug conjugates (ADCs), a novel class of biopharmaceutical agents, as a successful treatment modality for cancer. More than 50 ADCs are already in clinical development against diverse targets, encompassing various hematological malignancies and solid tumors (1). These “armed antibodies” are a chemical combination of monoclonal antibodies (mAbs) and chemotherapeutic agents, attached via a linker. The targeting capability of a mAb along with the cell-killing potential of a chemotherapeutic agent renders increased efficacy and minimal toxicity for ADCs in vivo, leading to widened therapeutic window. Typical mechanism for an ADC involves specific high-affinity binding of the mAb to highly expressed cell surface antigens on tumor cells, followed by receptor-mediated endocytosis. Following internalization, differential properties of the linker in intracellular conditions determines the subsequent trafficking and release of the drug, which subsequently exhibits the cytotoxic effect. Of note, the chemical nature of the linker used for ADC design determines the stability of the ADC in vivo, intracellular processing of the ADC, as well as its off target toxicities. Once the ADC is administered in vivo, the mAb and the released drug exhibits distinctive dispositional characteristics, making it challenging to characterize the pharmacokinetics (PK) and resultant pharmacodynamics (PD) of ADCs. Thus, to generate a translatable multiscale PK model for ADC, it is imperative to integrate all the different processes that determine the disposition of ADC and its component, especially the intracellular processes that determine drug release inside the cells. Once developed, these models can be used to further identify the important pathways and rate-limiting steps, modulations of which could result in the development of better ADCs (2, 3).

Previously, we have described a multiscale mechanistic PK model for tumor disposition of ADCs, which has been applied to two different ADCs, brentuximab-vedotin (4) and A1mcMMAF (5). While both of these ADCs were anatomically very similar (i.e., auristatin based ADCs conjugated via random conjugation at inter-chain disulfide bonds), they differed in their linker chemistry. Brentuximab-vedotin consists of anti-CD30 mAb (cAC10) attached to potent tubulin polymerization inhibiting payload monomethyl auristatin E (MMAE) via a cleavable linker valine-citrulline (vc). Whereas, A1mcMMAF consists of an anti-5 T4 mAb (A1) linked to monomethyl auristatin F (MMAF) via a non-cleavable linker maleimidocaproyl (mc). In the present work, we have augmented our ADC tumor disposition model and have extended its application to a lysine-based ADC, ado-trastuzumab-emtansine (T-DM1, Kadcylla®). T-DM1 is a clinically approved ADC for the treatment of patients with human epidermal growth factor receptor 2 (HER2)-positive metastatic breast cancer, who have been previously treated with trastuzumab (Herceptin®) as a monotherapy or in combination with other chemotherapeutic agents (6). T-DM1 is composed of humanized anti-HER2 mAb trastuzumab attached to DM1 (a derivative of maytansine), via a non-cleavable thioether linker succinimidyl-trans-4-[maleimidylmethyl] cyclohexane-1-carboxylate (SMCC). Overexpression of HER2 (ErbB2) in 20–25% of breast cancer patients along with the easy accessibility of its extracellular domain makes it an ideal target for antibody-based therapeutics (7). The mechanisms of action for trastuzumab include inhibition of PI3K/AKT signaling pathway, inhibition of HER2 shedding, and antibody-dependent cellular cytotoxicity (ADCC) (8). T-DM1 retains these mechanisms of trastuzumab, along with the additional cytotoxic effect of DM1. Proteolytic degradation of T-DM1 results in different catabolites composed of a combination of DM1, the linker SMCC, and the conjugating amino acid lysine. Preclinical and clinical studies have confirmed MCC-DM1 and lysine-MCC-DM1 as two major active catabolites generated following intracellular processing of T-DM1 (9, 10). These catabolites and DM1 are expected to inhibit microtubule polymerization with similar potencies (IC₅₀ ~ 1 μM) (11). Since most T-DM1 catabolites do not readily permeate cell membrane, they are expected to result in minimal bystander effect (10).

In this manuscript, we propose a more mechanistic cellular disposition model for ADCs that explicitly accounts for intracellular proteolytic degradation as well as passive diffusion of DM1 containing molecules across the tumor cell. The cellular model has been validated using cellular disposition data of T-DM1 in different cell lines and different biomeasures reported in the companion paper. The improved cellular model has been integrated into the in vivo tumor disposition model of ADC, and the ability of this augmented model to a priori predict tumor PK of T-DM1 and its components is assessed. The model has been further explored using global and local sensitivity analysis and pathway analysis.

MATERIALS AND METHODS

Datasets

Cellular Disposition of T-DM1 (10)

Intracellular PK of T-[H]³DM1 has been investigated by Erickson et al. (10) in three different HER2 expressing cell lines: BT-474EEI (resistant to trastuzumab), SK-BR3, and MCF-7/neoHER2. Briefly, they introduced a stable tritium label in the C-20 methoxy group of DM1. Cells were cultured in a T-75 flask and were treated with T-[H]³DM1 (30–40 nM) for 2 h at 4°C. Drug containing medium was then exchanged with fresh medium at room temperature and radioactivity associated with maytansinoids (in media and cell pellet) was assessed using liquid scintillation counting (LSC) over the period of 24 h. We have used the data reported by Erickson et al. (10) for cellular disposition of conjugated and unconjugated maytansinoids in intracellular and extracellular space of three different cell lines for the validation of our improved ADC cellular disposition model.

Plasma PK of T-DM1 and DM1

Plasma PK for T-DM1 in both tumor-bearing and non-tumor-bearing mice has been investigated by several groups. Erickson et al. (10) studied PK of total trastuzumab and T-DM1 after intravenous administration of T-DM1 at two different dose levels (2 and 3 mg/kg) in non-tumor-bearing mice. Whereas, Jumbe et al. (12) investigated plasma PK of T-DM1 in tumor-bearing mice after intravenous administration at three different dose levels (0.3, 3, and 15 mg/kg). It has been demonstrated that there is no significant difference in the PK of T-DM1 in tumor-bearing vs. non-tumor-bearing mice. Hence, datasets from both animal models were utilized simultaneously to build a plasma PK model for T-DM1. The systemic disposition model for ADC (explained later in manuscript) also requires the plasma PK of the released drug. However, mouse PK data for DM1 or related T-DM1 catabolites is not reported. Thus, in order to develop the full systemic disposition model for T-DM1, we employed rat plasma PK data for DM1 reported by Shen et al. (9), and scaled down the PK parameters derived from the rat data to mice using the principles of allometry and following equations:

$$\begin{array}{l}{CL}_{\mathit{mice}}={CL}_{\mathit{rats}}.{\left[\frac{25g}{100g}\right]}^{0.75}{\mathit{CLD}}_{\mathit{mice}}\\ ={\mathit{CLD}}_{\mathit{rats}}.{\left[\frac{25g}{100g}\right]}^{0.75}V{1}_{\mathit{mice}}=V{1}_{\mathit{rats}}.{\left[\frac{25g}{100g}\right]}^{1}V{2}_{\mathit{mice}}\\ =V{2}_{\mathit{rats}}.{\left[\frac{25g}{100g}\right]}^1\end{array}$$

All the three datasets (i.e., T-DM1 PK in tumor-bearing and non-tumor-bearing mice, and DM1 PK in rat) were digitized and fitted simultaneously using the integrated systemic disposition model of ADC described in Fig. 1b.

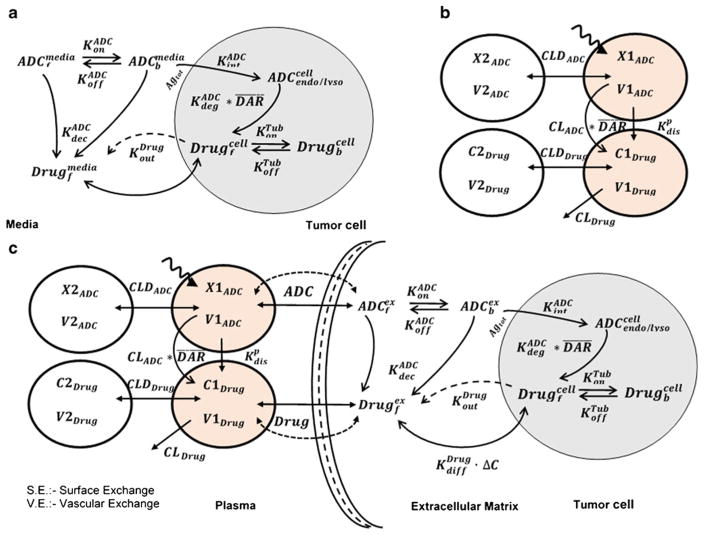
Fig. 1.

Schematics of PK models used to characterize the disposition of T-DM1. a Cellular disposition model for T-DM1 characterizing the intracellular processing and release of DM1 catabolites in the intracellular and extracellular space. b A combined PK model consisting of two integrated two-compartment models characterizing the disposition of T-DM1 and released DM1 catabolites simultaneously. c Full multiscale mechanistic tumor PK model capable of predicting tumor concentrations of released DM1 catabolites based on plasma T-DM1 PK

Tumor PK of T-DM1

In vivo tumor disposition studies for T-DM1 have been performed by Erickson et al. (10) (also well described in Wada et al. (13)) in BT-474EEI tumor-bearing xenograft models. Briefly, tumor-bearing mice were treated with an intravenous dose of T-[H]³ DM1 (300 μg/kg DM1 based dose) upon achieving the tumor volume of ~250 mm³. After treatment, mice were sacrificed at different time points up to 7 days to measure total plasma maytansinoids and tumor maytansinoids concentrations (total and unconjugated) using liquid scintillation counting (LSC). The dataset was digitized and used to validate the predictions made using the augmented mechanistic tumor disposition model of ADC (Fig. 1c), as described later in the manuscript.

Models

Cellular Disposition Model

Figure 1a describes the schematics of the cellular disposition model which was used to capture the intracellular processing of T-DM1. All the state variables drawn in the model diagram have been defined in Table I. Some of the key processes captured in the model includes cell surface binding (K_on^ADC and K_off^ADC) of T-DM1 in media to HER2 receptors (Ag_tot) followed by internalization (K_int^ADC) and degradation in the endosome/lysosome compartment (K_deg^ADC). It is assumed that the HER2 receptors are at steady-state, and total number of HER2 receptors does not change with time. The concentration of available cell surface receptors is calculated by subtracting the bound receptor concentration from the total. Upon degradation, each molecule of T-DM1 is assumed to yield unconjugated maytansinoids (DM1 catabolites) equivalent to the drug-antibody ratio (DAR) at that time. Free DM1 catabolites are assumed to escape into the cytoplasm where they are subjected to binding to intracellular tubulin (K_on^Tub and K_off^Tub) or diffuse (K_diff^Drug) outside the cells into the media. In the absence of many reports stating active efflux of DM1 containing catabolites across cell membrane, the parameter K_out^Drug was assumed to be zero. Non-specific deconjugation of drug in the media from T-DM1 (free or bound to HER2) was characterized using K_dec^ADC parameter. The final intracellular concentrations were calculated using the reported cellular volumes of 3955, 3823, and 3648 μm³ for BT-474EEI, SK-BR3 and MCF-7/neoHER2 cells (10). All the model equations along with initial conditions are as listed below:

$$\begin{array}{l}\frac{d\left({\mathit{ADC}}_f^{\mathit{media}}\right)}{dt}=-K_{on}^{\mathit{ADC}}·{\mathit{ADC}}_f^{\mathit{media}}·\left({Ag}_{\mathit{total}}-{\mathit{ADC}}_b^{\mathit{media}}\right)+K_{\mathit{off}}^{\mathit{ADC}}·{\mathit{ADC}}_b^{\mathit{media}}-K_{\mathit{dec}}^{\mathit{ADC}}·{\mathit{ADC}}_f^{\mathit{media}};IC\\ =AD{C}_{\mathit{media}}(0)\end{array}$$ (1)

$$\frac{d\left({\mathit{ADC}}_b^{\mathit{media}}\right)}{dt}=K_{on}^{\mathit{ADC}}·{\mathit{ADC}}_f^{\mathit{media}}·\left({Ag}_{\mathit{total}}-{\mathit{ADC}}_b^{\mathit{media}}\right)-\left(K_{\mathit{off}}^{\mathit{ADC}}+K_{\mathit{int}}^{\mathit{ADC}}\right)·{\mathit{ADC}}_b^{\mathit{media}}-K_{\mathit{dec}}^{\mathit{ADC}}·{\mathit{ADC}}_b^{\mathit{media}};IC=0$$ (2)

$$\frac{d\left({\mathit{ADC}}_{\mathit{endo}/\mathit{lyso}}^{\mathit{cell}}\right)}{dt}=K_{\mathit{int}}^{\mathit{ADC}}·{\mathit{ADC}}_b^{\mathit{media}}-K_{\mathit{deg}}^{\mathit{ADC}}·{\mathit{ADC}}_{\mathit{endo}/\mathit{lyso}}^{\mathit{cell}};IC=0$$ (3)

$$\begin{array}{l}\frac{d\left({\mathit{Drug}}_f^{\mathit{cell}}\right)}{dt}=K_{\mathit{deg}}^{\mathit{ADC}}·\overline{\mathit{DAR}}·{\mathit{ADC}}_{\mathit{endo}/\mathit{lyso}}^{\mathit{cell}}-K_{on}^{\mathit{Tub}}·{\mathit{Drug}}_f^{\mathit{cell}}·({\mathit{Tub}}_{\mathit{total}}-{\mathit{Drug}}_b^{\mathit{cell}})\\ +K_{\mathit{off}}^{\mathit{Tub}}·{\mathit{Drug}}_b^{\mathit{cell}}-K_{\mathit{out}}^{\mathit{Drug}}·{\mathit{Drug}}_f^{\mathit{cell}}+K_{\mathit{diff}}^{\mathit{Drug}}·\left({\mathit{Drug}}_f^{\mathit{media}}-{\mathit{Drug}}_f^{\mathit{cell}}\right);IC=0\end{array}$$ (4)

$$\begin{array}{l}\frac{d\left({\mathit{Drug}}_b^{\mathit{cell}}\right)}{dt}=K_{on}^{\mathit{Tub}}·{\mathit{Drug}}_f^{\mathit{cell}}·\left({\mathit{Tub}}_{\mathit{total}}-{\mathit{Drug}}_b^{\mathit{cell}}\right)-K_{\mathit{off}}^{\mathit{Tub}}·{\mathit{Drug}}_b^{\mathit{cell}};IC\\ =0\end{array}$$ (5)

$$\begin{array}{l}\frac{d\left({\mathit{Drug}}_f^{\mathit{media}}\right)}{dt}=K_{\mathit{out}}^{\mathit{Drug}}·{\mathit{Drug}}_f^{\mathit{cell}}+K_{\mathit{dec}}^{\mathit{ADC}}·\overline{\mathit{DAR}}·\left({\mathit{ADC}}_f^{\mathit{media}}+{\mathit{ADC}}_b^{\mathit{media}}\right)-K_{\mathit{diff}}^{\mathit{Drug}}·\left({\mathit{Drug}}_f^{\mathit{media}}-{\mathit{Drug}}_f^{\mathit{cell}}\right);IC\\ =0\end{array}$$ (6)

$$\frac{d\left(\overline{\mathit{DAR}}\right)}{dt}=-K_{\mathit{dec}}^{\mathit{ADC}}·\overline{\mathit{DAR}};IC={\overline{\mathit{DAR}}}^0$$ (7)

Table I.

Glossary of the state variables and model parameters used to build the model

Symbol	Definition	Unit
${\mathit{ADC}}_{\mathit{f}}^{\mathit{media}},{\mathit{ADC}}_{\mathit{b}}^{\mathit{media}},{\mathit{ADC}}_{\mathit{f}}^{\mathit{ex}},{\mathit{ADC}}_{\mathit{b}}^{\mathit{ex}}$	Free (f) and bound (b) concentrations of ADC in the media or extracellular space (ex).	nM
ADCendo/lysocell	Concentration of ADC internalized in the endosome/lysosome of a tumor cell.	nM
${\mathit{Drug}}_{\mathit{f}}^{\mathit{cell}},{\mathit{Drug}}_{\mathit{b}}^{\mathit{cell}}$	Intracellular concentrations of the unconjugated drug free (f) and bound (b) to Tubulin.	nM
${\mathit{Drug}}_{\mathit{f}}^{\mathit{media}},{\mathit{Drug}}_{\mathit{f}}^{\mathit{ex}}$	Free (f) drug concentrations in the media and extracellular space (ex).	nM
${\mathit{K}}_{\mathit{on}}^{\mathit{ADC}},{\mathit{K}}_{\mathit{off}}^{\mathit{ADC}}$	Association and Dissociation rate constants between ADC and tumor antigen.	1/nM/day, 1/day
KdecADC, KdecP	Deconjugation rate constant of drug from ADC in the cell-culture media and plasma, respectively.	1/day
${\mathit{K}}_{\mathit{out}}^{\mathit{Drug}},{\mathit{K}}_{\mathit{diff}}^{\mathit{Drug}}$	Active efflux and passive diffusion rates of drug between tumor cell and media/extracellular matrix	1/day
KdecADC	Endosomal degradation rate constant of the ADC to release free drug	1/day
${\mathit{K}}_{\mathit{on}}^{\mathit{Tub}},{\mathit{K}}_{\mathit{off}}^{\mathit{Tub}}$	Association and Dissociation rate constants between Drug and intracellular Tubulin.	1/nM/day, 1/day
KintADC	Internalization rate constant of the antigen inside the cell	1/day
$\overline{\mathit{DAR}},{\overline{\mathit{DAR}}}^0$	Average DAR values at time ‘t’ and time 0	1
X1ADC, X1mAb, X1drug	Amount of ADC, total mAb and Drug in the systemic circulation.	nMol.
X2ADC, X2mAb, X2drug	Amount of ADC, total mAb and Drug in the peripheral circulation	nMol.
C1drug, C2drug	Concentration of drug in the systemic and peripheral circulation	nM
V1ADC, V1mAb, V1Drug	Volume of distribution in the central compartment for ADC, mAb, and drug	L
CLADC, CLmAb, CLDrug	Central Clearance of ADC, mAb, and drug	L/day
V2ADC, V2mAb, V2Drug	Volume of Distribution in the peripheral compartment for ADC, mAb, and drug	L
CLDADC, CLDmAb, CLDDrug	Distributional Clearance of ADC, mAb, and drug	L/day
RCap, RKrogh	Radius of the tumor blood capillary (cap), and an average distance between two capillaries (known as the Krogh radius)	μm
PADC, DADC	Permeability and diffusion coefficients of ADC across and around the tumor blood vessels.	μm/day, cm2/day
PDrug, DDrug	Permeability and diffusion coefficients of released drug across and around the tumor blood vessels	μm/day, cm2/day
ADC, Drug	Tumor void volume for ADC and drug	Unitless
TV, RTumor	Total volume and radius of a spherical tumor where: $TV=\frac{4}{3}·\pi R_{\mathit{Tumor}}^3$	mm3, cm
Agtotal, ADC_Agbound	Total antigen and ADC bound antigen concentrations	nM
Tubtotal	Total drug binding tubulin concentration	nM
DoseADC	Amount of ADC injected in tumor-bearing mice	nMol
ADCmedia(0)	Initial concentration of ADC in media	nM

Plasma PK Model

Figure 1b describes the schematics of the plasma PK model for T-DM1. The biexponential profile of T-DM1 in mice is captured by a two-compartment PK model with linear clearance (CL_ADC) from central compartment and distributional clearance (CLD_ADC) to peripheral compartment. Extraclearance component, K_dec^p (non-specific deconjugation of DM1 in systemic circulation), accounts for faster clearance of conjugated antibody (T-DM1) cf. total antibody (TmAb). The disposition of released DM1, generated either by proteolytic degradation of T-DM1 (CL_ADC) or via non-specific deconjugation (K_dec^p), is also characterized using a two-compartment model with linear clearance (CL_Drug) and distributional clearance (CLD_Drug). Total clearance of T-DM1 as well as deconjugation clearance (via K_dec^p) feeds as an input to the DM1 PK model. The integrated PK model was used to characterize the PK of T-DM1 in tumor-bearing and non-tumor-bearing mice and the PK of DM1 in rats simultaneously. The associated model equations along with initial conditions are as listed below:

$$\begin{array}{l}\frac{d(X{1}_{\mathit{mAb}})}{dt}=-\frac{{CL}_{\mathit{mAb}}}{V{1}_{\mathit{mAb}}}·X{1}_{\mathit{mAb}}-\frac{{\mathit{CLD}}_{\mathit{mAb}}}{V{1}_{\mathit{mAb}}}·X{1}_{\mathit{mAb}}+\frac{{\mathit{CLD}}_{\mathit{mAb}}}{V{2}_{\mathit{mAb}}}·X{2}_{\mathit{mAb}};IC\\ ={\mathit{Dose}}_{\mathit{ADC}}\end{array}$$ (8)

$$\frac{d(X{2}_{\mathit{mAb}})}{dt}=\frac{{\mathit{CLD}}_{\mathit{mAb}}}{V{1}_{\mathit{mAb}}}·X{1}_{\mathit{mAb}}-\frac{{CL}_{\mathit{mAb}}}{V{2}_{\mathit{mAb}}}·X{2}_{\mathit{mAb}};IC=0$$ (9)

$$\begin{array}{l}\frac{d(X{1}_{\mathit{ADC}})}{dt}=-\frac{{CL}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}·X{1}_{\mathit{ADC}}-\frac{{\mathit{CLD}}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}·X{1}_{\mathit{ADC}}+\frac{{\mathit{CLD}}_{\mathit{ADC}}}{V{2}_{\mathit{ADC}}}·X{2}_{\mathit{ADC}}-K_{\mathit{dec}}^p·X{2}_{\mathit{ADC}};IC\\ ={\mathit{Dose}}_{\mathit{ADC}}\end{array}$$ (10)

$$\begin{array}{l}\frac{d(X{2}_{\mathit{ADC}})}{dt}=\frac{{\mathit{CLD}}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}·X{1}_{\mathit{ADC}}-\frac{{CL}_{\mathit{ADC}}}{V{2}_{\mathit{ADC}}}·X{2}_{\mathit{ADC}};IC\\ =0\end{array}$$ (11)

$$\begin{array}{l}\frac{d\left(C{1}_{\mathit{Drug}}\right)}{dt}=-\frac{{CL}_{\mathit{Drug}}}{V{1}_{\mathit{Drug}}}·C{1}_{\mathit{Drug}}-\frac{{\mathit{CLD}}_{\mathit{Drug}}}{V{1}_{\mathit{Drug}}}·C{1}_{\mathit{Drug}}+\frac{{\mathit{CLD}}_{\mathit{Drug}}}{V{1}_{\mathit{Drug}}}·C{2}_{\mathit{ADC}}+\frac{X{1}_{\mathit{ADC}}·\overline{\mathit{DAR}}·K_{\mathit{dec}}^p}{V{1}_{\mathit{Drug}}}+\frac{{CL}_{\mathit{ADC}}·\mathit{DAR}·\frac{X{1}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}}{V{1}_{\mathit{Drug}}};IC\\ =0\end{array}$$ (12)

$$\begin{array}{l}\frac{d(C{2}_{\mathit{Drug}})}{dt}=\frac{{\mathit{CLD}}_{\mathit{Drug}}}{V{2}_{\mathit{Drug}}}·C{1}_{\mathit{Drug}}-\frac{{\mathit{CLD}}_{\mathit{Drug}}}{V{2}_{\mathit{Drug}}}·C{2}_{\mathit{Drug}};IC\\ =0\end{array}$$ (13)

$$\frac{d\left(\overline{\mathit{DAR}}\right)}{dt}=-K_{\mathit{dec}}^p·\overline{\mathit{DAR}};IC={\overline{\mathit{DAR}}}^0$$ (14)

Tumor PK Model

Figure 1c describes the schematics of the complete tumor disposition model for ADCs, which is used to predict tumor T-DM1 PK in a preclinical xenograft model. All the state variables are defined in Table I and a detailed description of model has been published in our previous work (4, 5). Briefly, after administration in a tumor-bearing mouse, T-DM1 and DM1 disposition in the systemic circulation and peripheral tissues is described by the PK model described earlier (Fig. 1b). Both T-DM1 and released DM1 catabolites in the systemic circulation are exchanged with the tumor extracellular space using permeability and diffusion associated terms determined by respective molecular size. This portion of the model is based on the seminal work conducted by Dr. Wittrup’s lab regarding exchange of different molecules between systemic circulation and tumor microenvironment (14–16). Size of the tumor determines the extent of distribution via either surface exchange or vascular exchange. At lower tumor sizes, surface exchange predominates, and at higher tumor sizes when the tumor develops vasculature, the vascular exchange predominates. It is assumed that due to the higher interstitial pressure inside the tumor, drug distribution to the tumor is limited to diffusive processes only, and transport via convection is not considered. Size-specific values of diffusivity, permeability, and accessible tumor volumes (or void volumes) were used for T-DM1 and unconjugated DM1 catabolites as described in Tables I and II. Within the tumor extracellular space, T-DM1 binds to HER-2 receptors on the cell surface and gets internalized. It is assumed that the HER2 receptors are at steady-state, and total number of HER2 receptors does not change with time. The concentration of available cell surface receptors is calculated by subtracting the bound receptor concentration from the total. Internalized T-DM1 is degraded in the endosome/lysosomal compartment, yielding DM1 catabolites which are free to either bind to intracellular tubulin or diffused (viaK_diff^Drug) to extracellular space. The effluxed or generated DM1 (via non-specific deconjugation from free or bound T-DM1) in the extracellular space can distribute back into the systemic circulation via tumor exchange processes described earlier (14–16). The parameters obtained from earlier two analysis (i.e., cellular disposition model and plasma PK model) were fixed in this final step to a priori predict the tumor concentration of DM1 catabolites. All the model equations along with initial conditions are as listed below in Eq. 15–25:

$$\begin{array}{l}\frac{d(X{1}_{\mathit{ADC}})}{dt}=-\frac{{CL}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}·X{1}_{\mathit{ADC}}-\frac{{\mathit{CLD}}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}·X{1}_{\mathit{ADC}}\\ +\frac{{\mathit{CLD}}_{\mathit{ADC}}}{V{2}_{\mathit{ADC}}}·X{2}_{\mathit{ADC}}-\frac{2·P_{\mathit{ADC}}·R_{\mathit{Cap}}}{{R_{\mathit{Krogh}}}^2}·\left({\epsilon }_{\mathit{ADC}}·\frac{X{1}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}-{\mathit{ADC}}_f^{ex}\right)·TV\\ -\frac{6·D_{\mathit{ADC}}}{R_{\mathit{Tumor}}^2}·\left({\epsilon }_{\mathit{ADC}}·\frac{X{1}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}-{\mathit{ADC}}_f^{ex}\right)·TV;IC={\mathit{Dose}}_{\mathit{ADC}}\end{array}$$ (15)

$$\begin{array}{l}\frac{d(X{2}_{\mathit{ADC}})}{dt}=\frac{{\mathit{CLD}}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}·X{1}_{\mathit{ADC}}-\frac{{CL}_{\mathit{ADC}}}{V{2}_{\mathit{ADC}}}·X{2}_{\mathit{ADC}};IC\\ =0\end{array}$$ (16)

$$\begin{array}{l}\frac{d\left({\mathit{ADC}}_f^{ex}\right)}{dt}=\frac{2·P_{\mathit{ADC}}·R_{\mathit{Cap}}}{{R_{\mathit{Krogh}}}^2}·\left({\mathit{\epsilon }}_{\mathit{ADC}}·\frac{X{1}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}-{\mathit{ADC}}_f^{ex}\right)\\ +\frac{6·D_{\mathit{ADC}}}{R_{\mathit{Tumor}}^2}·\left({\epsilon }_{\mathit{ADC}}·\frac{X{1}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}-{\mathit{ADC}}_f^{ex}\right)\\ -K_{on}^{\mathit{ADC}}·{\mathit{ADC}}_f^{ex}·\left(\left({Ag}_{\mathit{total}}-{\mathit{ADC}}_b^{ex}\right)/{\mathit{\epsilon }}_{\mathit{ADC}}\right)\\ +K_{\mathit{off}}^{\mathit{ADC}}·{\mathit{ADC}}_b^{ex}-K_{\mathit{dec}}^{\mathit{ADC}}·{\mathit{ADC}}_f^{ex};IC=0\end{array}$$ (17)

$$\begin{array}{l}\frac{d\left({\mathit{ADC}}_b^{ex}\right)}{dt}=K_{on}^{\mathit{ADC}}·{\mathit{ADC}}_f^{ex}·\left(\left({Ag}_{\mathit{total}}-{\mathit{ADC}}_b^{ex}\right)/{\mathit{\epsilon }}_{\mathit{ADC}}\right)-\left(K_{\mathit{off}}^{\mathit{ADC}}+K_{\mathit{int}}^{\mathit{ADC}}+K_{\mathit{dec}}^{\mathit{ADC}}\right)·{\mathit{ADC}}_b^{ex};IC\\ =0\end{array}$$ (18)

$$\frac{d\left({\mathit{ADC}}_{\mathit{endo}/\mathit{lyso}}^{\mathit{cell}}\right)}{dt}=K_{\mathit{int}}^{\mathit{ADC}}·{\mathit{ADC}}_b^{ex}-K_{\mathit{deg}}^{\mathit{ADC}}·{\mathit{ADC}}_{\mathit{endo}/\mathit{lyso}}^{\mathit{cell}};IC=0$$ (19)

$$\begin{array}{l}\frac{d\left({\mathit{Drug}}_f^{\mathit{cell}}\right)}{dt}\\ =K_{\mathit{deg}}^{\mathit{ADC}}·\overline{\mathit{DAR}}·{\mathit{ADC}}_{\mathit{endo}/\mathit{lyso}}^{\mathit{cell}}-K_{on}^{\mathit{Tub}}·{\mathit{Drug}}_f^{\mathit{cell}}·\left({\mathit{Tub}}_{\mathit{total}}-{\mathit{Drug}}_b^{\mathit{cell}}\right)\\ +K_{\mathit{off}}^{\mathit{Tub}}·{\mathit{Drug}}_b^{\mathit{cell}}-K_{\mathit{out}}^{\mathit{Drug}}·{\mathit{Drug}}_f^{\mathit{cell}}\\ +K_{\mathit{diff}}^{\mathit{Drug}}·\left({\mathit{Drug}}_f^{ex}-{\mathit{Drug}}_f^{\mathit{cell}}\right);IC=0\end{array}$$ (20)

$$\frac{d\left({\mathit{Drug}}_b^{\mathit{cell}}\right)}{dt}=K_{on}^{\mathit{Tub}}·{\mathit{Drug}}_f^{\mathit{cell}}·\left({\mathit{Tub}}_{\mathit{total}}-{\mathit{Drug}}_b^{\mathit{cell}}\right)-K_{\mathit{off}}^{\mathit{Tub}}·{\mathit{Drug}}_b^{\mathit{cell}};IC=0$$ (21)

$$\begin{array}{l}\frac{d\left({\mathit{Drug}}_f^{ex}\right)}{dt}=\frac{2·P_{\mathit{Drug}}·R_{\mathit{Cap}}}{{R_{\mathit{Krogh}}}^2}·\left({\epsilon }_{\mathit{Drug}}·C{1}_{\mathit{Drug}}-{\mathit{Drug}}_f^{ex}\right)\\ +\frac{6·D_{\mathit{Drug}}}{{R_{\mathit{Tumor}}}^2}·\left({\epsilon }_{\mathit{Drug}}·C{1}_{\mathit{Drug}}-{\mathit{Drug}}_f^{ex}\right)\\ +K_{\mathit{out}}^{\mathit{Drug}}·{\mathit{Drug}}_f^{\mathit{cell}}\\ +K_{\mathit{dec}}^{\mathit{ADC}}·\overline{\mathit{DAR}}·\left({\mathit{ADC}}_f^{ex}+{\mathit{ADC}}_b^{ex}\right)\\ -K_{\mathit{int}}^{\mathit{Drug}}·\left({\mathit{Drug}}_f^{ex}-{\mathit{Drug}}_f^{\mathit{cell}}\right);IC\\ =0\end{array}$$ (22)

$$\begin{array}{l}\frac{d(C{1}_{\mathit{Drug}})}{dt}=-\frac{{CL}_{\mathit{Drug}}}{V{1}_{\mathit{Drug}}}·C{1}_{\mathit{Drug}}-\frac{{\mathit{CLD}}_{\mathit{Drug}}}{V{1}_{\mathit{Drug}}}·C{1}_{\mathit{Drug}}\\ +\frac{{\mathit{CLD}}_{\mathit{Drug}}}{V{1}_{\mathit{Drug}}}·C{2}_{\mathit{ADC}}-\frac{2·P_{\mathit{Drug}}·R_{\mathit{Cap}}}{{R_{\mathit{Krogh}}}^2}\left({\epsilon }_{\mathit{Drug}}·C{1}_{\mathit{Drug}}-{\mathit{Drug}}_f^{ex}\right)\\ -\frac{6·D_{\mathit{Drug}}}{{R_{\mathit{Tumor}}}^2}·\left({\epsilon }_{\mathit{Drug}}·C{1}_{\mathit{Drug}}-{\mathit{Drug}}_f^{ex}\right)\\ +\frac{X{1}_{\mathit{ADC}}·\overline{\mathit{DAR}}·K_{\mathit{dec}}^p}{V{1}_{\mathit{Drug}}}+\frac{{CL}_{\mathit{ADC}}·\mathit{DAR}·\frac{X{1}_{\mathit{ADC}}}{V{1}_{\mathit{ADC}}}}{V{1}_{\mathit{Drug}}};IC=0\end{array}$$ (23)

$$\begin{array}{l}\frac{d\left(C{2}_{\mathit{Drug}}\right)}{dt}=\frac{{\mathit{CLD}}_{\mathit{Drug}}}{V{2}_{\mathit{Drug}}}·C{1}_{\mathit{Drug}}-\frac{{\mathit{CLD}}_{\mathit{Drug}}}{V{2}_{\mathit{Drug}}}·C{2}_{\mathit{Drug}};IC\\ =0\end{array}$$ (24)

$$\frac{d\left(\overline{\mathit{DAR}}\right)}{dt}=-K_{\mathit{dec}}^p·\overline{\mathit{DAR}};IC={\overline{\mathit{DAR}}}^0$$ (25)

Table II.

Estimated, experimentally obtained, or literature-derived values of the model parameters supporting the three models

Parameters	Value (CV %)	Unit	Source	Category
Intracellular model parameters
KonADC	0.37	1/nM/h	(17)	Drug-specific
KoffADC	0.014	1/h	(17)	Drug-specific
KintADC	0.11	1/h	(17)	System-specific
KdegADC	0.03	1/h	(17)	System-specific
KonTub	0.03	1/nM/h	(5)	Drug-specific
KoffTub	10.6	1/h	(25)	Drug-specific
Tubtotal	65	nM	(5)	System-specific
KdecADC	0.0226	1/h	(24)	Drug-specific
KdiffDrug	0.092 (17.4%)	1/h	Estimated	Drug-specific
KoutDrug	0	1/h	Fixed	Drug-specific
AgtotalBT – 474EEI	0.594 (12.4%)	nM	Estimated	System-specific
AgtotalSK – BR3	1.6 (11.3%)	nM	Estimated	System-specific
AgtotalMCF – 7/neoHER2	1.96 (11.8%)	nM	Estimated	System-specific
Systemic PK Parameters
CLADC	0.0093 (4.4%)	L/day	Estimated	Drug-specific
CLDADC	0.118 (12.6%)	L/day	Estimated	Drug-specific
V1ADC	0.043 (7.3%)	L	Estimated	Drug-specific
V2ADC	0.0948 (5.2%)	L	Estimated	Drug-specific
CLDrug	11.29 (78.2%)	L/day	Estimated	Drug-specific
CLDDrug	155.4	L/day	Fixed	Drug-specific
V1Drug	3.30 (48%)	L	Estimated	Drug-specific
V2Drug	2.01	L	Fixed	Drug-specific
KdecP	0.241 (8.8%)	1/day	Estimated	Drug-specific
${\overline{\mathit{DAR}}}^0$	4.0	1	Fixed	Drug-specific
Tumor distribution parameters:
RCap	8	mm	(5)	System-specific
RKrogh	75	mm	(5)	System-specific
PADC	334	μm/day	(5)	Drug-specific
PDrug	21000	μm/day	(5)	Drug-specific
DADC	0.022	cm2/day	(5)	Drug-specific
DDrug	0.25	cm2/day	(5)	Drug-specific
RKrogh	75	mm	(5)	System-specific
ADC	0.24	Unitless	(5)	Drug-specific
Drug	0.44	Unitless	(5)	Drug-specific
TV	250	mm3	(10, 13)	System-specific

Biomeasures and Chemomeasures

T-DM1 binding coefficients (K_on^ADC and K_off^ADC) to HER2, the antigen-antibody internalization rate (K_int^ADC), and the lysosomal degradation rates (K_deg^ADC) were measured in-house and are well described in the accompanying manuscript (17). The rest of the parameters were either extracted from literature or were estimated using the model fitting criteria, details of which are provided in the Table II.

Modeling and Simulation

All the datasets were digitized from original publications using Grab It!® software package. Models were simulated using the software Berkeley Madonna (University of California at Berkeley, CA) and were fitted to the data using maximum likelihood (ML) estimation methods in ADAPT-5 software (BMSR, CA) (18). For the model fitting, following variance model was used, where σ_intercept refers to the additive error to the data and σ_slope refers to the proportional error to the model output.

$$\mathit{Var}(t)={\left({\sigma }_{\mathit{intercept}}+{\sigma }_{\mathit{slope}}·Y(t)\right)}^2$$ (26)

Local Sensitivity and Pathway Analysis

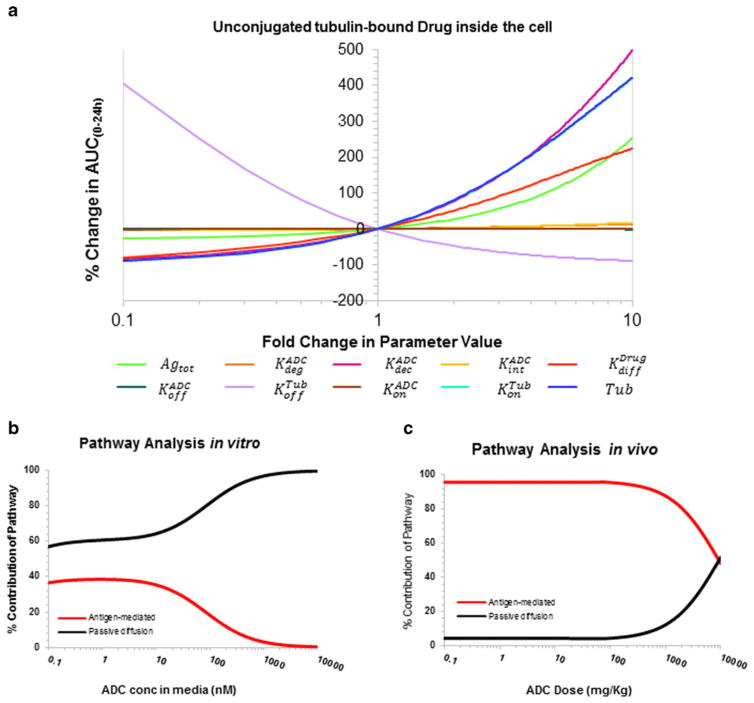
Local sensitivity analysis was performed using Berkeley Madonna on the proposed cellular PK model for ADC (Fig. 1a). The changes in relevant state variables were assessed with progressive changes in individual parameter values. Model-based exposures (AUC_(0–24h)) of total $\left({\mathit{ADC}}_f^{\mathit{media}}·\overline{\mathit{DAR}}+{\mathit{Drug}}_f^{\mathit{media}}\right)$ and unconjugated maytansinoids (Drug_f^media) in the extracellular space as well as free unconjugated (Drug_f^Cell) and tubulin-bound unconjugated maytansinoids (Drug_b^cell) in the intracellular space were simulated based on 0.1–10-fold change in parameter values. Percent changes in the exposure of each variable were plotted against the changes in the parameter values, to identify the most important model parameters. Pathway analysis was performed on the cellular disposition model (Fig. 1a) and tumor disposition model (Fig. 1c) using Berkeley Madonna to quantify the relative contribution of antigen-mediated and passive diffusion pathways in generating the amount of unconjugated drug inside a cell.

Global Sensitivity Analysis

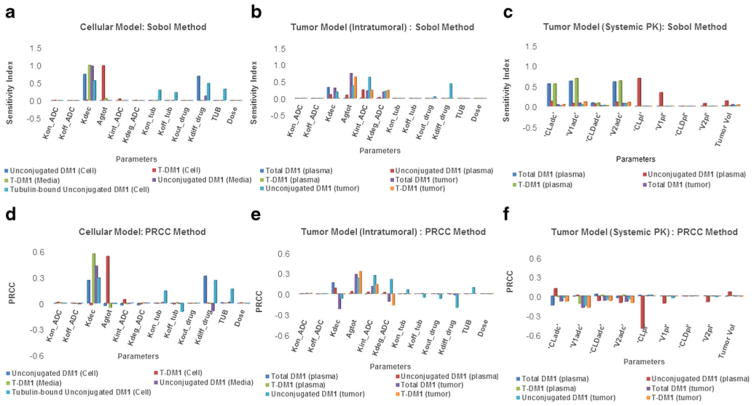
Considering the complexity of the underlying system, global sensitivity analysis (GSA) was performed where all parameters in a cellular model (Fig. 1a) and full tumor disposition model (Fig. 1c) were simultaneously varied to deduce the overall uncertainty described in the model output by an individual parameter. The analysis was performed using Sbtoolbox2 in Matlab® (19) using two methods, i.e., Partial Rank Correlation Coefficient (PRCC) and Sobol method with a sampling size of 100,000 and parameter range of 1 (100% lower or higher). PRCC describes the relative importance of a parameter along with positive/negative correlation to the desired model output (20), whereas Sobol method describes the overall effect (either individually or via interaction with other parameters) on a model output (21). The model-based exposures (AUC_(0–24h)) of total unconjugated DM1, tubulin-bound DM1, and T-DM1 in the intracellular and extracellular space were used as model outputs for GSA of the cellular model (Fig. 1a). Whereas exposures (AUC_(0–10day)) of total DM1, unconjugated DM1, and T-DM1 in tumor and systemic circulation were used for the full model (Fig. 1c).

RESULTS

Cellular Disposition Model

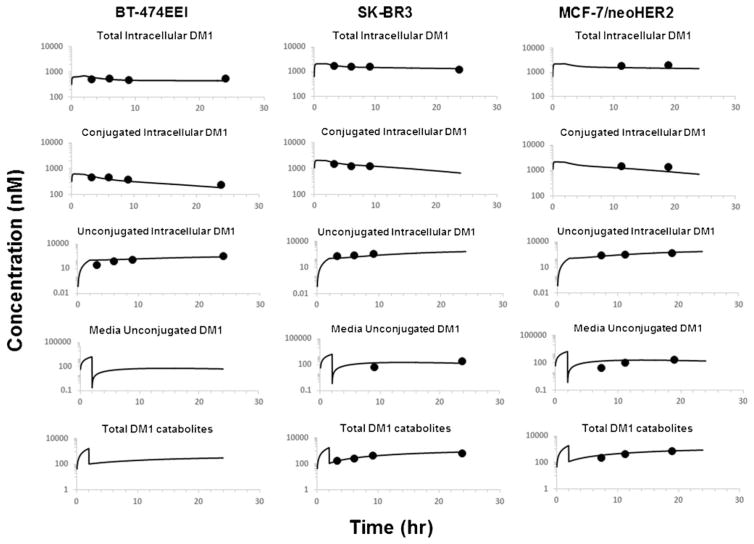
Figure 2 shows the observed and model generated profiles of total, conjugated, and unconjugated DM1 inside the cells, and unconjugated and total DM1 in the media, after treating BT-474EEI, SK-BR3, and MCF-7/neoHER2 cells with T-DM1. The cell volumes of 3955, 3823, and 3648 μm³ for BT-474EEI, SK-BR3 and MCF-7/neoHER2 cells were used in the model building while predicting the intracellular concentrations of T-DM1 and DM1 metabolites, to account for the number of cells that could be packed in a liter volume. The washing step after 2 h of treatment (as described in experimental design) was captured in the model by resetting the media state variables to zero at that time (10). All the fixed parameters obtained experimentally or from literature, as well as fitted parameter estimates, are reported in Table II.

Fig. 2.

Observed and model generated profiles of total, conjugated, and unconjugated maytansinoids inside the cells, and unconjugated and total DM1 in the media, after treating BT-474EEI, SK-BR3, and MCF-7/neoHER2 cells with DM1 (10)

Plasma PK Model

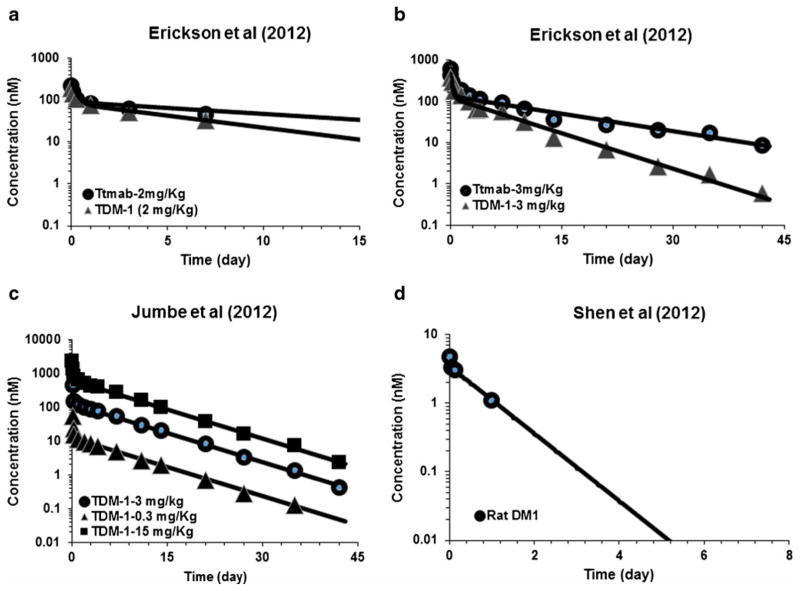
Figure 3 shows the observed and model generated plasma PK profiles of T-DM1 and DM1 in mice and rats, respectively. The model shown in Fig. 1b was fitted to all the data simultaneously. The upper 2 panels of Fig. 3 show the average PK data of total trastuzumab and T-DM1 in non-tumor-bearing mice after IV administration of 2 and 3 mg/kg doses. The lower left panel shows the average PK profile of T-DM1 in tumor-bearing mice after IV administration of 0.3, 3, and 15 mg/kg doses. The lower right panel shows the model fitted DM1 profile in rats, which was used to obtain mouse parameters following allometric scale-down. All parameter estimates are reported in Table II.

Fig. 3.

Observed and model generated plasma PK profiles of total trastuzumab and T-DM1, after a 2 mg/kg and b 3 mg/kg dose of T-DM1 in non-tumor-bearing mice. c Observed and model generated plasma PK profile of T-DM1 after 0.3, 3, and 15 mg/kg intravenous dose of T-DM1 in tumor-bearing mice. d Observed and model generated plasma PK profile of DM1 after intravenous DM1 administration in rats

A priori Predictions of Tumor PK

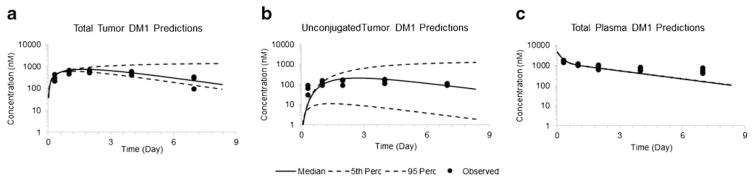
Figure 4 shows the model predicted PK profiles of total maytansinoids (i.e., T-DM1 + unconjugated DM1) in tumor and plasma, as well as unconjugated DM1 profile in tumor. The a priori model predictions were overlaid with experimentally obtained data in BT-474EEI xenograft, after IV administration of 300 μg/kg [H]³DM1-based dose of T-[H]³DM1(10, 13). While making predictions, the cellular disposition parameters specific to BT-474EEI cell line as well as the plasma PK parameters for T-DM1 were fixed to estimates obtained in the previous sections. The tumor distribution parameters associated with T-DM1 and DM1 were fixed to what has been reported in our earlier work (4, 5). The diffusion rate constant of drug across the cell membrane (K_diff^Drug) was fixed to a value estimated based on the in vitro system. Since K_diff^Drug is an important parameter whose value has not been previously reported in the literature, we also assessed the importance of uncertainty in this parameter. The estimated uncertainty in cellular model fitting (i.e., CV% of 17.4) was used to run Monte-Carlo simulations to generate 5th and 95th percentile confidence intervals around the median, which are shown by dotted lines in Fig. 4. The predicted exposure (AUC_(0–24h)) values were quantitatively compared with observed values using the percentage prediction error (% PE) using the expression: $\frac{\mid \mathit{Pred}-\mathit{Obs}\mid }{\mathit{Pred}}\times 100$. The %PE values for plasma, total tumor, and unconjugated tumor maytansinoid exposure were found to be 2.5, 20.5, and 22.8%. The parameter values associated with the final model are listed in Table II.

Fig. 4.

Observed and a priori model predicted profiles of a total maytansinoids and b unconjugated maytansinoids in the tumor, and c total plasma maytansinoids, obtained after IV administration of 300 μg/kg [H]³DM1-based dose of T-[H]³DM1 in BT-474EEI tumor-bearing mice

Local Sensitivity and Pathway Analysis of Cellular Disposition Model

Figure 5a shows the local sensitivity analysis profile for tubulin-bound drug inside the cell (Drug_cell^b) generated using the improved cellular disposition model for ADC shown in Fig. 1a. The non-specific deconjugation rate (K_dec^ADC) and passive diffusion rate (K_diff^Drug) were identified as the most sensitive parameters for free and bound unconjugated maytansinoid exposures in the intracellular space. Additionally, total and unconjugated maytansinoid levels in the intracellular space were also dependent on the total antigen expression (Ag_tot). The sensitivity analysis for other state variables is provided in the Supplementary Figures 1–3. Figure 5b and c shows the pathway analysis profiles of cellular model (Fig. 1a) and full tumor PK model (Fig. 1c), respectively, as a function of ADC dose. Both antigen-mediated and passive diffusion pathways start out with approximately equal contribution in an in vitro setting (Fig. 5b), with saturation of antigen-mediated pathway with increasing ADC dose. However, in the in vivo setting, the antigen-mediated pathway predominates at pharmacological relevant doses (Fig. 5c), mainly because the unconjugated drug outside the cells in the tumor is readily available for diffusion outside the tumor.

Fig. 5.

a Local sensitivity of the improved cellular disposition model with respect to intracellular unconjugated (tubulin) bound drug as an output, b pathway analysis of in vitro cellular disposition model for assessing relative importance of antigen-mediated and diffusion pathways of intracellular drug delivery, and c pathway analysis of in vivo tumor disposition model for assessing relative importance of antigen-mediated and diffusion pathways of intracellular drug delivery

Global Sensitivity Analysis Using Sobol and PRCC Method

The results from GSA are provided in Fig. 6. Figure 6a–c provides the results obtained using the Sobol method, and Fig. 6d–f provides the results obtained using PRCC method. Panel 6A and 6D provide the sensitivity analysis for cellular disposition model shown in Fig. 1a. The remaining four panels provide sensitivity analysis for the tumor disposition model shown in Fig. 1c. In general, the magnitude of sensitivity remained the same for all the parameters for a given output between Sobol and PRCC methods. PRCC sensitivity index also provided additional information about the direction of the effect of a parameter on a given output. Using the cellular disposition model for ADC it was found that the non-specific deconjugation rate (K_dec^ADC) of drug from the ADC and passive diffusion rate (K_diff^Drug) of the drug across tumor cell were the most sensitive parameters for unconjugated drug exposure within the cell. Deconjugation rate was also an important parameter for ADC and unconjugated drug exposure in the media. Antigen expression level was the most important parameter for cellular concentration of ADC. The in vivo PK model for ADC disposition revealed that the cellular disposition parameters were key determinant for tumor exposure of the ADC, and the systemic PK parameters were key determinant for plasma exposure of the ADC.

Fig. 6.

Results from global sensitivity analysis. Sobol analysis on: a in vitro cellular disposition model of ADC, b in vivo tumor disposition model of ADC using intra-tumoral kinetic parameters, and c in vivo tumor disposition model of ADC using systemic PK parameters. PRCC analysis on: d in vitro cellular disposition model of ADC, e in vivo tumor disposition model of ADC using intra-tumoral kinetic parameters, and f in vivo tumor disposition model of ADC using systemic PK parameters

DISCUSSION

An ability to mathematically characterize the disposition and efficacy of ADCs at the discovery, preclinical, and clinical stage is crucial for successful development of future ADCs. While there is an array of PK-PD models available to characterize systemic deposition of ADCs (2, 22), cellular disposition of ADCs is rarely quantified (10, 23) and mathematically characterized. In this publication, we have continued our efforts towards this, by augmenting our previously published (4, 5) cellular PK model for ADCs with more intracellular details.

The anticancer effect of ADC molecules is assumed to depend on their uptake by cancer cells expressing the target antigen, via receptor-mediated internalization process. However, there may be other rate-limiting processes involved before intracellular generation of pharmacologically active unconjugated drug molecules. For example, the release of the cytotoxic agent, especially in ADCs designed with non-cleavable linkers, is dependent on the proteolytic degradation of mAb in the late endosome/early lysosomal compartment. In our companion manuscript, parameters associated with intracellular processing of the T-DM1 were quantified, and it was observed that the intracellular degradation of T-DM1 was slower than the net internalization rates in different cell lines (17). To account for these novel findings, we have evolved our cellular PK model for ADCs. We have evaluated the application of this new cellular model to T-DM1 by utilizing the experimental data obtained from Erickson et al. (10), who studied intracellular processing of T-DM1 in different cell lines. With the augmented cellular disposition model (Fig. 1a), we were able to characterize the disposition of T-DM1 in HER2 expressing cell lines well. In order to characterize the data, we incorporated experimentally obtained values of different biomeasures (17, 24, 25) and estimated unknown parameters such as passive diffusion rate of drug across the cell membrane (K_diff^Drug). We consider this parameter to be ADC/drug-specific and expect it to differ based on the linker design and attached cytotoxic agent in an ADC molecule. To experimentally obtain this parameter, one needs to perform cellular uptake studies using the observed drug metabolite (e.g., lysine-mcc-DM1 for T-DM1). Nonetheless, the model estimated diffusion rate of DM1 containing catabolites across cell membrane was much less than the rate of MMAE diffusion, corroborating literature reports suggesting that T-DM1 catabolites are charged and relatively less permeable to cell membrane. In addition, the model estimated value for the half-life of diffusion for DM-1 catabolites across the cell membrane was coincidently found to be similar to the reported half-life for diffusion of lysine-mcc-DM1 across the lysosomal membrane (i.e., <10 h) (26). We have also estimated the HER2 expression levels in different cell lines, which came out to be very consistent with the reported values by Erickson et al. (10). In the future, we plan to expand our cellular PK model to incorporate multiple cell populations (e.g., antigen positive and antigen negative), and to account for dynamically changing cell numbers with time, similar to the single-cell kinetic model reported by Krippendorff et al. (27).

Following the local sensitivity analysis, we identified non-specific deconjugation rate (K_dec^ADC), passive diffusion rate of drug across the cell (K_diff^Drug), and antigen expression levels (Ag_tot) as the most sensitive parameters associated with the exposure of total and unconjugated maytansinoids (DM1) in the media and inside cell (Fig 5a, supplementary data). Additionally, the dissociation rate of DM1 (K_off^ADC) from the tubulin-DM1 complex and concentration of tubulin (Tub) were also important parameters determining the extent of bound DM1 exposure in the intracellular space (Fig. 5a). Of note, the importance of K_deg^ADC parameter may be underrepresented in this analysis, as with increase in degradation rate beyond certain value the net internalization rate (K_int^ADC) becomes rate-limiting, restricting the net change in unconjugated DM1 exposures. The results from the global sensitivity analysis (Fig. 6a, d) corroborated the results from the local sensitivity analysis, suggesting non-specific deconjugation rate of drug from the ADC and passive diffusion rate of the drug across tumor cell as the most important parameters for unconjugated drug exposure within the cell.

We further investigated the translational potential of the cellular model in vivo by integrating it with the ADC tumor disposition model described in our previous work (4, 5). Plasma PK data for T-DM1 in mice from different studies along with DM1 PK in rats were utilized to support the integrated plasma PK model shown in Fig. 1b. Most of the obtained systemic PK parameters for T-DM1 were similar to the values reported by Jumbe et al. (12) and Erickson et al. (7). The systemic disposition of released lysine-mcc-DM1 in the systemic circulation is not experimentally investigated or mathematically characterized by any other group and hence available data on radiolabeled DM1 disposition in rats was used and then scaled down to mice to complete the model (Fig. 1b). In the final step, new cellular model (Fig. 1a) and plasma PK model (Fig. 1b) were integrated with the tumor disposition model (Fig. 1c) to a priori predict plasma and tumor concentration of unconjugated and total maytansinoids in BT-474EEI tumors bearing mice (13) (Fig. 4). The model was able to a priori predict maytansinoid levels in plasma and tumors well with median going through the middle of the data and most of the data in the 90% confidence interval. Some of the observed deviations in the plasma PK predictions of total maytansinoids may be due to the fact that disposition of DM1 in mice was characterized using PK parameters scaled down from rat. In addition, in the absence of average DAR vs. time profile for T-DM1 in mice, we estimated the drug deconjugation rate based on total antibody and conjugated antibody profiles, which may not yield the most accurate parameter estimates for drug deconjugation (K_dec^ADC) from ADC. Nonetheless, our estimated value of DM1 deconjugation rate from T-DM1 in mice (0.241 1/day) was consistent with the reported values by Bender et al. in rat (0.114–0.543 1/day) and monkey (0.0939–0.341 1/day) (24). The DM1 catabolites obtained after non-specific deconjugation (in systemic circulation or extracellular matrix) can be different than the DM1 catabolites obtained after intracellular processing (e.g., lysine-mcc-DM1). These different DM1 containing molecules may have significantly different disposition in vivo, which can also result in the deviation of model prediction from observed data. A dedicated systemic and tumor distribution study of DM1 metabolites (lysine-mcc-DM1) in xenograft mice could further bolster our understanding of PK parameters for the released drug.

Since the tumor disposition model for T-DM1 presented in this manuscript stems from our previously published models, it is important to compare these models. Our previously published precursor models (4, 5) were similar to the presented model in terms of the plasma and tumor distribution components of the ADC, but differed in the structural model for cellular disposition of ADC. The parameters associated with the exchange of ADC and released drug between plasma and tumor, which are dependent on the molecular size of antibody and attached cytotoxic agent, were identical to what has been reported in precursor models. The systemic PK parameters for T-DM1 were estimated using the reported plasma PK of total antibody and conjugated antibody following T-DM1 administration. These parameters were different but comparable to the parameters used previously to describe the disposition of other ADCs (4, 5). The cellular model used in this manuscript has an additional degradation parameter not used in the previous manuscript, which was included based on our companion manuscript that has experimentally shown that for T-DM1 the intracellular degradation rate is slower than the internalization. As such, the estimates for this parameter cannot be compared with our precursor models. The non-specific cellular influx (K_in) and efflux (K_out) parameters used in our previous cellular model for characterizing the exchange of released drug between extracellular and intracellular compartments were replaced by bidirectional diffusion (K_diff) and unidirectional efflux (K_out) parameters. Therefore, the estimates for this set of parameters cannot be compared between the two versions of the model. Other antibody-dependent parameters for cellular disposition of ADC, such as binding kinetics, internalization, and degradation, were specific to trastuzumab. Whereas the parameters pertaining to the intracellular target tubulin were similar to what has been used in our previous models. Thus, the basic structure of the proposed model is very generic, and applicable to a variety of ADCs with diverse set of antibodies and drug-liner combination. However, the drug-specific parameters and some system specific parameters (e.g., antigen abundance and internalization) need to be adjusted to meet the specifications of a given ADC. In addition, with the advent of site-specific ADCs where one may be able to observe the PK of different DAR species, the model may have to be modified to account for each ADC species like it is done in references (22) and (24).

Detailed mathematical analysis of the systems PK models presented in this manuscript using pathway analysis and GSA provides novel insight into the disposition of ADC. Comparison of the pathway analysis between in vitro and in vivo system (Fig. 5b, c) reveals that the contribution of antigen-mediated uptake and passive diffusion of drug within the cell is not only dependent on the ADC dose level (because of the saturation of antigen-mediated pathway), but it is fundamentally different between the two systems. The main reasons for this difference can be the different range of concentrations cells are exposure to in vitro vs. in vivo, and the ability of unconjugated drug to easily leave the extracellular space of a tumor by diffusing to the central circulation. The GSA (Fig. 6) revealed that plasma exposure of ADC and unconjugated drug is mainly dependent on the systemic PK parameters for ADC and the unconjugated drug (e.g., clearance and volumes). However, the tumor exposure of ADC and unconjugated drug is very much dependent on the parameters associated with the stability of ADC and intracellular processing of ADC. Thus, accurately understanding and characterizing the cellular processing of ADC is paramount for our ability to accurately predict tumor exposure of ADC and unconjugated drug.

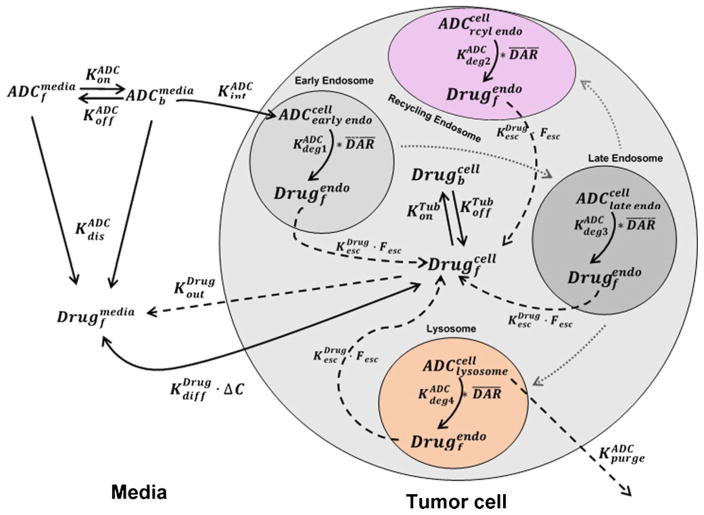
Intracellular activation of ADC molecules in a cancer cell entails intracellular trafficking in different endosomal and lysosomal compartments, eventually leading to the release of conjugated drug that induces the cytotoxic effect. However, currently available data on cellular disposition of ADCs limits our capability to mathematically characterize all these processes. We intend to perform further intracellular trafficking studies to better understand the intracellular fate of ADC and released drug, in order to further bolster our cellular model. Figure 7 depicts the schematic of a proposed systems PK model for ADC based on our current understanding about the disposition of an ADC molecule on a cellular level. In an in vitro system, the ADC in the media (ADC_media^f) is expected to bind to cell surface antigens (Ag_tot), followed by antigen-mediated internalization (K_int^ADC). Upon internalization, ADC follows the intracellular trafficking route from early endosome to late endosome, and eventually lysosome. Fraction of the ADC bound to target/FcRn receptors gets recycled back to the extracellular space via recycling endosome. The nature of a chemical linker determines the non-specific deconjugation of drug outside the cell (K_dec^ADC) as well as the generation of unconjugated drug (K_deg^ADC) in different endosomal/lysosomal compartments. For example, an acid-labile linker will cleave immediately following changes in pH in early endosomal space, a valine-citrulline linker will be cleaved more in the late endosome/lysosomal space with abundance of cathepsin B enzyme, a non-cleavable SMCC linker will be proteolytically degraded in lysosomal space, and a disulfide linker will be cleaved by the cytoplasmic glutathione molecules. The rate (K_esc^Drug) and extent (F_esc) of endosomal escape of the unconjugated drug/drug metabolite in the cytoplasm could be a salient factor determining the efficacy, as sequestration of weakly basic drugs in the lysosome is widely acknowledged (28). Recent studies performed on anti-CD70 Ab-mcc-DM1 have shown that upon 24 h after internalization, there is still 17% of lysine-mcc-DM1 sequestered in lysosomes (26). Hamblett et al. have recently shown that SLC46A3 is responsible for the endosomal/lysosomal escape of lysine-mcc-DM1 to the cytoplasm (29). The unconjugated free drug in the cytoplasm is able to bind to cellular tubulin (Drug_b^cell) and elicit its pharmacological action (based on the mechanism of action) or efflux (K_out^Drug) outside the cells (via passive or active processes). To mathematically characterize all these processes however, different analytes (i.e., unconjugated and conjugated drug) need to be quantified in extracellular and different intracellular spaces, along with experimental measurements of different biomeasures. Once developed, the cellular level systems PK model for ADCs can be utilized to identify the most sensitive and rate-limiting pathways, evaluate the effect of different linker types, and develop strategies for successful intracellular drug release from future ADCs.

Fig. 7.

Schematics of a proposed systems pharmacokinetic model for intracellular processing of ADCs, which highlights our current understanding about the determinants responsible for ADC activation in a cell

In summary, here we have improved previously published in vivo tumor disposition model for ADCs, and have demonstrated the application of this augmented model to T-DM1. We have also performed pathway analysis and global sensitivity analysis of the models to understand the key pathways and parameters responsible for intracellular exposure of pharmacologically active unconjugated drug. Finally, we have proposed an ideal model for characterizing intracellular PK of ADC and its components, which is not feasible to develop yet because of our lack of understanding about the disposition of ADC in intracellular compartments.