Are coarse-grained models apt to detect protein thermal stability? The case of OPEP force field

Abstract

We present the first investigation of the kinetic and thermodynamic stability of two homologous thermophilic and mesophilic proteins based on the coarse-grained model OPEP. The object of our investigation is a pair of G-domains of relatively large size, 200 amino acids each, with an experimental stability gap of about 40 K. The OPEP force field is able to maintain stable the fold of these relatively large proteins within the hundrend-nanosecond time scale without including external constraints. This makes possible to characterize the conformational landscape of the folded protein as well as to explore the unfolding. In agreement with all-atom simulations used as a reference, we show that the conformational landscape of the thermophilic protein is characterized by a larger number of substates with slower dynamics on the network of states and more resilient to temperature increase. Moreover, we verify the stability gap between the two proteins using replica-exchange simulations and estimate a difference between the melting temperatures of about 23 K, in fair agreement with experiment. The detailed investigation of the unfolding thermodynamics, allows to gain insight into the mechanism underlying the enhanced stability of the thermophile relating it to a smaller heat capacity of unfolding.

1. Introduction

Proteins are marginally stable soft-matter entities, with a free energy difference between the folded and the unfolded states of only a few kcal/mol [1]. This small difference, about 3 to 30 kcal/mol, which microscopically corresponds to just a few hydrogen bonds, results from a delicate balance of intramolecular and solvation forces that causes a large enthalpy-entropy compensation.

The design of proteins of enhanced stability is a key goal for many applications in biotechnology and chemical processing aimed at exploiting the catalytic power of enzymes in non-native harsh conditions [2]. In this regard, proteins from thermophilic organisms, which thrive at temperatures as high as the boiling point of water, represent a natural template [2, 3]. Understanding both the thermodynamics as well as the molecular basis of their resistance to high temperatures could be fundamental for de novo protein design.

It is widely accepted that thermophiles gain stability, with respect to their mesophilic homologues that work at ambient conditions, by a combination of molecular factors [2, 4, 5]. The commonly observed surplus of charged amino-acids is for example associated to an extended network of hydrogen bonds (HB) and ion-pairs that eventually rigidify strategic regions of the protein matrix [6, 7] and enhance the coupling with the solvent. In addition, the extension of hydrophobic contacts has been proposed as a source of cohesive forces that stabilize the folded state [8]. Structurally speaking, the shorter loops and flexible regions detected in the structure of thermophilic proteins as well as their distribution along the sequence reduce the number of weak spots on the protein surface preventing unfolding [9]. As a consequence of these and other factors, several thermodynamic mechanisms have been identified as responsible for an enhanced thermal stability [10, 2, 11, 5, 12].

Nowadays, the increase of computational power makes feasible an extended investigation of the kinetic and thermodynamic properties of this class of proteins by computer simulations, although limitations still exist [5]. For example the behavior of homologue proteins can be explored via brute force atomistic molecular dynamics at the microsecond time scale and longer, allowing to compare their folded-state flexibilities or track their different kinetic stabilities at high temperature. Unfortunately, for all atom (AA) models in the explicit water the calculation of thermodynamic properties like the exact melting temperature, the heat capacity of unfolding or the overall shape of stability curves are still a challenge even for medium-size molecules. For that reason the use of coarse-grained (CG) potentials in combination with enhanced-sampling techniques is an appealing alternative [13].

Simplified models have been already successfully applied to the design of proteins of enhanced stability, for example by targeting specific structural patterns [14] or optimising electrostatic interactions [15]. However, these approaches rely on static protein structures. Accounting for molecular flexibility would open alternative routes for in silico design by including, in some sense, entropic effects and kinetic stabilization. Here we make a first attempt to use a protein CG model in combination with standard MD and an enhanced sampling technique in order to explore the different thermal stabilities of two homologous proteins.

The model recruited for the task is the Optimized Potential for Efficient protein structure Prediction (OPEP), a coarse-grained force field designed to fold peptides and small proteins that has already been used successfully in a wide variety of cases, see [16, 17, 18, 13, 19] and references therein. The model is used here to study the different stabilities of two relatively large homologous proteins, having about ∼ 200 amino acids each. The first one is the catalytic domain of the elongation factor thermo unstable (EF-Tu) from Escherichia coli [20], a mesophile, while the second one is the catalytic domain of the homologous EF-1α from the archaeon Sulfolobus solfataricus, a hyperthermophile [21]. This pair of homologues is a very good study-case for several reasons; their thermal stabilities are separated by a large gap of about 40 K, their fold contains both α and β structures, and the hyperthermophile is enriched in charged amino acids as commonly observed in thermophiles. We recently studied these two proteins using all-atom molecular dynamics, with which we probed the enhanced stability of the hyperthermophilic variant at high temperature and analyzed the folded state at ambient conditions [22, 23, 9]. This all-atom investigation represents a reference state for benchmarking the capability of the OPEP force field.

Herein, we verify that OPEP can extend standard MD simulations of rather large proteins in the hundrend-nanosecond timescale without compromising their overall structures. Furthermore, specific features of the two homologues, such as the different number of sub-states characterizing the conformational landscape or their collective motion, qualitatively reproduce the results from the all-atom simulations. Using this folded-state characterization we provide a first mapping of the OPEP CG time-scale versus the all-atom one for internal protein dynamics. Finally, with the use of replica-exchange molecular dynamics simulations we investigate the different thermal stabilities of the proteins; not only we reproduce the proteins’ stability gap, but also gain an insight into the underling thermodynamic mechanism.

2. Methods

As mentioned briefly above, the two homologous proteins under study are the G-domains of the Elongation Factor thermo unstable (EF-Tu) and 1α (EF-1α). The mesophilic protein, ℳ (EF-Tu, PDB code 1EFC [21]) belongs to Escherichia coli bacterium while the hyperthermophilic one, ℋ (EF-1α, PDB code 1SKQ [20]) belongs to the Sulfolobus solfataricus archaeon. The G-domain corresponds to the N-terminal part of the protein. In our simulations the mesophilic homologue covers the residues T8-E203 and its size is 196 amino acids while the hyperthermophilic G-domain encompasses the stretch of residues K4-V229 and has 226 amino acids. Details about the setup of the systems can be found in [22].

2.1. Simulation Setup

The coarse-grained Molecular Dynamics simulations (MD) are performed using the Optimized Potential for Efficient protein structure Prediction (OPEP) for proteins with implicit solvent, see the recent review [13]. The model represents each amino acid by six centers of force: the side-chain is represented by a unique bead, while atomistic resolution is reserved for the backbone that includes N, H_N, C_α, C, O atoms. Exception is proline whose side-chain is represented by all heavy atoms. As many force fields, the Hamiltonian consists of short-range interactions for bond lengths and angles, improper torsions and rotations, and long-range nonbonded interactions. The functional forms are described in detail in [16, 17, 18] as well as reported in the electronic supplemental information of [13]. Here we only highlight that the energy scale of the model is set by both the optimised weighting factors of each term of the Hamiltonian and a global scaling factor. In numbers: the minimum of the non-bonded Ile/Ile interaction, used here as reference, is set to 3.89 kcal/mol. For some applications and tests the weaker value 3.49 kcal/mol has also been used. In this work we employ the version 4 of the force field [17].

MD simulations run using an in-house developed code implementing the OPEP Hamiltonian. The trajectory is evolved using a time-step of 1.5 fs, and the temperature of the system is kept constant by applying the Berendsen thermostat (τ_B = 0.1 ps). Before the production phase at temperatures T=300 K, T=325 K, and T=350 K, the systems were progressively equilibrated at lower temperatures, T=250 K and T=275 K for about 50 ns. The replica exchange molecular dynamics is done using 24 parallel replicas and an exponential temperature distribution in the range 260-582 K. Exchanges between two neighbouring replicas is attempted every 7.5 ps. Each replica is extended for 230 ns. Specific heat curves, C_V and free energy profiles are computed using the PTwham algorithm [24].

The ambient temperature (300 K) all-atom MD simulation is performed using the CHARMM22 Force Field for proteins [25] and TIP3P-CHARMM model for water. We used the NAMD software [26] with the simulation parameters as mentioned in [9].

2.2. Collective variables

The radius of gyration is given by

$${\text{R}}_g(t)=\sqrt{\frac{1}{N_B}{\displaystyle \sum _{i=1}^{N_B}{({\mathit{\text{r}}}_i(t)-\langle {\mathit{\text{r}}}_i(t)\rangle )}^2}}$$ (1)

where the summation is over all the heavy backbone atoms, that is N_B =C, C_α, N and O, r_i(t) is the position of the i-th atom at time t and 〈r_i(t)〉 is the average position of all backbone atoms at time t.

The Root Mean Square Displacement (RMSD) is computed via the following expression

$$\text{RMSD}(t)=\sqrt{\frac{1}{N_{C_{\alpha }}}{\displaystyle \sum _{i=1}^{N_{C_{\alpha }}}{({\mathit{\text{r}}}_i(t)-{\mathit{\text{r}}}_i^{\prime })}^2}}$$ (2)

where N_Cα is the number of C_α atoms in the chain, again r_i(t) is the position of the i-th atom at time t and ${\mathit{\text{r}}}_i^{\prime }$ is its reference position in the equilibrated structure, see above. Rigid body motions were removed by super-imposing the set of rigid-core C_α atoms of the protein configuration at time t on those of the equilibrated structure. We compute the RMSD for the rigid-core of the proteins: the stretches for ℳ and ℋ that correspond to well defined secondary structure elements (i.e. excluding coil or loop) in the crystal structure.

The fraction of native torsion angles is given by

$$n_t(t)=\frac{1}{N_{\theta }}{\displaystyle \sum _{i=1}^{N_{\theta }}\text{exp}\left[-\frac{{({\theta }_i(t)-{\theta }_i^{\prime })}^2}{{\sigma }^2}\right]}$$ (3)

where N_θ is the number of torsion angles θ, having values ${\theta }_i^{\prime }$ in the equilibrated structure and values θ_i(t) at time t and σ = 60°. In our calculations the torsion angles along the sequence include both ϕ and ψ dihedrals.

The fraction of secondary structure corresponds to the number of residues belonging to a well-defined secondary structure, namely α-helix or β-strand (codes G, H, I, E or B) as calculated by the DSSP algorithm [27] divided by total number of residues in the sequence.

2.3. Clustering

The clustering is done using the leader algorithm [28] and it is based on the pairwise root mean square deviations, as defined in Eq. 2 above, between different snapshots of the trajectory after removing rigid body motions. The RMSD clustering of the trajectories was fed as an input to the Markov clustering algorithm (MCL) [29] in order to group together the most kinetically relevant substates. MCL is based on a random walk on a network and the basic steps have been described elsewhere [29, 9].

2.4. Diffusion

The diffusion coefficient for the proteins in the folded state was calculated for n_t. In the harmonic approximation [30, 31] the diffusion coefficient is given by $D=\frac{\langle \delta n_t^2\rangle }{{\tau }_{corr}},$ where δn_t = n_t − 〈n_t〉 is the instantaneous fluctuation of the collective variable and τ_corr its correlation time, being defined as:

$${\tau }_{corr}=\frac{{\displaystyle \int \langle \delta n_t(t)·\delta n_t(0)\rangle dt}}{\langle \delta n_t^2\rangle }$$ (4)

The autocorrelation in Eq. 4 decays exponentially after an initial short transient time. We used an exponential fit to estimate τ_corr. The correlation functions were calculated for the last 20ns of each trajectory that correspond to the final stationary stretch of the simulation.

3. Results and discussion

3.1. Stability on long time scale

So far the OPEP force field has been extensively applied to study small peptides, and it was only recently tested on mid-size proteins with generally less than 80 amino-acids [32, 17, 23]. Therefore, given their size, the mesophilic (ℳ) and hyperthermophilic (ℋ) G-domains, are a challenging study-case. The capability of the force field to maintain the fold of the two proteins in MD simulations extending up to 100 ns is first probed and discussed below.

After an equilibration phase at low temperatures (250 K and 275 K), three independent trajectories, of length 100 ns each, were generated at temperatures 300 K, 325 K and 350 K in order to monitor the kinetic stability of the two systems and characterize the dynamics of their folded state.

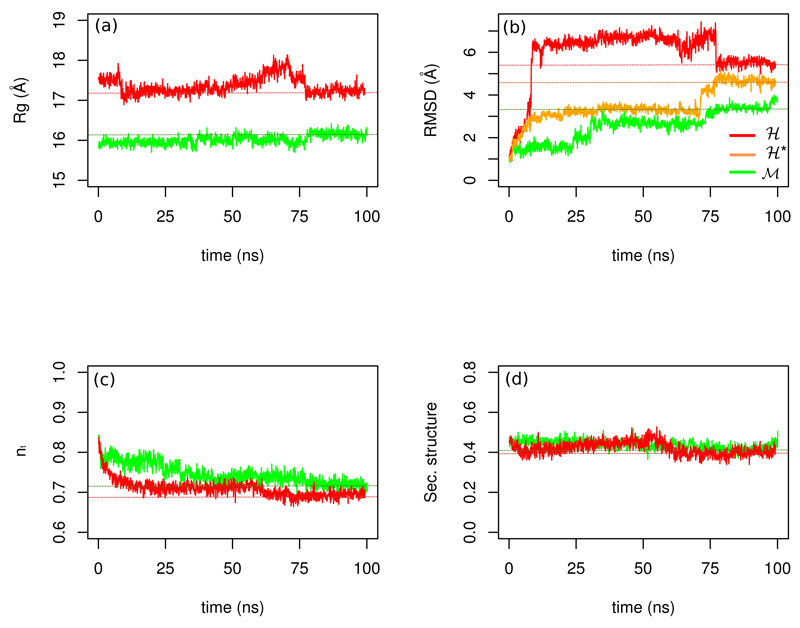
Figure 1 shows, for the MD simulations at T=300 K, the time evolution of four collective variables (CV) that monitor conformational properties, namely the radius of gyration R_g, the root mean square deviation (RMSD) calculated with respect to the equilibrated configuration, the fraction of native torsion angles n_t and the fraction of secondary structure. The average values of these CVs are reported in Table 1 along with the respective values from AA simulations. Overall, the fold of the two proteins is stable during the simulation time; the ℳ and ℋ domains remain folded in a compact globular state of radius R_g= 16.0 Å and R_g=17.3 Å, respectively. We note that these values are about 3-5% smaller than those obtained by all atoms simulations. This stronger cohesive packing is caused by several factors characteristic of the CG model, such as the lack of “adhesive” interactions with the solvent treated as implicit, the preferential filling of the space due to the spherical graining of the amino-acid side-chains, the specific weight of hydrophobic mimicking potentials and the lack of repulsive electrostatic interactions. While the fraction of native torsion angles n_t and the percentage of secondary structure show a steady behavior, when looking locally, we observe several instabilities. For either protein, two helices and two small β-strands located around the middle and the end of each sequence are not well preserved. For ℳ these stretches are lost during the equilibration phase at low temperature (250 K). For ℋ, one small helix is similarly lost during the equilibration and a second short peripheral helical stretch unwinds at the beginning of the 300 K simulation (Q128-G140). It is however noteworthy that at a later time, part of this helix refolds and that even the short helix lost during the equilibration phase (E118-M123) is also recovered. The main contribution to the initial RMSD jump of ℋ comes from a specific region of the ℋ domain, two helices located at the switch I region of the protein, α¹ [E32-L45] and α² [E48-E63], see Fig. S1 of SI. These two helices mantain very well their secondary structure however they do move in a rather flexible way as a rigid body. By removing the contribution from this region the RMSD shifts down and follows the behavior of the ℳ protein as shown by the orange curve in the Figure 1 (b). The functional role of the switch I region and how this region contributes to the different stabilities of the ℳ and the ℋ proteins is discussed in [9]. The timeline of the secondary structure for both systems is reported in SI, Figure S2.

Figure 1.

Timeline of (a) radius of gyration R_g (b) rigid-core C_α RMSD, (c) fraction of native torsion angles n_t and (d) fraction of secondary structure along the sequence for the OPEP MD simulations of the two systems at 300 K. Data in red refer to the ℋ protein and data in green to the ℳ protein. In panel (b) the orange curve ℋ* refers to a calculation performed after removing the contribution from helices α¹ and α² of the switch I region (see Fig. S1 of SI).

Table 1.

Average values of radius of gyration R_g, rigid-core C_α RMSD, fraction of native torsion angles n_t and fraction of secondary structure along the sequence for the OPEP MD simulations at 300 K, 325 K and 350 K. For T=300 K the reported data in parenthesis correspond to the AA simulations. Errors correspond to standard deviation.

	CV	T=300 K	T=325 K	T=350 K
	Rg (Å)	16.0 ± 0.1 (16.3 ± 0.1)	16.0 ± 0.2	16.3 ± 0.1
ℳ	RMSD (Å)	2.5 ± 0.7 (3.0 ± 0.5)	4.4 ± 0.6	4.4 ± 0.3
	nt	0.70 ± 0.03 (0.85 ± 0.01)	0.71 ± 0.01	0.70 ± 0.02
	sec. structure	0.44 ± 0.02 (0.65 ± 0.01)	0.44 ± 0.02	0.41 ± 0.02
	Rg (Å)	17.4 ± 0.1 (18.0 ± 0.1)	17.3 ± 0.1	17.4 ± 0.1
ℋ	RMSD (Å)	5.9 ± 0.7 (3.4 ± 0.3)	5.8 ± 0.3	5.8 ± 0.2
	nt	0.71 ± 0.02 (0.86 ± 0.01)	0.69 ± 0.01	0.69 ± 0.01
	sec. structure	0.42 ± 0.03 (0.52 ± 0.02)	0.39 ± 0.02	0.40 ± 0.02

The examined CVs attest that the overall structure of ℳ is more rigid and better maintained than that of ℋ. The somewhat floppy dynamics of the ℋ domain is caused by the larger number of flexible regions [9], turns and coils, located at the surface of the protein and which, as a consequence of the absence of the viscous aqueous medium, move more freely. Such behaviour is also expected to impact the rigid core since α-helices and β-strands are on average shorter and more frequently interrupted by coils and loops.

The average values of the four CVs for the two simulations at the higher temperatures of 325 K and 350 K are given in Table 1 whereas a timeline is also shown in Figure S3 of the SI. At these timescales, we do not observe any temperature-driven kinetic instability for both systems, something also verified by two simulations at the higher temperatures of T=375 K and T=400 K (data not shown). We recall that in the all-atom simulations the early steps of unfolding are observed in a well localized region of the ℳ protein and occur between 200 and 500 ns at T=360 K. As we discuss later in detail, the OPEP force field like other CG models in general, as compared to the all atom simulations, impacts both the effective time scale of relaxation processes (kinetics) as well as their energy scales (thermodynamics). Therefore it is important to quantify this shift when discussing the relative stability of proteins and its time and temperature dependence.

3.2. Exploring the folded-state dynamics

According to several experimental studies, thermophilic proteins have been considered more rigid at ambient conditions than their mesophilic homologues [2]; in fact the mechanical rigidity was postulated as the main source of thermal stability as well as the cause of the lack of activity of thermophiles at ambient temperature [5]. Only at the optimal growth temperature of the host organism, thermophilic proteins function efficiently because the thermal excitation activates conformational motions that eventually match those of mesophiles at ambient condition [33]. This corresponding-states picture for mechanical rigidity has been however questioned recently, both experimentally [34, 35] and theoretically [36, 9]. Indeed, depending on the time and length scales considered, thermophilic proteins show, at ambient conditions, comparable if not enhanced flexibility with respect to their mesophilic variants. In other words, the entropic route to stability also exists [12]. Moreover quality matters. As put forward in our recent study of the G-domains [9] the spatial distribution of flexible and rigid stretches differs substantially between the ℋ and ℳ domains; the ℋ homologue gains kinetic stability via a more uniform alternation of flexible and rigid structural patterns.

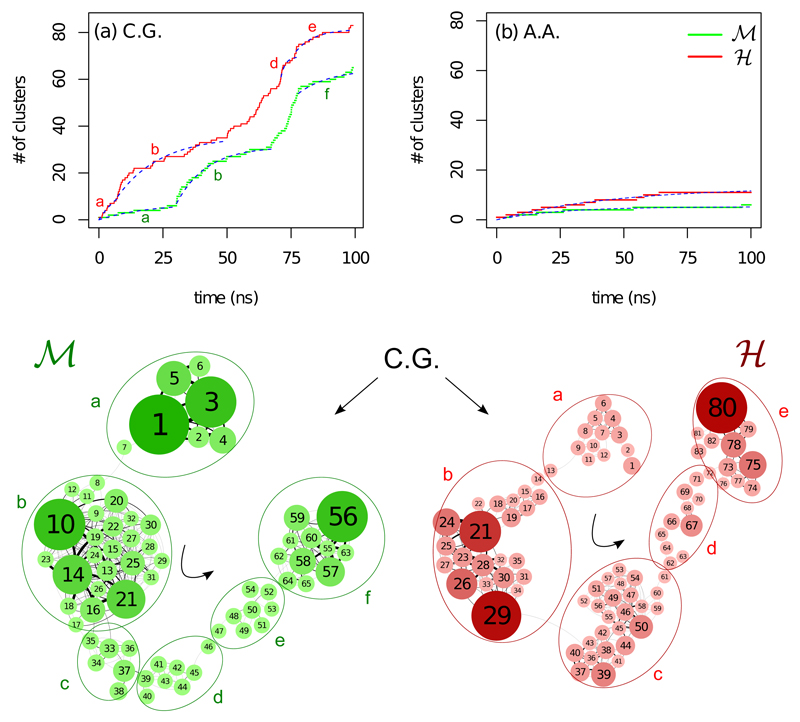
In the lines of our previous all-atom investigation [9], we now focus on the dynamics at ambient temperature in order to characterize the conformational landscape of the proteins. This is achieved by performing a conformational clustering on the trajectories, where we use the C_α RMSD as a distance between two configurations and a cut-off of 2.5 Å to separate the clusters. The results are shown in Figure 2. In the top panels, the cluster growth versus time is plotted for the OPEP CG simulations (Fig. 2(a)) in comparison to the results from all-atom simulations of equal length (Fig. 2(b)). Bearing in mind that the clustering cutoff for both systems and models is the same we observe a striking difference in the final number of clusters between the two models. As expected, the sampling of the available conformational space is much more effective using a CG model over an AA one. Interestingly, for this CV, we also note that in the OPEP simulations the ℋ protein visits a larger number of sub-states than ℳ, in agreement with the reference all-atom result [9], albeit the effective time-scales in CG and all-atom simulations are different [13] as we will discuss later on.

Figure 2.

Conformational substates at 300 K. Top: Number of clusters versus time for (a) the CG and (b) the AA MD simulations at 300 K. The dashed blue lines correspond to an exponential fit on the function N = N_∞(1 −e^−t/τ). Bottom: Network representations [37] of the coarse-grained MD simulations clusters shown in (a) drawn with a force based algorithm for ℳ on the left and ℋ on the right. The larger ellipsoidal borderlines outline the basins of attraction extracted using a Markov clustering algorithm with a granularity parameter equal to 1.2 [29]

In the all-atom simulations, the number of clusters visited as a function of time can be successfully fitted using a simple exponential model, N = N_∞(1 − e^−t/τ), obtaining N_∞ = 5 and τ = 24 ns for ℳ and N_∞ = 13 and τ = 46 ns for ℋ. However, the same model cannot be fitted on the totality of the CG data that actually show sudden jumps.

To elaborate more on the above, in the bottom panel of Figure 2, a network representation of the CG clustering is drawn using a force based algorithm, with the size of the nodes and edges being proportional to their occupancy and number of interconversions, respectively (the edge weights have been normalized so that all edges that exit one node sum up to one). With the use of a Markov clustering algorithm [29, 9] we identified the substates where random-walks representing protein motion in the network of states get confined. These clusters are grouped together in larger bundles and outlined by the larger ellipsoidal lines in Fig. 2 (bottom). We call those basins of attraction and, for the same granularity parameter of the algorithm that set the height of the kinetic barrier confining the walkers, we identified 5 and 4 of them for ℳ and ℋ respectively. We then went back to the cluster growth of the CG model and tried to fit the exponential model to the parts of the trajectory that correspond to each of the basins. As can be seen in Figure 2(a) for three cases in ℳ and one in ℋ the fit was not possible suggesting that the trajectory was only transiting those substates. Similar fast transitions have been observed previously in all atom simulations of a protein in crystal environment and could be associated to Lévy flight motion [38].

Our findings show that with respect to AA, the CG dynamics not only is faster in exploring the conformational space as shown by the larger number of clusters visited in simulations of numerically equal length, but it also explores more efficiently the hierarchical organisation of the conformational states [39, 40, 41] as demonstrated by the sudden jumps in the clustered trajectories. The larger number of clusters identified by the OPEP simulations suggests a speed-up of at least 5-6 times with respect to the AA model. This finding agrees with previous validations of the model [13] as well as by monitoring relaxation processes as discussed below.

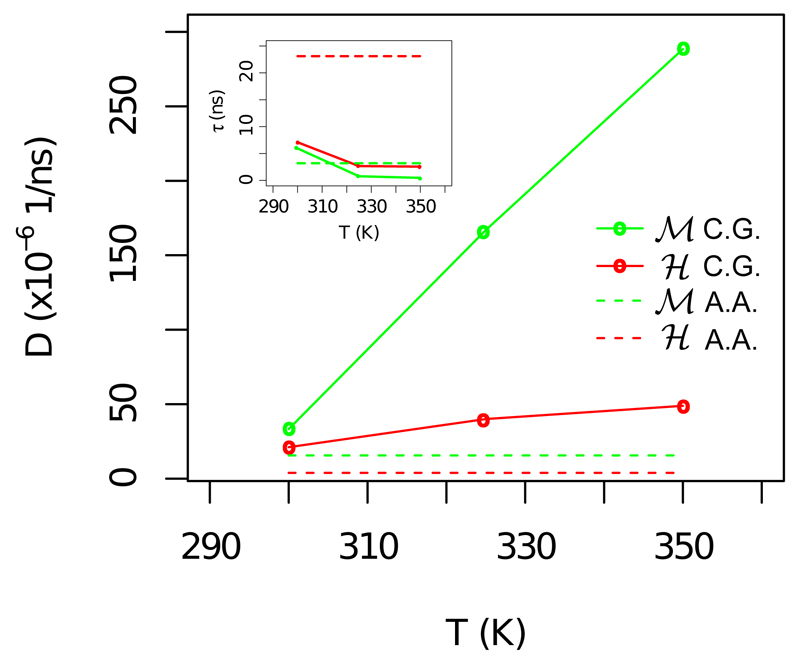
Although the OPEP CG force field allows us to explore more efficiently the conformational landscape, it is at this point not safe to compare the global flexibility of the two systems since it is clear from Figure 2(a) that longer simulations are needed to achieve a convergence. However, we can try to quantify the diffusivity of the systems along the conformational landscape, a property that relates to the local disorder of the surface [42] and represents a key parameter in the theory of protein folding [43]. In this context, the motion of a protein with respect to a given collective variable X is associated to a diffusion constant D. Within the harmonic approximation, D is given by D = 〈δX²〉/τ_corr, see Methods. This approximation is valid for the fraction of native torsion angles n_t for which the autocorrelation of fluctuations decays exponentially, c(t) = 〈δn_t(t) · δn_t(0)〉 ≃ e^−t/τ_c. We only stress that when the CV does not show a harmonic behavior, more sophisticated approaches are needed to estimate the local diffusivity on the projected landscape [44, 45, 9].

The obtained results for n_t are shown in Figure 3. The main plot shows, in solid lines, the diffusion coefficient D with respect to the temperature for the two systems whereas in dashed lines we report the value of D as estimated in our previous all-atom approach for the n_t at T=300 K [9]. The values are systematically higher for ℳ, meaning that the internal motion of the ℋ domain is slowed down by a distribution of higher barriers separating substates [42]. At ambient temperature, the value of D for both systems is shifted, for OPEP, to slightly larger values as compared to the AA force field. This verifies, as we expected, that dynamics is more diffusive in the CG model. The ratio of the computed diffusion constants, D^CG/D^AA ∼ 2 − 7 provides a supplemental estimate of the effective time-scale characterizing the OPEP internal protein dynamics with respect to all-atom simulations.

Figure 3.

Diffusion in a harmonic basin of attraction. Main plot: In solid lines we report the diffusion coefficients versus temperature for n_t as estimated for the OPEP simulations. In dashed lines we report the value of D as estimated in our previous all-atom approach for n_t at T=300 K [9]. Inset: Characteristic decorrelation time of δn_t with respect to the temperature. The decorrelation time is always smaller for ℳ in agreement with our previous AA results.

Moreover, as the temperature increases the values of D increase as well with a notable resilience for ℋ as compared to ℳ. Since the dynamics depends on temperature, as the temperature increases it allows for more frequent transitions among substates; thus, the above picture reveals again the presence of higher kinetic barriers for ℋ than for ℳ.

3.3. Towards thermodynamics

The OPEP force field has been routinely used in combination with a variety of simulation techniques [13, 46, 47, 48], among which is replica exchange molecular dynamics (REMD) [49] that enhances the sampling of the protein folding/unfolding process yielding correct thermodynamical properties of the systems under study.

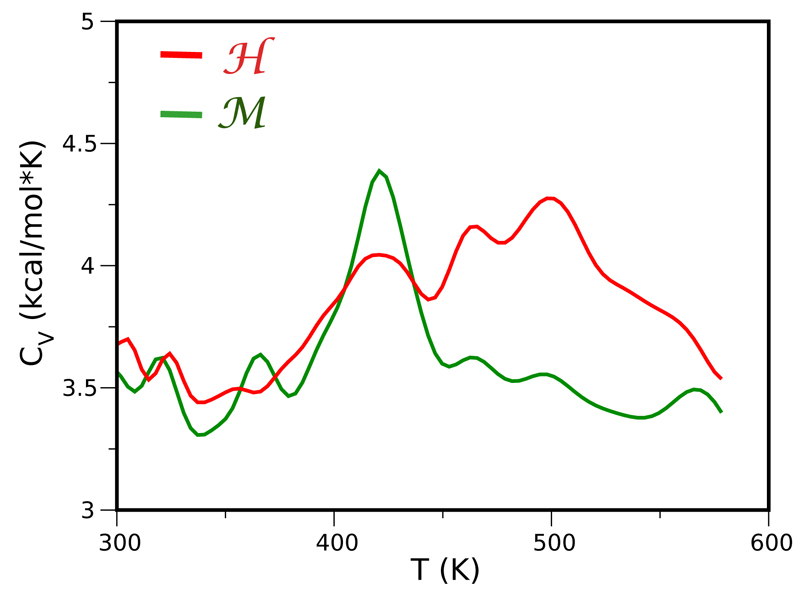
A first attempt to probe the different thermal stabilities of the homologous G-domains was already reported for a weak energy scaling factor of the force field [13], see Methods. It was indeed verified that the curve of the specific heat C_V (T) of the ℋ protein was systematically shifted at higher temperatures with respect to that of ℳ, mirroring the enhanced stability of the hyperthermophile. Here, we report the results from REMD simulations using a higher energy scaling factor (the same used for the MD simulations discussed previously). The curves of the specific heat are plotted in Figure 4. Likewise, we observe for this set up, a systematic shift towards higher temperatures for the ℋ domain as compared to ℳ. We also note the presence of several peaks that signal the onset of unfolding of different secondary structures as well as unpacking. In particular, the ℳ protein is characterized by two peaks, a minor one at T=366 K and a large one at T=420 K. The hyperthermophilic protein also presents a peak at T=420 K, but also a series of others at the higher temperatures of T=460 K and 500 K. While the absolute value of the temperatures at the C_V peaks is generally too high as compared to experimental data [50, 51] the stability gap between the two proteins is actually within the correct range of 40-50 K.

Figure 4.

Specific heat C_V for ℳ (green) and ℋ (red) domains of the EF-Tu and 1α proteins, respectively, calculated from OPEP-REMD simulations. The presence of multiple peaks in the C_V profile is caused by the unfolding events of different secondary structure motifs as well as progressive unpacking. In a simple two-state model, the C_V is expected to show a single peak at the melting temperature T_m where the populations of the folded (p_f) and unfolded (p_u) states are equal.

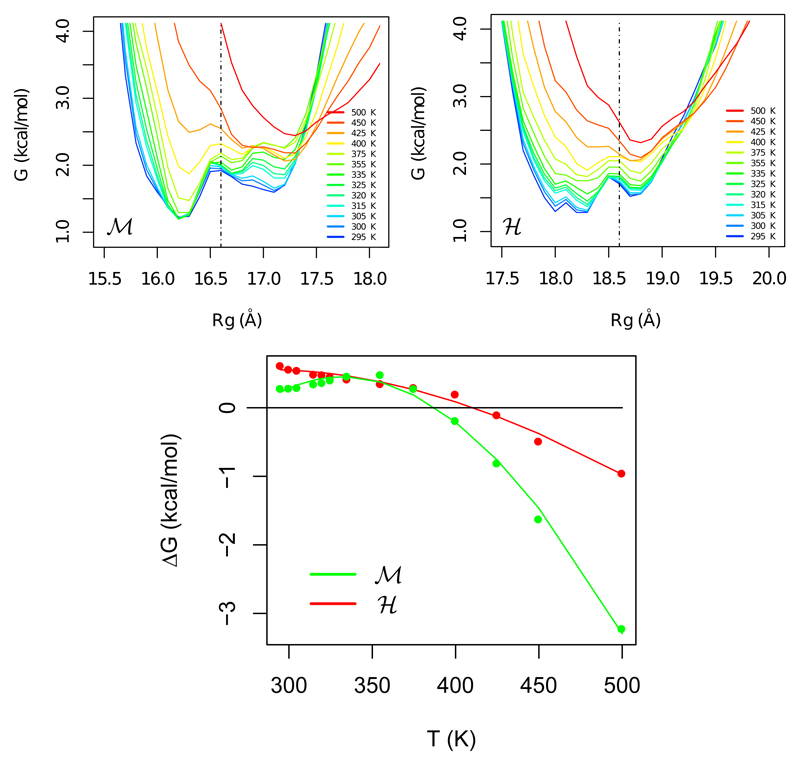
Subsequently, from the same simulation data, we attempt to extract the stability curves for the two proteins. We use the gyration radius as an order parameter to distinguish between the folded and unfolded states. From the trajectories of all the replicas we reconstruct the free energy landscape projected on the reaction coordinate R_g, G(R_g) = −k_bTln P(R_g). This is done by calculating the probability distribution of the variable P(Rg) using the PTwham unbiasing technique [24]. The probability distributions P(Rg) display a well defined bimodal profile, thus allowing for a clear a separation of the folded and unfolded states at all temperatures and for both systems. This can be appreciated by looking at the top panel of Figure 5 where the free energy profiles for different temperatures are shown with respect to the radius of gyration for ℳ (left) and ℋ (right) proteins. The dividing value between folded and unfolded states is indicated with a vertical dashed line, being 16.6 Å for ℳ and 18.6 Å for ℋ. As temperature increases the population of unfolded proteins (p_u) increases at the expense of the folded ones (p_f). In the bottom panel of Fig. 5, the free energy difference between folded and unfolded states, $\Delta G=-k_{b}Tln\frac{p_u}{p_f}$ is calculated as a function of temperature. This is the so-called stability curve, intersecting the x-axis at the melting temperature T_m. The obtained data were fitted to the Gibbs-Helmholtz equation given by

$$\Delta G_{f\to u}(T)=\Delta H_m\left[(T_m-T)/T_m\right]-\Delta C_p\left[T_m-T\left(1-ln(T/T_m)\right)\right]$$

estimating the values of T_m = 388 ± 2 K, ΔC_p = 0.103 ± 0.005 kcal/mol·K and ΔH_m = 6.2 ± 0.3 kcal/mol for ℳ and T_m = 411 ± 3 K, ΔC_p = 0.020 ± 0.004 kcal/mol·K and ΔH_m = 3.5 ± 0.2 kcal/mol for ℋ.

Figure 5.

Stability curves. Top: Free energy profiles for different temperatures w.r.t. the radius of gyration for the mesophilic (left) and hyperthermophilic (right) proteins. As temperature increases the population of unfolded proteins increases at the expense of the folded population. The dividing value between folded and unfolded states is indicated with a vertical dashed line, being 16.6 Å for ℳ and 18.6 Å for ℋ. Bottom: Free energy difference, a.k.a. stability curves, as extracted from the data of the top panel. The melting temperature is where the stability curve intersects the x-axis, estimated at 388 K and 411 K for ℳ and ℋ, respectively.

With the use of a single reaction coordinate, the simple OPEP model allows to detect a thermal stability gap of about 25 K between the two proteins. This is not far from the experimentally reported difference of the optimal enzymatic activity for the two domains (40 K). Of course, as already discussed above and reported in previous investigations, the OPEP force field is prone to a systematic deviation of ±23 K with respect to experiments [52, 18, 13]. At the same time we should stress that also all-atom force fields, although nowadays well-refined and capable to follow folding/unfolding events at long time scales [53], generally fail to estimate the exact temperature dependence of thermodynamic properties [54, 53].

Moreover, the values obtained for the heat capacity of unfolding ΔC_p and enthalpy of unfolding at the melting temperature ΔH_m, are out of scale. There are several causes to that starting from the absence of explicit water that is considered to give an important contribution to ΔC_p. Additionally, given the coarse-grained nature of system, the separation among entropic and enthalpic contribution is compromised. Finally, the lack of explicit electrostatic interactions should also be added to the list [55].

Up to date, no calorimetric data are available for the two G-domains. However, two detailed experimental studies on the thermal stability of the whole elongation factors -Tu and -1α, using circular dichroism and fluorescence, have been carried out determining the melting temperatures of the trimeric proteins at 320 K and 365 K respectively as well as showing that the G-domains set up a “basic” level of the thermostability for the whole proteins [50, 51]. Here, we verify in a qualitative manner that indeed the different thermal stability content of the two proteins is also reflected when the G-domains are taken isolated. More importantly, we observe the broadening of the hyperthermophilic’s stability curve over that of its mesophilic homologue suggesting that the thermodynamical mechanism behind the increase of its thermal stability is that of a smaller heat capacity of unfolding [10, 11, 9]. This is coherent with what deduced from AA simulations considering the conformational fluctuations in the folded state as well as the change of compressibility with temperature [9].

4. Conclusions

This is the first time that the thermal stability of two homologous thermophilic and mesophilic proteins is examined using the OPEP force field. In fact, to the best of our knowledge, this has never been attempted with any other coarse-grained force field of the same nature for such large systems consisting of about 200 residues. First, we show the capability of the force field to preserve the native state at the time scale of a hundred of nanoseconds by MD without the need of external constrains. This enables the characterization of the conformational landscapes of the homologues. More specifically, we show that the qualitative description of the conformational landscapes of the two proteins matches that from all atom simulations. The space visited by the hyperthermophilic protein is characterized by a large number of sub-states and its dynamics is slower and more resilient to temperature increase than that of the mesophilic variant. By using enhanced-sampling REMD, we also probe more explicitly the different thermal stabilities of the two proteins computing a stability gap of about 23 K in fair agreement with experiment. The shape of the extracted stability curve suggests that a smaller specific heat of unfolding for the hyperthermophilic protein is key for increasing its melting temperature.