Nucleotide diversity and linkage disequilibrium in loblolly pine

Abstract

Outbreeding species with large, stable population sizes, such as widely distributed conifers, are expected to harbor relatively more DNA sequence polymorphism. Under the neutral theory of molecular evolution, the expected heterozygosity is a function of the product 4N_eμ, where N_e is the effective population size and μ is the per-generation mutation rate, and the genomic scale of linkage disequilibrium is determined by 4N_er, where r is the per-generation recombination rate between adjacent sites. These parameters were estimated in the long-lived, outcrossing gymnosperm loblolly pine (Pinus taeda L.) from a survey of single nucleotide polymorphisms across ≈18 kb of DNA distributed among 19 loci from a common set of 32 haploid genomes. Estimates of 4N_eμ at silent and nonsynonymous sites were 0.00658 and 0.00108, respectively, and both were statistically heterogeneous among loci. By Tajima's D statistic, the site frequency spectrum of no locus was observed to deviate from that predicted by neutral theory. Substantial recombination in the history of the sampled alleles was observed and linkage disequilibrium declined within several kilobases. The composite likelihood estimate of 4N_er based on all two-site sample configurations equaled 0.00175. When geological dating, an assumed generation time (25 years), and an estimated divergence from Pinus pinaster Ait. are used, the effective population size of loblolly pine should be 5.6 × 10⁵. The emerging narrow range of estimated silent site heterozygosities (relative to the vast range of population sizes) for humans, Drosophila, maize, and pine parallels the paradox described earlier for allozyme polymorphism and challenges simple equilibrium models of molecular evolution.

New genetic variation within a species arises solely by the process of mutation. A new neutral variant may be lost rapidly from a population at the rate of one minus its initial frequency. If the new variant is not lost, genetic, demographic, and evolutionary processes, in addition to random genetic drift, determine its population frequency and its nonrandom association with adjacent sites (linkage disequilibrium, LD) along the segment of DNA on which it arose. Recombination is the primary genetic process that erodes LD over time. Therefore, two key parameters in simple population genetic models that govern the amount and distribution of intraspecific sequence variation are the population mutation parameter, θ = 4N_eμ, and the population recombination parameter, ρ = 4N_er, where N_e is the effective population size, μ is the per-generation, per-base pair mutation rate, and r is the per-generation recombination rate between adjacent sites.

Estimates of 4N_eμ can be readily calculated from DNA sequences obtained from population samples, even with relatively small data sets. Watterson's estimate of 4N_eμ as θ_W (1) is based on the number of polymorphic sites in a sample of sequences drawn at random from a population. A second estimate of 4N_eμ is nucleotide diversity, or π (2), which is the average number of pairwise nucleotide differences between sequences in a sample. π depends on both the number of polymorphic sites and their frequency, whereas θ_W is independent of frequencies. Tajima (3) developed a test statistic, D, to compare π and θ_W and to infer selection and demographic events by a skew in the site frequency spectra.

Estimating 4N_er (reviewed in refs. 4 and 5) is not as straightforward as 4N_eμ. One approach estimates N_e and r independently (6). N_e can be estimated from diversity and interspecific divergence data but estimates of r require knowledge of the ratio of genetic map distance to physical map distance, of which one or both may be inaccurate or unknown for many species. The second method estimates 4N_er directly from population DNA samples by using moment estimators, or more recently, full- and composite-likelihood approaches. The composite-likelihood method of Hudson (7), which considers only a single pair of segregating sites at a time and derives a point estimate of 4N_er by multiplying all pairwise likelihoods, is computationally fast and works as well or better than other methods (7).

Much of the pioneering research in estimating sequence variation and LD has arisen from large-scale sequencing surveys in humans (8, 9), Drosophila (10), and the angiosperm plant species Arabidopsis (11) and maize (12). In this study, we identified single nucleotide polymorphisms (SNPs) in ≈18 kb of DNA distributed across 19 loci from 32 alleles of the long-lived gymnosperm loblolly pine (Pinus taeda L.). Pertinent attributes of the species include a highly outcrossed mating system with extensive wind dispersal of pollen (13), a 50-million-acre distribution in the southeastern United States (14), abundant allozyme and microsatellite polymorphism with only weak population differentiation across its range (15, 16), and a very recent domestication history. Thus, natural, undisturbed stands of loblolly pine may be a good approximation to an idealized random mating population. In addition, the nutritive tissue of conifer seed (the megagametophyte) is maternally derived and haploid, greatly facilitating the analysis of sequence data. This study was motivated not only by an interest in the underlying processes determining the patterns of polymorphism, but also in the hope of identifying polymorphisms that have observable phenotypic effects. Our sampling strategy was focused primarily on the discovery of sequence variation and estimation of θ in genic regions representative of the genome as a whole in loblolly pine. The estimation of ρ requires that considerably larger segments of contiguous DNA be sequenced. Based on Hudson's (7) assertion that the estimate of ρ with the lowest variance is obtained for sites a known distance apart (in base pairs), when ρ_bp multiplied by distance is ≈5, the relatively short sequences obtained in this study are not sufficient to provide reliable locus-specific estimates of ρ. Instead, a genome-wide estimate of ρ was obtained from the two-site sample configurations pooled across loci.

Materials and Methods

Plant Material. The breeding of loblolly pine began only in the mid 1950s with mass selection of well adapted individuals from undisturbed natural stands. These individuals are conserved to this day as first-generation breeding material by grafting. The sample of 32 genotypes includes 14 first-generation selections archived in the 1950s by the North Carolina State University Industry Cooperative Tree Improvement Program and 18 individuals resulting from controlled crossing of the mass selections (second-generation breeding material). It was presumed that the first-generation breeding material is unrelated. The second-generation material introduced a slight bias, which should have minimal impact because of the expected high levels of heterozygosity and meiotic segregation, by the erroneous inclusion of two pairs of half sibs. The geographic distribution of the sample encompasses most of the natural range of loblolly pine with the exception of Florida; the origins of the first-generation selections or the two parents of the second-generation selections are included in Table 4, which is published as supporting information on the PNAS web site. Weyerhaeuser (Federal Way, WA) provided seeds from each individual, and, after seed germination, haploid DNA was extracted from the excised megagametophyte by using the Plant DNeasy kit (Qiagen, Valencia, CA).

PCR and DNA Sequencing. Sequencing of alleles was performed directly by using haploid megagametophyte DNA. Sequence data were obtained for 19 loci in most of the 32 samples. One to five fragments were amplified from each locus by using PCR primers designed from contig assemblies of loblolly pine EST sequences accessed through http://pine.ccgb.umn.edu. PCR primers and amplification conditions are provided in Table 5, which is published as supporting information at the PNAS web site.

Sequence data were obtained directly from PCR products on an ABI 377 automated sequencer by using the BigDye Terminator version 3.1 Cycle Sequencing kit (Applied Biosystems, Foster City, CA). All samples were sequenced in both directions at least once. For each allele, the forward and reverse reads were base-called initially by the phred program and assembled by the phrap program. To identify putative variants, multiple alleles from a locus were aligned by using the Multiple Alignment Consed Extensions (mace) program (Bill Gilliland and Charles Langley, University of California, Davis). A putative SNP was accepted as a genuine sequence variant if all chromatograms were unambiguous and all phred scores exceeded 25 at that site. Resequencing was performed when necessary to maintain these criteria.

Analyses. Sequence statistics were calculated by using dnasp software (version 3.53) (17) and are reported as per-site values. Insertion/deletions (indels) were excluded from all estimates. Nucleotide diversity was estimated as θ_W (1) and π (2). Heterogeneity of θ_W among loci was assessed by using a likelihood ratio test in which the probability of the observed number of segregating sites in a sample was calculated under the null hypothesis of a common, genome-wide 4N_eμ (P_g) and the alternative hypothesis of locus-specific values of 4N_eμ (P_l). This probability, calculated by using the recursion provided as equation 12 of ref. 18, was determined for both silent and nonsynonymous segregating sites. The likelihood ratio test statistic, -2ln(P_l/P_g), is distributed as a χ² with m - 1 degree of freedom, where m is equal to the number of loci. To investigate evidence of nonneutral evolution, the D test of Tajima (3) was applied. The two-tailed P value for each test was determined empirically from the distribution of D statistics across 10,000 data sets generated by coalescence (19). Simulated data sets for each locus were based on the observed number of segregating sites.

Several descriptors of the amount of LD in the sample were obtained. The number of haplotypes and the minimum number of historical recombination events, R_M, inferred from the four-gamete test (20) were determined by using dnasp. The descriptive statistic of LD, r² (21), and its significance, determined by a one-tailed Fisher's exact test, were calculated by using tassel (www.maizegenetics.net/bioinformatics/tasselindex.htm). The average decay of LD with distance was modeled similarly to previous research in maize (22). Under a standard Wright-Fisher model, the expected value of r², E(r²), is equal to 1/(1 + 4N_er) (21). It has been shown (23) that, with a low mutation rate and adjustment for sample size (n), this expectation is

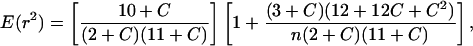1

where C = ρ = 4N_er. A least squares fit of the C parameter in this equation was obtained by the general algorithm described in ref. 24 implemented in kaleidagraph software (version 3.6.4, Syngergy, Reading, PA).

The composite-likelihood method of (7) was used to estimate 4N_er as described in ref. 25, but with haploid sample configuration probabilities. Frisse et al. (25) distinguished between 4N_er_bp (= ρ), where r_bp is the per-generation crossing-over rate between adjacent sites, and 4N_er_e, where r_e is the “effective” per-generation recombination rate between adjacent sites, equal to the probability that a gamete produced by a double heterozygote would be a recombinant by either crossing-over or gene conversion. The effective recombination rate is given by

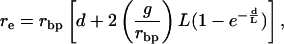2

where d is the distance in base pairs between two sites, (g/r_bp) is the ratio of gene conversion to crossing-over rate (also denoted as f), and L is the mean gene conversion tract length (25). We used the program makenewh (available at http://student-www.uchicago.edu/~rhudson1/source/twolocus.html) to estimate the two-locus sample configuration probabilities [designated h(n:ρ) in ref. 7] for a sample of 32 alleles and values of ρ between 0 and 100. To estimate ρ and f, the composite likelihood function given as equation 19 in ref. 7 was maximized by using the program maxhap (available at http://student-www.uchicago.edu/~rhudson1/source/maxhap.html) for all pairs of sites within each locus excluding singletons and a small number of sites with more than two variants in the sample. Note that, to the extent that the surveyed regions represent the loblolly pine genome, these estimates of 4N_er can be considered as genome-wide.

Results

Sequence Variation in Loblolly Pine. More than 575 kb of DNA sequence was obtained across 19 genes (Table 1). Sequence data for the complete set of 32 alleles was collected for 17 genes. High-quality sequence data for c3h and cad was obtained from only 28 samples, possibly because of the coamplification of a pseudogene (26). Summary statistics of nucleotide diversity, Tajima's D test, and the minimum number of recombination events are shown in Tables 2 and 3.

Table 1. Summary of 19 loci examined in this study.

			Base pairs screened
Gene	Locus	Linkage group	Total†	5′ UTR	Exon	Intron	3′ UTR	Indels*
Phenylalanine ammonia-lyase	pal	6	433		267		166	0
Cinnamate 4-hydroxylase	c4h-1	3	2,506	8	1,452	944	74	7 (28)
	c4h-2		522		522			0
4-coumarate:CoA ligase	4cl	7	2,438		1,341	902	56	7 (139)
Coumarate 3-hydroxylase	c3h	7	2,269		1,479	427	362	1 (1)
Caffeoyl CoA O-methyltransferase	ccoaomt	6	517		258	243		1 (16)
Cinnamoyl CoA reductase	ccr	7	1,044		378	487		2 (179)
Caffeate O-methyltransferase	comt-2	11	1,278		1,032	189	35	2 (22)
Cinnamyl alcohol dehydrogenase	cad	9	442		330	110		1 (2)
S-adenosyl methionine synthetase	sam-1	3	739	333	402			1 (4)
	sam-2	8	461		306	155		0
Glycine hydroxymethyltransferase	glyhmt	3	552		186	132	218	1 (16)
LIM transcription factor	ptlim1		425		126		299	0
	ptlim2		449		165		284	0
Cellulose synthase	cesA3	11	1,023		678	274	71	0
Arabinogalactan proteins	agp-like	3	886		633	253		0
	agp-4	7	367		177		188	2 (2)
	agp-6	5	884		609	88	169	3 (18)
α-Tubulin	tubulin	5	792	71	282	419		2 (20)
Total			18,027	412	10,623	4,623	1,922	30 (447)

^*Number of indels (total indel length in bp).

^†Includes total indel sequence length shown in last column.

Table 2. Summary statistics of sequence variation and Tajima's D.

	Total				Silent					NS*
Locus	L*	S†	τw	π	L	S	95% CI	τw	π	L	S	95% CI	τw	π	D‡
pal	433	6	0.00344	0.00197	231	6	0-13	0.00645	0.00370	202	0	0-5	0.00000	0	−1.20
c4h-1	2,478	40	0.00401	0.00308	1,365	36	16-67	0.00655	0.00463	1113	4	0-11	0.00089	0.00118	−0.85
c4h-2	522	11	0.00523	0.00489	125	9	0-8	0.01788	0.01887	397	2	0-5	0.00125	0.00046	−0.21
4cl	2,299	41	0.00443	0.00594	1,284	39	15-64	0.00754	0.01050	1015	2	0-10	0.00049	0.00018	1.25
c3h	2,268	6	0.00068	0.00027	1,131	4	12-55	0.00091	0.00042	1137	2	0-11	0.00045	0.00013	−1.73
ccoaomt	501	12	0.00595	0.01200	304	12	1-17	0.00980	0.01975	197	0	0-3	0.00000	0	2.81
ccr	865	21	0.00603	0.00524	580	21	5-30	0.00899	0.00782	285	0	0-4	0.00000	0	−0.45
comt-2	1,256	15	0.00297	0.00324	458	10	3-24	0.00542	0.00618	798	5	0-8	0.00156	0.00154	0.30
cad	440	6	0.00350	0.00602	186	5	0-11	0.00691	0.01147	254	1	0-4	0.00101	0.00203	2.09
sam-1	735	12	0.00405	0.00220	420	12	3-23	0.00709	0.00385	315	0	0-4	0.00000	0	−1.62
sam-2	461	3	0.00162	0.00220	226	3	0-13	0.00330	0.00447	235	0	0-4	0.00000	0	0.83
glyhmt	536	13	0.00602	0.00647	396	13	2-21	0.00815	0.00876	140	0	0-3	0.00000	0	0.24
ptlim1	425	3	0.00175	0.00058	326	3	1-18	0.00229	0.00075	99	0	0-2	0.00000	0	−1.55
ptlim2	449	5	0.00277	0.00095	321	4	1-18	0.00309	0.00078	128	1	0-2	0.00194	0.00137	−1.76
cesA3	1,023	9	0.00218	0.00087	513	9	4-27	0.00436	0.00173	510	0	0-6	0.00000	0	−1.84
agp-like	886	7	0.00196	0.00157	423	6	3-23	0.00352	0.00314	463	1	0-6	0.00054	0.00014	−0.58
agp-4	365	24	0.01633	0.01728	226	16	0-13	0.01758	0.01274	139	8	0-3	0.01429	0.02463	0.21
agp-6	866	34	0.00975	0.01086	433	25	3-23	0.01434	0.01727	433	9	0-5	0.00516	0.00446	0.19
α-tubulin	772	20	0.00643	0.00351	555	20	4-29	0.00895	0.00488	217	0	0-3	0.00000	0	−1.56
Total	17,580	288			9,503	253				8,077	35
Weighted average			0.00407	0.00398				0.00658	0.00640				0.00108	0.00114

NS, nonsynonymous sites; CI, confidence interval.

^*Length of sequence excluding indels.

^†Number of segregating sites.

^‡Tajima's D.

Table 3. The number of haplotypes and the minimum number of recombination events, R_M, in the history of the sampled loci.

Locus	No. of haplotypes	RM
pal	6	0
c4h-1	19	5
c4h-2	10	1
4cl	11	2
c3h	7	0
ccoaomt	5	0
ccr	15	2
comt-2	6	0
cad	3	0
sam-1	6	0
sam-2	4	0
glyhmt	6	0
ptlim1	3	0
ptlim2	6	0
cesA3	9	0
agp-like	8	0
agp-4	11	4
agp-6	12	1
α-tubulin	7	0

Across the 19 genes, 18,027 base pairs were aligned, including 10,623 bases from coding regions, 6,957 bases from noncoding regions (introns and untranslated regions), and 447 bases of indels. A total of 288 SNPs were detected, corresponding to one SNP per 63 base pairs and a (weighted) average θ_Wt = 0.00407. Diversity at silent (θ_Wsil) and nonsynonymous (θ_Wns) sites was 0.00658 and 0.00108, respectively.

The number of SNPs observed per locus varied from 3 to 41, giving rise to values of θ_Wsil ranging from 0.00091 to 0.01788 and θ_Wns ranging from 0 to 0.01429 (Table 2). We applied a likelihood ratio test to determine whether θ_Wsil and θ_Wns varied statistically among all loci. The probability (P_l or P_g) of observing the observed number of segregating sites or fewer at each locus was calculated conditioned on either a locus-specific estimate of θ or a genome-wide θ equal to the estimates of θ_Wsil and θ_Wns across all loci. The χ² tests were significant for both silent sites (df = 18; χ² = 43.25, P = 0.0007) and nonsynonymous sites (df = 18; χ² = 41.82, P = 0.0018) and, therefore, the homogeneity across loci of 4N_eμ governing silent and nonsynonymous substitutions was rejected. Assuming that the neutral equilibrium model is appropriate, fewer segregating silent sites than expected were observed at c3h, whereas c4h-2, agp-4 and agp-6 were more variable than expected (Table 2). At nonsynonymous sites, agp-4 and agp-6 revealed more variation than expected under a neutral model.

Indels. Indels were responsible for a larger proportion of mismatched nucleotides than SNPs. Among the 19 loci, 30 indels spanning 447 bases were observed (Table 1). Indel size ranged from 1 to 178 bases; a total of 52% of indels were 1-2 bp in length, and 93% were <19 bp. Only two indels >100 bp were found, including a complex indel in 4cl and a direct tandem repeat indel of 178 bp in ccr. Five additional direct repeats ranging from 7 to 19 bases in length were detected in addition to a tetranucleotide microsatellite in the 5′ untranslated region of sam-1. Direct repeats ranging in size from 10 to 217 bp have been reported in the alcohol dehydrogenase gene family of Pinus banskiana Lamb (27) and appear to be a common occurrence in conifer genomes.

Selection. Tajima's D statistic reflects the difference between π and θ_W. At equilibrium between genetic drift and selectively neutral mutation, the expected value of D is close to zero. Tajima's D was calculated for all loci (Table 2). To control for an elevated rate of false positives resulting from multiple testing, the two-tailed P value for each test was determined empirically from simulated data sets, and the standard Bonferroni correction applied. When this conservative approach was used, no evidence to contradict neutral evolution was observed.

LD and the Estimation of the Population Recombination Parameter. An examination of the distribution of polymorphic sites and minimum number of historical recombination events (R_M) at each locus (Table 3) provided little evidence of strong haplotype structure, by which most sequences would fall into one or a few classes with few intermediate types observed. At the six loci in which one or more historical recombination events were detected, 13 haplotypes were observed on average. The 13 loci without evidence for historical recombination had six haplotypes on average. Eleven of the 13 are characterized by a single predominant class making up as much as 60% of the sample, with the remaining classes differing only by one or several substitutions. The remaining two loci are ccoaomt and cad that consist predominantly of two haplotypes with many fixed differences, giving rise to large, positive, but not significant, Tajima's D statistics. Hudson and Kaplan's four-gamete test has very limited power to infer recombination. Nonetheless, this preliminary analysis suggests a relatively short range of LD in the sample of loblolly pine. It should be noted that no evidence for clustering of haplotypes by geographic distribution was observed at any locus.

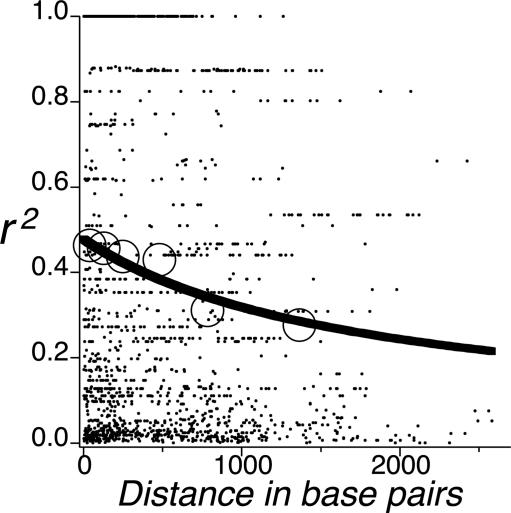
Because the average distance between sites was relatively small, and heterogeneity among loci in the decay of r² was not apparent by visual inspection (data not shown), we pooled site data across all loci to represent a genome-wide description of the short-range behavior of LD in loblolly pine. Fig. 1 shows the distribution of r² values for the 1,812 pairs of biallelic sites with minor allele frequencies >6%. Although few pairwise comparisons are available for sites >1500 bp apart, the curve, which represents the observed r² values fitted by least-squares to their expectation (24), clearly indicates that LD decays ≈50% over the short segments examined (from ≈0.5 to 0.25 within 2,000 bp). Also shown in Fig. 1 are the mean r² values for six subsets of the 1,812 site pairs, each consisting of 302 site pairs from adjacent intervals along the x axis. The fit of these mean values to the regression line is quite good.

Fig. 1.

Plot of the squared correlations of allele frequencies (r²) versus distance in base pairs between polymorphic sites across 19 loci. The fitted curve (solid line) of Hill and Weir (23) is shown along with the mean r² values (open circles) for subsets of the 1,812 site pairs, each consisting of 302 site pairs from adjacent intervals along the x axis.

Intergenic LD was assessed across three regions where two or more genes had been mapped genetically (28). These regions are described, where the number in parentheses is approximate Kosambi centiMorgan (cM) distances between loci, as [glyhmt-(19)-c4h-1-(9)-agp-like-(38)-sam-1] on linkage group 3, [agp-6-(6)-α-tubulin] on linkage group 5, and [4cl-(14) agp-4-(42)-ccr] on linkage group 7. According to Fisher's exact test, 35 of a total of 1,812 site pairs were significantly correlated. However, after Bonferonni correction, no evidence of intergenic LD was found.

Under simple population genetic models, the extent of LD is determined by ρ = 4N_er. Using a maximum composite likelihood method (7), ρ was estimated from the pooled data of sample configurations between pairs of sites within the 19 loci. In the absence of gene conversion, the estimate of ρ per base pair is 0.00175. Note that the fitted equation depicting the decay of LD (Eq. 1 and Fig. 1) provides an alternative (and very similar) least-squares estimate of ρ per base pair, 0.00115. If gene conversion tract lengths are fixed at 400 bp, near the lower bound of tract lengths reported in Drosophila and yeast (29, 30), then the joint maximum likelihood estimates of ρ and the gene conversion rate, f, are 0.0012 and 0.5, respectively. However, the likelihood surface for estimating f was quite flat and, therefore, other parameter values are compatible with the data.

Discussion

This study adds a taxonomically and ecologically important nonmodel species to the growing list of organisms for which estimates of fundamental population genomic parameters are available. The sample of loblolly pine germplasm is a good representation of the variation in natural populations of a large, long-lived, outcrossing plant species. Our sampling of the genome revealed a 10-fold difference in estimates of θ that underscores the perils of comparing variation among species when estimates of θ are based on one or only a few loci. Regions of intergenic, noncoding DNA where levels of variation are expected to be higher (31) may provide a different picture of diversity in loblolly pine and other species. With the caveat that comparisons among species of θ based on many loci should be restricted ideally to orthologous loci, this study places loblolly pine in an intermediate position among species for which similar sequencing surveys have been performed. θ_Wt is 2.3-fold lower than maize (12), 1.8-fold lower than Drosophila (10), 2-fold greater than Cryptomeria japonica (32), 4.2-fold greater than soybean (33), and 4.9- to 7.7-fold greater than humans (8, 9).

One limitation of this study is the omission of an outgroup species. To derive estimates of μ and N_e, the single best matching expressed sequence tag from the related species Pinus pinaster Ait. was selected as the putative ortholog of each loblolly pine gene sequenced. For loblolly pine genes sequenced over multiple amplification products, only a single P. pinaster sequence was used. A total of 6,522 base pairs were aligned across all genes with the exception of ccr. Divergence between the two species (d_A = 0.02799; ref. 34) was estimated from 4-fold degenerate sites. The best estimate of divergence time (T) for these two species is 120 million years (35, 36) and the per-year substitution rate was estimated to be μ_y = d_A/2T = 1.17 × 10^-10 substitutions per year. This value is similar to μ_y estimated at the pal locus in Pinus sylvestris (37) and is an order of magnitude lower than angiosperm mutation rates (37). Assuming a 25-year generation interval as the time to achieve substantial seed production in a typical, crowded natural stand of loblolly pine (Bruce Bongarten, personal communication), the per-generation mutation rate, μ_G, is equal to 25 μ_y. N_e was estimated as θ_Wsil/4 μ_G = 5.6 × 10⁵.

Despite the approximate nature of this calculation the estimate of N_e seems exceptionally low for a species with the life history and population attributes of loblolly pine. For argument's sake, if a minimum density of 1,000 trees per acre is assumed, the census population size is almost five orders of magnitude greater than N_e. The average N_e over a population's history is the harmonic mean over all generations, which tends to be dominated by the smallest value. Therefore, a simple explanation for this large difference is that extant communities of loblolly pine arose from postglacial migration out of one or more refugia, where the census population size was drastically reduced. A Pleistocene glacial refugium existed in southern Florida (38), and a second refugium has been proposed to exist in central Texas (15, 39). Sediments taken from the Florida peninsula and extending back 50,000 years revealed multiple pre-Holocene and Holocene fluctuations in pine pollen abundance. Pollen abundance after the height of the Wisconsin glaciation is representative of these fluctuations. Southern Florida landscapes 10,000 years B.P. were dominated by oak and scrub; pines contributed relatively little pollen (<10%) to the sediments and must have been reduced to very small populations (40), presumably of lower stand density. (Note that pollen morphology among many pines is indistinguishable, and several southern pine species, including loblolly pine, were implicated in this study.) Pine pollen becomes steadily more abundant, and then the dominant type, in sediments beginning as early as 7,000 years B.P., signifying the onset of expansion into present-day communities. These data indicate that glacial advances periodically reduced the population size of loblolly pine by orders of magnitude through a restriction of its geographic distribution and a decrease in stand density. Such drastic fluctuations certainly explain a large portion (if not all) of this disparity between the present-day census numbers, and the estimated equilibrium effective population size. We note that our sample size is likely too small to detect traces of these fluctuations, either as a positive Tajima's D or geographic structure in the distribution of haplotypes characteristic of recently bottlenecked populations or a negative Tajima's D after population expansion as new mutations accumulate.

Our observations on levels of LD in loblolly pine are consistent with population genetic theory as applied to a highly outcrossed species with large N_e and little evidence for strong population stratification or selection. Regardless of the low number of inferred minimum number of recombination events, there is evidence for considerable recombination in the history of the sampled alleles. LD decays over short distances at the loci examined, to values of r² approaching 0.2 within several kilobases, although the generality of this scale of LD across the entire loblolly pine genome remains to be established. There are strong suggestions that recombination rates vary dramatically across genomic regions in other species; although genetic map distances are similar among eukaryotes (≈100 cM per chromosome or one recombination event per chromosome per generation), the physical amount of nuclear DNA is highly variable. In humans, there is ample evidence for recombination hotspots 1-2 kb in length, which effectively partition the genome into haplotype blocks (41). In plants, recombination events may be restricted to genic regions. In maize, for example, this may be a consequence of the extensive repetitive retrotransposon makeup of the genome. Fu et al. (42) showed that recombination was two orders of magnitude lower in a gene-poor, retrotransposon-rich region of the bronze locus compared to a gene-dense, retrotransposon-free region. Gene conversion has also received little attention in studies modeling the decay of LD, but Frisse et al. (25) showed that LD data for an African population of humans were not consistent with a model that includes crossing-over only. If recombination by reciprocal crossing-over or gene conversion is restricted to genes in pines, then the modeling of LD presented here will overestimate the average genome-wide decay. This issue can only be addressed through a further analysis of more genes and much longer segments of contiguous DNA.

The results of nucleotide variation in loblolly pine contribute to an issue dating back to a curiosity in predictions of the neutral theory of molecular evolution described by Lewontin (43). At mutation-drift equilibrium, heterozygosity (H) is expected to increase with a species' effective population size according to the fundamental neutral theory equation H = 4N_eμ/(1 + 4N_eμ) (44). Lewontin (43) demonstrated that the observed heterozygosities at allozyme loci for most species were actually much lower than expected. Furthermore, he showed that the range of estimates of N_e required for the neutral theory to be true was unrealistically narrow for the diverse groups of higher organisms considered. In light of the increasing number of DNA studies surveying multiple regions of both model and nonmodel genomes, a reexamination of this issue will be possible. To date, the number of organisms with sufficient data are still limited, but a similar observation of a lower-than-expected range of heterozygosities at silent nucleotide sites is emerging. However, the prospects of now resolving this paradox are more favorable because of the detail and scale of population genomic data sets based on DNA sequences. Deeper sampling of both a species' genome and range-wide distribution will enable testing of alternative models to the equilibrium neutral model that incorporate both biogeographic and selection events.