ABSTRACT
Cells are interactive living systems where proteins movements, interactions and regulation are substantially free from centralized management. How protein physico‐chemical and geometrical properties determine who interact with whom remains far from fully understood. We show that characterizing how a protein behaves with many potential interactors in a complete cross‐docking study leads to a sharp identification of its cellular/true/native partner(s). We define a sociability index, or S‐index, reflecting whether a protein likes or not to pair with other proteins. Formally, we propose a suitable normalization function that accounts for protein sociability and we combine it with a simple interface‐based (ranking) score to discriminate partners from non‐interactors. We show that sociability is an important factor and that the normalization permits to reach a much higher discriminative power than shape complementarity docking scores. The social effect is also observed with more sophisticated docking algorithms. Docking conformations are evaluated using experimental binding sites. These latter approximate in the best possible way binding sites predictions, which have reached high accuracy in recent years. This makes our analysis helpful for a global understanding of partner identification and for suggesting discriminating strategies. These results contradict previous findings claiming the partner identification problem being solvable solely with geometrical docking. Proteins 2016; 85:137–154. © 2016 Wiley Periodicals, Inc.
Keywords: protein–protein interaction, geometrical docking, partner identification, binding site, complete cross‐docking, interface prediction
INTRODUCTION
The development of experimental and computational techniques for protein structure characterization has led to the emergence of integrative approaches for probing the “molecular sociology of the cell,”1 that is, how proteins interact within cellular functional modules. These approaches have proven successful in determining the structures of some macromolecular assemblies and hold great promises for the future.1, 2, 3 However, a number of challenges remain to be overcome before the building of 3D interactome networks becomes feasible. One of the most pressing challenge is that of specificity. In the context of a very crowded cellular environment, how can a protein distinguish its dedicated partners from non‐interactors? While in vitro/in vivo experiments can suggest and test putative partners, computations provide a unique way to characterize interactions at very large scale and to explore the space of negatives, that is, of what does not occur in the cell. Hence, the development, adaptation and optimization of in silico methods is of paramount importance.
Molecular docking has been addressed, for many years, toward the understanding of molecular behavior and its potential to infer protein–protein interactions (PPIs) has often been discussed.4, 5, 6 Although the development of docking algorithms, stimulated by the CAPRI competition,7 has shown great improvements over the years, scoring functions still struggle with a number of difficulties in correctly ranking near‐native complex conformations.4 That is why the identification of interaction partners has generally been regarded as beyond their scope.8, 9, 10 It is only very recently that molecular docking‐based strategies have been devised to this problem. The first proof‐of‐principle for such an approach applied to the reconstruction of biological networks was reported in Ref. 11. In 2007, the first large‐scale cross‐docking study12 for the prediction of interaction partners was launched on 168 proteins13 whose interactions are known. This study highlighted the importance to develop appropriate concepts and tools for improving the discriminative power of molecular docking.
Large‐scale modeling experiments dealing with hundreds of proteins can be computationally highly demanding and scaling up to thousands or tens of thousands of proteins asks for drastically reducing the computing time associated to molecular docking. In this respect, rigid‐body geometrical docking algorithms have been used to efficiently generate and rank candidate complex conformations.14, 15 It has been suggested that docking scores based only on the geometric complementarity of the two molecular surfaces can be used to identify binding partners.14 This finding goes against observations by other groups that docking scores, even from the most sophisticated current scoring functions, are poorly or mildly correlated with binding affinities16 (see Ref. 17 for recent improvements based on contacts). Here, we rigorously demonstrate that geometrical complementarity is not sufficient to distinguish between cognate partners and non‐binders. By doing so, we set questions that could be considered as benchmarks to test new approaches.
What type of information can be exploited to identify interacting partners? To what extent can geometrical docking localize protein binding sites? What is the link between partner identification and binding site localization? To contribute to answer to these questions, we revisit the concepts used in previous studies12, 14 and we propose to evaluate docking configurations by using two kinds of information that are different from shape complementarity docking scores: (1) the knowledge of the binding sites and (2) the knowledge of the global behavior of each protein relative to its potential partners (native and non‐native) inferred from docking calculations.
The first criterion relies on the assumption that each interacting surface encodes information about the specificity of the interaction between the two partners. The majority of protein interface prediction methods exploit sequence‐based, and optionally structure‐based, residue properties of a single protein.18, 19, 20, 21, 22, 23, 24, 25, 26, 27. Some of these methods already provide very accurate predictions, without any knowledge of a protein's partner(s). Likewise, several docking studies showed that some regions at the surface of a protein are preferentially targeted by any protein (partner or not).11, 12, 15 Nevertheless, a few recent works demonstrated that protein binding site predictions can be improved by including information about the native partner, provided that reliable structural data are available, and highlighted the specificity of interfaces involved in transient interactions.28, 29, 30, 31 Here, we show that the problem of localizing and delineating interaction surfaces is more tightly linked to that of discriminating protein partners than what is generally admitted. We reveal a correlation between the correct detection of the binding site and the identification of the correct partner. This correlation is observed using geometrical docking, and also using a more sophisticated docking/scoring methodology.
The second criterion postulates that the overall propensity of a protein to interact with many potential partners, in other words its global social behavior, should be accounted for to identify its cognate partners. Previous studies have characterized the tendency of proteins to form promiscuous interactions in terms of stickiness, defined based on the hydrophobicity of the protein surface.32, 33, 34, 35 Here, we propose to define a sociability index, called S‐index, that reflects the tendency of a protein to glue to other proteins, inferred from docking calculations. The notion of sociability goes beyond that of stickiness: while a sticky protein has no preferential partner, we show that a protein might be sociable with all other proteins but display different degrees of sociability, with proteins playing different functional roles in the cell. The information of protein sociability can help reveal evolutionary signals toward avoiding non‐functional interactions. We show that the S‐index scales obtained from different docking algorithms largely overlap. We use S‐indexes to normalize interaction scores computed between pairs of proteins with respect to all other proteins in the ensemble considered. In Ref. 14, this idea was not present and the complexes were evaluated independently. We propose a modified version of the normalization formula, compared to that reported in our previous works.11, 12 Our results clearly show that accounting for protein sociability greatly contributes to increasing the discriminative power of the approach. We highlight a higher chance of detecting the correct partner for pairs that are not both highly sociable nor both poorly sociable.
These two criteria have implications for our global understanding of how proteins interact with each other.
MATERIALS AND METHODS
Unbiased high‐throughput docking
Two types of docking experiments were realized. (i) The 352 proteins from the Protein‐Protein Docking Benchmark (PPDB) version 4 (http://zlab.bu.edu/benchmark4/)36 were docked against their known partner (from PPDBv4) and against a background set of 918 potential interactors belonging to different superfamilies.37 The original set was taken from Ref. 14 and comprised 922 structures. We removed four structures as they were not suitable for docking (the contained only C‐α atoms). (ii) A complete cross‐docking of PPDBv4 was also realized in which all 352 benchmark proteins were docked against each other and themselves [Fig. 1(c)]. Given a protein pair from the dataset, two docking calculations were performed where the two proteins alternatively played the role of the receptor and that of the ligand [Fig. 1(b)]. In total, 447 040 docking calculations were realized. Docking was performed with HEX v6.338 using the shape complementarity scoring function. HEX parameters are reported in Supporting Information Table S1. The precision of the molecular representation was defined from 18 and 25 expansion orders for the initial and final search steps. To avoid bias coming from the input PDB structures, the receptor and ligand models were positioned at a distance of 100 Å from one another prior to docking. Moreover, five starting positions were defined using HEX Macro‐Sampling module and were used to generate initial docking orientations for the ligand over the receptor and to derive appropriate local coordinate frames. Let us stress that in all docking calculations, we used the unbound conformations of the proteins from PPDBv4.
Figure 1.
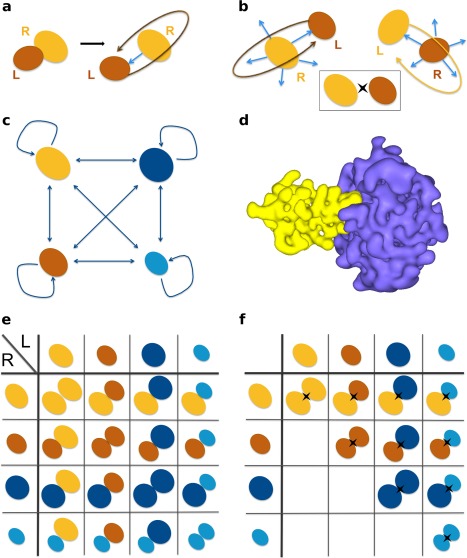
Schematic representation of the docking protocols. (a) Biased docking starts from the original PDB file recording the coordinates of the known complex. The relative orientation of the ligand (in brown) compared to the receptor (in orange) is randomized prior to docking, but not its position. (b) Unbiased docking starts from five randomly chosen orientations and positions (blue arrows) of the ligand with respect to the receptor. For any pair of proteins, two docking calculations are performed (on top and at the bottom), so that each protein alternatively plays the role of the ligand and that of the receptor. The insert on the right gives a simplified representation of the two docking calculations for a pair of proteins. (c) In a complete cross‐docking experiment applied on an ensemble of four proteins, each protein (for example here, the orange one) is docked to all the other proteins, including itself. (d) Representation of molecular surfaces by HEX, with the order of the 3D expansion N = 25. The complex is that of trypsin (in purple) and its inhibitor (in yellow). (e) To identify partners using geometrical ranking, each line of the matrix is considered separately. (f) To identify partners using interface‐based ranking, the interaction index of a protein pair is determined over the two docking calculations involving the two proteins. The II matrix is symmetrical.
Post‐processing of docking poses to discriminate native partners from non‐interactors
Different protocols for evaluating the docking poses were tested: (1) the protocol reported in Ref. 14 where the docking score distribution of each known complex is simply compared to those of the non‐interacting protein pairs, (2) a similar protocol where the comparisons are based on an interaction index that uses experimentally determined interfaces [see Eq. (1) below], (3) a more sophisticated protocol where the interaction index value of each protein pair is normalized with respect to all the other pairs.
Statistical testing of docking score distributions
Docking score distributions for the known complexes and the non‐interacting protein pairs were compared following the same protocol as that reported in Ref. 14. Given a protein P and its N potential partners (including its native partner and other proteins that are considered as non‐interactors), N docking runs were conducted and M best‐scored models were selected from each docking run. Therefore, N – 1 individual Wilcoxon rank‐sum tests were performed to compare the docking score distribution from P with its native partner with each one of the N – 1 distributions from P with the other proteins. For each test, the H0 hypothesis is that the two distributions are the same and the differences are simply due to random error. It is rejected when the P values is lower than 0.01 (changing this value for 0.05 or 0.10 did not impact the results, see Supporting Information Fig. S1). This way, one can rank the native partner of P and determine the percentage x of non‐interactors from which it is indistinguishable. We refer to x as the significance level of the test. For instance, when x = 1 the native partner of P has a better score distribution than 99% of the other proteins.
The number N of potential partners is 919 in experiment i and 352 in experiment ii. The number M of retained scores is 7 348 (maximum number of solutions given by HEX). Note that in Ref. 14, the authors considered the top 20,000 best‐scored models for their analyses but they showed that they could obtain essentially the same results using the 1,00,000, 10,000, 5000 and 1000 top scores.
The protein interaction index—II
With the aim of discriminating cognate partners from non‐interactors, we propose to evaluate docking models based on the agreement between the docked interfaces and the experimentally known interfaces. For every protein pair , we determined an interaction index (II):
| (1) |
where (Fraction of Interface Residues) is the overall fraction of the docked interfaces, obtained when P 1 is the receptor, composed of residues belonging to the experimentally identified interfaces for the two proteins: . , where P 2 is the receptor, is defined similarly. The docked interfaces are defined by the sets of residues that display a change of at least 10% decrease in accessible surface area compared to the unbound proteins (receptor and ligand). For each docking calculation, the maximum is determined >2 000 docking conformations, obtained by clustering the solutions generated by HEX with a 3 Å cutoff distance and retaining those with the best HEX scores. The receptor and the ligand do not play symmetrical roles in the docking calculations, so that the conformational ensemble obtained when docking P 1 to P 2 may be different from that generated when docking P 2 to P 1. To avoid any bias in the results, we estimated the interaction strength between each pair regardless of the role (receptor or ligand) each protein plays in the calculations. Hence, the maximum was defined over the 2 docking calculations involving P 1 and P 2. It follows that: .
The protein normalized interaction index—NII
We further propose to normalize the interaction indices, in order to account for the global social behavior of the proteins involved in each pair. Our assumption is that the ability of P 1 and P 2 to interact with all other proteins in the dataset should be accounted for to decide whether P 1 and P 2 interact together. The normalized interaction index NII between P 1 and P 2 was determined as:
| (2) |
where is a weighted version of the interaction index and it is defined as:
| (3) |
where is the ensemble of proteins considered. The normalization can be applied to the whole PPDBv4 dataset or to subsets. In either case, NII values vary between 0 and 1. For each protein Pi, we defined its predicted partner as the protein Pj that lead to . Note that this formula is simpler than the one we proposed in Ref. 12. This is because the II matrix computed here is symmetrical, which was not the case in Ref. 12.
Comparing with other docking programs
We repeated CC‐D of a subset of 33 enzyme‐inhibitor complexes from PPDBv4 (Supporting Information Table S2) with the docking program ZDOCK 3.0.2.39 Like HEX, ZDOCK performs rigid‐body docking using a grid‐based representation of proteins and a fast Fourier transform. The 2 000 best‐scored docking models were retained for docking score distribution statistical comparison, and the 500 best ones only for interface‐based ranking.
We also analyzed data issued from a complete cross‐docking study of the PPDBv2 benchmark13 (84 complexes, included in PPDBv4) realized using the MAXDo (Molecular Association via Cross Docking) algorithm.12 MAXDo uses a multiple energy minimization scheme based on the ATTRACT protocol.40 For each pair of proteins, one molecule (called the receptor) is fixed in space, while the other (called the ligand) is placed at different starting positions to cover the surface of the receptor. For each position of the ligand, 210 orientations were generated and only the one yielding the best interaction energy was retained. To analyze these data, we used an alternative version of the interaction index:
| (4) |
where and are the interaction energies computed by MAXDo (negative values) when docking P 1 against P 2 and reciprocally. For each docking calculation, the minimum was determined over all retained docking models (this number may vary depending on the size of the receptor) for the 2 docking calculations involving P 1 and P 2 so that . The normalization formula is the same as in Eq. (2).
Residue scoring based on docking
The interaction propensity index—IP
In order to characterize the docking conformational ensemble, we defined an interaction propensity (IP) index that estimates the frequency at which each residue i of a given protein P 1 appears in a docked interface:
| (5) |
where is the number of retained docking conformations of P 1 and is the number of these conformations where residue i belongs to the binding interface. Given a docking experiment, we retained the 2 000 best scoring clustered poses to compute IP. The IP index can be calculated from all the docking experiments involving P 1 or only from the two docking experiments with its native partner (IPnative) or only from the two docking experiments with any non‐interactor. The IP values computed for all proteins from PPDBv4 using HEX are available at http://www.lcqb.upmc.fr/CCDGeomDock/.
The normalized interaction propensity index—NIP
To allow comparison between residues belonging to the same protein P 1, the index IP was normalized as:
| (6) |
where is the average computed over all residues j at the surface of P 1, and is the maximum IP value obtained at the surface of P 1. NIP can be positive, indicating that the residue i is favored to occur at potential binding sites, or negative, indicating that it is disfavored. We considered residues with positive NIP values as predicted to be in interaction.
Comparison of NIP profiles
Given a protein P 1, we define its NIP profile as the vector of values, where i varies between 1 and the size of P 1, computed from docking P 1 to all the proteins in the dataset. Upon docking P 1 to its known partner P 2, one can define in a similar manner the vector of length equal to the size of P 1 containing the NIP values calculated from the two docking calculations involving both P 1 and P 2. The distance between and was calculated as the normalized angle between the two vectors:
| (7) |
The distance is comprised between 0 and 1. A small value indicates that P 2 binds to the same region(s) at the surface of P 1 as any other protein in the dataset, while a high value indicates that P 2 binds in a peculiar way to P 1 compared to the other proteins in the dataset.
Evaluation of IP and NIP performance
To evaluate the predictive power of IP and NIP indexes, we relied on the following quantities: the number of residues correctly predicted as interacting (true positives, TP), the number of residues correctly predicted as non‐interacting (true negatives, TN), the number of non‐interacting residues incorrectly predicted as interacting (false positives, FP) and the number of interacting residues incorrectly predicted as non‐interacting (false negatives, FN). We used the four standard measures of performance: sensitivity , specificity , accuracy and positive predictive value . The R software41 was used to compute all performance values and produce the corresponding graphs.
Species representation in PPDBv4
We analyzed the distribution of species within PPDBv4. For each protein P of the ensemble, we retrieved with Blast (e‐value threshold at , alignment coverage 70%) three lists of species where a homolog of that protein, at 100%, 80% or 60% sequence identity, is present. For each species identified, we then counted the number of known complexes whose two partners have homologs in that species. At 100% sequence identity, Homo sapiens is the most populated species, with 24 complexes. At 80% and 60% sequence identity, the species being the most populated are essentially mammals. Homo sapiens has 75 complexes at 80% and 85 complexes at 60%. The bacterium Escherichia coli has 11 complexes at 80% and 60% sequence identity.
RESULTS
In the following, we aim at singling out cognate partners based on docking calculations, and discriminating them from non‐interactors. We use a geometrical docking algorithm based on a rather crude representation of protein surfaces, which has the great advantage of being fast compared to other approaches. We are interested in understanding what the ingredients of the discrimination are: geometrical score, fit with the real interface, sociability of the protein. We refer to the protein pairs comprising the 176 binary complexes from PPDBv4 as known/native/cognate partners. Any other protein pair is considered as non‐interacting, even though interactions might be possible but unknown.
Geometrical ranking does not identify protein partners
We performed rigid‐body docking with the program HEX,38 using only the shape complementarity of the two molecular surfaces to score the docking poses [Fig. 1(a)]. HEX models proteins using 3D expansions of real orthogonal spherical polar basis functions [Fig. 1(c)], which allows for a very efficient sampling of the docking space. The order of the expansion determines the level of refinement of the description. Typically, >3 billions candidate ligand‐receptor orientations are generated for each docking calculation. Given two proteins, five randomly chosen initial positions and orientations of the ligand with respect to the receptor were considered (see Materials and Methods). Moreover, two docking calculations were performed, so that each protein alternatively played the role of the receptor and that of the ligand [Fig. 1(a)]. As benchmark set, we used the Protein‐Protein Docking Benchmark version 4 (PPDBv4) comprising 352 proteins, among which 52 enzymes, 52 inhibitors, 25 antibodies (12 bound), 25 antigens (12 bound), and 198 proteins with other function.36
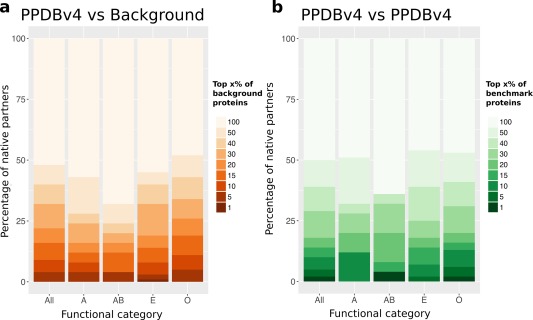
We performed two high‐throughput unbiased docking experiments, totaling about 4,50,000 docking calculations. In the first one, all the proteins from PPDBv4 (in unbound conformations) were docked against a background set of about 1000 structures belonging to different superfamilies37 (see Materials and Methods). The statistical distributions of the docking scores were then compared using the Wilcoxon rank‐sum test.42 For each protein P, we determined the percentage x of background proteins from which the native partner of P was indistinguishable. We then counted the number of native partners corresponding to different values of x [Fig. 2(a)]. Only 14 native partners (4% of the benchmark set) had significantly better scores than 95% of the background proteins (All, x = 5%, two darkest orange rectangles). About 50% of the partners were not even ranked in the first half, that is, they were no better than 459 background proteins (All, lightest orange rectangle). This indicates that docking scores obtained by unbiased geometrical docking do not carry sufficient information to distinguish cognate partners from a background set of potential interactors.
Figure 2.
Discrimination of cognate partners and non‐interactors based on geometrical ranking. (a) High‐throughput docking of PPDBv4 (352 proteins) against a background of 918 proteins. (b) Complete cross‐docking of PPDBv4. In y axis is reported the percentage of known interactors whose docking score distribution falls in the top x% of background distributions. The x% is indicated by the intensity of the color. For instance, the darkest orange rectangle in All, indicates that the known partners of 12 proteins from the benchmark set (12/372 = 3%, in y axis) are found in the top (x=) 1% of the background distributions (see color legend). In other words, 3% of the known interactors have a score distribution significantly better than 99% of the background distributions. The functional categories are the following: 26 antibodies‐antigens (A), 24 bound antibodies‐antigens (AB), 104 enzymes‐inhibitors (E), and 198 proteins with other functions (O).
The second experiment consisted in a complete cross‐docking (CC‐D) of all structures in PPDBv4, including themselves [Fig. 1(d)]. The score distributions obtained by docking each protein to all the proteins in the dataset were compared [Fig. 1(e)]. Only seven native partners (2%) were found in the top 5 potential partners [Fig. 2(b), All, x = 1%, darkest green rectangle]. And again, about 50% of the partners were not even ranked in the best half (All, lightest green rectangle). This protocol consistently displayed poor performance for the four functional classes represented in PPDBv4: enzymes‐inhibitors (E), antibodies‐antigens (A), bound antibodies‐antigens (AB) and others (O). These results are in agreement with those we previously obtained on the enzyme‐inhibitor dataset of PPDBv243 and clearly show that geometrical docking alone does not carry sufficient information to distinguish cognate partners from non‐interactors in an unbiased CC‐D experiment.
Partner identification using knowledge of binding sites
How can geometrical docking be useful in singling out cognate partners? Instead of relying on docking score distributions, we propose to rank potential partners based on the agreement between the docking interfaces and the experimental interfaces, without explicitly including the shape complementarity score. To this end, we defined an interaction index for any protein pair as:
| (8) |
where and (Fraction of Interface Residues) are the fractions of the docked interfaces, obtained when docking P 1 against P 2 and reciprocally, composed of residues belonging to the experimental interfaces for the two proteins (see Materials and Methods). The maximum is determined over the 2 × 2000 best‐scored poses from the two docking calculations involving P 1 and P 2 [as illustrated in Fig. 1(f)]. Consequently, geometrical docking scores are used only to select an ensemble of poses that are then evaluated based on an independent criterion. Experimental interfaces can be viewed as perfect predictions. Using them enables to estimate the maximum discriminative power one can expect from the interaction index II.
We ranked all protein pairs by their interaction index II and observed that we could retrieve the known partner of 47 proteins (13%) from PPDBv4 at the 5% significance level [Fig. 3(a), All, two darkest green rectangles]. This is almost three times as much as the value computed from geometrical ranking [16 proteins, see Fig. 2(b), All]. The results are consistently improved for all functional classes [Fig. 3(a)]. Consequently, using knowledge of the binding sites clearly helps identify cognate partners. The definition of FIR, dependent on the experimental binding sites, allows to evaluate the best result one can hope for when replacing it with predicted interfaces.
Figure 3.
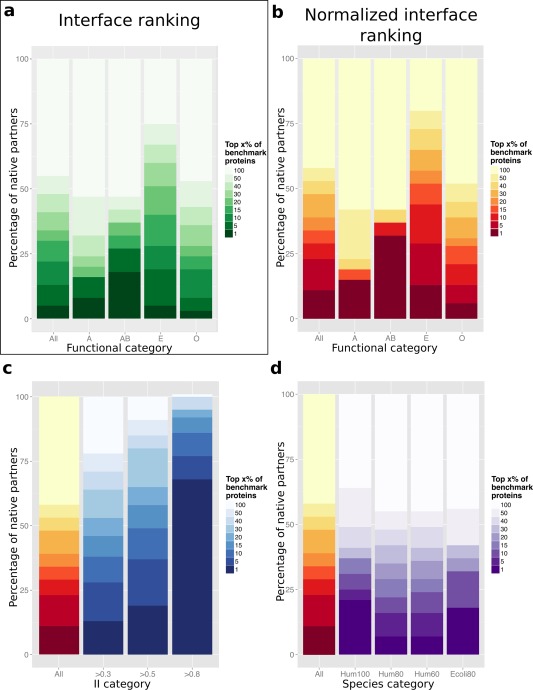
Discrimination of cognate partners and non‐interactors by using knowledge of the interfaces and of the global behavior of protein. In y axis are reported the percentages of cognate partners identified within the top x% of non‐interactors, where x varies between 1 and 100 (color scale). Each protein from PPDBv4 was docked against its native partner and 371 non‐interactors (including itself) from PPDBv4. The proteins were ranked using: (a) interaction indexes II, (b–d) normalized interaction indexes NII. Different subsets are considered based on: (a,b) functional categories, (c) II values, (d) the presence of homologs of the studied proteins in the same organism (Human or E. coli) at different degrees of sequence identity (100%, 80% or 60%).
Partner identification using binding sites and social behavior
We then considered a more sophisticated protocol in which we normalized the II values before comparing them. To do so, we defined a sociability index, or S‐index, computed for each protein Pi as:
| (9) |
that represents the degree of “sociability” of a protein: the higher the value of S, the more sociable the protein in the CC‐D. The distribution of sociability indexes is reported on Figure 4(a). They are used in the normalization formula to weight interaction indexes II (see Materials and Methods). This allows to estimate the ability of two proteins to interact together, knowing how they interact with all other proteins in the dataset. This strategy yielded strikingly improved results [Fig. 3(b)]. The known partners of 80 proteins (23% of the benchmark set) were identified in the top 5% (All, two darkest red rectangles). In all classes, the number of proteins whose known partner was ranked first largely increased: four (15%) antibodies‐antigens, seven (32%) bound antibodies‐antigens, 14 (13%) enzymes‐inhibitors, and 12 (6%) proteins with other function.
Figure 4.
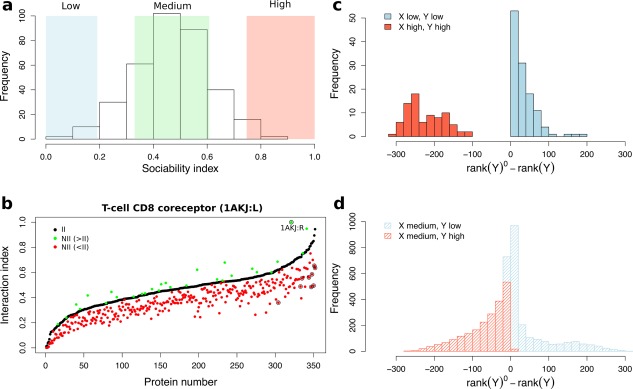
Global social behavior of the proteins. (a) Distribution of the sociability index S values for all proteins from PPDBv4. The colored rectangles correspond to different levels of sociability: in blue, in green and in red, where and are the mean and standard deviation computed over all proteins. (b) Effect of the normalization for T‐cell CD8 co‐receptor. Interaction index values are reported for T‐cell CD8 co‐receptor (1AKJ:L) before (II, black dots) and after (NII, red and green dots) normalization. Values of NII lower (resp. higher) than those of II are colored in red (resp. green). The values are sorted in ascending order of II. The protein displaying the highest increase upon normalization (1AKJ:R) is labelled and circled in black. The nine proteins displaying high sociability ( ) are also indicated by black circles. (c, d) Effect of the normalization on proteins depending on their sociability. Given a protein X, the NII values enable to rank all the proteins from the dataset, from 1st to 352nd. We report the distributions of the number of ranks lost (negative values) or gained (positive values) by any protein Y. (c) Both X and Y and either highly (in red) or poorly (in blue) sociable. (d) X has medium sociability while Y is highly (in red) or poorly (in blue) sociable.
Given a protein pair , the normalization accounts for the sociability of P 1 and P 2 in the following way: if the proteins are highly (resp. poorly) sociable, that is, their S values are high (resp. low), the interaction index will be lowered (resp. raised). This procedure has a direct impact on the ranks of the potential partners [Fig. 4(c,d)]. Poorly sociable proteins ( ) generally gain ranks upon normalization [Fig. 4(c,d), in blue]. By contrast, highly sociable proteins ( ) are systematically penalized by the normalization [Fig. 4(c,d), in red]. Given a protein P with medium sociability, the down‐shifting of highly sociable proteins [Fig. 4(d), in red] may greatly help singling out its cognate partner. The case of T‐cell CD8 coreceptor and its partner MHC class 1 HLA‐A2, both mildly sociable (SI of 0.49 and 0.40), illustrates this effect. The interaction index for this native pair is high (>0.6) and is further increased by the normalization formula [Fig. 4(b), circled green point]. Meanwhile, highly sociable competitors, such as CMTI‐1 squash inhibitor (S = 0.85), are disqualified by the normalization [Fig. 4(b), circled red points]. This results in the cognate partner of T‐cell CD8 coreceptor being ranked first after the normalization (32nd before). The rank differences for all pairs of mildly sociable proteins are normally distributed around zero (data not shown).
This analysis revealed that to decide whether P 1 and P 2 interact together, the way P 1 and P 2 behave with all the other proteins in the dataset should be accounted for. The tendency to get together at a given protein interface and the sociability effect perform better than geometry.
Avoiding interactions within the same functional class
Are there general trends in the way proteins dock to each other, depending on their functional classes? To answer to that question, we represented the matrix of NII values with the rows and columns ordered so that proteins from the same functional class are grouped together [Fig. 5(a)]. One can clearly observe that the distribution of NII values is not uniform. Specifically, the squares on the diagonal corresponding to antibodies‐antibodies (Ar and ABr), bound antigens‐antigens (ABl) and enzymes‐enzymes (Er) display mostly low values: 98%, 97%, 97% and 94% of them are below 0.55 [Fig. 5(c)]. This indicates that the proteins within these functional groups have evolved to avoid interactions between them. This is also true for the proteins with other function (O) and the inhibitors (El), but to a smaller extent (88% and 86% values <0.55, respectively). By contrast, the squares corresponding to enzymes‐inhibitors display the highest values (only 71% of the values in the square are <0.55). Overall, the antigens (Al), the inhibitors (El) and the proteins with other function (O) are the most interacting: the corresponding columns contain 22%, 21% and 17% of values above 0.55 (versus 8–15% for the other classes).
Figure 5.
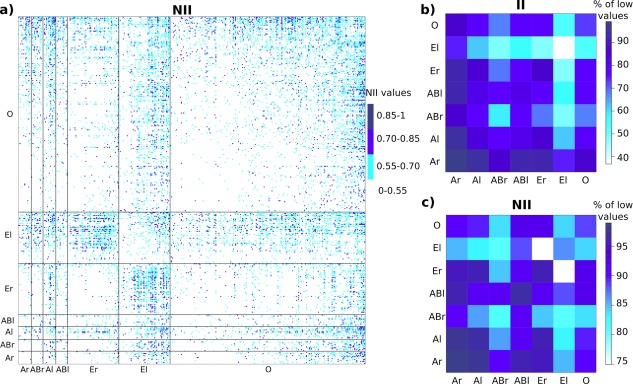
II and NII matrices ordered by functional classes. (a) The colors indicate the values of NII. The rows and columns are ordered so that proteins belonging to the same functional class are grouped together: antibodies (Ar), bound antibodies (ABr), antigens (Al), bound antigens (ABl), enzymes (Er), inhibitors (El), proteins with other function (O). (b, c) Proportion (in percentages) of low (<0.55) II values (b) and NII values (c) within and between classes. A high proportion means that the proteins within the class (diagonal) or between the two classes (off‐diagonal) avoid each other.
This analysis of the NII matrix revealed the evolutionary constraints that apply to proteins within and between functional classes. Interestingly, when comparing the NII matrix with the II matrix [Fig. 5(b)], one can observe that accounting for the sociability of the proteins contributed to unveiling evolutionary signals. In the II matrix, the inhibitors (El) appear as highly sociable, displaying high interaction indexes between them and with the proteins from almost all the other classes [Fig. 5(b)]. By treating each protein according to its S‐index, the normalization formula enables to refine the structure of the benchmark set. In the NII matrix, the inhibitors (El) are specifically attracted to the enzymes (Er) while they tend to avoid each other and the bound antigens (ABl) [Fig. 5(c)].
Partner identification within species
The PPDBv4 dataset comprises complexes coming from a wide range of species and for some complexes, the two partners are from different organisms (for example one from Human and the other one from a virus). In order to test whether this variability could introduce some noise in the analysis, we defined subsets of complexes for which the two partners have homologs in the same species. We considered homologs at 100%, 80% and 60% sequence identity. Such homologs are expected to display the same structural and functional characteristics of the original structure, and homologs up to 30–40% of sequence identity have been shown to interact the same way.44, 45
The organism that is the most represented in PPDBv4 is Human, with 24 complexes at 100% sequence identity, 75 at 80% and 85 at 60%. The performance of NII in discriminating known partners from non‐interactors within the subset of 24 complexes is significantly better than that obtained on the whole dataset [Fig. 3(d), Hum100]. About one quarter of the proteins have their known partner ranked first, versus 4% for the whole dataset. However, such improvement is not observed for lower sequence identity levels [Fig. 3(d), Hum80 and Hum60]. We also considered the bacterium Escherichia coli, in which 22 proteins (11 complexes) have a homolog at 80% sequence identity [Fig. 3(d), Ecoli80]. 4 and 3 proteins had their known partners ranked first and second respectively, representing about one third of the subset. This is relatively slightly better than the performance on the whole dataset. These results suggest that the identification of known partners can be slightly improved by considering proteins coming from the same organism. The presence of compartments in the cell does not seem to influence the results.
Partner identification connects to binding site localization
For each benchmark complex, the II value, defined from the FIR, directly reflects the best agreement with the experimental interface one can found in the docking conformational ensemble. There are 56 complexes (112 proteins, almost one third of the set) for which geometrical docking did not produce any docked interface resembling the experimental one (II < 0.3). Among them, 36 complexes are classified as rigid (no significant conformational change upon association), eight as medium and 12 as difficult (root mean square deviation over the interface >2.2 Å). Hence, the quality of the selected docking ensembles is not directly correlated to the extent to which the unbound structures deviate from the bound ones. To investigate the link between partner identification and binding site localization, we removed those proteins from the dataset, and we evaluated the discriminative power of NII on three inclusive subsets comprising complexes with II values >0.3, 0.5 and 0.8 [Fig. 3(c)]. The known partner of 68 (out of 240, 28%), 65 (out of 176, 37%) and 26 (out of 34, 76%) proteins could be retrieved in the top 2 within the three subsets. The discrimination increases as the threshold increases and is almost perfect for proteins with very high II values ( 0.8). This indicates that cognate protein pairs for which there exists one docked interface that resembles very well the experimental one can be singled out with very high accuracy.
Binding site detection by partners and non‐interactors
We then investigated whether geometrical docking could be used to predict binding sites. For this, we extended the analysis of the best fitted docked interfaces to the analysis of the whole docking conformational ensembles. We computed interaction propensity (IPnative) indexes for the benchmark complexes, by counting the number of docking models where each protein residue lies at the interface (see Materials and Methods). The complex between the enzyme Streptogrisin B and its inhibitor Ovomucoid gives an example of good overall agreement between docked and experimental interfaces (Fig. 6, on top). 70% and 64% of the binding sites of the two partners are frequently hit in the docking poses (see residues colored in red, purple and dark red on the front view). Such good overlap between docked and experimental binding sites is observed for about one quarter of the benchmark set. More examples are displayed on Supporting Information Figure S3, the case of bovine trypsin and its inhibitor CMTI‐1 (1PPE) being particularly impressive. By contrast, the binding sites of about 15% of the proteins are rarely visited by their partner in the docking calculations (>80% of the interacting residues detected in <10% of the docking models).
Figure 6.
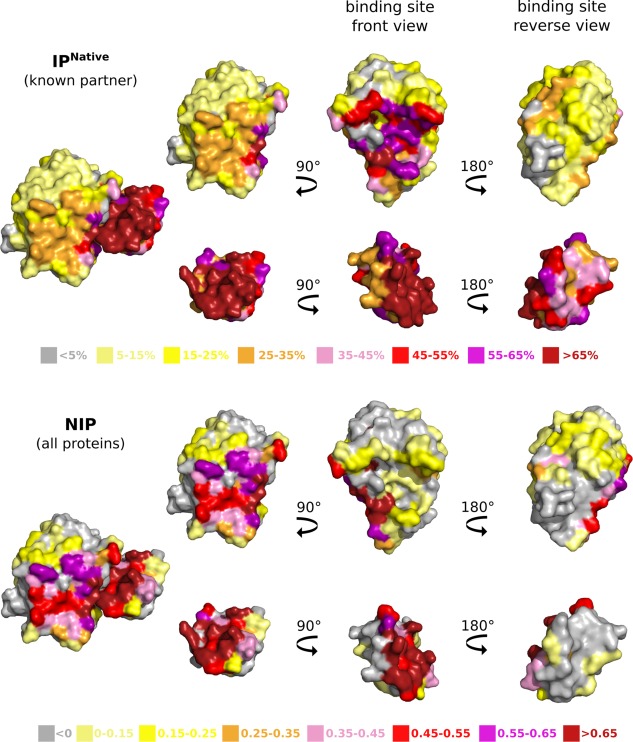
Interaction propensity indexes computed from geometrical docking. The values of IPnative (on top) and NIP (at the bottom) computed for the enzyme Streptogrisin B and its inhibitor Ovomucoid (3SGQ) are mapped onto the molecular surfaces of the two proteins. IPnative measures how often each residue is found at the interface between the two partners upon docking them together. NIP measures the tendency of each residue to be found at the docked interfaces between each partner and all the proteins from PPDBv4.
To quantitatively evaluate the predictive power of geometrical docking, we normalized the interaction propensity indexes (NIPnative, see Materials and Methods) and considered residues with as predicted to interact. On average, the predictions cover about 51% of the experimental interfaces with an accuracy of 60% (Table 1, NIPnative). The precision (PPV) achieved is rather low (20%), indicating a substantial variability in the positions and orientations sampled by the docking algorithm. The interfaces of enzymes are the best predicted ( 65%, 66%) while the antigen‐binding sites of antibodies are particularly difficult to detect (Table 1).
Table 1.
Normalized Interaction Propensity Index Performance
| NIP | NIP native | |||||||
|---|---|---|---|---|---|---|---|---|
| Category | Sen | PPV | Spe | Acc | Sen | PPV | Spe | Acc |
| All (352) | 52.12 | 19.51 | 59.43 | 59.3 | 51.36 | 19.70 | 60.21 | 59.98 |
| antibodies (13) | 12.08 | 2.83 | 62.17 | 58.44 | 13.93 | 3.26 | 62.25 | 58.55 |
| antigens (13) | 46.49 | 15.21 | 54.84 | 54.15 | 48.92 | 14.58 | 53.34 | 53.45 |
| bound antibodies (12) | 21.46 | 4.87 | 65.29 | 62.60 | 26.76 | 5.63 | 64.06 | 61.93 |
| bound antigens (12) | 46.78 | 14.37 | 54.32 | 54.89 | 40.96 | 11.57 | 50.97 | 50.94 |
| enzymes (52) | 65.20 | 20.02 | 62.19 | 63.00 | 64.80 | 22.10 | 66.07 | 66.49 |
| inhibitors (52) | 59.37 | 32.24 | 56.87 | 57.53 | 56.66 | 31.79 | 57.01 | 57.19 |
| others (198) | 51.96 | 18.6 | 59.45 | 59.26 | 51.17 | 18.65 | 60.15 | 59.95 |
| II>0.3 (240) | 59.43 | 23.65 | 59.00 | 59.36 | 57.86 | 23.74 | 60.17 | 60.24 |
| II>0.5 (176) | 61.84 | 25.72 | 59.13 | 59.80 | 60.70 | 26.12 | 60.64 | 61.04 |
| II>0.8 (34) | 60.38 | 29.95 | 59.46 | 59.79 | 64.97 | 32.61 | 62.16 | 63.28 |
Statistical performance values, given in percentages, were computed by considering residues displaying positive NIP values as predicted to be in interaction. NIP values were computed from docking all proteins (on the left) or only known partners (on the right). Within each classification, the maximum values for sensitivity (Sen), positive predictive value (PPV), specificity (Spe) and accuracy (Acc) are highlighted in bold.
Previous studies11, 15, 46 have suggested that proteins tend to dock to their cognate partners and also to non‐interactors via the same region at their surface. This observation has led to the development of arbitrary or cross docking‐based strategies for the prediction of protein binding sites.12, 15, 47 To test this in our experiment, we computed a normalized interaction propensity (NIP) index for each residue of each protein P from PPDBv4 by considering all docking experiments involving P (see Materials and Methods). Visual inspection of NIP‐colored molecular surfaces reveals that highly scored residues often form localized patches (Fig. 6, at the bottom, and Supporting Information Fig. S6). The average performance values for NIP (all proteins) are very similar to those for NIPnative (native partner only) (Table 1), and this observation holds true when considering a smaller number of docking models (50, 200 and 500, data not shown). Nevertheless, in some cases, the native partner samples residues known to be part of the interface more often than non‐binders. The example of Streptogrisin B is particularly striking (Fig. 6): the cognate inhibitor preferentially targets the experimental binding site (on top) whereas non‐interactors prefer another location (at the bottom).
To rigorously and systematically evaluate such differences, we compared, for each protein P, the NIP profile (vector of NIP values along the protein sequence) obtained from docking P to all other proteins in the dataset, with the NIPnative profile obtained from docking P to its known partner . The distance between the two vectors was calculated as their normalized angle (see Materials and Methods). The distribution of distances is centered around 0.16 ± 0.07 and is homogeneous among the different functional classes of PPDBv4 [Fig. 7(a)]. Examples of low (0.06) and relatively high (0.37) distances are given by Rac GTPase and Ran GTPase [Fig. 7(b)]. In the first case, the partner binds to the correct (experimental) site, as do the other proteins from the dataset, on average (Supporting Information Fig. S2, on top). In the second case, neither the partner nor the other proteins target the experimental site (Supporting Information Fig. S2, at the bottom). The large majority of proteins (78%) display small ( 0.2) distances [Fig. 7(a)], indicative of a similar behavior between the known partner and non‐binders.
Figure 7.
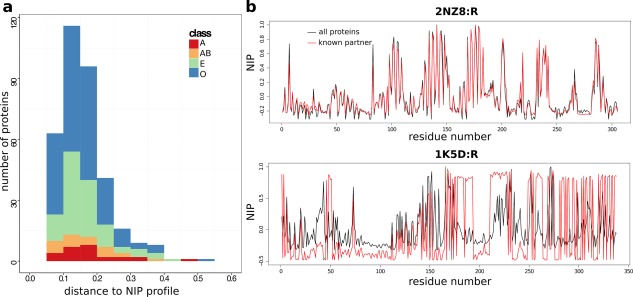
Properties of the docking conformations. (a) Distribution of distances computed between the NIP profiles obtained from docking known partners and those obtained from docking all proteins. (b) NIP profiles computed from docking Rac GTPase (2NZ8:R) and Ran GTPase (1K5D:R) to all the proteins from PPDBv4 (black curves) or only their known partners (red curves). The distance between the two profiles is 0.06 for Rac GTPase and 0.37 for Ran GTPase.
This analysis showed that: (1) the docking models produced for the known complexes are of variable quality, (2) the surface of a protein is globally sampled in the same manner by its cognate partner and by non‐binders. This confirms previous findings11, 12, 15, 46, 47 obtained using different docking algorithms. Some of the targeted patches match well experimental binding sites. Others might correspond to alternative interfaces. However, a previous study15 put in evidence a bias of HEX shape complementarity scoring function toward regions with geometrical and physico‐chemical properties that are not characteristic of protein binding sites. Here, we observed that in the case of the antibodies, a flat and slightly concave surface region is preferred over the antigen‐binding site (see 1DQJ in Supporting Information Fig. S6).
Comparison with a previous study based on geometrical docking
Wass and co‐authors previously reported results suggesting that geometrical docking could distinguish the cognate partners of 56 benchmark proteins (>6 times smaller than PPDBv4) from a background of about 1 000 structures belonging to different superfamilies.14 They performed docking with HEX,38 using the shape complementarity score. Contrary to us, they used the original PDB files as starting conformations [Fig. 1(b)]. By comparing docking score distributions using Wilcoxon rank‐sum tests (geometrical ranking), they found that 14 benchmark complexes (25% of the set) displayed significantly better scores than 99% of the background proteins (see Table 1 in Ref. 14). In our calculations, we found that only 4% of the benchmark complexes were better than 95% of the background proteins [Fig. 2(a)]. Consequently, the results reported in Ref. 14 are not generalizable to unbiased docking realized on a bigger benchmark set.
We compared our heat map style figures with those displayed in Ref. 14 and observed substantial differences. For instance, the most frequently hit patches at the surface of fasciculin 2 (1MAH:L) and transthyretin (1RLB:R) do not match the experimental interfaces in our experiment (Supporting Information Fig. S4), while it was the case in Ref. 14. Overall, we observe much more variation in the quality of the docking models from one protein to another than what was reported in Ref. 14, even when considering only the subset of benchmark proteins studied in Ref. 14. The signal from our docking calculations also seems sharper (compare Supporting Information Figs. S4 and S5 with Fig. 2 and Supporting Information S13 in Ref. 14).
Transferability to other docking tools
To assess the transferability of our results, we repeated CC‐D of a subset of 33 enzyme‐inhibitor complexes from PPDBv4 (Supporting Information Table S2) with the docking program ZDOCK 3.0.2.39 Like HEX, ZDOCK is very efficient to sample the docking space as it uses a grid‐based representation of proteins and a 3D fast Fourier transform. The scoring function includes shape complementarity, electrostatics, and a pairwise atomic statistical potential.48 We analyzed the data generated by ZDOCK using the three strategies described above and compared with the HEX results (Supporting Information Fig. S7). Geometrical ranking (docking score distributions comparison) with ZDOCK does not enable to discriminate potential partners (Supporting Information Fig. S7b, grey tones), as observed with HEX (Supporting Information Fig. S7a, grey tones). Interface‐based ranking (Supporting Information Fig. S7b) slightly improves partner identification (8 partners identified in the top 10% in green, instead of 5 in grey) but to a much smaller extent than when using HEX (Supporting Information Fig. S7a). This is due to a stronger competition from the non‐interacting pairs, as the quality of the docking models produced by ZDOCK for the 33 benchmark complexes is similar to that of HEX docking models (Supporting Information Fig. S8b). Accounting for the sociability of the proteins significantly improves the discrimination (Supporting Information Fig. S7b, orange tones). The relative improvement is the same for ZDOCK and HEX (+50% partners in the top 10%), although the discriminative power achieved with ZDOCK (Supporting Information Fig. S7b) is much lower than that achieved with HEX (Supporting Information Fig. S7a). The Pearson correlation between the S‐index scales computed from HEX and ZDOCK is 0.70. The sets of the 20 most sociable proteins (among the 66 in the subset) identified by the two docking algorithms share 15 proteins in common.
We also analyzed docking data generated using a more sophisticated docking and scoring methodology. The data consist in a CC‐D of the PPDBv2 benchmark (84 complexes, included in PPDBv4) by using the MAXDo (Molecular Association via Cross Docking) algorithm.12 MAXDo uses a reduced protein model and an energy function comprising a Lennard‐Jones type potential and a term to account for electrostatic interactions.40 The quality of the conformational ensembles generated by MAXDo is much better than those generated by HEX and ZDOCK (Supporting Information Fig. S8c). To analyze these data, we used an alternative version of the interaction index for any protein pair (see Materials and Methods). Without normalization, we could retrieve the known partner of 35% of PPDBv2 (58 proteins) at the 5% significance level (Supporting Information Fig. S9a, All). This is more than twice as much as with HEX (24 proteins in the top 5%). Applying the normalization formula (Supporting Information Fig. S9b) enabled to significantly increase this percentage, up to 45% (75 proteins, versus 43 with HEX). As observed with HEX, the closer the known complexes docked interfaces to the experimental interfaces, the better the identification of cognate partners (Supporting Information Fig. S9c). The Pearson correlation coefficient between the S‐index scales computed with MAXDo and with HEX is 0.62. The sets of the 20 most sociable proteins (among the 168 in PPDBv2) identified by HEX and MAXDo share 15 proteins in common. The predictive performances of NIP and NIPnative computed from MAXDo are very similar (data not shown). Contrary to HEX, MAXDo predicts very well the antigen binding sites at the surface of antibodies.
This analysis showed that the tendencies highlighted with HEX are also highlighted by ZDOCK, a similar (fast Fourier transform‐based) docking algorithm, and also by MAXDo, a more sophisticated docking algorithm based on a coarse‐grained protein model and including an empirical energy function. With all three docking programs, we could put in evidence the significant contribution of the normalization step in discriminating potential partners. Moreover, we found very good overlap between the sociability scales computed from the different programs. The intersection between the three sets to which the three programs were applied comprises 34 proteins. When considering only this subset, the three lists of the 15 most sociable proteins identified by HEX, ZDOCK and MAXDo are almost identical, with 13 proteins in common (Supporting Information Table S3). Noticeably, MAXDo yielded strikingly better enrichments in native partners, over the whole dataset and over functional classes, than HEX and ZDOCK.
DISCUSSION
In this study, we have addressed the question of the identification of protein partners at large scale by using geometrical docking. We performed two high‐throughput completely unbiased docking experiments, one involving a benchmark set of 372 proteins and a background environment of almost 1 000 proteins, and the other one consisting in docking the 372 proteins to each other and to themselves (CC‐D). We investigated different strategies to evaluate the docking results and predict who interacts with whom. By contrast to a previous study,14 our results clearly indicate that this difficult problem is yet far from being resolved. We can also highlight some important points that contribute to a better understanding of the articulation between binding site prediction and partner identification.
First, we found that geometrical ranking is largely insufficient to discriminate cognate partners from non‐interactors. The success of the docking algorithm in localizing the interaction surfaces varies greatly from one protein to another and the docking ensembles often contain no to few near‐native conformations. One might think that this poor quality is due to the particular docking code and to the use of unbound structures, and may prevent the shape complementarity score to perform well. However, HEX was designed to very efficiently sample the docking search space and we used 5 different initial positions, so that we are fairly confident that the 2000 models retained for our analysis represents only a tiny fraction of the ensemble of docking models actually generated. This set is already the result of a selection performed by the surface complementarity score. Moreover, we did not find a direct correlation between the quality of the docking models and the extent of conformational changes between unbound structures (used in the calculations) and bound ones. Consequently, the poor quality of the docking models reflects the inability of the score to correctly rank near‐native conformations. These observations strikingly contrast with results reported in Ref. 14 showing that areas of shape complementarity are systematically identified for the benchmark complexes but not for the non‐interacting pairs. We clearly show here that this previously reported observation cannot be generalized to a complete unbiased cross‐docking experiment involving different types of proteins.
Second, consistent with our previous studies,11, 12, 43 we showed here that the knowledge of the binding sites is instrumental in retrieving known partners. This means that even though the surface of a protein is globally targeted in the same way by partners and non‐interactors in the docking calculations, two native partners often achieve a better fit of their interfaces (higher FIR) than two non‐interacting pairs. In general, the binding sites are not known a priori and one has to predict them. Here, we used experimentally determined interfaces, which represent “perfect predictions,” to precisely evaluate the maximum performance one can expect from interface‐based rankings. Our results clearly show that the limited and variable quality of the interfaces generated and selected by geometrical docking bridles the discriminative power of the approach. Experimental knowledge can be incorporated to drive the docking process (like in HADDOCK49) rather than evaluate the docking poses. We tested this approach on 13 antibody‐antigen complexes. The cognate partners were docked with HEX, restricting the search space to the region around the experimental interface. Unfortunately, the docked interfaces poorly resembled the experimental ones. Using the more sophisticated force‐field based scoring function implemented in MAXDo12 enabled to enrich the docking ensemble with near‐native conformations and to obtain better discrimination indices. However, the drawback of these scoring schemes is that they are significantly more time‐consuming. Our goal here was to test whether efficient docking algorithms based only on shape complementarity could be used instead.
Nevertheless, geometrical docking proved sufficient to reveal a fundamental characteristic of PPIs. Specifically, to decide whether two proteins are likely to interact in the cell, their global social behavior must be taken into account. Normalizing the interaction indexes, so as to lower down values obtained for proteins that are amenable to dock well to many proteins and increase values obtained for proteins that display antisocial behavior, greatly helped partner identification (+70% identified partners at the 5% significance level). Repeating our calculations with other docking algorithms and scoring functions confirmed the importance of protein sociability for partner identification. Moreover, we found very good overlap between the S‐index scales computed from the different tools. This suggests that we capture some real properties of proteins and possibly some aspects of their behavior in the cell.
Do the highly sociable proteins identified in the docking calculations correspond to sticky proteins in the cell? The notion of stickiness is usually defined based on the content of hydrophobic residues at the surface of the protein.34 Our notion of sociability is not directly defined based on the physico‐chemical properties of the surface residues and thus may deviate from the notion of stickiness. The most sociable proteins in the dataset are inhibitors and proteins with other function (Supporting Information Fig. S10a, El and O). Their interacting surfaces are small, containing <40 residues (Supporting Information Fig. S11a), although the S‐index is not overall correlated to the interface size (Supporting Information Fig. S11a). It is not correlated to the hydrophobic content of the protein surface (data not shown), indicating that the notion of sociability is different from that of stickiness. By contrast, the S‐index is strongly correlated to the IP averaged over the protein and anti‐correlated to the number of residues covered in the docked interfaces (Supporting Information Fig. S11b). Highly sociable proteins have a rather small number of surface residues and most of them are frequently hit in the docking models.
Important efforts have been dedicated to characterizing sticky proteins and their interactions.32, 33, 34, 35 It was shown that sticky proteins have stronger than average non‐functional interactions and that avoiding such non‐functional PPIs is an important constraint in protein evolution.32, 33 Here, we demonstrated that accounting for the propensity of proteins to glue to anyone in the docking calculations (whether this is due to stickiness or not) could help identify specific cellular partners and reveal evolutionary constraints toward avoiding non‐specific interactions within functional classes. This observation, together with experimental evidence that proteins may have multiple partners possibly interacting through the same interface to perform different functions (e.g., moonlighting proteins, see examples in Ref. 18), emphasizes the fact that how well proteins accomplish what they are designed to accomplish depends on what other proteins do. Whom they interact to depends on whom they meet, and on which potential partner is already engaged. Their way to interact and their binding affinity depend on the way and on the binding affinity other proteins display. Let us stress that to unveil this type of properties, one has to consider a huge ensemble of negatives (the non‐interacting pairs) compared to the positive (native partners). This cannot be done experimentally and requires high‐throughput computational approaches.
Finally, we highlighted a positive correlation between partner identification and binding site localization. This finding has major implications for the design of strategies to predict and characterize PPIs, that is, the problem of identifying interface residues and that of identifying protein partners should not be considered as independent as they are actually tightly linked and solving the former can greatly contribute to solving the latter.
A recent study suggested that the structural space of protein‐protein interfaces is degenerate, close to complete, and highly connected.50 This implies that forming a native‐like interface is likely and thus the probability of finding a physically favorable association between non‐cognate partners is high, even though this association is not biologically relevant. This reasoning may explain why singling out cognate partners is such a challenging task for docking algorithms and give a structural basis for the many promiscuous interactions detected by yeast two‐hybrid experiments.51 To model specificity, specific sequence information may be useful.
Deciphering the network of protein interactions for a given proteome (that is, the set of proteins within a given organism) is the goal of many experimental and computational efforts in systems biology. The information identified by docking programs on PPIs is complementary to the one provided by other methods and encoded in PPI networks. In fact, protein docking allows to reach at least a residue level resolution of the interaction, in contrast to usual PPI networks that simply express the existence or absence of an interaction. This would extend our knowledge on the interactome of an organism and improve our capacity to perform systematic studies on them, to determine new strategies to engineer pathways to protein control and new targets for drug design.
Supporting information
Supporting Information
ACKNOWLEDGMENTS
The MAPPING project (ANR‐11‐BINF‐0003, Excellence Programme “Investissement d'Avenir”); funds from the Institut Universitaire de France; the access to the HPC resources of the Institute for Scientific Computing and Simulation (Equip@Meso project ‐ ANR‐10‐EQPX‐ 29–01, Excellence Program “Investissement d'Avenir”); the World Community Grid (WCG,www.worldcommunitygrid.org) and WCG volunteers that allowed us to perform cross‐docking experiments with MAXDo on the PPDBv2.0.
REFERENCES
- 1. Robinson CV, Sali A, Baumeister W. The molecular sociology of the cell. Nature 2007;450:973–982. [DOI] [PubMed] [Google Scholar]
- 2. Lasker K, Phillips JL, Russel D, Velázquez‐Muriel J, Schneidman‐Duhovny D, Tjioe E, Webb B, Schlessinger A, Sali A. Integrative structure modeling of macromolecular assemblies from proteomics data. Mol Cell Proteomics 2010;9:1689–1702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Karaca E, Melquiond ASJ, de Vries SJ, Kastritis PL, Bonvin AMJJ. Building macromolecular assemblies by information‐driven docking: introducing the haddock multibody docking server. Mol Cell Proteomics 2010;9:1784–1794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Fleishman SJ, Whitehead TA, Strauch EM, Corn JE, Qin S, Zhou HX, Mitchell JC, Demerdash ON, Takeda‐Shitaka M, Terashi G, Moal IH, Li X, Bates PA, Zacharias M, Park H, Ko JS, Lee H, Seok C, Bourquard T, Bernauer J, Poupon A, Aze J, Soner S, Ovali SK, Ozbek P, Tal NB, Haliloglu T, Hwang H, Vreven T, Pierce BG, Weng Z, Perez‐Cano L, Pons C, Fernandez‐Recio J, Jiang F, Yang F, Gong X, Cao L, Xu X, Liu B, Wang P, Li C, Wang C, Robert CH, Guharoy M, Liu S, Huang Y, Li L, Guo D, Chen Y, Xiao Y, London N, Itzhaki Z, Schueler‐Furman O, Inbar Y, Potapov V, Cohen M, Schreiber G, Tsuchiya Y, Kanamori E, Standley DM, Nakamura H, Kinoshita K, Driggers CM, Hall RG, Morgan JL, Hsu VL, Zhan J, Yang Y, Zhou Y, Kastritis PL, Bonvin AM, Zhang W, Camacho CJ, Kilambi KP, Sircar A, Gray JJ, Ohue M, Uchikoga N, Matsuzaki Y, Ishida T, Akiyama Y, Khashan R, Bush S, Fouches D, Tropsha A, Esquivel‐Rodriguez J, Kihara D, Stranges PB, Jacak R, Kuhlman B, Huang SY, Zou X, Wodak SJ, Janin J, Baker D. Community‐wide assessment of protein‐interface modeling suggests improvements to design methodology. J Mol Biol 2011;414:289–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Lensink MF, Wodak SJ. Blind predictions of protein interfaces by docking calculations in CAPRI. Proteins 2010;78:3085–3095. [DOI] [PubMed] [Google Scholar]
- 6. Mendez R, Leplae R, Maria LD, Wodak SJ. Assessment of blind predictions of protein‐protein interactions: current status of docking methods. Proteins 2003;52:51–67. [DOI] [PubMed] [Google Scholar]
- 7. Janin J, Henrick K, Moult J, Eyck LT, Sternberg MJ, Vajda S, Vakser I, Wodak SJ. CAPRI: a Critical Assessment of PRedicted Interactions. Proteins 2003;52:2–9. [DOI] [PubMed] [Google Scholar]
- 8. Russell RB, Alber F, Aloy P, Davis FP, Korkin D, Pichaud M, Topf M, Sali A. A structural perspective on protein‐protein interactions. Curr Opin Struct Biol 2004;14:313–324. [DOI] [PubMed] [Google Scholar]
- 9. Aloy P, Russell RB. Structural systems biology: modelling protein interactions. Nat Rev Mol Cell Biol 2006;7:188–197. [DOI] [PubMed] [Google Scholar]
- 10. Gray JJ. High‐resolution protein‐protein docking. Curr Opin Struct Biol 2006;16:183–193. [DOI] [PubMed] [Google Scholar]
- 11. Sacquin‐Mora S, Carbone A, Lavery R. Identification of protein interaction partners and protein‐protein interaction sites. J Mol Biol 2008;382:1276–1289. [DOI] [PubMed] [Google Scholar]
- 12. Lopes A, Sacquin‐Mora S, Dimitrova V, Laine E, Ponty Y, A Carbone. Protein‐protein interactions in a crowded environment: an analysis via cross‐docking simulations and evolutionary information. PLoS Comput Biol 2013;9:e1003369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Mintseris J, Wiehe K, Pierce B, Anderson R, Chen R, Janin J, Weng Z. Protein‐Protein Docking Benchmark 2.0: an update. Proteins 2005;60:214–216. [DOI] [PubMed] [Google Scholar]
- 14. Wass MN, Fuentes G, Pons C, Pazos F, Valencia A. Towards the prediction of protein interaction partners using physical docking. Mol Syst Biol 2011;7:469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Martin J, Lavery R. Arbitrary protein‐protein docking targets biologically relevant interfaces. BMC Biophys 2012;5:7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Kastritis PL, Bonvin AM. Are scoring functions in protein‐protein docking ready to predict interactomes? Clues from a novel binding affinity benchmark. J Proteome Res 2010;9:2216–2225. [DOI] [PubMed] [Google Scholar]
- 17. Vangone A, Bonvin AM. Contacts‐based prediction of binding affinity in protein‐protein complexes. Elife 2015;4:e07454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Laine E, Carbone A. Local geometry and evolutionary conservation of protein surfaces reveal the multiple recognition patches in protein‐protein interactions. PLoS Comput Biol 2015;11:e1004580–e1004Dec. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Jordan RA, El‐Manzalawy Y, Dobbs D, Honavar V. Predicting protein‐protein interface residues using local surface structural similarity. BMC Bioinform 2012;13:41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Segura J, Jones PF, Fernandez‐Fuentes N. Improving the prediction of protein binding sites by combining heterogeneous data and Voronoi diagrams. BMC Bioinform 2011;12:352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Innis CA. siteFiNDER—3D: a web‐based tool for predicting the location of functional sites in proteins. Nucleic Acids Res 2007;35:W489–W494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Liang S, Zhang C, Liu S, Zhou Y. Protein binding site prediction using an empirical scoring function. Nucleic Acids Res 2006;34:3698–3707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Fernandez‐Recio J, Totrov M, Skorodumov C, Abagyan R. Optimal docking area: a new method for predicting protein‐protein interaction sites. Proteins 2005;58:134–143. [DOI] [PubMed] [Google Scholar]
- 24. Neuvirth H, Raz R, Schreiber G. ProMate: a structure based prediction program to identify the location of protein‐protein binding sites. J Mol Biol 2004;338:181–199. [DOI] [PubMed] [Google Scholar]
- 25. Pupko T, Bell R, Mayrose E, Glaser IF, Ben‐Tal N. Rate4Site: an algorithmic tool for the identification of functional regions in proteins by surface mapping of evolutionary determinants within their homologues. Bioinformatics 2002;18:S71–S77. [DOI] [PubMed] [Google Scholar]
- 26. Zhou HX, Shan Y. Prediction of protein interaction sites from sequence profile and residue neighbor list. Proteins 2001;44:336–343. [DOI] [PubMed] [Google Scholar]
- 27. Armon A, Graur D, Ben‐Tal N. ConSurf: an algorithmic tool for the identification of functional regions in proteins by surface mapping of phylogenetic information. J Mol Biol 2001;307:447–463. [DOI] [PubMed] [Google Scholar]
- 28. Xue LC, Dobbs D, Bonvin AM, Honavar V. Computational prediction of protein interfaces: a review of data driven methods. FEBS Lett 2015;589:3516–3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Minhas F. u, Geiss BJ, Ben‐Hur A. PAIRpred: partner‐specific prediction of interacting residues from sequence and structure. Proteins 2014;82:1142–1155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Xue L, Dobbs CD, Honavar V. HomPPI: a class of sequence homology based protein‐protein interface prediction methods. BMC Bioinform 2011;12:244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Ahmad S, Mizuguchi K. Partner‐aware prediction of interacting residues in protein‐protein complexes from sequence data. PLoS ONE 2011;6:e29104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Heo M, Maslov S, Shakhnovich E. Topology of protein interaction network shapes protein abundances and strengths of their functional and nonspecific interactions. Proc Natl Acad Sci USA 2011;108:4258–4263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Zhang J, Maslov S, Shakhnovich EI. Constraints imposed by non‐functional protein‐protein interactions on gene expression and proteome size. Mol Syst Biol 2008;4: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Deeds EJ, Ashenberg O, Gerardin J, Shakhnovich EI. Robust protein protein interactions in crowded cellular environments. Proc Natl Acad Sci USA 2007;104:14952–14957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Deeds EJ, Ashenberg O, Shakhnovich EI. A simple physical model for scaling in protein‐protein interaction networks. Proc Natl Acad Sci USA 2006;103:311–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Hwang H, Vreven T, Janin J, Weng Z. Protein‐protein docking benchmark version 4.0. Proteins 2010;78:3111–3114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Gough J, Karplus K, Hughey R, Chothia C. Assignment of homology to genome sequences using a library of hidden Markov models that represent all proteins of known structure. J Mol Biol 2001;313:903–919. [DOI] [PubMed] [Google Scholar]
- 38. Ritchie DW, Kemp GJ. Protein docking using spherical polar Fourier correlations. Proteins 2000;39:178–194. [PubMed] [Google Scholar]
- 39. Pierce BG, Hourai Y, Weng Z. Accelerating protein docking in ZDOCK using an advanced 3D convolution library. PLoS ONE 2011;6:e24657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Zacharias M. Protein‐protein docking with a reduced protein model accounting for side‐chain flexibility. Protein Sci 2003;12:1271–1282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. R Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria; 2014. [Google Scholar]
- 42. Wilcoxon F. Individual comparisons by ranking methods. Biometrics Bull 1945;1:80–83. [Google Scholar]
- 43. E Laine, A Carbone. Identification of protein interaction partners from shape complementarity molecular cross‐docking In International Conference on Image Analysis and Processing, Lecture Notes in Computer Science, Volume. 8158, pages 318–325, 2013, Springer Berlin Heidelberg. [Google Scholar]
- 44. Faure G, Andreani J, Guerois R. InterEvol database: exploring the structure and evolution of protein complex interfaces. Nucleic Acids Res 2012;40:D847–D856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Aloy P, Ceulemans H, Stark A, Russell RB. The relationship between sequence and interaction divergence in proteins. J Mol Biol 2003;332:989–998. [DOI] [PubMed] [Google Scholar]
- 46. Fernandez‐Recio J, Totrov M, Abagyan R. Identification of protein‐protein interaction sites from docking energy landscapes. J Mol Biol 2004;335:843–865. [DOI] [PubMed] [Google Scholar]
- 47. Vamparys L, Laurent B, Carbone A, Sacquin‐Mora S. Great interactions: how binding incorrect partners can teach us about protein recognition and function. Proteins 2016;84:1408–1421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Mintseris J, Pierce B, Wiehe K, Anderson R, Chen R, Weng Z. Integrating statistical pair potentials into protein complex prediction. Proteins 2007;69:511–520. [DOI] [PubMed] [Google Scholar]
- 49. Dominguez C, Boelens R, Bonvin AM. HADDOCK: a protein‐protein docking approach based on biochemical or biophysical information. J Am Chem Soc 2003;125:1731–1737. [DOI] [PubMed] [Google Scholar]
- 50. Gao M, Skolnick J. Structural space of protein‐protein interfaces is degenerate, close to complete, and highly connected. Proc Natl Acad Sci USA 2010;107:22517–22522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. P, Uetz L, Giot G, Cagney TA, Mansfield RS, Judson JR, Knight D, Lockshon V, Narayan M, Srinivasan P, Pochart A, Qureshi‐Emili Y, Li B, Godwin D, Conover T, Kalbfleisch G, Vijayadamodar M, Yang M, Johnston S, Fields JM, Rothberg A. Comprehensive analysis of protein‐protein interactions in Saccharomyces cerevisiae. Nature 2000;403:623–627. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


