Structure of Penta-Alanine Investigated by Two-Dimensional Infrared Spectroscopy and Molecular Dynamics Simulation

Abstract

We have studied the structure of (Ala)₅, a model unfolded peptide, using a combination of 2D IR spectroscopy and molecular dynamics (MD) simulation. Two different isotopomers, each bis-labeled with ¹³C=O and ¹³C=¹⁸O, were strategically designed to shift individual site frequencies and uncouple neighboring amide-I′ modes. 2D IR spectra taken under the double-crossed 〈π/4, −π/4, Y, Z〉 polarization show that the labeled four-oscillator systems can be approximated by three two-oscillator systems. By utilizing the different polarization dependence of diagonal and cross peaks, we extracted the coupling constants and angles between three pairs of amide-I transition dipoles through spectral fitting. These parameters were related to the peptide backbone dihedral angles through DFT calculated maps. The derived dihedral angles are all located in the polyproline-II (ppII) region of the Ramachandran plot. These results were compared to the conformations sampled by Hamiltonian replica-exchange MD simulations with three different CHARMM force fields. The C36 force field predicted that ppII is the dominant conformation, consistent with the experimental findings, whereas C22/CMAP predicted similar population for α₊, β, and ppII, and the polarizable Drude-2013 predicted dominating β structure. Spectral simulation based on MD representative conformations and structure ensembles demonstrated the need to include multiple 2D spectral features, especially the cross-peak intensity ratio and shape, in structure determination. Using 2D reference spectra defined by the C36 structure ensemble, the best spectral simulation is achieved with nearly 100% ppII population, although the agreement with the experimental cross-peak intensity ratio is still insufficient. The dependence of population determination on the choice of reference structures/spectra and the current limitations on theoretical modeling relating peptide structures to spectral parameters are discussed. Compared with the previous results on alanine based oligopeptides, the dihedral angles of our fitted structure and the most populated ppII structure from the C36 simulation are in good agreement with those suggesting a major ppII population. Our results provide further support for the importance of ppII conformation in the ensemble of unfolded peptides.

TOC image

1. Introduction

The solution structure of unfolded proteins and peptides has long been an intriguing problem. The unfolded state is common in peptides, intrinsically disordered proteins and even folded proteins. Structural knowledge of the unfolded state is needed to understand the conformational propensities of sequences and protein unfolding. In the last two decades, the notion that the unfolded state is much more restricted in the Ramachandran space compared to the random coil model has gained increasing experimental support.^1–22 These studies implicate polyproline II (ppII) as an important conformation in the ensemble of disordered states of peptides and proteins. This view, if confirmed, could impact the prediction of protein folding, and merit further experimental verification.

Alanine (Ala) based oligopeptides are simple yet important model systems to understand the intrinsic propensity of protein folding because Ala is abundant in proteins. However, determining the conformational sampling of these short peptides is challenging because ensembles of structures rapidly interconvert in solution.^{19–20, 23–24} Multiple spectroscopic techniques have been used to investigate this problem, from the simplest systems of trialanine^{10–12, 16–19, 25–26} and Ac-Ala-NHMe (Ac: acetyl)^27–29 with only two peptide bonds, to longer alanine-rich peptides including (Ala)_n (n = 4 – 7)^{6, 13–14, 20} and Ac-X₂A₇O₂-NH₂ (XAO, here X = diaminobutyric acid, and O = ornithine),^{5, 15, 21–22} and host–guest peptides like GGXGG.^7–8 Kim et al. suggested ppII-like conformation for Ac-Ala-NHMe in aqueous solution, employing 2D IR in combination with DFT calculation.²⁸ Woutersen et al. determined (ϕ, ψ) on the central residue of (Ala)₃ to be ppII-like (−60°, 140°) using 2D IR spectral fitting.^17–18 They then estimated the ppII population to be 80% from the spectral diffusion experiment assuming the other conformer is α-helix.¹⁹ Schweitzer-Stenner et al. investigated (Ala)₃ using a joint fitting procedure combining FTIR, isotropic and anisotropic Raman and vibrational CD spectra.¹⁰ They suggested that the conformation is a 50:50 mixture of ppII and an extended β-strand-like structure,^11–12 which was also supported by their temperature-dependent CD study.^11–12 Later, by considering the conformational distribution explicitly, they updated the ppII population to 80%.¹⁶ NMR can extract residue-specific information. Kallenbach and coworkers first showed that the seven alanine residues in XAO mainly adopted ppII at 2°C, and the β strand content increased by 10% at 55°C.⁵ Later a joint NMR and MD simulation study of (Ala)_n (n = 3 – 7) peptides showed that the population distribution is almost independent from their chain length, with 90% ppII, 10% β, and no detectable population of the α conformation.²⁰ However, Hummer and coworkers studied (Ala)₅ conformations using MD simulations, and argued that the NMR data can be consistent with force fields that give a small α population and do not require exclusive formation of the ppII structure.³⁰ Cho and coworkers developed a self-consistent singular value decomposition based method to fit CD spectra and NMR J-coupling constant simultaneously, and determined the ppII population of the central residue in (Ala)₃ is 66%.³¹

Many studies on the structural propensity of alanine oligopeptides suggested a high ppII population, but the quantitative results depend on different molecular environments and spectroscopic methods utilized. Most, if not all, of the residue-specific studies on peptides containing more than two alanine peptide units were conducted by NMR spectroscopy. Although Schweitzer-Stenner et al. extended their joint fitting procedure to oligopeptides as long as XAO based on an excitonic coupling model,^{13–14, 32} it still did not offer direct interrogation of a single residue like NMR. These studies also showed that it is essential to invoke a large set of spectral constraints to determine peptide conformation distribution. In NMR, although it has been argued that different Karplus parameters give different quantitative results,³⁰ several different J-coupling constants can be measured independently for each residue,²⁰ which makes structural determination more robust. Similarly, in vibrational spectroscopy, it is necessary to combine data from FTIR, isotropic and anisotropic Raman scattering, and vibrational CD to obtain results consistent with all techniques.^{10–11, 13–16}

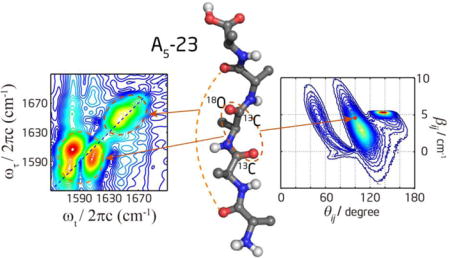
In this work, we investigated the conformation of (Ala)₅ by 2D IR spectroscopy to provide multiple spectral constraints and by isotope labeling to achieve residue specificity. This peptide has four peptide units and three pairs of dihedral angles describing the backbone conformation (Figure 1). To determine these angles in a site specific manner, we designed two bis-labeled pentapeptides: A₅-23 has ¹³C and ¹³C=¹⁸O at the second and third peptide units, respectively, and A₅-43 has ¹³C and ¹³C=¹⁸O at the fourth and third peptide units, respectively. This design enabled us to differentiate the four amide-I′ modes and strategically probe the interaction between specific pairs of vibrators. Spectral fitting was performed to determine the vibrational coupling and angles between transition dipoles. These spectral parameters were connected to structural parameters though the DFT-calculated transition dipole orientation and coupling map. The effects of multiple conformations on spectral features were explored. Previous studies have already demonstrated that 2D IR spectroscopy can be very useful for testing and validation of force fields.^{24, 33–35} Here we performed MD simulation with three different CHARMM force fields and compared the results with the experimental 2D spectra and cross peak intensities. The relative efficacies of different force fields in generating realistic structural ensembles were analyzed and discussed. We also attempted to extract conformational population based on reference spectra defined by the MD simulated structural ensembles. The results were discussed in the context of the literature.

Figure 1.

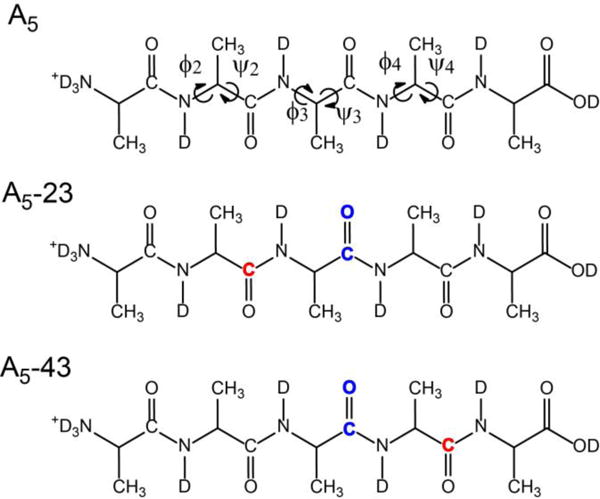
Structure formula of (Ala)₅ in D₂O with pD = 1. Three different isotopomers were studied: unlabeled (A₅); bis-labeled with ¹³C=O and ¹³C=¹⁸O at the second and third peptide units, respectively (A₅-23); and bis-labeled with ¹³C=O and ¹³C=¹⁸O at the fourth and third peptide units, respectively (A₅-43). ¹³C and ¹³C=¹⁸O are colored in red and blue, respectively. The middle three pairs of dihedral angles are indicated by the arrows.

2. Experimental and Computation

2.1 Experimental details

Unlabeled (L-Ala)₅ was purchased from Sigma-Aldrich. Ala-(¹³C)Ala-(¹³C,¹⁸O)Ala-Ala-Ala (A₅-23) and Ala-Ala-(¹³C,¹⁸O)Ala-(¹³C)Ala-Ala (A₅-43) were purchased from CPC Scientific, Inc. The uncapped peptides were used without further purification. The isotope purity of the labeled peptides was examined with mass spectrometry. The ¹³C labeling is almost 100%, and ¹⁸O labeling purity is about 92% by comparing the signal intensity of (m+2)/z and m/z peaks.

Peptides were lyophilized in 5 mM DCl/D₂O solution at least three times before use in order to remove trifluoroacetic acid and deuterate the NH groups.³⁶ The peptide was then dissolved in pD = 1 DCl/D₂O solution to convert the carboxyl groups into acidic form to minimize the spectral overlap with amide-I′ modes. For FTIR and 2D IR measurements, the concentration of peptides solution was ~30 mM and the sample solution was held in between two CaF₂ windows with a 25 μm spacer. FTIR measurements were performed using a Nicolet magna-IR 860 spectrometer with a 2-cm⁻¹ resolution and averaged over 32 scans. The solvent background and water vapor peaks were removed by programs written in MATLAB. Concentration dependent measurements were performed to confirm that no aggregation occurred.

The principles of 2D IR spectroscopy and our experimental setup for obtaining 2D IR spectra have been described in detail elsewhere.^37–39 Experimental parameters relevant to the current study are briefly described below. Ultrafast broadband mid-IR pulses were generated at 1 kHz with a pulse width of ~110 fs and spectral bandwidth of ~180 cm⁻¹. The mid-IR pulses were always tuned to be resonant with the center of peptide amide-I′ modes. For isotope-labeled peptides, the mid-IR wavelength was centered at around 1625 cm⁻¹, which is in the middle of the labeled and unlabeled regions. The effect of finite spectral width can be taken into account by a simple convolution procedure.⁴⁰ The 2D IR experiments were performed by focusing the excitation beams with wavevectors k_a, k_b, and k_c onto the samples in boxcar geometry. The nonlinear signal emitted in the phase-matching direction (k_d = −k_a + k_b + k_c) was spatially overlapped with the local oscillator pulse to do spectral interferometry with a 4-cm⁻¹ resolution. The polarizations of all beams were controlled individually and denoted as 〈a, b, c, d〉. The signal was recorded as a function of two time intervals, τ (time interval between first and second pulses) and T (time interval between second and third pulses), and the detection frequency ω_t. The data was processed using the double Fourier transform methods^{28, 41} to produce the 2D IR spectrum $S({\omega }_{\tau },{\omega }_t;T)$. We employed rephasing (R, a–b–c) and nonrephasing (NR, b–a–c) pulse sequences. The time intervals were controlled by moving the translation stages. τ was scanned from 0 to 3.6 ps for the rephasing sequence, and 0 to 3.0 ps for the nonrephasing sequence, with a step of 4.5 fs. T was set to 0 for the double-crossed 〈π/4, −π/4, Y, Z〉 polarization spectra, and 300 fs for the 〈ZZZZ〉 and 〈YYZZ〉 polarization spectra to minimize nonresonant solvent response. The local oscillator was set to precede the signal by 1.0 ps. Absorptive 2D IR spectra were obtained by summing the real part of rephasing and nonrephasing spectra that were properly phased against a dispersed broadband pump-probe spectrum measured at the same waiting time.^{28, 42–43}

2.2 MD simulation

(Ala)₅ was solvated in a cubic water box of ~31.5 Å per side containing 988 water molecules and one Cl⁻ ion. MD simulations were carried out using three different force fields, including two additive (CHARMM22/CMAP^44–45 and its recent refinement CHARMM36⁴⁶) force fields, and a fully polarizable Drude-2013 force field⁴⁷ based on the classical Drude oscillator model.

Hamiltonian replica exchange molecular dynamics (H-REMD) simulations were performed in the NPT ensemble at 293 K and 1 atm. The Hamiltonian was biased using a CMAP potential applied to all backbone ϕ and ψ dihedrals. For the zeroth (unbiased) replica the unperturbed CMAP from the corresponding CHARMM protein force field was used, whereas for the highest replica a biasing potential CMAP (bpCMAP) generated by inverting the 2D ϕ and ψ potential energy surface of Ac-Ala-NHMe was applied. Eight replicas were used for each H-REMD simulation using the additive force fields with linear scaling between the adjacent bpCMAPs, while twelve replicas were used for the Drude-2013 force field.

Periodic boundary conditions were applied and Lennard-Jones interactions were truncated at 12 Å with a smoothing function (force switch smoothing for the C22/CMAP and C36 simulations and switch smoothing for the Drude-2013) from 10 to 12 Å. The non-bonded interaction lists were generated with a distance cutoff of 16 Å and updated heuristically. Electrostatic interactions were calculated using the particle mesh Ewald method⁴⁸ with a real space cutoff of 12 Å on an approximately 1 Å grid with a sixth-order spline. Covalent bonds to hydrogen atoms were constrained by SHAKE.⁴⁹ Temperature control was performed based on the Nose-Hoover thermostats^50–51 and pressure control performed with the Andersen barostats.⁵² For the polarizable simulations, the Drude particles were kept at low temperature (1 K) using a dual thermostat Nose-Hoover algorithm,⁵³ imposing the electronic degrees of freedom to approach the adiabatic SCF limit.

The integration time step was set to 2 fs for the additive simulations and 1 fs for the polarizable simulations. Exchanges were attempted every 1 ps, and coordinates were saved every 10 ps. The acceptance ratio for exchange between two replicas ranged from 20% to 50%. H-REMD simulations were run for 100 ns for the additive force fields and 60 ns for the polarizable Drude-2013 force field. Analysis was performed to check that the populations of the (Ala)₅ conformations had converged in the H-REMD simulation. The coordinates and velocities at every 100 ps during the last 50 ns H-REMD simulations were used to start NVT simulations that were run for 40 ps with the coordinates saved every 20 fs. This leads to 500 short MD trajectories for spectral calculations. All the simulations were carried out using CHARMM.⁵⁴ We checked the conformational distribution of the 500 short trajectories, and found that they gave very similar results to the last 50 ns of REMD simulation. The difference between the two is about 1–2%. All further analysis and calculations below were based on the 500 short trajectories.

3. Results and discussion

3.1 Experimental results of unlabeled (Ala)₅

As shown in Figure 2a, the four amide-I′ modes in (Ala)₅ are congested in a single FTIR band centered at 1650 cm⁻¹, with a small shoulder around 1670 cm⁻¹. The band at 1720 cm⁻¹ is due to the carboxylic acid CO stretch.⁵⁵ The shoulder around 1670 cm⁻¹ can be attributed to the N-terminal amide-I′ mode. It is blue shifted from the other amide-I′ modes due to the presence of the -ND₃⁺ group, as suggested in previous studies.^{17–18, 55} The broad and featureless FTIR spectrum does not intuitively provide useful information about the structures.

Figure 2.

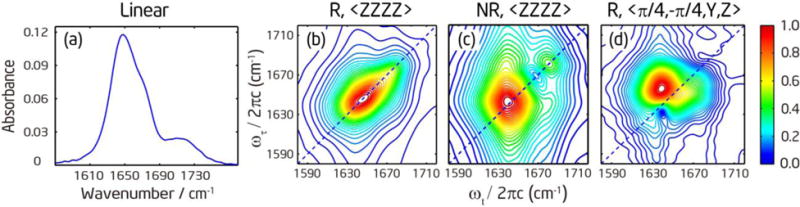
(a) Linear absorption spectra of deuterated (Ala)₅ in D₂O at pD = 1. (b) and (c): Rephasing and nonrephasing spectra under the 〈ZZZZ〉 polarization at T = 300 fs, respectively. (d) Rephasing spectrum under the double-crossed 〈π/4, −π/4, Y, Z〉 polarization at T = 0.

The 2D IR spectra of (Ala)₅ shown in Figure 2b–d also do not provide significant structural information. The rephasing spectrum under the 〈ZZZZ〉 polarization has only one broad peak. The nonrephasing spectrum has a higher resolving power for closely spaced spectral features,^{37, 39, 56–57} and reveals two peaks at 1673 and 1648 cm⁻¹. The higher frequency peak corresponds to the first amide-I′ mode and the lower frequency peak corresponds to the second-fourth amide-I′ modes. There appears to be some cross peaks between the two peaks, but no internal spectral features can be distinguished within the broad lower frequency peak. We then measured the 2D IR spectra under the double-crossed 〈π/4, −π/4, Y, Z〉 polarization since it has been shown theoretically and experimentally that this polarization^{33, 37–38, 58–60} and its variations^{37, 61–62} can suppress the strong diagonal peaks and retain only the cross peaks. As shown in Figure 2d, the double-crossed spectrum exhibits a cross-peak pattern that has an intense and broad peak above the diagonal line and tails into two regions below the diagonal. This pattern is different from the doublet and multiple peak patterns observed in the 3₁₀- and α-helical structures, respectively.^{38, 59} To model this four-vibrator system, a 4×4 matrix is needed to describe the one-exciton Hamiltonian which contains six independent coupling terms describing the interactions between amide-I′ local modes, four local frequencies, and some dynamics parameters. The poor peak separation and lack of spectral features in the unlabeled peptide spectra do not allow unique determination of these parameters.

3.2 Experimental results of labeled (Ala)₅

To resolve separate peaks, we designed two different isotope-edited peptides: A₅-23 and A₅-43. The first amide-I′ mode is close to the positively charged N-terminal, so it always has the highest frequency. The third amide-I′ mode is always double-labeled with ¹³C=¹⁸O, so it has the lowest frequency. As shown in Figure 3, the isotope-labeled and unlabeled regions are well separated in FTIR spectra. However, within each amide-I′ band, two peaks are only partially resolved because the frequency separation is comparable to the linewidth. The frequency separation is about 20 cm⁻¹ between two peaks within the same band, and about 45 cm⁻¹ between the lower frequency peak in the unlabeled region and the higher frequency peak in the labeled region. The frequency ordering (from high to low wavenumber) for the four amide-I′ modes is 1-4-2-3 for A₅-23, and 1-2-4-3 for A₅-43, as labeled in Figure 3.

Figure 3.

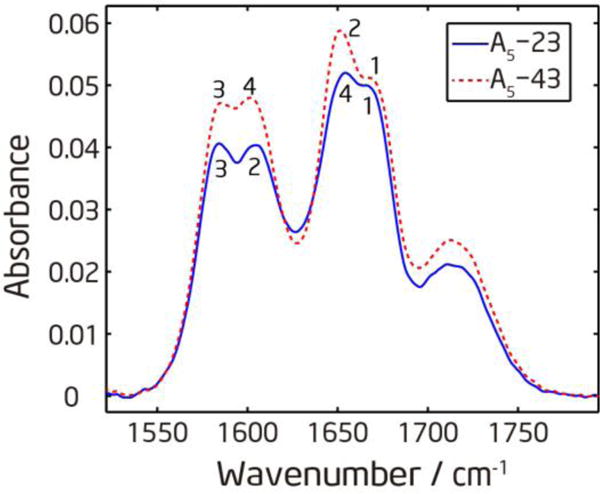
Linear absorption spectra of isotope labeled (Ala)₅ in D₂O at pD=1. The numbers labeled on the peaks indicate which amide-I′ mode the peak belongs to.

Figure 4a–d and f–i show the rephasing and nonrephasing spectra collected under the 〈ZZZZ〉 and 〈YYZZ〉 polarization for the labeled (Ala)₅ peptides. The rephasing spectra are similar to the FTIR spectra, where the isotope labeled band is well separated from the unlabeled band, but within each band the two peaks are not well resolved. The nonrephasing spectra have better resolution, so all four peaks are resolved in both A₅-23 and A₅-43. In all 2D spectra the unlabeled band is stronger than the labeled band, which is also consistent with the intensity profile of the FTIR spectra. Since the mid-IR spectrum is centered at 1625 cm⁻¹ (between the labeled and unlabeled regions), the difference should not come from the spectral bandwidth convolution effect. Previous studies^63–64 and our ab initio calculation on deuterated N-methylacetamide (see Section 3 in the Supporting Information) both showed that isotope labeled amide-I′ modes have smaller transition dipole strengths μ. Therefore, the difference is most possibly due to weaker transition dipole strength for the labeled amide-I′ modes. Because 2D IR intensity is proportional to μ⁴, the contrast is more apparent compared to linear IR where the intensity is proportional to μ².

Figure 4.

2D IR absolute magnitude spectra of isotope labeled (Ala)₅ in D₂O at pD=1. (a) and (b): Rephasing and nonrephasing spectra of A₅-23 under the 〈ZZZZ〉 polarization at T = 300 fs, respectively. (c) and (d): Rephasing and nonrephasing spectra of A₅-23 under the 〈YYZZ〉 polarization at T = 300 fs, respectively. (e) Rephasing spectra of A₅-23 under the 〈π/4, −π/4, Y, Z〉 polarization at T = 0 fs. The corresponding spectra for A₅-43 are plotted in (f) – (j).

The cross peaks in 2D IR reflect vibrational couplings between different vibrational modes, which can be related to the dihedral angles describing the polypeptide conformation. The intensity of cross peaks, in the weak coupling limit, is proportional to the off-diagonal anharmonicity Δ_ij⁶⁵

$${\mathrm{\Delta }}_{ij}=4{\beta }_{ij}{ }^2\mathrm{\Delta }/{({\omega }_i-{\omega }_j)}^2$$ (1)

where β_ij is the coupling constant between the local modes i and j, Δ is the diagonal anharmonicity of the local modes, and ${\omega }_i$ and ${\omega }_j$ are local mode frequencies. To show strong cross peaks, β_ij needs to be large whereas the frequency separation needs to be small. Our strategy was to isotope labeled some amide C=O bonds to introduce a larger frequency separation to simplify the cross peak patterns, so that we can use a set of smaller Hamiltonians to model the peptide instead of using the full Hamiltonians. In this labeling scheme, for the six pairs of nearest-neighbor amide-I′ modes in two isotopomers, only three pairs (1–2 pair and 3–4 pair in A₅-43, and 2–3 pair in A₅-23) have a frequency separation of ~20 cm⁻¹, whereas the other three pairs (2–3 pair in A₅-43, 1–2 pair and 3–4 pair in A₅-23) are separated by ~65 cm⁻¹. For (i, i+2) pairs, the frequency separation between the 1–3 pair of amide-I′ modes is always ~85 cm⁻¹, and that between the 2–4 pair is always ~45 cm⁻¹.

In the rephasing spectra in Figure 4, the cross peaks are buried under the strong diagonal peaks. In the nonrephasing spectra, the cross peaks are more visible but still overlap with strong diagonal peaks. In the 2D absorptive spectra plotted in the top row of Figure 5, the cross peaks are less clearly discerned from the strong diagonal peaks compared to the nonrephasing spectra. In both the absolute magnitude and absorptive spectra, cross peaks are more pronounced in the 〈YYZZ〉 polarization than the 〈ZZZZ〉 polarization. When comparing the nonrephasing spectra at different polarizations, the peak patterns between the 1–2 pair in the unlabeled region and the 3–4 pair in the labeled region of A₅-43 change significantly between the 〈ZZZZ〉 and 〈YYZZ〉 polarizations, so do the pattern between the 2–3 pair in the labeled region of A₅-23, indicating the presence of strong cross peaks between these nearest-neighbor amide-I′ modes. In contrast, the peak patterns between the 1–4 pair in the unlabeled region of A₅-23 are very similar in the 〈ZZZZ〉 and 〈YYZZ〉 polarizations, suggesting that the cross peaks between these two amide-I′ modes are quite weak.

Figure 5.

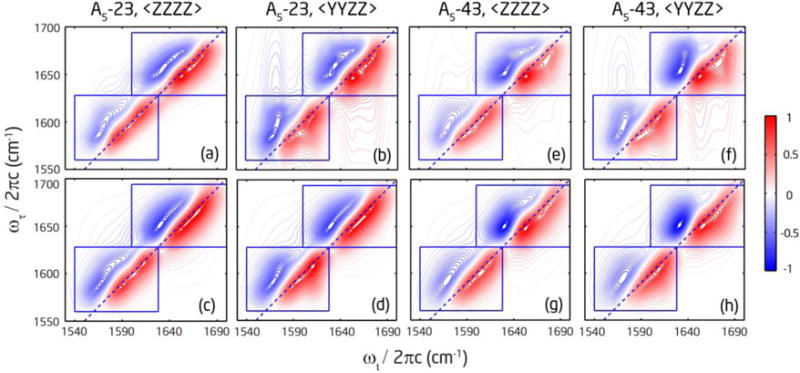
2D IR absorptive spectra of isotope labeled (Ala)₅ at T = 300 fs. (a) and (b): Measured absorptive spectra of A₅-23 under the 〈ZZZZ〉 and 〈YYZZ〉 polarization, respectively. (c) and (d): Fitted absorptive spectra of A₅-23 under the 〈ZZZZ〉 and 〈YYZZ〉 polarization, respectively. The corresponding spectra for A₅-43 are plotted in (e) (f) (g) (h). The blue square boxes indicate the areas for fitting.

The existence and relative strength of cross peaks can be further examined by the double-crossed rephasing spectra. Figure 4e and j show three pairs of strong cross-peak doublets together with residual diagonal peaks: the 2–3 pair in the labeled region of A₅-23, the 1–2 pair in the unlabeled region and the 3–4 pair in the labeled region of A₅-43. Between the 1–4 pair in A₅-23, only the residual diagonal peaks are observed which excludes the possibility of strong coupling. Except for the 1–4 pair, the cross peaks between two modes within the same region (labeled or unlabeled) are stronger, whereas the cross peaks between a mode from the labeled region and another mode from the unlabeled region are much weaker. Figure S3 in the Supporting Information displays slices of the double-crossed spectra to more clearly illustrate the different strengths in the cross peaks. It is clear from these spectra that the three pairs of amide-I′ modes that show strong cross peaks are nearest neighbors and have about 20-cm⁻¹ frequency separation. The other pairs exhibit much weaker peaks either due to a large frequency separation, or a small β_ij, or a combination of two factors. Figure S3 also includes slices of the nonrephasing spectra to illustrate how cross-peak intensities change with polarization. Large changes are seen for the cross peaks between nearest-neighbor modes within the same region, but not for those from different regions. This behavior is consistent with the results from the double-crossed polarization spectra.

Although there are still diagonal peaks remaining in the double-crossed polarization spectra that are not fully suppressed, they are relatively weak compared to the cross peaks. The residual diagonal peaks may originate from several reasons, including the non-collinear beam geometry, some nonrephasing contribution from smaller τ when pulses overlap, and internal rotation of peptide molecules. In our setup, the diagonal peak can be suppressed to 0.6–1% with the double-crossed polarization for a single amide-I mode.³⁸ For (Ala)₅, the intensity of the cross peaks under the double-crossed polarization are about 2% of the intensity of the diagonal peaks under the 〈ZZZZ〉 polarization, about 2–3 times the intensity of the residual diagonal peaks.

3.3 Conformational analysis by fitting the 2D spectra

As discussed above, only three pairs of amide-I′ modes (2–3 pair in A₅-23, 1–2 pair and 3–4 pair in A₅-43) have strong cross peaks. As a first order approximation, the four-oscillator system can then be effectively reduced into three sets of two-oscillator systems in the two isotopomers. The cross peaks between them contain information of dihedral angles that are pertinent to the middle three residues. Because the frequency separation is only about 20 cm⁻¹ which is comparable to the diagonal peak linewidth, there is a lot of diagonal peak contribution at the cross peak positions. This renders direct extraction of structural information from cross peaks impossible. We fit the experimental 2D spectra using a vibrational exciton model and a sum-over-states approach to extract the structural parameters (using the same equations as reported in ref 38 to calculate the R and NR spectra). One-exciton Hamiltonians and the transition dipole operator were constructed in the site basis with ${\omega }_i$ as the diagonal elements, β_ij as the off-diagonal elements in the Hamiltonian, and θ_ij as the angle between two transition dipoles. Assuming Bloch dynamics, the spectral line shapes were broadened by homogeneous and inhomogeneous contributions. The homogeneous broadening was described by γ and γ′, the dephasing rate for the v = 0→1 and 1→2 transitions, respectively. The static inhomogeneous distribution of the site energies were approximated by 2000 sets of uncorrelated normally distributed random frequencies centered at ω_i and ω_j with standard deviations of σ_i and σ_j, respectively. The two-exciton Hamiltonian was then built from the one-exciton Hamiltonian with the harmonic approximation. Diagonalization of the Hamiltonians provides the eigen-frequencies and the corresponding transition dipoles in the exciton basis. 2D spectra were calculated with the exciton basis in the frequency domain, averaged over the inhomogeneous distribution and finally convoluted with the mid-IR spectrum. There are eight free parameters: center frequencies ω_i and ω_j, coupling constant β_ij and angle θ_ij between two transition dipoles, inhomogeneous widths σ_i and σ_j, and dephasing rates γ and γ′. Because the ¹⁸O isotope purity is 92%, the spectral fitting also included 8% isotopomers bis-labeled with ¹³C=O.

To maximize the information content extracted from the experimental spectra, we fit the model to either the absolute magnitude spectra or the absorptive spectra and check their consistency. The absolute magnitude spectra have individual rephasing and nonrephasing components, but do not have phase information. The absorptive spectra have phase information, but rephasing and nonrephasing components are combined. The spectra under the 〈ZZZZ〉 and 〈YYZZ〉 polarization were given the same weighting in the fitting. Because we used a two-oscillator model, the off-diagonal regions between isotope labeled and unlabeled bands were not included in the fitting. The spectral regions for fitting are inside the blue square boxes, as illustrated in Figure 5. Either the spectrum inside each box was fitted individually with a single two-oscillator model, or the spectra inside both boxes were fitted together by adding up contributions from two two-oscillator models. We fitted both ways to check the consistency because the isotope labeled and unlabeled bands partially overlap and interfere with each other, which mainly affects the diagonal peaks rather than the cross peak region. When fitting the spectrum inside each box individually, multiple initial guesses were used to find the global minimum. When fitting the spectra inside both boxes together, the fitted parameters from individual box fitting were used as the initial guess. The Levenberg–Marquardt algorithm was used to do least-square fitting, and the final fitted parameters (more details are provided in Section 4 of the Supporting Information) are β₁₂ = 4.3 +1.3/−1.2 cm⁻¹ and θ₁₂ = 101° +10°/−8°, β₂₃ = 4.6 +2.0/−2.6 cm⁻¹ and θ₂₃ = 100° +9°/−8°, and β₃₄ = 4.4 +1.8/−2.4 cm⁻¹ and θ₃₄ = 100° +10°/−9°. The estimation of the confidence interval was performed by changing the parameters until the fitting error was doubled, similar to the method adopted in literatures.⁶⁶ The fitted parameters are very similar across different residues.

3.4 Conformational distributions from MD simulations

We analyzed the conformation distributions of MD trajectories based on three secondary structure definitions commonly used in the MD community,^{30, 46}

$$\begin{array}{l}{\mathrm{\alpha }}_{+}:-160°<\mathrm{\varphi }<-20°\text{and}-120°<\mathrm{\psi }<50°\hfill \\ \mathrm{\beta }:-180°<\mathrm{\varphi }<-90°\text{and}50°<\mathrm{\psi }<180°\text{or}\hfill \\ -180°<\mathrm{\varphi }<-90°\text{and}-180°<\mathrm{\psi }<-120°\text{or}\hfill \\ 160°<\mathrm{\varphi }<180°\text{and}110°<\mathrm{\psi }<180°\hfill \\ \begin{array}{l}\text{ppII:}-90°<\mathrm{\varphi }<-20°\text{and}50°<\mathrm{\psi }<180°\text{or}\\ -90°<\mathrm{\varphi }<-20°\text{and}-180°<\mathrm{\psi }<-120°\end{array}\hfill \end{array}$$ (2)

Here (ϕ, ψ) are the peptide backbone dihedral angles, α₊ is a broader definition of α helix often used in the force-field related discussion.⁴⁶ Although (Ala)₅ has five residues, only the middle three residues have both well-defined ϕ and ψ based on which secondary structures are defined. The population fractions of each secondary structure for the middle three residues are listed in Table 1. From the table, it is clear that different force fields predict very different conformational distributions. C22/CMAP force fields predict almost equal population for the three secondary structures, C36 force fields predict more ppII and less α₊ compared to C22/CMAP, whereas the Drude-2013 force fields predict predominately β structure. The conformational distributions across the three residues are similar in the C36 force fields, but there are some variations in the C22/CMAP and Drude-2013 force fields.

Table 1.

Population fractions of different conformations at each residue under different force fields.

Force Field	Conformation	(ϕ2, ψ2)	(ϕ3, ψ3)	(ϕ4, ψ4)
	α+	0.26	0.39	0.30
C22/CMAP	β	0.32	0.23	0.32
	ppII	0.36	0.31	0.32
	α+	0.11	0.13	0.12
C36	β	0.24	0.21	0.21
	ppII	0.58	0.60	0.59
	α+	0.02	0.08	0.10
Drude-2013	β	0.86	0.75	0.77
	ppII	0.12	0.16	0.13

3.5 Comparison of fitting results with MD

The spectral parameters obtained by fitting experimental spectra are nearest-neighbor coupling constant β_ij and angle θ_ij, whereas the MD simulation gives conformational distributions. To convert conformational parameters into spectral parameters, we invoke the mapping shown in Fig. S1 of Supporting Information. For every MD snapshot, β_ij was determined using the nearest-neighbor coupling map (Table S1), and θ_ij was calculated from the directions of transition dipoles on neighboring amide units. In this way, each single conformation in the Ramachandran plot can also be represented by a point in the coupling-angle plot which is directly related to the observables from experiment. Figure 6 shows the overall conformation distribution for all three middle residues predicted by different force fields, in both the Ramachandran plot (top row) and β_ij–θ_ij plot (second row). To more clearly illustrate how the different regions in the β_ij–θ_ij plot correspond to the secondary structures defined in eq (2), the points within each colored box in the top row are plotted in the corresponding β_ij–θ_ij plot in the third row of Figure 6. It is clear that the mapping between two plots is very complex. The relatively narrow distribution of ppII in the Ramachandran plot corresponds to a relatively broad distribution in the β_ij–θ_ij plot, whereas the relatively broad distribution of β structure in the Ramachandran plot translates to a very narrow distribution in the β_ij–θ_ij plot. The latter is the reason why the β structure always gives rise to the strongest peak intensity in Figure 6d–f even when its total population is not the highest.

Figure 6.

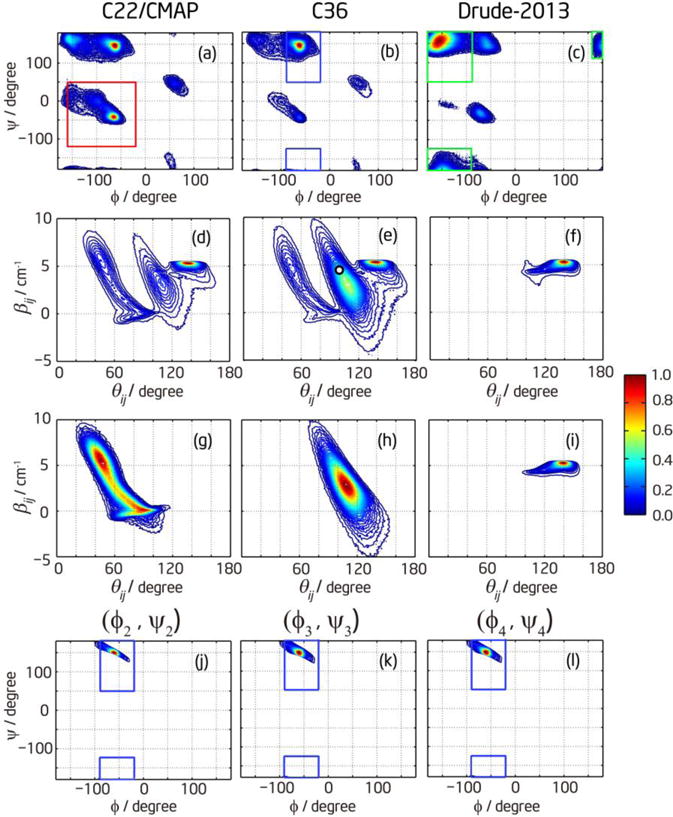
The conformational distributions of (Ala)₅ from the MD simulations. The first row shows the Ramachandran plots for different force fields including all conformers, and the corresponding β_ij-θ_ij plots are in the second row. (a, d) are for C22/CMAP, (b, e) are for C36, and (c, f) are for Drude-2013. The third row is the β_ij–θ_ij plot for each conformer. The red box in (a) shows the definition of α₊, and the corresponding distribution in the β_ij–θ_ij plot is shown in (g). The blue boxes in (b) and the corresponding distribution in (h) are for ppII. The green boxes in (c) and the corresponding distribution in (i) are for β structure. (a)–(i) include statistics from all three middle residues. The fourth row shows the region of Ramachandran plot in (b) allowed by the confidence interval from spectral fitting for each residue: (j) is for (ϕ₂, ψ₂), (k) is for (ϕ₃, ψ₃), and (l) is for (ϕ₄, ψ₄). The blue boxes show the definition of ppII.

On the basis of above discussion, we can invert the problem and find the corresponding Ramachandran angles from the (β_ij, θ_ij) parameters obtained from spectral fitting. In general the inversion problem is neither unique nor robust since a single set of (β_ij, θ_ij) can correspond to more than one set of (ϕ, ψ) (see, for example, Figure 4 in ref¹⁷), and a small change in (β_ij, θ_ij) might lead to a big change in (ϕ, ψ). However, based on the realistic conformational distribution sampled by MD simulation, we can find the unique distribution of (ϕ, ψ) that corresponds to the confidence interval of (β_ij ± Δβ, θ_ij ± Δθ) from fitting. The results are plotted in the fourth row of Figure 6. From the plots, it is clear that the distribution of (ϕ, ψ) allowed by the confidence interval of fitting parameters are mostly within the definition of ppII for all three residues. The allowed (ϕ, ψ) distribution is very asymmetric due to the nonlinear nature of mapping between (β_ij, θ_ij) and (ϕ, ψ). The center of the allowed (ϕ, ψ) distribution is then the solution of the inversion problem. Taking for example the fitted parameters β₁₂ = 4.3 cm⁻¹ and θ₁₂ = 101°, denoted as the white dot in Figure 6e, the corresponding (ϕ₂, ψ₂) = (−60°, 150°). It is only (1°, 5°) off from the most populated point (−61°, 145°) in the C36 MD simulation. The dihedral angles for other two residues are only 1~2 degrees off from (ϕ₂, ψ₂), which is a natural consequence of similar fitted parameters. It should also be noted that, in the spectral fitting, (β_ij, θ_ij) and (−β_ij, 180°−θ_ij) give exactly the same results. The fitted parameters β_ij = 4.3 cm⁻¹ and θ_ij = 101° can also be β_ij = −4.3 cm⁻¹ and θ_ij = 79°. However, the latter set of parameters corresponds to a structure that is physically unrealizable and is very far from any distribution in the β_ij–θ_ij plot. Therefore, comparing the results from spectral fitting and MD simulation, we can conclude that the C36 force field yields the best agreement with the experimental data for (Ala)₅ by predicating the most ppII population (Table 1), while the Drude-2013 and C22/CMAP force fields are in poorer agreement.

Further examination of conformational distribution in the β_ij–θ_ij plot shows that these two spectral parameters play different roles in the determination of secondary structures. Figure 7 shows the histogram of β_ij and θ_ij taken from the C36 simulation in Figure 6e. It is apparent that the distributions of coupling constants from different secondary structures significantly overlap with each other, whereas the distributions of angles can be better distinguished from each other.

Figure 7.

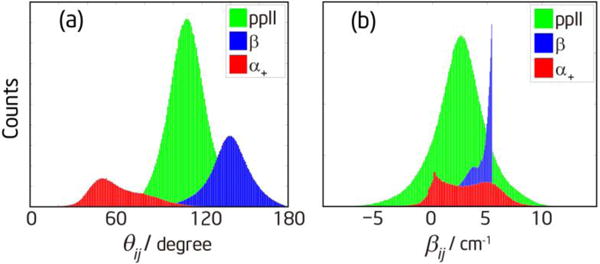
(a) Histogram of the angles between two transition dipoles on nearest-neighbor amide-I modes for different conformations. (b) Histogram of the coupling constants between nearest-neighbor amide-I modes for different conformations. This distribution is calculated for the C36 force field.

To check the validity of two-oscillator model, we also calculated the coupling constant and angle between transition dipoles for non-nearest-neighbor amide-I modes using the C36 MD simulation trajectories.⁶⁷ The coupling constant was calculated by the transition charge coupling method.⁶⁸ The distribution of the coupling constant for 1–4 pair is most populated at 0.5 cm⁻¹ and they can be considered as totally uncoupled. The distributions of coupling constants for 1–3 and 2–4 pairs are most populated at about −2.2 cm⁻¹, smaller than the nearest-neighbor coupling. Because the frequency separations between the (i, i+2) pairs are 2–4 times larger than that between the nearest neighbors, the effect of their coupling can be neglected. These results are consistent with the observed cross peak patterns in our double-crossed spectra in Figure 4(e, j), and also the slices shown in Figure S3.

3.6 Spectral signatures of different conformers

To demonstrate the dependence of linear and 2D IR spectra on peptide conformations, we performed spectral calculation for the 1–2 pair of A₅-43 using a single representative conformation of ppII, α₊ and β structure. Figure 8 shows the comparison with the measured and fitted spectra. The representative conformation was chosen as the most populated position in the Ramachandran plots in Figure 6(g–i). The parameters for ppII are (ϕ, ψ) = (−61°, 145°) and (β_ij, θ_ij) = (3.0 cm⁻¹, 109°). The parameters for β are (ϕ, ψ) = (−156°, 156°) and (β_ij, θ_ij) = (5.3 cm⁻¹, 139°). The parameters for α₊ are (ϕ, ψ) = (−65°, −42°) and (β_ij, θ_ij) = (5.5 cm⁻¹, 46°). For other spectral parameters, we used the fitted values listed in Table S2 in the Supporting Information. The results clearly show that ppII conformation produces spectra that closely resemble the experimental and fitted spectra, but β (α₊) conformation produces spectra that are too intense on the low (high) frequency side.

Figure 8.

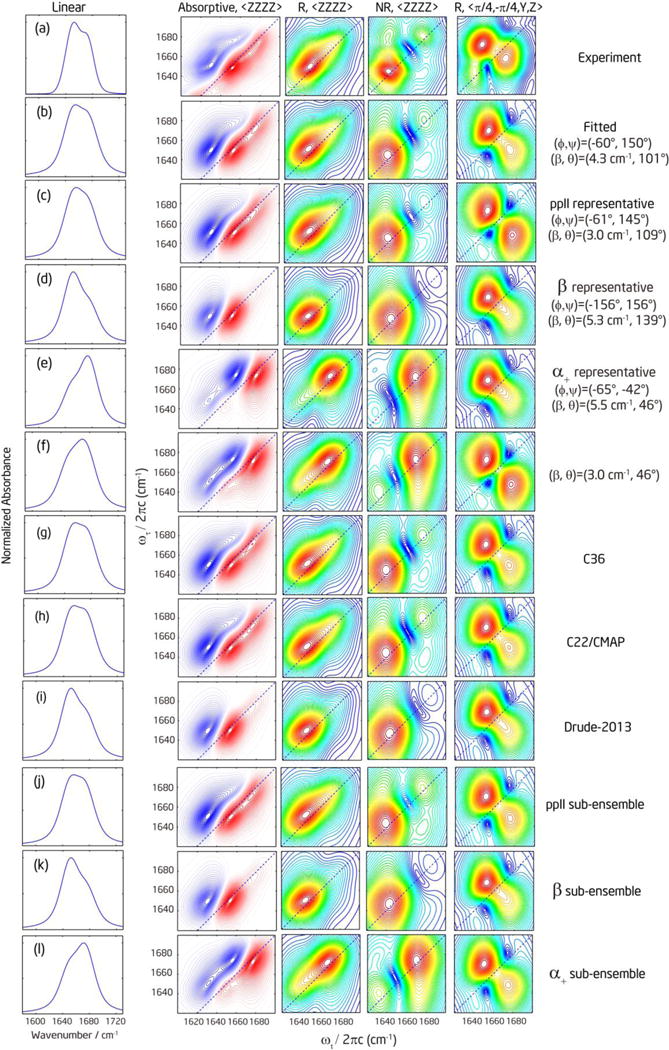
Comparison of experimental, fitted, and simulated spectra of representative conformations and different MD simulation trajectories. Each row represents (a) Experimental spectra for the 1–2 pair of A₅-43. The linear spectrum of the unlabeled band was obtained from fitting the FTIR spectra of A₅-43 with multiple Voigt functions. (b) Fitted spectra. (c–f) Simulated spectra for representative conformations: (c) ppII; (d) β; (e) α₊; (f) a conformation with (β_ij, θ_ij) = (3 cm⁻¹, 46°). (g–i) Simulated spectra using MD simulation trajectories with different force fields: (g) C36; (h) C22/CMAP; (i) Drude-2013. (j–l) Simulated spectra averaged over the MD C36 simulated distribution of each conformer: (j) ppII; (k) β; (l) α₊ distribution. The color scales are the same as those used in Figure 2 and Figure 5.

So far we fit the experimental spectra with a single set of β_ij and θ_ij, and compare the experimental spectra with the simulated spectra of some representative conformations which are also described by a single set of β_ij and θ_ij. However, real peptides can adopt multiple conformations, and the measured spectra will be a population-weighted sum of contributions from different conformations. In that case, the fitted β_ij and θ_ij may not necessarily correspond to any real structure, although it is quite close to ppII here. Therefore, getting reasonable results from single conformation fitting is not sufficient. As shown in Figure 8(d, e), the β conformation produces spectra with the intensity mainly located at the low frequency, and α₊ conformation produces spectra with the intensity mainly located at the high frequency. Therefore, a question is raised: whether the peptide can adopt a mixture of β and α₊ conformations rather than mainly ppII; and whether there are some spectral observables of ppII that cannot be a weighted-average of the other two conformations.

As discussed in Section 3.4 and illustrated in Figure 7, the three conformations are better distinguished by θ_ij, and hence we first focus on the spectral observables as a function of θ_ij.⁶⁰ One useful spectral observable is the cross-peak anisotropy, which is given by

$$\begin{array}{l}{R}_{\mathit{cross}}=\frac{I_{\mathit{ZZZZ}}-I_{\mathit{YYZZ}}}{I_{\mathit{ZZZZ}}+2I_{\mathit{YYZZ}}}\\ =\frac{1}{5}\left(\frac{13P_2+5}{2P_2+7}\right)=\frac{13{\text{ cos}}^2{\theta }_{ij}^{\prime }-1}{10{\text{ cos}}^2{\theta }_{ij}^{\prime }+20}\end{array}$$ (3)

in the weak coupling limit for the experimental configuration used in this study. Here $I_{\mathit{ZZZZ}}$ and $I_{\mathit{YYZZ}}$ are the cross-peak intensity in absorptive 2D IR spectra taken with the 〈ZZZZ〉 and 〈YYZZ〉 polarization, respectively. P₂ = P₂(cos ${\theta }_{ij}^{\prime }$) is the second order Legendre polynormial. ${\theta }_{ij}^{\prime }$ is the angle between transition dipoles in the eigen basis. In the weak coupling limit, ${\theta }_{ij}^{\prime }$ is very close to ${\theta }_{ij}$ or 180°− ${\theta }_{ij}$, (this ambiguity comes from the fact that eigenvectors are indifferent to sign), and hence R_cross exhibits basically the same dependence on ${\theta }_{ij}^{\prime }$ and ${\theta }_{ij}$. R_cross is at the lowest value at 90° which is close to the ppII conformation (around 110°). Because both α₊ (around 45°) and β (around 140°) give higher values, they cannot be mixed to get the same value as ppII. When the frequency separation between the diagonal peaks is large enough, R_cross can be determined directly from measured cross peak intensities.¹⁷ Unfortunately, in the current system the intensity of cross peaks cannot be obtained directly because they are in close proximity to the strong and broad diagonal peaks. They can only be obtained by fitting over the entire range including the strong diagonal peaks. Therefore, the result on R_cross is nevertheless obscured.

Another choice is to use the double-crossed polarization by which the diagonal peaks are mostly removed. We did not include the double-crossed polarization spectra in our fitting due to the incomplete suppression of the diagonal peaks. Using the fitted parameters, we simulated the double-crossed polarization spectra and checked that the consistency with experimental spectra in the cross peak region is reasonable (Figure 8b). For comparison, we also calculated the double-crossed spectra of representative conformations in Figure 8, and included another spectra with (β_ij, θ_ij) = (3.0 cm⁻¹, 46°) which has the same θ_ij as that of the representative α₊ conformation, but the same β_ij as that of the representative ppII conformation. Comparing Figure 8d with e, and Figure 8c with f, we found that the shape of double-crossed spectra is invariant with different θ_ij. However, comparing Figure 8e with f, the shape of double-crossed spectra is very sensitive to the change in β_ij. This different dependence of spectral shape on θ_ij and β_ij has been further confirmed by simulating the double-crossed spectra with many different combinations of (β_ij, θ_ij). This behavior seems to be a special case for two-vibrator systems only, because it has been previously shown that the shape of double-crossed spectra for many-vibrator systems are very sensitive to structures.^{33, 38–39} Compared to the experimental spectrum (Figure 8a), with the cross peaks above the diagonal line being normalized to the same intensity, the cross peaks below the diagonal line in the ppII and (β_ij, θ_ij) = (3.0 cm⁻¹, 46°) spectra (Figure 8c and f, both have β_ij = 3.0 cm⁻¹) are marginally stronger than the experiment, but they are weaker and smeared in the α₊ and β spectra (Figure 8d and e, β_ij ~ 5.4 cm⁻¹). To show a clear doublet cross-peak feature, β_ij needs to be smaller than 5 cm⁻¹, although this condition alone is not sufficient to rule out any conformations because the distributions of β_ij are very broad and significantly overlap (see Figure 7b).

On the other hand, the intensities of the cross peaks are sensitive to both θ_ij and β_ij. In the weak coupling limit, the orientation factor for cross peaks under the double-crossed polarization is $\left({\text{sin}}^2{\theta }_{ij}^{\prime }\right)/6$ which peaks at ${\theta }_{ij}^{\prime } ~ {\theta }_{ij}=\mathrm{90}°$. Let us define a quantity, R_cross/diag, that is dependent on both θ_ij and β_ij:

$$R_{\text{cross}/\text{diag}}=\frac{I_{\text{cross}, \langle \frac{\pi }{4}, -\frac{\pi }{4} ,\text{ Y},\text{ Z}\rangle }}{I_{\text{diag},\langle \text{ZZZZ}\rangle }}$$ (4)

Here the numerator is the maximal intensity of the cross peaks in the absolute magnitude 〈π/4, −π/4, Y, Z〉 rephasing spectrum, and the denominator is the maximal intensity of the diagonal peaks in the absolute magnitude 〈ZZZZ〉 rephasing spectrum. The experimental R_cross/diag ratio is 2.2 ± 0.2% (The double-crossed polarization spectrum was taken at T = 0, but the parallel polarization spectrum was taken at T = 300 fs. The fitted and simulated values reported below are corrected by a factor of 0.74 to account for the ~ 1-ps population decay). Using the fitted parameters (β_ij = 4.3 cm⁻¹, θ_ij = 101°), we obtained R_cross/diag = 2.4%, comparable to the experiment. Although the double-crossed spectrum contains residual diagonal peaks, their effect on the R_cross/diag ratio is estimated to be less than 10% (see Section 5 in Supporting Information).

If β_ij is fixed at the fitted value and θ_ij takes the values of the representative conformations, R_cross/diag is 2.0% for ppII (θ_ij = 109°), close to the experimental result, but it becomes 1.2% for α₊ (θ_ij = 46°) and 0.77% for β (θ_ij = 139°), much smaller than the experiment. If β_ij is allowed to arbitrarily vary, it needs to be 6.1 cm⁻¹ for α₊, and 9.2 cm⁻¹ for β in order to reach R_cross/diag = 2.0%, but the doublet feature in the double-crossed spectra will completely disappear with these large values of β_ij. To see whether it is possible to mix α₊ and β conformers in different ratios to increase R_cross/diag, we tested many mixing ratios under the constraints of maintaining the experimental diagonal profile of 〈ZZZZ〉 and 〈YYZZ〉 spectra and the double-crossed spectral shape. It should be noted that when mixing α₊ and β conformers, the resultant R_cross/diag is not a simple population-weighted average of their respective values because the maximal diagonal peaks of the two conformers are located at different frequency positions. We found that it is impossible to find a mixing ratio that gives a higher R_cross/diag than that of the individual conformer (see Section 5 in Supporting Information), and hence the R_cross/diag of the mixture is always much lower than the experimental value. Therefore, based on the double-crossed spectral shape and R_cross/diag, we can rule out the possibility that the spectral features well-represented by the fitted ppII conformation actually resulted from a weighted average of α₊ and β conformations.

3.7 Spectral simulation with MD trajectories

In this section, we will simulate 2D IR spectra by the sum-over-states method using the fluctuating conformations (ϕ, ψ) from the MD simulation trajectories. Each structure corresponds to one (β_ij, θ_ij) with normally distributed random local mode frequencies and other dynamic parameters taken from the fitting. The results are shown in Figure 8g–i. Compared to the simulation above for single representative conformations, the calculation here incorporates the conformational heterogeneity sampled in the MD simulation. The spectra simulated using Drude-2013 force fields MD trajectories are very similar to those of the β representative conformation, and are not consistent with the experimental spectra. This is expected because Drude-2013 force field predicts 86% β conformation. The spectra simulated by the additive C22/CMAP and C36 force fields are very similar and both consistent with the experimental and fitted spectra, even though they predict different conformational distributions. However, the ensemble-averaged R_cross/diag is 1.59% for the C36 simulation, 1.57% for C22/CMAP, and 1.22% for Drude-2013, all of which are quite off from the experimental and fitted values. These results suggest that none of the three MD conformational ensembles is an ideal representation of the actual conformational distribution.

When comparing the simulation results between C22/CMAP and C36, it is somewhat unexpected that they predict very similar spectral shape as well as R_cross/diag values. As we discussed in the previous section, the ppII spectra under the parallel and perpendicular polarizations can be somewhat approximated by a weighted average of α₊ and β spectra, which rationalizes the similarity in spectral shape between the C22/CMAP and C36 simulations. Although C22/CMAP has a lower percentage of ppII than C36, the higher percentages of α₊ and β combined in a way that gives spectral features similar to C36. However, it is not obvious why R_cross/diag values are also very similar. To elucidate the reason, we simulated the spectra averaged over the MD simulated sub-ensemble of each conformer (within the range inside the boxes in Figure 6a–c). The spectra are shown in Figure 8j–l. We found the ratio to be 1.8% for ppII, 1.6% for α₊, and 1.0% for β. Compared to the ratios given previously for representative conformations at a fixed β_ij = 4.3 cm⁻¹, the sub-ensemble-averaged ratio is smaller for ppII, but larger for α₊ and β. The behavior is mainly due to the difference in the calculated β_ij. As shown in Figure 6, the ppII conformation is most populated around β_ij = 3.0 cm⁻¹, which is smaller than the fitted value and will result in weaker cross-peak intensities. The most populated β_ij is around 5.5 cm⁻¹ for α₊ and 5.3 cm⁻¹ for β conformer, both of which are larger than the fitted value and will result in stronger cross-peak intensities. Therefore, the ensemble-averaged R_cross/diag values are quite similar even though population distributions are quite different from the C22/CMAP and C36 force fields.

To quantitatively estimate the population distribution of different conformers, we took the sub-ensemble-averaged 2D spectra of each conformer, as shown in Figure 8j–l, as the reference spectra and mixed them in different population ratios to find the combination that can reproduce the experimental spectra and R_cross/diag. Our result shows that for any possible population distributions constrained by the diagonal peak intensity profile, the R_cross/diag value can never be larger than 1.8%. Decreasing the population of ppII reduces the ratio. Therefore, 100% ppII population produces the closest spectra (Figure 8j) and R_cross/diag to the experiment, within the accuracy of our MD simulation and current model.

The above spectral simulation based on the C36 structure ensemble suggested an almost exclusive population of ppII. This conclusion supports the validity of single conformation fitting. However, the most populated ppII conformation from the MD simulation has different (ϕ, ψ) and (β_ij, θ_ij) from those of the fitted conformation. Also, the 1.8% ratio is still much smaller than the measured ratio, indicating that there are still some problems with the current spectral simulation using MD structures. Several reasons can contribute to the discrepancy. First, let us focus on the double-crossed spectra because they are more sensitive to the small changes of (β_ij, θ_ij). As we showed in Figure 8, 1~2 cm⁻¹ of increase in β_ij can erase the doublet feature of cross peaks. We can also calculate how sensitive R_cross/diag is around the fitted (β_ij, θ_ij) = (4.3 cm⁻¹, 101°). At θ_ij =101°, R_cross/diag changes from 2.4% at β_ij =4.3 cm⁻¹, to 1.5% at β_ij =3.0 cm⁻¹. At β_ij =4.3 cm⁻¹, R_cross/diag changes from 2.4% at θ_ij =101° to 2.0% at θ_ij = 109°. If we calculate the dependence of (β_ij, θ_ij) on (ψ, ϕ) around (−61°, 145°), β_ij has a slope of 0.2 cm⁻¹/degree against ψ, and 0.1 cm⁻¹/degree against ϕ, whereas θ_ij has a slope of −0.75 degree/degree against ψ or ϕ. Therefore, even a small difference of ~5° in dihedral angles can introduce remarkable difference in both the shape and intensity of double-crossed spectra, and affect the calculated R_cross/diag value. A deviation of several degrees is quite normal for the accuracy of MD force fields, especially for a highly flexible peptide where the distribution of ψ can range by ±25° or more for the ppII conformation, as seen in Figure 6a–c.

Another uncertainty comes from the current nearest-neighbor coupling map. Depending on the calculation details, the coupling maps from different references^68–71 are quite different in magnitude, although they have similar shape. For example, at (ϕ, ψ) = (−61°, 145°), Torri’s map gives 6.2 cm⁻¹,⁶⁹ Cho’s map gives 1.8 cm⁻¹,⁷² Jansen’s map gives 3.3 cm⁻¹,⁶⁸ Stock’s map gives 3.0 cm⁻¹,⁷⁰ and our map (Figure S1) gives 2.5 cm⁻¹. The more recent maps (including ours) are closer to one another compared to the earlier map⁶⁹ used in the (Ala)₃ and other studies.^{17–18, 26} However, it has been shown that Torri’s map predicts β_ij closer to the experimental value for the fully extended conformation.⁶² At this point, it is still unclear which map is the best due to the lack of systematic experimental validation. Another contributing factor is the direction of transition dipoles. We calculated the angle between transition dipole and C=O bond to be 15.8°, whereas the literature values vary between 10° and 25°,^{28, 69, 73} depending on both the calculation details and specific model peptides used. Instead of using a fixed angle, it may be beneficial to introduce a model which can account for how this angle varies with local environments.

3.8 Comparison with literatures

In this section we summarize some results from previous studies on alanine-based oligopeptides (Table 2), and compare their conformational distribution or single reference conformations to our fitted and MD simulated conformations. From the table, the reference structures of ppII (including the canonical conformation from the protein structural database^{3, 74}) cited in these papers vary by 10–15°. Both our fitted (ϕ, ψ) = (−60°, 150°) and simulated ppII (ϕ, ψ) = (−61°, 145°) are within or close to this range. Additionally, our residue-specific fitting result shows that the conformation is insensitive to the residue position which is consistent with the NMR study.²⁰

Table 2.

Summary of reference results on ppII. The red As represent the studied residues.

Reference	System	Methodology	(ϕ, ψ) of ppII	ppII population	other population
Tamburro3, 74		PDB	(−75°, 145°)
Hamm17–19	A $\mathrm{A}$A	2D IR	(−60°, 140°)	80%	α = 20%
Schweitzer-Stenner11–12	A $\mathrm{A}$A	Polarized Raman, FTIR, VCD and ECD	(−60°, 150°)	50%	β = 50%
Schweitzer-Stenner16	A $\mathrm{A}$A	Polarized Raman, FTIR, and VCD	(−70° ± 20°, 150° ± 20°)	84%	β = 16%
	A $\mathrm{A}$A		(−69° ± 10°, 140° ± 10°)	84%	β = 8%, α = 4%, γ = 5%
Schweitzer-Stenner14	A $\mathrm{A}$KA	Polarized Raman, FTIR, VCD, ECD and NMR	(−65°, 150°)	63%	β = 7%, α = 30%
	A $\mathrm{A}$AA		(−65°, 150°)	66%	β = 14%, α = 20%
	AA $\mathrm{A}$A		(−70°, 140°)	73%	β = 17%, α = 10%
Cho31	Averaged A $\mathrm{AA}$	NMR, used 3J(HN,Hα) from Ref20	AMBER ff03	65%	β = 35%
			Gromos 43A1	88%	β = 12%
Graf20	A $\mathrm{AAA}$A	NMR	Gromos 43A1	84%	β = 16%
This work	A $\mathrm{AAA}$A	Fitting	(−60°, 150°)
		C36 prediction	(−61°, 145°)	59%	β = 22%, α = 12%
		Simulation based on C36 ensemble	(−61°, 145°)	~100%

The ppII population predicted from C36 MD simulation is 59%. On the basis of spectral calculation where the C36 structure ensemble was used to define the reference spectra, we determined the ppII population for (Ala)₅ to be almost 100%. Therefore, our result is consistent with these previous studies that concluded ppII is the predominating conformation in aqueous solution. In this sense, the C36 force field is improved over C22/CMAP by predicting more ppII conformation, but there is still too much sampling of the α₊ and β conformers. The Drude-2013 force fields significantly over samples the β conformer and sampling of α₊ is also observed; efforts towards improving the Drude force field are ongoing. It should be noted that the quantitative results of population distribution are highly dependent on the way reference structures are defined, and also on the theoretical modeling of the relationship between peptide structure and spectra. The latter factor has already been discussed in Section 3.7. The effect of the former factor has been shown in previous studies on alanine based oligopeptide by Schweitzer-Stenner et al,^{11–12, 14, 16} where they obtained reference structures of each conformer from protein libraries or to reproduce the NMR J-coupling constants, and then fit the vibrational spectra for the population distribution. Different choices of reference structures yielded different population distribution,^{11–12, 14, 16} and sometimes it was necessary to modify the coordinates of reference structure to obtain satisfactory fitting.¹⁴ When more conformers were included in the fitting, the population distribution also changed.¹⁶

The explicit inclusion of conformational distribution also makes a big difference in population determination.¹⁶ For example, if we had chosen the representative ppII structure at the most populated position as our reference structure, it could affect the conclusion because its R_cross/diag is only 1.4%, much smaller than 1.8% obtained for the whole ppII sub-ensemble. For a given conformer, spectral calculation using its averaged or most populated structure cannot in general reproduce the 2D spectra averaged over its sub-ensemble because both the mapping from (ϕ, ψ) to (β_ij, θ_ij), and the relationship between (β_ij, θ_ij) and 2D spectra are quite complex. Therefore, it is important to use sub-ensemble-averaged 2D spectra as the reference spectra. If different structure ensembles from a different force field are used in the simulation analysis, they will give rise to different reference spectra, and hence result in a different population distribution. Cho and co-workers showed that the average ppII population over two peptide bonds in (Ala)₃ changes from 88% to 65% by simply changing the reference structure ensembles from Gromos 43A1 to AMBER ff03 but using the same experimental J-coupling constants and Karplus equations.³¹ Such dependence on force fields demonstrates the need for accurate MD simulations and validation.

4. Conclusion

We have determined the conformation of (Ala)₅ using a combination of 2D IR spectroscopy, isotope editing, and MD simulation. Fitting the experimental 2D IR spectra under the 〈ZZZZ〉 and 〈YYZZ〉 polarizations to a simple two-vibrator exciton model allowed us to extract the coupling constants and angles between transition dipoles for the 1–2, 2–3 and 3–4 peptide unit pairs. DFT-based maps were developed to relate the fitted parameters to the Ramachandran angles on residue 2, 3 and 4. All three residues adopt very similar structures located within the range of ppII conformation. Because 2D IR spectra under the 〈ZZZZ〉 and 〈YYZZ〉 polarizations are insufficient to distinguish between whether single or multiple conformations coexist in solution, we explored other spectral parameters and found that both the spectral shape under the double-crossed polarization and the R_cross/diag ratio are good spectral indicators to check the validity of fitting and spectral simulation. The spectral shape mainly provides a constraint for β_ij, whereas R_cross/diag provides a constraint for both β_ij and θ_ij for the case of two coupled vibrators. For (Ala)₅, both indicators in the fitted double-crossed spectra are consistent with the experimental spectra, suggesting the validity of single conformation fitting.

Spectral simulations based on the C22/CMAP, C36, and Drude-2013 conformational ensembles show that none can fully reproduce the experimental R_cross/diag ratio. Defining the 2D reference spectra based on the C36 conformational ensemble, the simulated R_cross/diag ratio is the closest to the experiment when the ppII population is maximized to 100%. This finding provided further validation for single conformation fitting. Compared to the literature, the dihedral angles of our fitted structure and the most populated ppII structure from the C36 simulation are within the same range as previous studies on alanine based oligopeptides, although our work is the only study to suggest exclusive ppII population. We can conclude that ppII is the dominating conformation for (Ala)₅ at ambient temperature, but the quantitative results on conformer population are subjected to the definition of reference structures and accuracy in theoretical modeling. More reliable spectral simulation methods and MD force fields are important to elucidate peptide structures, and require further theoretical development.