Elucidating important sites and the mechanism for amyloid fibril formation by coarse-grained molecular dynamics

Abstract

Fibrils formed by the β-amyloid (Aβ) peptide play a central role in the development of Alzheimer’s disease. In this study, the principles governing their growth and stability are investigated by analyzing canonical and replica-exchange molecular dynamics trajectories of Aβ_(9–40) fibrils. In particular, an unstructured monomer was allowed to interact freely with an Aβ fibril template. Trajectories were generated with the coarse-grained united-residue force field, and one- and two-dimensional free-energy landscapes (FELs) along the backbone virtual-bond angle θ and backbone virtual-bond-dihedral angle γ of each residue and principal components, respectively, were analyzed. Also, thermal unbinding (unfolding) of an Aβ peptide from the fibril template was investigated. These analyses enable us to illustrate the entire process of Aβ fibril elongation and to elucidate the key residues involved in it. Several different pathways were identified during the search for the fibril conformation by the monomer, which finally follows a dock-lock mechanism with two distinct locking stages. However, it was found that the correct binding, with native hydrogen bonds, of the free monomer to the fibril template at both stages is crucial for fibril elongation. In other words, if the monomer is incorrectly bound (with nonnative hydrogen bonds) to the fibril template during the first “docking” stage, it can remain attached to it for a long time before it dissociates and either attempts a different binding or allows another monomer to bind. This finding is consistent with an experimentally-observed “stop-and-go” mechanism of fibril growth.

Graphical Abstract

Introduction

Alzheimer’s disease (AD), one of the largest health problems nowadays with a significant rise in the number of affected patients and cost of care,¹ is a neurodegenerative disorder whose pathology is associated with the formation and deposition of amyloid plaques and fibrils in the brain.^2,3 These plaques contain filamentous forms of a protein known as β-amyloid (Aβ) peptide, which originates by cleavage of a large and multifunctional membrane protein called amyloid precursor protein (APP). Aβ is produced by almost every cell in the body, and in the brain, at physiological concentrations, it plays a role in synaptic plasticity and memory.^4,5 However, elevated levels of Aβ and the accumulation of Aβ plaques lead to cognitive dysfunction and cell death. Despite great progress achieved in the field, the exact role of Aβ is still not well understood.⁶ Numerous therapeutic approaches (such as use of Aβ-degrading enzymes,⁷ the ultrasound technique,^8,9 mid-infrared free-electron laser technology,¹⁰ etc.) that target the production, toxicity and removal of Aβ have been developed during the past decade. Moreover, great progress has been made in the elucidation of the three-dimensional structure of amyloid fibrils.^11–16 Despite this progress and huge effort (both through in vitro and in vivo studies), there is still no remedy that can slow the progression of AD. A number of drugs available currently are effective only for a short period of time and for half of the patients with milder forms of AD.¹⁷ There are several reasons making this problem so difficult to solve,¹⁸ including non-fully-comprehended mechanisms by which small oligomers evolve into their fibrillar form and then how these fibrils grow.

Because of the inability to identify and follow the low concentration of oligomers over time experimentally, it is difficult to determine the fundamental microscopic reactions taking place during aggregation.¹⁹ Molecular dynamics (MD) simulation is the only method with which to study the details of fibril formation; however, the timescales, over which fibrils form,^20–22 limit its usefulness. Due to this limitation, most all-atom MD studies are focused on small fragments of Aβ,^23–28 missing the full complexity of the complete system. Nevertheless, these studies have provided useful insights into the process of fibril growth. Nguyen et al.²⁴ studied the elongation of Aβ_(16–22) fibrils at the all-atom level and showed that this small fragment follows a two-stage dock-lock mechanism. The complexity of the second stage, locking, was further described in two more studies from Thirumalai’s group.^25,26 These studies illustrated that, for six-residue fragments from the C-terminus of Aβ, the locking state coincides with the formation of a dry interface between monomer and fibril, and that even small peptides undergo a series of failed docking attempts before they can be natively locked into the fibril.

Due to the computational cost of simulating larger systems, fibril growth for longer Aβ fragments have mostly been studied using implicit solvent²⁹ or coarse-grained simulations,^30–32 and they have often been coupled with sampling enhancing techniques such as REMD^29,31 or umbrella sampling.³² Perhaps the most impressive work was that of Takeda and Klimov,²⁹ in which µs long all-atom simulations of the elongation of Aβ₄₀ were carried out and the complex mechanism leading to monomer deposition was revealed. However, even these simulations were not long enough to reproduce the assembly process in full. In the Takeda and Klimov simulations, as well as in other studies,^30–31 the free monomers were seen to dock onto the fibril with conformations that resembled the fibrillar one, but the hydrogen bond pattern was slightly different from the native one, suggesting that some structural rearrangement had yet to take place.

Both experimental^33,34 and theoretical^{24–26,31,32,35,36} studies have shown that the deposition of soluble Aβ onto amyloid fibrils has two distinguishable kinetic steps: A reversible step in which an Aβ monomer docks onto an amyloid template and an irreversible lock step in which the Aβ monomer fully associates with the amyloid fibril. Since Aβ monomers can easily dissociate in the first “docking” step, it is of interest to know which residues play a crucial role in docking, and if there is a way to avoid the docking of monomers onto the fibrils.

The objective of this paper is to model the entire process of Aβ fibril elongation, which would enable us to identify not only dock and lock steps of Aβ monomer, but also the details of those microscopic reactions, which take place during aggregation and very difficult to be observed by experiment.

The timescale problem in this study was surmounted by employing a physics-based coarse-grained united-residue (UNRES) force field,^37,38 which is not biased towards Aβ fibril conformation, and is able to simulate folding of multichain systems within reasonable time, starting from completely unstructured conformations and without using any information from the native structure of these systems.^31,38 Global (principal component)^39–41 and local (free-energy profiles along the amino acid sequence)^40–42 analyses were used to scrutinize the molecular dynamics of trajectories, generated with the UNRES force field, for the assembly of a free and unrestrained Aβ_(9–40) monomer onto a fibril template based on Tycko’s Aβ wild-type fibril model (Figure 1).^12,13 In particular, 120 canonical and replica-exchange molecular dynamics (REMD) simulations were carried out for ~ 35×10⁶ steps for each trajectory. The time step in MD simulations was δt = 0.05 mtu (1 mtu = 48.9 fs is the “natural” time unit of molecular dynamics,⁴³ which should be multiplied by ~ 1000, when it is compared to the experimental time, because the fast degrees of freedom are averaged⁴⁴ in UNRES), resulting in effective simulation times of approximately 85.5 µs per replica. The role of the different residues along the Aβ_(9–40) sequence in the stability of Aβ_(9–40) fibrils is also studied by canonical MD simulations at different temperatures.

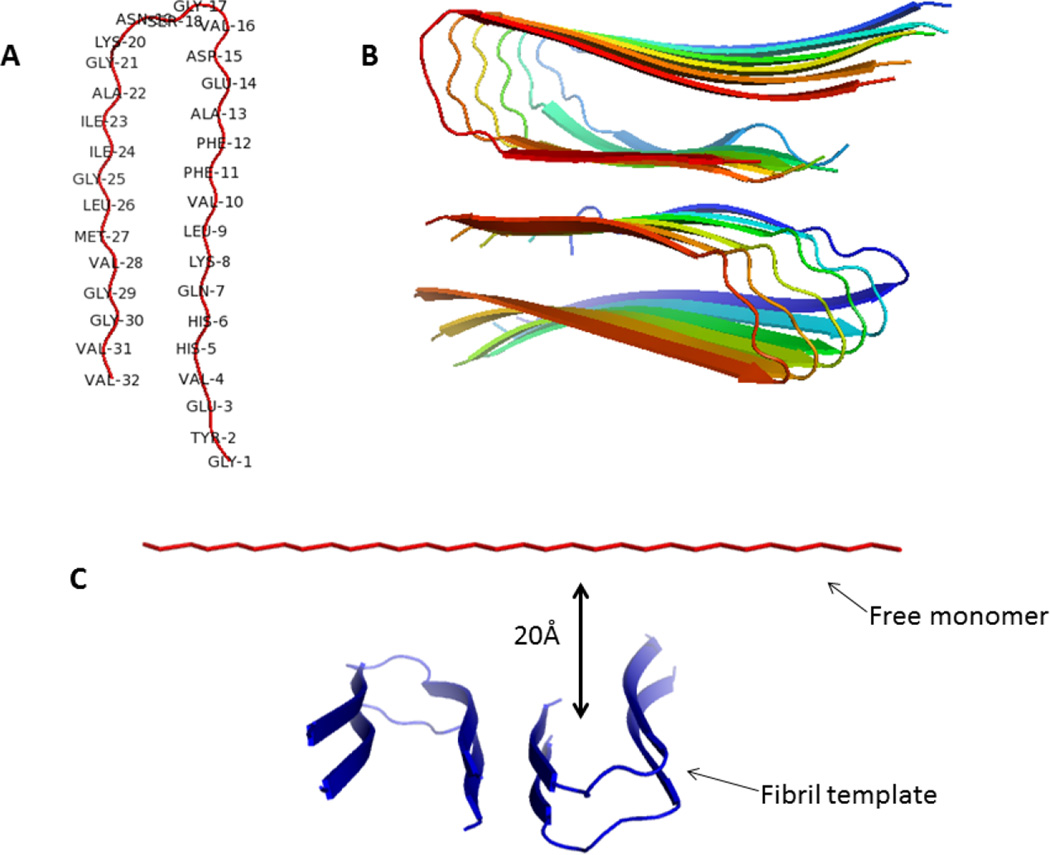
Figure 1.

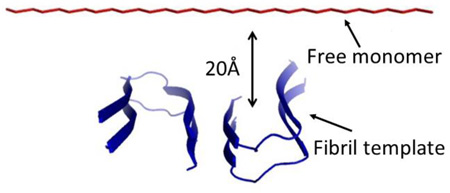
Backbone representation of an Aβ_(9–40) monomer (A) and structural model of an Aβ_(9–40) fibril with a striated-ribbon morphology (B). The Figure was produced with PYMOL, based on the coordinates provided by Tycko for the structural model of an Aβ_(1–40) (Petkova et al¹³). Residues 1–8 are omitted from the diagram because they were conformationally disordered in the NMR model.¹³ Therefore, residue numbers in this paper are shifted by 8 compared to an Aβ_(1–40) (e.g., Gly1 in this paper corresponds to Gly9 of an Aβ_(1–40), etc.). The initial conformation for the simulations of fibril elongation (C). A two-layers fibril (four chains) acts as a template for the free monomer to bind. Restraining forces are used to stabilize the chain in the template, but no restraints are applied on the free monomer, which is initially placed 20 Å away from the concave end of the template.

Results and Discussion

Monomer assembly

As in our earlier work,³¹ each REMD simulation started with the monomer in an extended conformation at a distance of 20 Å from the surface of the template. The monomer was placed facing the concave end of the fibril (see Fig. 1C). The fibril template consisted of two layers (i.e., four chains). As was shown earlier,³¹ at least 14 chains are required to retain the stable initial structure in the fibril template. Simulating a system of that size is computationally too costly; therefore, restraining forces were used to stabilize the template chains in the fibrillar conformation. In order to describe how a free monomer first docks onto an amyloid template and then locks, the hydrogen bonds (HBs) between the free monomer and the chains in the template were classified into native and nonnative hydrogen bonds (NHBs and nNHBs). NHBs are those hydrogen bonds made between peptide groups with the same indices (often referred as “in-register” HBs¹³), while all other hydrogen bonds are considered nNHBs.

An initial set of 120 REMD simulations were carried out for ~ 18×10⁶ steps, which when translated to experimental time is equivalent to ~ 44 µs per replica. Several different binding scenarios were observed during the search for the fibril conformation by a free monomer. In particular, in ~ 24% of the trajectories the monomer was bound to the template with the incorrect (anti-parallel) orientation; in ~ 27% of the trajectories the monomer was bound to the template with parallel orientation, but was shifted by ≥1 residue; in ~ 46% of the trajectories the monomer had bound to two different chains of the template at both parallel and antiparallel orientation; in ~2% of the trajectories the monomer was not bound to the template at all.

That the monomer did not bind the template with the native conformation in any of the trajectories is not surprising. Experiments of Aβ₄₀ elongation have estimated that, even at the high concentrations used in our simulations (50 mM), the fibrils would add a monomer approximately every few hundred microseconds,²² which is still longer than our simulation times. Moreover, µslong all-atom REMD simulations of Aβ_(9–40) elongation carried out by Takeda and Klimov²⁹ also failed to show complete native binding of a monomer into a fibril template. However, these simulations²⁹ did contain conformations with parallel but shifted binding of the monomer, similar to what we encountered in ~ 27% of our trajectories.

In those trajectories in which the monomer binds the template making HBs that are shifted with respect to native only by one or two residues, the total number of HBs is almost as large as in the native conformation. This makes the binding quite stable because, in order to adopt the native binding, a long β-strand has to be unzipped. Interestingly, simulations of fibril elongation with smaller, 6-residue, peptides have also reported shifted binding, but these shifted conformations were identified as an intermediate preceding native binding.^27,28 Therefore, it is possible that the shifted conformations seen in our simulations, and in those of Takeda and Klimov,²⁹ are an intermediate along the pathway of Aβ₄₀ fibril elongation.

Even if the shifted conformations were an intermediate, extending the simulation time might not be sufficient to see the transition because many HBs have to be broken and rearranged. To increase the chances of this happening, one of the conformations with shifted binding was selected to be used for further investigation. This conformation had NHBs along the C-terminal β-strand, but the HBs along the N-terminal β-strand were shifted by one. Final conformations matching this description were seen in 13% of the trajectories. The selected conformation was used as the initial state for another set of 17×10⁶ steps long REMD simulations. One of the trajectories resulting from the combination of the first and second set of simulations is the object of scrutiny in the present work. Combining the first and second interval of simulations, this trajectory was ~ 35×10⁶ steps long, which is approximately equivalent to 85.5 µs.

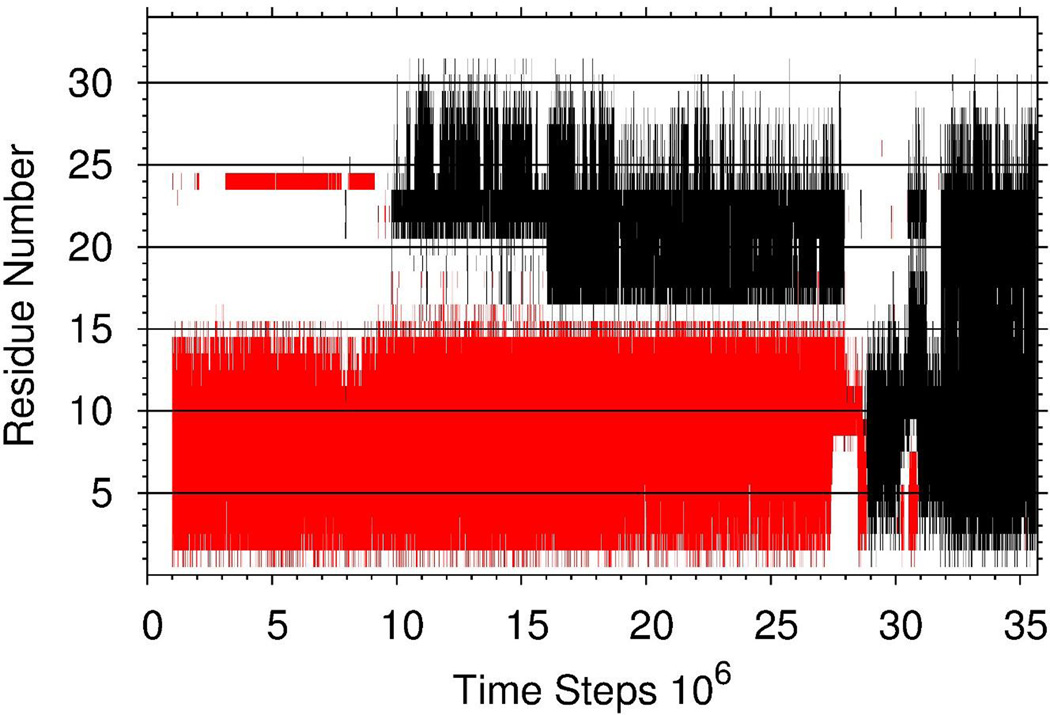
For the aforementioned trajectory, Figure 2 illustrates how the free monomer binds to the fibril template and locks itself into the fibril making NHBs along both β-strands (black lines correspond to NHBs and red lines correspond to nNHBs). In particular, the first β-strand of the free monomer binds nonnatively to one of the chains in the template from the beginning of the trajectory (docking step). At ~1×10⁷ time step the second β-strand of the free monomer starts to make NHBs with the same chain in the template, and then at ~1.6×10⁷ time step, the loop connecting the first and second β-strands (except for residue Val16) joins the second β-strand in the native binding (locking step). Although both native and nonnative bindings last quite long (until ~2.8 – 2.9×10⁷ time steps), the free monomer completely unbinds from the template, and right after that, almost instantly, residues Leu9, Val10, Phe11, and Phe12 of the first β-strand of the free monomer bind natively to that same chain in the template (docking step) followed by the rest of the monomer (locking step). Moreover, these residues remain natively bound to the template throughout the time interval of 3.03 – 3.1×10⁷, during which the rest of the first β-strand is unbound.

Figure 2.

The native hydrogen bonds (black), and the nonnative hydrogen bonds (red) between the free monomer and the fibril template formed during the entire trajectory.

Thus, these results indicate that the native binding of residues Leu9, Val10, Phe11, and Phe12 to the fibril template plays a crucial role in aggregation of the free monomer.

Describing Aβ peptide aggregation by a free-energy landscape

In order to describe, in details, the pathway along which the free monomer binds to the fibril template and successfully propagates the fibrillar conformation, we built the free-energy landscape (FEL) along the principal components. The energy landscape language, which has emerged for experimentalists and theorists to describe how proteins fold and function,^45,46 can also be used successfully for the description of Aβ-peptide aggregation. It is impossible to present an FEL as a function of all degrees of freedom of a protein. Consequently, it is very important to find the coordinates along which the intrinsic pathways of aggregation can be viewed. To this end, principal components, obtained from a covariance-matrix-based mathematical technique, called principal component analysis (PCA),⁴⁷ are good alternatives. Here, instead of traditional Cartesian PCA, we employ internal-coordinate PCA^41,48,49 based on UNRES backbone coordinates (θ,γ) (see Fig. S1), because, as was shown earlier,^39,49–51 FELs of small systems constructed by traditional Cartesian PCA can contain artifacts arising from strong mixing of overall and internal motions.

Internal-coordinate PCA decomposes the structural mean-square-fluctuations (MSF) of the angles θ and γ into collective (principal) modes. These modes have “frequencies” and directions corresponding to the eigenvalues and eigenvectors of the PCA covariance matrix. The projection of the trajectory on the eigenvector is named the principal component. The modes with the largest eigenvalues λ_k (named slow modes) contribute the most to the structural fluctuations of the protein. The contribution of the i^th angles θ and γ to a mode k is the so-called influence ${\nu }_i^k$, and the $MS{F}_i={\mathrm{\Sigma }}_k{\lambda }_k{\nu }_i^k$.

Figure 3 illustrates the FEL along the first two PCs at 300K with representative structures, in which two major basins are identified. Each basin contains several minima. The representative structures of minima clearly show the aggregation pathway of the free monomer, which is in agreement with the results illustrated in Figure 2. In particular, most of the conformations (except minimum 3), in which the free monomer (rainbow chain) is partially and nonnatively (the first β-strand is shifted by one residue from the corresponding residues of the chain in the template) bound to the fibril template, are found in the left basin; and the conformations, in which both β-strands of the free monomer are bound (nonnatively and natively) to the template, are found in the right basin.

Figure 3.

Free-energy landscape (in kcal/mol) along the first two PCs with representative structures at the minima for the free monomer aggregation trajectory.

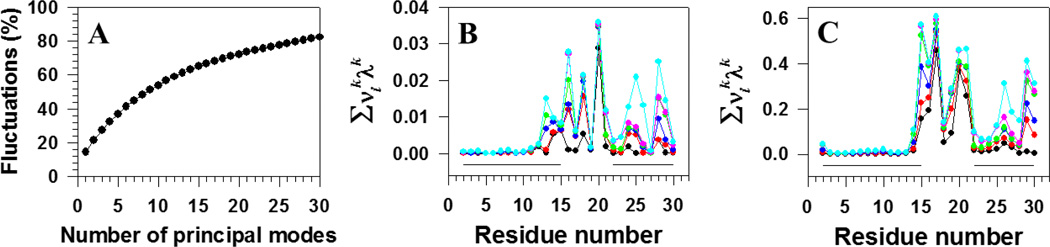
We have shown previously that the FEL constructed along PCs can describe the folding dynamics correctly if these PCs can capture at least 40% of the total fluctuations.⁴⁹ It appears that here ~ 40% of the total fluctuations can be captured by the first six principal modes (Fig. 4A); therefore, we also examined the trajectory in higher-dimensional (3D, 4D, 5D and 6D) PC spaces (one of them, 3D FEL, is illustrated in Fig. S2); however, we could not find any new major basins (Fig. S2C clearly demonstrates this). An additional check for whether the trajectory has sampled an FEL sufficiently for convergence was done by calculating the cosine contents of the first two PCs. The values of the cosine content for both PCs were less than 0.5 (0.42 for PC₁ and 0.26 for PC₂)^48,51 indicating convergence of sampling. Thus, 2D FEL is sufficient for this trajectory. We also computed the contributions of the first (black), first two (red), first three (blue), first four (green), first five (pink), and first six (cyan) principal modes to the MSFs along the angles θ (Fig. 4B) and γ (Fig. 4C). The main contributions to the fluctuations in this trajectory come from the loop and the second β-strand, and partially from the first β-strand edge, which indicates that the main players in the binding of the free monomer to the template are residues along the first β-strand.

Figure 4.

Percentages of the total fluctuations captured by principal modes (panel A), and contributions of the principal modes $({\nu }_i^k{\lambda }^k)$ [black $({\nu }_i^k{\lambda }^1)$, red $({\sum }_{k=1}^2{\nu }_i^k{\lambda }^k)$, blue $({\sum }_{k=1}^3{\nu }_i^k{\lambda }^k)$, green $({\sum }_{k=1}^4{\nu }_i^k{\lambda }^k)$, pink $({\sum }_{k=1}^5{\nu }_i^k{\lambda }^k)$, and cyan $({\sum }_{k=1}^6{\nu }_i^k{\lambda }^k)$ lines with filled circles] to the MSFs along the θ (panel B) and γ (panel C) angles for the free monomer aggregation trajectory. The solid black lines on the bottoms of panels B and C correspond to the β-strand regions.

Free-energy profiles along θ_i and γ_i angles of Aβ peptide aggregation trajectory

As was demonstrated earlier,^40–42 free-energy profiles (FEPs) are very helpful to identify the key residues in the folding process; therefore, we employ here FEPs along the θ_i and γ_i angles to identify the key residues in Aβ peptide fibril elongation. The analysis of the FEPs of the entire trajectory does not provide information about the way in which each residue explores its own FEP in the course of time; therefore, we have computed FEPs along the θ_i and γ_i angles (Fig. 5) over the entire trajectory (black lines) and over ~ 29×10⁶ time steps, i.e. before the first β-strand starts to natively bind to the fibril template (red lines).

Figure 5.

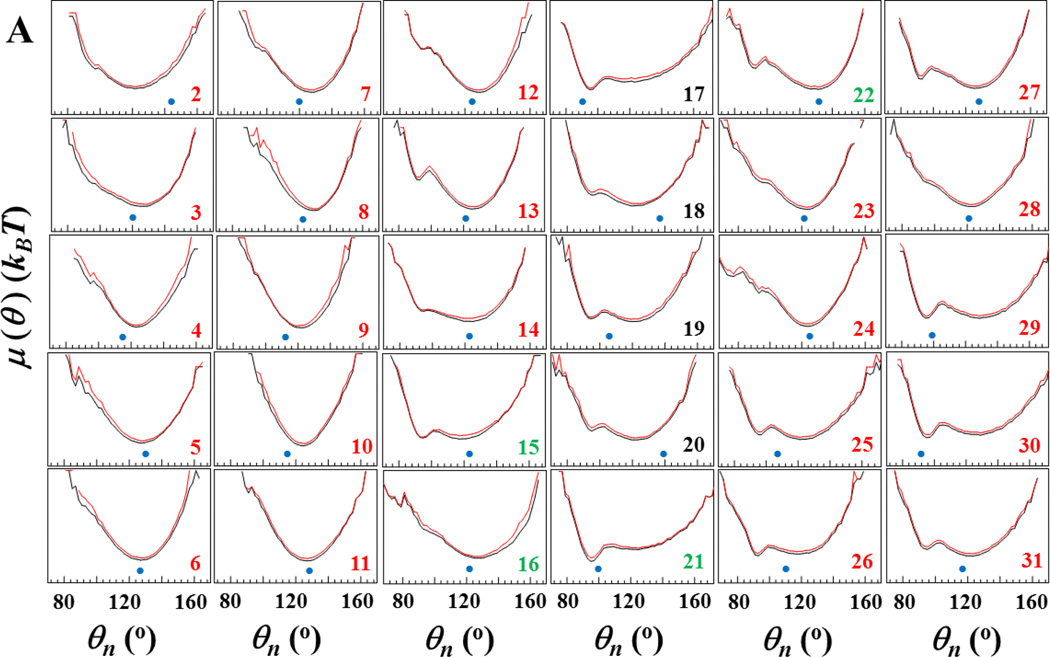
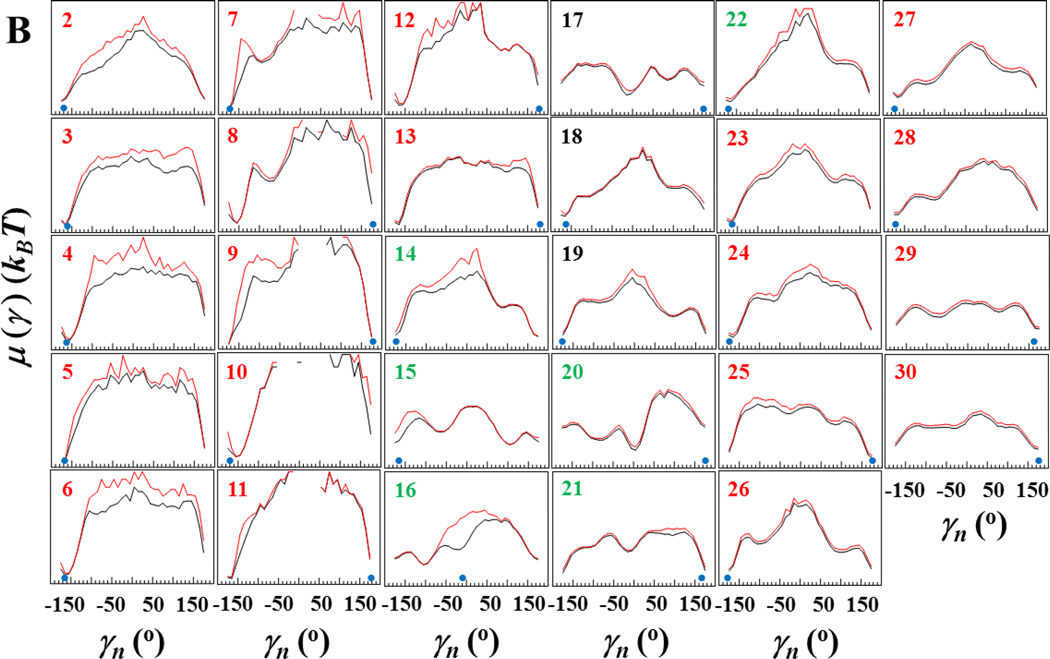
Free-energy profiles (FEPs), μ(θ) and μ(γ), along the θ and γ angles (panels A and B, respectively) for the free monomer aggregation trajectory. Black curves correspond to FEPs computed over the entire trajectory, red curves correspond to FEPs computed over ~29×10⁶ time steps (i.e. before the native hydrogen bonds of the first β-strand start forming). The black numbers pertain to FEPs along the θ and γ angles which include only residues of the loop; the red numbers pertain to FEPs along the θ and γ angles which include only residues of β-strands; the green numbers pertain to FEPs along θ and γ angles which include the residues from both loop and β-strands. The NMR-derived structural data are computed from the coordinates provided by Tycko for the structural model of an Aβ_(1–40) (Petkova et al¹³) (blue circles at the bottom of each panel).

Two main (representative) shapes in the FEPs computed over the entire folding trajectory (black lines in Fig. 5A) can easily be distinguished along the sequence of the θ_i angles. The first shape, with one broad, deep minimum at ~ 120° – 130°, represents FEPs of most of the first β-strand residues (FEPs along θ_i, i = 2 – 12, 14) and FEPs of some of the second β-strand residues (FEPs along θ_i, i = 23, 24, 28); the second shape, with broad and narrow, deep minima at ~120° – 130° and ~90°, respectively, represents FEPs of loop residues (FEPs along θ_i, i = 17 – 20) and FEPs of most of the second β-strand residues (FEPs along θ_i, i = 25 – 27, 29 – 31); the shapes of FEPs along the θ_i angles, which include residues from both loop and β-strands (FEPs with green numbers) resemble either the first shape (FEPs along θ_i, i = 16), or the second shape (FEPs along θ_i, i = 15, 21); FEPs along θ_i, i = 13, 22 exhibit “transition” shape between these two shapes; i.e., a broad, deep minimum at ~120° –130° and a narrow, shallow local minimum at ~90°. These results indicate that the second β-strand is not as conformationally stable as the first β-strand. Moreover, FEPs along the θ angles of the full trajectory (black lines) and the first 29×10⁶ time-steps-interval (red lines) do not reveal any noticeable differences, which indicates that the θ angles do not detect the differences between natively and non-natively (shifted by one residue) bound monomer to the fibril template.

Unlike the FEPs along the θ_i angles, shown in Fig. 5A, the shapes of the FEPs along the γ_i angles of the full trajectory (black lines in Fig. 5B) are diverse. However, most of the FEPs along the γ_i angles exhibit one deep minimum at ~180° along with a few shallow minima in different regions of FEPs. The second β-strand and loop are very flexible and explore the entire range of γ_i angles, which is manifested in an absence of regions in which the FEPs are undefined. The first β-strand is less flexible, which is manifested by some regions of γ angles in which the FEPs are either undefined (γ_i, i = 9 – 11) or the γ angles spend very short time (γ_i, i = 5 – 8). Moreover, there are noticeable differences between the FEPs of the entire trajectory (black lines in Fig. 5B) and those of the first 29×10⁶ time-steps-interval (red lines in Fig. 5B) along the γ₇, γ₈, γ₉, γ₁₀ and γ₁₆ angles. After native binding of the first β-strand to the template, these angles exhibit different behavior. In particular, angles γ₇, γ₈, γ₉, γ₁₀ explore new regions of the conformational space, and angle γ₁₆ forms a new minimum. Since the new regions explored by γ₇, γ₈, γ₉, γ₁₀ angles are far from the global minima, and the time spent in these regions by each angle is very short, exploration of the new regions is an indication of “reorganization process” in binding: from nonnative to native. A formation of new minimum by γ₁₆ angle, which coincide with the experimental global minimum, indicates the formation of native binding of Val16, which was missing during the first 29×10⁶ time-steps-interval (Fig. 2). These results indicate that except for these γ angles and corresponding residues to these angles the behavior of θ and γ angles is similar no matter how the monomer is bound to the fibril template, natively or nonnatively.

We also examined the local dynamics of each residue and the global dynamics of the entire system for three trajectories with different binding scenarios selected from the initial set (18×10⁶ time steps). In the first trajectory the free monomer binds to one of the chains of the fibril template completely, but it is shifted by one residue (Fig. S3A); in the second trajectory the free monomer binds to two different chains of the fibril template at both parallel and antiparallel orientation (Fig. S3B); in the third trajectory the free monomer does not bind to the fibril template at all (Fig. S3C). This local and global analysis enabled us to determine how different the behavior of each angle (and corresponding residues) is in the trajectories with completely different binding scenarios. Based on the FEPs along the θ_i angles (Figure S4A), the main differences are revealed in the N-terminal β-strand and loop regions. Interestingly, there is no difference in the behavior of θ angles in the C-terminal region. As was expected, the shapes of the FEPs along the γ_i angles (Figure S4B) are more diverse, and the differences can be seen all over the chain except for the C-terminal region.

Thermal unbinding (unfolding) of Aβ peptide from the fibril template

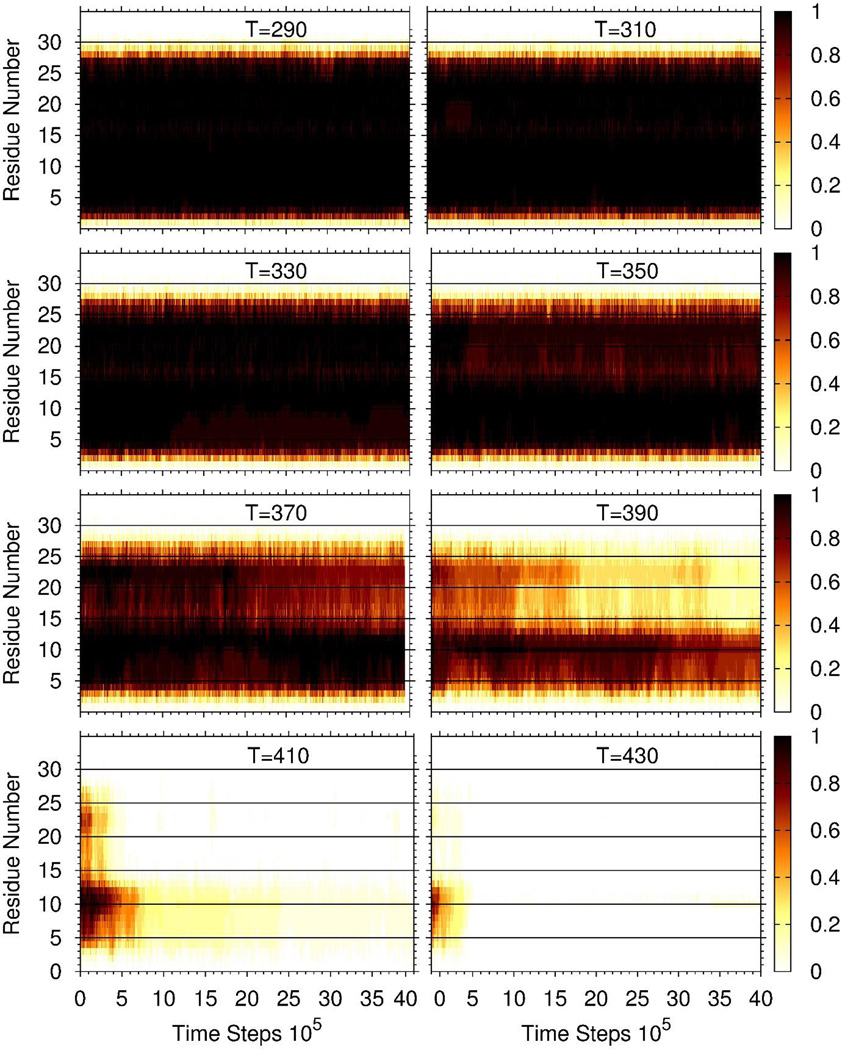
Another study toward elucidation of the residues playing a crucial role in the stability of Aβ fibrils was carried out. In particular, we selected, as an initial structure, the same template with four chains plus the free monomer natively bound to the fibril template, and examined the thermal unbinding (unfolding) of the free monomer from the template. We carried out 16 MD trajectories at 4 × 10⁶ time-step-intervals at eight different temperatures from 290K to 430K. As in the binding simulations, the four chains in the template were restrained to the fibrillar conformation, and the monomer was allowed to move freely. The values on the right side of panels and corresponding colors in Figure 6 indicate the probabilities of the native hydrogen bonds between the residues in the free monomer and the corresponding residues in the template to remain formed at any time along the entire trajectories. As it can be seen, the hydrogen bonds are very stable up to 370K for most of the residues, and they start breaking at 390K. The most stable hydrogen bonds remained formed, albeit for a short time, at the highest temperature of 430K. Those are the hydrogen bonds formed by residues Lys8, Leu9, Val10, Phe11, and Phe12.

Figure 6.

Thermal unfolding of the free monomer from the fibril template. The values on the right side of panels and corresponding colors indicate the probabilities that the native hydrogen bonds between the residues in the free monomer and the corresponding residues in one of the chains of the template remained formed over the entire trajectories. The probability at any time was calculated by counting the fraction of trajectories (over 16 trajectories) in which a particular hydrogen bond was still formed at that specific time.

By analyzing the MD trajectories of the Aβ_(9–40) oligomer, generated with the coarse-grained UNRES force field, in terms of the local motions of each residue and PCA, and by examining the thermal unfolding of the Aβ_(9–40) free monomer, we have studied amyloid fibril elongation.

Adopting strict criteria for classification of the native and nonnative hydrogen bonds, we were able to identify a pathway for fibril elongation, which might be consistent with an experimentally-observed “stop-and-go” type mechanism.^20,22,52 The point is that in many trajectories we observed the free monomer binding the fibril template in an ”almost-in-register” conformation; i.e., the monomer makes in-register (native) hydrogen bonds along the C-terminal β-strand, but the hydrogen bonds are shifted by one residue along the N-terminal β-strand. There is no experimental evidence for such an “almost in-register” structure in fibrils, since experimentalists know very little about the molecular structures at the ends of fibrils. Only bulk structures can be identified by experiments (private communications with Dr. Tycko). It is logical, although not proven experimentally, that peptide molecules may bind to the ends of fibrils in a somewhat disordered or imperfectly aligned manner, or in a mixture of parallel and antiparallel alignments (all these cases were observed in our trajectories), consequence of which might be the “stop-and-go” mechanism observed in amyloid fibrils grow experimens.^20,22,52 These experiments^20,22,52 suggest that incorrect intermolecular structures at the ends of fibrils can be rather stable and persist for long periods of time (seconds time-scale) before these incorrect structures dissociate or anneal. Most of our simulations agree with this finding in microsecond time range. Unfortunately, current computational power does not allow us to simulate, with the MD technique, events that occur beyond the microsecond time-scale. However, truncation of the N-terminus (residues 1–8 were not resolved in the NMR¹³ structure, and therefore were also excluded from the simulations) and the use of the REMD technique in this study could have significantly speeded up the dissociation process, and made it possible for the simulations to show an event that normally happens on the time-scale of seconds. Only in one trajectory, an incorrectly bound free monomer dissociated from the fibril template and then correctly folded within the microsecond time-scale, which was the object of scrutiny in this study. It also should be noted that we carried out the same thermal unfolding on an incorrect intermolecular structure (in which the free monomer was bound to the template with the hydrogen bonds shifted by one residue) as we did for the correctly bound monomer (Fig. 6) to test the stability of incorrect intermolecular structure. The result showed that the incorrect binding of the free monomer to the template is almost as stable as correct binding (not shown) within 4×10⁶ time-step-intervals.

The results obtained here from different approaches suggest that Lys8, Leu9, Val10, Phe11, Phe12 (KLVFF) portion of the N-terminal β-strand plays a crucial role in aggregation. These findings are very important for the prevention of fibril formation. In other words, if experimentalists can find a way to break the KLVFF hydrophobic core or cleave this part of the monomer, then there is a big probability to avoid amyloid fibril growth. It is also important to mention that the findings in the presented work are in agreement with earlier experimental^{20,22,33,34,52,53} and computational studies,^{23–26,30,32,35,36} which indicates that the UNRES force field can correctly determine the mechanism and crucial sites for amyloid fibril formation, and makes UNRES a powerful tool to study amyloid diseases.

Methods

MD and REMD simulations

Force field

Simulations were carried out using the UNRES force field.^31,37,38 Details of the force field and its MD implementation can be found in refs. 37, 54–57 and 38, 43, 44, respectively. In the UNRES model (Figure S1) a polypeptide chain is represented as a sequence of virtual peptide groups (p's) connecting C^α-carbons atoms. United side chains (SC's) are represented by ellipsoids attached to the C^α atoms. Only SC's and p's are interaction sites. The UNRES energy function contains terms accounting for site-site as well as multibody interactions. The effect of the solvent is implicitly included in SC-SC interaction energy.^37,56 The force field is not biased towards amyloid formation, but it has been optimized to reproduce the structure and thermodynamics of small proteins.^54–57 Here, a version of the force field parameterized with the formin-binding WW domain (PDB ID: 1E0L) is used.⁵⁵

Simulation of an Aβ fibrils

Aβ_(9–40) fibrils were simulated based on the model by Tycko's group.¹³ Our previous work³¹ showed that at least 7 layers (14 chains) are needed to obtain a stable fibril with this model. However, MD simulations with such a large number of chains would result in extremely long computation times and, therefore, would be intractable. Instead, we simulated a fibril by building a two-layers (i.e., 4-chains) template. As in our previous work,³¹ to give this template the stability of a real fibril, distance restraints were applied to the virtual peptide groups of the chains in the template. The system was forced to remain inside a sphere, the size of which resulted in a concentration of 50 mM.

Fibril elongation

For simulations of fibril elongation, an Aβ_(9–40) monomer was placed, in the extended conformation, at a distance of 20 Å away from one of the edges of the template (Fig. 1C). Because our earlier simulations with this same system³¹ showed that placing the monomer closer to one edge does not prevent it from binding on the opposite edge, all trajectories were started from the same initial conformation, with the monomer closer to the concave edge of the template. Simulations were carried out using replica exchange molecular dynamics. A total of 120 trajectories were simulated with temperatures ranging from 280 to 350 K. Each trajectory was 18×10⁶ steps (9×10⁵ mtu ≈ 44 µs) long. Temperature exchanges were attempted every 20,000 steps, and the temperature was held constant between exchanges with the Berendsen thermostat.⁵⁸ This choice of parameters resulted in exchange acceptance rates of 30% or higher. The last conformation of one of the trajectories was chosen as the initial state of another set of REMD simulations. This conformation had the largest number of NHBs, and thus we wanted to study it in more detail. Starting from the chosen conformation, 120 replicas were simulated with temperatures ranging from 280 to 390 K. Each of the 120 trajectories were 17×10⁶ steps (8.5×10⁵ mtu ≈ 41.5 µs) long.

Thermal unfolding

For simulations of thermal unfolding, canonical MD simulations were carried out at 8 different temperatures between 290 and 430 K (Fig. 6). For each temperature, 16 independent trajectories where carried out. For all trajectories, the initial conformation was a two-layers Aβ_(9–40) template with a natively bound monomer (obtained from the simulations of fibril elongation). As in the simulations of fibril elongation, the template was restrained but the monomer was not. The temperature was held constant using the Berendsen thermostat. All trajectories were 4×10⁶ steps long (2×10⁵ mtu ≈ 10 µs).