Computational modeling reveals how interplay between components of a GTPase-cycle module regulates signal transduction

Abstract

Heterotrimeric G protein signaling is regulated by signaling modules composed of heterotrimeric G proteins, active G protein-coupled receptors (Rs), which activate G proteins, and GTPase-activating proteins (GAPs), which deactivate G proteins. We term these modules GTPase-cycle modules. The local concentrations of these proteins are spatially regulated between plasma membrane microdomains and between the plasma membrane and cytosol, but no data or models are available that quantitatively explain the effect of such regulation on signaling. We present a computational model of the GTPase-cycle module that predicts that the interplay of local G protein, R, and GAP concentrations gives rise to 16 distinct signaling regimes and numerous intermediate signaling phenomena. The regimes suggest alternative modes of the GTPase-cycle module that occur based on defined local concentrations of the component proteins. In one mode, signaling occurs while G protein and receptor are unclustered and GAP eliminates signaling; in another, G protein and receptor are clustered and GAP can rapidly modulate signaling but does not eliminate it. Experimental data from multiple GTPase-cycle modules is interpreted in light of these predictions. The latter mode explains previously paradoxical data in which GAP does not alter maximal current amplitude of G protein-activated ion channels, but hastens signaling. The predictions indicate how variations in local concentrations of the component proteins create GTPase-cycle modules with distinctive phenotypes. They provide a quantitative framework for investigating how regulation of local concentrations of components of the GTPase-cycle module affects signaling.

The timing and amplitude of signaling in cellular signaling networks depends on the local concentrations and kinetics of component proteins. The complexity of these networks has precluded comprehensive quantitative analysis of signaling. However, the networks can be divided into discrete signaling modules that can be quantitatively modeled and analyzed independently (1–5). Later, such models of modules can be experimentally verified and then reconnected to build larger signaling networks.

G protein-mediated signaling networks (6) are ideal for such quantitative analysis. A key signaling module in these networks is the GTPase-cycle module, which controls signaling by regulating G protein activity. This module consists of a heterotrimeric G protein, a guanine nucleotide exchange factor (GEF) such as agonist-bound and active G protein-coupled receptor, a GTPase-activating protein (GAP) such as regulator of G protein signaling (RGS) protein or phospholipase C-β, GTP, GDP, and P_i. The extent of G protein activation reflects the balance between the rates of GDP/GTP exchange, which activates the G protein, and GTP hydrolysis, which deactivates it (7–9). GEFs facilitate GDP/GTP exchange (9), and GAPs accelerate GTP hydrolysis (10, 11). Additional roles of GEFs (12) and GAPs (10, 11, 13, 14) are not included in this module. At present, we lack quantitative understanding of how local concentrations and kinetics of G proteins, receptors, and GAPs regulate G protein activity in cells.

Local concentrations of G proteins, receptors, and GAPs are spatially regulated by movement between membrane microdomains (15–19), translocation of G proteins and GAPs between the plasma membrane and cytosol (14, 20), desensitization and internalization of receptors (12, 21), and perhaps by receptor oligomerization (22). For example, β2-adrenergic receptors leave caveolin-rich membrane fractions upon agonist stimulation (18, 19), and the δ-opioid receptor, Gαi3, and the RGS protein GAIP are concentrated at the neck of clathrin-coated pits (17). No quantitative data are available on the local concentration of receptors, G proteins or GAPs.

Furthermore, it is unclear how receptors and GAPs coordinately regulate the amplitude and timing of G protein activity. GAPs are expected to decrease amplitude and hasten G protein deactivation upon removal of active receptor. However, RGS proteins do not affect the amplitude of G protein-induced changes in K⁺ channel current, but do accelerate the timing of both current onset upon agonist addition and current desensitization upon agonist removal (23–26).

To address the aforementioned issues, we developed a computational model of the kinetics of the GTPase-cycle module. The model is distinct from previous models (27–33) in that (i) it includes GAP, which many previous models have excluded; (ii) it is based on a general mechanism that allows several modes of coupling of G proteins with active receptors and GAPs, including a ternary complex of receptor, G protein, and GAP; and (iii) it is based on data pertaining to a single mammalian GTPase cycle module; i.e., the m1 muscarinic acetylcholine receptor (m1 MAchR), Gq, and RGS4 (34–37). The predictions of the model elucidate how changes in concentrations of molecules can result in a variety of G protein signaling properties, both in terms of dynamics as well as steady-state behavior, and how these properties are governed by the kinetics of the GTPase-cycle module.

Methods

Our model contains three parts: (i) a biochemical reaction scheme of the GTPase-cycle module (Fig. 1), (ii) the mathematical formulation of the scheme, and (iii) the computational implementation of the mathematical equations.

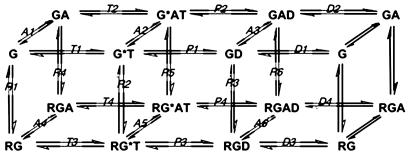
Fig. 1.

Biochemical reaction scheme of the GTPase cycle. The GTPase reaction is described as GTP (T) binding to G protein (G) to form the Michaelis complex G*T, followed by hydrolysis of bound GTP to form the G protein–GDP complex (GD) and subsequent dissociation of GDP (D). Each G species can bind agonist-bound receptor (R), GAP (A), or both at each stage of the GTPase reaction. All reactions are reversible. The asterisk denotes activation of G protein by GTP. Free GTP, GDP, and P_i are not shown in the reaction scheme for simplicity. Reaction rates are listed in Table 1.

Biochemical Reaction Scheme. We devised a reaction scheme based on experimental data that is depicted in Fig. 1. The scheme includes the following simplifications: (i) two multistep reactions, GTP binding and G protein activation, and (ii) GTP hydrolysis, P_i dissociation, and G protein deactivation (38) are considered single-step reactions; all receptors are considered active. Increasing concentration of the active G protein-coupled receptor (R) mimics increasing fractional binding of agonist by a fixed cellular concentration of receptor; Gβγ subunits, which modulate interaction of Gα with nucleotides, receptors, and GAPs, are not included.

Mathematical Formulation. The biochemical reaction scheme was mathematically formulated in accordance with mass action kinetics as 17 ordinary differential equations, one for each chemical species, with 48 reaction-rate parameters. For example, the equation for d[G]/dt is

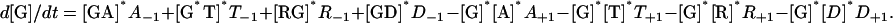Rate constants such as A₊₁ are for association and A_–1 are for dissociation; they correspond to the reaction labeled A1 in Fig. 1. Reaction rates are given in Table 1. All equations are available from us. The equations were solved simultaneously at each time step of a simulation to track changes in the concentration of each chemical species over time.

Table 1.

Reaction-rate parameters (labeled per Fig. 1)

Reaction	Kd, nM	k+, M-1·s-1	k-, s-1
A1	911	8.78 × 106	8.00
A2	106	3.86 × 105	0.0408
A3	1.48 × 104	6.41 × 104	0.950
A4	77.0	7.43 × 104	0.00572
A5	75.8	6.30 × 106	0.478
A6	5.28 × 104	1.30 × 104	0.685
R1	0.0282	6.36 × 108	0.0179
R2	9.74	1.32 × 108	1.28
R3	0.0239	9.47 × 107	0.00227
R4	0.00238	2.28 × 107	0.0000543
R5	6.99	6.20 × 106	0.0433
R6	0.0853	4.94 × 107	0.00421
T1	0.0158	5.29 × 105	8.38 × 10-6
T2	0.00184	4.47 × 104	8.32 × 10-8
T3	5.48	8.53 × 105	0.00468
T4	5.40	1.62 × 106	0.00875
P1	3.34 × 109	9.03 × 10-7	0.0130
P2	2.38 × 107	0.244	25.0
P3	1.36 × 1012	2.22 × 10-9	0.0130
P4	1.95 × 109	0.00297	25.0
D1	1,600	62.3	0.000100
D2	2.61 × 104	3.83	0.000100
D3	1,360	1.47 × 106	2.00
D4	9.35 × 105	2,940	2.75

k₊, association rates; k_-, dissociation rates.

Computational Implementation. Reaction-rate parameters. Parameters used in the equations were based on data from an experimental system in which purified m1 MAchR, Gq, and RGS4 were reconstituted into large, unilamellar phospholipid vesicles (34–37). Direct measurements were not available for several parameters. These measurements were constrained between upper and lower bounds evident from experimental data and either optimized (39) to fit other experimental data or calculated to satisfy constraints of the second law of thermodynamics. Details of the parameters are available in Tables 3 and 4, Figs. 6 and 7, and Supporting Text, which are published as supporting information on the PNAS web site.

Software. The equations were programmed and solved by using gepasi 3.30 (40) and matlab (Mathworks, Natick, MA) software. Output of computation. The computational model output is the concentration of all chemical species at any time or steady state. From these data, we calculated Z, the fractional activity of G proteins, and v, the GTP hydrolytic rate:

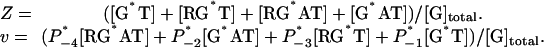Simulation of vesicle experiments. The concentrations of molecules derived from the vesicle experiments were used in the computer simulation of these experiments, unless otherwise noted; details of this conversion can be found in Supporting Text. Measurements of steady-state GTPase rate and G protein fractional activity from vesicle experiments were simulated by using the steady-state values of the functions v and Z. K_m (GTP), EC₅₀ (GAP), and EC₅₀ (R) were derived from plots of steady-state Z and v versus the initial concentration of GTP, GAP, or R, respectively. In gepasi simulations, steady state occurred when the concentration of each chemical species changed by <10^–18 M/s; in matlab simulations, it was assumed at 1,000 s.

Computational characterization of the GTPase cycle. We simulated the effect of large variations in R, G protein, GAP, GTP, GDP, and P_i concentrations on Z and v. In many simulations, average cellular concentrations of GTP (468 μM), GDP (149 μM), and P_i (4.4 mM) were used (41).

Results and Discussion

Parameters of the Model. Our model contains 48 reaction-rate parameters (Table 1). Several were not directly measured but were rigorously optimized or calculated within constraints of all available data, as described in Methods. That procedure resulted in 16 similar parameter sets that fit the available data (Comparison of these parameter sets can be seen in Supporting Text). These in essence represent 16 competing versions of the computational model. Predictions made by these parameter sets were similar, and in the remainder of this paper figures and discussion are based on the parameter set (Table 1) that best fits all available experimental data.

Validation of the Model Against Vesicle Experiments. Simulations agreed well with data from the m1 MAchR-Gq-RGS4 vesicle system, reproducing steady-state GTPase rates that span 4 orders of magnitude, as well as K_m (GTP) and EC₅₀ (GAP) (Fig. 2). Simulations also agreed with fractional activity of Gq in the presence of carbamoylcholine-stimulated m1 MAchR with and without GAP (i.e., 0.62 and 0.12, respectively, in ref. 28; 0.53 and 0.12, respectively, in our simulations. Details of this simulation can be found in Supporting Text). Additionally, simulations fit an important experimental result that was not used in the optimization, namely that GAP increases EC₅₀ (agonist) (Fig. 8, which is published as supporting information on the PNAS web site; additional details can be found in Supporting Text). Furthermore, the K_d values of the reaction scheme reproduced the known free energy of GTP hydrolysis (42) and maintained material equilibrium in accordance with the second law of thermodynamics. Finally, we verified that the simulations reached the same steady state from any initial conditions with identical total R, G, GAP, GTP, GDP, and P_i concentrations (unpublished data). The model agrees well with diverse experimental data, and, in the next sections, we describe its predictions.

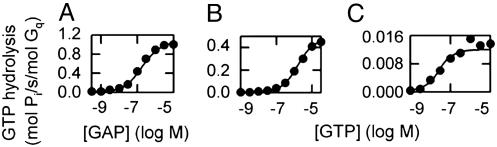
Fig. 2.

Comparison of steady-state GTPase activities derived from simulations with those from vesicle experiments. Simulations of the best parameter set are shown by lines and experimental data (35) by circles. Notably, some data in A and B that were measured under the same experimental conditions differ in GTPase rate, an error probably due to variability of protein distributions in the membrane preparations and/or variability in the proportion of G proteins that coupled to R in the membrane preparations. To compensate, we allowed the concentration of receptor used in simulations (R_sim) to vary slightly from that used in vesicle experiments (R_exp). (A) Dependence on GAP concentration in the presence of 10 μM GTP; R_exp = 3 nM and R_sim = 5.4 nM. (B) Dependence on GTP concentration in the presence of 4 μM GAP (simulation and experiment; R_exp = 3 nM and R_sim = 2.2 nM. (C) Dependence on GTP concentration in the absence of a GAP; R_exp = 3 nM and R_sim = 3 nM. In experiments and simulations, [G] = 10 nM. In experiments, 1 mM (saturating) carbamoylcholine agonist was used.

Variations in Active Receptor and GAP Concentrations Lead to Diverse Signaling Behavior, Bounded by Four Limiting Signaling Regimes (LSRs). Cells spatially regulate the concentrations of components of the GTPase-cycle module to regulate G protein activity, but little is known about how specific changes in these concentrations affect G protein activity. We used the model to examine the effect of changes in R and GAP concentrations on G protein activity. The simulations show that variations in R and GAP concentrations lead to a wide range of steady-state Z and v (Fig. 3). There are four signaling regimes that are stable to changes in R and GAP concentrations (plateaus in Fig. 3) that we term LSRs. The LSRs represent the physiological cases of G protein activity in the: (i) absence of R and GAP (G), (ii) presence of saturating R but absence of GAP (RG), (iii) presence of saturating R and GAP (RGA), and (iv) presence of saturating GAP but absence of R (GA), respectively. Along the transitions between the LSRs, a large variety of G protein signaling behavior occurs. Overall, the four LSRs and transitions between them provide a quantitative framework for understanding how local R and GAP concentrations affect G protein activity.

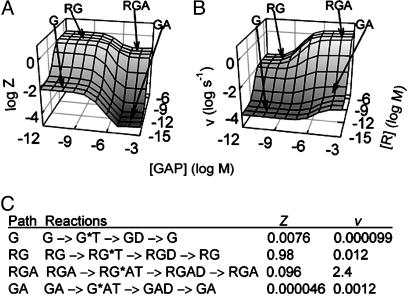
Fig. 3.

The concentrations of active receptor (R) and GAP determine steady-state fractional G protein activation and GTPase activity. Three-dimensional logarithmic plots show the output of simulations of Z (A) and v (B) at various concentrations of R and GAP, with 10 nM G protein and cellular concentrations of GTP, GDP, and P_i. The labeled plateaus (G, RG, RGA, and GA) show the four LSRs of the GTPase cycle and indicate the proteins contributing to regulation of G protein activity in each limit. Among the LSRs, a large range of intermediate signaling behavior occurs, and to transition between LSRs changes in R or GAP concentration of ≈50- to 1,000-fold are required. (C) The four extreme paths and their values of Z and v.

The LSRs Arise from the Kinetics of the GTPase Cycle Module. Each LSR arises from the reactions along one of the four horizontal edges of the biochemical reaction scheme (Fig. 1). These extreme paths have distinct kinetics, distinct values of Z and v, and are the mechanisms underlying the LSRs (Fig. 3C). Path G keeps Z and v low in LSR G by slow GDP/GTP exchange. Path RG keeps Z high by fast GDP/GTP exchange and slow GTP hydrolysis, resulting in moderate v in LSR RG. Path RGA has substantial Z and high v by coupling fast GTP hydrolysis and GDP/GTP exchange rates, as shown in LSR RGA. Path GA maintains low Z and v in LSR GA by fast GTP hydrolysis with slow GDP/GTP exchange. In cells, changes in local R and GAP concentrations lead to changes in the proportion of G proteins following any one extreme path, resulting in the large range of G protein signaling activity predicted in Fig. 3 and observed in biological systems.

All GTPase-cycle modules obey the mechanism in Fig. 1 and thus have the four extreme paths. We therefore expect the four LSRs and transitions between them to be a feature of all GTPase-cycle modules, not only the m1 MAchR, Gq, and RGS4 module that we have modeled. However, the kinetics of GTPase-cycle modules differ, and, hence, we expect that among GTPase-cycle modules, Z and v of each LSR, and the changes in concentration for transitions between LSRs will differ. These differences determine specialized GTPase-cycle modules with unique properties of signal amplitude and timing that regulate diverse cellular signaling pathways in cells.

The GTPase-Cycle Module Responds Rapidly to Changes in R and GAP Concentrations. Fig. 3 shows Z and v for a range of R and GAP concentrations at steady state; however, regulation of R and GAP concentrations in vivo is dynamic, and, hence, the GTPase-cycle module might not occur at steady state in vivo. We simulated the time of return to steady state after a change in R or GAP concentrations. The simulations (Fig. 4) predict that if large amounts of R or GAP are present, the GTPase-cycle module reaches steady state in <1 s, regardless of the change in R or GAP concentration, and that the fastest return to steady state (t_1/2 = 0.03 s) requires saturating GAP. However, several minutes (t_1/2 = 50–60 s) are needed to relax to basal G protein activity after removal of both R and GAP. These predictions show that it is sufficient to study only steady-state activity of the GTPase-cycle module because the presteady state is short-lived. Moreover, they show that saturating GAP is required for the fastest return to steady state and therefore suggest that GAP is required for the fastest signal modulation during cellular signaling.

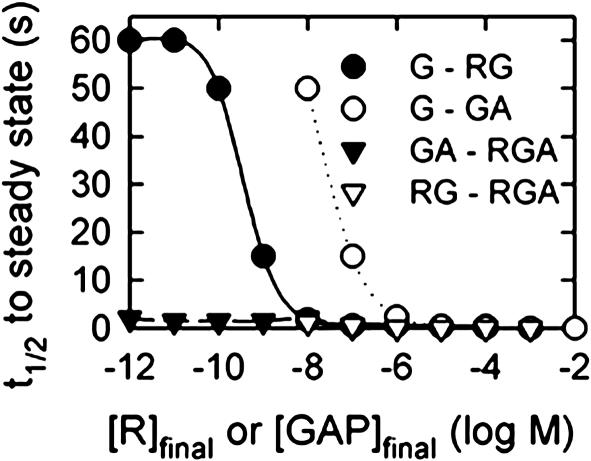
Fig. 4.

The GTPase cycle responds rapidly to changes in R or GAP concentration and saturating GAP is required for the fastest response. Shown is the t_1/2 for steady-state approach after perturbing the steady state of one LSR by adding or removing concentrations of R or GAP that mediate transitions between LSRs (Fig. 3). Only the curves for addition of R or GAP are shown; curves for removal are often similar and were removed for clarity. On the transition from the LSR G to RG, the t_1/2 to steady state decreases with increasing R concentration to 0.5 s. Addition of GAP, the transition from LSR RG to LSR RGA, then decreases the t_1/2 further to 0.03 s with saturating GAP. If R or GAP is removed, the t_1/2 to steady state remains rapid, at ≈1 s or less. However, if both R and GAP are removed, or if R is removed from LSR RG or GAP is removed from LSR GA, the t_1/2 to steady state takes up to 60 s. In all simulations, [G] = 10 nM, and GTP, GDP, and P_i are at cellular concentrations.

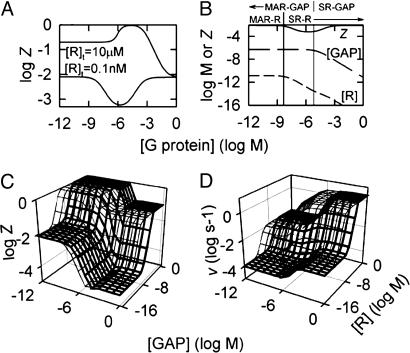
G Protein Concentration Determines the Effect of R or GAP by Selecting Between Mass Action Regimes (MARs) and Stoichiometric Regimes (SRs). In the previous sections, we reported the effect of changes in R and GAP concentration on Z and v, whereas G protein concentration was constant. In this section, we report the effect of changes in G protein concentration on Z and v for specified R and GAP concentrations. To provide a deeper understanding of the main results, we introduce the MAR, which occurs at relatively low G protein concentrations, and the SR, which occurs at relatively high G protein concentrations. These are epiphenomena of the model and in each of them R and GAP have different capacities to regulate Z and v. In the MAR, R increases Z and v if the association rate of R with G–GDP (reaction R₊₃, pseudo-first-order rate = ≈10⁸ M^–1·s^–1 × [R]) exceeds the rate of GDP dissociation from G-GDP (reaction D_–1 = 0.0001 s^–1). However, R can no longer increase Z and v when the association rate of R with G-GDP exceeds the rate of R-stimulated GDP dissociation (reaction D_–3 = 2 s^–1). Thus, R influences Z and v over the range of concentrations, ≈1 pM ≪ ≈10 nM (Fig. 3). Alternatively, if the concentration of G protein nears or exceeds the concentration of R that results in saturation of the R–G–GDP complex in the MAR, excess G proteins have no access to free R. Under these circumstances, the concentration of R must increase to approximately that of the concentration of G protein to be maximally effective. This equimolar stoichiometry between G and R characterizes the SR. Similar principles govern the MAR and SR for G–R interactions in the presence of saturating GAP (D_–2, R₊₆ and D_–4 in Fig. 1), and for G–GAP interactions in the absence of R (P_–3, A₊₅ and P_–4) or presence of saturating R (P_–1, A₊₂, and P_–2). Transitions between MAR and SR occur at one G protein concentration for G–R interactions and yet another for G-GAP interactions, because the relevant reaction rates differ. Thus, as G protein concentration increases, a trough or peak in Z may form (Fig. 5A). The trough is used to illustrate the phenomenon of MAR and SR in Fig. 5B.

Fig. 5.

The G protein concentration determines whether the MAR or SR is active and influences the effect of R and GAP on G protein activity. (A) Increasing G protein concentration leads to a trough and peak in Z.(B) Z for the trough is shown with the concentrations of free R and GAP and the divisions between the MAR and SR to demonstrate how interplay between the MAR and SR causes the trough. As G protein concentration increases from the MAR to the SR (transition at ≈6 nM), R is increasingly bound to G proteins, causing the concentration of free R to decrease (R_total = 0.1 nM); thus, R cannot access all G proteins and Z decreases. A similar process occurs for GAP–G interactions (transition at ≈7 μM; [GAP]_total = 500 nM), and in the SR GAP cannot access all G proteins so Z increases. Alternatively, in A, the peak forms because free GAP ([GAP]_total = 500 nM) is depleted at lower G protein concentrations than free R ([R]_total = 10 μM), allowing R to act on G proteins in the absence of GAP. (C and D) In the SR, higher concentrations of R and GAP are needed to regulate G protein activity. Each image (the Z is shown in C and the v is shown in D) contains two plots: the hairline plot has 1 nM G protein (MAR) and the thick line plot has 100 μM G protein (SR). In both images, significantly more R and GAP are required to affect transitions between LSRs in the SR than in the MAR. However, the values of Z and v in the LSRs are unchanged. Additionally, the potency of GAP to affect a change from LSR RG to RGA is greatly enhanced in the SR, as seen by the steeper downward slope: an x-fold change in [GAP] leads to only a 0.3-fold change in Z in the MAR, but to an ≈3-fold change in the SR. In all simulations GTP, GDP, and P_i are at cellular concentrations.

The significance of MAR and SR is that, together, they provide a mechanism whereby the local G protein concentration determines what effect the local R or GAP concentrations have on G protein activity. As G protein concentration is increased from MAR to SR, the concentrations of R and GAP needed to regulate G protein activity also increase, as shown quantitatively in Fig. 5 C and D. Furthermore, the potency of GAP to deactivate G proteins is increased ≈10-fold in the SR (Fig. 5C), which suggests that signaling in the SR is more rapidly modulated compared with the MAR. The MAR and SR add new detail to the four LSRs described above, and because each LSR can occur when G–GAP interactions are in the MAR or SR and when G–R interactions are in the MAR or SR, there are in essence 16 distinct signaling regimes of the GTPase-cycle module, with infinite gradations between them.

We predict that MAR and SR are general characteristics of GTPase-cycle modules. Whether particular GTPase-cycle modules operate in the MAR, SR, or both must be tested experimentally. In the next section, we use available data and simulations from the model to discuss the conditions under which the MAR and SR occur in vivo.

Little is known about the range of local concentrations of G proteins, G protein-coupled receptors, and GAPs in vivo, soitis difficult to determine whether the MAR or SR is active in vivo. The whole-cell ratio of G protein to receptor (G:R, where R includes active and inactive receptors) is ≥10 for many G protein-receptor pairs (16) (measurements of GAP are unavailable, to our knowledge). As shown in Table 2, this ratio is insufficient to significantly activate G proteins in all cases except when GAP is absent in either the SR or the transition between the MAR and SR. In the other cases, which include the MAR with and without GAP and the SR with GAP, local R concentration must increase substantially for any signaling to occur. A similar pattern exists for GAP–G interactions, although relatively less GAP is required for the IC₅₀ effect. These predictions suggest that signaling can occur by means of two alternative mechanisms, one in which G proteins, Rs, and GAPs are unclustered, and another in which they are clustered.

Table 2. Ratio of G:R (and G:GAP) required for activation (or deactivation) of G proteins in MAR and SR as predicted by simulations.

	Ratio G:R				Ratio G:GAP
	-GAP		+GAP		-R		+R
	EC50	MAX	EC50	MAX	IC50	MAX	IC50	MAX
MAR	<6	<0.06	<0.8	<0.08	<28	<0.5	<2.3	<0.23
Transition	6 to 50	0.06 to 1	0.8 to 2	0.08 to 0.5	28 to 280	0.5 to 2	2.3 to 3	0.23 to 1
SR	≈50	≈1	≈2	≈0.67	≈333	≈2	≈3	≈1

When GAP or R is added (+GAP or +R), it is saturating. Ratios are shown for half-maximal activation (EC₅₀) or deactivation (IC₅₀) of G proteins, and for maximal (MAX) activation or deactivation. The transition is considered as ±5-fold about the transition point between the MAR and SR (6 nM for G—R interactions and 7 μM for G—GAP interactions); the MAR contains all G protein concentrations below the transition, and the SR contains all G protein concentrations above the transition. In data for the MAR, < is used because the number of G proteins can decrease to 0 in this regime, but the EC₅₀ and MAX do not change.

The classical view of G protein signaling invokes the collision-coupling model in which receptors are unclustered and agonist binds to and activates receptors, which then interact with and activate many more G proteins to amplify the original ligand signal (28, 43–45). Interpreted in the light of our computational model's predictions, this type of G protein signaling occurs only in the absence of GAP in either the SR or at the transition from MAR to SR.

An alternative view of G protein signaling is that Rs, and perhaps GAPs and effectors, are clustered or complexed together with G proteins. This view is supported by evidence from several GTPase-cycle modules. For instance, rhodopsin occurs at extremely high concentrations in the visual pathway and in ≈10-fold excess of transducin, the G protein it activates (46). Many receptors are known to dimerize and possibly oligomerize (22), thereby increasing their local concentrations. δ-Opioid receptor Gi3 and the RGS protein GAIP colocalize upon agonist challenge in human embryonic kidney 293 cells (17). The GAPs RGS2 and RGS4 can bind m1 and other MAchRs in a two-way physical scaffolding complex, increasing the concentration of both with respect to the G protein (ref. 47; also see ref. 48). Also, steady-state GTPase rates of the GAPs RGS4 and phospholipase C-β1 in reconstituted vesicles with m1 MAchRs and Gq support a mechanism in which GAP-catalyzed GTP hydrolysis out-competes R–G*T dissociation, thus maintaining receptor–G complexes by kinetic scaffolding (34).

A hypothesis called spatial focusing that resulted from another computational model suggests how clustering may regulate signaling (31). It posits a signaling region of R, G protein, and GAP that allows limited G protein activity, and a nonsignaling region enriched in GAP relative to R. We suggest that in some cases the signaling region may exclude GAP for higher G protein activity.

Our computational model schematizes the aforementioned types of clustering and predicts quantitatively the concentration regimes under which each type is required. Clustering of R and GAP is represented by path RGA (Fig. 3), clustering of R by path RG, and clustering of GAP by path GA. Clustering of R and GAP is required for signaling in the MAR and in the SR in the presence of saturating GAP (Table 2). In the absence of GAP, clustering of R is required for signaling in the MAR. In the absence of R, clustering of GAP to inhibit signaling is more important in the MAR than in the SR. Notably, the predictions do not specify whether clustering occurs before or after agonist binding to receptor.

The computational model also predicts that clustering of R, G, and GAP may be characterized by fast-signal modulation. For instance, the fastest response to changes in local R and GAP concentrations occurs when R or GAP or both are saturating (Fig. 4), and the potency of GAP is enhanced in the SR (Fig. 5C). Furthermore, substantial G protein activity (Z ≈ 10%) is maintained even in the presence of saturating GAP in extreme path RGA (Fig. 3). Physiological conditions that may require this type of G protein signaling include regulation of some ion channels and the phototransduction pathway (49, 50).

We examined whether the computational model explains experimental data on ion-channel activation. Ion-channel data come from the m2 MAchR, Gi, RGS4, and G protein-gated inward rectifier K⁺ ion channel in oocytes (23), which is closely related to the m1 MAchR-Gq-RGS4 system we have modeled. As mentioned in the Introduction, these data appear paradoxical because RGS proteins do not necessarily alter G protein-stimulated ion-channel current amplitude but do accelerate the onset and desensitization of current (23–26). In our simulations, we cannot directly assess the activation of ion channels; however, we predict that Z decreases from 0.98 (path RG) to 0.096 (path RGA) in the presence of RGS4 and speculate that Z = 0.096 is sufficient to saturate ion channels. For signal timing, RGS4 decreased the t_1/2 for signal activation in the oocyte system from ≈1.5 to ≈0.6 s and the t_1/2 for signal deactivation (upon removal of agonist) from ≈20 to ≈4 s; our simulations predict 0.5 to 0.03 s and ≈50 to 0.03 s, respectively. Qualitatively, the experimental data and our simulations agree. Quantitative differences may arise from (i) G_i–ion-channel interactions and R desensitization, which are ignored by the model, (ii) differences in the kinetics of the two GTPase-cycle modules, or (iii) differences in component concentrations between oocytes and simulations. Additionally, data on signaling kinetics in the phototransduction cascade with and without RGS9 (51) resemble the K⁺ channel data. Thus, the computational model also explains the phototransduction data, even though important proteins such as Gβ5, cGMP phosphodiesterase, and cGMP-gated ion channels (50) are not included. These examples quantitatively validate extreme path RGA and the hypothesis that R and GAP are clustered together with G proteins. Furthermore, they demonstrate that the model, by using reaction-rate parameters from a specific GTPase-cycle module, captures features of related GTPase-cycle modules.

The model has demonstrated how the concentrations of receptor, GAP, and G protein govern the activation of G proteins. However, the question of whether there is a threshold local concentration of active G proteins at which downstream pathways are significantly activated remains unanswered and merits further investigation.

Conclusion. In a paradigm systems biology approach involving biochemical, mathematical, and computational modeling, we examine quantitatively how the interplay between concentrations and reaction parameters regulate the biochemical events of G protein activity. Our model provides mechanistic insights into the regimes under which distinct GTPase-cycle modules function and yield a wide range of biochemical phenotypes. These regimes provide the quantitative framework for experimental investigations of GTPase-cycle modules. Furthermore, the mechanisms implied in these regimes provide a molecular picture of two varieties of GTPase-cycle module function, one where the active receptor is intimately coupled to the G protein and perhaps its regulatory partner, and the other variety, in which the coupling is through kinetic processes. In addition to explaining currently available data, the predictions put forth here pave the way for a large number of future experiments.