Abstract
Globular proteins are not permanently folded but spontaneously unfold and refold on time scales that can span orders of magnitude for different proteins. A longstanding debate in the protein-folding field is whether unfolding rates or folding rates correlate to the stability of a protein. In the present study, we have determined the unfolding and folding kinetics of 10 FNIII domains. FNIII domains are one of the most common protein folds and are present in 2% of animal proteins. FNIII domains are ideal for this study because they have an identical seven-strand β-sandwich structure, but they vary widely in sequence and thermodynamic stability. We assayed thermodynamic stability of each domain by equilibrium denaturation in urea. We then assayed the kinetics of domain opening and closing by a technique known as thiol exchange. For this we introduced a buried Cys at the identical location in each FNIII domain and measured the kinetics of labeling with DTNB over a range of urea concentrations. A global fit of the kinetics data gave the kinetics of spontaneous unfolding and refolding in zero urea. We found that the folding rates were relatively similar, ∼0.1–1 s−1, for the different domains. The unfolding rates varied widely and correlated with thermodynamic stability. Our study is the first to address this question using a set of domains that are structurally homologous but evolved with widely varying sequence identity and thermodynamic stability. These data add new evidence that thermodynamic stability correlates primarily with unfolding rate rather than folding rate. The study also has implications for the question of whether opening of FNIII domains contributes to the stretching of fibronectin matrix fibrils.
Keywords: fibronectin, kinetics, protein folding, protein stability, spectroscopy, FNIII domains, irisin, thiol exchange
Introduction
Fibronectin (FN)3 assembles into a fibrillar extracellular matrix, which is the primordial matrix in embryonic development and wound healing. The FN molecule is a dimer of 250,000-Da subunits, which are modular proteins that fold into a string of globular domains. There are three types of domains, which differ in size, structure, and the presence of internal disulfide bonds (1). FNI and FNII domains are 5,000 and 6,500 Da, respectively, and are stabilized by internal disulfide bonds. FNIII domains are 10,000 Da and have no internal disulfide bonds.
The present study focuses on FNIII domains. The FN monomer contains 15–17 FNIII domains, depending on splicing. The domain structure is a β-sandwich (Fig. 1), with three strands on one side, four on the other, and a compact hydrophobic core (2). First discovered in fibronectin, FNIII domains are incorporated as a folding motif in many animal proteins. Although different FNIII domains share only ∼20% sequence identity, they all fold with the same β-sandwich structure. These domains have been implicated in cell adhesion, matrix assembly and elasticity, and membrane receptors and are the main focus of our present study.
FIGURE 1.
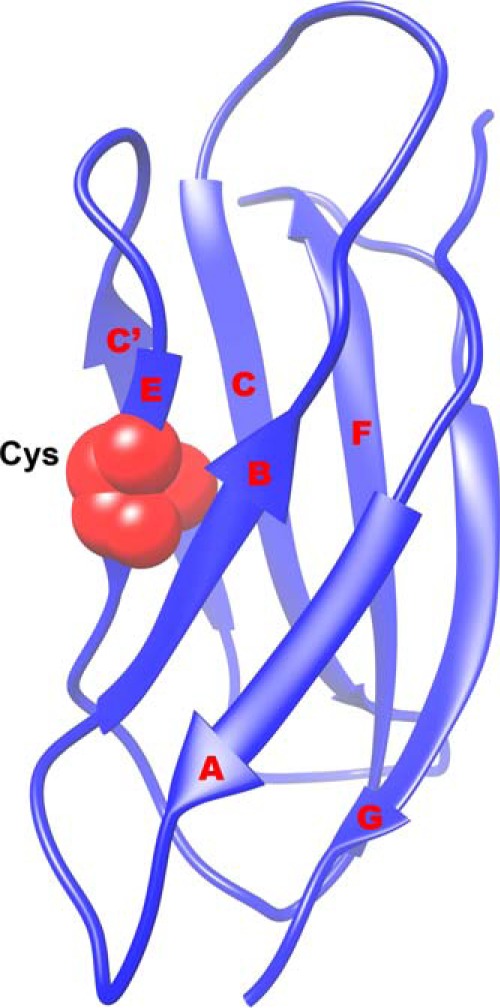
Structure of FNIII 7 showing the seven strands (A, B, C, C′, E, F, and G). The buried Cys in the E strand used in the thiol exchange assay is shown in red. Figure based on the coordinates from 1FNF.pdb (2).
FN matrix fibrils are very elastic; those in cell culture are typically stretched up to 4 times their rest length (3, 4). The mechanism of the stretch is controversial. One hypothesis is “tension-induced domain unfolding,” which proposes that individual FNIII domains unravel when the fibril is under tension (5–7, 40). A folded FNIII domain is 3.5 nm long, and the 90 amino acids of the unfolded polypeptide chain have a contour length of 30.5 nm, providing a potential source of stretch. An alternative model proposes that the stretch involves a conformational change of the FN dimer from a compact pretzel shape to an extended form, without unfolding FNIII domains (8–11). To explore the mechanism of FN fibril elasticity, Lemmon et al. (12) used the technique of chemical labeling of a Cys buried in a globular domain as an indication of domain unfolding. This technique was previously developed by Johnson et al. (13) to show that tension can expose buried Cys in two isoforms of spectrin in red blood cells. In fibronectin, only FNIII 7 and 15 have a free Cys (Fig. 1). These two Cys are buried, and with FN in solution, they can only be labeled after denaturation (7). Lemmon et al. (12) found that these two domains did not label in FN matrix fibrils assembled in cell culture. To explore the state of other FNIII domains, Lemmon et al. (12) created thirteen full-length mutant FNs, each containing a buried Cys in a single FNIII domain. When incorporated into cell culture matrix, 6 of the 15 FNIII domains were sufficiently open that their buried Cys could be labeled by 1-h incubation with fluorescein maleimide. The domain unfolding could be due to (a) tension-induced unfolding, (b) unfolding as part of FN–FN bond formation during fibril assembly, or (c) spontaneous unfolding and refolding of domains. Our study addresses quantitatively this third mechanism.
All globular proteins and protein domains spontaneously unfold and refold, with a very wide range of kinetics (14). The kinetics in dilute aqueous buffer can be described by two rate constants, kuH2O for unfolding and kfH2O for folding. Three FNIII domains have been extensively studied for unfolding-folding kinetics: FNIII 9 and 10 and TNfn3, an FNIII domain from tenascin (15–17). Recently, the unfolding and refolding kinetics of FNIII 3 have also been studied (18). These studies monitored the unfolding by the increase in fluorescence of the single conserved and buried Trp in most FNIII domains.
An alternative to Trp fluorescence is to use a buried Cys and assay its accessibility to a thiol-reactive reagent to measure the population of the unfolded state. This approach has been termed thiol exchange (SX). In SX, the opening and closing kinetics, which are defined by the rate constant of opening (kop) and the rate constant for closing (kcl), determine the accessibility of the Cys to the dye. In many cases, the opening and closing kinetics correspond to global unfolding and folding; then kop = ku and kcl = kf. In other cases, the Cys can be exposed by subglobal or by local opening and closing, and these mechanisms need to be accounted for separately. We will use the terms kop and kcl to describe our kinetic measurements, although most domains fit a two-state global unfolding mechanism.
SX was first used by Ballery et al. (19, 20), and it has been subsequently applied to several proteins. Each of these studies focused on a single protein and placed the Cys at different locations to determine how folding varied at different positions (21–23). Two papers provide an excellent background for our study because they used a very similar experimental approach and interpretation (22, 23). These studies probed unfolding-folding at various locations in a single protein and compared it with global unfolding-folding of that protein as measured spectroscopically. Feng et al. (22) used SX to study global and local unfolding events in ferric aquomyoglobin. They introduced a buried Cys at 10 different sites in the protein, to explore how local unfolding varied over the structure. Malhotra and Udgaonkar (23) used SX to study high energy intermediate states during protein unfolding. They created four single Cys mutants at buried locations of the single-chain protein monellin.
In the present study, we have applied SX with a different strategy. We have surveyed the opening-closing kinetics of 10 different protein domains related by homology, specifically the family of FNIII domains. We have included the six domains of FN that were labeled in matrix fibrils and two that were not (12), as well as TNfn3 and irisin, which is the ectodomain of the transmembrane protein FNDC5 (24, 25). For this purpose, we engineered a single buried Cys at the same location in each of the FNIII domains, at the site of the natural Cys in FNIII 7 and irisin. The kinetics of Cys labeling were measured in different concentrations of urea. Most domains could be fit to a two-state model of global unfolding, but for three domains, the Cys was partially exposed by a local or subglobal unfolding. Our study provides new evidence that thermodynamic stability correlates most closely with unfolding rates.
Results
Equilibrium Studies of FNIII Domains by Trp Fluorescence Show a Wide Range of Chemical Stability
Conventional protein folding studies use a direct spectroscopic probe to measure the fraction of folded protein in various concentrations of denaturant. Almost all FNIII domains have a single buried Trp at sequence position 22 or 23 in β strand B. In folded FNIII domains, the buried Trp has an emission peak at 320 nm when excited at 280 nm. Solvent exposure of Trp by protein denaturation in urea shifts the emission peak to 350 nm. An example of these changes for FNIII 3C is shown in Fig. 2A. In 0–1 m urea, the emission peak is at 320 nm, and it shifts to 350 nm at 3 m urea, in which it is predominantly unfolded.
FIGURE 2.
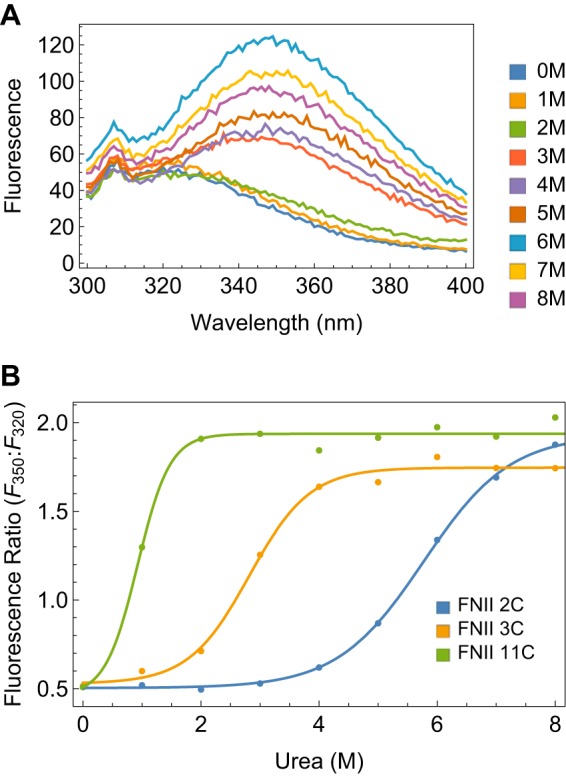
Stability of FNIII domains assayed by Trp fluorescence. A, emission spectra of 1 μm FNIII 3C in 0–8 m urea, excited at 280 nm. B, ratio of 350 nm/320 nm fluorescence intensities as a function of urea for FNIII 11C, 3C, and 2C.
We determined the thermodynamic stabilities of the 11 domains in this study from Trp fluorescence urea denaturation curves. To eliminate variations due to protein concentration, we used the emission ratio 350/320 nm as a measure of the extent of unfolding. A ratio of 0.3–1.8 indicates a buried Trp; the ratio increases to 1.5–2.8 when the Trp is exposed to the solvent (12). We fit the emission ratio versus urea concentration for each domain to a simple two-state equilibrium (see “Experimental Procedures”). Examples of Trp denaturation curves for three FNIII domains that span the stability range are shown in Fig. 2B. The fitted stabilities and their urea dependence for all 11 domains are listed in Table 3. FNIII 11C is the least stable with ΔGF→UH2O of 1.59 ± 0.65 kcal/mol. FNIII 10C is the most stable, with a ΔGF→UH2O greater than 10 kcal/mol, which was too stable to measure accurately by the non-ionic denaturant urea. FNIII 3C has intermediate stability with a ΔGF→UH2O of 3.3 ± 1.0 kcal/mol.
TABLE 3.
Comparison of thermodynamic parameters obtained from Trp fluorescence and SX
The parameters obtained by SX are extrapolated to 0 m for all FNIII domains studied. FNIII 2C*, FNIII 9C*, and FNIII 10C* were fit using a more complex mechanism (Equation 13). Trp(SVD) means the Trp fluorescence data were analyzed using singular value decomposition. S.E. values (see Table 1) are shown in parentheses.
| FNIII domain | Technique | ΔG | meq | C1/2 |
|---|---|---|---|---|
| kcal/mol | m | |||
| 1C | Trp | 6.1 (0.1) | −1.06 (0.17) | 5.7 (0.1) |
| 2C | SX | 5.9 (0.07) | −1.05 (0.02) | 5.6 (0.1) |
| 2C | Trp | 4.7 (0.4) | −0.81 (0.07) | 5.8 (0.04) |
| 3C | SX | 3.4 (0.03) | −1.39 (0.012) | 2.5 (0.03) |
| 3C | Trp | 3.3 (1.0) | −1.16 (0.34) | 2.8 (0.2) |
| 3C | Trp (SVD) | 3.8 (0.2) | −1.15 (0.07) | 3.4 (0.04) |
| 6C | SX | 5.6 (0.03) | −1.03 (0.0041) | 5.4 (0.05) |
| 6C | Trp | 3.4 (0.8) | −0.51 (0.16) | 6.7 (0.7) |
| 7 | SX | 5.9 (0.01) | −1.3 (0.02) | 4.6 (0.02) |
| 9C* | SX | 3.7 (0.01) | −1.0 (0.004) | 3.6 (0.02) |
| 9C | Trp | 3 (1.6) | −0.87 (0.44) | 3.4 (0.4) |
| 10C* | SX | 8.2 (0.009) | −0.93 | 8.8 |
| 10C | Trp | 10.6 (2.1) | −1.21 (0.24) | 8.8 (0.09) |
| 11C | SX | 0.78 (0.03) | −1.64 (0.002) | 0.48 (0.03) |
| 11C | Trp | 1.6 (0.7) | −1.79 (0.66) | 0.88 (0.1) |
| 12C | SX | 4.3 (0.02) | −1.45 (0.006) | 2.96 (0.02) |
| 12C | Trp | 5.4 (1.27) | −1.47 (0.34) | 3.7 (0.1) |
| Irisin | SX | 4.1 (0.01) | −1.42 (0.02) | 2.9 (0.01) |
| Irisin | Trp | 3.4 (0.8) | −1.41 (0.31) | 2.4 (0.1) |
| TNfn3 | SX | 2.9 (0.04) | −1.51 (0.03) | 1.9 (0.04) |
| TNfn3 | Trp | 2.5 (2.4) | −0.65 (0.6) | 3.9 (0.9) |
Global Fitting of Thiol Reactivity Data Gives Kinetic and Thermodynamic Information
Our SX assay measures the labeling of the buried Cys and fits it to the general scheme (developed in detail under “Experimental Procedures”).
| (Eq. 1) |
In this model, a closed domain PC opens with an opening rate constant kopD, and the open domain PO closes with a closing rate constant kclD. The superscript D in the kinetic constants indicates that they are dependent on the concentration of denaturant. The Cys is only exposed in PO, so this population was assayed by its reaction with the thiol-reactive reagent: 5,5-dithiobis-(2-nitrobenzoic acid) (DTNB). The major goal is to extrapolate the data to determine the rates at zero denaturant, indicated by kopH2O and kclH2O.
Our global fitting approach, developed under “Experimental Procedures,” differs from that of previous SX studies, which fit individual labeling curves for each urea concentration to an exponential to obtain kobs ([urea]) (21–23). These intermediate data were then fit again to obtain thermodynamic and/or kinetic parameters for the conformational reactions. Our approach globally fits all labeling curves over the full range of urea concentrations to a model that includes the urea dependence of opening and closing.
Differential equations describing the time dependence of all species were solved either with the kinetic matrix method or by numerical integration in MathematicaTM (see “Experimental Procedures”). Global fitting of SX data can determine both thermodynamic and kinetic parameters, provided that there are sufficient data in the so-called EXX regime. In this regime, both the conformational opening and DTNB reactions contribute to the observed kinetics (Equation 16). However, if the conformational opening reaction is rate-determining at all urea concentrations (EX1 regime, Equation 17), kop can be determined, but not kcl or the stability. In contrast, if conformational kinetics at all urea concentrations are much faster than the DTNB reaction (EX2 regime, Equation 18), then the equilibrium constant can be determined, but not kop or kcl. With sufficient data in the EXX regime, the global fitting determines the best values of five parameters: kop, kcl, mop, mcl, and kchem.
The complete kinetics data for FNIII 2C at various urea concentrations are shown in Fig. 3 as an example of a data set and the global fitting. To obtain this data set, FNIII 2C was incubated for 10 min in buffers containing 0–8 m urea to establish unfolding equilibrium. DTNB was then added to the protein, and the reaction was monitored by absorbance at 412 nm. At low concentrations of urea, the reaction is slow and was monitored with a spectrophotometer after manual mixing (Fig. 3A), whereas at high urea concentrations, the reaction is much faster and required stopped-flow mixing (Fig. 3B). The data for FNIII 2C follows the EX2 regime from 0 to 1 m urea and the EXX regime from 2 to 6 m urea, where kcl and kint are within a factor of 10 of each other. Above 6 m urea, the domain is predominantly unfolded, and the Cys is completely exposed to the dye. In this regime, no information is provided about the conformational reaction, but the labeling curves help determine kchem, which is another globally fitted parameter. The thermodynamic and kinetic parameters extrapolated to 0 m urea and the mop and mcl, fit from the complete data set, are shown in Table 1.
FIGURE 3.
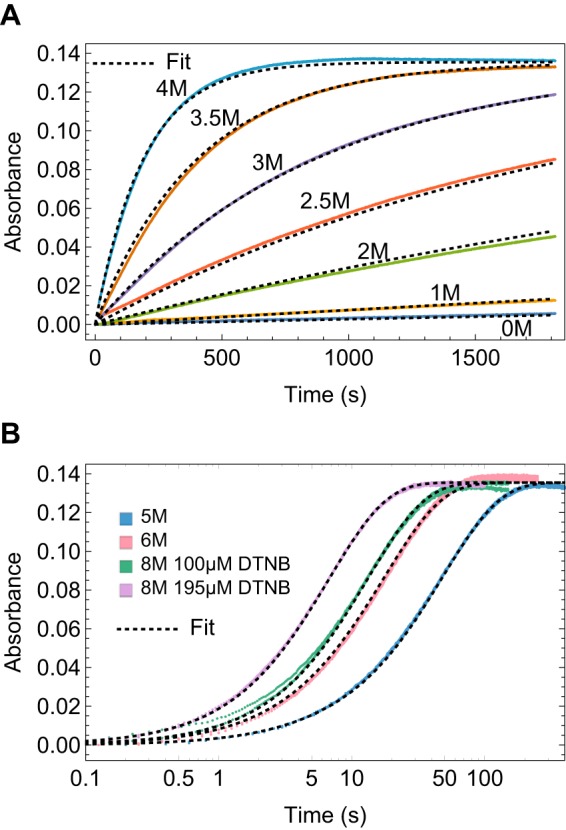
Kinetics of labeling the buried Cys in FNIII 2C in 0–8 m urea by manual spectrophotometer (A) and stopped flow (B). Colored curves, kinetic data; dotted black lines, global fit. The transients in B are shown with a log(time) axis to better exhibit differences at short times.
TABLE 1.
Parameters extrapolated to 0 m from the global fit for FNIII 2C
Fitted parameters are indicated with an asterisk; all others have been derived from the fitted parameters. The S.E. values were determined by Monte Carlo sampling of the best-fit model using the MathematicaTM NonlinearModelFit function.
| Parameter | Value | S.E. |
|---|---|---|
| kopH2O (s−1)* | 2.67 × 10−4 | 1 × 10−5 |
| kclH2O (s−1)* | 4.83 | 0.2 |
| Closed state half-life (s) | 2,590 | 100 |
| Open state half-life (s) | 0.143 | 0.007 |
| mcl (m−1)* | −0.648 | 0.01 |
| mop (m−1)* | 1.11 | 0.008 |
| kopH2O (kcal mol−1) | 5.88 | 0.04 |
| kopH2O* | 5.52 × 10−5 | 3.3 × 10−6 |
| meq (m−1) | −1.05 | 0.008 |
| kchemH2O (m−1 s−1)* | 1,720 | 2 |
| KopLH2O* | 3.21 × 10−5 | 7 × 10−7 |
The kinetics data and global fits for all domains are shown in supplemental Figs. 1–11. The extrapolation to 0 m urea, kopH2O, kclH2O, and the mop, mcl, and kchem values are summarized in Table 2.
TABLE 2.
Kinetic parameters extrapolated to 0 m for all FNIII domains studied
FNIII 2C* and FNIII 9C* were fit by a more complex model (Equation 13).
| FNII domain | kop | kcl | mop | mcl | ΔG | meq | kchem | KopL |
|---|---|---|---|---|---|---|---|---|
| s−1 | s−1 | m−1 | m−1 | kcal mol−1 | kcal mol−1 m−1 | m−1 s−1 | ||
| 2C* | 2.7 × 10−4 (1 × 10−5) | 4.8 (0.2) | 1.1 (0.008) | −0.65 (0.01) | 5.9 (0.04) | −1.1(0.008) | 1,700 (2) | 3.2 × 10−5 (7 × 10−7) |
| 3C | 1.9 × 10−3 (2 × 10−5) | 0.55 (0.01) | 1.5 (0.007) | −0.78 (0.01) | 3.4 (0.01) | −1.4 (0.006) | 2,100 (2) | |
| 6C | 1.3 × 10−5 (1 × 10−7) | 0.14 (0.003) | 1.5 (0.002) | −0.20 (0.006) | 5.6 (0.02) | −1.0 (0.002) | 2,200 (2) | |
| 7 | 6.9 × 10−5 (4 × 10−7) | 1.4 (0.01) | 0.95 (0.001) | −1.2 (0.002) | 5.9 (0.007) | −1.3 (0.008) | 1,200 (0.3) | |
| 9C* | 3 × 10−5 (4 × 10−7) | 0.015 (0.0003) | 1.2 (0.004) | −0.53 (0.006) | 3.7 (0.01) | −1.0 (0.004) | 12,000 (40) | 2.7 × 10−4 (1 × 10−6) |
| 11C | 0.016 (2 × 10−4) | 0.06 (0.001) | 1.8 (0.02) | −0.93 (0.04) | 0.78 (0.02) | −1.6 (0.001) | 1,400 (2) | |
| 12C | 2.3 × 10−4 (1 × 10−6) | 0.3 (0.005) | 1.1 (0.003) | −1.3 (0.006) | 4.3 (0.01) | −1.5 (0.003) | 3,700 (3) | |
| Irisin | 2.1 × 10−3 (1 × 10−5) | 1.9 (0.01) | 0.72 (0.002) | −1.7 (0.004) | 4.1 (0.005) | −1.4 (0.008) | 5,200 (5) | |
| TNfn3 | 6 × 10−3 (1 × 10−4) | 0.72 (0.02) | 0.55 (0.008) | −2 (0.02) | 2.9 (0.02) | −1.5 (0.01) | 6,200 (6) |
Stability of FNIII Domains Determined by SX Range from 0.8 to 8.1 kcal/mol
We also determined the stability of domains from our SX data. The stability (ΔGH2O in 0 m urea) and urea dependence of stability (meq), determined by Trp fluorescence and by SX, are compared in Table 3. SX values are missing for FNIII 1C, which could not be fit to a two- or three-state opening model. FNIII 11C is very unstable and has the lowest ΔGH2O = 0.78 ± 0.03 kcal/mol, whereas FNIII 10C is very stable to global opening and has the highest ΔGH2O = 8.17 ± 0.009 kcal/mol. The SX and Trp data generally agree closely. As an example, for FNIII 3C, ΔGH2O = 3.4 ± 0.03 kcal/mol by SX versus 3.8 ± 0.24 kcal/mol by Trp fluorescence. A value of 4.0 kcal/mol was determined in a separate study of FNIII 3 (without the buried Cys) using Trp fluorescence and denaturation in guanidine HCl (18).
Most FNIII Domains Fit a Two-state Unfolding Mechanism; Some Exhibit Local or Subglobal Unfolding
A central finding of this study is that the global opening reaction to expose the engineered Cys buried in the FNIII domains is the same as global unfolding. This finding is supported by the good fit to a two-state unfolding mechanism for most domains and the agreement between the stabilities measured by Trp fluorescence and SX (see Table 3). However, it is important to properly model all of the possible routes by which the Cys residues can be exposed to DTNB. In addition to global opening, Cys residues can become exposed through subglobal opening, which corresponds to a partial unfolding reaction, or they could open via local fluctuations in the structure. These three opening mechanisms are distinguishable by their urea dependence, which is greater for global unfolding, lower for subglobal unfolding, and urea-independent for local state fluctuations.
The domains whose Cys residues react exclusively via global unfolding include FNIII 3C, 6C, 7, 11C, 12C, irisin, and TNfn3. The SX data for these domains fit well to the simplest model (Equation 11). The key parameters describing the folding and unfolding kinetics of these domains are the rate constants for opening (unfolding) and closing (folding) at 0 m urea (kopH2O and kclH2O, respectively). These parameters, which are listed in Table 2, are also used to determine the global stability of the domain, ΔGopH2O.
The SX data for two domains, FNIII 9C and 2C, did not fit well to a global opening alone model but did fit to a model that included an additional local opening reaction (local state fluctuations (22)) that allows the Cys to react without global unfolding. This model is described in Equation 13. For FNIII 2C, the model parameters include the equilibrium constant for local opening (KopL), which is unfavorable and much less than 1 and global opening parameters kopH2O and kclH2O (see Tables 1 and 2).
The SX data for FNIII 10C did not fit well to either of these models. Instead, it was necessary use a model (Equation 14) that includes an additional subglobal opening (unfolding) reaction along with a global opening reaction. The rate constants for subglobal opening (kopSH2O) and closing (kclSH2O) define the rates at 0 m urea for this conformational reaction. The kinetics for labeling for FNIII 10C lie predominantly in the EX2 regime. This gave thermodynamics parameters, but no kinetic parameters could be obtained (see supplemental Fig. 7).
We initially tested FNIII 1C with the Cys located on the E strand, at the position of the natural Cys in FNIII 7 and irisin. FNIII 1 is a very stable domain, as assayed by Trp fluorescence, but the kinetics of labeling of FNIII 1C were rapid and did not change with an increase in urea concentration from 0 to 2 m. The NMR structure of FNIII 1 (26) shows that the Tyr-666 in FNIII 1, the amino acid on the E strand that we changed to Cys, appears to be only partially buried. The Ile at position 668, two amino acids away, was totally buried. Hence, we created a Cys mutant of FNIII 1 at position 668. The kinetics of labeling of this mutant were also rapid and did not change with an increase in urea concentration from 0 to 3 m (supplemental Fig. 1). We tried fitting the data to a three-state mechanism that included a subglobal event but were unsuccessful. Attempts to fit the labeling of the Y666C mutant were also unsuccessful. We conclude that the E strand of FNIII 1 has complex unfolding/refolding kinetics involving more than one partially folded intermediate, and we have not included it in the analysis.
Reactivity of the Cys in Different FNIII Domains Varies by a Factor of 10
The best-fit bimolecular rate constant for the reaction of a fully exposed Cys with the thiol-reactive dye varied by a factor of 10 between FNIII domains. The kchem ranges from 1,400 s−1 m−1 for FNIII 11C to 11,600 s−1 m−1 for FNIII 9C. The next highest kchem is for TNfn3: 6,200 s−1 m−1. The data points that determined these rate constants came from high urea conditions, where the protein was predominantly unfolded. According to Snyder et al. (27), in ionic strengths >20 mm, positive charges in the flanking domains increase the reactivity of the Cys. For TNfn3, the Cys mutant has a flanking Arg, whereas for FNIII 11C, there is a flanking Glu. For most of the FNIII domains, the amino acids flanking the Cys are neutral. Thus, the wide range of kchem observed cannot be explained by electrostatics alone. However, other interactions that affect solvent accessibility of the thiol in the unfolded state may also contribute to the wide variation of kchem that we observed.
Flanking Domains Modestly Perturb the Kinetics of FNIII C
So far, we have discussed the kinetics and thermodynamics of individual FNIII domains. FNIII domains in fibronectin are flanked by neighboring FNIII domains, with which they make a significant interface (2, 28). To study the effect of flanking domains on the kinetics and thermodynamics of individual FNIII domains, we made two multidomain constructs with a buried Cys in only one internal FNIII domain. FNIII 4–7(6C, 7A) contained FNIII domains 4–7, with the Cys in FNIII 6 and the natural Cys in FNIII 7 changed to Ala. Fig. 4B shows the kinetics data for FNIII 4–7(6C, 7A). Comparing the curves for the multidomain construct with those of individual FNIII 6C (Fig. 4A), we see that the kinetics of labeling are somewhat slower in FNIII4–7(6C, 7A), suggesting that FNIII (6C) is slightly stabilized by the flanking domains. In addition, the kinetics of labeling in the multidomain construct had a faster burst phase (demonstrated by the rising level of the first data point) followed by a slower phase. Similar results were obtained with the multidomain construct FNIII 1–5(2C), where FNIII 2 has the buried Cys mutation (supplemental Fig. 12). Neither of these multi-domain constructs could be fit by a simple two-state model.
FIGURE 4.
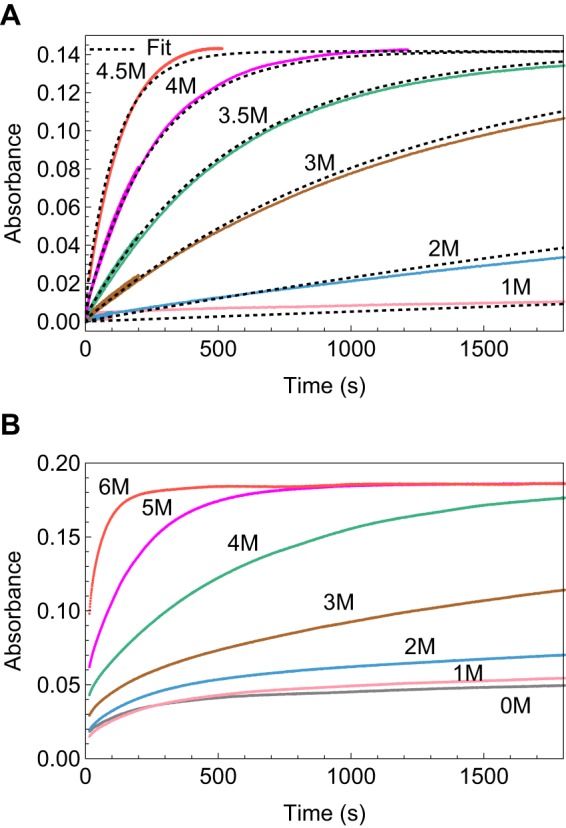
Kinetics of labeling the buried Cys in FNIII 6C as a single domain (A) and when it is flanked by other domains in the multidomain construct FNIII 4–7 (6C) (B). The kinetics of labeling in the multidomain construct are visibly somewhat slower than for the single domain. They were also more complex and could not be fit by our models.
Correlation of Unfolding and Refolding Kinetics to Thermodynamic Stability
The half-lives for the closed and open states, which are more intuitive than rate constants, are plotted together on a log scale in Fig. 5. The important general conclusion is that the open state half-lives varied <2 orders of magnitude (excluding FNIII 11C, the variation is 0.6–6 s), whereas the closed state half-lives varied by 3 orders of magnitude.
FIGURE 5.
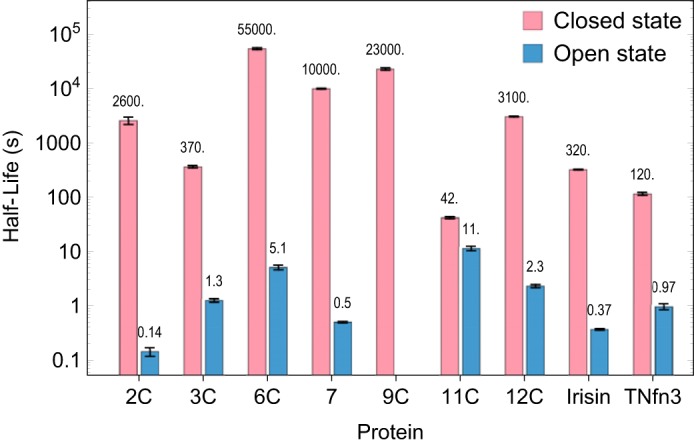
Comparison of the closed and open state half-lives of FNIII domains as measured by SX. The error bars represent the 95% confidence intervals as estimated by Monte Carlo sampling of the fitted model against the data by the NonlinearModelFit function of MathematicaTM.
Fig. 6 plots the ln of kop and kcl against the unfolding ΔG. kop is correlated with ΔG (R2 = 0.77), whereas kcl is poorly correlated (R2 = 0.34, and it drops to 0.04 if we remove the point for FNIII 11). These observations support the conclusion that among FNIII domains, the wide variation of thermodynamic stability is due primarily to variations in folded state lifetimes.
FIGURE 6.
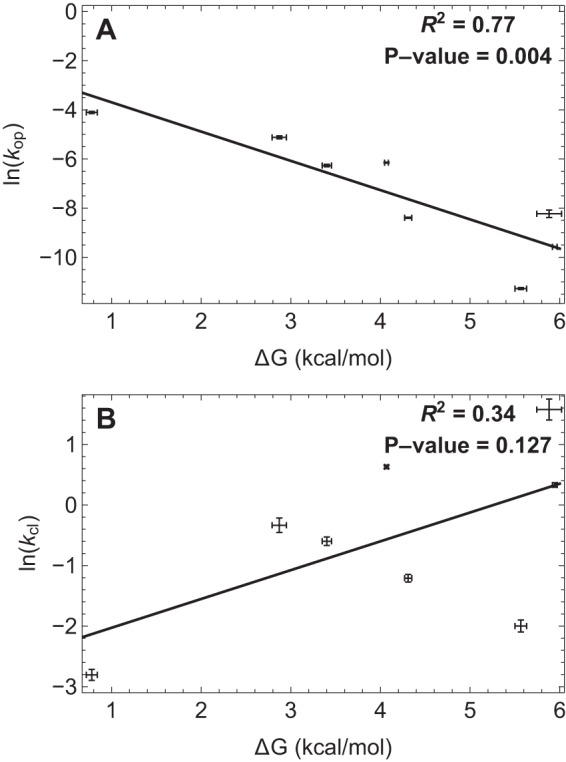
Relationship between change in free energy of unfolding with ln(kop) (A) and ln(kcl) (B). The correlation coefficient of ΔG with ln(kop) is much higher than that with ln(kcl), which drops to 0.04 if we remove the point for the extremely unstable FNIII 11. Error bars, 95% confidence intervals as described in the legend to Fig. 5.
Discussion
Opening and Closing Kinetics That Expose the Buried Cys in Most FNIII Domains Are Due to Global Unfolding and Folding
Labeling the buried Cys can be due to global, subglobal, or local unfolding (29). If the rate of labeling increases with denaturant concentration, then the opening event is global. On the other hand, if the rate of labeling shows no urea dependence, then the opening is due to local unfolding/fluctuations. Local unfolding is only observable if the domain is sufficiently stable. If the rate of labeling shows less urea dependence than global unfolding, then the opening is due to subglobal unfolding. For most of the FNIII domains, the rate of labeling of the buried Cys increased with increase in urea concentration (supplemental Figs. 1–11), and the data were fitted to the two-state, global unfolding mechanism. For these FNIII domains, ku = kop and kf = kcl.
For FNIII domains 1C, 10C, and 9C, the rate of DTNB labeling had little or no urea dependence at low urea concentrations. However, at higher urea concentrations, the rate of labeling became strongly urea-dependent. The conventional interpretation of these results is to attribute labeling at low urea to local or subglobal unfolding reactions.
Global Fits of Thiol Reactivity Data Are More Constrained than Two-step Fits
Global fitting of SX data is a powerful method for data analysis. This approach allows simultaneous fits to a single set of parameters of a data set comprising a wide range of denaturant and thiol-reactive reagent concentrations. This allows the data to span all of the kinetic regimes, EX1, EX2, and EXX, and leads to a single and accurate estimate of the rate constant of folding and unfolding at 0 m urea. Previous analyses of SX have fit separate curves to obtain the kobs for each concentration of thiol-reactive dye and denaturant, and the separate results were then extrapolated to zero denaturant (21). Our global fitting treats all data together to determine the five model parameters: kopH2O, kclH2O, mop, mcl, and kchemH2O. These parameters allow comparison between the model and data at each denaturant concentration, as shown in supplemental Figs. 1–11.
The Refolding Rate Constant Is Similar for All of the FNIII Domains; the Unfolding Rate Constant Varies with Thermodynamic Stability
FNIII domains have a wide range of thermodynamic stability, as measured by chemical denaturation. There has been a debate in the literature over whether stability of protein domains is correlated primarily to the folding or the unfolding rate constant. Earlier studies, based on FNIII 9 and 10 from FN and TNfn3 from tenascin, suggested that stability correlated with the folding rate constant (15, 16, 30). All three proteins are included in our study. These early studies focused heavily on FNIII 10, whose high stability and folding and unfolding rate constants anchored the top of the curves. In our study, FNIII 10 was completely in EX2 and therefore gave no rate constants. However, the folding rate constant for FNIII 10 determined previously (15, 16), 155 s−1, is now seen to be 2 orders of magnitude higher than those of the other FNIII domains and is a distinct outlier. Removing it weakens the correlations noted in these earlier studies.
The other school of thought is that the folding rate constant is affected primarily by contact order and hence topology. Plaxco et al. (31) studied a set of 12 single-domain proteins that lacked disulfide bonds and cis prolines and folded with simple two-state kinetics. They found no significant correlation between the stability of the protein and refolding kinetics. Instead, they found that the refolding rate constant was highly dependent on relative contact order, a measure of local and non-local contacts in a protein's native structure. Broom et al. (32) corroborated their result and showed that the unfolding rate constant also correlated with contact order, although less well. They concluded, “Unfolding rates correlate better with thermodynamic stability.”
Our study is the first to use the technique of thiol exchange to compare 10 homologous proteins sharing the same topology but widely divergent sequence and stability, and it is largely consistent with the conclusion of Plaxco et al. (31). All FNIII domains have the same β-sandwich structure and hence should have very similar contact orders. Eight of them have folding rate constants that vary by a factor of ∼10. In contrast, the equilibrium constants and hence stability vary by a factor of 5 × 103, similar to the 2 × 103 range of the unfolding rate. Because the refolding rate constants are similar for all of these homologous domains, the unfolding rate constant is necessarily strongly correlated with stability.
This correlation is illustrated in Fig. 6, which plots the ln of kop and kcl against the unfolding ΔG. ΔG is well correlated with ln kop, whereas correlation of ΔG with kcl is low and becomes insignificant if we remove the point for FNIII 11.
It is worth noting that the folding rate constants for these FNIII domains are at the very slow end of small proteins and domains. Jackson (14) tabulated values for ∼50 small proteins, and with few exceptions, kf ranged from 50 to 10,000 s−1. For our FNIII domains, kf mostly ranged from 0.6 to 6 s−1. Small β-sandwich proteins, including FN III domains and immunoglobulin domains, have a contact order between 17 and 19.7 (30), but the immunoglobulin domains fold much faster than the FNIII. Thus, contact order is probably not the only factor that determines folding rate constants.
The FNIII domains of FN and tenascin are arranged as tandem repeats, and one might propose that the folding rates are related to the modular structure. However, irisin is the ectodomain of a transmembrane protein, and it exists as a single FNIII domain. It had a similar slow folding rate. Additional insight will be needed to determine the underlying origin of the slow folding of FNIII domains.
Biological Significance of the Wide Range of Stabilities and Kinetics
FNIII domains are topologically identical yet have a wide range of stabilities and unfolding rates. A range of stabilities, controlled by the unfolding rates, or vice versa, may be important for the physical properties of FN. The fact that cognate FNIII domains in FN from different species are well conserved raises the question of whether the unfolding rates are an evolved trait or just an accident in nature.
FNIII 11C is the most unstable domain, being unfolded 20% of the time. We suggest that this unfolded state might provide a point of flexibility. The major segment of FN comprising FNIII 2–14 has no linkers, and crystal structures of FN7–10 and FN12–14 suggest that it behaves like a rigid rod (2, 28). FNIII 2–14 plays an important role in the compact conformation of FN (9). To form the pretzel, a region of flexibility is required in the otherwise rigid section of the FN. The unstable FNIII 11C might provide a bending point.
Comparison of Our Refolding and Kinetics of FNIII Domains with Past Studies
Previous studies of three FNIII domains, FNIII 10, FNIII 9, and TNfn3, have measured the kinetics at temperatures and pH values different from those used in the present study and therefore cannot be compared in detail with our numbers. However, Stine et al. (18) studied the kinetics of folding and unfolding of FNIII 3 at 23 °C and pH 7.4 in guanidine using Trp fluorescence. Our SX experiments were at 25 °C and pH 7.5 in urea, very similar to the conditions of Stine et al. (18). The free energy change for unfolding was very similar for the two studies (Table 4), although our SX value is a bit lower. However, the kinetics measured in the study by Stine et al. (18) were 30–60-fold faster for both unfolding and folding in the guanidine/Trp study compared with our SX kinetics. This discrepancy in the rate constants might be due to the difference in probes used, but we do not have a good explanation at present.
TABLE 4.
Comparison of the free energy of unfolding III 3 in our study (top two lines, bold) and in Stein et al. (18) (bottom two lines)
S.E. values (see Table 1) are shown in parentheses.
| Method | ΔG |
|---|---|
| kcal/mol | |
| SX | 3.4 (0.03) |
| Trp equilibrium (SVD) | 3.8 (0.2) |
| Trp equilibrium | 4 (0.26) |
| Trp kinetics | 3.89 (0.12) |
An alternative assay of domain folding kinetics was obtained in studies that used an atomic force microscope to mechanically unfold FN or tenascin. The refolding rates were determined by relaxing the stretched polypeptide and determining the number of domains that refolded after variable lag times. For the 15 FNIII domains of tenascin, a minor component refolded at 42 s−1, and the major component refolded at 0.5 s−1 (33). For polyproteins of domains FNIII 12–13, the refolding was at 0.6 s−1 (6). These rates, determined by a completely different assay, agree remarkably with the slow refolding rates that we determined with SX.
Labeling FNIII Domains in Cell Culture
Lemmon et al. (12) generated FN molecules with a buried Cys in a single FNIII domain and assayed their labeling after incorporation into FN matrix fibrils. Six of the 15 FNIII domains could be labeled by fluorescein maleimide during a 1-h incubation (12). The labeling of the domains could be due to several mechanisms: (a) tension-induced unfolding; (b) unfolding as part of FN–FN bond formation during fibril assembly; or (c) spontaneous unfolding and refolding of domains. From our study (Fig. 5), we conclude that domains FNIII 11C and 3C are open spontaneously enough to be labeled in the 1-h labeling time. On the other hand, for domains FNIII 2C, 6C, 9C, and 12C, spontaneous unfolding cannot explain their labeling. Labeling of these domains in cell culture may be due to tension-induced unfolding or to a domain opening that occurs upon bond formation in matrix assembly. The latter seems most likely, especially for FNIII 2, which was the most stable domain to mechanical unfolding (6).
Experimental Procedures
Protein Expression and Purification
BL21 or C41 bacteria were transformed with pET15b vectors containing His-tagged individual FNIII domains with the Cys mutation introduced at the location of the natural Cys in FNIII 7 (12). Irisin has a native Cys at the exact same location as the Cys in FNIII 7 (25). The sequences of the FNIII domains and the locations of the Cys are summarized in Table 5. Except for TNfn3, all domains had an N-terminal polyhistidine tag and were purified by the same procedure. A 500-ml culture in LB broth containing 1 μg/ml ampicillin was grown with shaking at 37 °C. When it reached an optical density of 0.6, isopropyl 1-thio-β-d-galactopyranoside was added to a final concentration of 400 μm to induce protein expression, and cells were harvested after 4 h. Cells were collected by centrifugation, resuspended in 10 ml of phosphate-buffered saline, and stored at −20 °C. The bacteria were thawed, and PMSF was added to a final concentration of 4 mm. Cells were sonicated for 1 min and then put on ice for 1 min. This cycle was repeated five times. The lysed cells were then centrifuged at 30,000 rpm for 20 min in a Beckman type 42.1 rotor. The His-tagged protein was purified from the supernatant using a 4-ml cobalt column. The protein eluted with 150 mm imidazole in phosphate-buffered saline. EDTA was added to 5 mm, and the protein was dialyzed against PBS. TNfn3 was purified as described by Aukhil et al. (34).
TABLE 5.
Amino acid sequences of the FNIII domains studied
The letters in lowercase type represent the His tag, the underlined letters represent the extra amino acids due to the cloning sites, and the native or introduced Cys is marked by bold and underline.
| Domain | Amino acid sequence |
|---|---|
| FNIII 1C | (m)gsshhhhhhssglvprgshmHMTSSGPVEV…SYTCKGL…FDFTTTGT |
| FNIII 2C | (m)gsshhhhhhssglvprgshmHMTSSPLVAT…ATSCNID…STSQTTGT |
| FNIII 3C | (m)gsshhhhhhssglvprgshmHMTSAPDAPP…ANSCTLS…GTPRSDGT |
| FNIII 6C | (m)gsshhhhhhssglvprgshmHMTSLQPGSS…SGSCVVS…VNKVVTGT |
| FNIII 7 | (m)gsshhhhhhssglvprgshmHMTSPLSPPT…QSSCTFD…SDTIIPGT |
| FNIII 9C | (m)gsshhhhhhssglvprgshmHMTSGLDSPT…RNSCTLT…IGQQSTGT |
| FNIII 10C | (m)gsshhhhhhssglvprgshmHMTSVSDVPR…KSTCTIS…SINYRTGT |
| FNIII 11C | (m)gsshhhhhhssglvprgshmHMTSEIDKPS…QTECTIE…VQTAVTGT |
| FNIII 12C | (m)gsshhhhhhssglvprgshmHMTSIPAPTD…SSSCVVS…VVTTLEGT |
| Irisin | (m)gsshhhhhhssglvprgshmSPSAPVN…TRSCALW…KDEVTMKE |
| TNfn3 | (m)RLDAP…SLICRRG…ETFTT |
Protein Stability Assay by Trp Fluorescence
Almost all FNIII domains have a single buried tryptophan in the B strand. When excited at 280 nm, this Trp has an emission peak at 320 nm. Denaturation of the protein in urea exposes the Trp to solvent, and the emission peak shifts to 350 nm. We used the ratio of emission at 350/320 nm as the measure of unfolding in 0–9 m urea. Individual FNIII domains were added to phosphate-buffered saline (1.4 mm KH2PO4, 0.14 m NaCl, 2.5 mm KCl, 5 mm NaH2PO4, pH 7.2) containing different amounts of urea so that the final concentration of protein was 1 μm and that of urea was 0–9 m. Phosphate-buffered saline, pH 7.2, was prepared by mixing salts in the specified proportion. The protein was incubated in the buffers for 10 min before the assay. A Shimadzu RF5301PC spectrofluorometer was used to measure the fluorescence emission spectrum between 300 and 400 nm, with excitation at 280 nm and slit widths of 3 nm for both excitation and emission. The ratio of emission at 350/320 nm was used as the measure of denaturation at each urea concentration. These data were fit to a simple two-state equilibrium model for protein folding and unfolding (Equation 2),
| (Eq. 2) |
where F represents folded protein, U is the unfolded protein, kuD is the rate constant for unfolding that varies with denaturant (D), and kfD is the rate constant for folding that varies with denaturant.
| (Eq. 3) |
| (Eq. 4) |
where KeqH2O represents the equilibrium constant for unfolding in H2O = kuH2O/kfH2O; keqD is the equilibrium constant for unfolding in denaturant (D) = kuD/kfD; R is the gas constant; T is temperature; ΔGH2O is the free energy for unfolding in H2O (the positive value indicates that unfolding is unfavorable); and ΔGD is the free energy for unfolding in denaturant concentration D.
Rearranging Equation 4 yields the following.
| (Eq. 5) |
According to the linear extrapolation theory,
| (Eq. 6) |
| (Eq. 7) |
where Dhalf represents the denaturant concentration where 50% of protein is unfolded; meq is a constant defining the denaturant dependence of ΔG (this is a negative number, meaning that higher denaturant makes unfolding favorable); and D is denaturant concentration. At equilibrium, the fraction of unfolded protein and folded protein is as follows.
| (Eq. 8) |
| (Eq. 9) |
Both fraction of unfolded protein and fraction of folded protein contribute to the total fluorescence signal, and these populations vary with denaturant concentration,
| (Eq. 10) |
where signal unfolded represents fluorescence intensity of a completely unfolded protein and signal folded is fluorescence intensity of a completely folded protein.
The equilibrium denaturation data obtained by Trp fluorescence are fit to Equation 10 to obtain the meq, Dhalf, and fluorescence intensities of a completely folded and unfolded protein. We also analyzed the denaturation of FNIII 3 by singular value decomposition analysis (35).
DTNB Is a Choice Reagent for SX
Previous work from our laboratory used 7-diethylamino-3-(4′-maleimidylphenyl)-4-methylcoumarin (CPM) to assay the spontaneous folding and unfolding of selected FNIII domains in solution (12). CPM is a thiol-reactive coumarin that is very weakly fluorescent. Upon reacting with a thiol, it forms a thioether conjugate that is highly fluorescent. Thus, the labeling of thiols can be followed over time using fluorescence. Product descriptions for CPM from different vendors give different opinions on the solubility of CPM in water, from “soluble” to “partly miscible,” to “insoluble.” Our preliminary experiments with CPM (data not shown) showed that the maximum concentration of CPM in aqueous buffer is ∼1.5 μm. The previous study (12) used a nominal 100 μm CPM concentration, resulting in an effective 1.5 μm soluble CPM in all cases. For our study, we wanted the labeling reactions to be pseudo-first order, with the dye concentration >10-fold higher than the protein. Using CPM as the thiol-reactive dye would mean that the protein concentration would have to be 150 nm or lower. Hence, we used DTNB (Ellman's reagent) (36) in our work. This dye has been used extensively for thiol quantification and is soluble in phosphate buffer up to 5 mm.
Thiol Labeling to Assay Domain Unfolding-Folding
When DTNB reacts with a Cys, a displacement reaction cleaves it to form 2-nitro-5-thiobenzoic acid anion (TNB−). This anion absorbs at 412 nm, providing a measure of the reaction.
FNIII domain and DTNB solutions were prepared separately in 50 mm phosphate buffer, pH 7.5 (14 mm KH2PO4, 37.3 mm K2HPO4). A 10 m urea stock solution was made in 50 mm phosphate buffer, and the pH levels of urea, FNIII, and DTNB stocks were adjusted to 7.5, as described in detail (37). Before the experiment, the FNIII domain and DTNB were diluted into the desired urea concentration to give 20 μm FNIII and 200 μm DTNB. The protein was incubated in the buffer containing 0–9 m urea for 10 min before mixing. We tested the 10-min incubation for the very stable FNIII 12C. We incubated FNIII 12C in urea for 1 min, 10 min, and overnight and repeated the DTNB labeling reaction at 0 m urea, 3.5 m urea (its Dhalf), and 8 m urea. The labeling kinetics were identical (data not shown) with the exception of a small loss of protein to disulfides formed overnight at the higher urea concentrations.
For slow reactions, which reached a plateau after ∼200 s, the absorbance at 412 nm was monitored with a Shimadzu UV-2401PC spectrophotometer in the kinetic mode. A quartz cuvette was used with a path length of 10 mm. 300 μl of DTNB solution was added to the cuvette followed by 300 μl of protein solution, each containing the same urea concentration. The final concentrations in the cuvette were 10 μm FNIII and 100 μm DTNB. The protein and dye were mixed by hand for 15 s in the cuvette, after which absorbance was monitored. The sample chamber was maintained at 25 °C.
For fast reactions, which reached a plateau before 200 s, we used an SX20 stopped-flow instrument from Applied Photophysics. The apparatus was first rinsed with distilled water followed by urea solution in phosphate buffer. One syringe was rinsed and filled with 20 μm protein solution in urea-phosphate buffer, and the other was rinsed and filled with 200 μm DTNB. The concentration of urea solution used to rinse the apparatus was the same as that of the protein and DTNB solutions for a particular run. The protein and DTNB were mixed 1:1 in the stopped-flow cell to initiate the reaction. FNIII and DTNB solutions were maintained in a water bath at 25 °C for 10 min before mixing, and the sample chamber was maintained at 25 °C.
Models Used for Fitting Cys Labeling Data
For each protein, the data files for all urea concentrations, from both the stopped-flow apparatus and manual spectrophotometer, were imported into a Mathematica notebook. For the spectrophotometer data, a 15-s lag was added to the data set. This lag is the time before the start of data acquisition required for manual mixing. For the stopped-flow data, the first data point was subtracted from the data set to ensure that all kinetic data started at the same point. These manipulated data were combined into one data set for fitting. This data set was globally fit to one of the models shown below. Most of the data sets fit to Model 1.
Model 1: Global Unfolding
| (Eq. 11) |
In this model, a closed domain PC opens with an opening rate constant, kopD, and the open domain PO closes with a closing rate constant, kclD. Rate constants that vary with denaturant have a superscript D. We are using kopD and kclD to designate the rates of exposure of the buried Cys. When the exposure of Cys is due only to global unfolding, then kopD = kuD and kclD = kfD (more complex cases are discussed below in Models 2 and 3).
Only the open state with the Cys exposed can react with DTNB, and it reacts with an intrinsic rate constant, kintD. This rate constant is a product of the DTNB concentration, [DTNB], and the second order rate constant for DTNB reacting with a free Cys, kchemD. Because the labeling can be affected by amino acids flanking the Cys, we determined kchemD separately for each domain. The DTNB labeling reaction is a pseudo-first order reaction, so kchemD can be determined by changing the DTNB concentration (it is the slope of the plot kobsD versus DTNB concentration). To accurately determine the kchemD, we added an additional curve at 8 m urea, where we doubled the DTNB concentration (to ∼200 μm). We also gave kchemD a urea dependence, as described by Equation 12, and used the fixed value mchem = −0.1, determined by the mchem value of FNIII 11C (the most unstable domain), for all FNIII domains except FNIII10 C (this domain gave a satisfactory fit only if mchem was adjusted to −0.35). Sridevi and Udgaonkar (21) previously suggested including mchem in the fit, and they attributed the denaturant dependence to changes in the viscosity of the buffer while increasing the denaturant concentration ([U]).
| (Eq. 12) |
Their value was mchem = −0.1, which we have used here.
Model 2: Global Unfolding Plus Local Structural Fluctuation
| (Eq. 13) |
In this model, the buried Cys is exposed to DTNB in two ways: in the unfolded state due to global unfolding and also in the folded state due to a local structural fluctuation (LSF) (22). The exposed Cys interacts with DTNB with the same rate constant kintD = kchemD [DTNB] in both cases. The LSF is represented by the equilibrium constant KopL, assuming that it occurs in the EX2 regime only. LSFs are denaturant-independent.
Model 3: Subglobal Unfolding
| (Eq. 14) |
In this model, the buried Cys is exposed to DTNB in two ways: in the unfolded state due to global unfolding and also in the folded state due to a subglobal opening event (29). The exposed Cys interacts with DTNB with the same rate constant kchemD [DTNB] in both cases. The subglobal opening event is represented by two rate constants, kopSD and kclSD, that have their individual urea dependence: mopS and mclS, respectively.
Model 4: An Alternative Mechanism to the Conventional Subglobal/Local Unfolding That Will Fit the Data Equivalently, at Least in the EX2 Regime
| (Eq. 15) |
This mechanism assumes that the dye can penetrate to the Cys thiol even in the closed state, with no opening necessary at all. By this interpretation, the conformational state of the protein determines the local environment of the thiol, which in turn determines the second-order rate constant for chemistry (kchem2D versus kchemD). All of the rate constants vary with the addition of denaturant; hence, the superscript D. The reactivity of Cys can be very sensitive to its local environment, especially the presence of charges (38). For instance, a perturbation of the thiol pKa of just 0.3 units would alter kchem by a factor of 2 (27). We note that this mechanism gives mathematically equivalent reaction kinetics to the conventional local opening mechanism; the two mechanisms cannot be distinguished from SX data alone. We describe it here as an alternative mechanistic interpretation.
For Model 1, the simplest case, the observed rate constant of labeling is given by the following.
| (Eq. 16) |
Kinetics of labeling can occur via three regimes: EX1, EX2, and EXX. These regimes apply to the native state and low urea, where kopD ≪ kclD. They do not apply to higher urea, where kopD ≃ kclD, nor in any case where kopD ≥ kintD. In all previous SX studies, these regimes were identified to simplify the analysis of SX data by fitting the individual transients to an observed rate constant, kobs. Because this introduces unnecessary fitting errors, we chose not to fit to kobs but instead to globally fit all of the SX transients for a given domain, collected over a wide range of urea concentrations, to the parameters of the fitting model. This made designation of the SX regime unnecessary except to enable proper interpretation of parameter values (see “Results”). In the EX1 and EX2 regimes, the relationship of kobsD to the other rate constants shown in Equation 16 reduces to simpler forms.
EX1 Regime
When kclD ≪ kintD, the observed rate constant (kobsD) is approximately equal to the opening rate constant kopD (Equation 17). The kinetic parameter kop can be obtained directly from data in this regime. Keq and meq can be determined if denaturation is achieved at high [urea]. Thus, kcl can be deduced, even though in the EX1 regime the observed kinetics are determined only by kop.
| (Eq. 17) |
EX2 Regime
When kclD ≫ kintD, the observed rate constant (kobsD) is equal to the product of the equilibrium constant of opening (keqD = kopD/kclD) and the intrinsic rate constant kintD (Equation 18). The thermodynamic parameter keqD can be obtained directly from data in this regime. Kinetic parameters are not obtained in this regime
| (Eq. 18) |
EXX Regime
When the ratio between kclD and kintD is within the range 0.1–10 (i.e. kclD ≃ kintD), the observed rate constant (kobsD) is the more complex function of all rate constants (Equation 16). Although mathematically complex, this is the regime that provides the most powerful fitting of the kinetic parameters.
It is important to emphasize that we do not fit our kinetics data at each denaturant concentration to kobsD. Equations 16–18 are presented only to emphasize the importance of the data spanning these different regimes and the different parameters obtained in each regime.
Our kinetics data obtained over a wide range of urea for a particular domain were globally fit to a model (Model 1, Model 2, or Model 3) that includes the urea dependence of opening and closing. Differential equations describing the time dependence of all species were solved either with the kinetic matrix method (39) or by numerical integration in Mathematica. For all of the FNIII domains studied here except for FNIII 10C, we used the rate matrix method. FNIII 10 was fit using Model 3 and was too complicated for Mathematica to fit using the rate matrix method. Hence, we used the numerical integration method to fit those data.
As an example, the differential equations describing Model 1 are presented below (see Equation 1). The rates of formation of PC, PO, and P-TNB are given by the following.
| (Eq. 19) |
| (Eq. 20) |
| (Eq. 21) |
The kinetic matrix method represents Equations 19–21 as a rate matrix, whose off-diagonal elements correspond to the rate constants for the reaction from the column state to the row state and whose diagonal elements are the negative sum of all other elements in the same column.
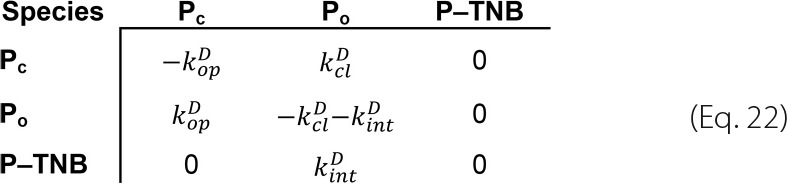 |
The time-dependent concentrations of all species are determined from eigenvalues and eigenvectors of this rate matrix (39).
The addition of urea shifts the equilibrium toward the open state by altering the rate constants kopD and kclD. For a two-state process, the logarithm of the rate constants of opening and closing show a linear dependence on the concentration of denaturant ([U]), as described by Equations 23 and 24. This is the formalism used in previous SX studies (22, 23).
| (Eq. 23) |
| (Eq. 24) |
Hence, in our fitting model we include this linear dependence.
On the other hand, for FNIII 10, Equations 19–21 were numerically integrated to obtain the population of all species as a function of time. The absorbance signal (Abs) is due to the formation of the reacted protein with DTNB (P*TNB). Thus, the detected signal is a reflection of the concentration of only this species. The maximum absorbance is reached when the population of P*TNB reaches 1 (AbsMax), so the time-dependent absorbance is as follows.
| (Eq. 25) |
This is the function fitted to the experimental data. The function describing the time dependence of the population of P*TNB is mathematically complex and depends on the following parameters: kopD, kclD, kintD, and AbsMax. It is important to note that we are primarily interested in obtaining the kopH2O and kclH2O for all of the domains studied because, in most cases, these parameters correspond to kfH2O and kuH2O constants for these domains (buried Cys is exposed due to global unfolding).
The AbstD is now a set of complex mathematical equations comprising the following parameters: kopH2O, kclH2O, mop, mcl, kintH2O, and AbsMax. Mathematica fits the kinetics data from all of the different urea concentrations globally to these parameters, and the rate constants in water and their urea dependences are obtained.
The equilibrium constant and its associated free energy vary linearly with denaturant, giving an meq. This is related to the mop and mcl by the following.
| (Eq. 26) |
| (Eq. 27) |
| (Eq. 28) |
Finally, the rate constants kopH2O and kclH2O can be transformed into the more obvious half-life as follows.
| (Eq. 29) |
| (Eq. 30) |
Author Contributions
R. S. designed the study, did the experimental measurements, and wrote the paper. T. O. contributed to the initial conception and design of the experiments. H. P. E. and T. G. O. participated in study design and refinement of procedures and analysis and participated in writing the paper. T. G. O. established the global fitting procedure. All authors analyzed the results and approved the final version of the manuscript.
Supplementary Material
This work was supported by National Institutes of Health Grant CA 47056 (to H. P. E.). The authors declare that they have no conflicts of interest with the contents of this article. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

This article contains supplemental Figs. 1–12.
- FN
- fibronectin
- SX
- thiol exchange
- DTNB
- 5,5-dithiobis-(2-nitrobenzoic acid)
- CPM
- 7-diethylamino-3-(4′-maleimidylphenyl)-4-methylcoumarin
- TNB
- 2-nitro-5-thiobenzoate
- LSF
- local structural fluctuation.
References
- 1. Skorstengaard K., Jensen M. S., Sahl P., Petersen T. E., and Magnusson S. (1986) Complete primary structure of bovine plasma fibronectin. Eur. J. Biochem. 161, 441–453 [DOI] [PubMed] [Google Scholar]
- 2. Leahy D. J., Aukhil I., and Erickson H. P. (1996) 2.0 Å crystal structure of a four-domain segment of human fibronectin encompassing the RGD loop and synergy region. Cell 84, 155–164 [DOI] [PubMed] [Google Scholar]
- 3. Ohashi T., Kiehart D. P., and Erickson H. P. (1999) Dynamics and elasticity of the fibronectin matrix in living cell culture visualized by fibronectin-green fluorescent protein. Proc. Natl. Acad. Sci. U.S.A. 96, 2153–2158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Sivakumar P., Czirok A., Rongish B. J., Divakara V. P., Wang Y. P., and Dallas S. L. (2006) New insights into extracellular matrix assembly and reorganization from dynamic imaging of extracellular matrix proteins in living osteoblasts. J. Cell Sci. 119, 1350–1360 [DOI] [PubMed] [Google Scholar]
- 5. Erickson H. P. (1994) Reversible unfolding of FN3 domains provides the structural basis for stretch and elasticity of titin and fibronectin. Proc. Natl. Acad. Sci. U.S.A. 91, 10114–10118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Oberhauser A. F., Badilla-Fernandez C., Carrion-Vazquez M., and Fernandez J. M. (2002) The mechanical hierarchies of fibronectin observed with single-molecule AFM. J. Mol. Biol. 319, 433–447 [DOI] [PubMed] [Google Scholar]
- 7. Smith M. L., Gourdon D., Little W. C., Kubow K. E., Eguiluz R. A., Luna-Morris S., and Vogel V. (2007) Force-induced unfolding of fibronectin in the extracellular matrix of living cells. PLoS Biol. 5, e268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Erickson H. P., and Carrell N. A. (1983) Fibronectin in extended and compact conformations: electron microscopy and sedimentation analysis. J. Biol. Chem. 258, 14539–14544 [PubMed] [Google Scholar]
- 9. Johnson K. J., Sage H., Briscoe G., and Erickson H. P. (1999) The compact conformation of fibronectin is determined by intramolecular ionic interactions. J. Biol. Chem. 274, 15473–15479 [DOI] [PubMed] [Google Scholar]
- 10. Erickson H. P. (2002) Stretching fibronectin. J. Muscle Res. Cell Motil. 23, 575–580 [DOI] [PubMed] [Google Scholar]
- 11. Maurer L. M., Ma W., and Mosher D. F. (2015) Dynamic structure of plasma fibronectin. Crit. Rev. Biochem. Mol. Biol. 51, 213–227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Lemmon C. A., Ohashi T., and Erickson H. P. (2011) Probing the folded state of fibronectin type III domains in stretched fibrils by measuring buried cysteine accessibility. J. Biol. Chem. 286, 26375–26382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Johnson C. P., Tang H. Y., Carag C., Speicher D. W., and Discher D. E. (2007) Forced unfolding of proteins within cells. Science 317, 663–666 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Jackson S. E. (1998) How do small single-domain proteins fold? Fold Des. 3, R81–R91 [DOI] [PubMed] [Google Scholar]
- 15. Plaxco K. W., Spitzfaden C., Campbell I. D., and Dobson C. M. (1997) A comparison of the folding kinetics and thermodynamics of two homologous fibronectin type III modules. J. Mol. Biol. 270, 763–770 [DOI] [PubMed] [Google Scholar]
- 16. Clarke J., Hamill S. J., and Johnson C. M. (1997) Folding and stability of a fibronectin type III domain of human tenascin. J. Mol. Biol. 270, 771–778 [DOI] [PubMed] [Google Scholar]
- 17. Cota E., Hamill S. J., Fowler S. B., and Clarke J. (2000) Two proteins with the same structure respond very differently to mutation: the role of plasticity in protein stability. J. Mol. Biol. 302, 713–725 [DOI] [PubMed] [Google Scholar]
- 18. Stine J. M., Sun Y., Armstrong G., Bowler B. E., and Briknarová K. (2015) Structure and unfolding of the third type III domain from human fibronectin. Biochemistry 54, 6724–6733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Ballery N., Desmadril M., Minard P., and Yon J. M. (1993) Characterization of an intermediate in the folding pathway of phosphoglycerate kinase: chemical reactivity of genetically introduced cysteinyl residues during the folding process. Biochemistry 32, 708–714 [DOI] [PubMed] [Google Scholar]
- 20. Ballery N., Minard P., Desmadril M., Betton J. M., Perahia D., Mouawad L., Hall L., and Yon J. M. (1990) Introduction of internal cysteines as conformational probes in yeast phosphoglycerate kinase. Protein Eng. 3, 199–204 [DOI] [PubMed] [Google Scholar]
- 21. Sridevi K., and Udgaonkar J. B. (2002) Unfolding rates of barstar determined in native and low denaturant conditions indicate the presence of intermediates. Biochemistry 41, 1568–1578 [DOI] [PubMed] [Google Scholar]
- 22. Feng Z., Butler M. C., Alam S. L., and Loh S. N. (2001) On the nature of conformational openings: native and unfolded-state hydrogen and thiol-disulfide exchange studies of ferric aquomyoglobin. J. Mol. Biol. 314, 153–166 [DOI] [PubMed] [Google Scholar]
- 23. Malhotra P., and Udgaonkar J. B. (2014) High-energy intermediates in protein unfolding characterized by thiol labeling under nativelike conditions. Biochemistry 53, 3608–3620 [DOI] [PubMed] [Google Scholar]
- 24. Erickson H. P. (2013) Irisin and FNDC5 in retrospect: an exercise hormone or a transmembrane receptor? Adipocyte 2, 289–293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Schumacher M. A., Chinnam N., Ohashi T., Shah R. S., and Erickson H. P. (2013) The structure of irisin reveals a novel intersubunit β-sheet fibronectin type III (FNIII) dimer: implications for receptor activation. J. Biol. Chem. 288, 33738–33744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Vakonakis I., Staunton D., Rooney L. M., and Campbell I. D. (2007) Interdomain association in fibronectin: insight into cryptic sites and fibrillogenesis. EMBO J. 26, 2575–2583 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Snyder G. H., Cennerazzo M. J., Karalis A. J., and Field D. (1981) Electrostatic influence of local cysteine environments on disulfide exchange kinetics. Biochemistry 20, 6509–6519 [DOI] [PubMed] [Google Scholar]
- 28. Sharma A., Askari J. A., Humphries M. J., Jones E. Y., and Stuart D. I. (1999) Crystal structure of a heparin- and integrin-binding segment of human fibronectin. EMBO J. 18, 1468–1479 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Englander S. W., and Kallenbach N. R. (1983) Hydrogen exchange and structural dynamics of proteins and nucleic acids. Q. Rev. Biophys. 16, 521–655 [DOI] [PubMed] [Google Scholar]
- 30. Clarke J., Cota E., Fowler S. B., and Hamill S. J. (1999) Folding studies of immunoglobulin-like β-sandwich proteins suggest that they share a common folding pathway. Structure 7, 1145–1153 [DOI] [PubMed] [Google Scholar]
- 31. Plaxco K. W., Simons K. T., and Baker D. (1998) Contact order, transition state placement and the refolding rates of single domain proteins. J. Mol. Biol. 277, 985–994 [DOI] [PubMed] [Google Scholar]
- 32. Broom A., Gosavi S., and Meiering E. M. (2015) Protein unfolding rates correlate as strongly as folding rates with native structure. Protein Sci. 24, 580–587 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Oberhauser A. F., Marszalek P. E., Erickson H. P., and Fernandez J. M. (1998) The molecular elasticity of the extracellular matrix protein tenascin. Nature 393, 181–185 [DOI] [PubMed] [Google Scholar]
- 34. Aukhil I., Joshi P., Yan Y., and Erickson H. P. (1993) Cell- and heparin-binding domains of the hexabrachion arm identified by tenascin expression proteins. J. Biol. Chem. 268, 2542–2553 [PubMed] [Google Scholar]
- 35. Gualfetti P. J., Bilsel O., and Matthews C. R. (1999) The progressive development of structure and stability during the equilibrium folding of the α subunit of tryptophan synthase from Escherichia coli. Protein Sci. 8, 1623–1635 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Ellman G. L. (1959) Tissue sulfhydryl groups. Arch. Biochem. Biophys. 82, 70–77 [DOI] [PubMed] [Google Scholar]
- 37. Walters J., Milam S. L., and Clark A. C. (2009) Practical approaches to protein folding and assembly: spectroscopic strategies in thermodynamics and kinetics. Methods Enzymol. 455, 1–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Jensen K. S., Pedersen J. T., Winther J. R., and Teilum K. (2014) The pKa value and accessibility of cysteine residues are key determinants for protein substrate discrimination by glutaredoxin. Biochemistry 53, 2533–2540 [DOI] [PubMed] [Google Scholar]
- 39. Pogliani L., Berberan-Santos M. N., and Martinho J. M. (1996) Matrix and convolution methods in chemical kinetics. J. Mathemat. Chem. 20, 193–210 [Google Scholar]
- 40. Soteriou A., Clarke A., Martin S., and Trinick J. (1993) Titin folding energy and elasticity. Proc. Biol. Sci. 254, 83–86 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


