Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Jan 20;7:40596. doi: 10.1038/srep40596

Dynamical states, possibilities and propagation of stress signal

Md Zubbair Malik 1,2, Shahnawaz Ali 1,2, Soibam Shyamchand Singh 1,2, Romana Ishrat 2, R K Brojen Singh 1,a
PMCID: PMC5247771  PMID: 28106087

Abstract

The stress driven dynamics of Notch-Wnt-p53 cross-talk is subjected to a few possible dynamical states governed by simple fractal rules, and allowed to decide its own fate by choosing one of these states which are contributed from long range correlation with varied fluctuations due to active molecular interaction. The topological properties of the networks corresponding to these dynamical states have hierarchical features with assortive structure. The stress signal driven by nutlin and modulated by mediator GSK3 acts as anti-apoptotic signal in this system, whereas, the stress signal driven by Axin and modulated by GSK3 behaves as anti-apoptotic for a certain range of Axin and GSK3 interaction, and beyond which the signal acts as favor-apoptotic signal. However, this stress system prefers to stay in an active dynamical state whose counterpart complex network is closest to hierarchical topology with exhibited roles of few interacting hubs. During the propagation of stress signal, the system allows the propagator pathway to inherit all possible properties of the state to the receiver pathway/pathways with slight modifications, indicating efficient information processing and democratic sharing of responsibilities in the system via cross-talk. The increase in the number of cross-talk pathways in the system favors to establish self-organization.

Natural systems are generally self-organized. Such systems, which evolve with the emergence of global coherent patterns out of local interactions1, are non-linear in nature2 with diverge equilibrium states3. Their spatio-temporal cross-talk with the environment and systems surrounding them try to resist any significant change in them3,4, but adapted to the changes if they find better fit new combinations provided the possibilities of adaptation subjected to a large number of stable states5. The responsibilities in their organization are distributed democratically among the individual components in the system6, favouring the coherence of the functions of individual components in the systems via interaction. To characterize such complex systems, emergent properties of both the systems and individual components constituting the systems at fundamental level are needed to be studied7,8. If one studies the dynamics of such complex system, there could be possibilities of existence of a number of perturbation driven dynamical states exhibiting distinct dynamical behavior in each state, which may have short or long life span, on which the system looks for its comfortable and adaptable state to exist. Since the system is generally far from equilibrium3 and non-linear2, it will hang around these dynamical states for better survival. In such studies, the systems’ properties are inherited to their respective time series data. Systematic dealing with these time series data could provide inherent properties of the complex system. Starting from the classical Mandelbrot’s mutifractal definition9, for a heterogeneous time series of window size T(ϕt), with scale factor ϕ and time sequence ‘t’, the multifractal function M follow the following relationships,

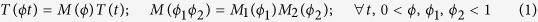graphic file with name srep40596-m1.jpg

Self-similar process satisfy the simpler scaling law, M(ϕ) = ϕD, where, D is self-similarity dimension10. Hence, time series data of a system’s dynamics generally have statistically independent multiple of such scaling behaviors exhibiting multifractal nature due to scale dependent broad probability distributions of the time series, and different long and short range correlations amplified by small and large fluctuations in the time series11. Then we can address fundamental issues of the system, namely, interference of noise in system dynamics, patterns of order driven by fluctuations2, perturbation induced change of dynamical states12, system’s adaptation to a change, and their implications in real biological systems.

Cellular processes are generally driven by intrinsic and extrinsic fluctuations due to random inter-molecular interaction in various cellular pathways and molecular cross-talks with the surrounding environments respectively13,14. Stress in such processes, due to external influences, abnormalities in the genetic regulations and failures of some molecular mechanisms, are propagated spatio-temporally throughout the network perturbing the pathways encountered along its path. However, the nature of stress propagation and management in the complex cellular processes is still an open question. We address these issues by modeling cross-talk of Notch-Wnt pathways in animal sometogenesis15,16,17,18 and p53 regulatory network19 via stress inducer nutilin molecule20,21,22. Somitogenesis, a process of periodic formation of somites in the presomitic mesoderm23, is regulated by the periodic expression of genes responsible in the interaction of Notch, Wnt and fibroblast growth factor pathways18,24, but control mainly by Notch and Wnt cross-talk via GSK325. This Notch-Wnt cross-talk regulates their transcriptional activities and their stabilities26; and is responsible for variety of biological functions, for example, wing development in Drosophila27, T-cell development and differentiation28, self-renewal capacity of stem cells29, in a variety of carcinogenesis, such as, positive regulation in colorectal cancer cells30, and enhancing their expression in ovarian cancer31. Then p53, which is negative regulator of cellular proliferation, differentiation, and apoptotic inducer32, acts antagonistically to the Notch; whereas Notch can either hold back or elevates p53 activity33. This cross-talk of p53 and Notch-Wnt pathways by means of stress imparted in the pathways can have different regulatory mechanisms, namely, p53 activated apoptosis in T-cell Lymphocytes is suppressed by Notch signaling34, Notch activates p53 in neuronal progenitor cell35,36, alteration of p53 and Notch in cancer cell37 etc. However, these complicated cross-talks are still far from proper understanding at fundamental level. In the present work we study the interaction of p53 and Notch-Wnt pathways via stress signal which compel the system at different dynamical states, and how the system selects comfortable state out of various possibilities and adapts on it.

Results

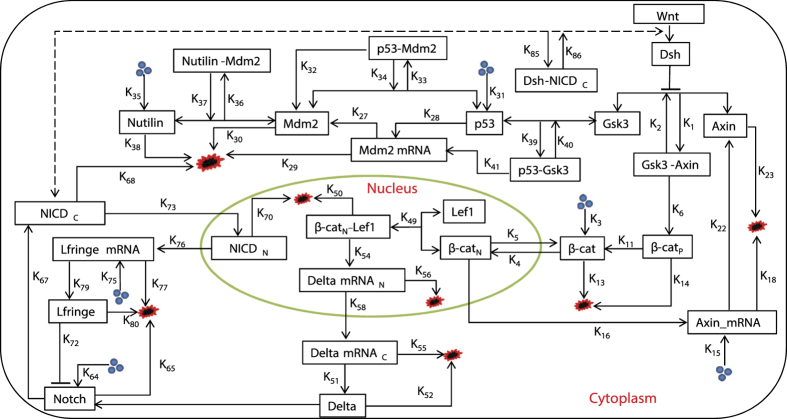
Regulatory biochemical network model (Fig. 1), which allows cross-talk between p53 and Wntch (Wnt and Notch) signaling pathways, are proposed based on some experimental reports (see Methods) to investigate complex signaling processes among them and behaviors of possible dynamical states those could correspond to certain cellular states.

Figure 1. The schematic diagram of Notch − Wnt − p53 cross-talk model.

Figure 1

Open in a new tab

Dynamical states driven by stress signal

The dynamical state of a system, we define here, is the dynamics of the system governed by a time series, T(t) which follow Mandelbrot’s Multifractal behavior38 throughout the time series,

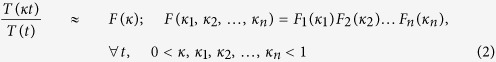graphic file with name srep40596-m2.jpg

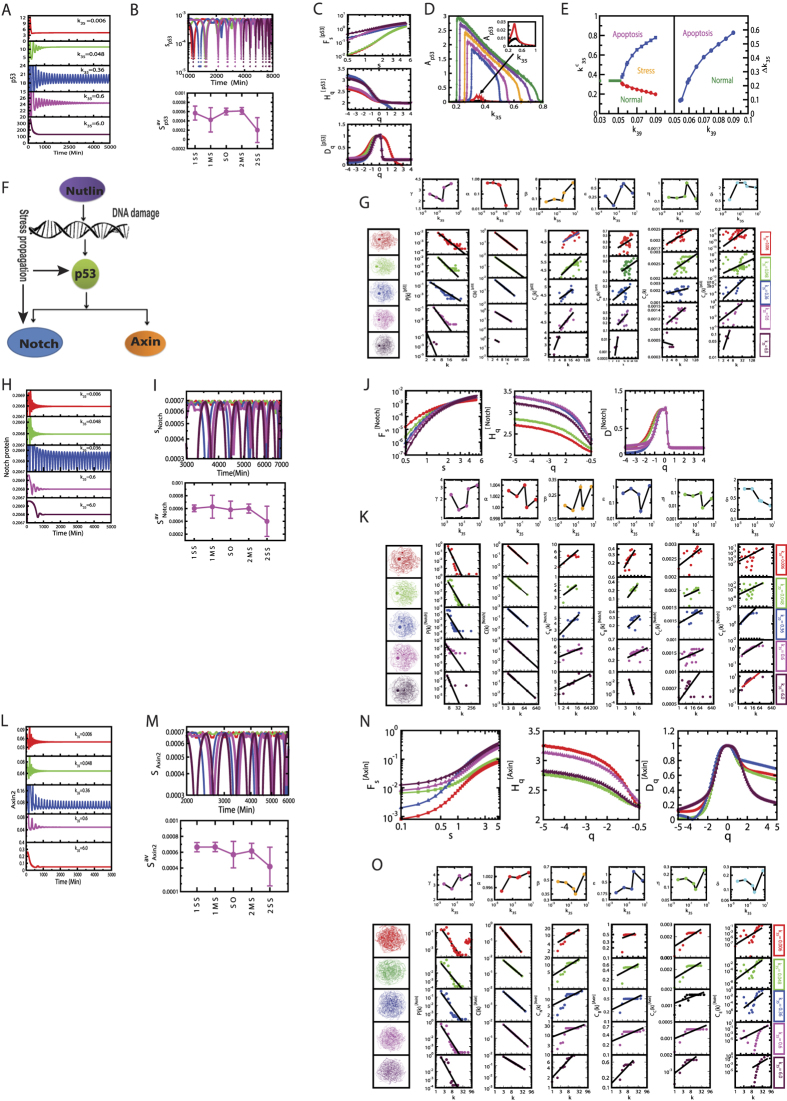
where, the fractal function Fi(κi) follows simple power law Fi(κi) ~ κD with fractal dimension D. Variation in concentration of nutlin trigger DNA damage20,21,22 (larger the nutlin concentration in the system, stronger the DNA damage), as a consequence stress signal is imparted to the system via p53 which is very sensitive to the stress signal. p53 dynamic become stabilized for low concentration of nutlin (small value of k35 ≤ 0.006), where, 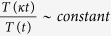Inline graphic, which may correspond to nearly normal dynamical state of the system (Fig. 2A upper panel). Increase in k35 (0.006 < k35 < 0.31) drives the p53 dynamics in the mixed dynamical state, damped for a certain range of time and then stabilized, which can be expressed as, 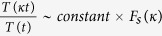Inline graphic, where, Fs(κ) is for certain range of time (time period and wavelength are constant, but amplitude decays). This may indicate that the system is activated first due to induced stress, and upon expended the stress the system comes back to normal. As k35 increases the range of Ts(κ) also increases. For significant strong stress (0.32 < k35 < 0.52), the p53 dynamics become sustain oscillation dynamical state (range of Ts becomes infinite), which can be represented by, 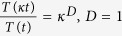Inline graphic, κ is an integer, and T(t) becomes time period in this case. This dynamical state may correspond to activated state of the system where active interaction of the molecular species is involved. Further increase in k35 (0.58 < k35 < 5.1) again brings back to the mixed dynamical state. Excess stress due to nutilin (k35 > 5.3) drives the dynamics to stabilized dynamical state, which may correspond to apoptosis. Thus we could able to find five such dynamical states as listed in Table 1. The system switch to these various dynamical states in response to the stress signal.

Figure 2.

Figure 2

Open in a new tab

Dynamical states of stress p53 driven by nutlin, and stress propagation: (A) dynamical states of p53 for different k35 values, (B) complexity measurement characterized by calculated permutation entropy Sp53 values of the corresponding dynamical states. (C) Multifractal calcualations of the dynamical states: plots of Fs vs s, 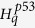Inline graphic vs q and Dq vs q, (D) Ap53 as a function of k35 for various values of k39:…., (E) phase diagram in the parameter space (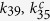Inline graphic), where 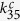Inline graphic are the values of k35 cut by horizontal line, and Δk35 is the range of k35 occupied by sustain oscillation, (F) schematic diagram of stress signal propagation, (G) topological properties of networks constructed from the time series of corresponding dynamical states: P(k), C(k), Cn(k), CB(k), CC(k) and CE(k) as a function of degree k, (H) the propagated signal received by Notch and corresponding dynamical states, (I) permutation entropy (HNotch) calculation of the dynamical states, (J) Multifractal measures of dynamical states of Notch: plots of Fs vs s, 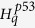Inline graphic vs q and Dq vs q, (K) topological properties of the corresponding dynamical states: P(k), C(k), Cn(k), CB(k), CC(k) and CE(k) as a function of degree k, (L) dynamical states of Axin due to propagated signal, and (M) corresponding permutation entropy (HAxin) values, (N) Multifractal calculations, (O) topological properties of the networks constructed from the Axin dynamical states.

Table 1. Different Dynamical state.

S.No. Dynamical state Description Reference
1. First steady state May correspond to normal cell. 72, 73, 74, 75
2. First damped oscillation state Stress (weak) induced cell that could able to repair back the changes in the cell and may come back to the normal condition. 72, 73, 74, 75
3. Sustain oscillation state Active state of the cell where active interaction of molecules are going on in the cell. 72, 73, 74, 75
4. Second damped oscillation state Damped oscillation state where the strong stress in p53 due to stress inducer nutlin and axin may become toxic to the system. In this state cell is associated with large stress, which cannot be repaired back and may probably go to apoptosis after some time. see Supplementary information
5. Second steady state Apoptotic state where repairment of pathways cannot force cell to become normal in excess stress condition, thus cell chooses to destroy itself. 72, 73, 74, 75
Open in a new tab

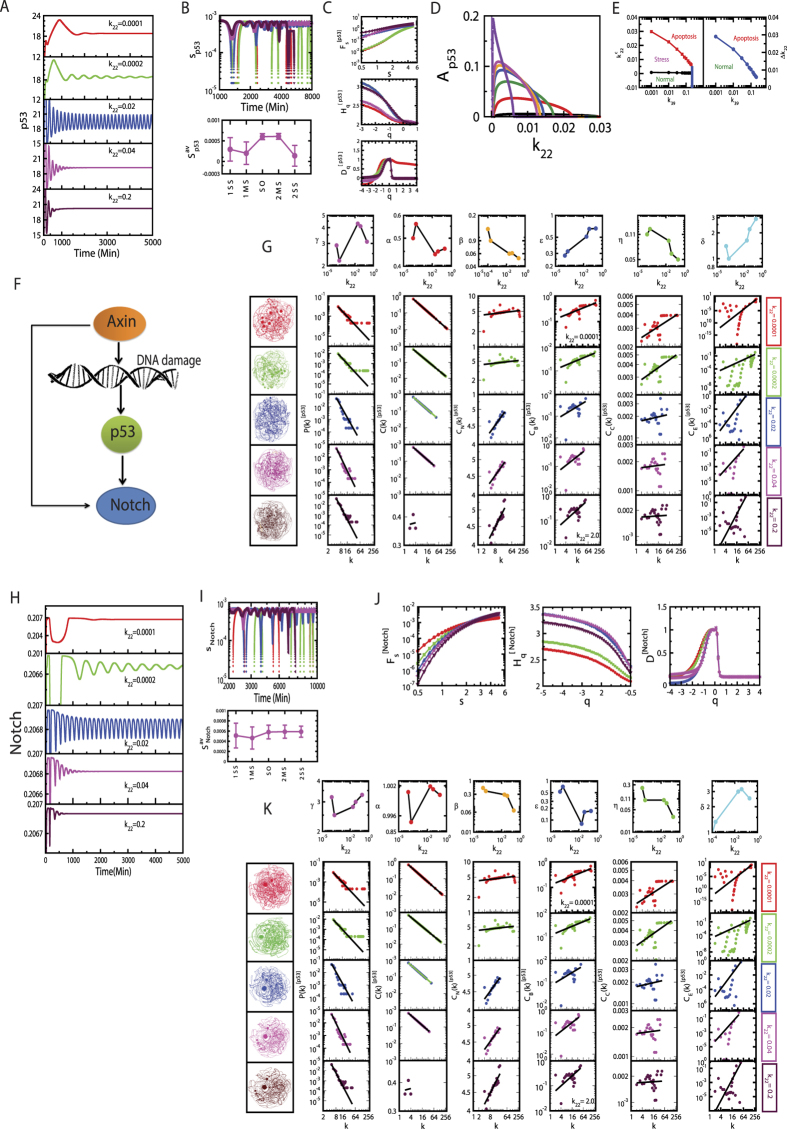
Another way to impart stress signal to the system could be by changing Axin concentration (changing k22) in the system which is reflected in the dynamics of p53 (Fig. 3A). Similar dynamical states, as obtained in the case of nutlin, can also be seen driven by Axin.

Figure 3.

Figure 3

Open in a new tab

Dynamical states of stress p53 driven by Axin, and stress propagation: (A) dynamical states of p53 for different k22 values, (B) permutation entropy Sp53 values of the corresponding dynamical states. (C) Multifractal calulations: plots of Fs vs s, 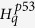Inline graphic vs q and Dq vs q, (D) Ap53 as a function of k22 for various values of k39:…., (E) phase diagram in the parameter space (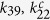Inline graphic), and Δk22 is the range of k22 occupied by sustain oscillation, (F) schematic diagram of stress signal propagation, (G) topological properties of networks of corresponding dynamical states: P(k), C(k), Cn(k), CB(k), CC(k) and CE(k) as a function of degree k, (H) the propagated signal receied by Notch and corresponding dynamical states, (I) permutation entropy (HNotch) calculations, (J) Multifractal measures, (K) topological properties of the corresponding dynamical states.

Complexity in the dynamical states

The complexity of the dynamical states (Figs 2A,H,L and 3A,H) driven by stress inducer nutlin and Axin can be measured by calculating permutation entropy (Si, i → p53, Notch, Axin) of these states (see Methods). The calculated Si magnitudes are in the order: Si(first stabilized state) < Si(first mixed state) < Si(sustain oscillation state) < Si(second mixed state) < Si(second stabilized state) (Figs 2B,I,M and 3B,I). The first stabilized dynamical state may correspond to normal, which is an ordered state, giving the minimum value of Si. Whereas, the second stabilized dynamical state corresponds to apoptotic state, which is a disorder state, providing maximum value of Si.

Multifractal due to long range correlation

The stress driven p53 time series are multifractal due to short and long correlations in the time series and they might follow some probability distributions. The fluctuation variation function Fs (Fig. 2C upper panel) follows power law with fluctuation parameter s (log-log plots show approximately straight line) for all five dynamical states (Fig. 2C) with varied slopes which correspond to Hurst exponents Hq. The Hq magnitudes with respect q for different dynamical states are as follows: Hq(sustain oscillation) > Hq (second stabilized state) > Hq(first and second mixed state)Hq(first stabilized state). Since large Hq value corresponds to large fluctuations introduced in the system due to active molecular interaction driven by stress signal or internal molecular mechanisms constituted, active (sustain oscillation) dynamical state associates maximum fluctuations on an average, whereas stabilized dynamical states (both first and second) have comparatively much lower fluctuations. Since natural systems are far from equilibrium3, fluctuations driven systems might incorporate the fluctuations in positive way2 to establish their own adaptable state for better existence5. Further, Hq variation is prominent mainly in negative q regime as compared to the positive q regime, indicating multifractal nature in the time series is contributed mainly by long range correlation. This behavior is also reflected in the singularity function Fα as the function of α.

The multifractal properties of the p53 time series for various dynamical states induced by Axin show similar behavior as obtained in the case of nutlin driven p53 dynamical states (Fig. 3C). The only slight change in the nature of singularity function Fα which show similar behavior for all dynamical states.

Complex stress management

The amplitude death scenario in p53 dynamics (Ap53) as a function of k35 (Fig. 2D) could be signatures of normal (first stabilized dynamical state) and apoptotic (second stabilized dynamical state) cellular states. Monotonic is increasing and decreasing of Ap53 as a function of k35 correspond to first and second mixed states, where removing the stress may come back to either normal or apoptotic state. Slow change in Ap53 corresponds to sustain oscillation dynamical state, where the system is strongly activated due to active molecular interaction induced by strong stress in the system.

GSK3, the main mediator of the Notch-Wnt-p53 cross-talk, could probably regulate the transition of the system at these dynamical states by managing the stress signal. Permitting the increase in GSK3 concentration through biochemical mechanism in the system allows the system to stay in active state (sustain oscillation dynamical state) for larger range of k35 (Fig. 2D and E), trying to save the system from apoptotic phase. Therefore, GSK3 favors the system to stay in normal state for small stress signal, whereas for significantly larger stress signal, it forces the system or the system itself prefers to stay in the active state to prevent from apoptotic state (Fig. 2E). Therefore, nutlin induced stress signal along with GSK3 acts as anti-apoptotic signal in the system.

On the other hand, this stress management by GSK3 is quite different for this system when stress in it is introduced by Axin via k22 (Fig. 3D and E). Even though the dynamical states, which we found in the case of nutlin driven stress p53 dynamics, also obtained in this case, the pattern is quite opposite. In this case, increase in the concentration of mediator GSK3 (k39) the range of k22 within which sustain oscillation dynamical state can be observed becomes decreased (Fig. 3D). This increase in k39 force the available, accessible area of active state to diminish (Fig. 3E), favoring the system to go to apoptotic state. Hence, the stress signal modulated by Axin along with GSK3 acts as favored-apoptotic signal.

Complicated self-organization

The time series of the dynamical states of stress p53 induced by nutlin (Fig. 2A) can be transformed into their respective complex networks (Fig. 2G) using visibility graph algorithm (see Methods), where, properties of the system, reflected in p53 dynamical states, can be studied using topological properties of the constructed networks. The probability of degree distribution P(k), clustering co-efficient C(k) and neighborhood connectivity Cn(k) follow power law behaviour as a function of the degree k,

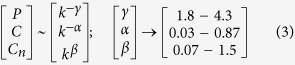graphic file with name srep40596-m6.jpg

The power law behaviour in these topological properties are verified and confirmed by using the fitting technique to test power law distribution proposed by Clauset et al.39, where all statistical p-values for all data, calculated against 2500 random samplings, are found to be larger than 0.1 which is the critical limit, and goodness of fits are found to be less than and equal to 0.3. The power law behaviours of these three topological parameters are the signatures of Hierarchical features40 in these networks exhibiting multifractal nature in their structures. The lowest value of γ = 2.3 in sustain oscillation dynamical state exhibits importance of, not only system level organization of modules, but also few hubs in the network regulation. Networks corresponding to other dynamical states also follow these hierarchical properties, but the network constructed from second stabilized state (apoptotic state) lacks most of the network properties (γ = 4.3, α = 0.03, β = 1.5) due random distribution in the dynamics.

Centrality measurements, namely, betweenness CB, closeness CC, and eigen-vector CE centralities (see Method), which provide the nature of information processing and to identify most influencing nodes in the network, again follow power low behaviors as a function of k (Fig. 2G),

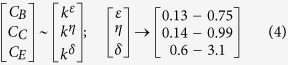graphic file with name srep40596-m7.jpg

We again verify the qualification of the respective power laws to the corresponding data with the statistical technique applied above39. The increase in these centrality values as a function of degree (k) indicate that hubs are most influencing nodes, and take significant roles in information processing in the network. Even though the absence of these hubs do not cause network breakdown, they and their interaction among them have better responsibilities in regulating the network in each dynamical state.

The constructed networks from the dynamical states of stress p53 triggered by Axin (Fig. 3G) also show similar hierarchical properties as obtained in nutlin induced stress p53 networks. The calculated values of exponents of power law topological parameters are,

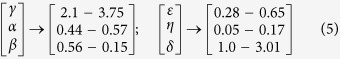graphic file with name srep40596-m8.jpg

The first set of parameter values in (5) shows significant roles of hubs after sustain oscillation dynamical state. The second set of parameter shows weaker information processing as compared to nutlin induced p53 case.

Propagation of stress signal

The stress signal exhibited in p53 dynamics induced either nutlin or Axin concentration variation is propagated to Notch and Wnt pathways through intermediate molecular interaction, and are showing up in the dynamical states of Notch and Axin (Fig. 2H and L), and Notch (Fig. 3H) respectively. The multifractal properties of dynamical states of Notch due to stress signal propagated from p53 either induced by nutlin (Fig. 2J and N), or Axin (Fig. 3J) show very similar nature as compared to that of p53 dynamical states (Fig. 2C). Further, topological parameters of the networks corresponding to dynamical states of stress receivers Notch and Wnt (due to stress inducer nutlin) (Fig. 2K and O); and Notch (due to stress inducer Axin) (Fig. 3K) exhibit similar properties as compared to the properties of the networks corresponding to dynamical states of stress propagator p53. This closely similar properties of the stress signal propagators and receivers reveals the inheritance of fundamental properties of the stress signal from propagators to receivers. Hence, the responsibilities, beneficials and injuries due to stress signal are approximately equally distributed among the important candidate proteins and/or genes in the interacting pathways. However, depending on the nature of stress signal and magnitude, and stress receivers, the inherited properties are modified according to their needs and comfortability.

Since the response of the stress propagated among the cross-talking pathways are received excellently via various mediators, the responsibilities of protecting the system as whole from any change due to external perturbations or failures in internal mechanisms might be distributed approximately equally among these pathways.

Signature of assortivity

Hierarchically organized networks generally qualify most of the features of self-organization, namely, fractal behaviours of topological parameters, system level organization of modules and absence of central control mechanism (removal of hubs do not cause network breakdown)41,42. However, neighborhood connectivity in these networks constructed from the dynamical states of stress p53 driven by either nutlin or Axin follows, Cn(k) ~ kβ, which is power law of positive exponent (Figs 2G and 3G). The fractal behaviour is the signature of importance of few hubs and their interaction exhibiting assortivity nature of the network topology43,44. Even though the few hubs do not have the capability of full control of the network, their significantly strong cross-talks can have the possibilities of regulating the network up to some extent. In these time series of dynamical states, there could be few hubs corresponding to few time states which are responsible for signal processing and management.

The propagation of this stress signal from the propagator p53 pathway to the receivers Notch and Wnt pathways associates the assortivity characteristics. This indicates that in the time series corresponding to dynamical states of the system, interaction of few hubs (formation of the rich-club) is probably essential for efficient signal propagation and stress management.

Active state is preferred state

The active dynamical state (sustain oscillation state) generally has maximum Hq values (Figs 2C,J,N and 3C,J middle pannels) due to large fluctuations than the other dynamical states. Since the system is perturbed with stress signal, the fluctuations coming from active molecular interaction due to stress signal becomes optimal, which could probably be utilized by the system in a constructive way2, to establish simple fractal law 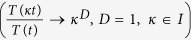Inline graphic, where the system can stay comfortably with this possibility. The network, corresponding to this dynamical state, exhibit topological properties closest to hierarchical network properties40,43,

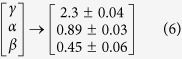graphic file with name srep40596-m10.jpg

However, the noise associated with this dynamical state is far smaller than the noise at second mixed and stabilized (apoptotic) states, as evident from permutation entropy Sp53 calculations.

Cross-talks favor to establish self-organization

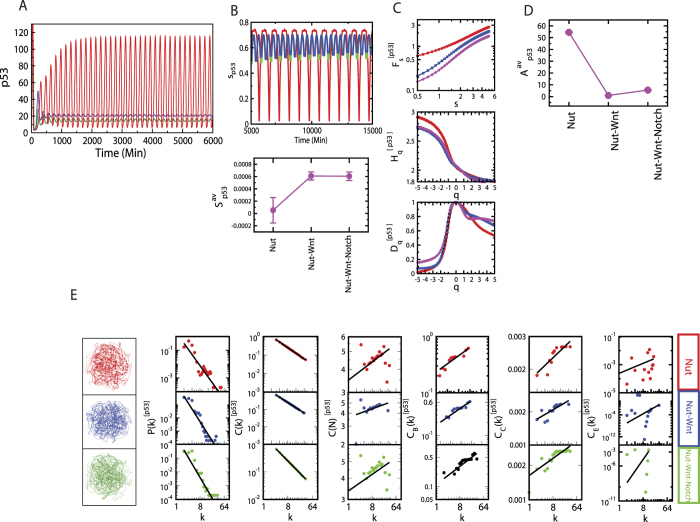
Stress p53 dynamics driven by nutlin exhibits optimized active dynamical state as number of cross-talks of pathways are increased (Fig. 4A–E). Si for p53 in the p53 pathway (direct stress is introduced via nutlin) is maximum, then the Si is pulled down drastically as it just cross-talks to Wnt pathway. When Notch-Wnt-p53 cross-talk is established Si is slightly increased, may be trying to optimize the fluctuations imparted by active molecular interaction due to stress in the system. Calculated Hq value is minimized as number of cross-talks of pathways is increased (Fig. 4C), but amplitude Ap53 is optimized (Fig. 4D).

Figure 4. Cross-talk of pathways and properties.

Figure 4

Open in a new tab

(A) Dynamics of stress p53 triggered by nutlin (red), nutlin plus Wnt (blue), and nutlin plus Wnt plus Notch (maroon), (B) permutation entropy measures of these cross-talks, (C) corresponding multifractal measures: Fs vs s, Hq vs q, and Dq vs q plots, (D) Ap53 corresponding to the cross-talks, (E) topological properties of the corresponding networks: P(k), C(k), Cn(k), CB(k), CC(k) and CE(k) as a function of degree k.

The constructed networks from these p53 dynamics corresponding to different combinations of cross-talks of the pathways (Fig. 4E) show that the topological properties of the network corresponding to Notch-Wnt-p53 interaction exhibits better organized and closer to hierarchical features,

graphic file with name srep40596-m11.jpg

The assortivity property, indicating the importance of hubs in the network, is still one of the important properties of the network. The important responsibilities of these hubs in information processing in the network are reflected and become clear in the fractal nature of the centrality measurements.

Discussion and Conclusion

Natural systems always try to be self-organized, subjected to a number of possibilities to change and corresponding states which are far from equilibrium, try to adapt to the preferred changes beneficial to their own organization for better and comfortable survival. During this struggle, the system tries to optimize any change (such as fluctuations due to stress in the system) in a constructive manner, utilize and distribute it, and look for better stability. If the system cannot able to face the change, it will break down.

Stress induced in Notch-Wnt-p53 cross-talk by stress inducing molecules (nutlin and Axin in our case), which are exhibited in stress p53 dynamics, drives the system at various dynamical states defined by different fractal laws, and the system switch to these dynamical states depending on the amount of stress induced. This stress system prefers to stay in an active dynamical state which has simple fractal rule subjected to the optimal fluctuations available due to active molecular interaction driven by stress. However, the system still associates a group of few hubs (assortive topology), but not in dependent manner (absence of these hubs do not cause system’s breakdown), for better signal processing and system regulation. Then this stress signal is propagated throughout the pathways, and found to inherit all the properties of the propagator pathway to the receiver pathways may be with slight modifications in them. This excellent co-ordination in cross-talk helps the system to save it from one directional apoptosis (once the system falls in this phase, it can never come back to normal situation) by regulating available active molecular interaction. This regulating mechanism could be different depending on the type of stress induced in the system (nutlin and Axin in our case).

The dynamical states obtained in our simple model are simple governed by simple fractal rules with limited possibilities. Multifractal studies show that these states are triggered by long range correlations with varied fluctuations. However, natural complex systems can have complex dynamical states defined by complex fractal rules allowing large number of possibilities in it.

The increase in the number of cross-talk pathways allows the system to optimize the imparted fluctuations, and therefore favours to establish self-organization in the whole system. This cross-talk regulates various biological functions out of which is regulating apoptosis. In the case of nutlin induced stress system, nutlin along with cross-talk mediator GSK3 acts as anti-apoptotic signal. Whereas, Axin induced stress along with GSK3 acts in two fold, first as an anti-apoptotic within a certain range of their interaction range, second favour-apoptotic signal beyond that regime. Since this Notch-Wnt-p53 cross-talk is involved in many important cellular processes in normal and cancerous cells, one needs to investigate these cellular activities with a number of open questions to understand how they work at a fundamental level.

Methods

Coupled Wntch (i.e. Wnt/Notch) Signaling in development

The notion Wntch signaling was introduced by Martinez Arias in 2008, for the elements of integrated system controlling cell fate i.e. Wnt and Notch45. The most important part of multicellular organisms is development which requires the proliferation of cell that decides its fate46. This decision for fate determination converge on the enhancement of specific genes that create a combination of transcription factors that determine the state and behaviour of the cell47. According to this analysis obtained from the study of Dorsophila genetics it can be proposed that Wnt is involved in regulating the probability of cell fate adoption48. The current understanding of Wnt signalling gives two striking features as reviewed by Martinez Arias and Hayward 2006, first is that many elements of this pathway take part in many other signaling processes, and second, is the ability of Wnt signaling to co-operate with other transcription factors and modulate their effect in other signaling pathways48. Thus, it acts as a noise filter, i.e making fluctuation in gene expression less strong49. However, there is one pathway that is consistent with Wnt, which is generally known as Notch signaling pathway48. Since Notch is involved in lateral inhibition, it together with Wnt plays crucial role in patterning the Notch inhibitory process47. Since, the development of wings in Dorsophila was first established by Couso and Martinez Arias in 1994, it also gave us a strong proof of interaction of notch and Wnt with strong sensitivity50. These evidences indicate that the elements of Notch and Wnt form a closed pathway for information processing, where Notch is available for NICD and Wnt regulate the Notch traffic using the β-catenin and activity of GSK3 in specific cells. Thus, Wntch signaling gives a clear picture of transition of states in cell during development51.

Notch-Wnt-p53 cross-talk biochemical network

Notch-Wnt cross-talk is a well-studied model16,17,18,25,52,53 which regulates variety of biological functions in normal and cancer cells, from lower to higher level organisms. On the other hand, p53 is very sensitive in responding stress in the system, may be via DNA damage or due to other molecular mechanisms, and drives the cell at various cellular states and lets the cells to decide their fate of survival19,54. The cross-talk between Notch-Wnt and p53 pathways are particularly important to understand, (i) how does p53 interfere Notch-Wnt interaction, and vice versa, (ii) nature of stress signal propagation in interacting pathways, and (iii) regulation of apoptosis. We present here Notch-Wnt-p53 regulatory biochemical network (Fig. 1) by incorporating simplified versions of the above models and other experimental findings.

Model Description

Wnt signaling pathway allows Wnt to interact with Dsh (Desheilved protein) to inhibit the formation of ubicutinaceous complex between Gsk3β and Axin2, which de-phosphorylate β-catenin (k6) to enter the nucleus (with a rate k4) and initiates the expression of Axin2-mRNA (k16). Then Axin2-mRNA is transported into the cytoplasm as part of the negative feedback loop between Wnt and Axin2. Free Gsk3β available in the system will allow to communicate Wnt with p53 by competing with the binding of p53 and Mdm2, with the formation of complex Gsk3β with p53 (k39). The process then activates the transcription of Mdm2-mRNA (k41), and it is translated (k27) and translocated to the cytoplasm where it binds to unbound p53 to degrade (k33). On the other hand, β-catenin present in the nucleus binds to Lef1 (k49) to increase the expression of mRNA of Delta gene (k54), followed by translation of Delta (k51) and translocated to the cytoplasm (k58). Now, this Delta protein interacts with Notch–NICD binary complex present on the cell membrane55 to initiate the release of NICD to form ternary complex (k67) and facilitating its transport to the nucleus (k73). The release of NICD in the cytoplasm is due to the ligand Delta that performs two activities cis-inhibition (intracellular i.e degradation of Notch) and trans-activation (intercellular) of Notch53,55. In our case cis-inhibition and trans-activation goes simultaneously within the cell, where cis-inhibition degrades Notch with rate constant k65 and trans-activation of Notch releases NICD in Cytoplasm (see Supplementary Fig. 1) followed by the nuclear transportation55. Further, NICD in the nucleus triggers the expression of Lfringe (mRNA) (k76)56 followed by its translation (k79). After translation, Lfringe goes to bind to its site on Notch followed by the inhibition of formation Notch delta complex to inhibit its own (Lfringe) transcription (k76) exhibiting negative feedback loop between Notch and Lfringe57. Lfringe does not prevent the binding of DSL ligands to Notch, while it potentiates both via Notch58. On the other hand, Lfringe decreases the binding of Notch and Delta by modifying (O-linked fucose glycosylation) the extracellular region of Notch259. However, Wnt directly inhibits the formation of Lfringe by direct transfer of information via interaction of Dsh and NICD present in cytoplasm (k86). The periodic expression of Lfringe is essential for somite formation56. Notch pathway interacts with Wnt via a mediator molecule Dsh, that bind to the cytoplasmic form of NICD (NICDc) (k85). This Dsh inhibits the formation of the destruction complex (formed by the association of GSK3β, Axin and β-catenin). GSK3β from this complex binds to p53 in the presence of Mdm2 forming binary complex p53-GSK3β (k39). This binary complex activates the transcription of Mdm2 with a rate constant of 0.042 min−1 (k41), increasing the concentration of Mdm2 inside the cell. This hike in the Mdm2 decreases the p53 concentration (k33). The bound p53 is restored by Nutilin (k36), a small molecule that compete to the binding site of p53 on Mdm2. On the other hand activated β-catenin is translocated into the nucleus (k4) and bind with the Lef1 (k49) to activate the transcription of Delta in the nucleus (Delta mRNA). This Delta mRNA is translated in cytoplasm to the protein that go to Notch to promote the cleavage of NICD (k51). The interaction of Notch-Wnt-p53 pathways allows to regulate apoptosis as well as stress propagation.

Mathematical framework of the network

The Notch-Wnt-p53 regulatory network model (Fig. 1) is defined by N = 28 molecular species (Table 2) corresponding to the reaction network description provided in Table 3. The state of the system at any instant of time ‘t’ is given by the state vector, 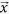Inline graphic (t) = (x1, x2, …, xN)T, where, N = 28 and ‘T’ is the transpose of the vector. By considering feedback mechanism of in p53, Wnt and Notch oscillators and coupling reaction channels of the two oscillators, we could able to reach the following coupled ordinary differential equations (ODE),

Table 2. List of molecular species and their initial concentration.

S.No. Species Name Description Notation Initial Concentration (nM)
1. Axin2 Initial Concentration Axin2 protein x1 10.1
2. Axin2 mRNA Initial Concentration Axin2 mRNA x2 0.02
3. β-catenin UnPhosphorylated β-catenin x3 0.1
4. β-cateninP Phosphorylated β-catenin x4 0.1
5. β-cateninN Nuclear β-catenin x5 0.01
6. Gsk3 Gsk3 protein x6 5.0
7. p53 unbound p53 protein x7 10.0
8. Mdm2 Unbound Mdm2 protein x8 10.0
9. Mdm2 mRNA Mdm2 Messsenger mRNA x9 0.0
10. p53-Mdm2 Mdm2 and p53 complex x10 95.0
11. Nutlin Unbound Nutlin x11 5.0
12. Nutlin-Mdm2 Nutlin Mdm2 complex x12 0.0
13. p53-Gsk3 p53 and Gsk3 complex x13 0.0
14. Dsh-activated Activated Dsh protein x14 0.5
15. Dsh-Axin The complex of Dsh and Axin2 x15 2.0
16. Gsk3-Axin2 The complex of Gsk3 and Axin2 x16 2.0
17. Lef1 The Lef1 protein in nucleus x17 0.1
18. β-catN-Lef1 The complex of β-catenin and Lef1 protein x18 0.01
19. Delta The Delta protein x19 1.68
20. Delta mRNAC The mRNA of Delta in the cytoplasm x20 0.1
21. Delta mRNAN The mRNA of Delta in the nucleus x21 0.1
22. Axin2 mRNAC The mRNA of Axin2 in the cytoplasm x22 0.1
23. Notch The Notch protein x23 0.5
24. NICDC Active Notch protein in the cytoplasm x24 0.2
25. NICDN Active Notch protein in the nucleus x25 0.0
26. Lfring mRNA The mRNA of Lunatic fringe protein x26 0.01
27. Lfring The Lunatic fringe protein x27 0.1
28. Dsh-NICDC The complex of Dsh and active Notch protein in cytoplasm x28 0.1
Open in a new tab

Table 3. List of parameters.

S.No. Notation Description Values Reference
1. K1 Rate constant for binding of Gsk3 to Axin2 0.23 nMmin−1 16
2. K2 Rate constant for dissociation of Gsk3-Axin2 0.1 min−1 16
3. K3 Rate constant of β-catenin synthesis 0.087 nMmin−1 16
4. K4 Rate constant of β-catenin entry into the nucleus 0.7 min−1 16
5. K5 Rate constant of β-catenin exit from the nucleus 1.5 min−1 16
6. K6 Rate constant of phosphorylation of β-catenin by the Gsk3 5.08 nMmin−1 16
7. K7 Concentration of Dishevelled(Dsh)protein 2.0 nM 16
8. K8 Total Gsk3 Concentration 3.0 nM 16
9. K9 Rate constant of inhibition by Dsh forβ-cateninP by the Axin2-Gsk3 complex 0.5 nM 16
10. K10 Michaelis rate constant for β-cateninp by the Axin2-Gsk3 complex 0.28 nM 16
11. K11 Maximum rate constant of dephosphorylation of β-catenin 1.0 nMmin−1 16
12. K12 Maximum rate constant for β-catenin phosphoration 0.003 nM 16
13. K13 Rate constant for degradation of unphosphorylated β-catenin 0 16
14. K14 Rate constant for degradation of phosphorylated β-catenin 7.062 min−1 16
15. K15 Rate constant of transcription of the Axin2 gene 0.06 nMmin−1 16
16. K16 Rate constant of transcription of the Axin2 gene induced by nuclear β-catenin 1.64 nMmin−1 16
17. K17 Rate constant for induction by nuclear β-catenin of Axin2 gene trascription 0.7 nM 16
18. K18 Maximum rate constant of degradation of Axin2 mRNA 0.8 nMmin−1 16
19. K19 Rate constant for degradation of Axin2 mRNA 0.48 nM 16
20. K20 Rate constant of transcription of Axin2 gene induced by transcription factor 0.5 nMmin−1 16
21. K21 Rate constant for induction by transcription factor of Axin2 gene transcription 0.05 nM 16
22. K22 Rate constant of synthesis of Axin2 protein 0.02 min−1 16
23. K23 Maximum rate constant of degradation of Axin2 protein 0.6 nMmin−1 16
24. K24 Michaelis rate constant for degradation of Axin2 protein 0.63 nM 16
25. K25 Hill coefficient 2.0 16
26. k26 Scaling factor for Wnt oscillator 1.5 16
27. k27 Rate constant of Mdm2 synthesis 0.297 min−1 19
28. k28 Rate constant of Mdm2 transcripton 0.006 min−1 19
29. k29 Rate constant of Mdm2 mRNA degradation 0.006 min−1 19
30. k30 Rate constant Mdm2 degradation 0.2598 min−1 19
31. k31 Rate constant of p53 synthesis 4.68 min−1 19
32. k32 Rate constant of p53 degradation 0.0495 min−1 19
33. k33 Rate constant of p53-Mdm2 binding 0.693 min−1 19
34. k34 Rate constant of p53-Mdm2 dissociation 0.00693 min−1 19
35. k35 Rate constant of Nutilin formation 0.001 min−1 Estimated
36. k36 Rate constant of Nutilin-Mdm2 formation 0.012 min−1 Estimated
37. k37 Rate constant of Nutilin-Mdm2 dissociation 0.03 min−1 Estimated
38. k38 Rate constant of Nutilin degradation 0.06 min−1 Estimated
39. k39 Rate constant of p53-Gsk3 complex formation 0.04 min−1 76
40. k40 Rate constant of p53-Gsk3 complex dissociation 0.12 min−1 76
41. k41 Rate constant of Mdm2 mRNA synthesis 0.042 min−1 76
42. k42 Rate constant of activation of Dsh by Wnt 5.0 min−1 25
43. k43 Wnt protein concentration 5.0 min−1 25
44. k44 Michaelis rate constant for activation of Dsh by Wnt 1.5 min−1 25
45. k45 Michaelis rate constant for activation of Dsh 0.95 min−1 25
46. k46 Rate constant of activation of inactivation of Dsh 1.0 min−1 25
47. k47 Michaelis rate constant for inactivation of Dsh 0.647 min−1 25
48. k48 Bimolecular rate constant for complex formation of Asin2 and Dsh 0.9 min−1 25
49. k49 Bimolecular rate constant for complex formation of β-catenin to Lef1 protein 0.9 min−1 25
50. k50 Bimolecular rate constant for degradation of complex of β-catenin to Lef1 protein 0.9 min−1 25
51. k51 Apparent first-order rate constant for the formation of Delta protein 0.1 min−1 25
52. k52 Maximum rate constant of degradation of Delta protein 0.9 min−1 25
53. k53 Michaelis rate constant for degradation of Delta protein 5.0 min−1 25
54. k54 Maximum rate constant of transcription of Delta gene induced by the complex of β-catenin and Lef1 in nucleus 1.12 min−1 25
55. k55 Maximum rate constant of degradation of mRNA of Delta protein in cytoplasm 2.0 min−1 25
56. k56 Michaelis rate constant for degradation of mRNA of Delta protein in cytoplasm 1.0 min−1 25
57. k57 Basal rat constant of transcription of the delta gene 1.0 min−1 25
58. k58 Apparent first-order rate constant for mRNA of Delta protein exit from the nucleus 1.725 min−1 25
59. k59 Apparent first-order rate constant for mRNA of Axin2 exit from the nucleus 2.0 min−1 25
60. k60 Maximum rate constant of degradation of mRNA of Axin2 in cytoplasm 1.2 min−1 25
61. k61 Michaelis rate constant for degradation of mRNA of Axin2 in cytoplasm 0.48 min−1 25
62. k62 Threshold rate constant for transcription of Delta induced by the complex of β-catenin and Lef1 protein in nucleus 2.46 min−1 25
63. k63 Threshold rate constant for transcription of Axin2 induced by the complex of β-catenin and Lef1 protein in nucleus 2.46 min−1 25
64. k64 Maximum rate constant of formation of Notch 0.23 min−1 16
65. k65 Maximum rate constant of degradation of Notch 2.82 min−1 16
66. k66 Michaelis rate constant for degradation of Notch 1.4 min−1 16
67. k67 Apparent first-order rate constant for Notch cleavage into NICD 3.45 min−1 16
68. k68 Maximum rate constant of degradation of NICD 0.01 min−1 16
69. k69 Michaelis rate constant for degradation of NICD 0.001 min−1 16
70. k70 Maximum rate constant of degradation of nuclear NICD 0.01 min−1 16
71. k71 Michaelis rate constant for degradation of nuclear NICD 0.001 min−1 16
72. k72 Threshold rate constant for inhibition of Notch cleavage into NICD by Lunatic fringe 0.5 min−1 25
73. k73 Apparent first-order rate constant for NICD entry into nucleus 0.1 min−1 16
74. k74 Apparent first-order rate constant for NICD exit from the nucleus 0.1 min−1 16
75. k75 Maximum rate constant of transcription of Lunaticfringe gene 3.0 min−1 16
76. k76 Threshold rate constant for activation of Lunaticfringe gene transcription by nuclear NICD 0.05 min−1 16
77. k77 Maximum rate constant of degradation of Lunaticfringe mRNA 1.92 min−1 16
78. k78 Michaelis rate constant of degradation of Lunaticfringe mRNA 0.768 min−1 16
79. k79 Apparent first-order rate constant for Lunatic fringe protein synthesis 0.3 min−1 16
80. k80 Maximum rate constant of Lunatic fringe protein degradation 0.39 min−1 16
81. k81 Michaelis rate constant of degradation of Lunatic fringe protein 0.37 min−1 16
82. k82 Inhibition constant for Gsk3 inhibition of Lunaticfringe transcription induced by NICD 2.5 min−1 25
83. k83 Hill coefficients for Notch oscillator 2.0 16
84. k84 Scaling factor for Notch oscillator 0.3 16
85. k85 Bimolecular rate constant for complex formation of NICD and Dsh 0.5 min−1 25
86. k86 Bimolecular rate constant for degradation of complex of NICD and Dsh 9.0 min−1 25
Open in a new tab
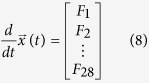graphic file with name srep40596-m13.jpg

where, the functions in the equation (8) {Fi(x1, x2, …, xN)}, i = 1, 2, …, 28 are given by,

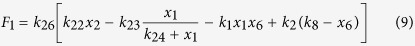graphic file with name srep40596-m14.jpg
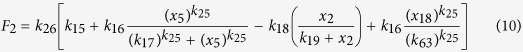graphic file with name srep40596-m15.jpg
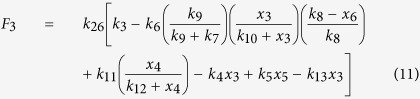graphic file with name srep40596-m16.jpg
graphic file with name srep40596-m17.jpg
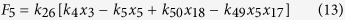graphic file with name srep40596-m18.jpg
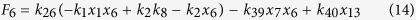graphic file with name srep40596-m19.jpg
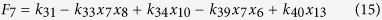graphic file with name srep40596-m20.jpg
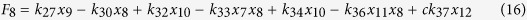graphic file with name srep40596-m21.jpg
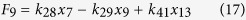graphic file with name srep40596-m22.jpg
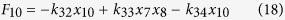graphic file with name srep40596-m23.jpg
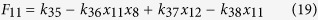graphic file with name srep40596-m24.jpg
graphic file with name srep40596-m25.jpg
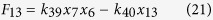graphic file with name srep40596-m26.jpg
graphic file with name srep40596-m27.jpg
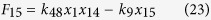graphic file with name srep40596-m28.jpg
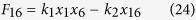graphic file with name srep40596-m29.jpg
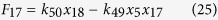graphic file with name srep40596-m30.jpg
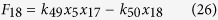graphic file with name srep40596-m31.jpg
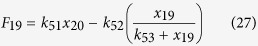graphic file with name srep40596-m32.jpg
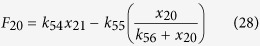graphic file with name srep40596-m33.jpg
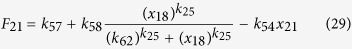graphic file with name srep40596-m34.jpg
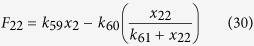graphic file with name srep40596-m35.jpg
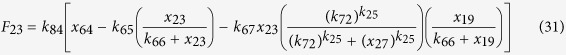graphic file with name srep40596-m36.jpg
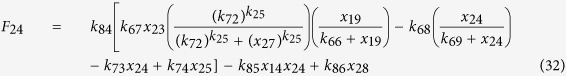graphic file with name srep40596-m37.jpg
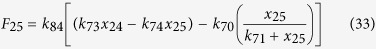graphic file with name srep40596-m38.jpg
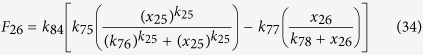graphic file with name srep40596-m39.jpg
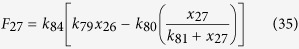graphic file with name srep40596-m40.jpg
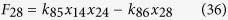graphic file with name srep40596-m41.jpg

We used standard Runge-Kutta method (order 4) of numerical integration to simulate equation (8) to find the solution of the variables listed in Table 2 for the parameter values given in Table 3. We then analyzed the constructed mathematical model to get possible approximate analytical solutions of the variables (slow variables) using quasi-steady state approximation.

Multifractal DFA approach

Fractal properties in non-stationary time series, and associated important correlations can studied using Multifractal detrended fluctuation analysis (MF-DFA)60. Important fractal parameters which characterize the time series, namely, Hurst exponent (H), generalized dimension (D) etc can be calculated numerically using a method adopted by Kantelhardt et al.11 as summarized below. First, the time series signal {xj} of length N is taken as random walk, and can be represented by the profile, 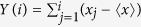Inline graphic, where, 〈x〉 is the mean value of the signal, and i = 1, 2, …, N. Second, the profile Y(i) is now divided into 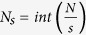Inline graphic equal non-overlapping equal segments of size s. To take into account all data points, 2Ns segments are considered by counting starting from both ends of the data. Third, the following variance is determined,

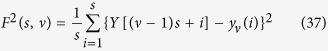graphic file with name srep40596-m44.jpg

where, ν = Ns + 1, …, 2Ns, and yν(i) is the fitting polynomial in segment ν. Fourth, the qth order fluctuation function is estimated by averaging over all segments,

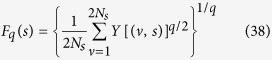graphic file with name srep40596-m45.jpg

Fifth, the scaling behavior of the function Fq(s) is represented by,

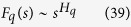graphic file with name srep40596-m46.jpg

where, Hq is the generalized Hurst exponent, which represents the measure of self-similarity and correlation properties of the signal. Then Hq is related to the classical scaling exponent τ(q),

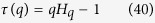graphic file with name srep40596-m47.jpg

and from the definition of Holder exponent, 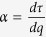Inline graphic, the singularity function f(α)60 is given by,

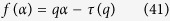graphic file with name srep40596-m49.jpg

Then, generalized fractal dimension of the signal is measured by,

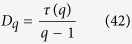graphic file with name srep40596-m50.jpg

Now, D0, for q = 0, is the fractal or Hausdorff dimension, D1 is information dimension and D2 represents correlation dimension60. Multifractal signature in the time series can be observed in the system if there exists significant dependence of Hq on q in the time series due to the different scaling nature of small and large fluctuations11. Positive dependence of Hq on q indicates short range correlations in the time series, whereas negative dependence of Hq on q exhibits long range correlations in the time series. Further, in multifractal time series, small and large fluctuations are characterized by large and small values of Hq.

Visibility graph of time series

This technique maps a time series to a network61, where each observation in time series is translated to a node and an edge between any two nodes is introduced when the following visibility condition is satisfied i.e. two nodes corresponding to observations x(ta) and x(tb) are connected if all intermediate states x(tc) with ta < tc < tb satisfy,

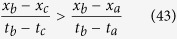graphic file with name srep40596-m51.jpg

These networks are undirected due to symmetry in visibility condition. Since the properties of the time series are inherited to the corresponding network, the studies of this network provide useful information which can’t be observed in traditional time series data.

Topological properties of networks

The following topological properties of the networks are studied to study the important behavior of the networks.

Degree distribution

The degree k of a node indicates the number of links the node connects with other nodes in the network. Consider a network defined by a graph G = (N, E), where N and E are number of nodes and edges respectively. The probability of degree distribution (P(k)) of the network is the probability that any chosen node will have a degree k, which is given by,

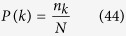graphic file with name srep40596-m52.jpg

where, nk is the number of nodes having degree k. P(k) in random and small-world networks follow Poisson distribution, whereas, it obeys power law P(k) ~ k−γ in scale-free and hierarchical networks depending on the value of γ which indicates the importance of hubs or modules in the network62.

Clustering co-efficient

Clustering co-efficient of a network characterize how strongly a node’s neighborhood nodes are interconnected. For an undirected network, clustering co-efficient (C(ki)) of ith node is the ratio of number of its nearest neighborhood edges to the total possible number of edges of degree ki, and can be calculated by,

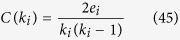graphic file with name srep40596-m53.jpg

where, ei is the number of connected pairs of nearest-neighbor of ith node, and ki is its degree. C(k) in scale free networks is independent of k, whereas in hierarchical network it follows a power law, C(k) ~ k−α, with α ~ 1.

Neighborhood connectivity

Neighborhood connectivity of a node of a network is a measure of the average connectivities of the nearest neighbors of the node in the network63, and is given by,

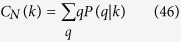graphic file with name srep40596-m54.jpg

where, P(q|k) is conditional probability that a link belonging to a node with connectivity k points to a node with connectivity q. The power law nature of CN(k), CN(k) ~ k−β is a signature of hierarchical topology in the network43. However, the positive power dependence of CN(k) could be an indicator of assortivity in the network topology44.

Betweenness centrality

Betweenness centrality of a node characterize the ability to (i) extract benefits from information flows in the network64, and (ii) extent to which the node has control over the other nodes in the network through communication65,66. If dij(v) indicates the number of geodesic paths from node i to node j passing through node v, and dij represents number of geodesic paths from node i to j, then betweenness centrality (CB(v)) of a node v can be measured by,

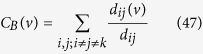graphic file with name srep40596-m55.jpg

If M denotes the number of node pairs excluding v, then normalized betweenness centrality is given by, 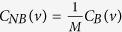Inline graphic.

Closeness centrality

Closeness centrality (CC) estimates how fast information is spread from a node to other nodes reachable from it in the network67. CC of a node i is the harmonic mean of geodesic distance between the node and all other nodes connected to it in the network,

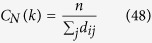graphic file with name srep40596-m57.jpg

where, dij is geodesic path length between nodes i and j, and n is the total number of nodes in the network connected to node i.

Eigenvector centrality

Eigenvector centrality of a node i (CE(i)) in a network is proportional to the sum of i′s neighbor centralities68, and it is measured by,

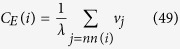graphic file with name srep40596-m58.jpg

where, nn(i) indicates nearest neighbors of node i in the network. λ is the eigenvalue of the eigenvector vi given by, Avi = λvi, where, A is the adjacency matrix of the network. The principal eigenvector of A, which corresponds to maximum eigenvalue λmax, is taken to have positive eigenvector centrality score69. Since node’s eigenvector centrality function smoothly varies over the network and depends on its neighbors, node with high eigenvector centrality is embedded in the locality of nodes of high eigenvector centralities, and chance of having isolated nodes in and around the locality is very low68. Hence, eigenvector centrality can be used as an indicator of node’s spreading power in the network.

Algorithm for calculating permutation entropy

Important information contained in a time series can be measured by calculating permutation entropy of the time series70,71. Permutation entropy H of a time series of a dynamical variable x(t) of a system can be calculated as follows. The time series x(t) can be mapped onto a symbolic sequence of length N: x(t) = {x1, x2, …, xN}. This sequence is then partitioned into M number of short sequences of equal length U i.e. x(t) = {w1, w2, …, wM}, where ith window is given by wi = {xi+1, xi+2, …, xi+U}. This window is allowed to slide along x(t) with maximum overlap. Permutation entropy of a window wi can be calculated by defining a short sequence of embedded dimension r, Si = {xi+1, xi+2, …, xi+r} in r-dimensional space, finding all possible inequalities of dimension r and mapping the inequalities along the ascendingly arranged elements of wi to find the probabilities of occurrence of each inequality in wi. Since q out of r! permutations are distinct, one can define a normalized permutation entropy as 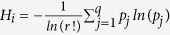Inline graphic, where 0 ≤ Hi(r) ≤ 1. The mapped permutation entropy spectrum of time series x(t) is represented by H = {H1, H2, …, HM}. In self-organized state one has H → 0.

Additional Information

How to cite this article: Malik, M. Z. et al. Dynamical states, possibilities and propagation of stress signal. Sci. Rep. 7, 40596; doi: 10.1038/srep40596 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information
srep40596-s1.pdf (141.2KB, pdf)

Acknowledgments

We would like to thank the reviewers of our work for their critical and important comments specially in the modeling of our work and the importance of the results in actual experimental situations. We would like to thank Prof. RNK Bamezai of Jawaharlal Nehru University for numerous discussions of our work. Finally we would like to thank our manuscript handling Editor for his help and kind cooperation. M.Z.M. and S.A. is financially supported by Indian Council of Medical Research under SRF (Senior Research Fellowship). R.K.B.S. is financially supported by DST-PURSE, department of Science Technology (DST), New Delhi, India, under sanction no. SB/S2/HEP-034/2012 and R.K.B.S is also financially supported by UPE-II under sanction no. 101, Jawaharlal Nehru University, New Delhi, India.

Footnotes

Author Contributions R.K.B.S. and M.Z.M. conceived the model and did the numerical experiment. M.Z.M. prepared the figures of the numerical results. R.K.B.S. and M.Z.M. analyzed and interpreted the simulation results, and wrote the manuscript. M.Z.M., S.A, S.S.S., R.I., and R.K.B.S. involved in the study and reviewed the manuscript.

References

  1. Heylighen F. The science of self-organization and adaptivity. The encyclopedia of life support systems. 5, 253–280 (2001). [Google Scholar]
  2. Prigogine I. & Stengers I. Order out of Chaos: Man’s New Dialogue with Nature (ed. Alvin T.) 1–349 (Bantam Books, 1984). [Google Scholar]
  3. Ashby W. R. Design for a Brain–The Origin of Adaptive Behavior (ed. Ashby W. R.) 1–304 (Chapman and Hall, London, 1952). [Google Scholar]
  4. Holland J. H. Hidden Order: How adaptation builds complexity (ed. Simmanons L. M.) 1–208 (Basic book, 1996). [Google Scholar]
  5. Holland J. H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology. 1–227 (Control and Artificial Intelligence, MIT Press, Cambridge MA, 1992). [Google Scholar]
  6. Kauffman S. A. The Origins of Order: Self-organization and Selection in Evolution. Oxford University Press, 1993). [Google Scholar]
  7. De Haan. How emergence arises. Ecol. Compl. 3, 293–301 (2006). [Google Scholar]
  8. Morin E. Restricted complexity, general complexity (ed. Gershenson C., Aerts D. & Edmonds B.) 1–25 (World Scientific, 2006). [Google Scholar]
  9. Mandelbrot B. B. Possible refinement of the lognormal hypothesis concerning the distribution of energy dissipation in intermittent turbulence (ed. Rosenblatt M. & Van Atta C.) 333–351 (In Statistical models and turbulence, Springer: Berlin Heidelberg, 1972). [Google Scholar]
  10. Peitgen H. O., Jurgens H. & Saupe D. Chaos and fractal: new frontiers of science. 1–184 (Springer-Verlag, New York, 1992). [Google Scholar]
  11. Kantelhardt J. W. et al. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A: Statistical Mechanics and its Applications. 316, 87–114 (2002). [Google Scholar]
  12. Nicolis G. & Prigogine I. Self-organization in Non-equilibrium systems (ed. Nicolis G.) 1–504 (Wiley, New York, 1977). [Google Scholar]
  13. Rao C. V., Wolf D. M. & Arkin A. R. Control, exploitation and tolerance of intracellular noise. Nature 420, 231–237 (2002). [DOI] [PubMed] [Google Scholar]
  14. Glas L. V. Synchronization and rhythmic processes in physiology. Nature. 410, 277–284 (2001). [DOI] [PubMed] [Google Scholar]
  15. Logan C. Y. & Nusse R. The Wnt signaling pathway in development and disease. Annu Rev Cell Dev Biol. 20, 781–810 (2004). [DOI] [PubMed] [Google Scholar]
  16. Goldbeter A. & Pourquie O. Modeling the segmentation clock as a network of coupled oscillations in the Notch, Wnt and FGF signaling pathways. J Theor Biol. 252, 574585 (2008). [DOI] [PubMed] [Google Scholar]
  17. Jensen P. B., Pedersen L., Krishna S. & Jensen M. H. A Wnt Oscillator Model for Somitogenesis. Biophys J. 98, 943950 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Rodrguez-Gonzalez J. G., Santillan M., Fowler A. C. & Mackey M. C. The segmentation clock in mice: Interaction between the Wnt and Notch signalling pathways. J Theor Biol. 248, 3747 (2007). [DOI] [PubMed] [Google Scholar]
  19. Proctor C. J. & Gray D. A. Explaining oscillations and variability in the p53-Mdm2 system. BMC Syst Biol. 2, 1–75 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fortini P. et al. DNA damage response by single-strand breaks in terminally differentiated muscle cells and the control of muscle integrity. Cell Death Differ. 19, 1741–9 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Valentine J. M., Kumar S. & Moumen A. A p53-independent role for the MDM2 antagonist Nutlin-3 in DNA damage response. BMC cancer. 11, 79 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Verma R., Rigatti M. J., Belinsky G. S., Godman C. A. & Giardina C. DNA damage response to the Mdm2 inhibitor nutlin-3. Biochem Pharmacol. 79, 565–74 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Dequeant M. L. & Pourquie O. Segmental patterning of the vertebrate embryonic axis. Nat Rev Genet. 9, 370382 (2009). [DOI] [PubMed] [Google Scholar]
  24. Hong. Y. W. et al. Modelling Coupled Oscillations in the Notch, Wnt, and FGF Signaling Pathways during Somitogenesis: A Comprehensive Mathematical Model. Compt. Intell.Neursc. 1, 1–16 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hong Y. W. et al. Mathematical models for the Notch and Wnt signaling pathways and the crosstalk between them during somitogenesis. Theoretical Biology and Medical Modelling. 10, 1–20 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Collu G. M., Hidalgo S. A. & Breman K. Wnt-Notch signaling cross-talk in development and disease. Cell Mol. Life Sc. 71, 3553–3567 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Klein T. & Arias A. M. The vestigial gene product provides a molecular contex for the interpretation of signals during the development of the wing in Drosophila. Development. 126, 913–925 (1999). [DOI] [PubMed] [Google Scholar]
  28. Germar K. et al. T-cell factor 1 is a gatekeeper for T-cell specification in response to Notch signaling. Proc. Natl. Acad. Sci. USA 108, 20060–20065 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Holland J. D., Klaus A., Garrat A. N. & Birchmeier W. Wnt signaling in stem and cancer stem cells. Curr. Opin. Cell Biol. 25, 254–264 (2013). [DOI] [PubMed] [Google Scholar]
  30. Ungerback J. et al. The Notch-2 gene is regulated by Wnt signaling in cultured colorectal caner cells.PLoS One. 6, e17952 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Chen X. et al. Jagged1 expression regulated by Notch 3 and Wnt/beta-catenin signaling pathways in ovarian cancer. Oncotarget. 1, 210–218 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Olivier M., Hollstein M. & Hainaut P. TP53 Mutations in Human Cancers: Origins, Consequences, and Clinical Use.Cold Spring Harbor perspectives in biology. 2, a001008 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Garg P. et al. Notch1 regulates the effects of matrix metalloproteinase-9 on colitis-associated cancer in mice. Gastroenterology. 141, 1381–1392 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Beverly L. J., Felsher D. W. & Capobianco A. J. Suppression of p53 by Notch in lymphomagenesis: implications for initiation and regression. Cancer Res. 65, 7159–68 (2005). [DOI] [PubMed] [Google Scholar]
  35. Yang X. et al. Notch activation induces apoptosis in neural progenitor cells through a p53-dependent pathway. Dev Biol. 269, 8194 (2004). [DOI] [PubMed] [Google Scholar]
  36. Vousden K. H. p53: death star. Cell. 103, 691–694 (2000). [DOI] [PubMed] [Google Scholar]
  37. Tsai J. H., Donaher J. L., Murphy D. A., Chau S. & Yang J. Spatiotemporal regulation of epithelialmesenchymal transition is essential for squamous cell carcinoma metastasis. Cancer Cell. 22, 725736 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Mandelbrot B. B. The fractal geometry of nature. 1–497 (New York, Freeman and Co., 1983). [Google Scholar]
  39. Clauset A., Shalizi C. R. & Newman M. E. J. Power-law distributions in empirical data. SIAM Rev. Soc. Ind. Appl. Math. 51, 661703 (2009). [Google Scholar]
  40. Ravasz E., Somera A. L., Mongru D. A., Oltvai N. & Barabasi A. L. Hierarchical organization of modularity in metabolic networks. Science 297, 15511555 (2002). [DOI] [PubMed] [Google Scholar]
  41. Singh S. S. et al. Scaling in topological properties of brain networks. Scientific Rept. 6, 24926 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Von Foerster H. On self-organising systems and their environments (ed. Yovits M. C. & Cameron S.) 30–50 (Pergamon Press, London, 1960). [Google Scholar]
  43. Romualdo P. S., Alexei V. & Alessandro V. Dynamical and Correlation Properties of the Internet. Phys. Rev.Lett. 87, 258701–4 (2001). [DOI] [PubMed] [Google Scholar]
  44. Barrat A., Barthlemy M., Pastor-Satorras R. & Vespignani A. The architecture of complex weighted networks. Proc. Natl. Acad. Sc. 101, 3747–3752 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Hayward P., Kalmar T. & Arias A. M. Wnt/Notch signalling and information processing during development. Development. 135, 411–424 (2008). [DOI] [PubMed] [Google Scholar]
  46. Davidson E. H. The regulatory genome: gene regulatory networks in development and evolution (Academic press, 2006). [Google Scholar]
  47. Arias A. M. New alleles of Notch draw a blueprint for multifunctionality. TRENDS in Genetics. 18, 168–170 (2002). [DOI] [PubMed] [Google Scholar]
  48. Hayward P., Balayo T. & Martinez Arias A. Notch synergizes with axin to regulate the activity of armadillo in Drosophila. Developmental dynamics. 235, 2656–2666 (2006). [DOI] [PubMed] [Google Scholar]
  49. Arias A. M. Wnts as morphogens? The view from the wing of Drosophila. Nature Reviews Molecular Cell Biology 4, 321–325 (2003). [DOI] [PubMed] [Google Scholar]
  50. Couso J. P. & Arias A. M. Notch is required for wingless signaling in the epidermis of Drosophila. Cell. 79, 259–272 (1994). [DOI] [PubMed] [Google Scholar]
  51. Descalzo S. M. & Arias A. M. The structure of Wntch signalling and the resolution of transition states in development. In Seminars in cell & developmental biology. 23, 443–449 (2012). [DOI] [PubMed] [Google Scholar]
  52. Santillan M. & Mackey M. C. A proposed mechanism for the interaction of the segmentation clock and the determination front in somitogenesis. PLoS ONE. 3, e1561 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Kazama A., Karashima A., Katayama M. & Nakao M. Modeling of segmentation clock mechanism in presomitic mesoderm. IEEE, Minneapolis, Minn, USA. 32673270 (2009). [DOI] [PubMed] [Google Scholar]
  54. Zubbair Malik M. et al. Dynamics of p53 and Wnt cross talk. Comput Biol Chem. 59, 55–66 (2015). [DOI] [PubMed] [Google Scholar]
  55. Sprinzak et al. Cis Interactions between Notch and Delta Generates Mutually Exclusive Signaling States Nature. 465, 86–90 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Gibb S., Maroto M. & Dale J. K. The segmentation clock mechanism moves up a notch. Trends Cell Biol. 20, 593600 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Dale et al. Periodic Notch inhibition by Lunatic Fringe underlies the chick segmentation clock. Nature. 421, 275–278 (2003). [DOI] [PubMed] [Google Scholar]
  58. Hicks et al. Fringe differentially modulates Jagged1 and Delta1 signalling through Notch1 and Notch2. Nature Cell Biology. 2, 515–520 (2000). [DOI] [PubMed] [Google Scholar]
  59. Shimizu et al. Manic Fringe and Lunatic Fringe Modify Different Sites of the Notch2 Extracellular Region, Resulting in Different Signaling Modulation. J. Biol. Chem. 276, 25753–25758 (2001). [DOI] [PubMed] [Google Scholar]
  60. Halsey T. C., Jensen M. H., Kadanoff L. P., Procaccia I. & Shraiman B. I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A. 33, 1141–1151 (1986). [DOI] [PubMed] [Google Scholar]
  61. Lacasa L., Bartolo L., Fernando B., Jordi L. & Juan C. N. From time series to complex networks: The visibility graph. Pro. Natl. Acad. Sc. 105, 4972–4975 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Albert R. & Barabas A. L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47 (2002). [Google Scholar]
  63. Maslov S. & Sneppen K. Specificity and stability in topology of protein networks. Science 296, 910–913 (2002). [DOI] [PubMed] [Google Scholar]
  64. Borgatti S. P. & Everett M. G. A Graph-theoretic perspective on centrality. Social Networks 28, 466–484 (2006). [Google Scholar]
  65. Brandes U. A faster algorithm for betweenness centrality. J. Math. Sociol. 25, 163–177 (2001). [Google Scholar]
  66. Mason O. & Verwoerd M. Graph theory and networks in biology. IET Syst. Biol. 1, 89–119 (2007). [DOI] [PubMed] [Google Scholar]
  67. Canright G. & Kenth E. M. Roles in networks. Sci. Comput. Program 53, 195–214 (2004). [Google Scholar]
  68. Canright G. & Kenth E. M. Spreading on networks: a topographic view. Complexus. 3, 131–146 (2006). [Google Scholar]
  69. Bonacich P. Power and centrality: a family of measures. Am. J. Sociol. 92, 1170–1182 (1987). [Google Scholar]
  70. Bandt C. & Pompe B. Permutation entropy: a natural complexity measure for time series. Phys Rev Lett. 88, 174102 (2002). [DOI] [PubMed] [Google Scholar]
  71. Cao Y., Tung W. W., Gao J. J., Protopopescu V. A. & Hively L. M. Detecting dynamical changes in time series using the permutation entropy. Phys Rev. E70, 046217 (2004). [DOI] [PubMed] [Google Scholar]
  72. Purvis J. E., Karhohs K. W., Mock C., Batchelor E., Loewer A. & Lahav G. p53 dynamics control cell fate. Science 336(6087), 1440–1444 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Shin S., Sung B. J., Cho Y. S., Kim H. J., Ha N. C., Hwang J. I. & Oh B. H. An anti-apoptotic protein human survivin is a direct inhibitor of caspase-3 and-7. Biochemistry 40(4), 1117–1123 (2001). [DOI] [PubMed] [Google Scholar]
  74. Carter B. Z., Mak D. H., Schober W. D., Koller E., Pinilla C., Vassilev L. T. & Andreeff M. Simultaneous activation of p53 and inhibition of XIAP enhance the activation of apoptosis signaling pathways in AML. Blood 115(2), 306–314 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Zhang Y., Fujita N. & Tsuruo T. Caspase-mediated cleavage of p21 Waf1/Cip1 converts cancer cells from growth arrest to undergoing apoptosis. Oncogene 18(5), 1131–1138 (1999). [DOI] [PubMed] [Google Scholar]
  76. Proctor C. J. & Gray D. A. GSK3 and p53-is there a link in Alzheimer’s disease? Mol Neurodegener. 5, 7 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep40596-s1.pdf (141.2KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES