Histidine Orientation Modulates the Structure and Dynamics of a de Novo Metalloenzyme Active Site

Abstract

The ultrafast dynamics of a de novo metalloenzyme active site is monitored using two-dimensional infrared spectroscopy. The homotrimer of parallel, coiled coil α-helices contains a His₃-Cu(I) metal site where CO is bound and serves as a vibrational probe of the hydrophobic interior of the self-assembled complex. The ultrafast spectral dynamics of Cu-CO reveals unprecedented ultrafast (2 ps) nonequilibrium structural rearrangements launched by vibrational excitation of CO. This initial rapid phase is followed by much slower ~40 ps vibrational relaxation typical of metal-CO vibrations in natural proteins. To identify the hidden coupled coordinate, small molecule analogues and the full peptide were studied by QM and QM/MM calculations, respectively. The calculations show that variation of the histidines’ dihedral angles in coordinating Cu controls the coupling between the CO stretch and the Cu–C–O bending coordinates. Analysis of different optimized structures with significantly different electrostatic field magnitudes at the CO ligand site indicates that the origin of the stretch–bend coupling is not directly due to through-space electrostatics. Instead, the large, ~3.6 D dipole moments of the histidine side chains effectively transduce the electrostatic environment to the local metal coordination orientation. The sensitivity of the first coordination sphere to the protein electrostatics and its role in altering the potential energy surface of the bound ligands suggests that long-range electrostatics can be leveraged to fine-tune function through enzyme design.

Graphical abstract

INTRODUCTION

De novo enzyme design offers opportunities to engineer new catalysts, while furnishing insights into natural biochemical function. There has been remarkable recent progress in designing novel macromolecules with enzymatic functionalities, adopting both “bottom up” and “top down” approaches.¹ Whereas top down strategies modify existing enzymes with well-defined scaffolds to alter their functions, bottom up schemes assemble catalysts that may range from models of natural enzymes to entirely novel macromolecules lacking any similarities to native enzymes. Refining selectivity and efficiency requires either an evolutionary strategy mimicking biology or a rational chemical approach based on principles of biophysical and bioinorganic chemistry. We seek to advance design optimization from a chemical perspective, bridging the expanse from small-molecule catalysts to biological macromolecules.

By borrowing binding site motifs found in natural enzymes, we have already established that metal ions coordinated within stable peptide matrices are potent catalysts. Using engineered metal binding sites, we have recently shown efficient hydrolytic (Zn) and nitrite reductase (Cu) activity.^2,3 In these first-generation de novo metalloenzymes, the metal binding sites are established within the stable scaffold of a coiled-coil, homotrimeric peptide. That is, these novel catalysts function despite a lack of any modifications to the active site pocket formed by the hydrophobic side chains that drive the peptide trimer self-assembly, though changes to residues near the active site can modulate efficiency.⁴ Hence, it is clear that optimizing the selectivity and efficiency will rest on the ability to modify and control the second coordination sphere by altering the side chains that line the active site within the hydrophobic coiled-coil interior. There is, however, another much less intuitive contribution to the chemistry at the active site, and it is due to the highly directional electrostatic landscape produced by the parallel α-helical protein matrix of TRI family peptide assemblies. Though common elements of structural proteins, parallel coiled-coils are rarely found in natural enzymes and offer both a challenge and an opportunity for new avenues of de novo enzyme optimization. A question arises regarding the degree to which the electrostatic environment can be tailored to specific chemical transformations, for example, by stabilizing transition states to bias the catalytic outcome.^5,6 Energetic modulations are often seen as paramount to the catalytic speedup performed by enzymes, for example, by lowering a reaction’s free energy barrier (ΔG‡). It can be challenging to isolate the role, if any, of the molecular dynamics in governing the rate and selectivity of an enzyme-catalyzed transformation.⁷ For high barrier, uncatalyzed reactions, dynamical phenomena such as friction and barrier height fluctuations influence reaction rates only negligibly. On the other hand, given that catalysts significantly reduce energetic barriers, dynamical aspects, which are neglected by conventional transition-state theory, may assume greater significance.^8–13 For low barriers, which typically also have small curvatures, dissipative interactions (i.e., friction) with the surrounding solvent or protein matrix tend to induce otherwise successfully reacting molecules to recross the barrier and return to the reactant basin.¹⁴ Another dynamical effect that is not included in traditional treatments of chemical kinetics is the time-dependent variation of barrier heights and shapes caused by fluctuations of the surroundings. Proteins exhibit dynamics on time scales ranging from picoseconds to longer than microseconds, and the degree to which these dynamics modulate the catalytic reaction dynamics has been difficult to determine experimentally. Despite the reasonable expectation from this perspective that dynamics should influence enzyme catalysis,¹⁵ there is significant computational support for the opposing conclusion that the reaction dynamics in the enzyme are quite similar to what would occur in solution.¹⁶ Separate from dynamics, it is widely recognized that electrostatics are central to enzyme function,⁵ but in situ experimental measures of the electric fields and potentials still remain open challenges. Recent progress by Boxer et al. has shown how vibrational probes at enzyme active sites can be especially powerful sensors of electric fields that drive catalysis.¹⁷ Ultrafast spectroscopy and computational chemistry investigations of designed de novo metalloenzymes should enable a promising new route to probe these fundamental aspects of enzyme catalysis.

The full picture of the reaction dynamics will need to be able to treat the catalysis from the points of view of both dynamical fluctuations and static energetic considerations. Based on the approach to elucidating the power of enzyme catalysis developed by Warshel, a complete description of catalysis requires an understanding of both the dynamics and energetics of the following processes: (1) the uncatalyzed reaction in water; (2) the enzymatic mechanism in solution (i.e., water); and (3) the catalysis reaction that takes place in the enzyme. In the context of de novo design, for a given net chemical reaction the uncatalyzed path is a constant reference, whereas the enzymatic reaction mechanism in solution may change with mutations to the de novo enzyme since they may change the enzyme mechanism. Nevertheless, it is possible to determine the static energetics using experiment or quantum chemistry.¹⁸ Since the reaction free energy barriers for the aqueous protein mechanism paths can be very similar to the uncatalyzed paths in solution,⁶ we would anticipate a relatively diminutive role for dynamics in all but the protein-catalyzed case, where the barrier is lowered substantially. For this reason, we focus in the current work on studying the structure and dynamics within the protein, but we do anticipate that future studies will need to take into consideration all three of the relevant reaction pathways. De novo enzyme design enables us to make minor modifications to the protein-catalyzed pathway, while essentially keeping the other two pathways constant, and we feel it is ideally suited to the approach devised by Warshel.

In metalloenzymes, it has been shown that electrostatics can influence electronic structure and energetics leading to altered redox potentials of metal sites.¹⁹ It remains a significant challenge to predict and design electrostatics, particularly over the large 0.1–10 nm range of distances spanned by the TRI peptide scaffolds. Since the protein environment is not static, an experimental probe should also be able to sense active site flexibility, which is directly related to substrate transport into and out of the active site as well as to the dynamics of a fluctuating reaction barrier resulting from temporal variations of both local structure and more delocalized electrostatics.^20,21 The transport properties relevant to enzyme catalysis are distinct from those operating in bulk solution due to the significant degree of structural heterogeneity, nanoscale confinement, and macromolecular crowding.^20,22

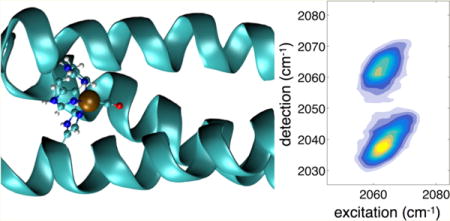
In this paper, we use two-dimensional infrared (2D-IR) spectroscopy²³ to study the ultrafast vibrational dynamics of a carbon monoxide ligand bound in the active site of a de novo metalloenzyme in which we have previously demonstrated nitrite reductase activity.⁴ The CO ligand is bound to a Cu(I) coordinated by three histidine side chains and provides an in situ probe of the active site (Figure 1). Many naturally occurring copper enzymes are capable of binding CO, such as hemocyanins²⁴ and the Cu_B site of cytochrome c oxidase,^25,26 and thus provide valuable references against which to compare our vibrational spectroscopy results. As numerous studies of CO-bound heme proteins have shown, the single CO oscillator bound to transition-metal atoms can be a particularly sensitive and tractable probe, offering a powerful sensor of structure and dynamics.^27–31

Figure 1.

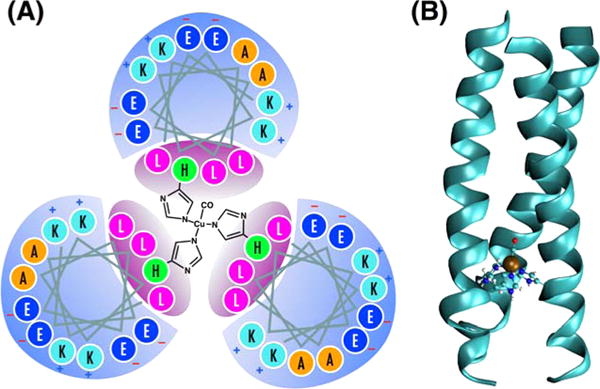
(A) The helix wheel diagram of TRI(L2W)L23H–Cu(I)CO metallopeptide, which is a coiled-coil of three parallel α-helices built from the repeating seven-residue motif LKALEEK. The leucine-rich interior provides a hydrophobic environment in which the type-II copper(I) site is coordinated by three histidine side chains in a distorted tetrahedral geometry. The bound CO ligand serves as a vibrational probe of the active site dynamics. (B) QM/MM optimized geometry of the protein showing the coiled-coil tertiary structure, and the distorted tetrahedral metal binding site with coordinated CO.

Here we show for the first time that Cu-CO within a metalloprotein displays an unexpected sensitivity to the electrostatic environment produced by the protein scaffold. For a single oscillator, the 2D-IR spectrum correlates excited and detected vibrational frequencies, resulting in two bands corresponding to the fundamental (v = 0 to 1) and excited-state (v = 1 to 2) transitions. The difference in the band center frequencies is the vibrational anharmonicity, and it reflects the curvature of the potential energy surface. With increased time delay between the excitation and detection steps, although the shapes of these bands typically evolve reflecting dynamics sensed by the probe, their frequency centers remain constant. Eventually the signal decays due to vibrational relaxation to the ground state.

In our measurements of the Cu-CO probe ligand, we find that following vibrational excitation, the spectrum of the bound CO ligand undergoes a surprising ultrafast frequency shift on a few picosecond time scale, where the two bands in the 2D-IR spectrum become closer in frequency. This band shifting phenomenon has not previously been observed in 2D-IR spectroscopy, but it appears to be analogous to a fluorescence Stokes shift in electronic spectroscopy, which arises due to nonequilibrium motion of the solvent around the fluorophore. Though we do not expect excitation of a CO vibration to cause the protein to move, it is possible that the CO itself could respond to its vibrational excitation by sampling new conformations, which may in turn lead to nonequilibrium spectral changes.

Determining the origin of these spectral changes requires information about the structure and the electrostatics, which we modeled using hybrid QM/MM calculations as well as DFT calculations of a small-molecule active site analogue. Our computational results are consistent with the intuitive picture, revealing a slight bending of the Cu–C–O bond angle caused by vibrational excitation, which is modeled by constraining the CO bond to be 10% longer than it is in the optimized geometry. Comparing the small-molecule (ethylimidizole)₃CuCO cluster to the full structure we show that the structural change arises almost entirely due to the protein scaffold’s distortion of the geometry of histidine coordination to the copper, which is found to be largely mediated by electrostatics by virtue of the substantial (~4 D) dipole moments of the histidine rings. Specifically, we find a dependence of the Cu–C–O bond angle on the C_δ–N_ε–Cu–C dihedral angle. The electrostatic interactions induce structural distortions of the histidines, which in turn activate the coupling between the CO stretch and the Cu–C–O bending motions. This finding suggests that active site energetics can be remotely tuned by modifying electrostatics, providing an avenue for directing mutation strategies or possibly for engineering long-range allosteric regulation into the de novo enzyme.

RESULTS AND DISCUSSION

Peptide Sequence

TRI-family peptides are designed based on the amphipathic heptad repeat approach. A heptad contains seven amino acid residues abcdefg, with hydrophobic residues at the a and d positions, and hydrophilic, salt-bridging residues at the e and g positions.³² The monomer peptides assemble into helical coiled coils upon dissolving in water through hydrophobic collapse.^33–36 Near neutral pH (6–8), it forms parallel three-stranded coiled coils (3SCC).^37,38 The sequence of the peptide TRIL2WL23H is Ac-G WKALEEK LKALEEK LKALEEK HKALEEK G-NH₂ with the N-terminus acetylated and C-terminus amidated. The peptide was synthesized on an Applied Biosystem 433A peptide synthesizer using standard protocols³⁹ and purified and characterized as previously reported.⁴⁰ Previous reports demonstrated that derivatives of TRI peptide, TRI(L2W)L23H, can bind to Zn(II) and Cu(I)/(II), forming metallopeptides that are excellent structural and functional models for carbonic anhydrase and copper nitrite reductase, respectively.^3,41 This system is particularly interesting to us because it maintains significant levels of protein complexity in a much-simplified scaffold.

Ultrafast 2D-IR Spectroscopy

2D-IR spectra recorded at a series of waiting time delays (t₂) between the excitation pulse pair and the detection pulse show an inhomogeneously broadened band centered near 2063 cm⁻¹. The band at lower detection frequency (2039 cm⁻¹) corresponds to excited-state absorption from the ν = 1 to 2 levels (denoted ν₁₂) and is red-shifted due to the vibrational anharmonicity of the CO oscillator. The 2063 cm⁻¹ fundamental (ν = 0 to 1, denoted ν₀₁) CO absorption frequency is typical of Cu-CO vibrations observed in other proteins such as the Cu_B site of cytochrome c oxidase, and within the bimetallic binding site of hemocyanins.^24,25 Relative to 1950–1960 cm ⁻¹ Fe-CO vibrations in heme proteins, the ~100 cm⁻¹ blue-shifted transition indicates that the copper–carbon bond is weaker, and the degree of π back bonding is also reduced. We note that under the low <1 mM protein concentration we used, it was difficult to record even linear FT-IR spectra, making the measurement of absorptive 2D spectra impossible given our 2D spectrometer’s sensitivity. Although the data shown in Figure 2 are absolute value rephasing spectra, from which accurate line shape information is not readily extracted, it is nevertheless clear that the antidiagonal spectral widths are very narrow. We attribute the preponderance of inhomogeneous broadening to the unique environment experienced by the CO vibrational probe. The CO resides in the hydrophobic core of the homotrimeric coiled-coil lined by nonpolar leucine side chains. Numerous previous studies by us and others have shown that metal carbonyl complexes in alkane solvents are generally homogeneously broadened due to the lack of spectral fluctuations induced by the motion of solvating nonpolar liquid molecules.⁴² Although the CO is effectively solvated by a nonpolar shell of alkane side chains, it is nevertheless embedded within a complex protein scaffold, which has charged residues on the solvent-exposed exterior, as well as highly oriented CO⋯NH bonds of the largely α helical peptide chains. In addition, as we detail below, the histidine side chains coordinating the Cu are significantly polar, having average dipole moments of 3.6 D.⁴³ The low polarity of the interior does not attenuate the electrostatic influence of the charges due to the low effective dielectric constant.⁴⁴ The substantial inhomogeneous broadening thus reflects the distribution of peptide conformations, including the coiled-coil packing, which induce shifts in the CO vibrational frequency.

Figure 2.

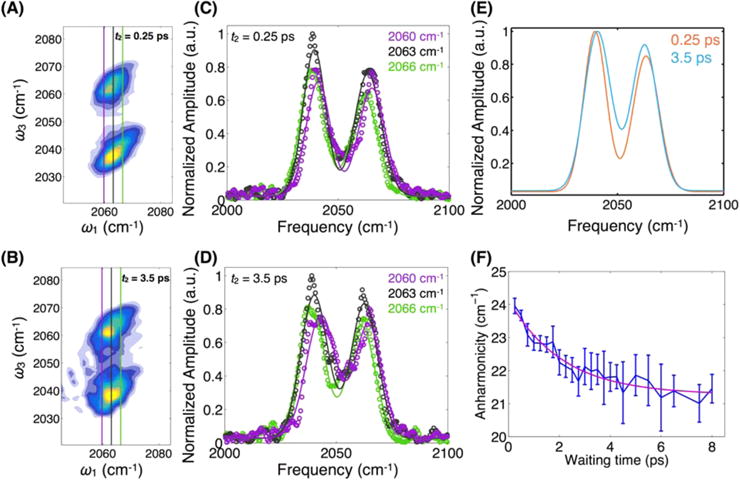
Absolute magnitude 2D rephasing spectra recorded at 0.25 ps (A) and 3.5 ps (B) waiting times. Diagonally elongated band shapes indicate inhomogeneous broadening and the detection frequency (ω₃) difference between the two bands gives the vibrational anharmonicity. Quantitative analysis of the detection frequency-dependent spectra at different values of the excitation frequency (ω₁) for t₂ = 0.25 ps (C) and 3.5 ps (D) shows waiting time-dependent changes to both amplitudes and centers. Three detection frequency spectra are shown for each waiting time in purple (2060 cm⁻¹), black (2063 cm⁻¹), and green (2066 cm⁻¹), shown in the 2D spectra as vertical lines. (E) Fitting the bands for all frequencies between 2060 and 2066 cm⁻¹ as described in the text and showing them together highlights the band coalescence. (F) The waiting time-dependent relaxation of the apparent vibrational anharmonicity is well fit with a decay constant of 2 ps.

Dynamic Evolution of the 2D-IR Bands

Waiting time-dependent changes in the 2D line shape are routinely monitored using the peak shape analysis of absorptive spectra or the inhomogeneity index.^45–47 The diagonal elongation of the line shape reflects the frequency correlation within the inhomogeneously broadened spectral band, and as stochastic modulations cause equilibrium fluctuations of the excited vibrations, the correlation becomes lost as a function of the waiting time. This stochastic frequency sampling is called spectral diffusion and is a powerful observable in 2D-IR spectroscopy. The decay of the correlation is related to the frequency fluctuation correlation function, ⟨δω(0)δω(t)⟩, where the instantaneous frequency ω(t) = ⟨ω⟩ + δω.⁴⁸ The meaning of this correlation function is somewhat poorly defined when the system is evolving out of equilibrium, as is the case for the vibrationally excited CO bound to the Cu active site.

On the few-ps time scale (Figure 2), increasing the waiting time in the 2D-IR pulse sequence does not lead to significant spectral reshaping besides that due to scattering from our weakly absorbing sample. The survival of spectral correlation on this time scale (<5 ps) indicates that much of the spectral diffusion takes place on slower time scales, as is expected in complex macromolecular environments.^49,50 We do note, however, a subtle but significant change in the 2D spectra that, to our knowledge, has not been described previously. The shift in wavenumber between the two bands in the 2D-IR spectrum gives the difference in energy between the 0–1 and 1–2 vibrational transitions, which is a measure of the vibrational anharmonicity. The value obtained at a waiting time of 250 fs is 24 cm⁻¹, which is typical of a single CO bound to a metal.⁵¹ With increased waiting time, we observe a surprising decrease in the frequency separation between the two detected bands.

The apparently time-evolving “anharmonicity” is more evident in a quantitative analysis of the bands. Taking slices along the detection frequency axis at each value of the excitation frequency between 2060 and 2066 cm⁻¹, we fit the two bands using Gaussian functions (Figure 2). We then average the differences of the fitted center frequencies over all of the excitation frequencies. Plotting the waiting time-dependent decay of the averaged differences reveals a clear dynamical signature. The decay of the apparent anharmonicity, due to the spectral evolution of the bands, is well fit to an exponential function with a 2.1 ± 0.8 ps decay constant, plus a constant offset determined by the long-time anharmonicity of 21 cm⁻¹. In addition to plotting the frequency differences between the fitted peak centers, we also show the centers themselves in Figure 3. The fitted centers show that the 0–1 transition red shifts, while the 1–2 transition blue shifts. It is interesting to note that the magnitude of the red shift of the 0–1 band is less than the blue shift of the 1–2 band. This difference may be due to the fact that roughly half of the amplitude of the 0–1 band arises from the ground-state evolution pathway, where we do not expect any frequency shift.

Figure 3.

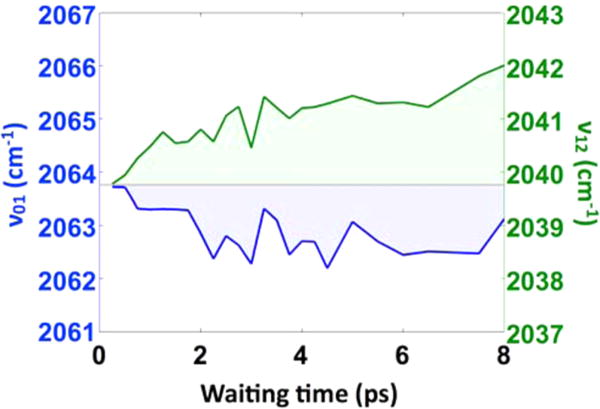
Waiting time-dependent fitted band centers for the 0–1 (blue) and 1–2 (green) transitions show that the apparent time-dependent anharmonicity arises due to the simultaneous red shifting of the 0–1 band and blue shifting of the 1–2 band. Within the simple Morse oscillator model, this trend requires that the dissociation energy D_e increases, while the Morse width parameter a decreases (defined in the SI). Both parameters influence the harmonic force constant since k_harm = 2a²D_e.

This observation of an apparent time-dependent anharmonicity is the central experimental finding of this work and provides the motivation for the subsequent computational efforts to identify the origin of this dynamical phenomenon. We note that we have observed nearly identical behavior in a different peptide sequence (shown in the SI) in which the positively charged lysine residues on the exterior of the peptide have been mutated to glutamine, indicating that this result is reproducible and is likely a general feature of the coiled-coil protein family we have investigated. Future studies will examine several other peptide sequences which have been shown to exhibit varying degrees of nitrite reductase activity. Importantly, we do not observe this dynamical anharmonicity in a small-molecule iron-monocarbonyl complex we have studied in earlier work (shown in the SI); this observation provides a hint that the dynamical evolution is due to the protein environment. Ideally we would compare the same active site structure experimentally in solution as well as embedded within the protein scaffold, but doing so would require synthesizing a complex such as (ethylimidizole)₃CuCO. There are monocarbonyl complexes of Cu that could provide useful comparison systems, but which lack the imidazole rings,⁵² which we have found to be essential in modulating the Cu–C–O potential energy surface.

2D-IR spectroscopy is often analyzed from the point of view where the spectral fluctuations that lead to decay of the correlation of frequency fluctuations are not influenced by the measurement process. For example, the slope of the 2D peak shape’s asymmetry is often taken to report the frequency correlation present at a given waiting time, and as the oscillators stochastically sample their full conformational space, including the solvent or other nearby environment, the frequency performs a random walk through the inhomogeneously broadened band.^46,53,54 The decay of frequency correlation is generally linked to molecular motions of the probe and of its surroundings. Since nearly all published examples analyze the diagonal 0–1 transition, it is tacitly assumed that the two pathways producing signal on the diagonal report the same equilibrium molecular dynamics. As shown in Figure 4, however, the two pathways are clearly distinct, since the ground-state bleach pathway corresponds to waiting-time evolution on the ground state, whereas the stimulated emission pathway corresponds to evolution on the excited vibrational state. If vibrational excitation launches nonequilibrium motion, the diagonal peak will not reflect solely the equilibrium frequency fluctuation correlation function often associated with spectral diffusion. Studies of methanol⁵⁵ and of acetic acid⁵⁶ have shown that vibrational population relaxation can produce “photoproducts” such as broken hydrogen bonds, as well as hot intermediates. We argue that our observation here of a continuously evolving spectral shift reflects nonequilibrium dynamics not due to cascaded population flow since the motion in the low-frequency coordinate is promptly launched by the v = 0 to 1 CO excitation, and the vibrational relaxation is quite slow (>30 ps, shown in the SI). Alternatively, this phenomenon is analogous to nonequilibrium dynamics commonly observed in fluorescent dyes, where solvation induces dynamically shifting Stokes emission.^57–60 Though the solvation coordinate is often treated only qualitatively, in the present case of nonequilibrium vibrational dynamics, it should be possible to identify a candidate for the coordinate along which motion is driven. Indeed the analogy with polar solvation is particularly apt, as discussed below, since our quantum chemistry calculations show a significant increase in CO bond dipole associated with vibrational excitation, which then potentially senses the collective electrostatic environment (see Table S2 in the SI). The central question of the remainder of this paper, therefore, is to determine the molecular origin of the otherwise hidden motional coordinate, as well as the degree to which the motion is driven by local, bonded interactions or by more collective electrostatic influences.

Figure 4.

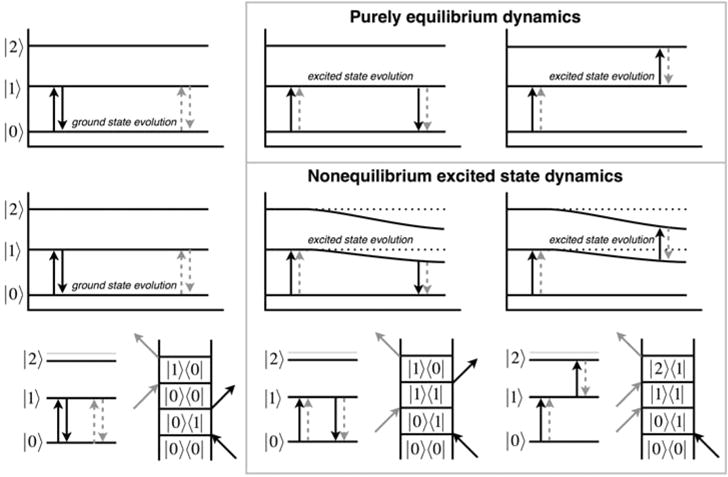
Energy level diagrams and rephasing Liouville space diagrams for the three accessible vibrational states of the copper-bound CO ligand show that two of the three pathways involve population evolution on the v = 1 vibrational excited state, whereas only one involves ground-state evolution. The three contributions to the 2D spectrum are shown in the columns: (left) ground-state bleach, GSB; (middle) stimulated emission, SE; and (right) excited-state absorption, ESA. The top row illustrates the conventional picture where vibrational excitation is fully uncoupled to the sensed ultrafast dynamics. The middle row shows a time-evolving CO vibrational energy level structure due to continuous modulation by anharmonic coupling to a slow degree of freedom. The bottom row shows the wave-matching energy level diagrams and double-sided Feynman diagrams corresponding to the GSB, SE, and ESA signal contributions.

Figure 2E shows that the two bands become closer to each other as a function of time, which requires the following interpretation regarding the shifts of the vibrational levels. For the ground-state bleach band (v = 0 to 1), the contribution due to the ground-state pathway is unshifted and only exhibits equilibrium spectral diffusion. The stimulated emission contribution evolving on the excited state, however, must red shift to cause the observed spectral change, whereas the excited-state absorption (v = 1 to 2) must blue shift. Therefore, one straightforward, though unusual, conclusion is that the CO vibration becomes more harmonic once it is excited. Within the Morse oscillator model, which describes single and multiple metal carbonyl complexes very well,⁶¹ a red-shifted fundamental and reduced anharmonicity means that the bond dissociation energy D_e must increase. Although it is counterintuitive to associate a red-shifted frequency with a stronger bond, that intuition is based on a one-dimensional harmonic oscillator picture where the bond strength is encoded in the force constant k; the simple harmonic model is necessarily not able to account for the anharmonicity of real bonding potential energy functions. We discuss this point further below in the context of our computational results.

Quantum Chemical Model of the Copper Site

To assess the likelihood that the nonequilibrium relaxation is due to the local bonding environment of the copper site, we first considered a small molecule analogue consisting of the copper ion with three 5-ethylimidazole ligands and a carbonyl ligand. In general, we are using the computational study to determine what degrees of freedom are coupled to the CO stretching mode. We investigate the small molecule analogue for two main reasons. First, the small molecule calculation enables a direct comparison to the case with the protein scaffold, which allows us to determine what role the protein plays in modulating the vibrational coupling. Second, the small molecule can be subsequently manipulated in order to understand why the protein is able to modulate the Cu–CO potential energy surface. The starting structure was based on the crystal structure of a similar peptide, Hg(II)_S[Zn(II)_N(H₂O)]-(CSL9CL23H)₃⁺ (PDB ID code 3PBJ), and the geometry of the small molecule was optimized in Gaussian 09 using the B3LYP functional and the 6-311G(d,p) basis set for all atoms as further described in the Methods section.⁶² To simulate the structural change associated with vibrational excitation, the C–O bond length was fixed at 110% of the globally optimized bond length, while the remaining atoms were allowed to reoptimize. This increase in bond length is the expected change for a Morse oscillator with a first excitation frequency of 2063 cm⁻¹, an anharmonicity of 24 cm⁻¹, and the same reduced mass as CO (see SI for details of the Morse potential). The calculated vibrationally excited geometry was very similar to the ground state (Figure 5A) with a RMSD of 0.023 Å for the atoms excluding the carbonyl. A more detailed discussion of the geometry change upon vibrational excitation can be found in the SI. The coordinate we expect to show the largest change from coupling to the CO displacement is the Cu–C–O bond angle, which changes by <1° upon vibrational excitation. To compute the expected thermal angle distribution, we froze the CO bond length at the ground- or excited-state value and then scanned through a range of angles between 160° and 180° while relaxing the other degrees of freedom. The results of this relaxed potential energy surface scan are shown in Figure 5D, where the only clear difference is the curvature of the potentials, which is 4.4 times greater in the ground state than in the excited state, indicating a difference in the stiffness of the Cu–C–O angle potential.

Figure 5.

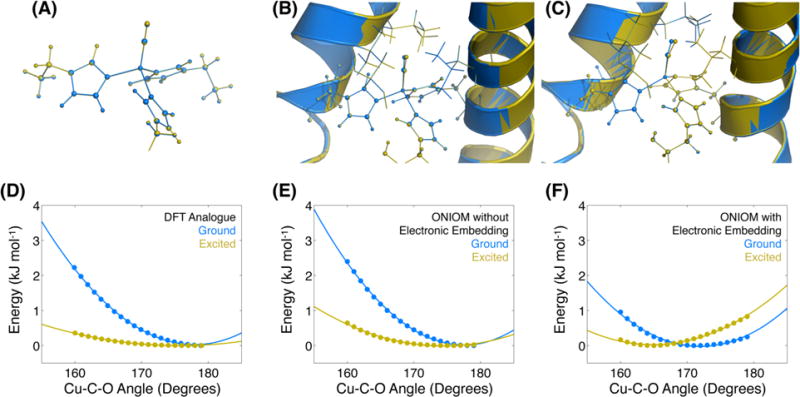
Optimized structures of the ground (blue) and vibrationally excited (yellow) states for the small molecule analogue (A), peptide calculated with ONIOM without electronic embedding (B), and peptide modeled with ONIOM including electronic embedding (C). The Cu–C–O bond angle tilting potential is shown for the three cases (D–F), with a clear difference between the ONIOM with ee potential and the other two. Calculated energies are shown as points with quadratic fits shown as curves.

QM/MM Model of the Full de Novo Enzyme

Since we were unable to identify an obvious candidate for the hidden motional coordinate by considering only the local bonding environment, we performed hybrid QM/MM calculations to account for the steric and electrostatic interactions arising from the entire peptide trimer. The QM/MM calculations were carried out with the ONIOM method (our own n-layered integrated molecular orbital and molecular mechanics) as implemented in Gaussian 09 using two layers (described in Methods).^63–65 With ONIOM the vibrational ground- and excited-state geometries can be compared in a similar way as was done for the small molecule analogue: optimizing the geometry for the ground state and then freezing the extended CO bond while optimizing the rest of the geometry for the vibrational excited state. In the ONIOM model, the optimized Cu–C–O bond angle is found to decrease by more than 6° upon vibrational excitation, as shown in Figure 5C. The relaxed potential energy surface scan is also included in Figure 5F and shows a clear difference between the ground- and excited-state Cu–C–O angle potential energy surfaces, although the change in curvature is less pronounced than for the small molecule analogue. In the peptide with electronic embedding, the curvature in the ground state is greater by a factor of 1.5 relative to the excited state, which is a considerably smaller difference than in the small molecule analogue. These calculations support the attribution of the hidden motional coordinate to the Cu–C–O bond angle, and the presence of the peptide enhances the coupling to the CO stretch. The identification of the bend as the coupled degree of freedom is consistent with the 1–2 ps time scale of the vibrational frequency shifting dynamics. Our frequency analyses yield normal modes that most closely resemble the bending motion to have frequencies of 27.37 cm⁻¹ (small molecule) and 31.30 cm⁻¹ (ONIOM with embedding). Both of these frequencies correspond to vibrational periods of about 1 ps, which is consistent with our measured time scale.

In order to separate the contributions due to electrostatic and other nonbonding interactions, we repeated the ONIOM calculations with electronic embedding disabled so that the electrostatic contribution from atoms not included in the QM layer would be ignored. Comparing the results obtained in the presence and absence of the MM charges enables us to isolate the electrostatic interactions from the excluded-volume, or hard-sphere collisions, for example, between the vibrationally excited carbonyl and the leucine residues above the active site in the interior of the peptide. The resulting potentials, shown in Figure 5E, are much more similar to those of the small molecule analog than the ONIOM calculations including electronic embedding. Both the ground and vibrationally excited states have Cu–C–O bond angles closer to 180°, and the difference between the two is <3°. The curvature of the ground-state potential is 2.6 times that of the excited state in this case, again showing that the ONIOM model without electronic embedding again falls between the values found for the other calculations. This comparison shows that the coupling of the Cu–C–O bond angle to the CO stretching frequency is more strongly influenced by the electrostatic interactions than by the van der Waals interactions.

Though there have been no previous reports of copper carbonyl proteins or small molecules studied with 2D-IR, there have been several experimental and theoretical investigations of heme proteins, which leverage the Fe–CO vibrational probe to study the dynamics of the heme site.^51,66–73 Though the present study does not rely upon computations to model the dynamics or 2D-IR spectra for comparison to experiment, several previous reports of heme proteins have taken this approach, and we summarize their basic characteristics here. A very successful strategy used to simulate 2D-IR spectra and associated dynamical observables employs classical molecular dynamics (MD) simulations coupled with an electrostatic-based mapping procedure for generating instantaneous vibrational frequencies at each simulation step.^74–79 In the case of myoglobin, which has received significant attention, two varieties of mapping approaches have been implemented and represent the range of complexity used in other 2D-IR simulation studies. To model three-pulse vibrational photon echo spectroscopy, which can be considered to be a subset of 2D-IR spectroscopy, Fayer and Loring’s groups used MD simulations of carboxymyoglobin, producing CO frequencies by using the experimental Stark tuning rate determined by Boxer et al.⁵¹ They used the frequency trajectories to construct the third-order response function and found good agreement with experiment.

An alternative approach was taken by Cho et al., using a much more sophisticated frequency mapping procedure based on a multisite evaluation of the electrostatic potential.⁷² This multisite approach enables the detailed treatment of directional hydrogen bonding, which is particularly important in capturing the subtle interactions between the histidine side chain and the CO ligand.

Recent theoretical and experimental investigations of heme proteins by Falvo et al. used an explicit quantum mechanical treatment of the CO vibrational frequency and transition dipole moment.⁷¹ In that approach, the CO vibrational potential is parametrized in such a way that electrostatics and anharmonic couplings are included, yielding a time-dependent CO potential energy surface.⁸⁰ Solving the 1D Schrödinger equation for that surface provides the vibrational frequencies, anharmonicities, and transition moments needed to compute linear and nonlinear response functions. Even this method, however, does not explicitly propagate the CO in an excited state to calculate the excited-state absorption and the stimulated emission pathways. Hence, the method essentially makes the assumption that vibrational excitation does not alter the spectral dynamics. Given the excellent agreement between experiment and simulation, it appears that the ground-state assumption is valid for hemoglobin. It is noteworthy that these investigators did include an explicit anharmonic coupling between the CO stretch and the Fe–C–O bend coordinates to reflect the red shift that occurs as the Fe–C–O bond angle is distorted from linear. Thus, the model treats the case where the protein environment’s distortion of the bond angle alters the CO stretch potential surface. This coupling necessarily works both ways, however, so that it is possible that exciting the CO also causes a bending motion. Evidently the effect is too weak to be seen in the experimental data, so neglecting the explicit CO stretch excitation seems to be a valid simplification.

In summary, these approaches to simulating 2D-IR spectra of heme proteins do not explicitly include the effect of vibrational excitation for the two paths that evolve in excited states since it is hypothesized that the dynamics of the surroundings will not be altered. This hypothesis seems quite reasonable in the case of myoglobin and hemoglobin since the major dynamical contribution is from the histidine motion.

There are cases where vibrational excitation does induce dynamics. For example, in methanol, exciting the OH (or OD) stretch can break the OH⋯O hydrogen bond, causing the dangling OH bond to blue shift.^55,81–84 This process has been denoted a vibrational photochemical reaction and leads to new cross peaks in the 2D-IR spectrum, which have been reproduced by theoretical modeling.^85,86 There are also examples of coupled, hydrogen-bonded dimers, such as those of acetic acid and of 7-azaindole.^87–92 In these cases, there are clear observations of vibrational quantum beats launched by excitation of the OH stretches that are anharmonically coupled to low-frequency interdimer motions. It is these types of couplings that are perhaps the most similar to our present studies of the de novo metalloenzyme, though in our case we find the anharmonic coupling to be highly dependent on the details of the coordination geometry at the metal site.

Electrostatic Potential is Indirectly Responsible for the Vibrational Coupling

The computational results suggest that the electrostatic environment of the peptide enhances the coupling of the carbonyl stretching mode to the Cu–C–O angle. The Adaptive Poisson–Boltzmann Solver (APBS) software⁹³ was used to calculate the electrostatic potential and from that the electric field projected along a vector defined by the carbonyl bond as described in the SI. The electric field magnitude along the carbonyl bond was found to vary greatly for two different conformers of the peptide, both optimized from different starting structures using the ONIOM scheme described above. The fields of the two conformers differ by about 35 MV/cm, principally in the contribution from the histidine residues, where a fairly small geometrical change (RMSD of (His)₃CuCO is 0.75 Å) results in a RMS Mulliken charge difference of 0.04 e for the same atoms. Despite the large field difference, the carbonyl tilts upon vibrational excitation in both conformers, and the electric field magnitude changes along the carbonyl in the ground and excited states are similar. So rather than the electric field directly affecting the carbonyl, it appears that the electric field from the peptide scaffold distorts the coordination of the histidines to the copper atom, which is responsible for inducing the coupling between the CO stretch and the Cu–C–O bend coordinates

To test the role of the three histidines in modulating the CuCO potential surface and to simulate a distortion of the histidines caused by the electric field, we performed DFT calculations on the small molecule analogue holding the C–N–Cu-C dihedral angles of each histidine fixed at values slightly larger than those of the optimal geometry. Without an applied field, we find that the Cu–C–O angle becomes tilted in the vibrational excited state, confirming the subtle coupling between the histidine coordination, the CO stretch and the Cu–C–O bend. Though the electric field will still likely cause a frequency shift and some of the CO tilting, the nonequilibrium dynamical signatures we observe appear to arise primarily from the bonding environment of the (His)₃Cu coordination. In other words, the histidines transduce their electrostatic interactions with the peptide scaffold to the copper active site via their coordination, which in turn alters the energetics of exogenous ligand binding, CO in this case. We note here that the link between histidine coordination geometry and the coupling between the CO stretch and Cu–C–O bend can be completely determined using the DFT calculations. Hence, we can regard the QM/MM calculations as providing a guide for the small molecule DFT calculation. That our structural finding is essentially independent of the QM/MM results is reassuring since there are more sophisticated QM/MM methods than ONIOM.

To investigate the histidine dihedral angle dependence further, we varied the C_δ–N_ε–Cu–C dihedral angles for each imidazole in the Cu(EtIm)₃CO cluster systematically, optimizing the other atoms at each angle. Figure 6 shows the optimized CuCO angle as a function of the histidine coordination geometry computed for both the CO vibrational ground state as well as the simulated CO v = 1 state. Whereas there is essentially no dependence on the histidine geometry in the vibrational ground state, the excited-state geometry is highly sensitive to the histidine coordination. These findings show that the CO excited state, more than the ground state, is remarkably sensitive to molecular and electronic structure changes in the first coordination sphere, which are themselves highly influenced by the overall electrostatics of the macromolecular construct. In general, the importance of histidine coordination and the structural changes upon ligand binding or dissociation is well-known.⁹⁴

Figure 6.

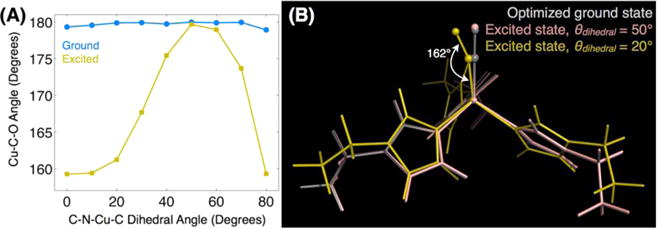
Propensity for excited-state structural changes appears to be controlled by the geometry of the histidine’s coordination with copper. Results of DFT calculations of the small Cu(EtIm)₃CO cluster in the absence of the protein matrix show that (A) the optimized Cu–C–O bond angle is insensitive to the C_δ–N_ε–Cu–C dihedral angle in the CO vibrational ground state. In the excited state, however, the bond angle and tilt become acutely sensitive to the histidine coordination geometry. (B) Structures selected from the full dihedral angle scan with dihedral angles of 20° and 50° illustrate the link between the histidine coordination and the copper-ligand bonding. This geometrical distortion only occurs in the CO excited state, suggesting the inadequacy of ground-state equilibrium structures to reveal reactivity. Similar structures showing no substantial changes on the ground state are shown in the SI.

It remains to be determined why the histidines are so susceptible to structural modification by electrostatics. By considering in detail the partial charges on the histidine CH and NH bonds, we find that, averaged over the three histidines, the N_δ–H and C_δ–H bonds are substantially more polar than the C_ε–H bonds, leading to a net dipole moment of roughly 3.6 D for each histidine side chain (Figure 7, see details in the SI). This computational result agrees very well with the value determined from microwave spectroscopy of imidazole.⁴³ The electric field presented by the protein applies a torque on the histidines through the charge asymmetry, which is enhanced relative to the uncoordinated histidines due to the metal coordination. This polarization has been observed in other copper binding sites, such as in cytochrome c oxidase’s Cu_B site.⁹⁵ It is interesting to note that in cytochrome c oxidase, it is the epsilon carbons that point toward the ligand binding site, rather than the present case of the delta carbons. In our QM/MM results, the C_δ–H bonds are more polarized than are the C_ε–H bonds in cytochrome c oxidase. The metal-induced polarization of CH bonds in histidines has been identified as a source of structure stabilizing CH⋯O hydrogen bonds in a series of metalloenzymes.⁹⁶ Indeed, CH⋯O hydrogen bonding to mutated side chains or substrates in the active site of our de novo metalloenzyme may also be leveraged to optimize catalytic efficiency and selectivity.⁹⁷

Figure 7.

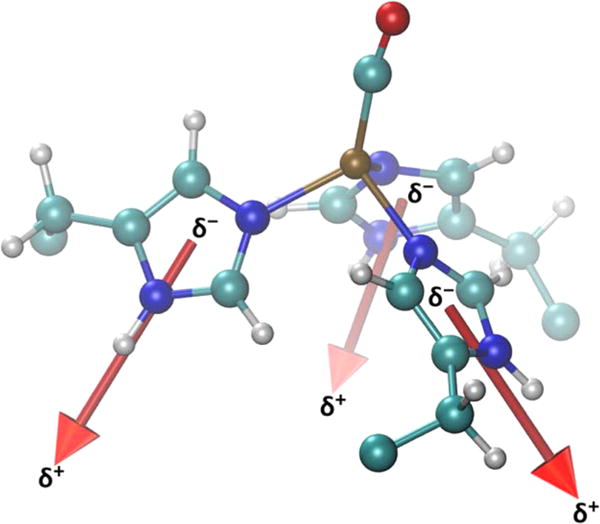
Dipole moment of each histidine ring, in Cu(I) (TRIL2WL23H)₃(CO)⁺ with average magnitude of 3.6 D. These dipolar side chains are able to couple to the electrostatic environment produced by the protein scaffold.

Relationship Between Bond Angle and CO Frequency

The identification of the Cu–C–O angle as the hidden coordinate coupled to carbonyl vibrational excitation does not necessarily explain why the CO frequencies appear to evolve dynamically. To compute the nonequilibrium vibrational transition energy would require a quantum dynamical treatment of a much higher dimensional potential energy surface. Nevertheless, there is ample evidence from previous studies of metal–CO bonding in heme proteins to help draw the link between bond angle and CO frequency. In contrast to smaller coordination complexes, where nonbridged metal–CO bonds rarely deviate from linear geometries,⁹⁸ influences from the protein do indeed induce distortions in ligand binding. One particularly well-known example is the heme protein myoglobin, where X-ray crystallography models showed significantly bent Fe–C–O bond angles, apparently in conflict with energetic constraints imposed by such highly distorted structures.^{28,29,31,99,100} The discrepancies were ultimately resolved by improvements in crystallography and by considering the results of picosecond IR transient anisotropy measurements, which indicated much more linear bond angles, even after careful consideration of finite sample thickness effects as well as accounting for the precise orientation of the CO transition dipole moment.¹⁰¹ The IR studies of myoglobin and hemoglobin, where the primary focus was on the geometry of the Fe–C–O and its orientation relative to the heme plane, are particularly helpful in understanding the dynamic frequency shifts we observe in the Cu–CO embedded within the peptide coiled-coil. Taking the values obtained in the heme proteins for CO wavenumber as a function of Fe–C–O bond angle determined from crystallography and IR spectroscopy, we can estimate a shift of roughly 5 cm⁻¹ for a 6° change in the angle assuming a linear regression of the angle-dependent vibrational frequency (details in the SI). While this frequency shift is larger than the 3–4 cm⁻¹ shift we observe in the CuCO case, in heme proteins the Fe–C bond is shorter, as evidenced by the considerably lower Fe–CO transition energy (1930–1950 cm⁻¹ in heme proteins in contrast to the 2063 cm⁻¹ in the CuCO peptide). Hence, for Cu–CO one would expect a reduced coupling between bond angle and CO bond strength. It is noteworthy that in the heme case, much of the distortion energy (~85%) can be attributed to the strong polar contact through hydrogen bonding to the nearby histidine residue,¹⁰⁰ whereas in the present CuCO case, the distortion from the linear form arises nearly entirely from variation in the histidine orientation, which itself reflects the longer range electrostatic interactions with the protein scaffold. Future work to understand the CO frequency dynamics will be undertaken following the approach of Falvo and Meier,^71,80 using a multidimensional potential surface combined with quantum dynamics to evaluate the nonequilibrium transition frequencies.¹⁰²

Rationale for Nonequilibrium Decreases in Fundamental Frequency and in the Vibrational Anharmonicity

The vibrational states of CO bound to transition metals are typically well described using Morse oscillators, even in the case of multiple coupled CO ligands.⁶¹ The Morse potential is characterized by two parameters D_e, the dissociation energy (from the potential minimum), and a term, a, that controls the stiffness.¹⁰³ Although the Morse potential can only be viewed as an approximate model of the CO bond, it is helpful in providing a chemical interpretation of the vibrational spectra. In the present case, we find that the nonequilibrium motion leads to both a red-shift of the carbonyl ν₀₁ (where ν₀₁ is the frequency difference between the ν = 0 and ν = 1 vibrational states) fundamental vibration and a decrease in the vibrational anharmonicity. Since ν₀₁ and Δ uniquely specify the Morse potential, we can extract Morse potential parameters from our 2D-IR data (details in the SI). A decrease in both ν₀₁ and Δ requires an increase in the dissociation energy. In chemical terms, vibrational excitation of CO bound to Cu within the protein’s electrostatic environment produces a slightly bent Cu–CO bond where the CO bond is actually stronger (as measured from the minimum of the V_CO potential surface). Within the Morse model, in order for a bond to become stronger while exhibiting a spectroscopic red shift, it must become more harmonic. The harmonic force constant for a Morse oscillator, evaluated at the position of the potential minimum, is k_harm = 2a²D_e, where a is the Morse width parameter, and D_e is the classical dissociation energy. Since both a and D_e determine the harmonic force constant, conventional linear spectroscopy will not be able to sense the competing influences of the two potential parameters. We do note, however, that unconventional IR spectroscopy performed on a crystal of carboxymyoglobin has been able to determine the vibrational anharmonicity using the overtone (i.e., 0–2) transition, which is 2 orders of magnitude weaker than the fundamental.¹⁰⁴ This method is not likely to be widely applicable, however, especially for proteins that are difficult to crystallize. There is evidence in recent ATR 2D-IR experiments of reduced anharmonicity for nonlinear metal–CO bonds relative to nearly chemically similar linear metal–CO bonds.¹⁰⁵ Standard arguments from inorganic chemistry provide the rationale for the increase in CO dissociation energy: the Cu– CO bond angle tilt reduces the spatial overlap between the metal d orbitals and the CO π* orbitals, reducing back bonding and returning electron density to the CO which strengthens the bond. In fact, these arguments appear to be able to explain the paradoxical observation in heme proteins that increased deviation from linear metal–CO bond angles correlates with red-shifted carbonyl vibrations, though those earlier experiments did not measure the vibrational anharmonicity. Finally, it is important to mention that the Morse oscillator is still a model of the CO interatomic potential and is not exact. The changes we have measured are quite small, and it is evident that future work will need to model the CO potential energy surface using quantum chemistry.

Role of Ultrafast Spectroscopy in Identifying the Anharmonic Coupling

The main result of this work is the identification of anharmonic coupling between the CO stretch and the Cu–C–O bend mediated by the histidine coordination geometry. In a sense it is a kind of three-body coupling requiring the knowledge of three distinct geometrical parameters. That we observe a 2 ps nonequilibrium dynamical signature is essentially a confirmation of the low-frequency motion of the bending motion launched by the CO excitation. That said, it is worth pointing out that observing the consequence of lengthening a bond on structure and dynamics requires nonlinear spectroscopy. Since linear spectroscopy measures only the coherence between the ground and excited vibrational states, in the present case of slow vibrational relaxation, the linear absorption spectrum does not contain information relating to the population of the excited vibrational state or to dynamics triggered by vibrational excitation. Figure 6A shows that there is no dependence of the ground-state geometry on histidine coordination, indicating that spectroscopy sensitive to the ground-state geometry (i.e., FTIR) would be unable to sense the coupling. Although we are exciting a vibrational probe, we note that one quantum of CO stretch, 2064 cm⁻¹, equals 6 kcal/mol, which is within a factor of 1–2 of catalyzed reaction barriers.⁵ Therefore, probing a potential energy surface through mode coupling may help to determine couplings near the transition state. For example, we should now be able to determine the reaction barrier to nitrite reduction computationally as a function of the histidine angle. Comparison of the barrier with and without the protein scaffold will enable us to extract the role of the enzyme in speeding up the reaction.

In choosing a reaction coordinate, it is common to treat the remaining degrees of freedom effectively. Although the reduction in dimensionality permits an intuitive understanding of the reaction, it becomes difficult to account for dynamical phenomena such as recrossings as well as barrier shape and height fluctuations. In a macromolecular environment, such as within a protein, structural fluctuations occur on time scales ranging from picosecond side chain motion to much slower motion of loops and domains. These fluctuations, in principle, can modulate reaction barriers by altering the path taken by a reacting species through the multidimensional energy landscape. When the time scales for motion toward and over the barrier are similar to those of the structural fluctuations, the observed rate constant can include these dynamical contributions. Though it is not impossible to include such effects in the transition-state theory rate constant,⁷ it is difficult to do so in the context of experiments alone. Controllable experimental constructs, such as the present de novo metalloenzyme, should provide a systematic means of assessing the degree to which dynamical fluctuations play a role in modifying the catalytic power of a designed enzyme, with the understanding that there may be no significant dynamical influence at all.

Prospects for Future Design Innovations

The central question driving this work—one that we have not answered yet—is how to leverage the finding that histidine coordination can modulate the metal–ligand potential energy surface which likely plays a role in the catalysis. While addressing this challenge is a focus of ongoing and future investigations, we can make some general comments. In particular, having the potential ability to tune the reactivity somewhat remotely through the histidine coordination geometry enables design flexibility, since modifications can be made both “above” the Cu site (i.e., in the substrate binding cavity) and below the Cu site. Modifications in the binding site can exert structural control, for example, by preforming the transition-state species via a differential binding mechanism, whereas mutations below the binding site may influence the reactivity without necessarily altering the structural preformation. The histidine coordination geometry will be influenced both by packing and sterics in the core of the coiled-coil as well as by the longer range coupling to the electrostatics through the imidazole ring dipole moments. By varying the packing near the histidines, the steric interactions may be able to constrain the ring planes to be alternatively more coplanar or more aligned with the long axis of the coiled-coil. Since structural consequences of side chain modifications are not necessarily straightforward to predict, inserting bulky side chains near the histidines may directly act on the imidazole rings, or they may push out the peptide chains, which in turn strain the imidazole rings. Implementing and testing these design principles will benefit from our combined approach integrating synthesis, experiment, and computational modeling.

CONCLUSIONS

Using 2D-IR spectroscopy to investigate the vibrational dynamics of a CO vibrational probe bound to the active site of a de novo copper metalloenzyme, we find unexpected nonequilibrium frequency evolution with a 2 ps time scale. This experimental observation suggests a coupling between the high-frequency CO vibration and a much lower-frequency motion. DFT studies of the model active site and QM/MM (ONIOM) calculations of the full peptide trimer point to the importance of electrostatics in mediating the coupling between the CO stretch and the Cu–C–O bending motions. Our results show that the multidimensional potential energy surface of a ligand bound to a metal active site is acutely sensitive to the geometry of the histidine side chains coordinating the copper atom. This conclusion was motivated by observations of a novel dynamical signature in 2D-IR spectroscopy, attributed to a nonequilibrium, vibrationally triggered structural distortion, manifested as a continuous dynamical spectral shift of both the ν₀₁ and ν₁₂ transition frequencies. Guided by our QM/MM calculations, we find using DFT to investigate the small molecule that the coordination of the histidine side chains to Cu determines the CuCO potential energy surface. The histidines derive some of their polarity from the metal coordination, which enhances their directional coupling to the protein’s electrostatics. Future work to modify the electrostatics through mutation or by the synthesis of asymmetric heterodimers will enable rational design of the reaction’s free energy surface, which we will be able to monitor with 2D-IR spectroscopy of the CO probe while comparing to QM/MM calculations that have been shown here to be consistent with experiment. Thus, there is promise that our combination of 2D-IR spectroscopy and quantum chemical modeling will enable directed, rational design of novel metalloenzymes by incorporating both long-range electrostatics and side chain modifications. When combined with measurements of the enzyme’s turnover frequency, we anticipate the combined approach will be able to provide a complete structural and dynamical picture of the catalysis.

METHODS

Full methods of the TRI peptide synthesis and analytical characterization as well as specific details of the 2D-IR experiments and additional results of the QM/MM calculations are provided in SI. Briefly, preparation of all solutions was carried out in an inert atmosphere box at room temperature. The apo-peptide solution was prepared by dissolving purified dry peptide powder in a degassed buffer solution in 100% D₂O (50 mM HEPES). One equiv (wrt. 3SCC) Cu(I) tetra(acetonitrile) tetrafluoroborate was added to form ~1 mM Cu(I)(TRIL2WL23H)₃⁺ complex. The pH of the solution was then adjusted to 7.5 by adding small aliquots of concentrated KOH in 100% D₂O. Carbon monoxide gas (MetroGas) was purged through the solution for 20 min. A dual-frequency optical parametric amplifier with independent difference frequency generation stages, pumped by a titanium-sapphire laser amplifier, produce 100 fs mid-IR pulses centered near 2060 cm⁻¹. 2D-IR spectra were recorded for both rephasing and nonrephasing pulse orderings using our chirped-pulse upconversion method of IR detection described in previous reports. The coherence time delay between the first two pulses in the photon echo sequence was scanned continuously over a range of roughly 10 ps, resulting in experimental resolution of 3 cm⁻¹. Waiting time delays were fixed at values between −0.25 and 4.5 ps in steps of 0.25, 5, and 20 ps in steps of 0.5 ps, 21 and 30 ps in steps of 1 ps, and 32 and 60 ps in steps of 2 ps. The complex signal field is obtained using spectral interferometry optical heterodyne detection. The local oscillator reference and generated signal fields are detected by sum-frequency generation in a MgO:LiNbO₃ crystal pumped with an uncompressed 800 nm pulse from the amplifier system. The resulting visible light centered at 685 nm is detected using a 0.5 m monochromator equipped with a 1200 grooves/mm diffraction grating and a 1300 × 100 pixel CCD camera synchronized to the 1 kHz laser pulses. All DFT calculations were performed in Gaussian 09 using the B3LYP functional and 6-311G(d,p) basis set on all atoms with symmetry disabled and tight optimization criteria. For the QM/MM ONIOM calculations, the QM layer (B3LYP/6-311G(d,p)) contains the active site and is almost identical to the smaller cluster calculation described above, consisting of the copper ion, three 5-methylimidazole ligands and a carbonyl ligand. The larger MM layer includes all atoms in the metalloenzyme, with atoms in residues located more than four residues away on either side of the histidine groups frozen to reduce computational cost. The MM layer was treated using the AMBER force field and relaxed prior to performing ONIOM calculations. Electronic embedding was enabled so that the atomic charges from the MM layer would be included in the QM calculations, reproducing the electrostatic interactions as well as the van der Waals interactions that are automatically included. Similarly to the DFT calculation, symmetry was disabled and tight optimization criteria were enabled. The structure was optimized using microiterations with a quadratic coupled algorithm.