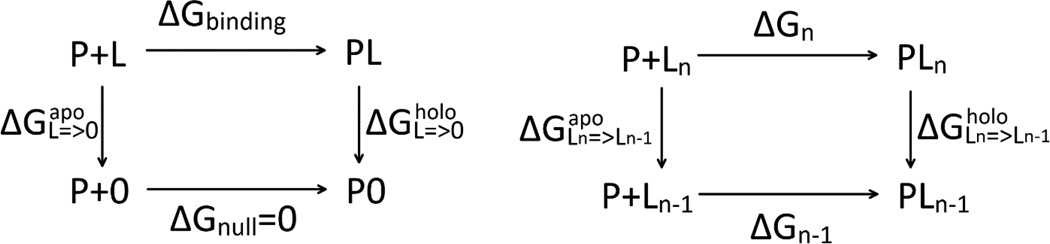Computing the binding affinity of a ligand buried deep inside a protein with the hybrid steered molecular dynamics

Abstract

Computing the ligand-protein binding affinity (or the Gibbs free energy) with chemical accuracy has long been a challenge for which many methods/approaches have been developed and refined with various successful applications. False positives and, even more harmful, false negatives have been and still are a common occurrence in practical applications. Inevitable in all approaches are the errors in the force field parameters we obtain from quantum mechanical computation and/or empirical fittings for the intra- and inter-molecular interactions. These errors propagate to the final results of the computed binding affinities even if we were able to perfectly implement the statistical mechanics of all the processes relevant to a given problem. And they are actually amplified to various degrees even in the mature, sophisticated computational approaches. In particular, the free energy perturbation (alchemical) approaches amplify the errors in the force field parameters because they rely on extracting the small differences between similarly large numbers. In this paper, we develop a hybrid steered molecular dynamics (hSMD) approach to the difficult binding problems of a ligand buried deep inside a protein. Sampling the transition along a physical (not alchemical) dissociation path of opening up the binding cavity---pulling out the ligand---closing back the cavity, we can avoid the problem of error amplifications by not relying on small differences between similar numbers. We tested this new form of hSMD on retinol inside cellular retinol-binding protein 1 and three cases of a ligand (a benzylacetate, a 2-nitrothiophene, and a benzene) inside a T4 lysozyme L99A/M102Q(H) double mutant. In all cases, we obtained binding free energies in close agreement with the experimentally measured values. This indicates that the force field parameters we employed are accurate and that hSMD (a brute force, unsophisticated approach) is free from the problem of error amplification suffered by many sophisticated approaches in the literature.

Graphical Abstract

INTRODUCTION

Accurately computing the free-energy of binding a ligand to a protein is a task of essential importance in biochemical and biophysical studies that still presents us considerable difficulty to overcome.[1–19] For example, the free energy perturbation (FEP) alchemical methods have been widely applied with many successes but they have also been found to have their share of producing false positives/negatives.[20] Examining the sources of the computation errors, the first is the errors in the force field parameters used for intra- and inter-molecular interactions, which can be regarded as intrinsic or systematic errors. Improvements of the force fields led to higher accuracy nearing the range of chemical accuracy in recent years. The second source of errors is extrinsic, which can simply be an amplification of the intrinsic errors. Errors also arise due to insufficient sampling of the relevant events for a given process. These extrinsic errors are dependent upon the computational approach used in a given study. For example, in an alchemical approach that involves thermodynamic (alchemical) cycles illustrated in Fig. 1, the absolute binding energy is computed as the difference, $\mathrm{\Delta }{G}_{\mathit{\text{binding}}}=\mathrm{\Delta }{G}_{L=>0}^{\mathit{\text{apo}}}-\mathrm{\Delta }{G}_{L=>0}^{\mathit{\text{holo}}}$, between the free energy of annihilating the ligand in the holo-protein state, $\mathrm{\Delta }{G}_{L=>0}^{\mathit{\text{holo}}}$, and the same in the apo-protein state, $\mathrm{\Delta }{G}_{L=>0}^{\mathit{\text{apo}}}$. If the two free energies of annihilation are large and similar, computing the free energy of binding is to extract the small difference between two large numbers, which typically amplifies the intrinsic errors. Hypothetically, if the free energy of annihilation in the apo state is 200±10 kcal/mol and the free energy of annihilation in the holo state is 190±10 kcal/mol, both with errors around 5%, then the computational result of the absolute binding energy is −10±14 kcal/mol with an uncertainty of 140%. It should be noted that other methods including docking and MM/GBSA/PBSA can have similar problems of error amplification when they involve small differences between large numbers.

Fig. 1.

Alchemical route/thermodynamic cycles for binding free energy. In the left panel, the ligand L is totally annihilated in the apo and the holo states respectively. In the right panel, only one fragment of the ligand is annihilated in the apo and the holo states respectively.

In the current literature, many efforts have been put forward to improve the accuracy of the force fields and to eliminate the extrinsic errors. In particular, various delicate approaches have been devised and refined to avoid the afore-illustrated amplification of errors, e.g., to compute the absolute binding energy as the sum of multiple relative binding energies (Fig. 1, right panel). For each of the N steps of annihilating a ligand, L, by part, L = L_N => L_N−1 => ⋯ L_n => L_n−1 => ⋯ L₁ => 0, we can compute the relative binding energy and then assemble the relative binding free energies together for the absolute binding free energy of the entire ligand, L, $\mathrm{\Delta }{G}_{\mathit{\text{binding}}}=\sum _n(\mathrm{\Delta }{G}_{L_n=>L_{n-1}}^{\mathit{\text{apo}}}-\mathrm{\Delta }{G}_{L_n=>L_{n-1}}^{\mathit{\text{holo}}})$. This assembly of a series of relative binding energies will be as accurate as the force fields we use if the major contributors to the sum are not small differences between similarly large numbers. Depending on how we choose the intermediates, L_n, we might be able to avoid the problem of error amplifications.

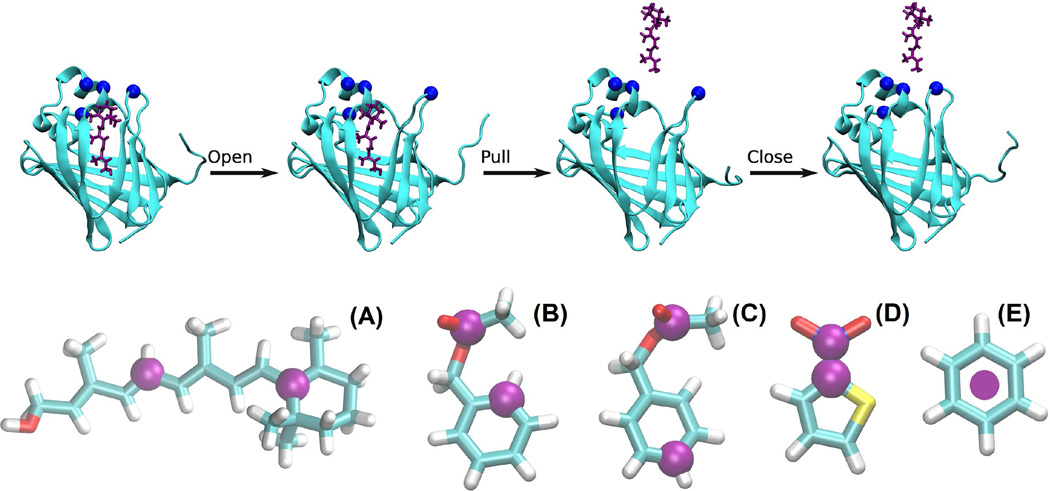
Approaches without invoking alchemical cycles can be free from the error amplification inherent in the process of extracting small differences between similarly large numbers, in which the potential of mean force (PMF) [21–25] is computed along a physical (not alchemical) dissociation path of the ligand leading from its binding site to a place far away from the protein. The PMF difference between the ends of the path (holo and apo states) is obtained not by subtracting the apo state PMF from the holo state PMF but instead by accumulating small PMF differences along the dissociation path. Each small PMF difference is computed not by subtraction but by conducting the statistical average of similar numbers from the equilibrium samplings with designed biases and constraints or from the nonequilibrium samplings with steered molecular dynamics (SMD). (Note that the brute force SMD has not been used reliably for free-energy calculations with quantitative accuracy without the specially designed correction factors. [16–19, 26, 27] The hybrid SMD (hSMD) method,[28, 29] also brute force in nature, has been shown to produce accurate results.) These PMF-based approaches, delicate equilibrium or brute force nonequilibrium, have proven to be effective in cases where a small molecule (or protein) adheres onto the surface of a protein or resides in an open binding site and, therefore, can be removed from the protein along an unhindered path.[12, 15, 16, 28–37] However, are they applicable to the cases where a ligand is completely buried in a deep binding site such as the complex of retinol (RTL) bound inside the human cellular retinol-binding protein 1 (CRBP1)[38] illustrated in Fig. 2?

Fig. 2.

An example of the open-pull-close pulling path and the pulling centers (purple spheres/disks) on the ligands. In the top panel, the protein (CRBP1) is shown as cyan ribbons and the ligand (RTL) in purple licorice. The blues spheres indicate the four pulling centers on CRBP1. In the bottom panel, the ligands are represented with licorices (colored by atom names: carbon, cyan; hydrogen, white; nitrogen, blue; oxygen, red; sulfur, yellow). (A) Retinol (RTL). The pulling centers on this ligand are atoms C6 and C11. (B) and (C) Benzylacetate (J0Z). The pulling centers on J0Z are, respectively, atoms CAJ and CAG in simulation Set I and atoms CAJ and CAC in Set II. (D) 2-Nitrothiophene (265). The pulling centers on this ligand are atoms CAG and NAH. (E) Benzene (BNZ). The pulling center is the center of mass of this ligand.

In this paper, we develop an hSMD sampling method for computing affinities of ligand-protein complexes similar to the RTL-CRBP1 complex. In essence, we will choose m pulling centers on the ligand and n pulling centers on the protein (Fig. 2). Starting from one initial state (set of coordinates for the m+n pulling centers), we will first steer the n centers on the protein to make an opening while holding the m centers on the ligand fixed at one chosen set of coordinates. Then we will hold those n centers on the protein fixed at their positions and steer the m centers on the ligand to pull it out of the protein. After that, we will steer the n centers on the protein back to their initial coordinates. In this manner, we choose a dissociation path which is simply a curve in the 3(m+n)-D phase space consisting of three straight lines. We compute the PMF along this open-pull-close path from the work done to the system during the pulling processes and combine the PMF with the fluctuations of the m+n pulling centers in the initial (holo) and the final (apo) states to extract the absolute binding free energy/binding affinity. We will apply this hSMD approach to four binding complexes including RTL buried inside CRBP1 and three well-studied complexes with different small molecules buried inside the L99A mutants of T4 lysozyme (T4L): benzylacetate (J0Z) in L99A/M102Q, 2-nitrothiophene (265) in L99A/M102Q, and benzene (BNZ) in L99A/M102H. For RTL-CRBP1, we obtained quantitative insights about the binding interactions (RTL induced fit of CRBP1, in particular) in agreement with experimental investigations and our computed binding free energy is in agreement with the experimental data within the known margin of error. For the T4L complexes, our computed binding energies are in close agreement with experiments in all the three cases where other computational studies in the literature are close to or far from the experimental data. With this hSMD approach for unbinding a ligand from a buried binding site, we now have a brute force method to compute binding affinities with quantitative/chemical accuracy that is only limited by the intrinsic errors in the force fields used to represent the intra- and inter-molecular interactions and that is free from the error amplifications inherent in the small-difference-between-two-large-numbers approaches.

METHODS

Following the standard literature,[1, 4] through the derivation detailed in the supplemental information (SI), we have the following formulas for the binding affinity (inverse dissociation constant k_D) and the Gibbs free energy of binding ΔG_binding, respectively,

$$\frac{1}{k_D}=\frac{Z_{m+n0}}{Z_{m-1\infty }^L{Z}_{n\infty }^P}\text{exp}[-\frac{\mathrm{\Delta }{W}_{0,\infty }}{k_{B}T}],\mathrm{\Delta }{G}_{\text{binding}}=k_{B}T\text{ ln}\left[\frac{Z_{m-1\infty }^L{Z}_{n\infty }^P}{Z_{m+n0}{c}_0}\right]+\mathrm{\Delta }{W}_{0,\infty }.$$ (1)

Here c₀ = 1M = 6.02×10⁻⁴ / ų is the standard concentration. k_B is the Boltzmann constant and T is the absolute temperature. ΔW_0,∞ is the PMF difference along the open-pull-close path (Fig. 2) in 3(m+n)-D phase space. The subscript 0 represents the holo state and ∞represents the apo state. The complex partition Z_m+n0 integrates over all the m+n pulling centers in the holo state (SI, Eq. S9). The protein partial partition $Z_{n\infty }^P$ integrates over the n pulling centers in the apo state (SI, Eq. S13). The ligand partial partition $Z_{m-1\infty }^L$ characterizes the fluctuations of the m-1 pulling centers on the ligand in the apo state when one center is fixed (SI, Eq. S14). The ratio between these three partitions in Eq. (1) naturally depends on the changes in the protein-ligand conformations and flexibilities from the holo to the apo state. When the conformation changes between the apo and the holo protein are small such as in the four complexes of this study, the Gaussian approximation (SI, Eq. S10/S14) is valid and accurate for the partial partitions. Otherwise, the Gaussian approximation will not be accurate.

In all the equilibrium molecular dynamics (MD) and nonequilibrium SMD runs, we used CHARMM36[39, 40] force field for all the intra- and inter-molecular interactions. We implemented Langevin stochastic dynamics with NAMD[41] to simulate the systems at constant temperature of 298 K and constant pressure of 1 bar. Full electrostatics was implemented by means of particle mesh Ewald (PME) at a resolution of 128×128×128. The time step was 1 fs for the short-range and 2 fs for the long-range interactions. The PME was updated every 4 fs. The damping constant was 5/ps. Explicit solvent was represented with the TIP3P model. In all sections, four forward and four reverse pulling paths were sampled.

The all-atom model system of RTL-CRBP1 complex (shown in SI, Fig. S1) was formed from the crystallographic structure (PDB code: 5HBS)[38] by rotating it to the orientation of RTL is approximately along the z-axis, putting the complex in the center of a water box of 80Å×80Å×100Å, and neutralizing the system and salinizing it to 150 mM with 61 Na⁺ and 55 Cl⁻ ions. During the 50 ns equilibrium MD run, the system settles down (after 4 ns) to fluctuate slightly around the dimensions of 78Å× 78Å×97Å. Similar system setups were done for the J0Z-M102Q (PDB code: 3HUK),[20] 265-M102Q (PDB code: 2RBO),[20] and BNZ-M102H (PDB code: 4I7J)[42] complexes (illustrated in SI, Fig. S2). The ligands are illustrated in Fig. 2.

The pulling centers and their pulling speeds are tabulated in Table I. It is noted here that the third part of the open-pull-close path was implemented not directly as closing back the binding cavity but as the inverse of opening up the binding cavity of the apo protein.

Table I.

Pulling centers and velocities (x,y,z- components in Å/ns).

Ligand/PDB code	RTL/5HBS	J0Z/3HUK (Set I)	J0Z/3HUK (Set II)	265/2RBO	BNZ/4I7J
Centers on Protein	m=4	m=3	m=3	m=3	m=3
Center (ResIDAtoma) Velocities	1. Leu29Ca (−0.5,0,0)	1. Ala99Ca (0,0,0)	1. Ala99Ca (0,0,0)	1. Leu84Ca (2.5,−2.5,0)	1. Lys83Ca (−1.25,0,0)
Center (ResIDAtom) Velocities	2. Ile32Ca (−0.5,0,0)	2. Leu118Ca (0,0,0)	2. Gln105Ca (0,0,0)	2. Val87Ca (2.5,−2.5,0)	2. Ala99Ca (0,0,0)
Center (ResIDAtom) Velocities	3. Phe57Ca (2.5,0,0)	3. Arg137Ca (−1.25,−1.25,0)	3. Gly110Ca (1.25,1.25,0)	3. Leu118Ca (0,0,0)	3. Leu118Ca (1.25,0,0)
Center (ResIDAtom) Velocities	4. Ile77Ca (0,0,0)	Not applicable	Not applicable	Not applicable	Not Applicable
Centers on Ligand	n=2	n=2	n=2	n=2	n=1
Center (Atom name) Velocities	1. C6 (0,0,2.5)	1. CAJ (0,0,2.5)	1. CAJ (0,0,2.5)	1. CAG (0,0,2.5)	1. bCoM (0,0,2.5)
Center (Atom name) Velocities	2. C11 (0,0,2.5)	2. CAG (0,0,2.5)	2. CAC (0,0,2.5)	2. NAH (0,0,2.5)	Not Applicable

^aIn the format of residue name-residue id-atom name.

^bCoM means the ligand’s center of mass.

RESULTS AND DISCUSSION

The hSMD results are tabulated in Table II along with the experimental data and some FEP results.

Table II.

hSMD results vs FEP results in comparison with experimental data (All in kcal/mol).

Ligand/PDB code	RTL/5HBS	J0Z/3HUK (Set I)	J0Z/3HUK (Set II)	265/2RBO	BNZ/4I7J
hSMD simulation time (ns)	728	480	480	440	378
$k_{\mathrm{B}}T\text{ ln}[Z_{m-1\infty }^L{Z}_{n\infty }^P/c_0{Z}_{m+n0}]$	+17.6	+6.1	+4.6	+7.8	+6.7
PMF difference ΔW0,∞	−30.2	−10.7	−10.1	−12.7	−11.5
hSMD ΔGbinding	−12.6±2.2	−4.6±1.2	−5.5±1.2	−4.9±1.2	−4.8±1.2
Experimental ΔGbinding	−10.9a	−4.5b	−4.5b	−4.9b	−4.5c
FEP alchemical ΔGbindingb		−1.3 (apo) −3.9 (holo)		−5.7 (apo) −11.4 (holo)

^aFrom Ref. [38].

^bFrom Ref. [20]. Top number computed with apo structure and bottom number with holo structure.

^cFrom Ref.[42].

Retinol

Retinol (Vitamin A₁) is essential for various aspects of human physiology. It is very labile and hydrophobic and, therefore, its storage and trafficking are assisted by the retinol-binding proteins. In particular, cellular retinol-binding protein 1 transports retinol by having it completely buried inside a pocket lined up with beta strands and fully covered by the residues on an alpha helix and three coils (Fig. 2). In a recent experimental study,[38] Silvaroli et al determined the coordinates of this ligand-protein complex to atomistic resolution. They also found that the holo protein (with retinol bound) is more rigid than the apo protein. This ligand-protein complex should be very challenging for binding-energy computations because the free energies of annihilating retinol inside the protein and away from the protein would both be large numbers. The difference between those two free energies inevitably cause amplification of errors contained in the force field parameters. Therefore, RTL-CRBP1 is an ideal candidate for testing our hSMD method.

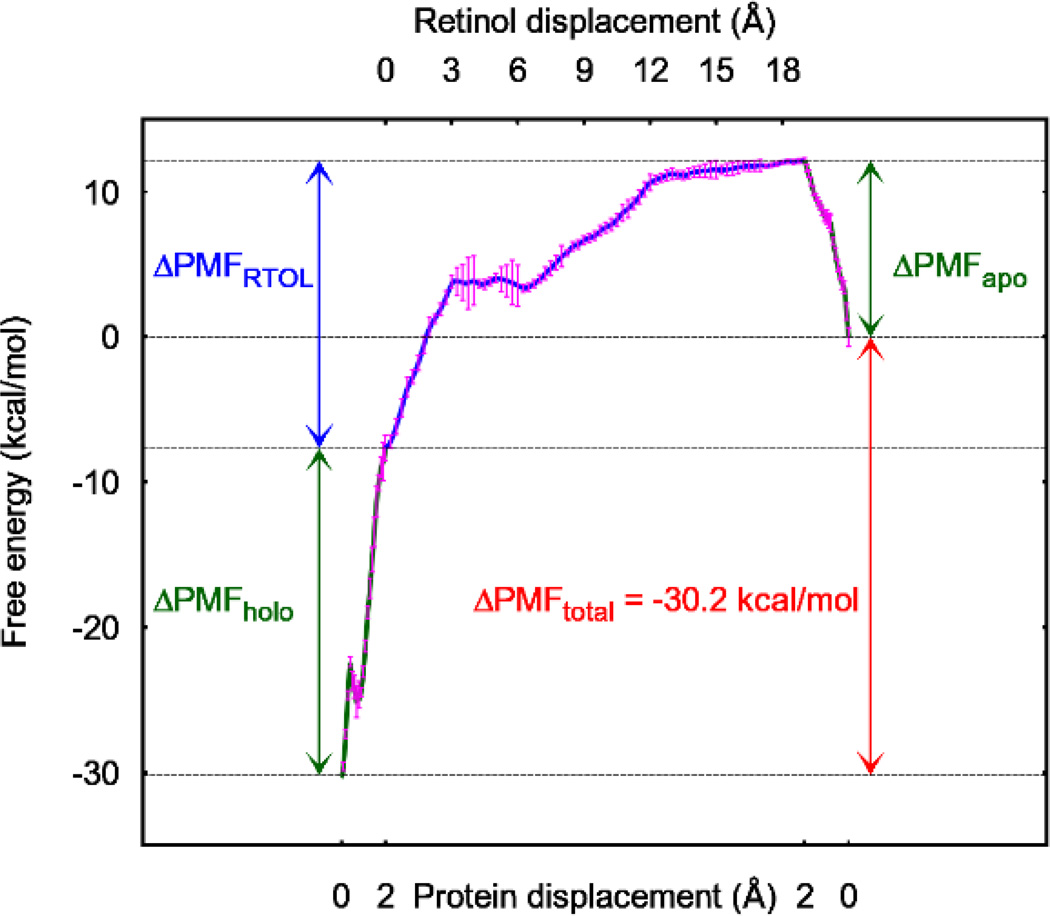
Indeed, in our study which is rather brute force, we were only deliberate to rotate the complex to an orientation so that the ligand was pulled along the z-axis and to pick the pulling centers to pull away the residues that cover up the binding site. In Fig. 3, we show the PMF curves for pulling open the holo protein (the green curve on the left hand side of Fig. 3), pulling out the ligand (the purple curve of Fig. 3), and closing up the apo protein (the green curve on the right hand side of Fig. 3). Combining the PMF difference and the fluctuations of the pulling centers in the holo and the apo states (SI, Figs. S3 and S4) in Eq. (1), we obtained the free energy of RTL-CRBP1 binding that is in agreement with the experimentally measured value.[38]

Fig. 3.

PMF curves along the path to open the holo protein up, to pull retinol out, and to close (reversely open) the apo protein back. The protein displacements are those of pulling centers 1 and 2 (Table I) on helix II of CRBP1. The error bars are most pronounced near the RTOL displacement of 4, which is taken as the error bar for our final result in Gibbs free energy of binding (Table II). The error bars represent the standard deviations from the work measurements along the four pulling paths for each section (shown in Figs. S14 to S16 of the SI).

It is also worth noting that the PMF curves in Fig. 3 quantitatively show that the holo protein is significantly more rigid than the apo protein (as do the fluctuations of the pulling centers shown in SI, Figs. S3 and S4). Pulling open the binding site of the holo protein costs more than 22 kcal/mol while the same for the apo is only 12 kcal/mol. This confirms the experimental insights of Ref. [38].

Benzylacetate

The structures of various mutants of T4 lysozyme have been abundantly available in the PDB and a wide range of studies have been conducted to elucidate how various ligands interact with the protein inside the binding site cavity generated/modified by L99A along with other mutations such as M102Q and M102H. Many binding complexes of this type have been successfully computed with the alchemical FEP approaches. Nonetheless, the J0Z-T4L-L99A/M102Q binding problem was not one of them. The computation based on the apo structure and the same based on the holo structure gave differing results that were both significantly off from the experimentally measured value (Table II). To test the hSMD method, we conducted two independent studies of the J0Z binding problem by choosing different sets of pulling centers. The PMF curves were obtained along the two independent dissociation paths (each has three legs: opening the protein to expose the ligand, pulling the ligand out, and closing the apo protein back (the reverse process of opening the binding site of the apo protein)). These PMF curves (SI, Figs. S5) and the fluctuation data of the pulling centers (SI, Figs. S6 to S9) combine to give the computed binding energies in Table II. The two results are within the error bar from one another.

It is worth noting that the pulling centers on the protein were chosen in the following manner: In Set I, they are on the most flexible parts of the protein. Accordingly, the PMF difference of opening up the binding cavity (the green curve on the left hand side of Fig. S5, top panel) and the same of closing back the binding cavity (the green curve on the right hand side of Fig. S5, top panel) are both small. And the overall result in the absolute binding free energy is in perfect agreement with the experimental data. This certainly evidences the accuracy of the CHARMM force field parameters for the ligand and the protein. It also indicates that hSMD does not amplify errors. In Set II, the pulling centers on the protein were much harder to pull (green curves in Fig. S5, bottom panel). Correspondingly, the final result deviates from the experimental data significantly more than Set I. Therefore, it is practically preferable to pick the soft spots on the protein as pulling centers for opening up the binding cavity.

2-Nitrothiophene

The binding complex of 265-T4L-L99A/M102Q is another example of the alchemical FEP approach being significantly off the experimental data. Again, the hSMD approach produced result in close agreement with the experiment (Table II) even though the choice of pulling centers on the protein was not made with much deliberateness. (The PMF curves and the fluctuation data are shown in SI, Figs. S10 to S12.)

Benzene

This is the simplest among the ligands we studied in this work. (The PMF curves and the fluctuation data are shown in SI, Figs. 13 to S15.) However, it proved to be most difficult to deal with in an hSMD study. It is worth noting that all carbons on BNZ are equivalent (indistinguishable). It is unwise to pull BNZ out by two pulling centers on it. If so done, the fluctuations of those two pulling centers in the bound state cannot be well approximated as Gaussian. In order to use the Gaussian approximation, we pulled BNZ by its center of mass (one single pulling center, m=1). However, then pulling the ligand out proved to be more difficult because BNZ constantly tumbled around its center of mass when pulled, which required wider opening of the binding cavity (larger rises in the green curves of Fig. S13). Otherwise, the steric clash between the ligand and the protein gave rise to large uncertainties in the PMF curve.

CONCLUSIONS

We have developed a hybrid steered molecular dynamics approach for computing absolute binding energy from the PMF along a dissociation path that consists of three parts: opening up the binding cavity to expose the ligand, pulling out the ligand from the buried binding site, and closing back the apo protein. Applying this hSMD approach with high-performance parallel processing, one can achieve, within a few wall-clock days, the computation of the binding affinity of one ligand-protein complex with accuracy comparable with experimental measurements. The hSMD approach is “brute force” in the sense that one does not have to delicately devise biasing and constraining potentials during the course of simulations. And it does not involve sophisticated ways of removing the artifacts introduced by biasing/constraining the ligand in other PMF-based and non-PMF-based approaches. For all the systems studied, our hSMD predictions based on the CHARMM force field are in very good agreement with the experimentally measured values. We assert that hSMD, a brute force approach, provides an alternative way to accurately compute the binding free energies in cases where the mature and sophisticated methods of the literature are successful or unsuccessful.