Abstract
Motivation
The advent of high-throughput DNA methylation profiling techniques has enabled the possibility of accurate identification of differentially methylated genes for cancer research. The large number of measured loci facilitates whole genome methylation study, yet posing great challenges for differential methylation detection due to the high variability in tumor samples.
Results
We have developed a novel probabilistic approach, differential methylation detection using a hierarchical Bayesian model exploiting local dependency (DM-BLD), to detect differentially methylated genes based on a Bayesian framework. The DM-BLD approach features a joint model to capture both the local dependency of measured loci and the dependency of methylation change in samples. Specifically, the local dependency is modeled by Leroux conditional autoregressive structure; the dependency of methylation changes is modeled by a discrete Markov random field. A hierarchical Bayesian model is developed to fully take into account the local dependency for differential analysis, in which differential states are embedded as hidden variables. Simulation studies demonstrate that DM-BLD outperforms existing methods for differential methylation detection, particularly when the methylation change is moderate and the variability of methylation in samples is high. DM-BLD has been applied to breast cancer data to identify important methylated genes (such as polycomb target genes and genes involved in transcription factor activity) associated with breast cancer recurrence.
Availability and Implementation
A Matlab package of DM-BLD is available at http://www.cbil.ece.vt.edu/software.htm.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
As the most well-studied epigenetic mark, DNA methylation has been demonstrated to play a crucial role in regulating gene expression without alterations to the DNA sequence (Bird, 2002). Although the underlying mechanism is still not completely known, DNA methylation is essential for cell differentiation and it is associated with various key biological processes such as embryonic development and genomic imprinting (Meissner, 2010). Besides its important role in normal cell development, recent studies show that DNA methylation abnormalities are associated with various diseases including cancer (Baylin and Jones, 2011; Feinberg, 2007). There is strong evidence that tumor-suppressor genes may be silenced because of hypermethylation; growth-promoter genes may be activated due to hypomethylation, consequently inducing cancer development (Feinberg and Tycko, 2004). Therefore, the identification of abnormalities in DNA methylation is of increasing interests in the field of cancer research. Moreover, DNA methylation is heritable and reversible (Ramchandani et al., 1999), which makes it a promising target for new therapeutic approaches in cancer treatment (Kulis and Esteller, 2010).
In the past decade, the development of high-throughput technologies provides the opportunity to obtain whole genome-wide DNA methylation mapping with high resolution. Illumina Infinium HumanMethylation450 BeadChip Kit (Illumina 450k) is one of the most popular, high-quality, cost-effective techniques for DNA methylation study. Illumina 450k measures >485000 CpG (5′-C-phosphate-G-3′) sites per sample at single-nucleotide resolution, which covers 99% of RefSeq genes with multiple sites in the functional regions, such as promoter, 5’UTR, 1st exon, gene body, and 3’UTR. The high coverage and low cost of the Illumina 450k array (Bibikova et al., 2011; Sandoval et al., 2011) make it a very powerful platform for exploring genome-wide DNA methylation landscape. By virtue of the high-throughput techniques, the methylation level of each gene is measured at multiple CpG sites across the genomic location, providing more comprehensive measurements for a methylation event.
Despite the advantage of high-throughput profiling, the high resolution poses challenges to computational analysis for detecting differentially methylated genes from the huge number of measured CpG sites. Early approaches attempt to identify differentially methylated sites by statistic tests. However, the statistical power is limited due to the problem of multiple hypothesis testing; moreover, it is biologically difficult to interpret individual CpG sites without considering the neighbors. Thus, the detection of differentially methylated regions (DMRs) is of prime interest, and several methods have been proposed, falling into two categories: annotation based methods and de novo methods. In the annotation based methods, the regions are predefined according to the annotation of CpG site location. IMA (Illumina Methylation Analyzer) (Wang et al., 2012) is a well-known annotation-based pipeline, which first generates an index of the methylation value of predefined regions, and then uses statistical tests, such as limma, to identify differentially methylated regions. The index of the methylation value of a region is derived from the methylation value of the involved CpG sites with metrics such as mean, median, and so on. As an alternative, de novo methods do not rely on predefined regions for DMR detection. Bumphunter (Jaffe et al., 2012) first estimates the association between the methylation level and the phenotypes for each site, and then identifies DMRs after a smoothing operation. DMRcate (Peters et al., 2015) is another approach agnostic to predefined regions. It first calculates a statistic from differential test for each site, and then uses a Gaussian kernel to incorporate the neighboring information for DMR detection. Comb-P (Pedersen et al., 2012) combines spatially assigned P-values to find regions of enrichment. Probe Lasso (Butcher and Beck, 2015) is a window based approach that detects DMRs using neighboring significant-signals. The region-based methods have demonstrated their capability in detecting biologically meaningful differential methylation events. However, most of the existing DMR detection methods are based on statistic tests, and the neighboring information is not jointly considered when estimating the methylation change of CpG sites.
In this article, we develop a novel method, differential methylation detection using a hierarchical Bayesian model exploiting local dependency (DM-BLD), to identify differentially methylated genes based on a Bayesian framework. In DM-BLD, CpG sites are first mapped or linked to genes according to their location information. For each gene, we then use a Gaussian Markov random field (MRF) model, Leroux conditional autoregressive (CAR) structure (Leroux et al., 2000), to capture the varying degree of dependency among nearby CpG sites. Based on the local dependency, it is reasoned that genes involving a sequence of CpG sites with methylation change are more likely to exhibit abnormal methylation activity. We use a discrete Markov random field (Wei and Pan, 2010) to model the dependency of methylation change (differential states) of neighboring CpG sites. A hierarchical Bayesian model is developed to fully take into account the local dependency for differential analysis, in which differential states are embedded as hidden variables. A Gibbs sampling procedure is then developed to estimate the methylation change of CpG sites jointly with other model parameters based on their conditional distributions, respectively. The proposed DM-BLD approach is a fully probabilistic approach with a hierarchical Bayesian model to account for the local dependency in both methylation level and differential state, capable of detecting less differentially methylated genes accurately and effectively.
2 Methods
2.1 Framework of the DM-BLD approach
Based on the observation that nearby CpG sites are significantly correlated (Supplementary Section S1), we propose to develop a probabilistic model incorporating the local dependency of CpG sites to identify differentially methylated genes. In our proposed method, CpG sites are mapped to genes according to their genomic locations. As is provided by the annotation file of Illumina 450k array, the probes/CpG sites are assigned to RefSeq genes of the reference genome hg19. For each gene, all of the CpG sites located within 1500bp from TSS to 3’UTR are used for differential analysis. Three major steps of the proposed method, DM-BLD, are summarized as follows (see Fig. 1): (i) within each gene, estimating the true methylation level of CpG sites by modeling the local spatial correlation of methylation level and the dependency of methylation change among neighboring CpG sites; (ii) calculating the differential methylation score of genes from the estimated methylation change of CpG sites; (iii) performing permutation-based significance tests on potential differentially methylated genes. Specifically in the first step, we use the Leroux model (Leroux et al., 2000), an advanced CAR structure, to capture the dependency of methylation level among neighboring CpG sites. Comparing with the intrinsic conditional autoregressive model (Clayton and Kaldor, 1987), the Leroux model is capable of accounting for different levels of correlation (Lee, 2011), which helps improve the accuracy in estimating the true methylation level of CpG sites. We then use a discrete Markov random field (Wei and Pan, 2010) to model the dependency of methylation changes (via differential states) of neighboring CpG sites. With differential states embedded as hidden variables, we use a hierarchical Bayesian model to take into account the local dependency fully for differential analysis. A Gibbs sampling procedure, based on conditional distributions, is designed to estimate the true methylation level and other model parameters. In the second step, the differential methylation score of a gene is calculated from the estimated methylation change of involved CpG sites. Genes can be prioritized according to the differential methylation score for further biological validation. Finally in the third step, permutation-based hypothesis tests are implemented and performed to assess the significance of the identified differentially methylated genes for real data analysis. More details of the three steps will be given in the following subsections.
Fig. 1.
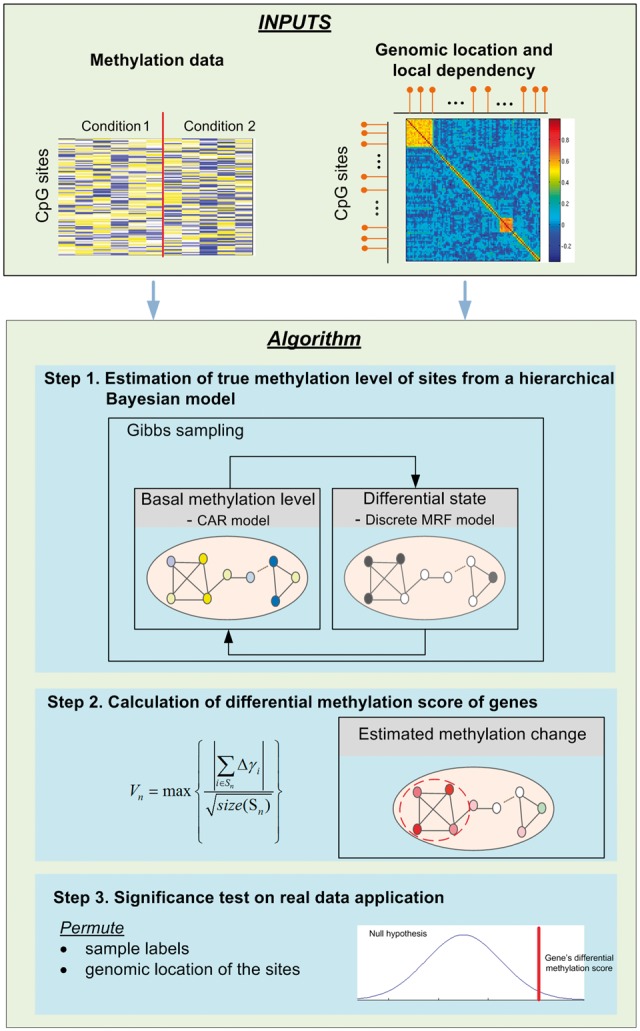
Flowchart of the proposed DM-BLD approach. DM-BLD consists of the following three major steps: (1) methylation level estimation; (2) differential methylation score calculation and (3) permutation-based significance tests (Color version of this figure is available at Bioinformatics online.)
2.2 Estimation of methylation change of the CpG sites within each gene
We first estimate the true methylation level of CpG sites by taking into account the neighboring CpG sites. Beta-value is conventionally used as the measure of the methylation level of CpG sites; beta-value is the ratio of the methylated probe intensity and the overall intensity (sum of the methylated and unmethylated probe intensity) (Bibikova et al., 2011). Beta-value is thus represented as a proportion value bounded by zero and one, which can be modeled by a logit-normal distribution. (Atchison and Shen, 1980)
Assume that there are N genes and gene n has Mn CpG sites. Let us denote as the beta-value of the () CpG site of gene n () in sample j (), which follows a logit-normal distribution. is the total number of samples associated with two biological phenotypes (or conditions), where J1 and J2 are the number of samples for phenotype 1 and phenotype 2, respectively. For gene n, denote yi,j as the logit transform of , as shown in Equation (1). yi,j (also called M-value) follows a normal distribution with mean and precision (Equation (2). (as defined by Equation (3) represents the true methylation level of CpG site i in gene n, where represents the basal methylation level of CpG site i, while represents the methylation level change of gene n between two conditions. di is a binary value representing the differential state of site i. If site i is differentially methylated, ; otherwise, . The above-mentioned equations are listed as follows:
| (1) |
| (2) |
| (3) |
where
Thus, for non-differentially methylated CpG sites, the methylation levels under two phenotypes are the same, ; for differentially methylated CpG sites, .
Within each gene, we use a Markov random field to capture the dependency among neighboring CpG sites. Leroux (CAR) structure (Leroux et al., 2000) is used to specify the between-site correlation of , where the methylation level of a CpG site depends on that of its neighbors but is independent of that of all other CpG sites. Denote as the set of the neighboring sites of CpG site . Under the Leroux model, the conditional distribution of given is defined by
| (4) |
where controls the dependency level among the nearby CpG sites and controls the variance. is a predefined design matrix for the neighborhood structure. , if CpG site i and CpG site j locate within a neighborhood; , otherwise.
Differential state is modeled by a discrete Markov random field (DMRF), which can be defined by the following equation (Besag, 1986; Wei and Pan, 2010):
| (5) |
where
In Equation (5), and are model parameters. Parameter controls the consistency of differential state in DMRF. The larger is, the more consistent the differential state is in a neighborhood. Note that in our implementation, we set and as default values for DMRF to control the neighborhood consistency of differential state. () is the number of neighboring CpG sites of site with differential state 1 (0).
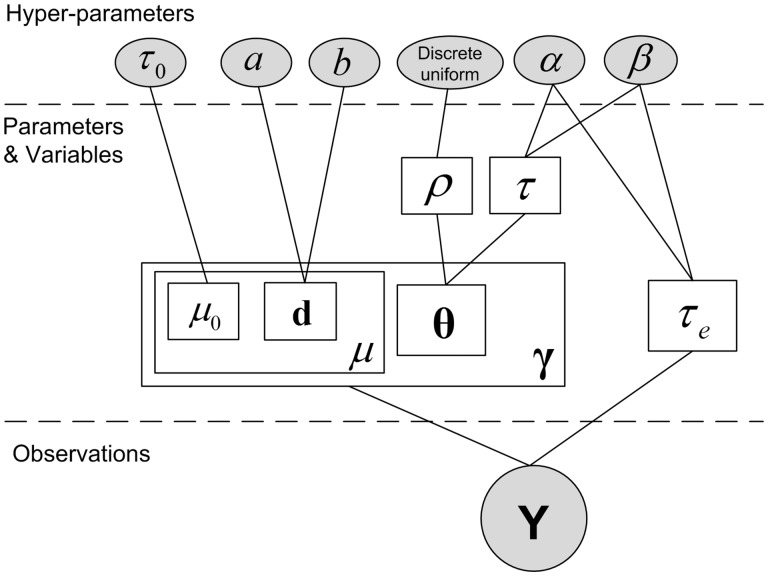
For differential methylation analysis, we devise a Bayesian approach to estimate the methylation levels ( and ) in two phenotypes, respectively. A hierarchical Bayesian model is used to model the dependency of random variables (basal methylation level), (methylation level change if differential) and (differential state), which fully determine the methylation levels ( and ). The dependency graph of the model is shown in Figure 2, where the differential state is embedded as hidden variables in the model. According to Bayes’ rule, the joint posterior distribution is given by
| (6) |
where , and are termed model parameters. For mathematical convenience, we further assume conjugate prior distributions (Gelman, 2004) for model parameters , and variable , and discrete uniform distribution as the prior distribution of parameter . The prior distributions (set as non-informative with hyper-parameters , , , and ) are defined by the following equations:
| (7) |
| (8) |
Fig. 2.
Dependency graph of the hierarchical Bayesian model in DM-BLD
Due to the complexity of the probabilistic model, we have developed a Markov Chain Monte Carlo method to jointly estimate the variables (, and ) and model parameters (, and ). In particular, we use Gibbs sampling to iteratively draw samples from the conditional distributions of the model variables/parameters. By virtue of the sampling process, the marginal posterior distribution can be approximated by the samples drawn. The conditional posterior distributions of the model variables/parameters can be found in Supplementary Section S2. The Gibbs sampling procedure can be summarized as follows:
INPUT: methylation data , neighborhood structure , number of iterations N
OUTPUT: Estimates of true methylation level in each group and other parameters in the probabilistic model
Algorithm:
Step 1. Initialization: each parameter is set an arbitrary value and non-informative prior knowledge is used for the parameters
- Step 2. Draw samples iteratively from conditional distributions of the parameters using Gibbs sampling:
- Sample θ from Gaussian distribution;
- Sample τ and τe from the corresponding Gamma distribution;
- Sample discrete variable and by first calculating the conditional probabilities and then random generating new samples according to the probabilities;
- Sample from Gaussian distribution.
Step 3. Estimate true methylation level as well as all the other parameters from the samples (after the burn-in period) generated from the sampling procedure. Then, for each CpG site, the estimated methylation change is calculated by , which will be used in the next step to calculate the differential methylation score of the genes
2.3 Calculation of the differential methylation score for each gene
We further assume that gene is more likely to have abnormal methylation activity, if it involves a sequence of CpG sites with methylation change. Thus, a searching method is used to determine the region of the sequence of CpG sites with methylation change, and the differential methylation score of the detected region represents the differential level of the corresponding gene.
With the estimate , the differential methylation score of gene n is defined by Equation (9), which contributes to highlighting the genes with more neighboring CpG sites with methylation change.
| (9) |
where denotes a subset of sequential CpG sites in a neighboring area within the genomic location of gene . Finally, genes are ranked according to their differential methylation scores.
2.4 Significance test on differentially methylated genes
When applying our proposed DM-BLD approach to real data, the confidence of the identified genes is a critical problem. In order to assess the significance of identified differentially methylated genes, we perform permutation-based significance tests. Specifically, we first rearrange the sample labels as well as the location of the CpG sites, and then apply DM-BLD onto the perturbed methylation data. The permutation of sample label disrupts the association between samples and phenotypes; the permutation of CpG site location disrupts the dependency among neighboring CpG sites. We generate the ‘global’ and ‘local’ null distributions of the differential methylation score of genes, from which the P-values of differentially methylated genes can be calculated. The ‘global’ null distribution is generated from all the genes in consideration, while the ‘local’ null distribution is generated for each individual gene; more details can be found in Supplementary Section S5.2. Finally, multiple testing corrections are used to calculate the adjusted P-values (Benjamini and Hochberg, 1995).
3 Results
3.1 Performance evaluation using simulation data
To systematically evaluate the performance of DM-BLD, we simulated multiple DNA methylation data sets with different scenarios (as detailed in Supplementary Section S4). In each experiment, the methylation values of all 450K probes were generated for 20 samples in two conditions, each with 10 samples. 30% out of the 20 758 genes with CpG sites in the promoter region were randomly selected as true differentially methylated genes, half hypermethylated and half hypomethylated. For each differentially methylated gene, a promoter-associated region was randomly selected as differentially methylated. The neighbors of each CpG site were defined as the CpG sites of both sides located within 1000bp from its location. The methylation values of CpG sites were simulated in two different ways: the first one is based on the simulation scheme used in DMRcate; the second one is based on our proposed Leroux model.
We compared the performance of DM-BLD in detecting differentially methylated genes with six existing region-based approaches, which are briefly described as follows:
Student’s t-test on mean value: the mean methylation value of all involved CpG sites was calculated as the methylation value of the gene; Student’s t-test was used for differential analysis.
Student’s t-test on median value: the median methylation value of all involved CpG sites was calculated as the methylation value of the gene; Student’s t-test was used for differential analysis.
Bumphunter: default settings with the null distribution and cutoff generated from 100 times of resampling, lambda = 1000.
DMRcate: default settings with the bandwidth of Gaussian kernel=1000 and the scaling factor = 2.
Probe Lasso: default settings with lassoRadius = 1000 and adjPval = 1.
comb-P: default settings with P-value from limma as the input, seed = 0.5 and dist = 1000.
To map the differentially methylated regions detected by Bumphunter, DMRcate, Probe Lasso and comb-P to genes, we used the associated region of the most significant adjusted P-value to represent the corresponding gene. Area-under-the precision-recall curve (AUCpr) was used to assess the overall performance on differentially methylated gene identification. Moreover, we calculated signal-to-noise ratio (SNR) to show the differential level of the generated simulation data in different scenarios. SNR measures the differential level of CpG sites taking into account both the methylation difference and the variance of the data, calculated as follows:
where and are methylation values in the two conditions, respectively.
We first generated the methylation values of CpG sites following the simulation scheme used in DMRcate. For the CpG sites in each DMR, two base beta levels were randomly chosen with a pre-defined difference, and the beta values within the DMR were randomly generated from a beta distribution with its mode equal to the base beta level and with pre-defined variance. The methylation levels of the CpG sites outside DMRs were randomly selected from two pre-defined beta distributions to mimic unmethylated and methylated sites, respectively. Following this simulation scheme, we generated multiple simulation data sets to evaluate the performances of the competing methods at different noise levels (see Supplementary Sections S4.2 and 4.3 for more details).
Figure 3A and B shows the performances of the competing methods in two scenarios with different noise levels. For each scenario, the SNRs of the differentially and non-differentially methylated sites were compared to show the differential level of the simulation data, as shown in Figure 3C and D. The differential levels of the true differentially methylated sites, indicated by SNR, decreased in the second scenario. We can see from the figure that DM-BLD outperformed the other six methods on both simulation data, especially when the differential level was lower (as shown in Fig. 3B). The competing methods, such as Bumphunter and comb-P, were quite effective in detecting a subset of DMRs with multiple sites of high differential level, yet missed the others (including many of less differential). DM-BLD was specifically designed based on an MRF framework, where the differential level was estimated considering the differential status of neighboring CpG sites. Hence, DM-BLD was more effective than other competing methods on data with high level of noise.
Fig. 3.
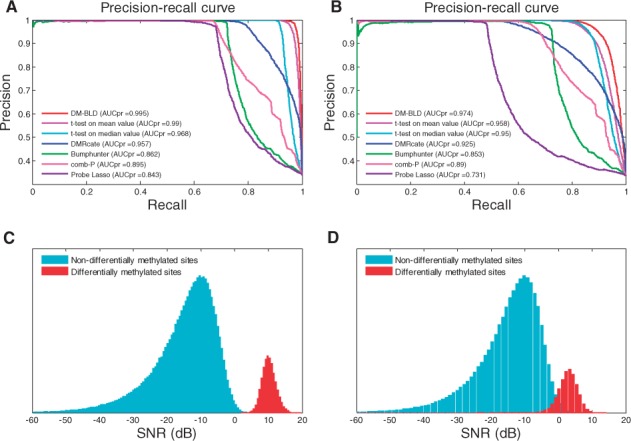
Performance on the detection of differentially methylated genes on simulation data generated by the DMRcate scheme. (A) and (B): Precision-recall curves on highly and moderately differential data; (C) and (D): SNRs of non-differentially methylated and differentially methylated sites in (A) and (B), respectively (Color version of this figure is available at Bioinformatics online.)
In the simulation data generated by the DMRcate scheme, the methylation levels of the CpG sites outside DMRs were generated randomly from two predefined beta-distributions. To better mimic real methylation data where the methylation values of neighboring CpG sites were dependent, we generated simulation data sets by the following steps. First, using the Leroux model, the methylation levels of all CpG sites in the control group were generated based on the methylated levels of the neighboring sites. Second, for the case group the methylation levels of the sites in DMRs were increased (or decreased) by a difference for hypermethylated (or hypomethylated) genes. For the sites outside DMRs, the methylation values in the case group are the same as in the control group. Third, the methylation data for the ten replicates in each condition were randomly sampled from a normal distribution with the methylation value as mean and variance controlled by . In each scenario, 10 random experiments were performed to assess the variance of performance measure. More details can be found in Supplementary Section S4.4.
Parameter and control the differential level of the ground truth differentially methylated CpG sites. Higher indicates lower variance among the samples in the same phenotype, resulting in higher differential level; higher indicates larger difference between two phenotypes, contributing to higher differential level. We first varied parameter to generate simulation data with different variance (noise) levels. Figure 4A, B and C shows the precision-recall curves at low, medium, and high variance levels, respectively, and Figure 4D presents the AUCpr of the 7 competing methods with error bar calculated from 10 random experiments. In the medium and high variance scenarios, Probe Lasso could not detect any differentially methylated regions, and thus, it was not included in those two scenarios. We can see that the performance of all methods dropped with a decrease of . However, DM-BLD consistently outperformed the other methods. With decreasing , the variance (noise) among the replicates in the same phenotype increased, which makes it more difficult to estimate the true methylation levels as well as to detect differentially methylated genes. The improved performance of DM-BLD can be attributed to its dependency modeling that borrows information from neighboring sites at estimated dependency level, thus becoming more effective in dealing with noise in replicates.
Fig. 4.
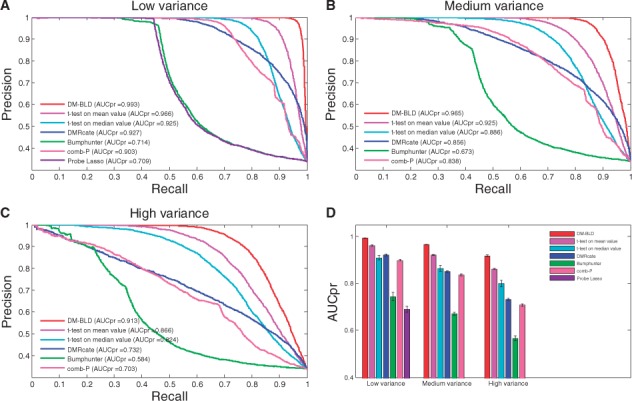
Performance on the detection of differentially methylated genes at varying noise levels. Precision-recall curves: (A) low variance; (B) medium variance; (C) high variance. (D) AUCpr in each scenario with 10 experiments performed (Color version of this figure is available at Bioinformatics online.)
We also varied parameter to evaluate the performance on varying differential levels between two phenotypes. Decreasing lowered SNR of true differentially methylated sites, since the difference of differentially methylated CpG sites between two phenotypes was reduced. The performance of all competing methods degraded when decreases, as shown in Supplementary Figure S6. However, DM-BLD achieved a much better performance than that of all other methods, even when the methylation change of genes was moderate. DM-BLD, with the full probabilistic model in a Bayesian framework, was evidently more effective in detecting moderate changes.
3.2 Identification of differentially methylated genes associated with breast cancer recurrence
We applied the proposed method, DM-BLD, to breast cancer data acquired from The Cancer Genome Atlas project (2012). The study was designed for the identification of differentially methylated genes associated with breast cancer recurrence. 61 estrogen receptor positive (ER+) tumors were collected from patients for this study, where 41 patients were still alive with the follow-up time longer than 5 years, labeled as ‘Alive’; 20 patients were dead within 5 years, labeled as ‘Dead’. The histogram of the survival time is shown in Supplementary Figure S8. The ‘Dead’ and ‘Alive’ groups represent the ‘early recurrence’ group and the ‘late recurrence’ group, respectively. We applied our method to identify differentially methylated genes by analyzing samples from the two groups. The significance of the differential level was calculated from two permutation tests (Supplementary Section S5.2). With adjusted P-value < 0.05 in both permutation tests, DM-BLD detected 1543 differentially methylated genes.
We compared our DM-BLD method with Bumphunter, DMRcate, and comb-P. Probe Lasso was not included since it did not detect any DMR. The details of the implementation of Bumphunter, DMRcate, and comb-P can be found in Supplementary Section S5.3. With P-value < 0.05, Bumphunter, DMRcate, and comb-P detected 236, 3347, and 721 differentially methylated genes, respectively. Consistent with the simulation studies and what reported in (Peters et al., 2015), Bumphunter and comb-P are more conservative than DMRcate and DM-BLD.
Among the 1543 differentially methylated genes detected by DM-BLD, 720 (common) genes were also detected by other methods yet 823 (unique) genes were detected by DM-BLD only. We compared the CpG sites in the detected DMRs associated with the common genes with those associated with the unique genes in terms of noise level and number of CpG sites. As a result, the absolute difference of beta value and SNR were significantly lower for the unique set than those for the common set; the number of sites associated with genes was significantly smaller for the unique set (P-value = 1.77e-7), while the number of sites in DMRs was significantly higher for the unique set. This observation supported that DM-BLD was more effective in detecting genes of less differentially methylated by virtue of its capability in detecting regions consisting of a sequence of sites with moderate methylation change (resulted in part from relatively large variance observed among tumor samples). Moreover, DM-BLD was effective in detecting genes with fewer measured CpG sites that might be missed by other methods biased to dense CpG regions. More details can be found in Supplementary Section S5.4.
As there was no ground truth of differentially methylated genes for real data, we used the corresponding mRNA expression change as the benchmark to assess the performance. We detected differentially expressed genes from RNA-seq data of the same set of tumor samples (as detailed in Supplementary Section S5.5). Figure 5 shows the proportion of differentially expressed genes among the top ranked differentially methylated genes detected by the four competing methods, where genes were ranked by the P-value obtained from each method. We can see from the figure that DM-BLD detected more genes with mRNA expression change, which were benchmarked as functional differentially methylated genes.
Fig. 5.
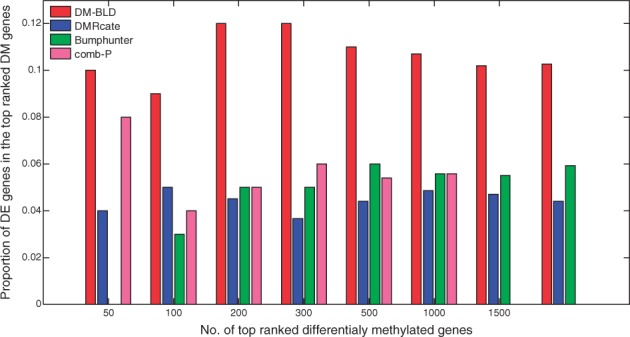
Proportion of differentially expressed (DE) genes among the top ranked differentially methylated (DM) genes detected by DM-BLD, DMRcate, Bumphunter or comb-P (Color version of this figure is available at Bioinformatics online.)
Among the differentially methylated genes detected by DM-BLD, 523 genes were hypermethylated in the promoter region. From functional annotation clustering using the Database for Annotation, Visualization and Integrated Discovery, http://david.abcc.ncifcrf.gov/home.jsp, the set of hypermethylated genes was enriched in transcription factor activity (82 genes, P-value = 4.5E-20), and homeobox (39 genes, P-value = 4.5E-19). The enrichment in transcription factor activity may indicate the interplay between transcription factor and DNA methylation. Methylation of homeobox genes has been reported as a frequent and early epigenetic event in breast cancer (Tommasi et al., 2009). Moreover, 159 genes out of the 523 genes were polycomb target genes (hypergeometric P-value = 3.19E-29). The polycomb target genes were the common genes detected from the ChIP-seq data of EZH2, SUZ12, H3K4me3 and H3K27me3 in embryonic stem cells (which were acquired in the ENCODE project (http://www.encodeproject.org/)) (Supplementary Section S6). Polycomb group proteins are well known epigenetic regulators that silence the target genes. The significantly large overlap between the identified hypermethylated genes in the promoter region and the polycomb target genes indicates that the two key epigenetic repression systems jointly regulate gene expression (Vire et al., 2006).
We further looked into functional differentially methylated genes, which are differentially methylated genes that are also differentially expressed. By incorporating the mRNA expression change estimated from the corresponding RNA-seq data, we detected 158 functional differentially methylated genes, which are enriched in cell adhesion, cell morphogenesis, cell to cell signaling, transcription factor activity, and so on. We also incorporated the protein–protein interaction network (Keshava Prasad et al., 2009) to further study the interaction of the functional differentially methylated genes. Supplementary Figure S7 shows that the major connected network is largely downregulated in the ‘Dead’ group as compared to that in the ‘Alive’ group (more detailed submodules, potentially regulated by DNA methylation, can be found in Supplementary Section S5.6). Literature has shown that hypermethylation in the promoter region repressed gene expression, contributing to cancer development. Thus, we focused on genes that are hypermethylated in the promoter region and down-regulated in the ‘Dead’ group (N = 52). 18 genes are also polycomb target genes, which may be regulated by polycomb group protein and DNA methylation jointly. Among the 18 genes, DBC1 and SLC5A8 are tumor suppressor genes. DBC1 has been demonstrated participating in cell cycle control (Nishiyama et al., 2001), and it was reported that the hypermethylation of DBC1 was an effective biomarker in predicting breast cancer (Hill et al., 2010; Li et al., 2015). SLC5A8, a putative tumor suppressor, was found that it inhibited tumor progression (Coothankandaswamy et al., 2013); the inactivation of SLC5A8 might result in tumor development (Elangovan et al., 2013). HTRA3 was reported as a candidate tumor suppressor and TGF-beta signaling inhibitor, which might be regulated by transcription factor CREB3L1 to affect the development of breast cancer (Rose et al., 2014). CMTM3, as a CMTM family protein linking chemokines and the transmenbran-4 superfamily, exerted tumor-suppressive function in tumor cells (Wang et al., 2009). The silencing of CMTM3 due to hyper-methylation would result in loss of function in inhibiting tumor cell growth and inducing apoptosis with caspase-3 activation. Note that DBC1, HTRA3 and CMTM3 were detected by our DM-BLD method only, yet missed by the other methods.
4 Discussion
It is important to accurately detect differentially methylated genes, yet with remarkable challenges, particularly in the field of cancer research where the variability of methylation among replicates/samples is high. We have developed a Bayesian approach, DM-BLD, for the identification of differentially methylated genes. A hierarchical and probabilistic model, with differential states as hidden variables, is devised to account for the local dependency of CpG sites and the variability among the samples/replicates of the same phenotype. Specifically, the Leroux model, which is capable of capturing varying degrees of local dependency, is used to model the unknown correlation among the true methylation levels of CpG sites in the neighboring region. A discrete Markov random field is then used to model the dependency of methylation change (via differential states) of neighboring CpG sites. A hierarchical Bayesian model, with differential states embedded as hidden variables, is then developed to take into account the local dependency for differential analysis.
The main advantages of our proposed method, DM-BLD, can be summarized as follows. First, it is a fully probabilistic approach that jointly models the methylation level of CpG sites and the differential state of methylation between two phenotypes. Rather than calculating the significance of the difference between two groups of samples using statistical tests (e.g., DMRcate, comb-P), DM-BLD uses a Bayesian framework to estimate the true methylation level and the differential state in a probabilistic way. Second, the varying local dependency among neighboring CpG sites is modeled by the Leroux model, an advanced CAR structure that can account for different levels of correlation. By virtue of using information from neighborhood with local dependency, the accuracy of the estimated methylation level is greatly improved, particularly when the variability among the replicates is high. Third, the Leroux model is embedded into the Bayesian framework. Thus, the posterior distributions of the true methylation levels in each group as well as other parameters are estimated jointly with the local correlation levels through a Gibbs sampling procedure, which provides an improved performance in detecting CpG sites of less differentially methylated. Finally, with the estimated methylation change of CpG sites between two groups, we detect differentially methylated genes as genes with a sequence of CpG sites exhibiting methylation change, and calculate the significance of differentially methylated genes by permutation tests.
We have compared the performance of DM-BLD with the existing methods using extensive simulation studies. DM-BLD consistently outperforms the other methods, particularly when the difference between two groups is less and the noise among the replicates is high. Moreover, we have applied DM-BLD to breast cancer data to identify differentially methylated genes associated with breast cancer recurrence, and demonstrated the advantage of DM-BLD as evaluated by the consistency with the differential expression of mRNA. The differentially methylated genes identified by DM-BLD are enriched in transcription factor activity and consisted of a significant portion of polycomb target genes. Moreover, several differentially methylated genes such as DBC1, HTRA3, and CMTM3, revealing the underlying biological mechanism related to breast cancer recurrence, have been uniquely identified by our DM-BLD method.
Funding
This work was supported in part by the National Institutes of Health (CA149653 to J.X., CA149147 & CA184902 to R.C. and CA164384 to L.H.-C.)
Conflict of Interest: none declared.
Supplementary Material
References
- Cancer Genome Atlas Network. (2012) Comprehensive molecular portraits of human breast tumours. Nature, 490, 61–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atchison J., Shen S.M. (1980) Logistic-normal distributions: some properties and uses. Biometrika, 67, 261–272. [Google Scholar]
- Baylin S.B., Jones P.A. (2011) A decade of exploring the cancer epigenome - biological and translational implications. Nat. Rev. Cancer, 11, 726–734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y., Hochberg Y. (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological), 57, 289–300. [Google Scholar]
- Besag J. (1986) On the statistical analysis of dirty pictures. Journal of the Royal Statistical Society. Series B (Methodological), B-48, 259–302. [Google Scholar]
- Bibikova M. et al. (2011) High density DNA methylation array with single CpG site resolution. Genomics, 98, 288–295. [DOI] [PubMed] [Google Scholar]
- Bird A. (2002) DNA methylation patterns and epigenetic memory. Genes & development, 16, 6–21. [DOI] [PubMed] [Google Scholar]
- Butcher L.M., Beck S. (2015) Probe Lasso: a novel method to rope in differentially methylated regions with 450K DNA methylation data. Methods, 72, 21–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton D., Kaldor J. (1987) Empirical Bayes estimates of age-standardized relative risks for use in disease mapping. Biometrics, 43, 671–681. [PubMed] [Google Scholar]
- Coothankandaswamy V. et al. (2013) The plasma membrane transporter SLC5A8 suppresses tumour progression through depletion of survivin without involving its transport function. Biochem. J., 450, 169–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elangovan S. et al. (2013) Molecular mechanism of SLC5A8 inactivation in breast cancer. Mol. Cell. Biol., 33, 3920–3935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinberg A.P. (2007) Phenotypic plasticity and the epigenetics of human disease. Nature, 447, 433–440. [DOI] [PubMed] [Google Scholar]
- Feinberg A.P., Tycko B. (2004) The history of cancer epigenetics. Nat. Rev. Cancer, 4, 143–153. [DOI] [PubMed] [Google Scholar]
- Gelman A. ( 2004) Bayesian Data Analysis. Chapman & Hall/CRC, Boca Raton, FL, USA. [Google Scholar]
- Hill V.K. et al. (2010) Identification of 5 novel genes methylated in breast and other epithelial cancers. Mol. Cancer, 9, 51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaffe A.E. et al. (2012) Bump hunting to identify differentially methylated regions in epigenetic epidemiology studies. Int. J. Epidemiol., 41, 200–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keshava Prasad T.S. et al. (2009) Human Protein Reference Database–2009 update. Nucleic Acids Res., 37, D767–D772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulis M., Esteller M. (2010) DNA methylation and cancer. Advances in genetics, 70, 27–56. [DOI] [PubMed] [Google Scholar]
- Lee D. (2011) A comparison of conditional autoregressive models used in Bayesian disease mapping. Spat. Spatio-Temporal Epidemiol., 2, 79–89. [DOI] [PubMed] [Google Scholar]
- Leroux B.G. et al. (2000) Estimation of disease rates in small areas: a new mixed model for spatial dependence In: Statistical Models in Epidemiology, the Environment, and Clinical Trials, Springer, New York, 179–191. [Google Scholar]
- Li Z. et al. (2015) Methylation profiling of 48 candidate genes in tumor and matched normal tissues from breast cancer patients. Breast Cancer Res. Treat., 149, 767–779. [DOI] [PubMed] [Google Scholar]
- Meissner A. (2010) Epigenetic modifications in pluripotent and differentiated cells. Nature biotechnology, 28, 1079–1088. [DOI] [PubMed] [Google Scholar]
- Nishiyama H. et al. (2001) Negative regulation of G(1)/S transition by the candidate bladder tumour suppressor gene DBCCR1. Oncogene, 20, 2956–2964. [DOI] [PubMed] [Google Scholar]
- Pedersen B.S. et al. (2012) Comb-p: software for combining, analyzing, grouping and correcting spatially correlated P-values. Bioinformatics, 28, 2986–2988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters T.J. et al. (2015) De novo identification of differentially methylated regions in the human genome. Epigenetics Chromatin, 8, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramchandani S. et al. (1999) DNA methylation is a reversible biological signal. Proceedings of the National Academy of Sciences of the United States of America, 96, 6107–6112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose M. et al. (2014) OASIS/CREB3L1 is epigenetically silenced in human bladder cancer facilitating tumor cell spreading and migration in vitro. Epigenetics, 9, 1626–1640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandoval J. et al. (2011) Validation of a DNA methylation microarray for 450,000 CpG sites in the human genome. Epigenetics, 6, 692–702. [DOI] [PubMed] [Google Scholar]
- Tommasi S. et al. (2009) Methylation of homeobox genes is a frequent and early epigenetic event in breast cancer. Breast Cancer Res., 11, R14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vire E. et al. (2006) The Polycomb group protein EZH2 directly controls DNA methylation. Nature, 439, 871–874. [DOI] [PubMed] [Google Scholar]
- Wang D. et al. (2012) IMA: an R package for high-throughput analysis of Illumina's 450K Infinium methylation data. Bioinformatics, 28, 729–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y. et al. (2009) CMTM3, located at the critical tumor suppressor locus 16q22.1, is silenced by CpG methylation in carcinomas and inhibits tumor cell growth through inducing apoptosis. Cancer Res., 69, 5194–5201. [DOI] [PubMed] [Google Scholar]
- Wei P., Pan W. (2010) Network-based genomic discovery: application and comparison of Markov random field models. J Roy. Stat. Soc. Series C, Appl. Stat., 59, 105–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.