Helical and rod-shaped bacteria swim in helical trajectories with little additional propulsion from helical shape

Helical bacteria, like the stomach pathogen H. pylori, swim only about 15% faster than their isogenic rod-shaped mutants.

Abstract

It has frequently been hypothesized that the helical body shapes of flagellated bacteria may yield some advantage in swimming ability. In particular, the helical-shaped pathogen Helicobacter pylori is often claimed to swim like a corkscrew through its harsh gastric habitat, but there has been no direct confirmation or quantification of such claims. Using fast time-resolution and high-magnification two-dimensional (2D) phase-contrast microscopy to simultaneously image and track individual bacteria in bacterial broth as well as mucin solutions, we show that both helical and rod-shaped H. pylori rotated as they swam, producing a helical trajectory. Cell shape analysis enabled us to determine shape as well as the rotational and translational speed for both forward and reverse motions, thereby inferring flagellar kinematics. Using the method of regularized Stokeslets, we directly compare observed speeds and trajectories to numerical calculations for both helical and rod-shaped bacteria in mucin and broth to validate the numerical model. Although experimental observations are limited to select cases, the model allows quantification of the effects of body helicity, length, and diameter. We find that due to relatively slow body rotation rates, the helical shape makes at most a 15% contribution to propulsive thrust. The effect of body shape on swimming speeds is instead dominated by variations in translational drag required to move the cell body. Because helical cells are one of the strongest candidates for propulsion arising from the cell body, our results imply that quite generally, swimming speeds of flagellated bacteria can only be increased a little by body propulsion.

INTRODUCTION

Bacteria come in a wide variety of shapes, and bacterial morphology affects selective adaptation (1). One important mechanism by which morphology could affect biological function is through motility (2); for example, cell length has been shown to affect the tumbling (3) and, hence, chemotactic ability in Escherichia coli. It is well known that the translational and rotational drag on the cell body depends on the shape and thus alters swimming speed (4, 5). For swimming bacteria, it has also been of interest how the cell body can directly contribute toward propulsion, obviously for species that propel themselves by deforming or twisting their bodies such as spiroplasma (6, 7) or spirochetes (8), but also for bacteria, which use a rotating flagellum or flagellar bundle like a propeller. For these flagella-propelled bacteria, Liu et al. (9) have recently shown that the counter-rotation and subsequent helical path of the cell body may contribute to swimming propulsion, but it is unclear how large this effect may be in general and how important it may be for adaptation. Here, we compare helical cells with their rod-shaped isogenic mutants to place quantitative bounds on the contribution of cell body shape to propulsion because a rotating helical cell body (like the helical flagellum) is well suited to provide maximal amounts of thrust; indeed, long ago, Berg and Turner (10) suggested that a helical cell shape would result in additional corkscrew-like propulsion for bacteria moving in viscous environments.

It has not been possible to draw firm conclusions from earlier studies addressing the role of helical cell shape on propulsion because many of these studies compare different species, which may have uncontrolled differences beyond cell morphology. Ferrero and Lee (11) compared the swimming speeds of the helical-shaped bacteria Campylobacter jejuni with rod-shaped bacteria, Vibrio cholerae, Salmonella enteritidis, and E. coli. They found that in viscous methylcellulose solutions, the helical-shaped C. jejuni were more motile than rod-shaped bacteria. Later work done by Karim et al. (12) compared the swimming speeds of the helical bacteria Helicobacter pylori and C. jejuni to rod-shaped E. coli bacteria, finding C. jejuni to be the fastest (median speed, 38 μm/s; range, 29 to 53 μm/s) compared to H. pylori (median speed, 25 μm/s; range, 12 to 29 μm/s), whereas the rod-shaped E. coli were the slowest (median speed, 12 μm/s; range, 8 to 18 μm/s). These studies seemed to indicate that helical cell shape resulted in increased swimming speed by factors of 2 to 3; however, because there are several other differences between these bacteria, it is unclear how much the observed differences in motility are due to cell body helicity. Furthermore, none of these studies measured the counter-rotational motion of the body of swimming bacteria nor did they measure speed and shape of individual bacteria to enable quantitative comparison between experiment and theoretical models.

Here, we use H. pylori, an important human pathogen that colonizes the epithelial surface of the gastric mucosa of the human stomach and is known to cause gastritis, gastric ulcers, and gastric cancer (13–15). Other Helicobacters with a larger number of helical turns [Helicobacter heilmannii, Helicobacter suis, Helicobacter felis, among others (16)] are also found in the gastric mucosa of humans, although they primarily infect other animals. As their name suggests, the helical shape of these bacteria is one of their most salient features and is purported to be an important factor in the ability of the bacterium to traverse the protective mucus barrier and colonize on the epithelial surface of the stomach mucosa. For example, it has been suggested that the helical shape enables the bacterium to bore its way like a corkscrew through the gastric mucus gel that covers the epithelial surface (17, 18). This commonly held view was questioned by previous studies of ours, which show that H. pylori can rotate its flagella but does not swim in mucin gels buffered at acidic pH 2 to 4 comparable to the stomach (19), as well as gelatin gels at neutral pH (20). In the case of mucus, gelation is related to a liquid-to-gel transition of the glycoprotein mucin at pH 4 and below (21, 22). We showed that H. pylori uses urease-mediated hydrolysis of urea to neutralize the pH of the mucin (19), enabling the non-acidophilic bacterium to not only survive in acidic conditions but also trigger a pH-dependent gel-to-liquid transition of mucin (19, 23, 24), enabling the bacterium to swim in a liquid environment. More recently, Mirbagheri and Fu (25) have developed a model that couples motility and diffusion to describe how H. pylori can swim as if in an unconfined medium by creating a moving pocket of fluid in a gel. However, it remains unknown to what extent the helical shape of the cell could be advantageous for swimming in a viscous fluid, which we address here.

To directly address the link between cell shape and motility, we use isogenic straight rod cell–shaped mutants of H. pylori, called Δcsd6 (26), which lack the Csd6 peptidoglycan carboxypeptidase responsible for cell helicity (27). These isogenic mutants differ only in cell shape due to the single csd6 gene mutation but are otherwise shown to have the same flagellation characteristics and motility as the wild type (WT) (26, 28). Rod- or C-shaped mutants of H. pylori lacking helical shape were found to show decreased halo formation in soft agar and impaired stomach colonization in a mouse model (26, 27); however, in these early studies, helical and straight rod bacteria were found to exhibit similar swimming speeds. Recently, we reported a detailed study on the relationship between H. pylori cell shape morphology and motility using live-cell microscopic imaging to track both helical and straight rod mutants of three different strains in several solutions (bacterial broth, gastric mucin, and methylcellulose) (28) and also measured the distribution of cell shapes and sizes from a separate microscopic imaging of bacteria fixed to a slide. The speed of individual bacteria was found to vary with time as well as due to the broad distribution of cell sizes (length, diameter, and pitch) and variation in the number of flagella among the bacteria population in the sample. Martinez et al. (28) concluded that, on average, helical bacteria had the same number of flagella and swam with a slightly increased median speed compared to their isogenic rod-shaped mutants, whereas other characteristics of the trajectories, such as linearity of tracks and frequency of reversals, were not significantly altered. They also noted that the effect of shape was larger in gastric mucin solutions than in culture broth or methylcellulose solutions, possibly due to specific interactions between H. pylori and mucin as well as viscoelasticity of mucin solutions. In that paper (28), resistive force theory (RFT) (29) was used to calculate the swimming speed using an average of all the cell shape measurements to define the bacterium. The RFT calculations overestimate the effect of shape, producing a significantly larger increase in the speed, ~30% for the helical bacterium relative to an elongated rod-like, ellipsoidal cell shape, as compared to the ~10% enhancement observed experimentally. However, crucially, Martinez et al. (28) found that variations in swimming speed are dominated by variations in the number of flagella and hence motor torque propelling the cells, meaning that the effect of body shape on swimming speed could be difficult to extract from population averages of bacteria differing not only in shape and size but also in number of flagella. By examining mutants with an average of one less flagella or one more flagella, they showed a direct correlation between the speed and number of flagella (28). In view of these variable factors of shape, size, and number of flagella within the population, it was not possible to clearly elucidate the relationship between cell body shape and swimming speed by comparing average speeds of rod-shaped mutants and helical WT bacteria.

Here, we take advantage of advances in high–frame rate digital tracking and image analysis (30) to design a study to directly address the question of shape and motility by simultaneously imaging and tracking individual cells as they rotate and translate. Whereas previous work to examine the rotational motion used a specialized, custom built three-dimensional (3D) tracking microscope (9), we use the more readily available 2D phase-contrast microscope to simultaneously measure both swimming properties and cell geometry for the same individual cell. Single-cell tracks in H. pylori have previously been reported (28, 31), but they did not address or analyze rotational motion and propulsion of the cell body. Using the high-resolution geometric and kinematic measurements reported here, we can quantitatively validate numerical models of swimming propulsion and thrust, and then use those numerical models to perform properly controlled investigations of how helical body shapes change in swimming speed while keeping other quantities, such as motor torque, fixed, leading to a physical mechanistic understanding of the contribution of cell body shape to thrust. These investigations are not possible without the combination of our simultaneous high-resolution tracking and numerical models.

To summarize our results, we present simultaneous shape and tracking measurements of individual H. pylori and its rod-shaped mutant (Δcsd6) while swimming in mucin and broth solutions using 2D phase-contrast imaging at high magnification and at high frame rates. The helical shape of H. pylori enables direct visualization of corkscrew motion. These measurements enable us to determine the rotational speed of the bacterium while simultaneously measuring the translational speed and cell shape parameters of a single bacterium for both forward and reverse motions, as well as the change in direction of rotation after a reversal event, providing detailed kinematic information that allows deduction of flagellar kinematics. We were able to confirm the previous finding that, during swimming, H. pylori’s multiple flagellar bundle together, forming a single left-handed bundle (19, 28). We used the measured geometry and the observed rotational rate to numerically calculate the swimming speed of both helical and rod-shaped bacteria moving forward as well as in reverse using the method of regularized Stokeslets (RSM) and find good quantitative agreement between theory and experiment for the swimming speed and the pitch of the trajectory. Using the observed rotation rate as an input, we circumvent the problems arising from not knowing the number of flagella in H. pylori, which as mentioned above is known to strongly affect the swimming speed (28). We find that because of the relatively slow counter-rotation rate of the cell body, the helical shape produces <15% extra propulsive thrust and <15% changes in swimming speeds as compared to the rod-shaped cell. Moreover, the accuracy of the theoretical model allows us to explore the influence of cell body shape on swimming speeds and enables us to predict how the speed depends on length, diameter, and helicity and to examine the effect of varying flagella geometry.

More generally, the helical shape might be considered a maximal case to produce thrust from cell body rotation. Thus, our result suggests that for flagellated bacteria, which usually have much slower cell body rotation rates than flagellar rotation rates, cell body shape has at most 10 to 15% effect on swimming speeds.

RESULTS

Helical trajectory

The swimming of bacteria can be easily visualized by time-resolved optical microscopy, and their trajectories can be obtained from frame-by-frame digital processing of movies to follow individual bacteria as they swim (30, 32). We use time-resolved phase-contrast microscopy to track the motion of live bacteria, although other types of microscopy have also been used in the literature (29, 30, 32). In our previous study (28), we tracked a hundred or more bacteria at a low–video frame rate [10 frames per second (fps)] to analyze the speed distributions of large populations of the WT helical H. pylori from three different strains and rod-shaped mutant Δcsd6. Here, we focus on imaging only a few bacteria from the LSH100 strain at higher magnification and faster frame rates to determine both the translational and rotational speeds of the swimmer and its relation to shape from a single trajectory. The experiments were done both in Brucella culture broth (BB10) and in porcine gastric mucin (PGM; 15 mg/ml solution at pH 6). This low concentration of PGM corresponds to the average concentration of mucin in the loose, nonadherent outer layer of mucus (33). At this concentration, PGM solutions in pH 6 buffer do not exhibit significant non–Newtonian effects (28, 34, 35). Movie S1 acquired at 100× with 200 fps shows a single helical bacterium swimming as a pusher in PGM at pH 6. An optical microscopic image from one frame of the movie shows the bacterium’s cell body (see Fig. 1A, inset) along with the contour (blue), centerline (red), and flagellar junction localization (J). The shapes of the images were analyzed using CellTool (36), as described in Materials and Methods. The 2D projection of the helix centerline was fit to a sinusoidal shape to obtain the cell body parameters. Figure 1A shows images from every fifth frame (about four images per body revolution) of this movie obtained by analyzing movie S1. Overlaid on this image is the trajectory obtained by tracking the centroid of the images, as explained in Materials and Methods.

Fig. 1. Trajectory and body rotation of H. pylori LSH100 helical bacterium (WT) and rod-shaped mutant (Δcsd6) swimming in PGM (15 mg/ml at pH 6).

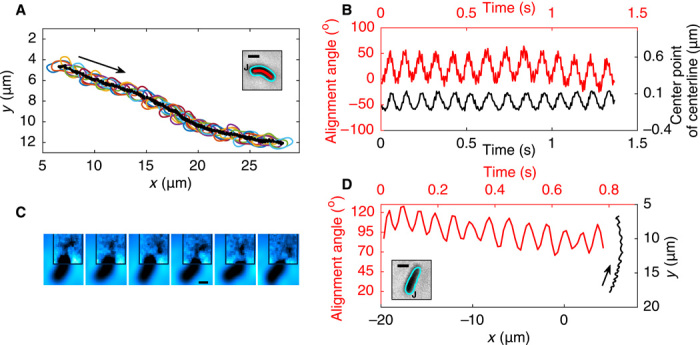
(A) Trajectory of helical bacterium plotted as body contours of cells (colors) every five frames from movie S1. From this trajectory, we measured a mean trajectory pitch P_T = 1.5 ± 0.2 μm (SD is based on the 13 full rotations observed in the entire movie S1). The inset shows the contour (blue), centerline of bacterium’s cell body (red), and the flagellar junction (J). The flagellar bundle cannot be seen in this image because of low contrast. (B) Rotation of helical bacterium as measured by the change of the axis angle as a function of time (red) and by the motion of the center point of the centerline (black) (more details in Materials and Methods). (C) Image of the flagellar bundle of helical bacterium for consecutive frames, giving an estimated rotation rate of 66 Hz with an uncertainty of 33%. This image sequence is from the same movie used in (A) and (B), with images rotated for display and filtered to increase contrast (movie S2), especially around the flagellar junction. (D) Trajectory of the rod-shaped mutant from movie S3 plotted on the right side of graph in black (bottom and right axis) and rotation of bacterium as measured by change of the axis angle as a function of time plotted on top in red (top and left axis). The inset shows the contour (blue) of the bacterium cell body with the flagellar junction indicated by J. Scale bars, 1 μm; arrows indicate the swim direction.

Figure 1B shows that the center point of the centerline and the axis of the body rotate as a function of time, and fig. S1 shows head and flagellar junction rotation independently. The rotation of the body causes the alignment angle between the body axis and the x axis of the image measured by CellTool (36) to oscillate in time. Measurement of the center point of the body (denoted by subscript b) and the alignment angle (denoted by subscript a) provide independent estimates of the rotation rates Ω_b = 10.3 ± 0.9 Hz and Ω_a = 10.4 ± 0.9 Hz, respectively. The 2D speed (V) during each revolution was calculated from the distance traveled on the image plane per revolution, as described in Materials and Methods. The rotation rate varies by ~9% during this run, whereas the speed varies about 12% with an average speed over the entire run of V = 17 ± 2 μm/s. The fact that body rotation and alignment angle precession have the same period is consistent with “wiggling” trajectories caused by flagellar bundles with fixed orientation relative to the cell body (37). For these trajectories, the oscillation amplitude of the alignment angle is roughly twice the precession angle between the cell body axis and the average swimming direction. The data follow a positive linear correlation between V and Ω. The ratio V/Ω is a useful measure of the distance traveled in one revolution and should be independent of the motor torque and only weakly dependent on the thickness of the flagellar bundle. However, it depends on cell and flagellar size parameters as well as flagellar bundle orientation.

For this bacterium imaged at high resolution, it was also possible to visualize the flagellar rotation in some frames, as shown in movie S2 and Fig. 1C. The flagellar rotation rate is much faster than the body rotation, leading to an estimate of around 66 Hz, which is about three frames on the 200-fps camera and thus estimated with an uncertainty of 33%. In the images, the orientation of the flagella appears to change with respect to the body. The diffraction blur makes it hard to make a definitive evaluation of this angle, but it seems to range from 0° to 45° from the body axis. Note that apparent changes in the flagellar orientation in these 2D images are also consistent with those of a bacterium with fixed flagellar orientation undergoing bodily rotation (37), although the observed slight temporal variation of swimming speeds, trajectories, rotation rates, and precession angles suggests that flagellar orientation may not be constant in time.

These direct observations of both body and flagellar rotation accompanied by a precession show that by tracking at high frame rate and high magnification, it is possible to directly observe the corkscrew motion of the bacterium as it swims. Additionally, because of the fact that as the flagellar bundle rotates the cell must counter-rotate to balance the flagellar torque, we can infer the sense of rotation of the flagella by imaging the rotation of the body. Flagellar rotation is very difficult to visualize, even under enhanced imaging conditions, because they are very thin and rotate much faster (~60 to 100 Hz), as well as by fluorescence microscopy, because the Helicobacter flagella are sheathed in the same cell membrane that covers the cell body. However, we have observed by looking at the movies that the end of the bacterium where the flagella are located (referred to as the junction J here) exhibits a more rapid variation in the contrast on the image as compared to the other end. Thus, we can identify the flagellar junction end even when the flagella cannot be imaged.

Comparison of helical with rod-shaped mutant

To address the question of how the shape affects swimming speed, we also tracked the rod-shaped mutant Δcsd6 in PGM and compared it to the helical bacterium (see movies S1 and S3). Figure 1D shows the trajectory of the rod-shaped mutant, indicating that it also swims in a helical track. The cell body image, its contour, and flagella junction localization are shown in the inset. The precession of the rod axis angle can be observed by looking at the orientation of the cell as it moves along a helical trajectory (see Fig. 1D), and the variation of the axis orientation with time provides a measure of the rotation rate. Although the 2D images of the cell body remain rod-shaped as the bacterium rotates, the length of the image of the rod changes in an oscillatory fashion with the same period as the axis. We were also able to see the flagella of this rod-shaped bacterium in some frames, but because it was not seen clearly in all successive frames, we cannot evaluate the flagellar rotation rate.

We also compared the helical H. pylori and its rod-shaped mutant in BB10 (see movies S4 and S5 and Fig. 2, A to D). Figure 2A shows the trajectory of a helical bacterium (from movie S4, recorded at 200 fps and 100× magnification) whose cell body image is shown in the inset, and Fig. 2C shows the trajectory for the rod-shaped mutant (from movie S5, recorded at 30 fps and 40× magnification). Both trajectories show forward and reverse swimming. The rotation of the alignment angle is shown for both the forward and reverse motions, in Fig. 2B for the helical bacterium and in Fig. 2D for the rod-shaped mutant. The inset in Fig. 2C shows that the axial length X_B and the diameter of this rod-shaped bacterium are close to the contour length of the cell body centerline L_arc and to the diameter of the helical bacterium shown in Fig. 2A (see Table 1), that is, the two bacteria have similar cell volumes.

Fig. 2. Trajectory, body shape, and body rotation rate of H. pylori LSH100 helical WT and rod-shaped Δcsd6 bacteria showing one reversal while swimming in BB10.

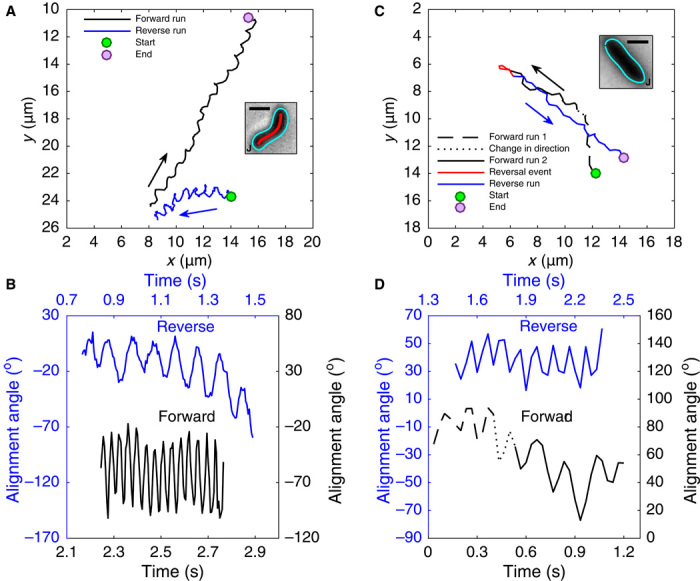
(A) Trajectory of helical bacterium from movie S4 starting at the green point and ending at the purple point; arrows indicate swimming direction. The forward (black) and reversed (blue) trajectories are not connected because the tracking software could not track the bacterium during the reversal event as it left the field of view. However, movie S4 captures part of the bacterium’s diffraction rings during the reversal event, confirming that it is the same bacterium for both tracks. The inset shows the contour (blue), centerline of cell (red), and the location of flagellar junction (J) of the helical bacterium; scale bar, 1 μm. (B) Rotation of helical bacterium measured by change of the axis angle with time for both runs, color-coded as in the track in (A). (C) Trajectory of rod-shaped mutant obtained from movie S5. The forward (black) and reversed (blue) trajectories are connected by the reversal event (red). The different lines in the forward run show changes in the direction of the trajectory and not from the reversals. The inset shows the contour (blue), centerline of cell (red), and the location of flagellar junction (J) of the rod-shaped bacterium; scale bar, 1 μm. (D) Rotation of rod-shaped mutant measured by change of the axis angle with time for both runs, color-coded as in the track in (C).

Table 1. Cell body shape parameters, translation, and rotation speeds of helical- and rod-shaped mutants of H. pylori in PGM and BB10.

NA, not applicable.

Medium		PGM (15 mg/ml)		BB10
Bacterium shape		Helical	Rod	Helical	Rod
Cell shape parameters	XB (μm)*	2.51 ± 0.09	2.74 ± 0.09	2.33 ± 0.09	2.6 ± 0.1
	Larc (μm)*	2.69 ± 0.09	2.74 ± 0.09	2.53 ± 0.09	2.6 ± 0.09
	dB (μm)*	0.83 ± 0.09	0.61 ± 0.09	0.61 ± 0.09	0.7 ± 0.1
	PB (μm)*	2.43 ± 0.09	—	2.32 ± 0.09	—
	RB (μm)*	0.15 ± 0.09	—	0.17 ± 0.09	—
Forward run	V (μm/s)†	17 ± 2	15 ± 4	31 ± 4	10 ± 2
	Ω (Hz)†	10.3 ± 0.9	17 ± 2	28 ± 3	7 ± 2
	V/Ω (μm) (measured)	1.6 ± 0.2	0.9 ± 0.3	1.2 ± 0.2	1.5 ± 0.4
	V/Ω (μm) (modeled)	1.66 ± 0.26	0.88 ± 0.15	1.13 ± 0.26	1.33 ± 0.12
	V/ΩXB (measured)	0.67 ± 0.08	0.3 ± 0.1	0.50 ± 0.07	0.6 ± 0.1
Reverse run	V (μm/s)†	NA	NA	10 ± 2	11 ± 2
	Ω (Hz)†	NA	NA	11 ± 2	10 ± 1
	V/Ω (μm) (measured)	NA	NA	0.8 ± 0.2	1.1 ± 0.2
	V/Ω (μm) (modeled)	NA	NA	0.82 ± 0.25	1.14 ± 0.13
	V/ΩXB (measured)	NA	NA	0.35 ± 0.09	0.44 ± 0.06

*The errors are given by 2_½ (pixel size of image).

†Averaged over the entire run; error is the SD for the run.

In Table 1, we list the observed speeds and also include the parameters V/Ω and V/(Ω X_B), which correspond to the distance traveled per rotation in dimensional and nondimensional units, respectively. A comparison of the observed speeds (Table 1) shows that the rod-shaped bacterium swims at a slower speed than the helical bacterium in both PGM and broth. We also observe that the relative change in speed of helical versus rod is larger in PGM than in broth, in agreement with the previous result reported by Martinez et al. (28) for the increase in median speed in viscous PGM as compared to broth. However, we cannot infer that this holds in general by comparing individual bacteria. The individual rod and helical bacteria examined here had different sizes as well as different rotation rates, which implies that they may have also differed in number of flagella in the bundle as well as flagellar geometry and orientation, features that we could not image.

Forward versus reverse motion

It is well known that bacteria change their swimming direction to explore their environment and respond to chemotactic gradients (32). In addition to the familiar run-tumble mechanism seen in many bacteria, such as E. coli (32), H. pylori also tends to reverse its swimming direction, which has been related to chemotactic sensing and quorum sensing in earlier works (28, 31, 38–41). Such run-reverse swimming has also been seen in several marine bacteria that swim in highly viscous environments (42–45) and in Caulobacter crescentus (9). We were able to observe reversal events in both the helical and rod-shaped bacteria tracks swimming in BB10, as shown in Fig. 2. We measured the average rotation rate before and after a reversal (see Table 1) and found that it increased by 40% for the rod-shaped mutant, whereas it decreased by 60% for the helical bacterium when swimming in reverse. The definition of forward/reverse relies on visualizing the rapid change in contrast at the flagella junction end further substantiated by actually seeing faint images of flagella in some frames (more details in the Supplementary Materials and movies S4 and S5). During the reverse run, the helical WT bacterium swims at V_WT,rev = 10 ± 2 μm/s and the rod-shaped mutant at a similar speed, V_Δcsd6,rev = 11 ± 2 μm/s. Moreover, in the reverse run, this rod-shaped mutant swims at a similar rotation rate Ω_Δcsd6,rev = 10 ± 1 Hz as compared to the helical one, Ω_WT,rev = 11 ± 2 Hz. Instead of comparing speeds for forward and reverse runs, it is better to measure distance traveled per rotation V/Ω [or the dimensionless quantity V/(ΩX_B)], which are slightly larger during forward versus reverse swimming for both the helical and rod-shaped bacteria tracked here (see Table 1). However, using either V/Ω or V/(ΩX_B) to compare the swimming ability of rod-shaped and helical cell bodies in this context is problematic because one should compare cells with the same motor torque, cell body diameter, and flagellar orientation angle, all of which could vary from cell to cell. For example, variations in the swimming speed are dominated by variations in the number of flagellar motors per cell, which alters the total torque (28). As discussed later, our numerical model circumvents these problems to allow direct tests of the effect of cell body geometry on propulsion while keeping all other parameters fixed.

Simultaneous imaging of the trajectory and cell body allows us to determine the sense of rotation of the cell body by analyzing the phase of the rotation angle (more details in Materials and Methods). Because the body counter-rotates relative to the flagellum to balance torques, we thereby deduce the sense of flagellar rotation. Relative to the cell body, such an analysis shows that the sense of rotation of the flagellar bundle appears to reverse on a reversal event, implying that during both pushing (forward motion) and pulling (backward motion), the propulsive flagella have the same left-handed configuration.

In addition to the results on the 4 individual bacteria reported in detail above, we imaged and tracked 22 other bacteria (16 helical and 6 rod-shaped) in PGM and broth, all showing cells rotating while swimming along their trajectory. Although the speeds and rotation rates of individual bacteria vary because of different cell and flagella sizes, the overall rotation rates and swimming speeds are in a similar range to those displayed in Figs. 1 and 2. Although the numbers are not large enough to do a detailed statistical analysis, we note that the average of both V/Ω and V/(Ω X_B) are larger for the helical versus rod-shaped mutant, irrespective of the swimming medium. The values we obtained for the dimensionless ratio V/(Ω X_B) are 0.5 for helical versus 0.4 for the rod in PGM, and 0.6 for helical versus 0.5 for rod in BB10, implying about 25% extra propulsion for the helical shape in PGM and 20% in broth.

Calculation of trajectory using RSM

We used RSM (46, 47) to calculate swimming trajectories and speeds of H. pylori with the same cell body shape, as shown in the inset in Fig. 1A. The bacterial geometry is specified by the helical pitch, helical radius, length, and cell body diameter, and the flagellar bundle is modeled as a single helix rotating around its helical axis at a fixed orientation relative to the cell body (Fig. 3A). Once the geometry is defined, all swimming kinematics are determined by a single input, the body rotation rate, which can be directly measured by experiment. This single input parameter incorporates the effects of varying flagella number, as well as any effects of medium viscosity on the rotation rate. Details of the numerical method, including convergence studies, are given in the Supplementary Materials, and the numerical parameters for both cell body and flagellum geometry are provided in Tables 1 and 2. The calculated trajectory for a particular choice of flagella geometry (as discussed later) shown in Fig. 3B is in reasonable agreement with the experimentally observed trajectory of Fig. 1A. The average velocity is the component of instantaneous velocity along the rotation direction, which is equivalent to the net translation over a revolution divided by the period of revolution.

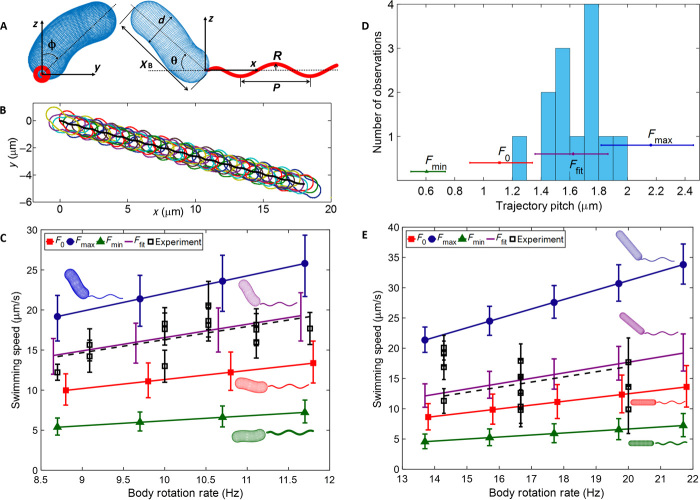
Fig. 3. Comparison of numerical model to experiment for bacteria in PGM.

(A) Discretized geometry used for numerical calculations. Cell body geometry is parameterized by diameter d and axial length X_B, and flagellar bundle geometry is parameterized by pitch P and helical radius R. Orientation of the helical centerline of the cell body with respect to the centerline of the flagellum is determined by angles θ and ϕ. (B) Calculated trajectory of the cell body with geometry measured from Fig. 1 and flagellar parameters F_fit (see text and Tables 1 and 2). Frame interval is the same as in Fig. 1A, and trajectory pitch is 1.62 ± 0.3 μm. (C) Swimming speed observed from Fig. 1B (helical WT) compared to those numerically calculated for different flagellar geometries, which are shown next to each line. (D) Histogram of the trajectory pitch observed in experiments and numerically modeled trajectory pitch for the same flagellar geometries as in (C). (E) Swimming speed observed from Fig. 1D (rod-shaped mutant Δcsd6) compared to those numerically calculated for different flagellar geometries, which are shown next to each line. Vertical error bars in (C) and (E) and horizontal error bars in (D) correspond to propagated uncertainty from experimental cell body measurements.

Table 2. Flagellar bundle parameters.

Flagellar geometry parameters following Martinez et al. (28) are inputs for our numerical calculations.

		PGM (15 mg/ml)		BB10
		Helical	Rod	Helical	Rod
Flagella (F0)	Xf (μm)*	2.97	2.97	2.97	2.97
	df (μm)†	0.07	0.07	0.07	0.07
	P (μm)‡	1.58	1.58	1.58	1.58
	R (μm)‡	0.14	0.14	0.14	0.14
	Ωf (Hz)	66§	—	—	—
Flagella (Ffit)	Θfwd (°)	40	30	30	50
	Φfwd (°)	0	0	0	0
	Θrev (°)	NA	NA	5	40
	Φrev (°)	0	0	0	0
Flagella (Fmin)	df (μm)	0.14	0.14	0.14	0.14
	Θ (°)	15	0	15	0
	Φ (°)	180	0	225	0
Flagella (Fmax)	df (μm)	0.035	0.035	0.035	0.035
	Θ (°)	45	50	45	50
	Φ (°)	0	0	0	0

*The end-to-end length X_f of the flagellum is calculated from a helical length of 3.4 μm following Martinez et al. (28) and was the same for the helical- and rod-shaped cells.

†The thickness of the flagellar bundle d_f is taken the same way as that used in the RFT calculation of Martinez et al. (28) for the F₀ and F_fit geometries and then varied for F_min and F_max geometries.

‡The flagella pitch P and helical radius R are taken the same way as that used by Martinez et al. (28), which are based on the values used for Vibrio alginolyticus (29).

§Flagellar rotation is estimated from only three frames per rotation (see Fig. 1C), and thus, the error would be about 33%.

Quantitative comparison between model and experiment

Figure 3C shows the predicted average speed as a function of cell body rotation frequency for the bacterium in Fig. 1. The error bars correspond to the propagated uncertainty from the measurements of cell body parameters (Table 1). The geometry and orientation of the bundle can affect the result, but flagellar geometry is difficult to measure precisely because it is difficult to visualize the flagella. Therefore, we investigate the effect of flagellar geometry by finding the range of swimming speeds possible for the observed cell body shape. Each of the different lines in Fig. 3C corresponds to different bundle geometries and orientations (pictorially represented beside the lines; see Table 2 for specific flagella geometrical parameters). The range of calculated speeds nearly spans all observed speeds: the minimum swimming speeds obtained for the bundle geometry F_min are below those observed in this experiment, whereas the maximum swimming speeds obtained for the bundle geometry F_max encompass the upper end of experimental measurements. The variation in swimming speed between the different bundle geometries is most strongly affected by the orientation angle. The flagellar configuration corresponding to the average flagellum geometry measured by Martinez et al. (28) using transmission electron microscopy (TEM) (Table 2) and bundle orientation parallel to the cell body helical axis (F₀) gives calculated swimming speeds smaller than the observed speeds. However, the geometry with the flagellum oriented at 40° from the helical axis (F_fit) yields swimming speeds that match experiments well. Note that a 40° orientation is consistent with the images in Fig. 1C.

We also investigated the dependence of trajectory on the flagellar bundle geometry. In Fig. 3D, the horizontal lines show the calculated trajectory pitch for the F_min, F₀, F_fit, and F_max bundle geometries. The F_fit geometry produces trajectories that have the most commonly observed trajectory pitch, calculated as V/Ω, further supporting the quantitative agreement between our model and experiment. The calculated overlay of images from trajectory for the flagellar geometry F_fit shown in Fig. 3B is comparable to the observed trajectory in Fig. 1A.

In addition to the helical bacterium shown in Fig. 1A, we also performed quantitative modeling of the rod-shaped mutant in PGM (Fig. 1D) as well as the helical bacterium and the rod-shaped mutant in BB10 (Fig. 2, A and B, respectively). We used the measured body parameters in Table 1 in combination with a range of flagellar bundle geometries as previously described (see Table 2 for specific geometric parameters). As in the previous case, the observed swimming speeds lie within the minimum and maximum values obtained by varying flagellar geometries. For the rod-shaped mutant in PGM (Fig. 3E), the best fit to observed speeds is obtained with the flagellar bundle at 30° from the body axis. For the bacteria in BB10 (Fig. 4), the best fits to observed speeds are obtained with the flagella at 50° and 40° from the helical axis for the rod-shaped bacterium swimming as a pusher (forward) and puller (reverse), and 30° and 5° for the helical bacterium swimming as a pusher and puller, respectively. Error bars for the calculated swimming speeds are the propagated uncertainty from errors in measured body parameters in Table 1. Note that the large errors in experimental frequencies for the Δcsd6 bacterium arise from the slower frame rate of the videos in that case. The slopes of the fitted lines in Figs. 3 (C and E) and 4 (A and B) correspond to V/Ω and can be used to compare swimming speeds at the same rotation rates. In our calculations, we assume that the flagellar bundle has a fixed orientation relative to the cell body during swimming, which results in a linear relationship between V and Ω. Deviations from linearity in the experimental data indicate that the flagellar bundle orientation relative to the cell body may vary in time along the trajectory.

Fig. 4. Comparison of numerical model to experiment for bacteria in broth.

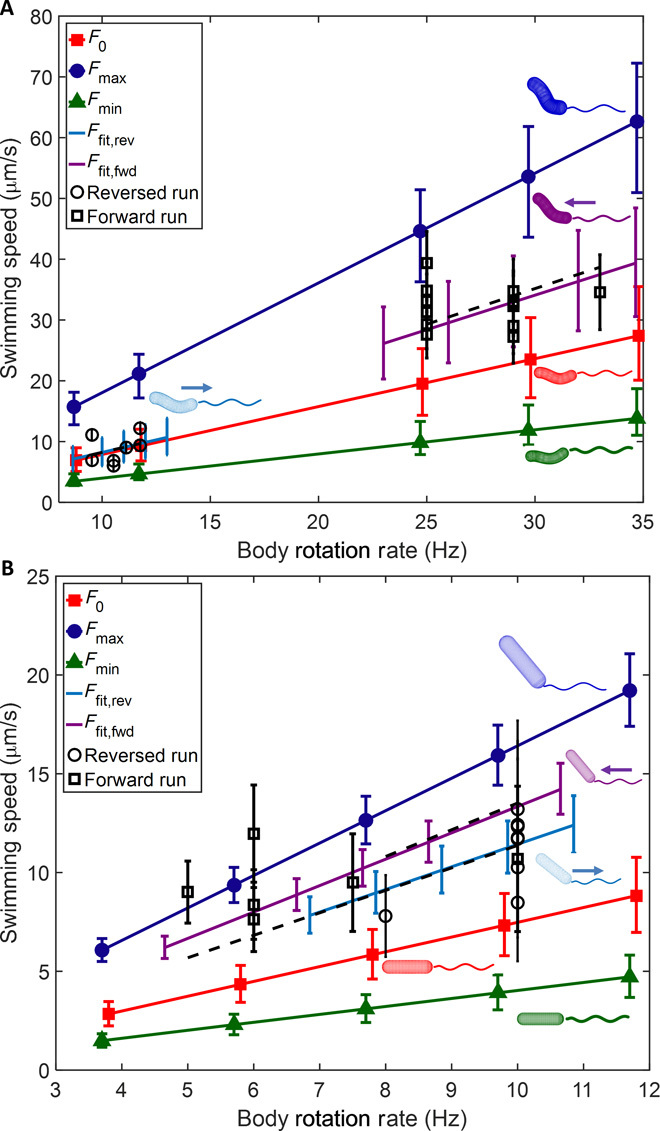
(A) Swimming speed calculated for LSH100 helical WT trajectory from Fig. 2A using measured cell body geometry and different flagellar geometries, which are shown next to each line. Isolated symbols are experimental observations from trajectory. (B) Swimming speed calculated for LSH100 rod-shaped mutant Δcsd6 trajectory from Fig. 2B using measured cell body geometry and different flagellar geometries, which are shown next to each line. Isolated symbols are experimental observations from trajectory. All parameters used for these models are described in Tables 1 and 2.

Effect of body helicity on swimming speeds

The above results provide quantitative validation of the numerical model, so we next use the numerical model to explore the effect of body helicity on swimming speeds. Although our experimental observations must only focus on individual examples, the numerical model allows us to continuously vary geometries. Numerical modeling circumvents the experimental difficulty of ensuring that flagellar geometries and cell body diameters are the same in comparison to helical and rod-shaped bacteria. To test the propulsive effect of the helical cell body, we first compare the swimming speed of helical and rod-shaped H. pylori cells with fixed flagellar geometry. In the following, we report speeds and angular velocities in nondimensional units by normalizing by T/(μX_f ²) and T/(μRX_f ²), respectively, where T is the motor torque, R is the flagellar helical radius, and X_f is the flagellar axial length. This choice of normalization amounts to keeping torque constant, as appropriate for flagellar motors under normal operating conditions, and provides a way to directly evaluate the effect of cell body shape on swimming speeds. In addition, the length scale X_f is derived from the flagellum and so remains constant as cell body geometry is altered.

To investigate the effect of cell body helicity on swimming speed, we compare three scenarios (Fig. 5A, inset): (i) the actual geometry with left-handed flagellum and right-handed cell body, (ii) a geometry with left-handed flagellum and left-handed cell body, and (iii) a geometry with left-handed flagellum and rod-shaped (nonhelical) cell body. For the helical cell body, we use the mean value of the helical radius (0.22 μm), pitch (2.4 μm), and body diameter (0.58 μm) (28). For the rod-shaped cell body, the pitch is 0 and other geometrical values are the same as the helical cell body. Figure 5A shows the swimming speed as a function of varying cell body axial length for these three scenarios. As expected, right-handed cell bodies have faster swimming speeds. The difference between swimming speeds for the left- and right-handed cell bodies is always less than 30%, whereas the swimming speed of the cylindrical cell body is usually between them. The inset in Fig. 5A shows the percent difference between the swimming speeds of left- and right-handed cell bodies. Typically, the cylindrical cell body has a swimming speed closer to that of the right-handed cell body (<10% difference) and further from that of the left-handed cell body (<20% difference). Note that because the geometry of the flagellum remains constant for all three cases, there is no overall symmetry relation between the left- and right-handed cell body scenarios, and the swimming speed of the ellipsoidal cell body is not expected to lie exactly in between that of the left- and right-handed cell bodies. These results support the idea that the effect of the body helicity on propulsion is quite small relative to a cell with a nonhelical geometry.

Fig. 5. Effect of body helicity on propulsion.

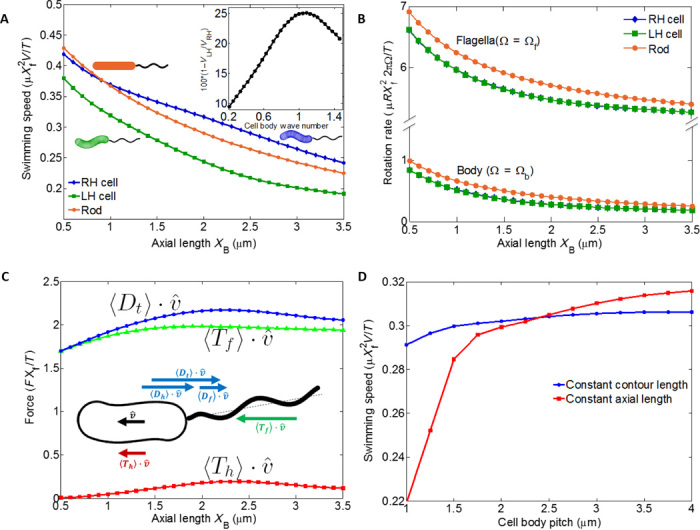
(A) Nondimensional swimming speed versus axial length for constant torque. Comparison between cell bodies of opposite helicity [blue/diamonds, right-handed (RH); green/square, left-handed (LH)] and a rod-shaped cell body (orange/circles) reveals the effect of helicity on swimming speed. Inset: Percent difference between swimming speeds for left- and right-handed cell bodies. (B) Nondimensional cell body rotation rate for different axial lengths. The body rotation rate is an order of magnitude slower than the flagellar rotation rate. Both rotation rates are virtually the same for RH and LH cells, as seen by the overlapping blue and green symbols. (C) Average swimming direction component of total drag and estimated thrusts from cell body and flagella. (D) Nondimensional swimming speed as a function of cell body pitch, which varies the helicity of the cell body. In the two curves, either cell body contour length or cell body axial length is kept fixed.

In addition to the direct comparison between the helical and rod-shaped bacterium presented above, we also examine our calculations relative to previous results comparing speed distributions for rod-shaped Δcsd6 and helical WT populations of the LSH100 strain (28). The measured speed distributions indicate that the rod-shaped mutants swim with an average swimming speed of ~10% slower, which is not too far from the result shown in Fig. 5A where the cylindrical body swimming speed is about 6% lower than that of a helical cell with a right-handed body. Because the swimming speed variation in the populations would be more strongly affected by variations in the number of flagella, this suggests that both the rod-shaped mutant and helical WT populations have similar distributions of number of flagella, as was confirmed from TEM measurements in (28). In addition, Martinez et al. (28) used RFT to calculate speed and found that the speed monotonically decreases with increasing length and increasing helical radius, whereas it showed a nonmonotonic dependence on pitch, increasing at low values of pitch and decreasing slightly for high pitch. These trends are the same as obtained here for the RSM calculation (Fig. 5, A and D, for constant contour length). However, the RFT predicted a much larger effect of helicity on speed, with the helical cell swimming about 40% faster than the rod [modeled as an ellipsoid (20)]. In contrast, RSM results are quite close to the observed speed increase of 10% for helix versus rod.

Little thrust produced by slowly rotating cell body

Physically, the small amount of cell body propulsion can be explained by the relatively small rotational speed of the cell body as compared to the flagella. Figure 5B shows the rotation rate for both the flagella and cell body for the scenarios in Fig. 5A. In all cases, the cell body rotation rate is less than ¹/₁₀ of the flagellar rotation rate (comparable within errors to the experimentally observed ratio of cell body to flagellar rotation rate shown in Fig. 1), implying that there is limited ability for the cell body to generate thrust. Because of hydrodynamic interactions between the cell body and flagellum, it is not possible to clearly define which portion of the total thrust arises from the cell body and flagellum separately. However, thrust and drag can be estimated from a model that ignores the hydrodynamic interactions between the cell body and flagellar bundle. We calculate the force and torque on the body and flagellar bundle separately using the RSM to calculate resistance matrices that express the forces and torques in terms of their linear and rotational velocities (48). Imposing the kinematic constraint of a fixed bundle-cell orientation and net force and torque balance yields swimming velocities and body rotations that are qualitatively in agreement to the full RSM calculations (see the Supplementary Materials for details).

In Fig. 5C, we plot the components of estimated total drag, flagellar thrust, and cell body thrust in the swimming direction as a function of axial length for the case of right-handed cell body and left-handed flagellum. In accord with the expectations arising from the smaller rotation rates of the cell body compared to the flagellum, the cell body thrust is estimated to be only about 15% of the flagellar thrust. Because of the net force constraint, the sum of the thrust from the cell body and flagellar bundle equals the total drag. Thus, the helicity of the cell body (which leads to thrust) should not affect swimming speeds through propulsion by more than that percentage.

Drag-dominated effect of cell body geometry on swimming speed

If the cell body shape does not affect the swimming speed through propulsion, then what dominates the changes in swimming speeds observed in Fig. 5A? In Fig. 5A, the dominant trend is that swimming speed decreases (by a factor of about 2) as the axial length increases. The trend in swimming speed can be explained by the following: for constant prescribed motor torque, the flagellar rotation rate should be relatively constant, yielding an approximately constant flagellar thrust and, hence, nearly constant total thrust, as apparent in Fig. 5 (B and C). The velocity is set by balancing the total thrust against the total drag, both of which are linearly related to the swimming velocity (Eq. 7 in the Supplementary Material). Thus, changes in the swimming speed are primarily due to changes in the translational resistance of the cell body, which increases with increasing axial length of the helix for fixed pitch, consistent with the results of Fig. 5A. Having the cell body affect swimming speeds through drag is the most commonly considered situation for bacteria as well as for sperm (4, 49, 50).

In addition to investigating the effect of cell body helicity by comparing left-handed, right-handed, and rod-shaped cell bodies, we can change the helical character of the cell body by varying the helical pitch: a small pitch yields a very tight helix, whereas a large pitch yields a loose helix. The resulting swimming speeds are shown in Fig. 5D. The blue curve (circle symbols) is the swimming speed versus pitch for constant arc length; the swimming speed increases by less than 5% as the pitch varies by a factor of 4. The small change in swimming speed suggests that helicity does not appreciably affect swimming speed. On the other hand, if the axial length of the helix is kept fixed instead of keeping the arc length of the helical cell body fixed (red curve, square symbols), the swimming speed increases by nearly 50% over the same range of pitches. However, changing the pitch changes not only the helical character of the geometry but also the quantities, such as rotational and translational drag of the cell body. Our results are consistent with the hypothesis that changes in drag are the dominant contributors to changes in swimming speed: translational drag increases with increasing contour length of the cell body, which increases with decreasing pitch for fixed axial length (red curve), whereas translational drag is relatively constant with pitch for fixed contour length of the cell body (blue curve).

Martinez et al. (28) also studied three different helical strains varying in shape parameters and found that some strains differed in average swimming speed by as much as a factor of 2. However, these observations cannot be directly compared to our calculation of dependence of speed on length or pitch of helical bacteria because these strains not only varied in their morphological parameters but also had a different number of flagella, which varied within each population as well. In accord with our investigation here, we believe that the latter may have a larger effect than variation in shape/size, as was observed in the experiments of Martinez et al. (28) by examining mutants with varying numbers of flagella. Such observations highlight the complicated variations within populations of a given bacterium and differences among strains, which make direct experimental evaluation of the changes in swimming speed due to cell body shape difficult. Even measures such as V/Ω should not be used to definitively compare swimming efficacy. Indeed, although Table 1 shows that V/Ω of the forward-swimming helical cell is equal within experimental error to that of the rod-shaped mutant bacteria in broth and that V/Ω of the forward-swimming helical cell is faster than that of the rod-shaped mutant in PGM, when we performed apple-to-apple comparisons by calculating swimming speeds of a rod-shaped bacterium with the same body diameter, length, and flagellar orientation as the helical bacterium (or vice versa), we found up to 50% differences in V/Ω. However, examining the constant-torque swimming speed between each rod-shaped/helical pair revealed less than 15% differences, in agreement with the calculations presented above.

Comparison to other bacteria species

The effect of propulsion arising from cell body rotation was also recently examined for the curved bacterium C. crescentus by Liu et al. (9). In that paper, the relative orientation of the cell body to the swimming trajectory is shown to affect swimming speeds, and it is hypothesized that tilted cell bodies significantly contribute to propulsive thrust. In contrast, our results suggest that helical cell bodies produce little propulsive thrust. Because helical cell bodies would be expected to have more propulsive thrust than the slightly curved cell bodies of C. crescentus, we reexamined the model of Liu et al., which presents a decoupled model treating the cell body as a rod-shaped body tilted from the flagellar axis by an angle θ. The resistance matrix for the cell body depends on the tilt angle θ and contains an off-diagonal term ϵ_c, which is nonzero when θ ≠ 0, describing cell body propulsion arising from rotation, and diagonal terms σ_c and τ_c, describing the cell body rotational drag arising from rotation or cell body translational drag arising from translation, respectively. In Fig. 6, we regenerate Liu et al.’s (9) Figure 4 for cell mobility versus precession angle, plotting the speed normalized by cell body rotation rate and cell body length, [K = V/(ΩL) = (bτ_c + ϵ_c)/(σ_c + c + bϵ_c)], which is Eq. 4 in the work of Liu et al. (9). The precise parameters we used are the following: $\mathit{L}=\mathrm{2 }\mathrm{\mu }\mathrm{m},\mathit{b}=\mathrm{1.1 }\mathrm{\mu }{\mathrm{m}}^{-1},\mathit{c}=\mathrm{0.65 }\mathrm{\mu }\mathit{m}\times 4\mathrm{\pi }\mathrm{\mu },\frac{{\mathit{c}}_{\perp }}{{\mathit{c}}_{\parallel }}=1.4,{\mathit{C}}_{\mathit{s}}=4\mathrm{\pi }\mathrm{\mu }, \text{and} 2\mathit{R}=\mathit{L}\text{sin}(\mathrm{\theta })$.

Fig. 6. Nondimensional swimming speed for C. crescentus predicted from flagellar thrust only (red) and cell body thrust only (green) compared to swimming speed predicted by model in Liu et al. (9).

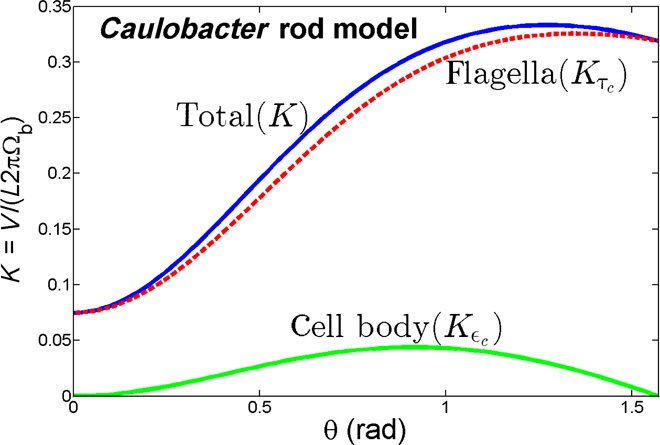
In Fig. 6, we examine the relative contribution of cell body propulsion by also plotting K_τc = bτ_c/(σ_c + c), which ignores the contribution of the cell body propulsion by setting ϵ_c = 0. It is apparent that the dependence of swimming speed on tilt angle is largely captured even without considering cell body propulsion. Furthermore, we also plot K_ϵc = ϵ_c/(σ_c + c + bϵ_c), which isolates the contribution of the cell body propulsion by setting τ_c = 0. This yields only a small variation of swimming speed, in accord with our results for H. pylori.

DISCUSSION

Our overall conclusion is that helical shape adds only a small advantage in motility. The results reported here and the earlier studies of Liu et al. (9) are consistent with the interpretation that cell bodies affect swimming speeds primarily through changes in rotational and translational drag rather than through changes in the cell body propulsion. This general statement should hold true when the propulsive thrust is largely generated by an external flagellum or flagellar bundle; on the other hand, in cases where propulsion is generated by cell body deformations, such as Spiroplasma or Spirochete bacteria, clearly the helicity of the cell body will play a dominant role in thrust. Likewise, the helicity of artificial swimmers where rotation rates can be controlled by external fields also plays a large role in thrust (51–54). In this manuscript, we have so far focused on swimming speed rather than efficiency because bacteria that live in the digestive tract are likely not limited by the power output needed for locomotion. However, for bacteria in other environments, such as marine bacteria, nutrient scarcity and higher swimming speeds may select for efficiency rather than speed. In the Supplementary Materials, we show the efficiencies of bacteria (defined as work done to translate the cell body divided by total power expended; Eq. 12 in the Supplementary Material) with the right-handed, left-handed, and rod-shaped cell bodies examined in Fig. 5A. We find that changes in efficiency are well-accounted for by the change in swimming speed, rather than changed resistance or changed power expended as the geometry varies. Because the work to translate the cell body scales as speed squared, one may expect that the 10% changes in swimming speed between rod and helical cell bodies would lead to larger changes in efficiency of a factor of ~1.2 (= 1.1² ), and 30% changes in swimming speed between left- and right-handed cell bodies would lead to changes in efficiency of a factor of ~1.7, which may be enough to play an important role in those bacteria that optimize efficiency and perhaps gain a fitness advantage in evolutionary terms. Furthermore, relatively small changes in swimming speeds may have large effects on chemotactability (1, 2, 55), which could be another way that the effects of body shape could be selected for.

To summarize, we have performed experiments and modeling to answer how much additional propulsion can be added by cell body shape, obtaining both quantitative results for H. pylori as well as a mechanistic, physical understanding of the dominant effects of cell body shape on propulsion. We show that bacteria rotation rates can be determined using readily available 2D microscopy tracking methods with fast time-resolution and high magnification (100×) phase-contrast microscopy along with a shape analysis program. More specialized 3D tracking microscopes are not essential, although they enable observation of longer tracks. We observed that the alignment angle of the 2D image of the cell precesses as the cell rotates about an axis aligned at a nonzero angle relative to the flagella, producing a helical trajectory, that is, proving that Helicobacters do indeed swim in a corkscrew fashion in a solution. However, this type of motion is not unique to the helical cell; rod-shaped cells also precess as they swim, in agreement with previous observations of other bacteria, such as E. coli (56) and Bacillus subtilis (37). The images of the helical-shaped bacterium change in shape and those of the rod-shaped bacterium change in length, further enabling us to visualize the rotation of the cell body.

We were also able to image the rotation of the flagellar bundle in a few bacteria in PGM and directly show that the rotation of the cell body is considerably slower than that of the flagella; the body rotation rate was one-sixth of the flagellar rotation rate for the bacterium swimming in PGM solution at pH 6. As the flagella rotate to provide thrust, the right-handed cell body counter-rotates in the opposite direction to produce net zero torque at the flagellar pole. Because the direction of the thrust is opposite for the right- and left-handed helices rotating in the same sense, it has been suggested that the helix of the cell body is right-handed rather than left-handed to provide additional propulsive thrust in the swimming direction. The sense of rotation of the flagella and cell body reverses on a reversal, implying that during both pushing (forward motion) and pulling (backwards motion), the propulsive flagella have the same left-handedness. Similar run-reverse motion and precession of the cell could also be seen for the rod-shaped Δcsd6 mutant, implying that this type of motion is not unique to helical bacteria, but rather it is similar to the motion previously observed in C. crescentus using a 3D tracking microscope.

Our quantitative measurements of the shape and speed of individual bacteria enable direct comparison and validation of theoretical models; previous experiments only provided indirect comparisons based on separate measurements of shape and speed distributions from a large population of bacteria. With the validated model, we were able to predict the effects of varying body helicity, length, and diameter, as well as flagellar configuration on swimming speeds and trajectories. Because of the relatively slow rotation of the cell body compared to flagella, we found that the body shape makes a small contribution to propulsive thrust—in agreement with our experimental observations—and swimming speed variations due to body shape are dominated by changes in translational drag due to length and diameter variations. Because helical cell bodies might be considered the strongest candidate for propulsion due to cell body, our results imply that quite generally, swimming speeds of flagellated bacteria are little affected by body geometry.

MATERIALS AND METHODS

H. pylori culturing

All experiments reported in this paper were done on the LSH100 strain of H. pylori, a derivative of the human clinical isolate G27 (38, 57) and its isogenic mutant with a straight rod shape, LSH100 Δcsd6 (26, 28). The culture procedure was identical to that used by Martinez et al. (28) and is described briefly here. Frozen aliquots of bacteria were grown on Brucella agar plates with 5% horse blood (BD Biosciences) for 2 days, after which, they were restreaked onto new plates. After 2 to 5 days, the grown cells were transferred into BB10 containing Brucella broth (BD Biosciences) with 10% heat-inactivated fetal bovine serum (GIBCO) and left to grow overnight under constant agitation. Both cultures in agar plate and BB10 were kept in an incubator at 37°C under microaerophilic conditions (6 to 16% oxygen and 2 to 10% carbon dioxide; BD Biosciences GasPak EZ Campy Container System Sachets).

Preparation of PGM

PGM was isolated from mucosal scrapings of pig stomach epithelium and purified by Sepharose CL-2B column chromatography followed by density gradient ultracentrifugation, as described by Celli et al. (19). Lyophilized PGM was weighed, and the appropriate amount of PGM was dissolved in sterile H₂O to prepare a solution (15 mg/ml). PGM solution was allowed to hydrate and equilibrate for 48 hours at 4°C, and an appropriate amount of 0.1 M phosphate-succinate buffer (pH 6) was added before use. A more detailed procedure is in the work of Martinez et al. (28).

Bacterial suspension in different media

Bacteria were removed from liquid culture during the exponential phase of growth (0.4 to 0.7 optical density at 600 nm) and diluted in BB10 or PGM solution (with buffer at pH 6) to produce 10% bacteria mixture by volume. To get adapted to the new environment, the bacteria in PGM were left in the incubator at 37°C for 45 min and used immediately. A more detailed procedure is in the work of Martinez et al. (28).

Microscopy and imaging

Bacteria samples were pipetted onto standard microscope slides with a 9-mm-diameter, 120-μm thick secure spacer (SecureSeal Imaging Spacers, Sigma-Aldrich) and sealed with a coverslip. The bacteria were imaged at room temperature using an Olympus IX70 inverted microscope. We were careful to focus in the center of the spacer to avoid swimming surface effects (58). We used a 100× phase-contrast lens with a numerical aperture (NA) of 1.25 and with Zyla 5.5 sCMOS Andor camera (6.5 μm per pixel) at 200 or 100 fps for most of the measurements. One series of measurements for the rod-shaped mutant in BB10 was done using a 40× phase-contrast lens with an NA of 0.65 and with QImaging Rolera CMOS camera (3.63 μm per pixel) at 30 fps. The 40× and 30-fps imaging conditions enabled us to track the bacterium for a longer time but with smaller spatial and temporal resolution than the 100× at 200 or 100 fps.

Cell shape analysis

The selected supplementary movies were individually and manually cropped to contain only one bacterium using ImageJ. The shape (which includes the cell body contour, diameter, and cell centerline) of each bacterium was extracted and aligned using the software program CellTool (36). The end-to-end axial length was measured as the distance between the front and back contour points of the aligned bacterium contour. For helical bacteria, the aligned centerline was imported to MATLAB v8.3.0.532 and fitted using a sine function, $\mathit{y}={\mathit{R}}_{\mathit{b}}(\frac{2\mathrm{\pi }}{{\mathit{P}}_{\mathit{b}}}\mathit{x}+\mathrm{\delta })$, from which the body helical pitch (P_b) and body helical radius (R_b) were obtained (28). Here, δ is a parameter that allows the sine function to have a phase shift. The cell shape parameters, reported in Table 1, are from the most in-plane image, and the errors were calculated as $\sqrt{2}\left(\frac{\text{pixel size of camera}}{\text{lens magnification}}\right)$.

Body rotation rate and sense of rotation

The body rotation rate for the helical bacterium was measured using CellTool to monitor the vertical change in the center point of the centerline of the aligned bacterium contour over time. CellTool saves the alignment angle of each aligned contour, so an independent measure of the body rotation rate was also obtained by monitoring the change in the alignment angle of the bacterium. Only the alignment angle method was used for determining the body rotation rate of the rod-shaped bacteria. The periodicity in both methods was obtained by measuring the time between two maximum points and showed consistent results. In addition to monitoring the alignment angle and change in vertical position of the center point, we also tracked a point at the head of the bacterium and one at the flagella junction pole, as shown in fig. S1. These points also give the same period of rotation. The rotation rate reported in Table 1 is an average of the rotation rates of each revolution during one run, and the error is the SD. At 30 fps, it was not possible to estimate the SD of the body rotation rate of fast rotating bacteria because the time resolution was not large enough to obtain the small variations in rotation rate over the duration of the track.

The sense of rotation can be obtained because of the helical shape of the body. Depending on the sense of rotation, the 2D projections over one revolution will go through a different sequence of shapes, analogous to a sinusoidal phase shift. When the bacterium is swimming as a pusher, its right-handed body rotates and the 2D shape projection sequence is given by Fig. 7A, and when it swims as a puller, the shape projection sequence is given by Fig. 7B.

Fig. 7. Method to obtain the sense of rotation of helical body of the bacterium.

(A) Forward run: Sequence of shape projections, a few frames apart, of the right-handed helical body rotating one way. (B) Reverse run: Sequence of shape projections, a few frames apart, of the right-handed helical body rotating the opposite way. Both sequences are obtained from the same bacterium before and after reversal, swimming in BB10 (from movie S4, same as Fig. 2A). The position of the flagellar junction is marked as J. Scale bars, 1 μm.

The flagellar bundle handedness of both pusher/puller cases can be inferred if one knows the localization of the flagellar bundle, sense of body rotation, and swim direction. To swim in the direction shown in Fig. 7 (A or B), the flagella have to generate a thrust in that same swimming direction. This thrust can be accomplished by a right-handed flagellar bundle rotating in the same sense as the body rotates or by a left-handed flagellar bundle rotating in the opposite direction of the body rotation. As mentioned before, the flagellar bundle has to rotate in the opposite direction of the body to balance torque. Consequently, the flagellar bundle has to be left-handed in both pusher and puller cases.

Tracking of bacteria and measuring 2D speed

The centroid of the bacterium obtained using CellTool for all frames provided the position over time of the swimmer and therefore was used for generating the tracks (shown in Fig. 1D). The same bacterium was also tracked using PolyParticleTracker (59), which generates tracks, as shown in Fig. 1B. Both methods show consistent results. Even though the bacterium is free to swim in a 3D volume, the supplementary movies only capture the bacterium swimming on a horizontal plane and thus measure the 2D speed. The distance traveled during one revolution was divided by the period of rotation to obtain the speed for each full revolution. The speed reported in Table 1 is given by the average of the speed per revolution during the run, and the error is the SD. The programs also give the instantaneous speed of the bacterium calculated from the displacement between successive frames.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/11/e1601661/DC1

movie S1. Motility of LSH100 WT (helical) H. pylori swimming in PGM (15 mg/ml) imaged with 100× lens, 200 fps.

movie S2. Flagellar bundle visualization.

movie S3. Motility of LSH100 Δcsd6 (rod mutant) H. pylori swimming in PGM (15 mg/ml) imaged with 100× lens, 100 fps.

movie S4. Motility of LSH100 WT (helical) H. pylori swimming in BB10 imaged with 100× lens, 200 fps.

movie S5. Motility of LSH100 Δcsd6 (rod mutant) H. pylori swimming in BB10 imaged with 40× lens, 30 fps.

fig. S1. Head and flagellar junction trajectories of LSH100 helical H. pylori swimming in PGM (15 mg/ml) (movie S1).

fig. S2. Swimming speed versus axial length, calculated by decoupled model.

fig. S3. Swimming power versus axial length for right- and left-handed helical cells and rod-shaped cell body.

Numerical calculation methods

References (60, 61)