Topological surface states in PbTaSe2 show fully gapped superconductivity, making it a potential topological superconductor.
Keywords: Topological superconductor, non-centrosymmetric superconductor
Abstract
The search for topological superconductors (TSCs) is one of the most urgent contemporary problems in condensed matter systems. TSCs are characterized by a full superconducting gap in the bulk and topologically protected gapless surface (or edge) states. Within each vortex core of TSCs, there exists the zero-energy Majorana bound states, which are predicted to exhibit non-Abelian statistics and to form the basis of the fault-tolerant quantum computation. To date, no stoichiometric bulk material exhibits the required topological surface states (TSSs) at the Fermi level (EF) combined with fully gapped bulk superconductivity. We report atomic-scale visualization of the TSSs of the noncentrosymmetric fully gapped superconductor PbTaSe2. Using quasi-particle scattering interference imaging, we find two TSSs with a Dirac point at E ≅ 1.0 eV, of which the inner TSS and the partial outer TSS cross EF, on the Pb-terminated surface of this fully gapped superconductor. This discovery reveals PbTaSe2 as a promising candidate for TSC.
INTRODUCTION
The helical spin-polarized electrons on the surface of topological insulators (TIs) can host exotic excitations, such as Majorana fermions (1–6), when a topological surface state (TSS) goes superconducting. Two primary proposals for realizing such a topological superconductor (TSC) are (i) spin-triplet pairing bulk superconductivity (1, 2, 4) and (ii) superconducting TSSs induced by the proximity effect through an s-wave superconductor (3, 7). A chiral p-wave superconductor is a natural choice as a bulk TSC, but electrons rarely form spin-triplet Cooper pairs in real materials. The order parameter of the prime candidate Sr2RuO4 remains under debate (8, 9), whereas the inhomogeneity within superconducting doped TIs hinders the confirmation of Majorana bound states (MBSs) at the vortex cores (10). Therefore, searching for a TSC remains one of the grand challenges in current TI research. Noncentrosymmetric superconductors (NCSs) offer one of the most promising routes to realizing TSCs (11, 12). Antisymmetric spin-orbit coupling (SOC) due to the broken inversion symmetry can lift spin degeneracy, giving rise to topological phases and allowing the mixing of spin-triplet and spin-singlet pairing channels. Hence, an NCS with dominating spin-triplet pairing can become a bulk TSC, whereas an NCS with dominating spin-singlet pairing in the bulk can still lead to a TSC on the surface if the fully gapped superconductivity were induced on TSSs. An NCS with a superconducting TSS is greatly desired to provide the required platform for TSC.
Noncentrosymmetric BiPd has been previously shown to exhibit a conventional Bardeen-Cooper-Schrieffer (BCS) s-wave superconducting state and TSSs above TC; however, TSSs in BiPd are absent at the Fermi level (EF) and are thus unable to become a TSC (13, 14). Similarly, the observation of TSSs in centrosymmetric superconducting β-PdBi2 also attracts great interest (15). Parity mixing of pair potential may occur near the surface because the inversion symmetry is broken at the surface. Furthermore, the presence of TSSs at EF in the normal state of β-PdBi2, determined by angle-resolved photoemission spectroscopy (ARPES) (15) and quasi-particle scattering interference (QPI) imaging (16), combined with the observation of fully gapped superconductivity in the bulk (16–18), makes β-PdBi2 a great candidate for TSC. The zero-energy bound states are absent at vortex cores of single-crystal samples (17); however, they have been observed on epitaxial β-PdBi2 thin films (19), indicating the possible existence of MBSs. This difference could be due to defects scattering or different surface/sample preparations, thus calling for further experiments. Recently, PbTaSe2 has emerged as a strong candidate for TSC (20). ARPES measurements observe topological nodal lines around and two surface bands (21). However, the existence of a Dirac point and the spin texture of these two surface bands have not yet been confirmed because the Dirac point energy (ED) is located at several hundred millielectron volts above EF and, hence, not accessible to ARPES. For the bulk superconducting state, although all recent bulk measurements indicate that PbTaSe2 is likely a conventional BCS s-wave superconductor (20, 22–25), it has been proposed that the superconductivity on TSSs induced by the proximity effect in PbTaSe2 can be stronger than that in TI/s-wave superconductor heterostructures (26). Therefore, it is critically important to confirm the existence of a superconducting TSS and to investigate the potential signature of any MBS in PbTaSe2.
Here, our density functional theory (DFT) calculations reveal that two TSSs with opposite helical spin polarization exist within the bulk gap at , touching at ED ≅ EF + 1.0 eV. The inner TSS is fully isolated from the nearby bulk states at EF, whereas the outer TSS heavily merges with the bulk states at EF. The characteristic wave vectors and their energy dispersion measured by our QPI imaging at the normal state show remarkable agreement with our theoretically calculated spin-polarized TSS band structures on PbTaSe2. The tunneling spectrum at T = 0.26 K reveals a full superconducting gap, indicating that the TSS becomes superconducting with bulk. Our vortex imaging also observes the zero-energy bound states at superconducting vortex cores. Our results demonstrate that stoichiometric PbTaSe2 is a strong candidate for TSC because its TSS can host Cooper pairs and becomes superconducting, providing a quintessential playground for nontrivial band topology and superconductivity.
RESULTS
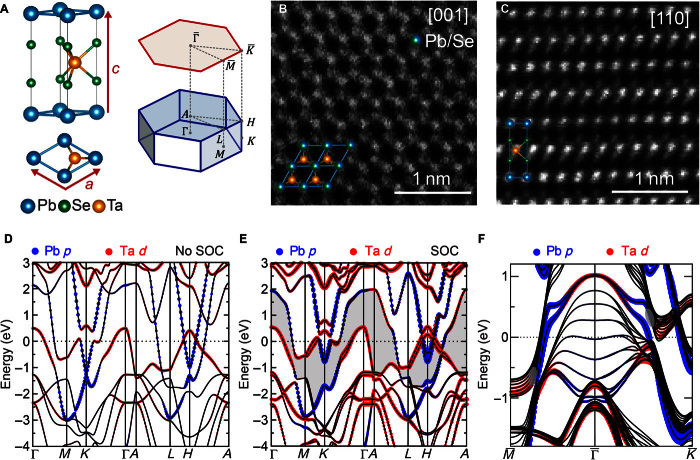
Our PbTaSe2 single crystals were grown by chemical vapor transport technique and exhibit a bulk superconducting transition at TC ~ 3.8 K [details are described elsewhere (23)]. The crystal structure of PbTaSe2 consists of alternating stacking of hexagonal 1H-TaSe2 and Pb layers (Fig. 1A). Within the TaSe2 layer, Ta atoms are suggested to reside at the same position within a unit cell (space group: ) (20), breaking the inversion symmetry. This is confirmed by our atomically resolved high-angle annular dark field (HAADF) imaging (Fig. 1, B and C, and fig. S1) in aberration-corrected scanning transmission electron microscopy (STEM), which unambiguously rules out the other possible crystalline structures reported in PbTaSe2 (23, 27). On the basis of our experimentally confirmed crystal structure, we carry out detailed DFT calculations for the bulk band structure and topological invariant. Our results on the bulk band structures with and without SOC (Fig. 1, D and E, respectively) demonstrate that SOC plays an important role in PbTaSe2, as previously reported (20, 26). A continuous gap throughout the Brillouin zone is present because of the gap opening by SOC, which is crucial for the topological property of PbTaSe2. Two groups of bands that lie below and above this continuous gap are completely separated from each other. In this case, the Z2 topological invariant is well defined regardless of the metallicity of the system (28). We use the method proposed by Yu et al. (29) to compute the Z2 invariant of the states below the continuous gap. The calculated Z2 = 1 reveals the necessity of TSSs of PbTaSe2. TSSs are further evidenced by the calculated surface band structure (Fig. 1F). The orbital decomposition of the surface Pb and Ta atoms reveals that two TSSs stem from Pb p orbitals, whereas Ta d orbitals also contribute significantly around the zone center. Apparently, the topological surface bands do not exhibit linear dispersion even in the vicinity of the crossing point at ED ~ EF + 1.0 eV at . Additional quadratic or cubic terms are required to describe the behaviors of Dirac electrons. Hereafter, we use “Dirac point” for brevity despite the nonlinearity. We note that the outer TSS, which represents the upper part of a Dirac cone, is present at EF because of this nonlinearity, and it strongly merges with the bulk states below E ~ 300 meV along and below E ~ −750 meV along , evident from the much smaller contribution of surface Pb atoms (gray circles in Fig. 1F). Consequently, only the inner TSS is well separated from the bulk states at EF, consistent with the Fermi surface revealed by ARPES (21). This is important because the odd number of TSSs at the Fermi surface is required for the stability of MBSs in TSC-related theoretical proposals (1, 2, 6, 7). The helical spin states of TSSs can be seen from the spin-decomposed band structures (fig. S2). From our DFT results, the TSS of PbTaSe2 is confirmed by the Z2 analysis and the fingerprints revealed in the surface band structure, consistent with a previous report (26). Experimentally, ARPES has been very successful in resolving the band structures in TIs. However, in the case of PbTaSe2, these calculated TSSs and the Dirac point are located above EF at , which is not accessible to ARPES. Thus, momentum-sensitive techniques that can probe both occupied and unoccupied states are required to resolve this issue.
Fig. 1. Crystal structure and calculated band structure.
(A) Crystal structure of PbTaSe2 and the Brillouin zone of bulk (blue) and the Pb-terminated surface (red). (B) The HAADF image projected along the c axis, overlapped with a crystal structure signifying Ta (Pb/Se) atomic columns. (C) The HAADF image along the [110] projection, revealing the characteristic Pb monolayer and 1H-TaSe2 cages of PbTaSe2. Calculated band structure of PbTaSe2 (D) without SOC and (E) with SOC. The size of blue and red dots indicates the Pb p and Ta d orbital contributions, respectively. Large SOC splitting can be observed in Pb p and Ta d bands. The gray-shaded area indicates the continuous gap. (F) The decomposed surface band structure on the Pb-terminated surface of PbTaSe2 shows the projection of the Ta d and Pb p orbitals of the surface atoms. The gray circles indicate where the outer TSS merges into the bulk conduction bands.
Spectroscopic imaging–scanning tunneling microscopy (SI-STM) is an ideal technique for investigating the calculated TSSs and superconductivity in PbTaSe2 by local density of states (LDOS) mapping in real space and QPI imaging in momentum space. Previous SI-STM and theoretical studies on topological materials have demonstrated that the band structures of TSS and the signature of its spin order can be visualized by QPI imaging (30–37). Our samples are cleaved in ultrahigh vacuum (UHV) at T < 20 K before SI-STM measurements. The cleavage plane is in between Pb and TaSe2 layers. A topographic image (Fig. 2A) shows a typical cleaved surface with several atomically flat terraces up to a few hundred nanometers. The step height between terraces is ~0.3 nm (Fig. 2B), comparable with the shortest distance between Pb and Se. Atomic-resolution STM topographic images taken at different terraces show two distinct surfaces. The lower area in Fig. 2A shows a hexagonal lattice (a ~ 0.34 nm) with atoms of 2 × 2 superstructure residing in between hexagons, consistent with the TaSe2 layer (Fig. 2C). We thus deduce this to be a Se-terminated TaSe2 layer. Our calculation shows that the 2 × 2 superstructure arises from the tiny shift in Ta atomic positions (fig. S3). In contrast, a topographic image taken at the higher area shows a hexagonal lattice (a ~ 0.34 nm) with a strong LDOS modulation from electronic surface states (Fig. 2, D and E). Because Pb p orbitals dominate TSSs near the bias voltage of topographic images, we identify this as a Pb-terminated surface. We further investigate LDOS in these two types of surfaces by differential tunneling conductance (dI/dV) measurements. Typical normalized spectra taken at Se-terminated and Pb-terminated surfaces at T = 0.26 K are shown in Fig. 2 (G and H, respectively). The spectrum acquired from a Se-terminated surface shows its metallic nature with increasing DOS below EF, which we associate with the contribution from bulk electronic states. In comparison, the spectrum taken at a Pb-terminated surface exhibits almost identical DOS but with two pronounced peaks at E ~ 0.5 eV and E ~ 0.95 eV, which are the signatures of a van Hove singularity due to the saddle point of TSSs near E ~ 0.5 eV and the local maxima at ED (Fig. 1F), respectively, indicating the existence of TSSs. Our tunneling spectra are also in agreement with our calculated surface-projected partial density of states (Fig. 2, G and H), affirming our surface identification. Pb p orbitals dominate these TSSs over the energy range of EF ± 0.5 eV (Fig. 1F). Even for the states close to the Dirac point where Ta d orbitals become significant, Pb p orbitals still have considerable contributions. Therefore, our QPI imaging will focus on the Pb-terminated surface to determine the TSS band structure.
Fig. 2. Topographic images and tunneling spectra.
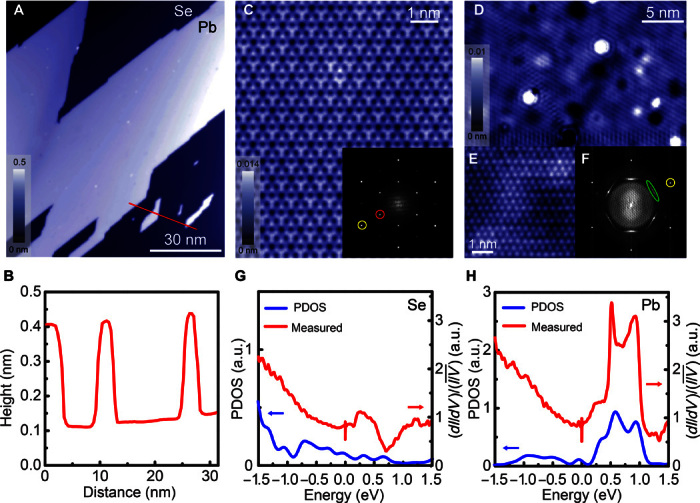
(A) Topography of PbTaSe2 showing atomically flat terraces and step edges (V = 100 mV and I = 2 pA). (B) The height profile deduced from the red line in (A). (C) The atomic-resolution topographic image on the Se-terminated surface (V = 10 mV and I = 300 pA). The inset shows the fast Fourier transform (FFT) of this topographic image. Yellow and red circles indicate the position of Bragg peaks and the peak of the 2 × 2 superstructure, respectively. (D) Topography on the Pb-terminated surface (V = 10 mV and I = 100 pA) shows strong LDOS modulation from QPI of TSSs. (E) The atomic-resolution topographic image on the Pb-terminated surface (V = −10 mV and I = 300 pA). (F) FFT of the topographic image in (D). Bragg peaks are marked by a yellow circle, and the dispersive signals from QPI are observed (green ellipse). The normalized tunneling spectrum and calculated partial density of states (PDOS) on (G) Se-terminated and (H) Pb-terminated surfaces, respectively (T = 0.26 K, V = 800 mV, I = 1 nA, and lock-in modulation = 0.5 mV). The superconducting gap near EF is not resolved clearly because of the large modulation in lock-in measurements. a.u., arbitrary units.
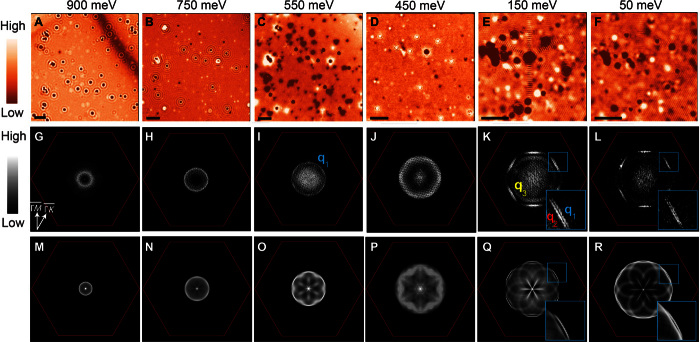
To resolve the k-space electronic structures by QPI imaging, we first measure energy-resolved differential conductance maps dI/dV(r, E = eV) on a Pb-terminated surface in the normal state (T = 6.0 K) with an energy range from E = −0.20 eV to E = 1.05 eV by using our homebuilt cryogenic UHV SI-STM (Materials and Methods). In Fig. 3 (A to F), we show simultaneous normalized dI/dV(r, E) maps at six different energies. It is apparent that the electron standing wave exhibits near-circular interference patterns at E ≳ 300 meV (Fig. 3, A to D), whereas sixfold symmetric patterns are visible at E ≲ 300 meV (Fig. 3, E and F). Then, we analyze the Fourier transform of dI/dV(r, E) maps as a function of energy, and we show dI/dV(q, E) maps at corresponding energies (Fig. 3, G to L). A q vector (q1) with a sharp circular closed contour is observed at E ≳ 500 meV (Fig. 3, G to I). Its length decreases with increasing energy and vanishes above E ~ 1.0 eV. From the helical spin texture of two TSSs and their energy dispersion, we deduce that q1 is the scattering vector connecting the opposite sides of two TSSs, which have the same in-plane spin orientation (Fig. 4A and fig. S4). When energy decreases from E ~ 500 meV to E ~ 300 meV, q1 becomes blurry and elongated (Fig. 3J), coinciding with the dispersion of both TSSs becoming flat and the out-of-plane spin components becoming larger, lifting the in-plane backscattering protection. When the energy is below E ~ 300 meV, another q vector (q2) is observed. Furthermore, both q1 and q2 disperse only along the direction with a sixfold symmetry below E ~ 300 meV (Fig. 3, K and L) because the warping effect on both TSSs (but helical spin polarization is still preserved) opens new scattering channels and the outer TSS overlapping with bulk states near suppresses QPI along the direction (Fig. 4B and fig. S4). A relatively isotropic q vector (q3) is also observed near EF (Fig. 3, K and L), which is due to intraband scattering from a bulk band at . In Fig. 3 (M to R), simulated dI/dV(q, E) images for these two TSSs at the corresponding energies appear to be in agreement with our measurements. In Fig. 4 (A and B), the scattering process of q1 and q2 is depicted on the constant energy contour plots of these TSSs, with calculated spin orientation near ED and at EF, respectively. The detail energy dispersion of three q vectors extracted from our QPI data along depicted in Fig. 4 (C and D) appears to be in remarkable agreement with our band calculation, and we can deduce that ED ~ 1.0 eV. Therefore, our QPI imaging demonstrates the signature of two TSSs with opposite helical spin polarization and the Dirac point in the unoccupied states of PbTaSe2, consistent with DFT calculations.
Fig. 3. Visualization of QPI on a Pb-terminated surface.
(A to F) A sequence of normalized differential conductance dI/dV(r, E) maps taken at normal state (T = 6 K). The field of view (FOV) of each image is adjusted to access the region of interest in q space. A larger FOV is required at higher energy near the Dirac point to resolve the smaller q vector. Scale bar, 10 nm (in each image). (G to L) The corresponding FFT of normalized dI/dV(r, E) maps taken in (A) to (F). (M to R) The simulated QPI images at the corresponding energy considering two topological surface bands, with band structures shown in Fig. 1F (details in note S4).
Fig. 4. Energy dispersion of topological surface bands by QPI.
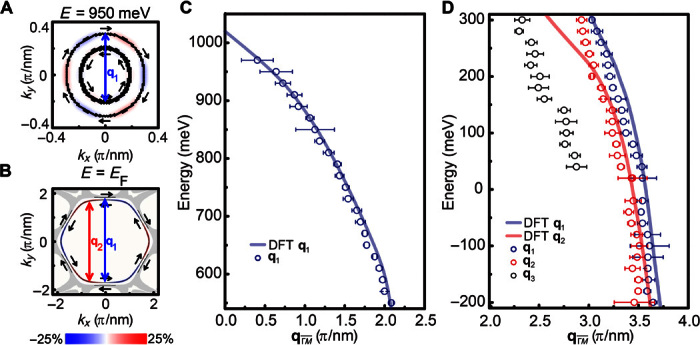
The calculated constant energy contours (CECs) of two TSSs with spin texture at (A) E = 950 meV and (B) EF. The black arrows represent the in-plane spin direction, and the blue/red contours show the sign and the magnitude of out-of-plane spin. The color scale indicates the ratio of out-of-plane spin to total spin polarization. The blue and red arrows in each image indicate the relation between topological surface bands with scattering vectors q1 and q2, respectively. The seemingly Rashba surface states are due to the unusual dispersion of the Dirac cone in Fig. 1F, in which the outer and inner CECs (upper and lower parts of the Dirac cone) exist at the same energy. The outer TSS and the bulk state strongly overlap below E ~ 300 meV around [gray regions in (B)], leaving a small portion near EF. The energy dispersion of (C) q1 from E = 500 meV to E = 1000 meV and (D) q1, q2, and q3 from E = −200 meV to E = 300 meV. Hollow circles are extracted from the measured QPI images along the direction, which are in agreement with the QPI dispersion obtained from our calculated topological surface band structure (solid lines). We do not extract the exact |q| in the energy range between 300 and 500 meV, in which blurry q1 occurs because of flat band dispersion and larger <Sz> in the TSS. q3 is associated with the intraband scattering on hole-like bulk bands at .
Next, we study the superconducting state of PbTaSe2 by temperature-dependent and magnetic field–dependent SI-STM measurements using our homebuilt 3He STM (Materials and Methods). The superconducting gap measured at T = 0.26 K does not show any spatial dependence on either Pb-terminated or Se-terminated surfaces (fig. S5). The representative tunneling spectrum reveals the fully gapped superconductivity (Fig. 5A). We then compare the tunneling spectrum taken by two STMs used in this study (fig. S7). The only noticeable difference in LDOS above and below TC is the opening of a full superconducting gap at EF, indicating that the superconducting gap opens on TSSs together with the bulk counterpart. By fitting our data with an isotropic BCS s-wave gap, the temperature dependence of superconducting gap exhibits a BCS-like behavior (Fig. 5, B and C). In addition, 2Δ/kBTC ~ 3.4 from our data is close to the BCS ratio of 3.5 and different from that of 4.3 in bulk Pb (38) and monolayer Pb on Si(111) (39), consistent with weakly coupled s-wave superconductivity by bulk measurements (20, 23, 24). The observed superconducting gap at TSSs in the presence of helical spin polarization shows that PbTaSe2 has the components necessary for realizing TSC (3, 7).
Fig. 5. Superconducting state and vortex imaging.
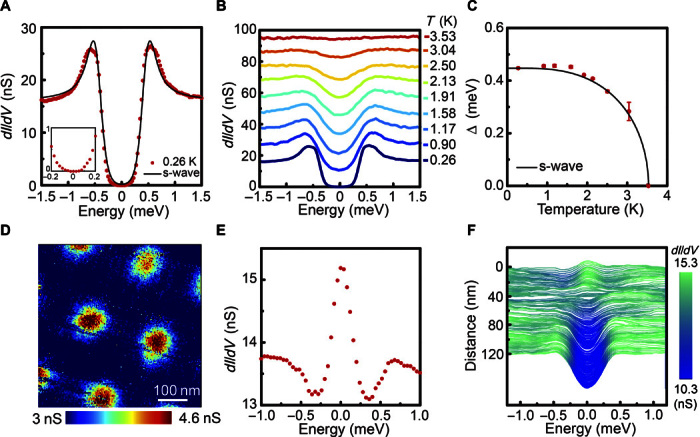
(A) The tunneling spectrum on the Pb-terminated surface at T = 0.26 K (V = 25 mV, I = 600 pA, and lock-in modulation = 50 μV). The black line is the result of a single BCS s-wave gap fitting (details in note S7). The inset shows the zoom-in of the spectrum between 0.2 and −0.2 meV. (B) Temperature evolution of a tunneling spectrum on the Pb-terminated surface. Each spectrum is shifted by 10 nS for clarity. (C) The temperature dependence of a superconducting gap. The black line represents the theoretical temperature dependence from the BCS theory. (D) Differential conductance map at EF shows the triangular vortex lattice, with an applied magnetic field of 0.05 T at T = 0.26 K (V = 10 mV, I = 60 pA, and lock-in modulation = 250 μV). (E) The tunneling spectrum at the vortex core shows the structure of a vortex bound state (V = 30 mV, I = 400 pA, modulation = 60 μV, applied magnetic field = 0.05 T, and T = 0.26 K). (F) The spatial dependence of a tunneling spectrum from the center of a vortex core toward the next nearest vortex core (V = 30 mV, I = 600 pA, lock-in modulation = 60 μV, applied magnetic field = 0.05 T, and T = 0.26 K).
A key question then is whether topological superconductivity indeed exists on the surface of PbTaSe2. The existence of MBSs at topological defects, such as vortices, would provide the definitive evidence by direct visualization of the vortex core states. Our vortex imaging at T = 0.26 K shows a nearly perfect triangular Abrikosov lattice (Fig. 5D) in a 550 × 550–nm2 field of view, from which we obtain the lattice constant of 239 nm with flux quanta Φ0 = 2.0 × 10−15 Tm2, consistent with the theoretical lattice constant of Abrikosov vortices of 218 nm at 0.05 T (fig. S8). To understand the detailed electronic structures of a single vortex core, we analyzed dI/dV(r, E) maps taken at several different magnetic fields. The vortex core exhibits a zero bias conductance peak (ZBCP), which can be the ordinary Caroli–de Gennes–Matricon (CdGM) bound state or the MBS (Fig. 5E). Although the MBS is predicted to dominate at vortex cores (26), the thermal broadening at T = 0.26 K overlaps the small energy-level spacing (Δ2/EF ~ 10−7 eV) of these vortex bound states, making it impossible to discriminate the CdGM bound state and the MBS (6). Owing to the difficulty of identifying the MBS by direct vortex imaging, the half-integer conductance quantization by point contact experiment or the thermal metal-insulator transition could provide alternative routes to detect the signature of Majorana fermions if PbTaSe2 is indeed a TSC (4). Recently, it has been proposed that spatial dependence of the vortex core bound state can be used as the signature of the MBS in Bi2Se3/NbSe2 heterostructures, within which a spin-polarized checkerboard pattern in LDOS is predicted (40, 41). The spatial dependence of LDOS along the line connecting two vortices is shown in Fig. 5F. The ZBCP decays as the superconducting gap emerges with increasing distance from the vortex core, which is identical with the spatial dependence of the vortex core state in topological trivial BiPd (13) and 2H-NbSe2 (42). It will also be of great interest to investigate this phase-sensitive quasi-particle excitation spectrum in the vicinity of vortex cores in PbTaSe2 by spin-polarized STM.
DISCUSSION
Here, we discuss the implication of our results for the realization of TSC in PbTaSe2. Bulk measurements have demonstrated PbTaSe2 to be a BCS s-wave superconductor with a full gap. The absence of a spin-triplet component in bulk superconductivity from the bulk measurements may be due to either the similar magnitude of the singlet and triplet components with the same sign (12) or the lack of strong electron correlations in PbTaSe2 (43). On the scenario of the superconductivity on the TSS induced by the proximity effect from bulk s-wave superconductivity, helical spin-polarized electrons on the TSS can pair into px + ipy symmetry and bound Majorana fermions in the vortices (3, 7). Thus, it is also essential to understand the nature of superconductivity on the TSS. For TI/s-wave superconductor heterostructures, if the proximity-induced superconductivity reaches the TI surface, the induced gap is expected to be smaller than the bulk gap because the pairing amplitude quickly decays with increasing distance between the TI surface and the interface (44). In contrast, for an intrinsic superconducting TI with bulk s-wave pairing, the induced gap magnitude is shown to be similar to the bulk gap (45). If we fit our tunneling spectrum with a model with two full gaps, we can obtain two gaps with comparable magnitudes. A larger superconducting gap on the TSS may also be induced as a result of parity mixing of the pairing potential enhanced by surface Dirac fermions (46). A tunneling spectrum on superconducting CuxBi2Se3 and SrxBi2Se3 also does not show an additional superconducting gap (10, 47, 48), which is proposed to be due to the doping evolution of the Fermi surface (46, 49). Meanwhile, recent nuclear magnetic resonance (50) and specific heat (51) measurements on CuxBi2Se3 report rotational symmetry breaking in spin rotation and superconducting gap amplitude, indicating topologically nontrivial superconductivity. Whether this also occurs in PbTaSe2 requires further investigation. In principle, bound states at magnetic and nonmagnetic impurities can be very helpful in determining the pairing symmetry of unconventional superconductors (52). Because no well-defined interface exists between TSSs and bulk states in stoichiometric PbTaSe2 and both states contribute to the measured tunneling current, which is evident from our QPI images, experimentally, it is not straightforward to separate the contribution between bulk and TSS superconductivity in a tunneling spectrum, and realistic theoretical models are required for comparison. Further experiments, such as band-selective superconducting gap mapping using QPI (53) or impurity-dependent spin-polarized QPI imaging (54), are more suitable for understanding the superconductivity on TSSs and bulk states in PbTaSe2.
In summary, our data unveil the nontrivial band topology of PbTaSe2 in the normal state, showing two TSSs with opposite helical spin polarization touching at ED ~ 1.0 eV at . The inner TSS is fully isolated from the nearby bulk states at EF, whereas the outer TSS heavily merges with bulk states at EF. The proximity-induced fully gapped superconducting TSS is observed for the first time in a stoichiometric bulk material. This reveals that stoichiometric bulk PbTaSe2 and closely related compounds hold promise as TSCs. PbTaSe2 is especially promising because it has all components necessary for TSC as a consequence of the surface-bulk proximity effect. It is now imperative to understand the nature of the superconductivity of the TSS and to explore the novel topological superconducting phases for future applications, such as topological quantum computation.
MATERIALS AND METHODS
The DFT calculations were carried out using Quantum Espresso (55) with norm-conserving pseudopotentials (56). SOC was included to study the topological properties. The k-meshes used to sample the Brillouin zone were 15 × 15 × 6 and 8 × 8 × 1 in the bulk and surface calculations, respectively. A slab consisting of a thickness of 8 unit cells (33 atomic layers), with both sides terminated at the layer of Pb, was used in surface calculations. The energy cutoff of the plane wave expansion was 50 Ry. The lattice parameters from the experiments were adopted in the calculations (a = 3.42 Å and c/a = 2.74).
The STEM investigations were conducted on a JEOL-2100F microscope operated at 200 keV and equipped with a CEOS spherical aberration corrector, and STEM HAADF imaging was performed at an annular collection angle of 72 to 192 mrad. Electron diffraction studies were performed on a FEI-Tecnai microscope at 200 keV. All images were unprocessed and taken at room temperature.
STM measurements
Single crystals of PbTaSe2 were cleaved at T < 20 K in UHV and immediately inserted into the STM head for measurement. For QPI measurements in the normal state, we used a homebuilt cryogenic UHV SI-STM with a base temperature of 1.6 K, a magnetic field of up to 9 T, and a hold time of ~10 days. For the study of the superconducting state, we used a homebuilt 3He STM with a base temperature of 0.25 K, a magnetic field of up to 7 T, and a hold time of ~24 hours. Etched tungsten wires were used for STM tips. A standard ac lock-in technique was used for differential conductance measurements. QPI maps were unprocessed, except that only q = 0 was suppressed to enhance the overall contrast of images.
Supplementary Material
Acknowledgments
We thank T.-K. Lee, S. Yip, J. C. Davis, A. W. Rost, M. H. Hamidian, H. Lin, W.-F. Tsai, T. Hanaguri, K. Iwaya, D.-H. Lee, P. Wahl, E.-A. Kim, M. H. Fischer, I. Garate, M. P. Allan, W.-C. Lee, W.-J. Li, S.-P. Chao, and T.-R. Chang for helpful discussions and communications. H.T.J. acknowledges the National Center for High-Performance Computing, the Computer and Information Network Center (CINC)–National Taiwan University (NTU), and the National Center for Theoretical Sciences, Taiwan, for technical support. Funding: This work was supported by Academia Sinica, NTU, and the Ministry of Science and Technology. T.-M.C. is grateful for the support of the Kenda Foundation. Author contributions: S.-Y.G. and T.-M.C. performed the SI-STM experiments and analyzed the data; R.S. synthesized the samples; and P.-J.C. and H.-T.J. performed the theoretical calculations. M.-W.C. performed the STEM experiments. F.C., H.-T.J., C.-S.C., and T.-M.C. supervised the project. S.-Y.G., P.-J.C., H.-T.J., and T.-M.C. wrote the paper with input from other authors. The article reflects the contributions of all authors. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/11/e1600894/DC1
note S1. Crystal structures and electron diffraction patterns of PbTaSe2.
note S2. Spin-decomposed surface band structures of PbTaSe2.
note S3. The 2 × 2 superstructure on a Se-terminated surface.
note S4. Verification of helical spin polarization in TSSs by QPI imaging.
note S5. Superconducting gap on a Se-terminated surface.
note S6. Single-s-wave gap and two-s-wave gap fitting.
note S7. Comparison of normalized differential conductance at normal and superconducting states on a Pb-terminated surface.
note S8. Upper critical field, lattice parameter of Abrikosov lattice, and normalized zero bias conductance of a vortex.
note S9. Spatial distribution of the superconducting gap on a Pb-terminated surface.
note S10. Topographic images and parameters of differential conductance maps on a Pb-terminated surface.
note S11. Setpoint effect of normalized differential conductance maps on a Pb-terminated surface.
note S12. Raw Fourier transform of normalized differential conductance maps on a Pb-terminated surface.
note S13. Differential conductance map at Fermi energy.
fig. S1. Electron diffraction patterns along [001] and [110] projection.
fig. S2. Projection of the spin polarizations of bands contributed from the surface atoms.
fig. S3. The simulated surface structure on the Se-terminated surface.
fig. S4. Spin-dependent QPI.
fig. S5. Temperature dependence of the superconducting gap.
fig. S6. BCS fitting of superconducting tunneling spectrum.
fig. S7. Normalized differential conductance taken on Pb-terminated surface.
fig. S8. Magnetic field dependence of superconducting vortex lattice and vortex bound states.
fig. S9. Homogenous superconducting gap on a Pb-terminated surface.
fig. S10. Topographic images of differential conductance maps on the Pb-terminated surface.
fig. S11. Bias independence of LDOS mapping and QPI imaging.
fig. S12. Raw data FFT of normalized differential conductance maps.
fig. S13. Visualization of QPI at Fermi energy.
movie S1. Normal-state QPI maps taken on a Pb-terminated surface.
REFERENCES AND NOTES
- 1.Hasan M. Z., Kane C. L., Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010). [Google Scholar]
- 2.Qi X.-L., Zhang S.-C., Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011). [Google Scholar]
- 3.Hosur P., Ghaemi P., Mong R. S. K., Vishwanath A., Majorana modes at the ends of superconductor vortices in doped topological insulators. Phys. Rev. Lett. 107, 097001 (2011). [DOI] [PubMed] [Google Scholar]
- 4.Beenakker C. W. J., Search for Majorana fermions in superconductors. Annu. Rev. Condens. Matter Phys. 4, 113–136 (2013). [Google Scholar]
- 5.Elliott S. R., Franz M., Colloquium: Majorana fermions in nuclear, particle, and solid-state physics. Rev. Mod. Phys. 87, 137 (2015). [Google Scholar]
- 6.Beenakker C. W. J., Random-matrix theory of Majorana fermions and topological superconductors. Rev. Mod. Phys. 87, 1037–1066 (2015). [Google Scholar]
- 7.Fu L., Kane C. L., Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008). [DOI] [PubMed] [Google Scholar]
- 8.Kallin C., Chiral p-wave order in Sr2RuO4. Rep. Prog. Phys. 75, 042501 (2012). [DOI] [PubMed] [Google Scholar]
- 9.Ando Y., Fu L., Topological crystalline insulators and topological superconductors: From concepts to materials. Annu. Rev. Condens. Matter Phys. 6, 361–381 (2015). [Google Scholar]
- 10.Levy N., Zhang T., Ha J., Sharifi F., Talin A. A., Kuk Y., Stroscio J. A., Experimental evidence for s-wave pairing symmetry in superconducting CuxBi2Se3 single crystals using a scanning tunneling microscope. Phys. Rev. Lett. 110, 117001 (2013). [DOI] [PubMed] [Google Scholar]
- 11.Sato M., Fujimoto S., Topological phases of noncentrosymmetric superconductors: Edge states, Majorana fermions, and non-Abelian statistics. Phys. Rev. B 79, 094504 (2009). [Google Scholar]
- 12.Yip S., Noncentrosymmetric superconductors. Annu. Rev. Condens. Matter Phys. 5, 15–33 (2014). [Google Scholar]
- 13.Sun Z., Enayat M., Maldonado A., Lithgow C., Yelland E., Peets D. C., Yaresko A., Schnyder A. P., Wahl P., Dirac surface states and nature of superconductivity in noncentrosymmetric BiPd. Nat. Commun. 6, 6633 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Neupane M., Alidoust N., Xu S.-Y., Belopolski I., Sanchez D. S., Chang T.-R., Jeng H.-T., Lin H., Bansil A., Kaczorowski D., Hasan M. Z., Durakiewicz T., Discovery of the topological surface state in a noncentrosymmetric superconductor BiPd. arXiv:1505.03466 (2015). [Google Scholar]
- 15.Sakano M., Okawa K., Kanou M., Sanjo H., Okuda T., Sasagawa T., Ishizaka K., Topologically protected surface states in a centrosymmetric superconductor β-PdBi2. Nat. Commun. 6, 8595 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.K. Iwaya, K. Okawa, T. Hanaguri, Y. Kohsaka, T. Machida, T. Sasagawa, Superconducting States of Topological Surface States in β-PdBi2 Investigated by STM/STS (APS Meeting, Baltimore, MD, 2016). [Google Scholar]
- 17.Herrera E., Guillamón I., Galvis J. A., Correa A., Fente A., Luccas R. F., Mompean F. J., García-Hernández M., Vieira S., Brison J. P., Suderow H., Magnetic field dependence of the density of states in the multiband superconductor β-Bi2Pd. Phys. Rev. B 92, 054507 (2015). [Google Scholar]
- 18.Kačmarčík J., Pribulová Z., Samuely T., Szabó P., Cambel V., Šoltýs J., Herrera E., Suderow H., Correa-Orellana A., Prabhakaran D., Samuely P., Single-gap superconductivity in β-Bi2Pd. Phys. Rev. B 93, 144502 (2016). [Google Scholar]
- 19.Lv Y.-F., Wang W.-L., Zhang Y.-M., Ding H., Li W., Wang L., He K., Song C.-L., Ma X.-C., Xue Q.-K., Experimental observation of topological superconductivity and Majorana zero modes on β-Bi2Pd thin film. arXiv:1607.07551 (2016). [DOI] [PubMed] [Google Scholar]
- 20.Ali M. N., Gibson Q. D., Klimczuk T., Cava R. J., Noncentrosymmetric superconductor with a bulk three-dimensional Dirac cone gapped by strong spin-orbit coupling. Phys. Rev. B 89, 020505(R) (2014). [Google Scholar]
- 21.Bian G., Chang T.-R., Sankar R., Xu S.-Y., Zheng H., Neupert T., Chiu C.-K., Huang S.-M., Chang G., Belopolski I., Sanchez D. S., Neupane M., Alidoust N., Liu C., Wang B., Lee C.-C., Jeng H.-T., Zhang C., Yuan Z., Jia S., Bansil A., Chou F., Lin H., Hasan M. Z., Topological nodal-line fermions in spin-orbit metal PbTaSe2. Nat. Commun. 7, 10556 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pang G. M., Smidman M., Zhao L. X., Wang Y. F., Weng Z. F., Che L. Q., Chen Y., Lu X., Chen G. F., Yuan H. Q., Nodeless superconductivity in noncentrosymmetric PbTaSe2 single crystals. Phys. Rev. B 93, 060506(R) (2016). [Google Scholar]
- 23.Sankar R., Rao G. N., Muthuselvam I. P., Bian G., Zheng H., Chen G. P.-J., Chang T.-R., Xu S., Murgan G. S., Lin C.-H., Lee W.-L., Jeng H.-T., Hasan M. Z., Chou F.-C., Single crystal growth and physical property characterization of PbTaSe2 as a noncentrosymmetric type-II superconductor. arXiv:1511.05295 (2015). [Google Scholar]
- 24.Zhang C.-L., Yuan Z., Bian G., Xu S.-Y., Zhang X., Hasan M. Z., Jia S., Superconducting properties in single crystals of the topological nodal semimetal PbTaSe2. Phys. Rev. B 93, 054520 (2016). [Google Scholar]
- 25.Wang M. X., Xu Y., He L. P., Zhang J., Hong X. C., Cai P. L., Wang Z. B., Dong J. K., Li S. Y., Nodeless superconducting gaps in noncentrosymmetric superconductor PbTaSe2 with topological bulk nodal lines. Phys. Rev. B 93, 020503(R) (2016). [Google Scholar]
- 26.Chang T.-R., Chen P.-J., Bian G., Huang S.-M., Zheng H., Neupert T., Sankar R., Xu S.-Y., Belopolski I., Chang G., Wang B., Chou F., Bansil A., Jeng H.-T., Lin H., Hasan M. Z., Topological Dirac surface states and superconducting pairing correlations in PbTaSe2. Phys. Rev. B 93, 245130 (2016). [Google Scholar]
- 27.Eppinga R., Wiegers G. A., A generalized scheme for niobium and tantalum dichalcogenides intercalated with post-transition elements. Physica B+C 99, 121–127 (1980). [Google Scholar]
- 28.Kane C. L., Mele E. J., Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005). [DOI] [PubMed] [Google Scholar]
- 29.Yu R., Qi X. L., Bernevig A., Fang Z., Dai X., Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection. Phys. Rev. B 84, 075119 (2011). [Google Scholar]
- 30.Roushan P., Seo J., Parker C. V., Hor Y. S., Hsieh D., Qian D., Richardella A., Hasan M. Z., Cava R. J., Yazdani A., Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009). [DOI] [PubMed] [Google Scholar]
- 31.Seo J., Roushan P., Beidenkopf H., Hor Y. S., Cava R. J., Yazdani A., Transmission of topological surface states through surface barriers. Nature 466, 343–346. (2010). [DOI] [PubMed] [Google Scholar]
- 32.Sessi P., Reis F., Bathon T., Kokh K. A., Tereshchenko O. E., Bode M., Signatures of Dirac fermion-mediated magnetic order. Nat. Commun. 5, 5349 (2014). [DOI] [PubMed] [Google Scholar]
- 33.Lee I., Kim C. K., Lee J., Billinge S. J. L., Zhong R., Schneeloch J. A., Liu T., Valla T., Tranquada J. M., Gu G., Davis J. C. S., Imaging Dirac-mass disorder from magnetic dopant atoms in the ferromagnetic topological insulator Crx(Bi0.1Sb0.9)2−xTe3. Proc. Natl. Acad. Sci. U.S.A. 112, 1316–1321 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zeljkovic I., Okada Y., Huang C.-Y., Sankar R., Walkup D., Zhou W., Serbyn M., Chou F., Tsai W.-F., Lin H., Bansil A., Fu L., Hasan M. Z., Madhavan V., Mapping the unconventional orbital texture in topological crystalline insulators. Nat. Phys. 10, 572–577 (2014). [Google Scholar]
- 35.Chang G., Xu S.-Y., Zheng H., Lee C.-C., Huang S.-M., Belopolski I., Sanchez D. S., Bian G., Alidoust N., Chang T.-R., Hsu C.-H., Jeng H.-T., Bansil A., Lin H., Hasan M. Z., Signatures of Fermi arcs in the quasiparticle interferences of the Weyl semimetals TaAs and NbP. Phys. Rev. Lett. 116, 066601 (2016). [DOI] [PubMed] [Google Scholar]
- 36.Inoue H., Gyenis A., Wang Z., Li J., Oh S. W., Jiang S., Ni N., Bernevig B. A., Yazdani A., Quasiparticle interference of the Fermi arcs and surface-bulk connectivity of a Weyl semimetal. Science 351, 1184–1187 (2016). [DOI] [PubMed] [Google Scholar]
- 37.Guo H.-M., Franz M., Theory of quasiparticle interference on the surface of a strong topological insulator. Phys. Rev. B 81, 041102(R) (2010). [Google Scholar]
- 38.Giaever I., Hart H. R. Jr, Megerle K., Tunneling into superconductors at temperatures below 1°K. Phys. Rev. 126, 941–948 (1962). [Google Scholar]
- 39.Zhang T., Cheng P., Li W.-J., Sun Y.-J., Wang G., Zhu X.-G., He K., Wang L., Ma X., Chen X., Wang Y., Liu Y., Lin H.-Q., Jia J.-F., Xue Q.-K., Superconductivity in one-atomic-layer metal films grown on Si(111). Nat. Phys. 6, 104–108 (2010). [Google Scholar]
- 40.Xu J.-P., Wang M.-X., Liu Z. L., Ge J.-F., Yang X., Liu C., Xu Z. A., Guan D., Gao C. L., Qian D., Liu Y., Wang Q.-H., Zhang F.-C., Xue Q.-K., Jia J.-F., Experimental detection of a Majorana mode in the core of a magnetic vortex inside a topological insulator-superconductor Bi2Te3/NbSe2 heterostructure. Phys. Rev. Lett. 114, 017001 (2015). [DOI] [PubMed] [Google Scholar]
- 41.Kawakami T., Hu X., Evolution of density of states and a spin-resolved checkerboard-type pattern associated with the Majorana bound state. Phys. Rev. Lett. 115, 177001 (2015). [DOI] [PubMed] [Google Scholar]
- 42.Hess H. F., Robinson R. B., Dynes R. C., Valles J. M. Jr, Waszczak J. V., Scanning-tunneling-microscope observation of the Abrikosov flux lattice and the density of states near and inside a fluxoid. Phys. Rev. Lett. 62, 214–216 (1989). [DOI] [PubMed] [Google Scholar]
- 43.Qi X.-L., Hughes T. L., Zhang S.-C., Topological invariants for the Fermi surface of a time-reversal-invariant superconductor. Phys. Rev. B 81, 134508 (2010). [Google Scholar]
- 44.Chiu C.-K., Cole W. S., Sarma S. D., Induced spectral gap and pairing correlations from superconducting proximity effect. Phys. Rev. B 94, 125304 (2016). [Google Scholar]
- 45.Hao L., Lee T. K., Surface spectral function in the superconducting state of a topological insulator. Phys. Rev. B 83, 134516 (2011). [Google Scholar]
- 46.Mizushima T., Yamakage A., Sato M., Tanaka Y., Dirac-fermion-induced parity mixing in superconducting topological insulators. Phys. Rev. B 90, 184516 (2014). [Google Scholar]
- 47.Du G., Shao J., Yang X., Du Z., Fang D., Zhang C., Wang J., Ran K., Wen J., Yang H., Zhang Y., Wen H.-H., Drive the Dirac electrons into Cooper pairs in SrxBi2Se3. arXiv:1604.08198 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Han C. Q., Li H., Chen W. J., Zhu F., Yao M.-Y., Li Z. J., Wang M., Gao B. F., Guan D. D., Liu C., Gao C. L., Qian D., Jia J.-F., Electronic structure of a superconducting topological insulator Sr-doped Bi2Se3. Appl. Phys. Lett. 107, 171602 (2015). [Google Scholar]
- 49.Lahoud E., Maniv E., Petrushevsky M. S., Naamneh M., Ribak A., Wiedmann S., Petaccia L., Salman Z., Chashka K. B., Dagan Y., Kanigel A., Evolution of the Fermi surface of a doped topological insulator with carrier concentration. Phys. Rev. B 88, 195107 (2013). [Google Scholar]
- 50.Matano K., Kriener M., Segawa K., Ando Y., Zheng G.-q., Spin-rotation symmetry breaking in the superconducting state of CuxBi2Se3. Nat. Phys. 12, 852–854 (2016). [Google Scholar]
- 51.Yonezawa S., Tajiri K., Nakata S., Nagai Y., Wang Z., Segawa K., Ando Y., Maeno Y., Thermodynamic evidence for nematic superconductivity in CuxBi2Se3. Nat. Phys. 10.1038/nphys3907 (2016). [Google Scholar]
- 52.Balatsky A. V., Vekhter I., Zhu J.-X., Impurity-induced states in conventional and unconventional superconductors. Rev. Mod. Phys. 78, 373–433 (2006). [Google Scholar]
- 53.Allan M. P., Rost A. W., Mackenzie A. P., Xie Y., Davis J. C., Kihou K., Lee C. H., Iyo A., Eisaki H., Chuang T.-M., Anisotropic energy gaps of iron-based superconductivity from intraband quasiparticle interference in LiFeAs. Science 336, 563–567 (2012). [DOI] [PubMed] [Google Scholar]
- 54.Hofmann J. S., Queiroz R., Schnyder A. P., Theory of quasiparticle scattering interference on the surface of topological superconductors. Phys. Rev. B 88, 134505 (2013). [Google Scholar]
- 55.Giannozzi P., Baroni S., Bonini N., Calandra M., Car R., Cavazzoni C., Ceresoli D., Chiarotti G. L., Cococcioni M., Dabo I., Dal Corso A., de Gironcoli S., Fabris S., Fratesi G., Gebauer R., Gerstmann U., Gougoussis C., Kokalj A., Lazzeri M., Martin-Samos L., Marzari N., Mauri F., Mazzarello R., Paolini S., Pasquarello A., Paulatto L., Sbraccia C., Scandolo S., Sclauzero G., Seitsonen A. P., Smogunov A., Umari P., Wentzcovitch R. M., QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009). [DOI] [PubMed] [Google Scholar]
- 56.Hamann D. R., Schlüter M., Chiang C., Norm-conserving pseudopotentials. Phys. Rev. Lett. 43, 1494–1497 (1979). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/11/e1600894/DC1
note S1. Crystal structures and electron diffraction patterns of PbTaSe2.
note S2. Spin-decomposed surface band structures of PbTaSe2.
note S3. The 2 × 2 superstructure on a Se-terminated surface.
note S4. Verification of helical spin polarization in TSSs by QPI imaging.
note S5. Superconducting gap on a Se-terminated surface.
note S6. Single-s-wave gap and two-s-wave gap fitting.
note S7. Comparison of normalized differential conductance at normal and superconducting states on a Pb-terminated surface.
note S8. Upper critical field, lattice parameter of Abrikosov lattice, and normalized zero bias conductance of a vortex.
note S9. Spatial distribution of the superconducting gap on a Pb-terminated surface.
note S10. Topographic images and parameters of differential conductance maps on a Pb-terminated surface.
note S11. Setpoint effect of normalized differential conductance maps on a Pb-terminated surface.
note S12. Raw Fourier transform of normalized differential conductance maps on a Pb-terminated surface.
note S13. Differential conductance map at Fermi energy.
fig. S1. Electron diffraction patterns along [001] and [110] projection.
fig. S2. Projection of the spin polarizations of bands contributed from the surface atoms.
fig. S3. The simulated surface structure on the Se-terminated surface.
fig. S4. Spin-dependent QPI.
fig. S5. Temperature dependence of the superconducting gap.
fig. S6. BCS fitting of superconducting tunneling spectrum.
fig. S7. Normalized differential conductance taken on Pb-terminated surface.
fig. S8. Magnetic field dependence of superconducting vortex lattice and vortex bound states.
fig. S9. Homogenous superconducting gap on a Pb-terminated surface.
fig. S10. Topographic images of differential conductance maps on the Pb-terminated surface.
fig. S11. Bias independence of LDOS mapping and QPI imaging.
fig. S12. Raw data FFT of normalized differential conductance maps.
fig. S13. Visualization of QPI at Fermi energy.
movie S1. Normal-state QPI maps taken on a Pb-terminated surface.