Tracking Equilibrium and Nonequilibrium Shifts in Data with TREND

Abstract

Principal component analysis (PCA) discovers patterns in multivariate data that include spectra, microscopy, and other biophysical measurements. Direct application of PCA to crowded spectra, images, and movies (without selecting peaks or features) was shown recently to identify their equilibrium or temporal changes. To enable the community to utilize these capabilities with a wide range of measurements, we have developed multiplatform software named TREND to Track Equilibrium and Nonequilibrium population shifts among two-dimensional Data frames. TREND can also carry this out by independent component analysis. We highlight a few examples of finding concurrent processes. TREND extracts dual phases of binding to two sites directly from the NMR spectra of the titrations. In a cardiac movie from magnetic resonance imaging, TREND resolves principal components (PCs) representing breathing and the cardiac cycle. TREND can also reconstruct the series of measurements from selected PCs, as illustrated for a biphasic, NMR-detected titration and the cardiac MRI movie. Fidelity of reconstruction of series of NMR spectra or images requires more PCs than needed to plot the largest population shifts. TREND reads spectra from many spectroscopies in the most common formats (JCAMP-DX and NMR) and multiple movie formats. The TREND package thus provides convenient tools to resolve the processes recorded by diverse biophysical methods.

Introduction

Plotting the course of biomolecular or physiological processes typically uses procedures specific to the field. In the case of spectroscopy and imaging, tracking the process can be laborious because of the steps of assigning the peaks of the spectra or features in the images, manually choosing peaks or image features subjectively judged optimal for monitoring the process of interest, and managing complications from any concurrent processes. Spectral overlap and peak broadening (e.g., from chemical exchange in NMR) can prevent correct fitting (1). A more elegant alternative to such efforts is to apply unsupervised, multivariate statistical pattern recognition such as principal component analysis (PCA). PCA has provided insight from series of measurements from diverse techniques of molecular biophysics that include magnetic resonance, vibrational, optical, and dichroic spectroscopies; x-ray scattering and diffraction; mass spectrometry; calorimetry; hydrodynamics; atomic force microscopy; electron microscopy; and imaging by fluorescence, Raman or light scattering, as well as functional magnetic resonance imaging (Table S1 in the Supporting Material and references therein). Biophysical studies have often used PCA to determine dependencies of various reactions upon time, concentration, or other conditions, e.g., in protein folding (Table S1). PCA applied directly to spectra, images, and movies appears to be a convenient and general way to determine the main trends of change among measurement frames that record many localized changes. PCA is much more accommodating of many data distributions than is often appreciated (2). It transforms many measured variables to far fewer and uncorrelated principal components (PCs) that each capture part of the trends of covariation among measured variables (2).

PCA of NMR peak lists was used to track equilibrium transitions of proteins due to pH (3) and binding of partners (4, 5, 6). Closely related singular value decomposition (SVD) of NMR peak pick lists was used to reconstruct filtered basis spectra for use in fitting biphasic ligand binding (7) or for identifying binding sites (8). The applications of PCA were recently extended directly to NMR spectra, images, and movies without choosing any peaks or features for analysis. Moreover, applying PCA directly to NMR spectra makes binding isotherms easily accessible in all chemical exchange regimes, including intermediate exchange where severe broadening and nonlinearity of peak shifts ordinarily mask the true course of molecular association (1, 9). Application of SVD to series of time-dependent two-dimensional (2D) images or spectra extracted the dominant time course as PC1. The approach also detected multiple time-evolving processes in magnetic resonance imaging (MRI) movies as PCs. Similarly, when two sequential steps of binding were monitored by NMR, PCA detected both binding steps and the intermediate state with a single ligand bound (9). Accomplishments with SVD (PCA) have usually been limited to the laboratories that wrote task-specific code to perform the calculations, however.

Independent component analysis (ICA) can complement PCA. ICA aims instead to find independent components (ICs) (2). The quest of ICA for statistical independence is more demanding than PCA’s aim of correlation coefficients of zero. These objectives are equivalent for Gaussian (normal) distributions. ICA can be regarded as more general than PCA and is effective for non-Gaussian data and situations where PCA fails (2). However, ICA can be very slow to compute compared with PCA, lower in convergence, and require repeated calculations. Like PCA, ICA has been used to reduce dimensionality and filter or separate data in processing signals, images (10), large biological data sets (11), and NMR spectra of mixtures (12, 13, 14).

To make these capabilities available for application to a variety of spectroscopic and imaging techniques used in biophysics, we have developed a software package named TREND (Tracking and Resolving Equilibrium and Nonequilibrium population shifts in Data). Its main means of tracking the shifts is PCA implemented with SVD. Its secondary means is an ICA algorithm, which recapitulates the PCA results we examined, provided the correct number of ICs is specified. We first sought to extract binding isotherms, equilibrium shifts, and time courses (all potentially with multiple components) from series of NMR spectra. Because of the suitability of PCA for many other kinds of series of 2D digital data frames, we utilized the Python community’s support of file I/O in multiple data formats (e.g., movies and spreadsheets) and wrote code for additional spectroscopic formats, enabling wide application (e.g., JCAMP-DX, Sparky peak list). For example, we analyzed a cardiac MRI movie (15) with TREND to isolate multiple aspects of the cardiac cycle and to reconstruct movies from combinations of PCs. This software package can resolve biologically relevant reactions and processes with relative ease from many biophysical sources of complicated spectral and imaging data.

Materials and Methods

Implementation of TREND

TREND was written in Python 2.7 and calls NumPy for linear algebra and random number generation. It implements PCA (SVD) with function calls to NumPy. We first wrote TREND for operation at the command line. We added a graphical user interface (GUI), supported by Gooey, using function calls to wxPython. Most users will prefer to use the GUI to operate TREND. TREND comprises three programs, each with both interfaces (Table 1). The executable files trendmaingui and trendmain compute the PCs or ICs across the 2D series of measurements, create temporary files used by the plotting or reconstruction programs run afterward, and plot the first three components plus benchmarks of their significance. Trendplotgui and trendplot provide optional plotting that is customizable in terms of the number and choice of normalization of the components. Optional reconstructions of the measurement series are available from trendreconstructgui and trendreconstruct (Table 1). Explanations of the flags and parameters for the command line versions are available online in the manual for TREND (https://trendmizzou.gitbooks.io/trend-manual/content/). For convenience of installation, we packaged TREND and the public domain software it depends upon using PyInstaller. Consequently, TREND does not need Python on the host system. Distributions are available for Windows 7 and later, Mac OS X 10.7 and later, and these versions of Linux: Ubuntu 14.04/Fedora 23, Ubuntu 16.04, and Red Hat 7.1/CentOS 7 (http://biochem.missouri.edu/trend).

Table 1.

Executable File Components of TREND

Executable File	Roles	Interface
trendmain.exe	preprocess and compute PCs or ICs	CLI
trendmaingui.exea	preprocess and compute PCs or ICs	GUI
trendplot.exe	plot selected PCs or ICs with choice of normalization	CLI
trendplotgui.exea	plot selected PCs or ICs with choice of normalization	GUI
trendreconstruct.exe	reconstruct spectra, images, or movies from PCs	CLI
trendreconstructgui.exea	reconstruct spectra, images, or movies from PCs	GUI

CLI is command-line interface; and GUI is graphical user interface.

^aExecutable files with GUI are trendmaingui.app, trendplotgui.app, and trendreconstructgui.app for OS X or macOS platforms.

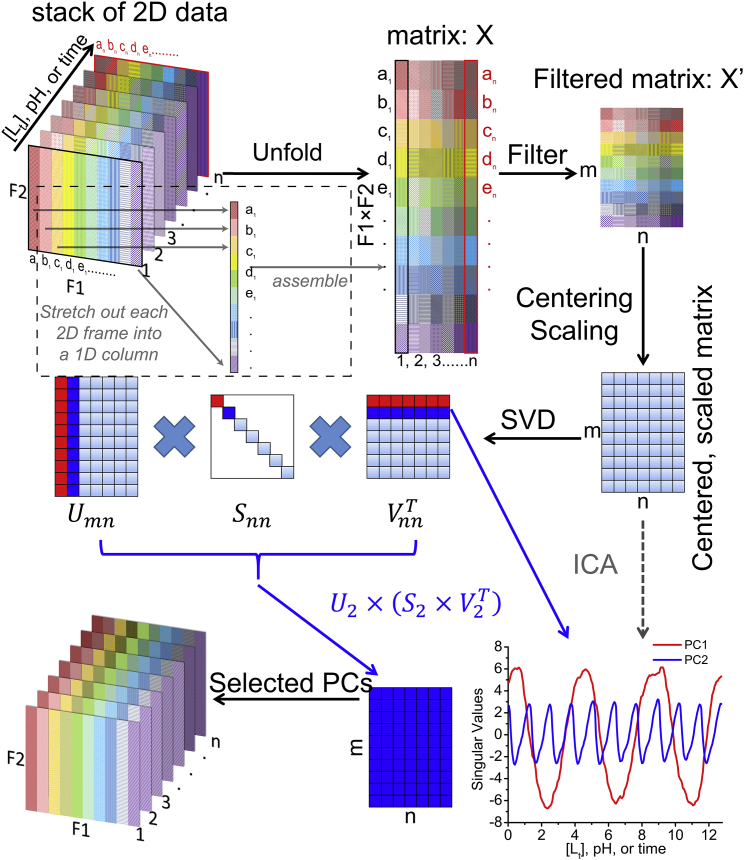
Conversion of a stack of 2D measurements into a matrix for analysis

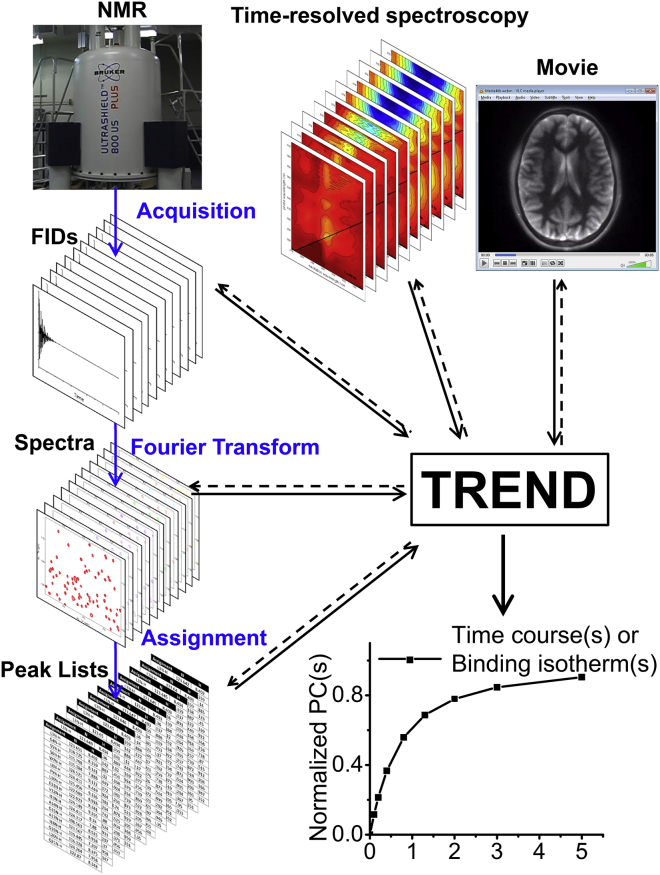
A wide variety of 2D measurements can be read and analyzed by trendmaingui and trendmain. This includes images or movie frames comprising pixels, one-dimensional (1D) and 2D spectra from many spectroscopies, lists of peak positions and heights, and unprocessed NMR spectroscopic data in the time domain (free induction decays, FIDs; Fig. 1). The program reads NMR spectra in NMRpipe, Sparky, and Bruker Topspin formats (as well as FIDs in NMRpipe and Topspin formats) (Table 2) using code from Nmrglue (16). Trendmaingui and trendmain also read Agilent (Varian) VNMRJ format and JCAMP-DX formats of Bruker, Agilent, and Jeol spectrometers. To analyze the measurements from many other kinds of spectroscopy and biophysical measurements (Table S1), the program reads the most common JCAMP-DX formats, as well as spreadsheet and text formats commonly written by instruments (Table 2). Trendmaingui and trendmain read NMR peak lists either in the format of Sparky peak lists (17) or plain text files, before converting them into column vectors (3, 7). Movies are read in multiple formats (i.e., avi, mov, mp4, ogv, webm) by the MoviePy module into three-dimensional (3D) arrays with color layers. Trendmaingui and trendmain convert the movie frames to gray-scale (8-bit depth) and rearrange them into 2D matrices (Fig. 2). Time-lapse series of PNG images are read, using the Scipy module of Python, and handled similarly.

Figure 1.

Workflows to TREND extraction of the main components of change across a series of measurements. TREND reads a series of spectra, peak lists, FIDs, images, or a movie and extracts the dominant trends from them. Spectral or electronic data series in general-purpose JCAMP-DX, text, or spreadsheet formats, NMR formats, and video formats are readable. The dashed lines signify reconstruction of measured data from the principal components chosen. To see this figure in color, go online.

Table 2.

File Formats Read and Reconstructed by TREND^a

Choice in Trendmaingui	Format	Reconstruction Support	Comment
NMR Data Formats
fid	NMRPipe FID	yes
ft2	NMRPipe Ft2	yes
ucsf	Sparky UCSF	yes
brukerfid	Bruker Topspin FID	yes	fid, ser in/1/pdata/subfolderb
brukerft2	Bruker Topspin spectra	yes	1r, 2rr files
agilentfid	VnmrJ, OpenVnmrJ FID	yes	fid
agilentspectra	VnmrJ, OpenVnmrJ spectra	no	Phasefilea
sparkylist	Sparky peak list	yes	duplicate peaks not allowed
JCAMP-DX (Joint Committee on Atomic and Molecular Physical data—Data Exchange format)
jcamp	JCAMP-DX	no	Only supports X..(Y+Y) and (XY..XY)c
Text File Formats
txt	floating point	yes	for series of text files
complextxt	complex numbers	yes	for series of text files
singletxt	complex or floating point	yes	for single .TXT file containing entire series
Spreadsheet Formats
csv	comma-separated floating point	no	for series of .CSV files
complexcsv	comma-separated complex numbers	no	for series of .CSV files
singlecsv	comma-separated complex or floating point	no	for single .CSV file containing entire series
excel	Excel format	no	for series of Excel files
singleexcel	Excel format with tabs	no	for single file with single or multiple tabs
Images and Movies
png	images in PNG format	yes	For series of .PNG files
movie	common video formats	yes	.ogv, .mp4, .mpeg, .avi, .mov, .webm

^aSee the online TREND manual (https://trendmizzou.gitbooks.io/trend-manual/content/).

^bCurrently the processed spectra must be saved by setting processed directory to 1.

^cJCAMP-DX is a general format for exchanging and archiving data from many instruments, including but not limited to infrared (IR), Raman, ultraviolet-visible (UV-Vis), fluorescence, NMR, and electron paramagnetic resonance (EPR). The data stored in JCAMP-DX files can be spectral plots, contours, or peak tables. TREND supports the most common JCAMP-DX formats. The digital data in JCAMP-DX can be AFFN (ASCII FREE FORMAT NUMERIC) form or ASDF (ASCII SQUEEZED DIFFERENCE FORM). TREND supports decoding compressed data, including PAC, SQZ, DIF, SQZDUP, and DIFDUP. Two most common tabular data forms, (X++(Y..Y)) and (XY..XY) are supported. TREND reads a series of JCAMP-DX files, or a single JCAMP-DX file with one or multiple blocks. TREND supports NTUPLE format (introduced by JCAMP-DX 5.0), which is designed for multidimensional techniques with data sets with multiple variables. For example, JCAMP-DX NMR uses NTUPLE to show mixed real/imaginary FID data sets. See format details in http://www.jcamp-dx.org/, https://badc.nerc.ac.uk/help/formats/jcamp_dx/, and http://wwwchem.uwimona.edu.jm:1104/spectra/testdata/index.html.

Figure 2.

TREND implementation of PCA (SVD), ICA, and reconstruction. The algorithm reorganizes a series of 2D measurements as a series of 1D columns. The dashed box indicates the unfolding of the first 2D data (marked by black edges) with F2 rows and F1 columns to a long 1D column with F1 × F2 points. The data matrix X is compressed to X′ and used for SVD. (No user selection of spectral peaks or image features is involved). The resulting first several right singular vectors in the decomposed matrix V^T represented the largest trend(s). ICA can be used to corroborate SVD results. Single or multiple PCs can be used to reconstruct the original data series. To see this figure in color, go online.

In the case of NMR data, spectra very recently emerged as probably the preferred format for application of PCA (9). In the examples below, NMR spectra (collected with a uniform set of parameters) were processed with NMRPipe (18) and converted to the UCSF format of Sparky (17, 19). NMR spectra in UCSF format were read by trendmaingui or trendmain for conversion into 2D matrices (Fig. 2). Unprocessed NMR data in the time domain (FIDs) can also be read, processed, and the solvent signal subtracted. (Analysis of time domain data is justified by Parseval’s theorem regarding the equivalency of signals in the time and frequency domains (20)).

Preprocessing

Regardless of original data format, columns from each 2D measurement read are positioned end-to-end into a single 1D vector for convenience (9) (Fig. 2). These 1D columns are arrayed over the experimental variable (concentration, pH, time, etc.) into the data matrix X, which has F1 × F2 points in the column dimension and n points per row for the n experimental conditions. To expedite manipulations of this matrix X and facilitate calculations on a modest laptop computer, each vector is compressed by deleting unchanging positions, resulting in matrix X′ (Fig. 2). For SVD of spectra, the user is encouraged to use a threshold that is three- to sevenfold the noise level to filter out low intensity regions of the spectra, which compresses matrix X′ further. However, it is better to use a lower threshold where intermediate exchange broadening significantly weakens NMR peaks.

As required by PCA and ICA algorithms, the rows of compressed matrix X′ are centered and then optionally scaled. Scaling enlarges weaker signals relative to large signals. The options for scaling methods include autoscaling, Pareto scaling, or no scaling (21). No scaling appears acceptable in most titrations, but autoscaling generally enhances fits to the binding isotherms. Autoscaling obviates the systematic scaling of ¹⁵N NMR peak shifts down by several-fold relative to ¹H shifts that were used in PCA of lists in (3). Autoscaling also generalizes to ¹H-¹³C correlation spectra. Pareto scaling is recommended for NMR titrations with substantial intermediate exchange broadening (9). Range, vast, and level scaling (21) are also implemented in trendmain but do not work well with NMR spectra. No scaling has been used for MRI movies. Column centering and scaling are not necessary in our experience, but are available in trendmaingui and trendmain as they are sometimes used for PCA (22) and ICA (11). The descriptions of the data scaling and centering methods (21) are listed in Table S2.

Calculating principal components via SVD

The compressed, preprocessed matrix X′ has m points per column and n points or experimental conditions in each row, with m > n. X′ can be decomposed into three matrices as follows:

$${\mathit{X}}_{\mathit{mn}}^{\text{'}}={\mathit{U}}_{\mathit{mn}}{\mathit{S}}_{\mathit{nn}}{\mathit{V}}_{\mathit{nn}}^{\mathit{T}},$$ (1)

where U and V^T are orthogonal matrices and S is a diagonal matrix that contains the square roots of eigenvalues for vectors in U or V in descending order. To obtain the trends of change across the measurements, we are interested in V^T, whose rows span X′ and are called the right singular vectors. The V^T matrix has row vectors ${\mathit{V}}_{\mathit{nn}}^{\mathit{T}}=\left({\mathit{V}}_1^{\mathit{T}},{\mathit{V}}_2^{\mathit{T}},{\mathit{V}}_3^{\mathit{T}}\dots {\mathit{V}}_{\mathit{n}}^{\mathit{T}}\right)$. Importantly, the first row in the V^T matrix is PC1 and the second row PC2, i.e., the two largest trends of change among the series of spectra or images measured. To obtain these PCs that record the relationships among columns in X′ (Fig. 2), it suffices to calculate V^T. The rows of V^T are orthonormal eigenvectors of the symmetric matrix ${\mathit{X}}^{\mathit{\text{'}T}}{\mathit{X}}^{\mathit{\text{'}}}$ (Fig. 2). (The normalized form of ${\mathit{X}}^{\mathit{\text{'}T}}{\mathit{X}}^{\mathit{\text{'}}}$ is equivalent to the covariance matrix, the alternative algorithm for computing PCA (2).) The normalized PC1 values from the first row of V^T indicate the fractional population of the main change at each measurement in the series of measurements. When obtained from a typical titration of ligand binding, PC1 represents the binding isotherm; a dissociation constant may be fitted to it (9).

Reconstruction of spectra, images, or movies by PCA

The reconstructed data set X_reconst, with size of m × n, can be calculated as follows:

$${\mathit{X}}_{\mathit{reconst}}={\mathit{U}}_{\mathit{a}}\left({\mathit{S}}_{\mathit{a}}{\mathit{V}}_{\mathit{a}}^{\mathit{T}}\right)+{\mathit{U}}_{\mathit{a}}\left({\mathit{S}}_{\mathit{b}}{\mathit{V}}_{\mathit{b}}^{\mathit{T}}\right)+{\mathit{U}}_{\mathit{c}}\left({\mathit{S}}_{\mathit{c}}{\mathit{V}}_{\mathit{c}}^{\mathit{T}}\right)+{\mathit{U}}_{\mathit{d}}\left({\mathit{S}}_{\mathit{d}}{\mathit{V}}_{\mathit{d}}^{\mathit{T}}\right)+{\mathit{U}}_{\mathit{e}}\left({\mathit{S}}_{\mathit{e}}{\mathit{V}}_{\mathit{e}}^{\mathit{T}}\right)\dots ,$$ (2)

where a, b, c, d, e … refer to the index of PCs generated by trendmain or trendmaingui to use in the reconstruction by trendreconstruct or trendreconstructgui. (Note a, b, c, d, e … can be nonconsecutive integers. To enable this, the “reconst” box should be selected in trendmaingui. When using trendmain, the –reconst flag should be included.) The U matrix is used for the reconstruction. It can be rewritten as column vectors: ${\mathit{U}}_{\mathit{mn}}=\left({\mathit{U}}_1,{\mathit{U}}_2,{\mathit{U}}_3\dots {\mathit{U}}_{\mathit{n}}\right)$, which lie in the column space of X′. U can be calculated similarly to V^T, by solving eigenvectors of the matrix ${\mathit{X}}^{\text{'}}{\mathit{X}}^{\text{'}\mathit{T}}$. To recover the original 2D data series, the preprocessing steps of centering, scaling, and compression (filtering) can be reversed as described in the manual for TREND. The user can choose to reconstruct the centered and scaled matrix, matrix X′, or matrix X in the format of the original data (Fig. 2).

ICA calculations

ICA is available in TREND and implemented using scikit-learn (http://scikit-learn.org/stable/modules/decomposition.html#ica). Despite the potential generality of ICA, two limitations need to be respected. Since the magnitudes of ICs cannot be determined, their contributions cannot be ranked. ICA is also prone to local minima during optimization, requiring comparisons of repeated calculations (10, 11). TREND implements the FastICA algorithm for computational efficiency. FastICA preprocesses data by PCA to reduce dimensions and avoid overlearning (23, 24, 25). (Overlearning is an underdetermined situation that interferes in obtaining parameters and introduces artifacts to ICs (24, 25)).

ICA decomposes the data matrix X as follows:

$$\mathit{X}=\mathit{AS},$$ (3)

where A is the unknown mixing matrix that is invertible, square, and mixes the components in X, and S is the matrix containing underlying independent sources. The aim of ICA is to solve for the mixing matrix A because it contains the ICs that may contain the meaningful trends sought. However, A and S both being unknown makes ICA calculations challenging (10). The equation can be rewritten as follows:

$$\mathit{S}=\mathit{WX}=\mathit{V}{\mathit{X}}_{\mathit{w}},$$ (4)

where W is the unmixing matrix that is calculated as A⁻¹. To simplify and improve convergence of ICA, X is preprocessed to remove correlations and to normalize it, a process called whitening, which generates X_w. FastICA implements this whitening step using PCA to calculate the whitened data matrix X_w as follows:

$${\mathit{X}}_{\mathit{w}}=\left({\mathit{D}}^{-\frac{1}{2}}{\mathit{E}}^{\mathit{T}}\right)\mathit{X}$$ (5)

Where E is the matrix whose columns are normalized eigenvectors of the covariance matrix of XX^T, and D is the diagonal matrix of the corresponding eigenvalues. The preprocessing with PCA also removes noise and reduces dimensions for ICA. The whitening simplifies the ICA problem to finding the unknown rotation matrix V that is defined as ${\mathit{D}}^{-\left(1/2\right)}{\mathit{E}}^{\mathit{T}}$. In FastICA, V is estimated by maximizing non-Gaussian character. The equations lead to the following:

$$\mathit{A}={\mathit{W}}^{-1}={\left(\mathit{V}{\mathit{D}}^{-\frac{1}{2}}{\mathit{E}}^{\mathit{T}}\right)}^{-1}$$ (6)

Results and Discussion

Workflows of TREND

For wide application of SVD or ICA to diverse series of 2D measurements, we wrote TREND in Python to read and analyze multiple types of data. These include diverse spectra, images, movies, or lists in text or spreadsheet formats available from many modern instruments (Fig. 1). The spectral formats include widely used JCAMP-DX standards and NMR formats. TREND can also apply PCA or ICA to a single 2D data matrix read in from a text file, spreadsheet file, or multiblock JCAMP-DX file containing multiple spectra (Table 2). The algorithm of the trendmain and trendmaingui executable files includes the following steps:

• 1)Convert each 2D measurement into a 1D vector arrayed by the experimental condition varied, in the data matrix X.
• 2)Preprocess X with compression to X′ and optional scaling.
• 3)Perform streamlined SVD or ICA to identify components (PC1, PC2, … or IC1, IC2, …) representing the major trend(s) varying with the experimental variable (Fig. 1).

The TREND package provides additional executable files for plotting the course of selected PCs or ICs or for rebuilding spectra, images, or movie from selected PCs (Table 1). For convenience, the plotting and reconstruction routines read temporary files just created by trendmain or trendmaingui; this frees the user from specifying input files, which is optional. The user may operate and customize these computations by a choice of GUI or command line arguments described in documentation for the software.

Although we used the Python routine NumPy to implement PCA (SVD) and scikit-learn (http://scikit-learn.org/stable/modules/decomposition.html#ica) to implement ICA calculations, corresponding routines are available in R (https://mran.microsoft.com/packages/), MATLAB (The MathWorks, Natick, MA, https://www.mathworks.com/matlabcentral/fileexchange/38300-pca-and-ica-package), and the MATLAB Statistics Toolbox. Recreating the workflows and functions depicted in Figs. 1 and 2 in an R or MATLAB environment would require code to parse the file formats of interest, reduce their dimensionality (i.e., “unfold” them), preprocess for readiness for the SVD or ICA routine, and interpret or reconstruct the results in the appropriate format. TREND spares the user this effort with a package that is user-friendly for NMR and other measurements from a variety of instrumentation, including spectroscopies and imaging; see Table 2 for data formats handled. TREND is free for academics, avoiding the cost of licensing MATLAB. TREND requires <200 MB of disk space whereas the MATLAB environment occupies 2 to 3 GB. TREND is portable and its installation lacks dependencies, other than the need for Internet access upon first usage.

We present examples of uses of TREND that illustrate 1) its performance in resolving two or more processes, which is nonroutine by conventional means, and 2) its wide applicability to trace and reconstruct concurrent, complex transformations recorded by biophysical means such as spectra or imaging.

Examples of ligand binding to two sites detected by NMR

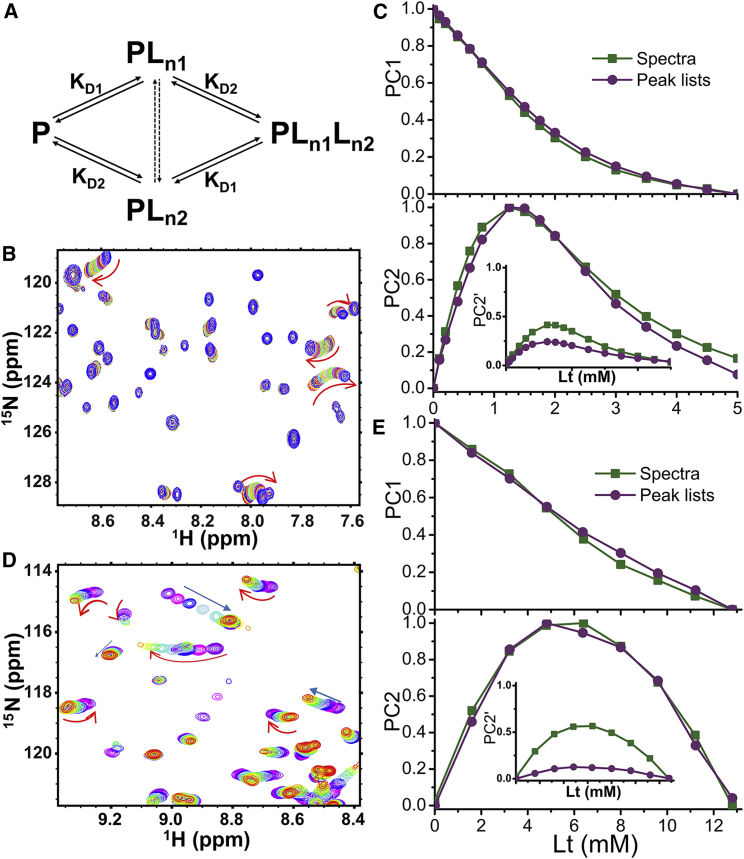
Antecedents to TREND’s direct application of PCA to spectra and images were previous PCA studies of NMR peak lists. SVD was used to filter noise out of the lists, in turn used to reconstruct clean basis spectra to resolve three pH transitions (3) or two binding events (4, 7). With TREND we demonstrate a direct spectrum-driven approach to the latter examples of two biphasic associations. Fig. 3 A plots a two-site binding scheme, where P and L denote [protein] and [ligand], respectively. K_D1 and K_D2 are dissociation constants from site 1 and 2. PL_n1 and PL_n2 are intermediates with ligand at site 1 or 2, where n1 and n2 indicate the numbers of ligand molecules that bind cooperatively to site 1 and 2, respectively. PL_n1L_n2 stands for the fully bound state. Equations 3 to 6 from (7) were used to simulate populations of species from the two-site binding scheme in a series of ¹⁵N HSQC spectra (Fig. 3 B) using methods given in Supporting Material. The curvature in the simulated shifts of several peaks (red arrows in Fig. 3 B) accompanies more than one mode of binding (7). PCA on the peak lists (chemical shifts) captures two smooth components, PC1 and PC2 (purple in Fig. 3 C), contributing 90% and 6% of the variance, respectively. The PC1 and PC2 components of the peak lists were recreated using trendreconstruct. PC1 captures from the curved trajectories of peak movements the main linear paths of change (Fig. S1, A and B). PC2 identifies the peak shifts orthogonal to PC1 (Fig. S1 C). Computing PC1 and PC2 instead directly from the simulated HSQC spectra using trendmain (green in Fig. 3 C) reproduces their counterparts extracted from peak lists very well, although each component contributes much less of the variance (38% and 15%, respectively). However, when PC2 values are normalized by PC1, there is a systematic difference in amplitude of PC2 consistent with its percentage of the variances listed above (inset in Fig. 3 C). This simulated two-site binding example and a number of 1:1 ligand-binding examples (2, 9) suggest that normalized PCs extracted from lists of picked peaks in the fast-exchange regime can be reproduced well by applying PCA to the series of spectra. However, PC1 and PC2 extracted by TREND from the FIDs from the simulated two-site binding example are skewed with sigmoidal deviation from the PCs obtained from either the peak lists or spectra (Fig. S2, A and B). In the investigation of a titration of β-lactoglobulin with 1-anilinoaphthalene-8-sulfonate (ANS), Konuma et al. resolved two binding components using PCA of the assigned peaks from the NMR spectra of the titration (4). They observed curved trajectories (red arrows in Fig. 3 D) and linear trajectories (blue arrows in Fig. 3 D), suggesting the presence of multiple binding sites. Fast exchange behavior supported reliable PCA of the chemical shift data in peak lists, which provided binding isotherms (4). TREND extracted the PCs from the spectra (green in Fig. 3 E) and unprocessed FIDs from the titration (green in Fig. S2, A and B). These PCs are compared with the previously reported binding isotherms (purple in Fig. 3 E). The binding populations of (4) are reproduced well by the normalized PC1 and PC2 derived from the spectra despite the t1-noise present (Fig. S3), and less well by PC1 and PC2 obtained from the FIDs. (The residual solvent signal was subtracted on-resonance from the FIDs using the trendmaingui option of a convolution difference window (26). In cases of especially poor solvent suppression, this subtraction might not be enough for reliable PCs.) When choosing the form of NMR data to analyze, application of TREND directly to spectra appears to be the most consistently accurate.

Figure 3.

TREND identifies two components in titrations of two binding sites. (A) Scheme of the two-site binding model is shown. The number of ligands that bind to sites 1 and 2 are n1 and n2, respectively. (B) ¹⁵N HSQC spectra simulated according to the two-site model, as described in Supporting Material, are plotted for ligand:protein ratios of 0, 0.1, 0.2, 0.4, 0.6, 0.8, 1.25, 1.5, 1.75, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0 with different contour colors. Both n1 and n2 equal 1 (7). In (B) and (D), linear and curved peak shifting are indicated by linear and curve arrows, respectively. (C) compares PCs from the spectra and peak lists from (B). PC1 and PC2 are normalized to the maximum amplitude of each. In the inset, each PC2 is instead normalized by the amplitude of PC1, which is symbolized by the PC2′ labeling of the ordinate. (D) Measured ¹⁵N HSQC spectra of β-lactoglobulin titrated with ANS additions of 0, 1.6, 3.2, 4.8, 6.4, 8.0, 9.6, 11.2, and 12.8 mM (4) are plotted with different contour colors; while n1 ≈ 2, n2 ≈ 1 (4). (E) compares PCs from the spectra and peak lists of (D). The circles plot the PCA results from peak lists reported by (4). The plots are normalized and labeled as in (C). To see this figure in color, go online.

Reconstruction of the spectra of the ANS titration with trendreconstructgui using only PC1 and PC2 introduces artifacts that are ghosts of the peaks from each spectrum of the titration (not shown). The cumulative contribution ratio (reported by trendmaingui) saturates at eight PCs, suggesting eight is sufficient to represent the series of spectra. Using eight PCs in the reconstruction removed the ghosts of peaks and reproduced well the spectra and their biphasic trajectories of peak shifts upon additions of ANS (Fig. S3). The need for eight or more PCs is typical of the need for faithful reconstruction of series of spectra and images. Nonlinearity is typical of such series and spreads their variances across many PCs; see Fig. S7 in (9). This spreading of variances to many PCs could account for the need for many PCs for faithful reconstruction. Inspection of the reconstructed and original spectra finds both fast and fast-intermediate exchange regimes (Fig. S3). Application of PCA directly to the spectra, followed by reconstruction, accommodated this mixture of behaviors, as recently proposed (9).

ICA for confirming components

TREND supports optional use of ICA. If the number or significance of PCs obtained comes into question, ICA can be used to test the significance and validity of the PCs. It is also conceivable that ICA may be able to resolve components from some experiments that are not resolvable by PCA. ICA of peak pick lists from the two-site binding example of Fig. 3 B yields ICs equivalent to PC1 and PC2 (Fig. S4). We tested ICA with various numbers K of trial components with series of spectra containing N true components. When K ≤ N, ICA derives components that are very similar to those from PCA (Fig. S5). However when K > N, which means trying to extract more “independent components” than true components, ICA always fails in our experience, as evident from components that are jagged and meaningless (Fig. S5, E and F). Consequently, we propose that this failure of ICA can be used to count the meaningful components. The ICA should be repeated with incrementally higher K trial components. The lowest value of K at which ICA fails implies K − 1 significant components (see Fig. S5 for two examples of the iterative process). The drawback of ICA validation of components is in repeating FastICA calculations N + 1 times for each trial number of components, preferably with three to five repetitions of each, to escape local minima. Though the process is repetitive, it requires no previous knowledge of the number of components. Deciding the PCs that are significant may be quicker by identifying the PCs that contribute the most to scree plots (the convention) and which have large autocorrelation coefficients (smoothness) (7). However, recapitulation of PCs by ICs may engender more confidence in the reproducibility of the analysis.

Cardiac MRI movie resolved into components

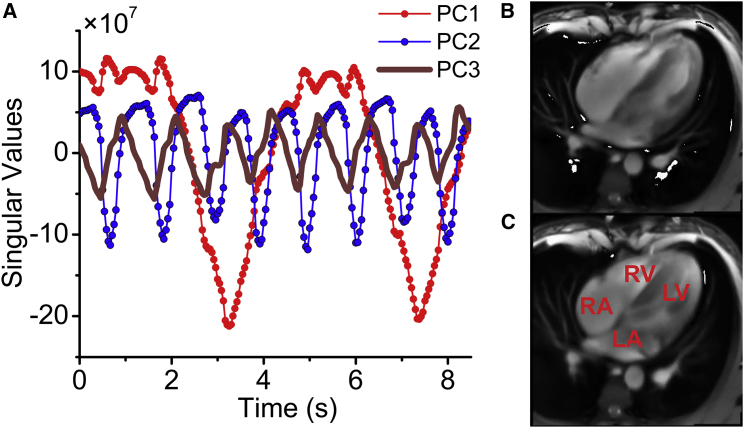
Real-time imaging by MRI generates complex movies that are suitable to showcase the capabilities of TREND. An MRI movie of a slice through the four chambers of the heart (15; http://www.biomednmr.mpg.de/images/stories/movies/Media18.ogv) was analyzed by TREND. A movie for each of the first four individual PCs was reconstructed using trendreconstructgui, aiding interpretation of the PCs. PC1 follows the time course of breathing where the trough represents inhalation (Fig. 4 A; Movie S1). Fig. 4 B plots a frame from the PC2 movie (Movie S2) where the left ventricle is relaxed and open, known as diastole. Fig. 4 C plots a frame from the PC2 movie where the left ventricle and heart overall are contracted in systole. The time course of PC2 follows the alternation between the crests representing diastole and narrow troughs representing systole (Fig. 4 A). In the crests of PC2, the phases of rapid filling and subsequent slower filling of the ventricles can be observed. (An overview of the cardiac cycle is provided by Cardiovascular Physiology Concepts, Indianapolis, IN, http://www.cvphysiology.com/Heart%20Disease/HD002b.htm). The troughs of PC3 coincide with the isovolumetric contraction phase that begins systole (Fig. 4 A). The left ventricle and atrium walls and interiors alternate in appearance in the PC3 movie (Movie S3). Bright density between the left ventricle and atrium in the PC3 movie at the troughs in the PC3 time course suggests the closed state of the left atrioventricular (mitral) valve. Coinciding with this is detectable rotation of the right atrium and ventricle. The PC4 movie represents sudden overall rotations of the heart (Movie S4). The time courses indicate synchronization of these rotations (PC4) with both the cardiac cycle (PC2) and each inspiration of a breath (PC1); see Fig. S6 A. The rotations appear largest when a breath in begins and ends. These observations illustrate the ability of TREND to resolve and aid interpretation of concurrent processes.

Figure 4.

SVD captures from a cardiac MRI movie the time courses of breathing, diastole, and systole from a “four-chamber” angle of view. (A) PC1 represents respiration is shown. PC2 tracks the oscillation between diastole and systole. (B) This frame in the reconstructed PC2 movie is during diastole with the open cavities especially evident in the ventricles (Movie S2). (C) In this frame from the same movie, all four chambers are contracted (systole). RA is right atrium; RV is right ventricle; LV is left ventricle; and LA is left atrium. To see this figure in color, go online.

A movie reconstructed from all four of these PCs using trendreconstructgui captures the major morphological changes of the cardiac cycle (Movie S5), but is not as smooth and nuanced as the original (15; http://www.biomednmr.mpg.de/images/stories/movies/Media18.ogv). Trendmaingui reports autocorrelation coefficients exceeding 0.7 for the first 44 PCs, suggesting their information content. Inspection of the scree plot and the cumulative contribution plot generated by trendmaingui indicates that the first four PCs account for ∼69% of the statistical variance across the movie, 10 PCs account for 85%, and 20 account for 93% (Fig. S6 B). Reconstruction of the cardiac MRI movie using the first 10 PCs imparts much increased realism to the depiction of the turbulent blood flow in the cardiac chambers and smoothness to the cardiac movement (Movie S6). Doubling the PCs to the first 20 enhances the fidelity further but more subtly (Movie S7). Omission of PC1 removes the largest background of breathing changes to the chest cavity, while preserving the cardiac cycle portrayal (Movie S8).

In reconstruction of other movies and NMR spectra, we also observed the faithfulness of the reconstruction to increase with number of PCs. Eight or more PCs may often be desirable for satisfying reconstruction of a measurement series. The scree plot and secondarily the autocorrelation coefficients appear useful for anticipating the number of PCs beneficial for reconstruction of the measurement series.

Conclusions

Direct application of PCA (or ICA) to 2D measurements using TREND will expand the accessibility of equilibrium and time-evolving processes measured by spectra and imaging. No curation, selection, assignment, or resolution of specific spectral peaks or image features is necessary using this unsupervised statistical approach. TREND can be applied “on-the-fly” on an instrument host computer during data collection to assess if the process or reaction has progressed far enough. Multiple concurrent processes, measured by biophysical techniques, have been readily resolved into principal or independent components. Movies and spectra can be reconstructed with TREND from the user’s choice of principal components. These capabilities will introduce, to our knowledge, new convenience and insight to analyses of spectrally detected reactions and imaging-detected processes studied by biophysics, physiology, and other disciplines.

Author Contributions

J.X. wrote the code. J.X. and S.R.V.D. designed the approach, performed the research, analyzed the results, and wrote the manuscript.

Editor: Jeff Peng

Supporting Citations

References 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58 appear in the Supporting Material.