Quantitative fluorescent microscopy measures vascular pore size in primary and metastatic brain tumors

Abstract

Tumors residing in the central nervous system (CNS) compromise the blood-brain barrier (BBB) via increased vascular permeability, with the magnitude of changes dependent on tumor type and location. Current studies determine penetrability of a cancer therapeutic by administering progressively larger molecules until cutoff is observed where little to no tumor accumulation occurs. However, decades-old experimental work and mathematical modeling document methods to calculate both the size of the vascular opening (pore) with solute permeability values. In this study, we updated this classic mathematical modeling approach with quantitative fluorescent microscopy in two preclinical tumor models, allowing simultaneous administration of multiple sized tracers to determine vascular permeability at a resolution of nearly one micron. We observed that three molecules ranging from 100 Da to 70 kDa permeated into a preclinical glioblastoma model at rates proportional to their diffusion in water. This suggests the solutes freely diffused from blood to glioma across vascular pores without steric restriction, which calculates to a pore size of >140 nm in diameter. In contrast, the calculated pore size of a brain metastasis of breast cancer was ~10 fold smaller than glioma vasculature. This difference explains why antibodies are effective against glioblastoma but generally fail in brain metastases of breast cancer. Based on our observations, we hypothesize that traztuzumab most likely fails in the treatment of brain metastases of breast cancer because of poor CNS penetration, while the similar sized antibody bevacizumab is effective in the same tumor type not because it penetrates the CNS degree better, but because it scavenges VEGF in the vascular compartment, which reduces edema and permeation.

Quick Guide to Equations and Assumptions

The unidirectional blood-to-brain tumor transfer constant K_in is calculated for fluorescent marker distribution according to established QAR methodology using a multiple-time uptake approach (1). Briefly, to determine the apparent terminal volume of brain and tumor distribution [V_d(app)] of the tracer at the time of sacrifice we used the following relationship:

$$V_{d\left(app\right)}=\frac{C_{br}\left(\tau \right)}{C_{bl}\left(\tau \right)}$$ (Eqn 1)

Where C_br is concentration of tracer in brain, C_bl is concentration of tracer in blood and t is sampling time. To measure the change of tracer concentration in brain over time in terms of uptake, and since C_bl is not constant with time we used the following relationship:

$$C_{br}\left(\tau \right)=K_{in}\left({\int }_0^t{C}_{bl}\left(\tau \right)d\tau \right)$$ (Eqn 2)

where K_in is the unidirectional brain uptake coefficient of the tracer. We solved for the integral of fluorophores or ¹⁴C-AIB plasma concentrations over time by sampling the concentration in blood in experimental animals by the equation:

$${\int }_0^t{C}_{bl}\left(\tau \right)d\tau =\sum _{i-0}^{n-1}\frac{t_{i+1}-t_i}{2}(C_{bl}+C_{bl+1})$$ (Eqn 3)

Where C_bl is concentration of tracer in blood, n is the number of blood concentrations sampled in each experiment which varied depending on size of the tracer, and t is time.

Lastly, multiple-time uptake analysis allowed us to use the tracer to serve simultaneously as the permeability and vascular marker, and by definition accounts for differing times of exposure, and therefore we divided equation 4 by the terminal blood concentration as previously described (2):

$$\frac{C_{br}\left(\tau \right)}{C_{bl}\left(\tau \right)}=K_{in}\frac{{\int }_0^t{C}_{bl}\left(\tau \right)d\tau }{C_{bl}\left(\tau \right)}+V_i$$ (Eqn 4)

Where V_i is the total vascular space or initial equilibrating space of the tracer in the brain vasculature (or bound to vascular endothelium) at the time of sacrifice.

Given the heterogeneity in metastatic tumors, a single-time uptake was used to measure K_in in individual animals with MDA-MB-231BR-Her2 tumors, using the following equation (3,4)

$$K_{in}=\frac{C_{br}\left(\tau \right)}{{\int }_0^t{C}_{bl}\left(\tau \right)dt}$$ (Eqn 5)

Where C_br is the amount of the compound in the lesion per unit mass of the tissue [less a 0.5% vascular correction (4)] at time T, and C_bl is the blood concentration of the compound. To provide an estimation of the pore diffusivity of the water soluble tracers and the number of cylindrical pores in tumor vasculature (per unit of mass of tissue) we used the following relationship (5):

$$K_{in}~PS=\frac{N{\left[D_w\pi (p-a)\right]}^2]}{\delta }$$ (Eqn 6)

Where δ is the mean thickness of the endothelial wall (~10 nm), a is the approximate radius of the tracer in aqueous solution (AIB: ~2.8A⁰; TX Red 625Da: ~7 A⁰; TX Red 3kDa dextran: ~15.9 A° and TX Red 70kDa dextran: ~60 A⁰) (6,7), p is the approximate radius of the vascular pore and N is the number of pores per unit of mass of tissue. D_w is the aqueous diffusion coefficient at 37° C and was estimated if not known, from the following relationship:

$$D_w\approx \frac{1}{\sqrt{MW}}{10}^{-4}$$ (Eqn 7)

where D_w in cm²/s × 10⁻⁷ was ~equal to: AIB: ~98; TX Red 625Da: 40; TX Red 3kDa dextran: 15 and TX Red 70 kDa dextran: 3.8) (8,9). To calculate the total pore area per gram (A_t) of tissue we rearranged Eqn 5 (5):

$$A_t~\frac{\delta K_{in}}{D_w}$$ (Eqn 8)

Major Assumptions

1. There is negligible post-mortem diffusion of tracer in brain given removal and freezing in isopentane occurs in less than 60 s

2. Solute uptake is unidirectional over the time period sampled

3. The permeability surface area product (PS) can be substituted for K_in from equation 5, since the measured K_in for all tracers are permeability limited with values that are significantly lower than 20% of cerebral vascular blood flow.

4. That a (solute radius) is at least six fold smaller than p (vascular pore radius)

Introduction

The incidence of brain metastasis has substantially increased and represents ~50% of intracranial lesions observed in humans (10,11). Yet the literature on permeability of the blood-tumor barrier stands in opposition with >90% of the work being performed in primary tumor models. This discrepancy must be addressed since it has recently been shown that permeability of brain metastases of breast cancer in two experimental metastasis model systems is highly heterogeneous, ranging nearly 30-fold between lesions and does not directly reflect what is observed in primary tumors (12). Therefore this study evaluates two critical permeability parameters in metastatic lesions; 1) size dependent permeability 2) size of pores in tumor vasculature, as both are critical to the understanding of the size of chemotherapeutics which can diffuse into metastatic lesions and potentially have therapeutic benefit.

Within the normal brain vasculature, endothelial cells are sealed together by tight-junction protein complexes. This unique structure coupled with pericytes, astrocytes and neuronal input creates a barrier that significantly restricts para-cellular diffusion of polar and or large molecules between the blood and brain (blood-brain barrier; BBB). However, the vasculature within a brain tumor is both anatomically and functionally different. Anatomically, tumors as small as 0.5 mm in diameter can promote the formation of new vessels which lack the classic BBB tight junction structure (13), have lost astrocytic contact and have both increased vesicular density (14) and fenestrations or pores which allow the free para-cellular passage of molecules from blood into brain (15). These anatomical changes functionally result in the brain tumor vasculature (Blood-tumor barrier; BTB) having an increased permeability (16-18) which is size dependent (19,20). For example, small molecules (<500 Da) have substantially increased diffusion rates (up to 30 fold) and larger molecules (>5000 Da) have only an ~two to three-fold increase (21-23).

Most non-biological chemotherapeutics (e.g., paclitaxel and doxorubicin) are typically less than 1500 Da in size and accordingly tend to penetrate tumors through angiogenic vascular BTB pores to a significantly greater degree than in normal brain (12). Recently numerous monoclonal antibodies have been approved for the treatment of breast, colon, squamous cell carcinomas, glioma and lymphomas/leukemias (24-26). These antibodies are ~100 fold larger in size than chemotherapeutics and, if they are able to cross the BTB, may have efficacy in treating both primary and metastatic tumors. Determining the size of molecules which can diffuse across the BTB is technically difficult but has been shown pre-clinically in models that have homogenous permeability from tumor to tumor (e.g., gliomas). In this report we describe novel imaging methodology that allows for the simultaneous measurement of size dependent permeability and prediction of vascular pore sizes in metastases which have heterogeneous permeability. This data is then directly compared to a primary tumor model as control, since to the best of our knowledge this is the first report which calculates pore size in metastatic lesions and/or any tumor in the brain that has substantial variability in permeability amongst different tumors.

Materials and Methods

Chemicals

Sulpho-rhodamine 101 (MW 625Da), TX Red 3kDa dextran lysine fixable, TX Red 70kDa dextran lysine fixable were purchased from Molecular Probes; Invitrogen (Eugene, Oregon, USA). ¹⁴C-AIB (specific activity: 55mCi/mmole) was purchased from American Radiolabelled chemicals (St. Louis, MO). All other chemicals are of analytical grade and were purchased from Sigma (St. Louis, MO).

In vivo Tumor Animals

Craniotomy and RG-2 Tumor implantation

All animal experiments were conducted in accordance with Institutional Animal Care and Use Committee and NIH guidelines. Intraperitoneal injection of Ketamine (100-200mg/Kg and Xylazine (5-10 mg/Kg) were used for anesthesia in all experiments. Human glioblastoma multiforme does not have a circumscribed border and as such we utilized the rat glioma (RG-2; obtained from ATCC in 2010 and in passage less than six months at the time of the experiment) tumor cell line since this model also displays an infiltrative growth pattern and is representative of human glioblastoma multiforme (27). Briefly male Ficher-344 rats (Charles River Laboratory, Kingston, N.Y., U.S.A.) were implanted stereotactically with ~100,000 stably eGFP transfected RG-2 cells in 5 μL (28) at coordinates of 4.5mm lateral to bregma and 5mm deep.

Seven days after implantation, one of the three fluorescent markers (6mg/kg body weight) was injected intravenously; TX Red 625Da (0-5 min circulation), TX Red 3kDa dextran (0-20min circulation), or TX Red 70kDa dextran (0-60 min circulation). Six blood samples were collected throughout each experimental time period (see Fig. 1) and after collecting the final blood sample animals were sacrificed and brain tissue was removed rapidly (<60 s) from the skull and flash frozen in isopentane (−50°C). Brains were then sectioned (20μm) using a cryostat (Shandon Cryotome ®) at −23 °C and sections were mounted on glass slides and air dried. Concentrations of the fluorophores in blood and brain were determined using fluorescent microscopy using matching tissue standards (as described previously (12); In a separate set of tumor bearing animals we injected ¹⁴C-AIB (100 μCi/Kg) along with a fluorophore to compare permeability differences of these tracers. After tissue preparation, fluorescent images were taken to analyze the TX Red 3kDa dextran permeability, and autoradiograms were generated by co-exposing the sections on Fuji film (FLA 7000, Stamford, CT) with tissue-calibrated ¹⁴C-standards for 4 days. The regional radioactivity was measured in tumor, contralateral regions. Quantitative analysis of the regional radioactivity was performed using MCID program (Interfocus Imaging, Cambridge, England).

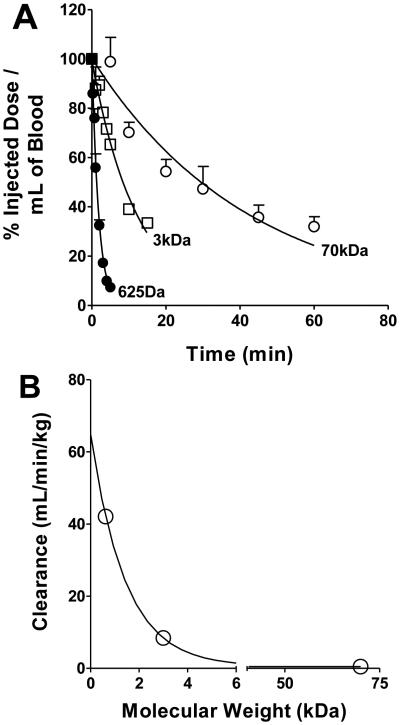
Figure 1.

Panel A shows the peripheral blood concentration of the three fluorescent dyes (TX Red 625Da, TX Red 3kDa and TX Red 70kDa) at various sampling times after an intravenous injection. Data are mean ± SEM (n=5-6). Panel B shows the relationship between clearance and molecular weight of the fluorescent marker. (r²=0.993)

Metastatic tumor development

Immune compromised female NuNu mice (Charles River Laboratories, Kingston, N.Y., U.S.A.) were inoculated with 175,000 eGFP transfected MDA-MB-231BR-Her2 cells (obtained as a gift from Pat Steeg in 2007 and in passage less than six months at the time of the experiments; have been confirmed with STR profiling) via left cardiac ventricle in serum free media. Tumors seeded the brain and were allowed to grow for 4-6 weeks. After tumor development animals were anaesthetized and administered and ¹⁴C-AIB and TX Red 625Da or TX Red 70 kDa dextran into femoral vein and allowed to circulate for 5-60 minutes. At the end of the circulation period the animals were euthanized by severing the cardiac ventricles and the brain was rapidly removed from the skull and flash frozen in isopentane (−50°C), cut coronally (20 μm), placed on slides and air dried.

Fluorescence Imaging and defining tumor regions

Fluorescence was observed with an Olympus MVX-10 stereo microscope using a 2X objective (numerical aperture; 0.5) and an optical zoom of 0.63 to 6.3x. The excitation and emission of TX Red and or the TX Red dextrans was accomplished using a chroma filter (Chroma Technology Corp., Rockingham VT) with an excitation filter of 560 ± 55 nm and an emission filter of 645 ± 75 nm. The dichromatic mirror inhibited the capture of emission wavelengths of light below 595 nm (Olympus America Inc., Center Valley, PA). Tumor bearing brain slices were analyzed using a binary mask methodology (i.e., voxel defined regions of interest) based upon eGFP fluorescence to define the tumor (Slidebook 4.2). Briefly, binary masking consisted of defining the tumor based upon the presence of eGFP fluorescence on a voxel by voxel basis. If eGFP fluorescence was present (approximately >3 fold above background) it was considered to be tumor, which was further confirmed by cresyl violet staining.

Statistical Analysis

K_in was determined with linear regression using least squares analysis. One-way ANOVA analysis followed by a Bonferroni’s multiple comparison test was used for the evaluation of regional brain uptake data. All data represent mean ± SD unless otherwise indicated. Differences were considered significant at the p < 0.05 level. (Graph pad Prism version 5.00 for Windows, Graph Pad Software, San Diego, CA USA).

Results

Method development for quantitative permeability measurements

In order to determine permeability changes we developed a quantitative fluorescent microscopy technique coupled to autoradiography that provides ~1 μm spatial resolution to evaluate permeability. Briefly, in the first set of experiments we ascertained the terminal concentrations of the permeability markers in blood, brain and RG-2 tumors using fluorescent standards to confirm previous results obtained with autoradiography and chromatography methods. Since concentration of the marker changed with time, we determined the blood-concentration time profiles at varying times from one to 60 min after injection (Fig 1A). A significant correlation (r²=0.99) was observed between the molecular weight of the fluorescent marker and clearance (Fig 1B), agreeing with previous literature showing dextran conjugates undergo renal elimination with filtration rates being dependent on size (29).

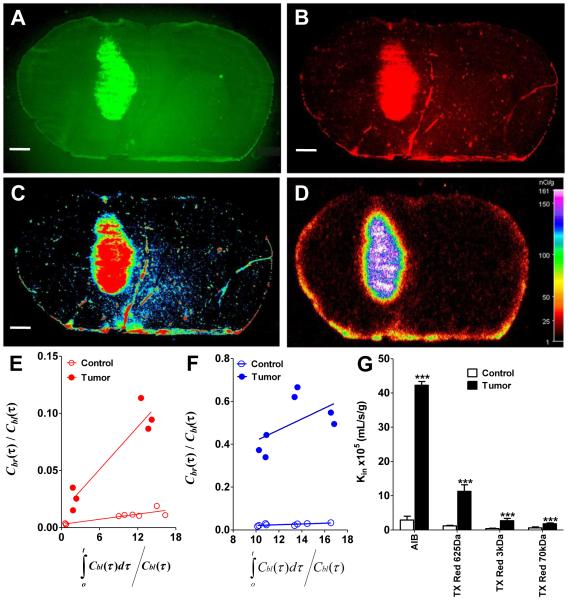
Tumor bearing brain slices were analyzed using a binary mask region of interest methodology based upon eGFP fluorescence to define the tumor (Fig 2A-D). Binary masking consisted of defining the tumor based upon the presence of eGFP fluorescence on a voxel by voxel basis. If eGFP fluorescence was present (approximately >3 fold above background) it was considered to be tumor. Once blood and tumor concentrations of the permeability markers were determined, we utilized an intravenous multiple uptake time approach to determine the transfer coefficient (K_in) in normal brain and tumor (Fig 2E and F) (1,2). The control K_in obtained from similar plots for all the molecules are shown in the first column of Fig 2G. The ordinate intercept for the TX Red 625Da and AIB was ~0.003 ± 0.008 mL/g (Fig 2E) and ~0.004 ± 0.009 mL/g (Fig 2F) respectively, which represents the vascular space (V_v) within brain. Similarly, the V_v was determined using similar plots for TX Red 3kDa dextran (0.0054 ± 0.0014 mL/g) and TX Red 70kDa dextran (0.0013 ± 0.0004). These data are consistent with previous work (30,31).

Figure 2.

Representative images from the simultaneous injection of ¹⁴C-AIB with TX Red 625Da are shown. A is the eGFP RG-2 tumor and B is the terminal accumulation of TX Red 625Da. The accumulation of dye is then converted to an intensity image where red is the highest areas of dye accumulation and blue is the lowest (C). This data is then directly compared to the ¹⁴C-AIB autoradiogram (D) which shows similar degrees of accumulation of tracer. This experiment provided concurrent QAR and fluorescent data which allows a direct comparison of permeability variances. Multiple time point graphical analysis of individual experiments to calculate the transfer constant K_in, in normal brain (open circles) and tumor (filled circles) for TX Red 625Da (red dots) and ¹⁴C-AIB (blue dots) are shown in E and F respectively. The slope of the regressed line is equivalent to K_in and the ordinate intercept is equivalent to the vascular volume of the tracer; V_i. A linear regressed line was the best fit for the data (goodness of fit; quantification of sum of squares). Scale bar represents 1mm. Blood to brain transfer coefficients for AIB, TX Red 625Da, TX Red 3kDa, and TX Red 70kDa in brain, and the tumor are shown in Fig 2G. The K_in values were obtained from individual multiple time point graphical analysis plots in each respective regions of interest. A ** and *** indicates a p value of <0.01 and <0.001 respectively. Data are mean ± SD; n=3-6 for all data points.

Determining the size pores in a single RG-2 tumor

One significant advantage of this method is that simultaneous permeability measurements of different sized markers can be done in the same tumor, where in previous studies multiple tumors in different animals were needed to determine if there were differences in size dependent permeability (3,17). As an example in this set of experiments we injected both ¹⁴C-AIB and TX Red 625Da in the same animal (Fig 2). At the time of sacrifice both brain and tumor (Fig 2A) concentrations of the fluorophores were determined using microscopy (representative raw image data shown in Fig 2B-C) and ¹⁴C-AIB concentrations were determined using QAR (representative raw image data shown in Fig 2D). The transfer coefficient K_in for ¹⁴C-AIB and TX Red 625Da in the tumor were 42 ± 1 × 10⁻⁵ mL/s/g and ~12 ± 0.2 × 10⁻⁵ mL/s/g. The magnitude of permeability changes (Fig 2E) compared to normal brain (¹⁴C-AIB: 2.9 ± 1.1 × 10⁻⁵ mL/s/g; TX Red 625Da: ~1.3 ± 0.1 × 10⁻⁴ mL/s/g) agreed with previously reported values. Similar to the control permeability data, linkage of the dye to a progressively larger dextran reduced vascular permeability changes in the tumor. For example, the K_in for TX Red 3kDa in tumor was only increased five-fold in the tumor and the larger TX Red 70kDa had only a two-fold increase (control: 0.63 ± 0.26 × 10⁻⁵ mL/s/g; tumor: 1.8 ± 0.3 × 10⁻⁵ mL/s/g) (Fig. 2E). Importantly, the ratio of unidirectional uptake of TX Red 625Da, TX Red 70kDa and ¹⁴C-AIB were nearly equal to the ratio of the tracers respective aqueous diffusion constant; D_w (Table 1). This data suggests all three sized molecules can freely diffuse from blood to the glioma across vascular pores without steric restriction suggesting a pore size in the glioma model of >140 nm in diameter. This data, while obtained simultaneously in a single tumor, is consistent with the previous literature evaluating pore sizes in the vasculature of multiple gliomas (5).

Table 1.

Blood to brain transfer and aqueous diffusion constants for glioma

	~ Kin (mL/s/g ×105)	~ Dw cm2/s ×107)
TX Red 70kDa	1.8	3.8
TX Red 625kDa	12	40
AIB	42	98
AIB / TX Red 70kDa Ratio	23.4	25.7
AIB / TX Red 625Da Ratio	3.5	2.5

The ratio of the unidirectional uptake of the water soluble tracers should be nearly equal to the ratio of the tracers respective aqueous diffusion constant; D_w. This ratio has >70% equality for TX Red 625Da , TX Red 70kDa dextran and ¹⁴C-AIB. The data suggests the vascular pores in glioma allow unrestricted diffusion of molecules greater than the size of IgG.

Further, using data from simultaneous injections and from all three fluorescent tracers we were able to calculate the surface area of the pores (Eqn 8) present in the glioma vasculature. Briefly, the total surface area of the pores which allow water soluble tracers to diffuse into tumor tissue was ~4.3 × 10⁻⁵ cm²/g. This data is consistent with previous work in RG-2 tumor models showing a calculated pore surface area of ~6.2 × 10⁻⁵ cm²/g (5). While our value is slightly lower, it may represent the difference between tumor stages; where 10 days of RG-2 tumor growth can increase vascular pore permeability ~20-30% (32) and ours were implanted for 7 days to minimize peripheral pathophysiological changes and to keep tumor and tumor vasculature normalized between animals.

Heterogenous permeability of metastatic MDA-MB-231BR-Her2 tumors

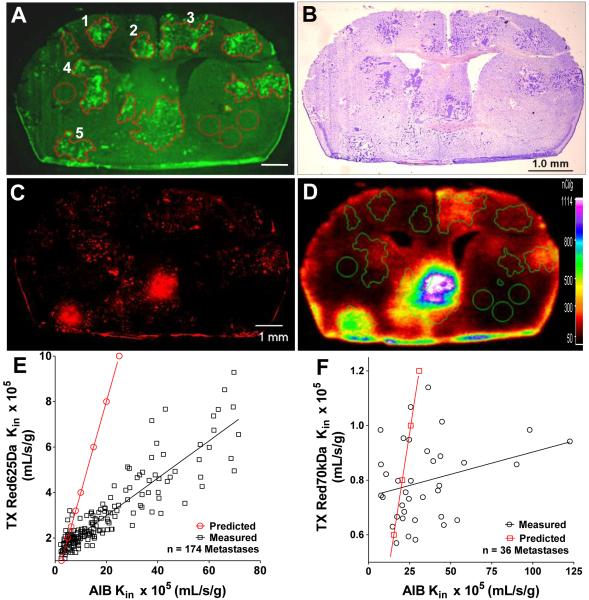
Once we had determined that our method was in general agreement for primary gliomas both in terms of regional permeability changes and in pore sizes/surface area, we applied the method to study brain metastases of breast cancer. We observed that changes in permeability from normal brain differed broadly among individual metastasis; representative images are shown in Fig 3A-D. As can be seen qualitatively in Fig 3, lesions one and two have an increased permeability compared to normal brain, yet are substantially less than lesion five. Of interest the mid-line lesion in Fig 3 had the highest permeability in this sample. We have recently shown that increased expression of a desmin+ subpopulation of pericytes and reduced CD13+ pericytes and laminin α2 correlates with increased permeability (33). The heterogeneous brain metastases of breast cancer model data is in sharp contrast to the relatively homogenous glioma to glioma permeability observed in different animals. Based on historical reports (18), it is important to note that the BTB permeability had only a weak correlation with metastasis size (Fig 3E and F). Quantitatively, of n=174 231BR-Her2 metastases ~9% showed no statistical difference in permeability form normal brain, whereas ~75% showed relatively modest permeability increases. Only ~15% of the metastases demonstrated TX Red 625Da permeability changes that were greater than 5 fold.

Figure 3.

Representative fluorescent and bright field images of metastases developed after left cardiac injection of MDA-MB-231Br-Her2 cells. Images of the same brain sections showing eGFP tumors (A), Cresyl violet stain (B), brain accumulation of TX Red 625Da (C), and ¹⁴C-AIB accumulation (D). Heterogenous permeability is evident in this image (A-D) where metastases 1 and 2 have relatively low tracer accumulation, lesion 3 and 4 have intermediate accumulation and lesion 5 has a relative high accumulation. A correlation of permeability between ¹⁴C-AIB and TX Red 625Da, TX Red 70kDa is shown in E and F. The red line in E and F is the predicted line of permeability for each tracer assuming there is no steric restriction in vascular pores for the water soluble molecules to enter into tumor tissue.

While there were significant permeability changes in most metastatic lesions in both models, the changes were much less on average compared to the glioma model. Therefore, we set out to determine if there were differences in the size of the pores in the metastatic vasculature which would limit accumulation of the tracer. In our analysis of the data we observed a highly significant correlation (r²=0.81) between the uptake of ¹⁴C-AIB and TX Red 625Da measured in the same metastases (Fig 3E). However, the observed diffusion rate for TX Red 625Da was only ~50% of what would be predicted (Table 2, Fig 3E red line) if the molecule was able to freely diffuse across vascular pores without steric hindrance. To verify this in a second set of experiments, we simultaneously injected the larger TX Red 70 kDa dextran with ¹⁴C-AIB in animal that had metastatic lesions. Evaluation of this data showed no correlation of uptake with ¹⁴C-AIB (Fig 3F) and the uptake of the larger dextran was also not consistent with pore diffusivity parameters predicted by ¹⁴C-AIB (Table 2; Fig 3F- red line). Using this data we then calculated the pore size present in the metastatic lesions to be ~10 fold smaller than what was observed in the glioma vasculature. This data strongly suggests that the metastatic vasculature is not near as porous or leaky as what is found in the primary glioma model. The implication is that chemotherapeutic uptake in metastases will be significantly restricted in comparison to gliomas.

Table 2.

Blood to brain transfer and aqueous diffusion constants for brain metastases

	Mean Kin (mL/s/g×105)	~ Dw (cm2/s×107)
TX Red 625Da	3	40
AIB	19.4	98
AIB/TX Red 625Da Ratio	6.3	2.5
TX Red 70kDa	0.8	3.8
AIB	34.2	98
AIB/TX Red 70kDa Ratio	42.8	25.7

The ratio of the unidirectional uptake of the water soluble tracers should be nearly equal to the ratio of the tracers respective aqueous diffusion constant; D_w. This ratio has <70% equality for TX Red 625Da, TX Red 70kDa dextran and ¹⁴C-AIB. The data suggests that the vascular pores in brain metastases restrict molecules the size of larger chemotherapeutics (~1000 Da) and biologic therapeutics (>100 kDa).

Discussion

Surprisingly, while metastases are the most common intracranial lesion (34) there has been very little quantitative data on permeability changes in metastases, especially compared to the primary tumor literature. Most information on brain metastasis permeability in humans is qualitative based upon CT or MRI enhancement (34) and there are only a few preclinical data sets which have used a physiological model of brain metastasis where the hematologic transfer, implantation, and lesion growth in brain is preserved (4,18,35,36). The permeability data presented herein is consistent with our previous report showing there is substantial variability between lesions (12), which differs from primary tumors (see Supplemental Figs s1-s3 for images showing variability in tumor permeability to the different dyes).

In this work we have examined the tumor vascular permeability using quantitative fluorescent microscopy. Crucial to the development of this methodology was the ability to quantify fluorescent dye concentration in tissue similar to what has been documented for radioisotopes in QAR studies. Briefly this was accomplished by summing the fluorescent intensity of each fluorophore in each pixel in a defined region of interest (e.g., brain homogenates, brain, tumor, etc…). Then all images (standards and experimental) were captured using the same settings for gain, exposure, optical zoom, on naïve samples (focus was obtained in the eGFP channel) to maintain consistency of fluorescence emission (37). Using this method the brain homogenates and blood standards had a range of linearity between fluorescent intensity and dye concentrations of ~ 3 log units which is consistent with most QAR standards (12). This range was large enough for us to give peripheral doses of dyes that produced at the time of sacrifice brain and tumor dye concentrations which fell within the midpoint of the standards.

One limitation in these studies, that had to be overcome, was that the standard curves of fluorescent intensity versus concentration had different slopes in blood and brain. This data, similar to previous work (38), suggested that tissue matrices can alter fluorescent emission. Attenuation of fluorescent signal by blood is a well-documented phenomenon where the emitted photons of fluorescence can be transferred to the heme moieties present in the red blood cell (39). The consequences of quenching the TX Red signal in our study had the possibility of altering two pieces of critical data. First, quenching could change the accuracy of our peripheral pharmacokinetics, by not allowing an accurate determination of dye concentration in blood. However, our pharmacokinetic parameters (Fig 1A; Table 3) are in close agreement with the two previous studies which used radiolabeled dextrans and scintillation counting (31). Further, the relationship between clearance and the molecular weight of the dextran shown Fig 1B is consistent with the clearance of fluorescein-labeled dextrans in rats using HPLC for analysis (29,40).

Table 3.

Peripheral pharmacokinetic parameters of TX Red and TX Red Dextran conjugates

	T1/2 (min)	AUC (mg.min/mL)	Clearance (mL/min/kg)
TX Red 625Da	1.3 ± 0.1	0.07 ± 0.01	42.1 ± 2.7
TX Red 3kDa	8.4 ± 0.2	0.7 ± 0.1	8.4 ± 0.8
TX Red 70kDa	29.2 ± 0.5	12.4 ± 0.7	0.49 ± 0.03

Pharmacokinetic parameters of the fluorophores used were calculated by sampling blood at various intervals and determining concentrations from the standard curve. Values represent Mean ±

The second concern that fluorescent quenching in blood created in this study was a potential misrepresentation of dye concentration for the end distribution volume of in brain. This could be compounded by differences in tissue accumulation in the active growing regions of the tumor versus a necrotic core. While some necrosis is evident in an RG-2 model, consistent with our previous work the brain metastases of breast cancer model, shows little evidence of necrosis (12,21). While this cannot be easily rectified, we believe that the small volume of blood per mass of tissue (assumed to be ~1% in normal brain and possibly as high as 4% in tumor or tumor core) did not significantly affect the calculated permeability value. For example, TX Red 3kDa dextran has a molecular radius in fluid of ~15.9 A° (41,42) for which we obtained a mean K_in value of ~4.0 × 10⁻⁶ mL/s/g in normal brain (Fig 3). In comparison, ¹⁴C-inulin (MW 5.5 kDa) has a similar radius of ~15 A° (31) for which a permeability value of ~2.2 × 10⁻⁶ mL/s/g was observed using radiolabeled isotopes and similar mathematical modeling (43). The observed permeability changes (fold increase) in tumor, which based upon size, is consistent with the magnitude of change observed in prior literature.

Once we had determined that our method was general validity in measuring the permeability alterations in tumor vasculature, we determined the size of pores in the tumors. Our data suggests that there is substantial discrepancy between the size of the molecule which can freely diffuse into gliomas and metastatic lesions. To make this comparison mathematically, we calculated the size of the vascular pores based upon theories of pore diffusivity. The pore theory model postulates water soluble tracers that are trapped to a large degree in the normal brain vasculature will enter into tumor tissue through “cylindrical pores” or channels in the newly formed vasculature. Further if the pores are large enough the molecules should enter into the tumor tissue at a transfer rate that is proportionately similar to their diffusion rates in water. For the glioma model the largest Dextran tested (70kDa) diffused across the tumor vasculature at approximately the same ratio rate (compared to ¹⁴C-AIB) as it would in water. This suggests that the 70kDa dextran (~12 nm in diameter) is able to freely diffuse from blood through angiogenic vascular pores into tumor. In order for this free diffusion to occur the diameter of the vascular pore must be at least 12x greater than the diameter of the largest molecule for which the diffusion constant remained proportionately constant (5), and accordingly the diameter of the vascular pore in the RG-2 tumor is ≥ 140 nm. These calculations assume that molecules with similar hydrodynamic radii have similar rates of permeability across a vascular pore. However, there are data demonstrating that nanorods have increased permeability rates across a tumor vessel compared to a similar hydrodynamic sized nanosphere. It is thought that the nanorod may have reduced steric hindrance and viscous drag during vascular flow and as it inters the vascular pore (44).

While tertiary and quaternary structured proteins are different in shape to an aqueous dextran, in theory, the pore size of the glioblastoma vasculature is sufficiently large to allow the 149 kDa, monoclonal antibody (~10 nm in size (45)) to freely accumulate into tumor tissue, and may be a reason bevacizumab and other monoclonal antibodies are showing promise in the treatment of gliomas (46). It can also be reasoned that VEGF (~3 nm) can exit from the tumor into the circulation through these vascular pores. Since the VEGR-2 is expressed approximately symmetrically on the luminal and abluminal side of the blood (47), we propose bevacizumab may pharmacologically act in the circulation as well to reduce effects of VEGF on the vasculature. This hypothesis is consistent and builds upon previous work that suggests normalization of the vasculature by blockade of the VEGFR-2 allows the permeability of smaller nanometer molecules (<12nm) across the tumor vasculature (48). This may be a primary reason there are concerns that bevacizumab may normalize the BTB and limit chemotherapeutic efficacy and allow tumor growth (49,50).

In contrast to glioma model which showed large pores allowing unrestricted passive diffusion of large molecules, in the brain metastases of breast of cancer model there was a ~40-60% restriction in both the TX Red and TX Red 70kDa compared to their proportionate diffusion rates in water. This degree of restriction suggests that there is steric hindrance in the pore for free diffusion of large molecules (5). Using similar calculations from the glioma model the pore size may be only ~9 nm in diameter and may be as small as ~5 nm based upon the size of free TX Red. Though these are average measurements and the spread of the actual pore sizes in the vasculature is most likely very heterogeneous. Importantly, if the free dye and the 70kDa dextran demonstrated significantly restricted permeability then trastuzumab at an approximate size of 5.5-6 nm will be restricted from diffusing across vascular pores into the metastatic lesion as well. However, we propose similar to gliomas, VEGF may be able to cross the vascular pores (though in a more restricted fashion) from the tumor into the circulation and this may be a factor in how bevacizumab is able to demonstrate anti-angiogenic effects in brain metastases.

In summary, the data presented herein have shown in pre-clinical models that: 1) permeability of brain metastases is highly heterogenous and significantly reduced compared to gliomas, 2) there are pore size restrictions which may limit the use of monoclonal antibodies in metastatic lesions and 3) the location for the action for bevacizumab in brain metastases may be limited to the luminal side of the vasculature.