Maximum Likelihood Reconstruction for Magnetic Resonance Fingerprinting

Abstract

This paper introduces a statistical estimation framework for magnetic resonance (MR) fingerprinting, a recently proposed quantitative imaging paradigm. Within this framework, we present a maximum likelihood (ML) formalism to estimate multiple parameter maps directly from highly undersampled, noisy k-space data. A novel algorithm, based on variable splitting, the alternating direction method of multipliers, and the variable projection method, is developed to solve the resulting optimization problem. Representative results from both simulations and in vivo experiments demonstrate that the proposed approach yields significantly improved accuracy in parameter estimation, compared to the conventional MR fingerprinting reconstruction. Moreover, the proposed framework provides new theoretical insights into the conventional approach. We show analytically that the conventional approach is an approximation to the ML reconstruction; more precisely, it is exactly equivalent to the first iteration of the proposed algorithm for the ML reconstruction, provided that a gridding reconstruction is used as an initialization.

I. Introduction

Magnetic resonance (MR) fingerprinting [1] provides a new quantitative imaging paradigm for simultaneously obtaining multiple tissue-specific parameters (e.g., T₁, T₂, spin density) in an efficient imaging experiment. The success of this technique is largely attributed to an ingenious design of incoherent signal excitation and data acquisition schemes. More specifically, it applies a set of randomized flip angles and repetition times to stimulate a sequence of images with randomly varied contrast weightings, contributing to the temporal incoherence; it further uses a set of highly undersampled variable density spiral trajectories to acquire k-space data, leading to the spatial incoherence.

With incoherent data, the conventional MR fingerprinting reconstruction in [1] employs a simple non-iterative procedure: it first performs a gridding reconstruction [2], [3], from which it then estimates unknown parameters by pattern matching. More specifically, given a range of parameters of interest, it constructs a dictionary that contains all possible signal (or magnetization) evolutions simulated from the Bloch equation. Afterwards, voxel-by-voxel pattern matching is performed. This selects a template signal evolution from the dictionary that yields the maximum correlation with the observed signal from the gridding reconstruction. Accordingly, the reconstructed parameters are assigned as those that generate the selected template signal evolution.

Although the conventional reconstruction approach is computationally efficient, it is heuristic in nature, i.e., there is no theoretic optimality associated with the reconstructed parameter maps. Moreover, its practical utility can often be limited by the inherent trade-off between accuracy and acquisition time, especially for applications requiring broad volumetric coverage [4]. Recently, a number of advanced reconstruction approaches, including [5]–[8], have been proposed, resulting in improved accuracy or even higher computational efficiency. For example, in the context of compressed sensing, low-dimensional signal models, including the sparse model [5] and manifold model [6], have been leveraged to enable accurate reconstruction with reduced acquisition time. To enhance the computational efficiency, [7] utilized a low-rank/subspace structure to reduce the dimensionality of the dictionary, whereas [8] developed a group matching strategy for rapid template search.

In this work, we introduce a statistical estimation framework for MR fingerprinting reconstruction, and formulate the reconstruction problem into a maximum likelihood (ML) estimation formalism. To solve the resulting optimization problem, a novel solution algorithm, based on variable splitting (VS) [9]–[11], alternating direction method of multipliers (ADMM) [11]–[13], and variable projection (VARPRO) methods [14]–[18], is described. The proposed algorithm features a unique variable splitting strategy that separates the Bloch equation based physical model from the data model. It allows simultaneous estimation of multiple parameters of interest, in a voxel-by-voxel fashion, through solving a subproblem of the ADMM iteration. This is done by using the VARPRO algorithm within the discrete optimization framework. Results from both simulations and in vivo experiments are shown to demonstrate the improvement in parameter estimation with the proposed approach.

The proposed framework also provides new theoretical insights into the conventional approach. In particular, we bridge the gap between the conventional approach and the statistically principled approach, i.e., ML reconstruction, by showing that with a gridding reconstruction as an initialization, the first iteration of the proposed algorithm for ML estimation exactly produces the conventional approach. With subsequent iterations, the reconstruction can be pushed toward an ML optimum, which has improved estimation performance. A preliminary account of this work was presented in [19].

II. Proposed Approach

A. Formulation

In MR fingerprinting, the contrast-weighted image I_m (x) can be parameterized as [6], [20], [21]:

$$I_m(\mathbf{x})=\rho (\mathbf{x}){\varphi }_m(T_1(\mathbf{x}),T_2(\mathbf{x}))),$$ (1)

for m = 1, ⋯, M, where ρ(x) denotes the spin density, T₁ (x) the longitudinal relaxation time, T₂ (x) the transverse relaxation time, and ϕ_m(·) the contrast-weighting function associated with the mth acquisition parameter (e.g., the flip angle α_m and repetition time TR_m). Note that ϕ_m(·) in (1) is determined by the Bloch equation based magnetization dynamics, driven by the acquisition parameters ${\{({\alpha }_t,{\text{TR}}_t)\}}_{t=1}^m$. However, distinct from conventional MR parameter mapping [20], [21], the analytical form of ϕ_m (·) can be difficult to obtain in MR fingerprinting (though it is feasible to determine ϕ_m numerically via Bloch simulations).

For simplicity, hereafter we use a discrete image model in which (1) can be represented as

$${\mathbf{I}}_m={\mathbf{\Phi }}_m({\mathbf{T}}_1,{\mathbf{T}}_2)\mathbf{\rho },$$ (2)

where I_m and ρ are N × 1 complex vectors, T₁, and T₂ are all N × 1 real vectors, and Φ_m (·) ∈ ℂ^N×N is a diagonal matrix with [Φ_m]_n,n = ϕ_m(T₁[n], T₂[n]). Moreover, under this setting, the imaging equation can be written as

$${\mathbf{d}}_{m,c}={\mathbf{F}}_m{\mathbf{S}}_c{\mathbf{I}}_m+{\mathbf{n}}_{m,c},$$ (3)

for m = 1, ⋯, M, and c = 1, ⋯, N_c, where d_m,c ∈ ℂ^P, and n_m,c ∈ ℂ^P respectively contain the measured k-space data and measurement noise from the cth receiver coil at TR_m, F_m ∈ ℂ^P×N denotes the undersampled Fourier encoding matrix, S_c ∈ ℂ^N×N is a diagonal matrix with the diagonal entries containing the coil sensitivities associated with the cth receiver coil, and N_c denotes the total number of receiver coils. Note that (3) includes both single-channel acquisitions (i.e., N_c = 1) and multichannel acquisitions (i.e., N_c > 1) as the special cases. For multichannel acquisitions, we have the following assumptions: 1) ${\{{\mathbf{S}}_c\}}_{c=1}^{N_c}$ is not time-varying; and 2) ${\{{\mathbf{S}}_c\}}_{c=1}^{N_c}$ is known or can be accurately pre-estimated (e.g., via a pilot scan).

Substituting (2) into (3), we have the following data model:

$${\mathbf{d}}_{m,c}={\mathbf{F}}_m{\mathbf{S}}_c{\mathbf{\Phi }}_m({\mathbf{T}}_1,{\mathbf{T}}_2)\mathbf{\rho }+{\mathbf{n}}_{m,c},$$ (4)

which describes the data generating process, from the underlying tissue MR parameters, to magnetization dynamics, to measured data. Equation (4) is a nonlinear model, due to the dependency of magnetization dynamics on {T₁,T₂} and the multiplicative coupling between Φ_m (T₁,T₂) and ρ. With respect to the noise, we assume: 1) for a fixed m and c, n_m,c can be modeled as additive complex white Gaussian noise; 2) n_m,c1 is correlated with n_m,c2, if c₁ ≠ c₂; and 3) n_m1,c1 is independent of n_m2,c2, whenever m₁ ≠ m₂. For multichannel acquisitions, we further assume that the noise covariance matrix is known or can be accurately pre-estimated (e.g., via a dummy scan), with which we can pre-whiten the colored Gaussian noise [22].

The goal of MR fingerprinting reconstruction is to estimate {T₁,T₂, ρ} from highly undersampled, noisy k-space data ${\{{\mathbf{d}}_{m,c}\}}_{m,c=1}^{M,N_c}$. Given the above data model and noise characteristics, the reconstruction problem can be formulated as the following ML estimation problem:

$$\left\{{\widehat{\mathbf{T}}}_1,{\widehat{\mathbf{T}}}_2,\widehat{\mathbf{\rho }}\right\}=arg\underset{{\mathbf{T}}_1,{\mathbf{T}}_2,\mathbf{\rho }}{min}\sum _{c=1}^{N_c}\sum _{m=1}^M{\Vert {\stackrel{\sim }{\mathbf{d}}}_{m,c}-{\mathbf{F}}_m{\stackrel{\sim }{\mathbf{S}}}_c{\mathbf{\Phi }}_m({\mathbf{T}}_1,{\mathbf{T}}_2)\mathbf{\rho }\Vert }_2^2,$$ (5)

where d̃_m,c and S̃_c respectively denote the measured data and sensitivity maps after noise prewhitening. Note that (5) enables direct parameter estimation from highly undersampled k-space data, as opposed to the conventional approach in which unknown parameters are estimated from severely aliased images generated by the gridding reconstruction. For notational simplicity, hereafter we use θ = {T₁,T₂} to denote the unknown parameters in Φ_m (·).

B. Solution Algorithm

Equation (5) results in a large-scale nonlinear least-squares problem. There are a number of key challenges associated with solving this problem:

• The cost function in (5) is a nonconvex, implying that the success of an iterative algorithm can critically depend on its initialization.

• Equation (5) optimizes over a large set of variables that are at very distinct scales. This leads to difficulty of applying a generic nonlinear optimization method, such as the nonlinear conjugate gradient (CG) method [23], which often needs careful variable rescaling (e.g., [21], [24]).

• The lack of an analytical expression for ϕ_m(·) makes it cumbersome to evaluate the cost function value and gradient in iterative algorithms, since each iteration involves Bloch simulations for all voxels, which can be computationally expensive.

Here we present a novel solution algorithm, integrating a variable splitting strategy, the alternating direction method of multipliers, and the variable projection method, to combat these difficulties. The main idea is to employ a special VS scheme and the ADMM method to convert (5) into a series of well-understood optimization problems that admit efficient solutions. In the following, we describe the proposed algorithm in detail.

First, we introduce a set of auxiliary variables ${\{{\mathbf{g}}_m\}}_{m=1}^M$ to split the parametric image model in (2) from the data consistency term in (5). For multichannel acquisitions, we also introduce another set of auxiliary variables, ${\{{\mathbf{h}}_{m,c}\}}_{m,c=1}^{M,N_c}$, to split the coil sensitivities [11]. As a consequence, (5) can be converted into the following equivalent constrained optimization problem:

$$\begin{array}{l}\underset{\mathbf{\rho },\mathbf{\theta },{\mathbf{g}}_m,{\mathbf{h}}_{m,c}}{min}\sum _{m=1}^M\sum _{c=1}^{N_c}{\Vert {\stackrel{\sim }{\mathbf{d}}}_{m,c}-{\mathbf{F}}_m{\mathbf{h}}_{m,c}\Vert }_2^2,\\ \text{s.t.}{\mathbf{g}}_m={\mathbf{\Phi }}_m(\mathbf{\theta })\mathbf{\rho }\text{and}{\mathbf{h}}_{m,c}={\stackrel{\sim }{\mathbf{S}}}_c{\mathbf{g}}_m,\end{array}$$ (6)

for m = 1, ⋯, M, and c = 1, ⋯, N_c.

Second, we apply the ADMM method [11]–[13] to solve (6). Specifically, the associated augmented Lagrangian function can be formed as follows:

$$\begin{array}{l}{\mathcal{L}}_A(\mathbf{\rho },\mathbf{\theta },\{{\mathbf{g}}_m\},\{{\mathbf{h}}_{m,c}\})=\sum _{m=1}^M\sum _{c=1}^{N_c}\{{\Vert {\stackrel{\sim }{\mathbf{d}}}_{m,c}-{\mathbf{F}}_m{\mathbf{h}}_{m,c}\Vert }_2^2+\\ \mathbf{Re}(<{\mathbf{x}}_{m,c},{\mathbf{h}}_{m,c}-{\stackrel{\sim }{\mathbf{S}}}_c{\mathbf{g}}_m>)+\frac{{\mu }_h}{2}{\Vert {\mathbf{h}}_{m,c}-{\stackrel{\sim }{\mathbf{S}}}_c{\mathbf{g}}_m\Vert }_2^2\}+\\ \sum _{m=1}^M\left\{\mathbf{Re}<{\mathbf{y}}_m,{\mathbf{g}}_m-{\mathbf{\Phi }}_m(\mathbf{\theta })\mathbf{\rho }>+\frac{{\mu }_g}{2}{\Vert {\mathbf{g}}_m-{\mathbf{\Phi }}_m(\mathbf{\theta })\mathbf{\rho }\Vert }_2^2\right\}\end{array}$$ (7)

where x_m,c and y_m are the Lagrangian multipliers, μ_g, μ_h > 0 are the penalty parameters, and Re takes the real part of a complex number. We iteratively minimize (7) by solving the following subproblems:

$$\{{\mathbf{\rho }}^{(k+1)},{\mathbf{\theta }}^{(k+1)}\}=arg\underset{\mathbf{\rho },\mathbf{\theta }}{min}{\mathcal{L}}_A(\mathbf{\rho },\mathbf{\theta },\{{\mathbf{g}}_m^{(k)}\},\{{\mathbf{h}}_{m,c}^{(k)}\}),$$ (8)

$$\{{\mathbf{g}}_m^{(k+1)}\}=arg\underset{\{{\mathbf{g}}_m\}}{min}{\mathcal{L}}_A({\mathbf{\rho }}^{(k+1)},{\mathbf{\theta }}^{(k+1)},\{{\mathbf{g}}_m\},\{{\mathbf{h}}_{m,c}^{(k)}\}),$$ (9)

$$\{{\mathbf{h}}_{m,c}^{(k+1)}\}=arg\underset{\{{\mathbf{h}}_{m,c}\}}{min}{\mathcal{L}}_A({\mathbf{\rho }}^{(k+1)},{\mathbf{\theta }}^{(k+1)},\{{\mathbf{g}}_m^{(k+1)}\},\{{\mathbf{h}}_{m,c}\}),$$ (10)

and updating the Lagrangian multipliers:

$$\begin{array}{lll}{\mathbf{x}}_{m,c}^{(k+1)}\hfill & =\hfill & {\mathbf{x}}_{m,c}^{(k)}+{\mu }_h\left[{\mathbf{h}}_{m,c}^{(k+1)}-{\stackrel{\sim }{\mathbf{S}}}_c{\mathbf{g}}_m^{(k+1)}\right],\hfill \\ {\mathbf{y}}_m^{(k+1)}\hfill & =\hfill & {\mathbf{y}}_m^{(k)}+{\mu }_g\left[{\mathbf{g}}_m^{(k+1)}-{\mathbf{\Phi }}_m\left({\mathbf{\theta }}^{(k+1)}\right){\mathbf{\rho }}^{(k+1)}\right],\hfill \end{array}$$

until the solution change between consecutive iterations is less than the tolerance ε, or the maximum number of iterations K_max is reached. Next, we describe the detailed solutions to (8)–(10).

1) Solution to (8)

The subproblem in (8) can be written as

$$\{{\mathbf{\rho }}^{(k+1)},{\mathbf{\theta }}^{(k+1)}\}=arg\underset{\mathbf{\rho },\mathbf{\theta }}{min}\sum _{m=1}^M{\Vert {\mathbf{g}}_m^{(k)}+\frac{1}{{\mu }_g}{\mathbf{y}}_m^{(k)}-{\mathbf{\Phi }}_m(\mathbf{\theta })\mathbf{\rho }\Vert }_2^2.$$ (11)

This is a nonlinear least-squares fitting problem, which is decoupled for each voxel, i.e.,

$$\{{\mathbf{\rho }}_n^{(k+1)},{\mathbf{\theta }}_n^{(k+1)}\}=arg\underset{{\mathbf{\rho }}_n,{\mathbf{\theta }}_n}{min}{\Vert {\mathbf{u}}_n^{(k)}-\mathbf{z}({\mathbf{\theta }}_n){\mathbf{\rho }}_n\Vert }_2^2,$$ (12)

for n = 1, ⋯,N, where ρ_n and θ_n respectively denote the nth element of ρ and θ, z(θ_n) = [ϕ₁(θ_n), ⋯, ϕ_M(θ_n)]^T, ${\mathbf{u}}_n^{(k)}={\left[{\mathbf{g}}_{1,n}^{(k)}+\frac{1}{{\mu }_g}{\mathbf{y}}_{1,n}^{(k)},\cdots ,{\mathbf{g}}_{M,n}^{(k)}+\frac{1}{{\mu }_g}{\mathbf{y}}_{M,n}^{(k)}\right]}^T$, and g_m,n and y_m,n denote the nth element of g_m and y_m, respectively.

Equation (12) has a separable structure, i.e., with a fixed value of θ, it reduces to a linear least-squares problem with respect to ρ. A class of algorithms based on variable projection (VARPRO) [14]–[18] can efficiently solve this type of problems. The VARPRO method expresses the update for { ${\mathbf{\rho }}_n^{(k+1)},{\mathbf{\theta }}_n^{(k+1)}$} as follows¹:

$${\mathbf{\theta }}_n^{(k+1)}=arg\underset{{\mathbf{\theta }}_n}{max}\frac{\left|<{\mathbf{u}}_n^{(k)},\mathbf{z}({\mathbf{\theta }}_n)>\right|}{{\Vert \mathbf{z}({\mathbf{\theta }}_n)\Vert }_2{\Vert {\mathbf{u}}_n^{(k)}\Vert }_2},$$ (13)

and

$${\mathbf{\rho }}_n^{(k+1)}=\frac{<{\mathbf{u}}_n^{(k)},\mathbf{z}({\mathbf{\theta }}_n^{(k+1)})>}{{\Vert \mathbf{z}\left({\mathbf{\theta }}_n^{(k+1)}\right)\Vert }_2^2},$$ (14)

Note that it can be shown that solving (13) and (14) together can yield the same set of optimal solutions as (12) (see [15] for more details). With VARPRO, ρ_n is separated from the optimization problem (12), resulting in a simpler problem in (13). This problem basically determines a set of parameters for the nth voxel, which generates magnetization dynamics having the maximum correlation with ${\mathbf{u}}_n^{(k)}$. Although (13) is more amenable to generic nonlinear optimization methods, applying these methods still involves Bloch simulations, which can be time consuming. Inspired by [16]–[18] and the idea from MR fingerprinting [1], here we bypass this issue by reformulating (13) as a discrete optimization problem. More specifically, we discretize the feasible search space of θ_n into a finite set of parameters ${\{{\mathbf{v}}_q\}}_{q=1}^Q$, with which we use Bloch simulations to generate a dictionary that contains all possible signal evolutions, i.e., ${\{\mathbf{z}({\mathbf{v}}_q)\}}_{q=1}^Q$. After that, a global optimization of (13) can be performed via a grid search, i.e.,

$$\begin{array}{lll}\hfill {\widehat{q}}_n& =\hfill & arg\underset{q=1,\cdots ,Q}{max}\frac{\left|<{\mathbf{u}}_n^{(k)},\mathbf{z}({\mathbf{v}}_q)>\right|}{{\Vert {\mathbf{u}}_n^{(k)}\Vert }_2{\Vert \mathbf{z}({\mathbf{v}}_q)\Vert }_2},\hfill \\ \hfill {\mathbf{\theta }}_n^{(k+1)}& =\hfill & {\mathbf{v}}_{{\widehat{q}}_n}.\hfill \end{array}$$ (15)

Note that the above scheme requires constructing the dictionary only once, which avoids repeating Bloch simulations for every voxel at each iteration.

2) Solution to (9)

The subproblem in (9) is a linear least-squares problem, which is decoupled for each g_m. It is equivalent to solving the following normal equation:

$$\left(\frac{{\mu }_h}{2}\sum _{c=1}^{N_c}{\stackrel{\sim }{\mathbf{S}}}_c^H{\stackrel{\sim }{\mathbf{S}}}_c+\frac{{\mu }_g}{2}\mathbf{I}\right){\mathbf{g}}_m^{(k+1)}={\mathbf{u}}^{(k+1)},$$ (16)

where

$${\mathbf{u}}^{(k+1)}=\frac{{\mu }_g}{2}\left[{\mathbf{\Phi }}_m\left({\mathbf{\theta }}^{(k+1)}\right){\mathbf{\rho }}^{(k+1)}-\frac{1}{{\mu }_g}{\mathbf{y}}_m^{(k)}\right]+\frac{{\mu }_h}{2}\sum _{c=1}^{N_c}{\stackrel{\sim }{\mathbf{S}}}_c^H\left({\mathbf{h}}_{m,c}^{(k)}+\frac{1}{{\mu }_h}{\mathbf{x}}_{m,c}^{(k)}\right).$$

Noting that $\left(\frac{{\mu }_h}{2}{\sum }_{c=1}^{N_c}{\stackrel{\sim }{\mathbf{S}}}_c^H{\stackrel{\sim }{\mathbf{S}}}_c+\frac{{\mu }_g}{2}\mathbf{I}\right)$ is a diagonal matrix, (16) can be efficiently solved by an entry-by-entry inversion.

Algorithm 1.

Proposed algorithm for (5).

3) Solution to (10)

The subproblem in (10) is also a linear least-squares problem, which is decoupled for each h_m,c. Its solution can be obtained by solving

$$\left({\mathbf{F}}_m^H{\mathbf{F}}_m+\frac{{\mu }_h}{2}\mathbf{I}\right){\mathbf{h}}_{m,c}^{(k+1)}={\mathbf{F}}_m^H{\stackrel{\sim }{\mathbf{d}}}_{m,c}+{\mathbf{v}}_{m,c}^{(k+1)},$$ (17)

where ${\mathbf{v}}_{m,c}^{(k+1)}=\frac{{\mu }_h}{2}\left({\stackrel{\sim }{\mathbf{S}}}_c{\mathbf{g}}_m^{(k+1)}-\frac{1}{{\mu }_h}{\mathbf{x}}_{m,c}^{(k)}\right)$. Note that for arbitrary k-space trajectories, the Gram matrix ${\mathbf{F}}_m^H{\mathbf{F}}_m$, or the coefficient matrix of (17), has a block Toeplitz structure [25]. A number of off-the-shelf numerical solvers taking advantage of this structure enables very efficient solution of (17), including the pre-conditioned CG solvers (e.g., [26], [27]) and hierarchically semiseparable (HSS) solvers (e.g., [28], [29]).

4) Algorithm initialization

Considering that (5) is a non-convex optimization problem, the solution of the algorithm generally depends on the initialization. Here, we initialize ${\mathbf{g}}_m^{(0)}$ with the gridding reconstruction (or coil-combined gridding reconstruction for the multichannel case), ${\mathbf{h}}_{m,c}^{(0)}={\stackrel{\sim }{\mathbf{S}}}_c{\mathbf{g}}_m^{(0)},{\mathbf{x}}_{m,c}^{(0)}=\mathbf{0}$, and ${\mathbf{y}}_m^{(0)}=\mathbf{0}$. Note that this initialization scheme is always feasible, and also very efficient to implement [3]. As will be demonstrated later, it consistently leads to good performance for the algorithm.

From a modeling/formulation standpoint, this initialization scheme eventually bridges the gap between the conventional MR fingerprinting reconstruction and ML reconstruction. In fact, the derivations in (11)–(15) for VARPRO has already yielded a matched filter based solution similar to the conventional approach. Here, given the above initialization (i.e., an appropriate ${\mathbf{u}}_n^{(0)}$), the proposed algorithm for ML estimation will exactly produce the conventional approach at its first iteration. Generally, the use of additional iterations can drive the solution toward an ML optimum, which has a number of desirable properties [30, Ch.7], such as asymptotic unbiasedness and asymptotic efficiency. In the next section, we will illustrate some of the benefits with concrete examples.

5) Computational complexity

It is worth analyzing the computational complexity of the proposed algorithm. For clarity, we summarize the overall algorithm in Algorithm 1. With the VS strategy and ADMM method, the original problem in (5) boils down to iteratively solving one parameter fitting problem and two structured linear least-squares problems. The parameter fitting problem in (8) is solved by the discrete VARPRO-based method on a voxel-by-voxel basis. For each voxel, this can be done in 𝒪(MQ) operations. Note that higher computational efficiency can be achieved by further integrating with the dictionary compression [7] or group search strategy [8]. The linear least-squares problem in (9) is decoupled for each time frame. Solving each subproblem only involves inverting a diagonal matrix, which can be done in 𝒪(N) operations. Regarding the linear least-squares problem in (10), it is decoupled with respect to each time frame and each coil, and each subproblem can be solved by the HSS solver in 𝒪(N log²N) operations [28].

III. Results

In this section, representative results from both simulations and in vivo experiments are shown to illustrate the performance of the proposed approach.

A. Simulation Results

A numerical brain phantom was designed to simulate single-channel MR fingerprinting experiments, in which the T₁, T₂, and spin density maps were taken from the Brainweb database [31], as shown in Fig. 1. The Bloch simulations were performed to generate a sequence of contrast-weighted images using the inversion recovery fast imaging with steady state precession (IR-FISP) sequence² in which the same set of flip angles and repetition times as in [32] were applied. For simplicity, we assume that the flip angle is uniform over the field of view. We set the acquisition matrix size as 256×256, and the field-of-view (FOV) as 300 × 300 mm². The same set of spiral trajectories as in [32] was used, and the k-space data were synthesized with the nonuniform fast Fourier transforms [33]. One spiral interleaf was acquired for each image frame (the fully sampled data consists of 48 interleaves). Complex white Gaussian noise was added to the measured data with the signal-to-noise ratio (SNR) defined as 20 log₁₀(s/σ), where s denotes the average signal intensity within a region of the white matter in the first contrast-weighted image, and σ denotes the standard deviation of the noise. For convenience, we use the number of TRs, as denoted by M, to measure the length of a MR fingerprinting acquisition, which corresponds to the total acquisition time $T={\sum }_{m=1}^M{\text{TR}}_m$.

Fig. 1.

Ground truth for the numerical phantom: (a) T₁ map, (b) T₂ map, and (c) spin density map.

We performed reconstructions using the conventional approach and the proposed ML approach. The gridding reconstruction involved in both approaches were performed on a 2X oversampled Cartesian grid, with an optimized Kaiser-Bessel convolution kernel [3] and Voronoi density compensation. Moreover, we used the same dictionary for both approaches based on the following parameter discretization scheme: 1) the possible T₁ values were set within [100, 5000] ms, with an increment of 10 ms for the range [100, 3000] ms and an increment of 200 ms for the range [3001, 5000] ms; and 2) the possible T₂ values were set within [1, 500] ms, with an increment of 5 ms. Additionally, we manually selected the penalty parameter to optimize the performance of the proposed ML reconstruction. Lastly, to assess the reconstruction accuracy, the following error metrics are used: 1) voxelwise relative error = |θ_n −θ̂_n|/θ_n, where θ_n and θ̂_n denote the true and reconstructed parameter at the nth voxel, respectively; and 2) overall error = ||θ − θ̂||₂/||θ||₂.³

1) General evaluation

We first demonstrate the benefit of the ML reconstruction in terms of improving the accuracy of parameter estimation. Specifically, we simulated a MR fingerprinting experiment with the acquisition length M = 300 and SNR = 40 dB, and performed reconstructions using the above two approaches. Fig. 2 (a), (c), and (e) respectively show the plots of overall error versus the number of iterations for the T₁, T₂, and spin density reconstructions using the ML reconstruction (the first iteration of the ML reconstruction produces the conventional approach). As can be seen, with the iterative procedure, the ML reconstruction leads to better accuracy than the conventional approach for all the parameter maps, where the improvements for the T₂ and spin density reconstructions are more pronounced. Furthermore, we show the reconstructed parameter maps and associated error maps produced at different number of iterations of the ML reconstruction in Fig. 2 (b), (d), and (f). This not only confirms the quantitative improvements shown before, but also illustrates how the iterative procedure refines the results qualitatively. In particular, notice that as the iteration progresses, the aliasing-like artifacts appearing in the T₂ and spin density maps are significantly reduced.

Fig. 2.

Evaluation of the ML reconstruction at different number of iterations with the acquisition length M = 300. (a) Overall error versus iteration number for T₁. (b) Reconstructed T₁ maps and associated relative error maps. (c) Overall error versus iteration number for T₂. (d) Reconstructed T₂ maps and associated relative error maps. (e) Overall error versus iteration number for spin density. (f) Reconstructed spin density maps and associated relative error maps. For each error map, the overall error is labeled at the lower right corner, and the regions associated with the background, skull, and scalp are set to be zero.

2) Influence of acquisition length

We have also evaluated the performance of the ML reconstruction with different acquisition lengths. Fig. 3 shows the reconstructed T₁, T₂, and spin density maps by the two approaches at M = 250, 500, and 1000. As expected, both approaches improve with the increase of acquisition length. However, note that the ML reconstruction not only outperforms the conventional approach for all three acquisition windows, but also exhibits better robustness to the change of acquisition length. It is worth noting that the ML reconstruction with M = 500 yields similar accuracy to the conventional approach with M = 1000, demonstrating its capability of reducing acquisition time. In Fig. 4, we plot the overall error versus acquisition length, which further confirms the benefit offered by the proposed ML approach.

Fig. 3.

Evaluation of the conventional approach and ML reconstruction with different acquisition lengths. (a)–(c): Reconstructed T₁ maps and associated relative error maps. (d)–(f): Reconstructed T₂ maps and associated relative error maps. (h)–(j): Reconstructed spin density maps and associated relative error maps. For each error map, the overall error is labeled at the lower right corner, and the regions associated with the background, skull, and scalp are set to be zero.

Fig. 4.

Overall error versus acquisition length for (a) T₁, (b) T₂, and (c) spin density maps from the conventional approach and ML reconstruction.

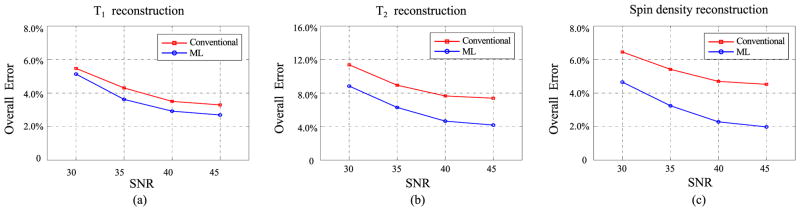
3) Influence of SNR

We have also evaluated the performance of the ML reconstruction at different noise levels. Specifically, we simulated the experiments at SNR = 30, 35, 40, and 45 dB, all of which were with M = 500. We performed reconstructions using the conventional approach and ML reconstruction. Fig. 5 shows the plots of overall error versus SNR for the reconstructed T₁, T₂, and spin density maps. It can be seen that the ML reconstruction consistently yields better accuracy than the conventional approach for all tested SNR levels.

Fig. 5.

Overall error versus SNR for (a) T₁, (b) T₂, and (c) spin density maps from the conventional approach and ML reconstruction.

4) Bias-variance analysis

We have also investigated the statistical properties of the proposed approach. Specifically, we conducted Monte Carlo (MC) simulations (with 100 trials) for the conventional approach and ML reconstruction at SNR = 35dB and M = 500. To compare the bias, variance, and mean square error at the same scale, the following normalized quantities are calculated for the nth voxel:

• 1)
  normalized bias:

  $${\text{NBias}}_n=\widehat{\mathbb{E}}\left[\left|{\mathbf{\theta }}_n-{\widehat{\mathbf{\theta }}}_n\right|\right]/{\mathbf{\theta }}_n,$$
• 2)
  normalized variance:

  $${\text{NVar}}_n=\sqrt{\widehat{\mathbb{E}}\left[{\left|{\mathbf{\theta }}_n-\widehat{\mathrm{E}}({\widehat{\mathbf{\theta }}}_n)\right|}^2\right]}/{\mathbf{\theta }}_n,$$
  and 3) normalized root-mean-square error:

  $${\text{NRMSE}}_n=\sqrt{\widehat{\mathbb{E}}\left[{\left|{\mathbf{\theta }}_n-{\widehat{\mathbf{\theta }}}_n\right|}^2\right]}/{\mathbf{\theta }}_n,$$

  where 𝔼̂(·) denotes the empirical mean evaluated for the MC simulations. Note that ${\text{NRMSE}}_n=\sqrt{{\text{NBias}}_n^2+{\text{NVar}}_n^2}$. Fig. 6 shows the maps of NBias, NVar, and NRMSE from the two reconstruction approaches. As can be seen, the ML reconstruction has significantly reduced bias compared to the conventional approach, which is consistent with the theoretical property that the ML estimation is asymptotically unbiased [30]. Moreover, it results in a similar level of variance to the conventional approach, except for the region of cerebrospinal fluid in the T₂ map and spin density map. But note that these regions are generally not of interest for neuroimaging. Lastly, by taking into account both the bias and variance, the ML reconstruction leads to improved NRMSE over the conventional approach.

Fig. 6.

Normalized bias, variance, and root-mean-square error for (a) T₁, (b) T₂, and (c) spin density estimation using the conventional approach and ML reconstruction at SNR = 35 dB and M = 500. Note that the regions associated with the background, skull, and scalp are set to be zero.

B. In Vivo Results

In this subsection, we show representative results of applying the proposed approach to in vivo MR fingerprinting experiments. Specifically, the experiments were performed on a 3T Siemens Tim Trio scanner (Siemens Medical Solutions, Erlangen, Germany) equipped with a 32-channel head coil. One healthy human subject was scanned using the IR-FISP sequence with the approval of the Institutional Review Board. The same sets of acquisition parameters and spiral trajectories as in [32] were used in the protocol, and one spiral interleaf was acquired for each acquisition parameter. Other relevant imaging parameters include: FOV = 300 × 300 mm², matrix size = 256×256, and slice thickness = 5 mm. Two slices were acquired with the acquisition lengths of 1400 and 1000 TRs, respectively. For each slice, we further collected a set of fully sampled data as reference by repeating the above acquisition multiples times, all with the same set of acquisition parameters, ${\{({\alpha }_m,{\text{TR}}_m)\}}_{m=1}^M$. But, in each repetition, we switched to a different spiral interleaf to acquire data for {(α_m, TR_m)} until all the interleaves had been collected.⁴ Here, to ensure that the magnetization returns to thermal equilibrium, a short delay was given before consecutive repetitions. Subsequently, we combined the measured data from different repetitions to form a set of fully sampled data for each {(α_m, TR_m)}. Additionally, we performed pilot scans with a rapid gradient echo (GRE) sequence, from which the coil sensitivity maps were estimated using the subspace method [34]. We also measured the actual spiral trajectories [35], rather than using the theoretical ones, to avoid the potential trajectory distortion caused by eddy currents and other hardware imperfections.

We performed the conventional MR fingerprinting reconstruction and ML reconstruction using the same set of data from a single acquisition. The same dictionary, as described in the simulations, was used for both approaches. We initialized the ML reconstruction with the coil combined gridding reconstruction, and manually selected the penalty parameters μ_g and μ_h for the optimized performance. Additionally, we reconstructed the contrast-weighted images from the fully sampled data, and then estimated the parameter maps as the underlying references.

For slice 1, we performed reconstructions with two acquisition lengths, i.e., M = 700 and 1400. Note that for M = 700, the data were retrospectively taken from the first half of the entire acquisition with 1400 TRs. Fig. 7 shows the T₁, T₂, and spin density maps obtained from the reference, conventional reconstruction, and ML reconstruction. Here, we also show the relative error map and overall error associated with each reconstruction for quantitative assessment. Clearly, both approaches yield improved performance, as the number of measurements doubles. However, the ML reconstruction outperforms the conventional approach for both acquisition lengths. Also, note that the ML reconstruction with M = 700 results in even higher accuracy than the conventional approach with M = 1400. In Fig. 8, we further show the relative error maps associated with the ML approach at different iterations with M = 700, illustrating how the accuracy was progressively improved. With respect to slice 2, we performed reconstructions at the original acquisition length, i.e., M = 1000. The related results are shown in the supplementary material, which further illustrates the performance of the proposed approach.

Fig. 7.

In vivo reconstructions for slice 1 with two acquisition lengths. (a) Reference T₁ map. (b)–(c): Reconstructed T₁ maps and associated relative error maps. (d) Reference T₂ map. (e)–(f): Reconstructed T₂ maps and associated relative error maps. (g) Reference spin density map. (g)–(h): Reconstructed spin density maps and associated relative error maps. For each error map, the overall error is labeled at the lower right corner, and the regions associated with the background, skull, and scalp are set to be zero.

Fig. 8.

Relative error maps associated with the ML reconstruction at different number of iterations. Here the acquisition length is M = 700. The three rows respectively show the relative error maps associated with the T₁, T₂, and spin density reconstructions. For each error map, the overall error is labeled at the lower right corner, and the regions associated with the background, skull, and scalp are set to be zero.

We also report the computational efficiency of the two reconstruction approaches, which were ran on a Linux workstation with 24 Intel Xeon E5-2643, 3.40 GHz processors and 128 GB RAM using Matlab R2013b. For both approaches, the dictionary for IR-FISP was pre-generated, which took about 14 min based on the extended phase graph formalism [32], [36]. Note that the dictionary only needs to be generated once, and then it can be saved for subsequent experiments. In terms of reconstruction, for the above in vivo data set, the conventional approach (including the gridding reconstruction and dictionary pattern matching) took about 1.5 min, whereas the ML reconstruction took about 32 min. Given the highly separable algorithmic structure, we expect that the computation time of the ML reconstruction could be substantially reduced with an optimized implementation on GPU. This is beyond the scope of this paper, but is worthwhile to explore in future work.

IV. Discussion

The effectiveness of the proposed ML reconstruction has been demonstrated for MR fingerprinting. It is worth making further comments on some points. First of all, it has been observed that both the conventional approach and ML reconstruction yield relatively accurate T₁ estimates, even when the acquisition time is short. This can be attributed to the design of the imaging sequence that applies an inversion preparation pulse at the beginning of acquisition, stimulating the T₁ recovery-like dynamics that dominate the early portion of signal evolutions (e.g., the first 200 TRs). Such type of magnetization dynamics typically exhibits higher sensitivity to the change of T₁ values, thus resulting in more accurate T₁ estimation.

The proposed formulation is based on the data model in (4), the fidelity of which impacts the accuracy of parameter estimation. In this work, we used the simple data model to illustrate the effectiveness of the ML-based formalism, although more sophisticated models could be adopted. For example, we could model the partial volume effect occurring at tissue interfaces by including more complex signal evolutions into the dictionary (e.g., [37]). Additionally, for certain applications, it may be desirable to incorporate an appropriate motion model (e.g., [38]) into (4) to compensate motion during acquisitions. However, these extensions generally lead to complex data models with more degrees of freedom, which often incurs higher SNR penalty for parameter estimation. Thus, their effectiveness depends on application-specific tradeoffs between model mismatch and noise contamination, which should be evaluated on a case-by-case basis.

Similar to the conventional approach [1], [32], this work assumes for simplicity that the transmit radiofrequency field (i.e., $B_1^{+}$) is homogeneous over the field of view. For in vivo brain imaging experiments at 3T, in which $B_1^{+}$ inhomogeneity is often not severe, such an assumption generally does not incur significant bias in parameter estimation. But for body imaging [39] or ultra-high field imaging [40], [41], strong B₁ inhomogeneity can result in severe bias for estimated parameter maps (especially for T₂ maps). In these scenarios, it is necessary to incorporate a spatially dependent $B_1^{+}(\mathbf{x})$ into the signal model (or signal evolution dictionary). To obtain $B_1^{+}(\mathbf{x})$, we can either conduct auxiliary scans (e.g., [42]) or perform joint estimation with other parameters of interest, although the latter may suffer from amplified variance in parameter estimation.

The proposed ADMM-based algorithm requires the selection of the penalty parameters μ_g and μ_h. For the nonconvex optimization problem in (5), we empirically observed that the solution of the algorithm did depend on the choice of penalty parameters⁵. In this work, we manually chose these parameters, with the reference to the fully sampled data, to optimize the performance of the algorithm. For practical applications, a useful way is to perform parameter selection based on a set of fully sampled calibration data acquired from a physical phantom (with a similar range of T₁ and T₂ values to the study), and then apply the selected parameters to subsequent experiments using the same imaging protocol and hardware configurations. Some preliminary investigations indicate the effectiveness of this approach, although it is worth studying the optimal parameter selection from a theoretical standpoint.

Statistical estimation provides a powerful framework to address the MR fingerprinting reconstruction problem. Within this framework, this paper described an ML approach for parameter estimation, and also proved that the conventional approach is equivalent to the first iteration of the proposed algorithm for ML estimation. There are a number of useful extensions that can be further pursued. For example, we can derive the estimation-theoretic bounds (e.g., [20], [21]) to characterize the performance of ML estimation. Also, these bounds can be utilized to optimally design MR fingerprinting experiments. Such an extension is under investigation, and will be reported in a subsequent work. Furthermore, we can incorporate a prior information on ${\{{\mathbf{I}}_m\}}_{m=1}^M$ and/or {ρ,θ} (e.g., [43]–[45]) to derive a penalized ML formulation for improved performance. A preliminary investigation along this line is presented in [46].

The proposed solution algorithm effectively tackles several key challenges of the ML reconstruction. It also provides a new way to address the computational problem associated with direct parameter estimation from k-space data arising in a variety of quantitative imaging applications, including the conventional MR parameter mapping⁶ (e.g., [20], [24]), quantitative diffusion imaging (e.g., [53], [54]), water-fat imaging (e.g., [55]), and contrast-enhanced imaging (e.g., [56]), which are worthwhile to explore in future research. Despite the empirical success, little is known about the convergence property of the proposed algorithm for solving the nonconvex optimization problem in (5), although the behavior of ADMM is well understood in the context of convex optimization [12]. Recently, there has been active research on analyzing alternating minimization algorithms for solving structured nonconvex optimization problems (e.g., [57]–[60]), which may provide useful insights into the theoretical characterization of the convergence of the proposed algorithm.

V. Conclusion

This work presented a maximum likelihood approach to MR fingerprinting reconstruction. A novel algorithm, integrating VS, the ADMM method, and the VARPRO method, was described to efficiently solve the resulting optimization problem. The proposed algorithm for the ML reconstruction includes the conventional approach as its first iteration, while rapidly improving reconstruction quality with additional iterations. The advantages offered by the proposed approach, including improving parameter estimation accuracy and reducing acquisition time, have been demonstrated with both simulations and in vivo experiments.