Probabilistic bias analysis in pharmacoepidemiology and comparative effectiveness research: a systematic review

Abstract

Purpose

We systematically reviewed pharmacoepidemiologic and comparative effectiveness studies that use probabilistic bias analysis to quantify the effects of systematic error including confounding, misclassification, and selection bias on study results.

Methods

We found articles published between 2010 and October 2015 through a citation search using Web of Science and Google Scholar and a keyword search using PubMed and Scopus. Eligibility of studies was assessed by one reviewer. Three reviewers independently abstracted data from eligible studies.

Results

Fifteen studies used probabilistic bias analysis and were eligible for data abstraction – nine simulated an unmeasured confounder and six simulated misclassification. The majority of studies simulating an unmeasured confounder did not specify the range of plausible estimates for the bias parameters. Studies simulating misclassification were in general clearer when reporting the plausible distribution of bias parameters. Regardless of the bias simulated, the probability distributions assigned to bias parameters, number of simulated iterations, sensitivity analyses, and diagnostics were not discussed in the majority of studies.

Conclusion

Despite the prevalence and concern of bias in pharmacoepidemiologic and comparative effectiveness studies, probabilistic bias analysis to quantitatively model the effect of bias was not widely used. The quality of reporting and use of this technique varied and was often unclear. Further discussion and dissemination of the technique are warranted.

Introduction

Stakeholders of pharmacoepidemiologic and comparative effectiveness research – including patients, clinicians, regulators, and policymakers – need to know the validity and degree of uncertainty of epidemiologic study findings to make important health-related decisions.^1–3 This includes an assessment of both random and systematic error (bias; e.g. confounding, misclassification, selection bias). Although researchers routinely estimate random error using confidence intervals or p-values,^4–6 few attempt to quantitatively evaluate the effects of bias despite concern that systematic error may be more impactful to study results in observational studies than random error;^7,8 this is particularly important when making causal claims and “arguably essential” when making policy recommendations.⁹

Quantitative bias analyses are sensitivity analyses that can assess the magnitude, direction, and uncertainty of bias through the simulation of bias parameters – the values required to estimate the effects of bias in an analysis.^{1–3,7,9–15} Probabilistic bias analysis offers several advantages because it balances incorporating uncertainty about bias parameters while requiring less expertise to implement than alternative strategies (e.g. Bayesian approaches);¹⁶ further, it can address common concerns of unmeasured confounding, misclassification, and selection bias when using claims data (see eTable 1).¹⁷ Probabilistic bias analysis is an extension of simple bias analysis applied by using Monte-Carlo techniques to repeatedly sample from investigator-assigned bias parameter distributions.^1–3,7,18 For each iteration, sampled bias parameter values are applied to simple bias analysis formulas to generate a single bias-adjusted estimate (Table 1); this process is repeated multiple times to generate a frequency distribution of bias-adjusted effect estimates (a simulation interval; most commonly summarized as a 95% simulation interval containing bias-adjusted estimates between the 2.5^th and 97.5^th percentiles).

Table 1.

General steps to implementing probabilistic bias analysis to simulate an unmeasured confounder, misclassification, or selection bias (modified from Lash, Fox, and Fink, 2009)^2*

Steps	Description
1. Identify source of bias to be addressed in probabilistic bias analysis	Prioritize modeling biases that may have the greatest impact on the conventional results based on a thorough review of the design, analysis, and limitations.9 Single or multiple biases can be readily incorporated into the bias analysis.2,7
2. Determine the bias model and whether it will be applied to crude estimates, adjusted estimates, or directly to individual records	Probabilistic bias analysis can be applied to crude effect estimates or stratified data. To apply probabilistic analysis to adjusted effect estimates (beyond stratification and pooling), investigators can simulate bias at the record-level or (in some cases) apply bias models directly to adjusted effect estimates. Applying probabilistic bias analysis to individual records can be time intensive but maintains the relationships between measured variables and allows for modeling.2,16 Unmeasured Confounder: can be applied to crude estimates,2,7,11 adjusted estimates,16 and to individual records.18 Misclassification: can be applied to crude estimates and individual records.2,3,7,11 It can only be applied to adjusted estimates under the assumption of nondifferential misclassification with perfect specificity and imperfect sensitivity.16 Selection bias – unequal selection probabilities: can be applied to crude summary estimates,2,7,11 adjusted summary estimates,2,7 or applied to individual records. Selection bias – loss to follow-up: can be applied to crude estimates of individual records.2,18
3. Identify bias parameters	Unmeasured confounder: Requires (when simulating binary confounder) estimates of the prevalence of the confounder in exposed groups and the strength between the confounder and outcome.† Misclassification: Requires estimates of classification probabilities (sensitivity/specificity and/or positive predictive value/negative predictive value). Addressing outcome misclassification in case-control studies also requires estimates of the sampling fractions for cases and controls.28 Selection bias – unequal selection probabilities: Requires estimates of each exposure-disease selection probability (assuming binary exposure and outcome) or the selection bias odds ratio.2,11 Selection bias – loss to follow-up: Requires estimates of outcome risk by exposure status and person-time to event.2,18
4. Assign probability distributions to bias parameters	Use internal validation data, external validation data, and expert judgement to define a range and central tendency of plausible values; choose a distribution shape that reflects the uncertainty about the bias parameters (see eFigure 1 for more detail).2,9
5. Sample from bias parameter distributions using Monte Carlo techniques and apply values to bias formulas to generate a single bias-adjusted estimate	Single bias parameters values are sampled from assigned probability distributions and applied to the bias model for a single bias-adjusted estimate. Investigators can create correlated bias parameter distributions.2,7,9 Misclassification: Under the scenario of differential misclassification, classification probabilities are hypothesized to be different between groups but are likely correlated; creating correlated bias parameter distributions is recommended.2,3,7,9
6. Save the single bias-adjusted estimate and repeat step 5	Repeatedly sample from bias parameters to generate a frequency distribution of bias adjusted estimates (a simulation interval).
7. Apply sensitivity analyses and diagnostics to bias model	Vary the location and spread of bias parameter distributions and applying different types of probability distributions to bias parameters.2,9 When using correlated bias parameter distributions, compare initial results to a bias model with independent bias parameter distributions.9 Diagnostics include generating histograms of bias parameters to ensure that the sampled distributions correspond to assigned distributions; the shape of the generated simulation interval should also be examined for implausible results.2,9 Misclassification: Some combinations of classification probabilities will generate implausible, negative cell-counts in contingency tables. These iterations are normally discarded. The frequency of discarded iterations should be reported.2,3,9
8. Summarize bias analysis results	Report median bias-adjusted estimate and simulation interval to summarize results of probabilistic bias analysis (also consider graphical presentations).2,9 Best practices include providing all methods, results, sensitivity analyses and diagnostics, and programming code used to implement the analysis (using online appendices).2,9
9. Interpret bias analysis results	Restate the assumptions of the bias analysis and focus on whether the modeled bias plausibly explains the conventional estimate.2,9 Do not interpret the simulation interval as having frequentist properties (e.g., null-hypothesis tests) or fully Bayesian properties (e.g., credibility interval).2,9 The simulation interval can be used for insight into the direction and magnitude of bias as well as providing a better estimate of total error (systematic and random error) about an effect estimate.2,9

^*Modified from the “General steps to probabilistic bias analysis” provided in Lash et al, 2009, p. 132.²

^†Alternative (but equivalent) formulas estimate only the relative risk due to confounding.^7,10,25 Other formulas to simulate multinomial or continuous unmeasured confounders, and unmeasured confounding in the presence effect-measure modification are available.^{2, 26}

Several factors have increased the ease of implementing probabilistic bias analysis including the availability of resources detailing best practices on implementation and reporting,^2,9 online appendices, and high-speed computing.¹⁹ However, no study has documented how probabilistic bias analyses have been conducted and reported in pharmacoepidemiologic and comparative effectiveness studies. To address this, we aimed to systematically review pharmacoepidemiologic and comparative effectiveness studies that used probabilistic bias analysis.

METHODS

Study selection

We implemented two separate search strategies: 1) MEDLINE (PubMed) and EMBASE (Scopus) from January 2010 to October 2015 using the keywords “bias analysis” OR “uncertainty analysis” OR “Monte-Carlo sensitivity analysis” OR “Monte Carlo sensitivity analysis” OR “MCSA” or “probabilistic sensitivity analysis”; and 2) Web of Science to perform citations searches of papers that referenced seminal papers.^3,14,18,20 Two key works were not indexed in Web of Science,^2,21 so we also used Google Scholar.

Eligible articles had to 1) be a pharmacoepidemiology or comparative effectiveness study with a pharmaceutical, biologic, medical device, or medical procedure as exposure and a health outcome; 2) be an observational study; and 3) apply probabilistic bias analysis to estimate the effects of systematic error including selection bias, unmeasured confounding, and/or exposure or outcome misclassification. We excluded 1) methodological studies or studies using simulated data only; 2) randomized control trials, mediation analyses, systematic reviews, meta-analyses, opinions, and non-research letters; 3) articles not published in English; and 4) duplicate publications.

We followed the Preferred Reporting Items for Systematic Reviews and Meta-Analyses guidelines.²² Article titles and abstracts were screened by one reviewer (JNH). Articles which met our eligibility criteria were included in our full text review. Three reviewers (JNH, KLL, SC) independently performed data abstraction on all eligible articles. Discrepancies were resolved through group discussion.

Data abstraction

We used two sources on implementing and reporting bias analysis to guide our data abstraction process.^2,9 Table 1 provides a general overview.^{1–3,9,14,18,20} We abstracted information on the specific bias addressed in the analysis, the bias model used, sources used for simulating the bias parameters (e.g., internal validation studies, external validation studies, expert judgement), believed location (central tendency and spread) and type of bias parameters distributions assigned (e.g. uniform, triangular, normal; see eFigure 1), the number of simulated iterations, and sensitivity analyses or diagnostics.

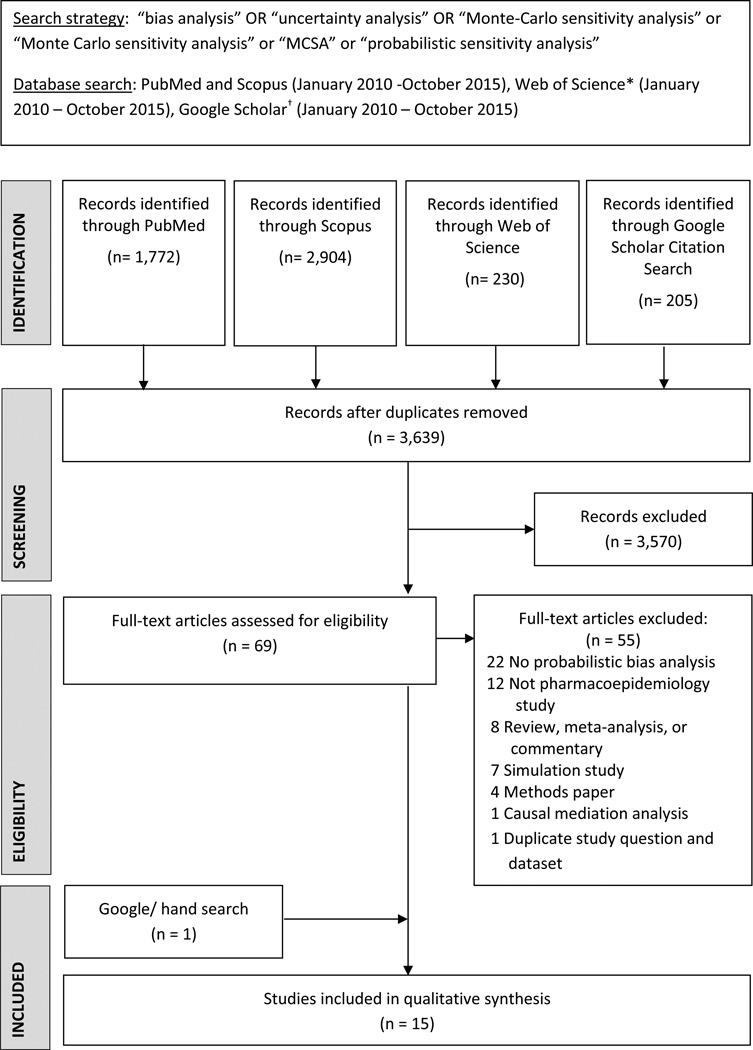
Figure 1.

Flow diagram of studies considered for inclusion

*Web of Science used to index any paper citing one of 4 seminal papers in probabilistic bias analysis.^3,14,18,20

^†Google Scholar used to index any paper citing a seminal book and paper that were not available in Web of Science database.^2,21

We abstracted information on the bias analysis results including the median bias-adjusted effect estimate and simulation interval and compared these results to the conventional analysis by calculating the percent change in effect estimates and interval widths. When many bias analyses were conducted, we abstracted information on the least and most extreme bias scenarios; if bias analysis results were visually displayed (without numeric data), we abstracted results discussed in the text. We abstracted how investigators interpreted bias analysis results in comparison to conventional estimates and whether frequentist or Bayesian properties were assigned to simulation intervals; simulation intervals do not have frequentist or purely Bayesian interpretations and should not be used for null-hypothesis testing or interpreted as Bayesian credible intervals.^2,7,9,21

We summarize issues in data abstraction for simulating an unmeasured confounder, misclassification, and selection bias below. See eTable 2 for bias analysis formulas.

Unmeasured confounding

Bias parameters needed to simulate an unmeasured confounder (assuming binary exposure, confounder, and outcome) include confounder prevalence in the exposed (p₁) and unexposed (p₀) and strength of the association between confounder and outcome (RR_CD);^2,11,23,24 alternative (but equivalent) formulations includes only parameterizing the relative risk due to confounding (RR_C) – the ratio of the crude effect estimate and the standardized risk ratio (standardized to the exposed group).^2,7,10,25 Finding literature to parameterize RR_C alone can be difficult; investigators may assign RR_C distributions that result in a narrower simulation interval due to incorporating less uncertainty in the range of values assigned to a single bias parameter distribution than would be incorporated when simulating multiple bias parameters (p₁,p₀, and RR_CD).² Extensions of basic formulas to continuous or multinomial confounders and unmeasured confounding in the presence of effect measure modification are available.^2,26

When applying probabilistic bias analysis to adjusted effect estimates (beyond stratification and pooling), approaches have been developed for directly adjusting the summary estimate or through simulating confounding at the record-level.^16,18,27 Data may be presented as: 1) a single discrete bias scenario; 2), multiple discrete scenarios showing the sensitivity of bias analysis results to varying bias parameter distributions; and 3) continuous changes in bias-adjusted estimates over a continuous interval of bias parameters.

We abstracted information on the specific unmeasured confounder being simulated; details on the approach implemented including bias parameters simulated and whether the method was applied to the effect estimate or individual records; and presentation of the results.

Misclassification

Bias parameters needed for binary exposure/outcome/confounder misclassification include classification probabilities (e.g., sensitivity/specificity or positive/negative predictive values (PPV/NPV)).^2,3,7,11,18 Probabilistic bias analysis can be applied to summary effect estimates to adjust for outcome misclassification with perfect specificity and imperfect sensitivity;^7,16 otherwise, record-level simulation is required.³ Record-level simulation involves sampling sensitivity/specificity or PPV/NPV values from the assigned bias parameter distributions to determine if individual records should be reclassified based on the assumed classification probabilities; for each simulated iteration, individuals are potentially reclassified based on Bernoulli trials;³ after reclassifying individual observations, standard statistical models are applied to the bias-adjusted dataset to generate a single bias-adjusted effect estimate. The process is repeated to generate a simulation interval. Investigators simulating nondifferential misclassification assume sensitivity/specificity are the same between groups; simulating differential misclassification assumes that sensitivity/specificity are different between groups, though introducing correlation between sensitivity/specificity between groups is recommended.^2,3,7

We abstracted information on the type of misclassification simulated; probability distribution assigned; diagnostics including counting the number of negative cell counts; and whether investigators adjusting for outcome misclassification in case-control studies appropriately accounted for differing sampling fractions for cases and controls.^7,28

Selection bias

Investigators can apply probabilistic bias analysis to selection bias when participation is related to exposure and outcome (differential selection) or loss to follow-up.^2,7,11 Bias parameters needed to simulate differential selection into the study (assuming binary exposure and outcome) include selection proportions for four combinations of exposure and outcome.^2,7,11 Alternatively, a single distribution can be assigned to the selection bias odds ratio, though the simulation interval may be narrower than when simulating unique selections proportion because it may incorporate less uncertainty than simulating multiple bias parameters.² Investigators can also assess the impact of loss to follow-up by simulating bias parameters for outcome risk by exposure status and person-time until the event by applying crude or record-level simulation.^2,18

RESULTS

Figure 1 shows that 69 articles were eligible for full text review. Of these, 55 were excluded: 22 studies did not conduct a probabilistic bias analysis; 12 were not pharmacoepidemiologic/comparative effectiveness studies; 8 were reviews, metaanalyses, or commentaries; 7 studies used simulated data only; 4 were methods papers, 1 applied probabilistic bias analysis to a causal mediation analysis, and 1 was a duplicate publication (we kept the earlier of the two publications).^{27, 29} Fifteen were eligible- 14 identified through our keyword and citation search^29–42 and 1 through Google/ hand searching.⁴³

Nine studies simulated an unmeasured confounder^29–37 and 6 simulated misclassification (eTable 3).^38–43 No studies applied probabilistic bias analysis to selection bias or multiple biases. Six studies simulating confounding were conducted by the same team,^{29, 32}-³⁶ as were 2 studies simulating misclassification.^{39, 40}

All studies addressing an unmeasured confounder^29–37 described a specific binary^30–37 or multinomial confounder(s)²⁹ to be simulated (Table 2). Sources used to assign bias parameter values varied; six studies^{31–35, 37} used prior literature to estimate bias parameters including observational studies,^{31–33,35, 37} trials,^31,33,37 government reports,³⁷ online databases,³⁷ and systematic reviews/meta-analyses.^{34, 35} Bias parameter estimates were sometimes based on small studies with imprecise estimates.^{32, 33} One study clearly reported the probability distributions assigned (including type and range of values) for all bias parameters.³¹ Two reported the number of simulated iterations applied - each used ≥5,000 iterations.^{29, 31}

Table 2.

Summary of probabilistic bias analysis when simulating unmeasured confounding, sorted by study design.

Study	Unmeasured confounder simulated	Source of bias parameter estimates	Type of probability distribution assigned to bias parameters*	Bias parameters for which assigned range of values were reported†	Simulated iterations
Cohort studies
Albert et al. (2012)30	Use of endocrine therapy (Binary)	Not reported	Not reported	Prevalence of confounder in exposed and unexposed	Not reported
Bannister-Tyrell et al. (2014)31	Severe labor pain intensity (Binary)	Expert judgement (prevalence); prior studies (association)	Trapezoidal	Prevalence of confounder in exposed and unexposed; association between confounder and outcome	10,000
Corrao et al. (2011)32	Depression (Binary)	Prior studies	Not reported	Not reported	Not reported
Corrao et al. (2014)33	Obesity (Binary)	Prior studies	Not reported	Not reported	Not reported
Corrao et al. (2014)34	Severity of hypercholesterolemia (Binary)	Prior study	Not reported	Not reported	Not reported
Case-control studies
Corrao et al. (2011)29	Severity of hypertension; CDS; BMI (Multinomial)	External dataset (prevalence); expert judgement	Normal	Association between confounder and outcome	5,000
Corrao et al. (2013)35	Severe hypercholest- erolemia (Binary)	Prior studies	Not reported	Not reported	Not reported
Ghirardi et al. (2014)36	Severity of osteoporosis (Binary)	Not reported	Not reported	Not reported	Not reported
Schmidt et al. (2010)37	Smoking (Binary)	Prior studies	Not reported	Association between confounder and outcome	Not reported

^*See eFigure 1 in the online supplementary appendix for further description of probability distribution types.

^†Bias parameters for unmeasured confounding include confounder prevalence in exposed and unexposed and strength of association between the confounder and outcome. We report whether investigators discussed the range of plausible values assigned to bias parameters

Three approaches to simulating an unmeasured confounder were used: 2 studies simulated a single bias scenario,^{31, 37} 5 studies presented multiple discrete bias scenarios with varying strength/prevalence of the unmeasured confounder,^{29, 30, 32, 35, 36} and 2 studies simulated a range of plausible bias-adjusted effect estimates over a predefined interval of the exposure-confounder odds ratio (the strength and overall prevalence of the confounder were held constant).^{33, 34} Most studies simulated an unmeasured confounder by applying bias-adjustment formulas to the summary estimate,^{29, 31}-³⁷ though one study performed record-level adjustment.³⁰

For misclassification (Table 3), 3 studies simulated outcome misclassification (2 cohort,^{39, 40} 1 case-control⁴¹) and 3 studies simulated exposure misclassification (2 cohort,^{38, 43} 1 case-control⁴²). Sources used to estimate the distribution of plausible bias parameters varied. Two studies simulating outcome misclassification used an internal validation study to estimate plausible distributions of sensitivity/specificity estimates of their outcome definitions.^{39, 40} One study simulating outcome misclassification used an external study with a similar patient population for sensitivity/specificity estimates.⁴¹ One study simulating exposure misclassification used validation data from three external studies with different patient populations to define bias parameter distributions.⁴³ One study used a combination of internal and external validation data to simulate misclassification of a time-varying exposure (simulating PPV, NPV and time-to-initiation).³⁸ One study provided no details on the bias analysis.⁴² Types and ranges of values assigned to probability distributions were discussed in 4 studies^{38, 39, 41, 43} and simulated iterations reported in three - each used ≥1,000 iterations.^{38, 39, 41}

Table 3.

Summary of probabilistic bias analysis when simulating misclassification, sorted by study design

Study	Type of misclassification simulated	Source of bias parameter estimates	Type of probability distribution assigned to bias parameters*	Bias parameters for which assigned range of values were reported†	Simulated iterations
Cohort studies
Ahrens et al. (2012)38	Differential exposure misclassification (binary)	Internal validation data and external validation study	Beta	PPV and time of initiation‡	100,000
Brunet et al. (2015)43	Nondifferential exposure misclassification (binary)	External validation studies	Trapezoidal	Sensitivity and specificity	Not reported
Huybrechts et al. (2014)39	Nondifferential outcome misclassification (binary)	Internal validation study	Triangular	Sensitivity and specificity	1,000
Palmsten et al. (2013)40	Nondifferential outcome misclassification (binary)	Internal validation study	Not reported	Not reported	Not reported
Case-control studies
Barron et al. (2013)41	Nondifferential Outcome misclassification; differential outcome misclassification (binary) §	External validation study; expert judgement	Trapezoidal	Sensitivity and specificity	5,000
					5,000
Mahmud et al. (2011)42	Nondifferential exposure misclassification	Not reported	Not reported	Not reported	Not reported

NPV, negative predictive value; PPV, positive predictive value

^*See eFigure 1 in the online supplementary appendix for further description of probability distribution types.

^†Bias parameters for misclassification include classification probabilities (sensitivity/specificity and/or PPV/NPV). We report whether investigators discussed the range of plausible values assigned to bias parameters

^‡Simulated a time-varying exposure required estimating time-to-initiation, which investigators simulated by fitting probability distributions to the range of times observed in their cohort. Only sensitivity and specificity point estimates were provided for the calculation of NPV.

^§Simulated both nondifferential and differential outcome misclassification

All studies reported adjusting for misclassification at the record-level; ^38–43 5 used the ‘sensmac’ SAS macro.^39–43 Two studies reported sensitivity analyses and diagnostics.^38,41 One case-control study modeled both nondifferential and differential outcome misclassification and was the only study to report introducing correlation between bias parameter distributions.⁴¹ They also shifted bias parameter distributions upwards to limit the number of simulations producing negative cell counts.;⁴¹ this study did not report accounting for differing sampling fractions for cases and controls in the bias adjustment formulas.²⁸ The cohort study adjusting for misclassification of a time-varying exposure used different probability distributions (beta or empirical distribution) as a sensitivity analysis and provided histograms of the simulation interval in comparison to conventional results.³⁸

Probabilistic bias analysis changed the conventional effect estimate by ≥10% in 8 studies^{30–33,36,37,40,41} and by ≥30% in 4 studies (eTables 4–5).^30,31,40,41 In the 13 studies that reported simulation intervals (incorporating both systematic and random error),^{29– 36,38–41,43} the bias analysis interval was generally larger relative to the conventional confidence interval reported (range: −30.6–1090.0%).

Seven of 9 studies simulating an unmeasured confounder used the simulation interval to conduct null-hypothesis testing;^29–34,36 6 of these studies referred to the simulation interval as a confidence interval.^{29,31–34,36} Two studies interpreted the probabilistic bias analysis by comparing the median bias-adjusted estimates to the conventional effect estimates.^35,37

One study applying probabilistic bias analysis to misclassification reported using the simulation interval to conduct null-hypothesis testing,⁴¹ and one referred to the simulation interval as a confidence interval.⁴⁰ Interpretations of bias analysis varied: 2 described differences in effect estimates and interval widths,^38,41 2 described differences in effect estimates only,^39,40 and 2 stated that there were no changes in results^42,43 – 1 of which only provided qualitative information on the bias analysis.⁴²

DISCUSSION

Given the pervasiveness and concern about bias in observational studies, we found few studies that quantitatively examined the effects of bias through the application of probabilistic bias analysis between January 2010 and October 2015. Dissemination of the technique was limited with many of the included papers being published by the same teams of researchers or including a primary proponent of bias analysis as a coauthor (Timothy Lash).^37,38 In general, we found that there was large variation in how probabilistic bias analysis was used and reported and that in many cases, key information needed to understand and critique the bias analysis was missing.

We identified several common deficiencies in the implementation of probabilistic bias analysis to address unmeasured confounding. First, for studies presenting multiple bias scenarios,^{29,30,32–36} authors did not generally provide enough guidance to suggest which scenarios were most plausible. Although these approaches show how sensitive bias analysis results were to varying bias parameters estimates, drawing conclusions on the most plausible effects of unmeasured confounding is difficult when unrealistic scenarios are simulated and emphasized within the text. Second, it was not always clear from where bias parameter estimates were derived,^30,36 and in some cases small studies were used to estimate the strength and prevalence of the unmeasured confounder.^32,33 This may result in inaccurately describing the range of values for the bias parameters. Third, in all but one study,³¹ the type and range of probability distributions assigned to bias parameters was unclear. We found this surprising given that the incorporation of uncertainty about bias parameters is one of the largest strengths of probabilistic bias analysis.^2,9 More transparency is needed to understand the methods used.

Studies applying probabilistic bias analysis to adjust for misclassification were in general more transparent when reporting the type and range of values assigned to probability distributions and the sources for these estimates. However, important details of the bias analysis were not always reported and discussions of sensitivity analyses and diagnostics were only reported in two studies.^38,41 Whether the lack of sensitivity analyses and diagnostics presented was due to the computational intensity and/or technical difficulties in applying probabilistic bias analysis to misclassification, or journal word limits is unknown.¹⁹

Probabilistic bias analysis has been described as semi-Bayes because it assigns prior distributions to the bias parameters but no other model parameters.² Although probabilistic bias analysis results can closely approximate a fully Bayesian analysis in many but not all situations,^2,21,44,45 simulation intervals should not be interpreted as having frequentist (e.g., to conduct null-hypothesis tests) or fully Bayesian properties (e.g., as a credibility interval). Despite this, we found the practice of using the simulation interval to conduct null-hypothesis tests to be highly prevalent,^{29–34,36,41} especially when simulating unmeasured confounding with many authors even referring to a simulation interval as a confidence interval.^29–34,36 Prior work suggests using the simulation interval to 1) gain insight into the direction and magnitude of bias given the assumed strength and distributions of the bias parameters by comparing the median bias-adjusted estimate to the conventional point estimate and 2) compare the width of the simulation interval (incorporating random and systematic error) to the confidence interval (random error only) to have a better understanding of the uncertainty about the effect estimate.^2,9

Regardless of the bias modeled, few studies reported probabilistic bias analysis as previously suggested.^2,9 Descriptions of the technique must be thorough to facilitate understanding and transparency.⁹ At a minimum, the investigator should state the purpose of the bias analysis, the values and probability distributions assigned to bias parameters, how these values were derived, the number of simulated iterations, and describe the sensitivity analyses and diagnostics implemented to ensure that the probabilistic bias analysis is as accurate as possible.^2,9 The use of online appendices can provide further information on the analysis and are available for most journals.^2,9

Probabilistic bias analysis is not an alternative to good study design and conduct, and several limitations must be recognized. Probabilistic bias analysis can be difficult to implement when there is limited information available to guide assigning probability distributions to bias parameters such as when simulating selection bias.^2,28 Implementing a full probabilistic bias analysis can be time-intensive and technically complex such as when addressing multiple biases.^14,19 However, probabilistic bias analysis is a flexible approach that readily complements common statistical methods as a sensitivity analysis and can produce simulation intervals with more accurate coverage probabilities than confidence intervals when bias parameter distributions adequately describe the underlying (but unknowable) bias present.^7,46

This systematic review has several strengths. We used a comprehensive search strategy that included both keyword searches and citation indexes of key sources of probabilistic bias analysis. We considered multiple applications of the technique to different types of systematic error. We examined both the implementation and results of the bias analysis. However, our review also has some limitations. We focused on studies published between January 2010 and October 2015 that applied probabilistic bias analysis in pharmacoepidemiology or comparative effectiveness research. We recognize that the reporting of bias analysis can be restricted by journal word limits and may not reflect what the authors originally wrote. Probabilistic bias analyses are one way to implement a quantitative bias analysis and authors could have implemented other approaches (e.g., Bayesian).^15,47–50 The background knowledge and programming expertise needed to implement such approaches can be a barrier.¹⁶

In conclusion, probabilistic bias analysis is underused in pharmacoepidemiologic and comparative effectiveness studies. The application and reporting of the technique is suboptimal despite recent publications on best practices for implementing and reporting. Further discussion/dissemination of the technique may enhance reporting and implementation of probabilistic bias analysis.

Take-Home Messages.

• Probabilistic bias analysis is a type of quantitative bias analysis that can be used to evaluate the effects of systematic error (e.g. confounding, misclassification, and selection bias).

• Probabilistic bias analysis uses Monte Carlo sampling techniques to repeatedly sample plausible values from probability distributions assigned to bias parameters (values required to estimate the effect of bias in an analysis) and apply these values to simple bias analysis formulas to generate a frequency distribution of bias-adjusted effect estimates.

• Commentaries have provided guidance on how to apply and report probabilistic bias analysis, no study has systematically investigated how probabilistic bias analysis has been used and applied in the pharmacoepidemiology and comparative effectiveness literature.

• Reporting of probabilistic bias analysis in pharmacoepidemiology or comparative effectiveness studies is suboptimal. The probability distributions assigned to bias parameters, number of simulated iterations, sensitivity analyses, and diagnostics were not discussed in the majority of studies.

• Further discussion and dissemination of probabilistic bias analysis are warranted given the concern of bias in observational studies and the varying quality of implementation and reporting.