Significance
Understanding how randomness in the timing of intracellular events is buffered has important consequences for diverse cellular processes, where precision is required for proper functioning. To investigate event timing in noisy biochemical systems, we develop a first-passage time framework in which an event is triggered when a regulatory protein accumulates up to a critical level. Formulas quantifying event-timing fluctuations in stochastic models of protein synthesis with feedback regulation are developed. Formulas shed counterintuitive insights into regulatory mechanisms essential for scheduling an event at a precise time with minimal fluctuations. These results uncover various features in the biochemical pathways used by phages to lyse individually infected bacterial cells at an optimal time, despite stochastic expression of lysis proteins.
Keywords: first-passage time, event timing, stochastic gene expression, feedback control, single cell
Abstract
In the noisy cellular environment, gene products are subject to inherent random fluctuations in copy numbers over time. How cells ensure precision in the timing of key intracellular events despite such stochasticity is an intriguing fundamental problem. We formulate event timing as a first-passage time problem, where an event is triggered when the level of a protein crosses a critical threshold for the first time. Analytical calculations are performed for the first-passage time distribution in stochastic models of gene expression. Derivation of these formulas motivates an interesting question: Is there an optimal feedback strategy to regulate the synthesis of a protein to ensure that an event will occur at a precise time, while minimizing deviations or noise about the mean? Counterintuitively, results show that for a stable long-lived protein, the optimal strategy is to express the protein at a constant rate without any feedback regulation, and any form of feedback (positive, negative, or any combination of them) will always amplify noise in event timing. In contrast, a positive feedback mechanism provides the highest precision in timing for an unstable protein. These theoretical results explain recent experimental observations of single-cell lysis times in bacteriophage . Here, lysis of an infected bacterial cell is orchestrated by the expression and accumulation of a stable protein up to a threshold, and precision in timing is achieved via feedforward rather than feedback control. Our results have broad implications for diverse cellular processes that rely on precise temporal triggering of events.
Timing of events in many cellular processes, such as cell-cycle control (1–3), cell differentiation (4, 5), sporulation (6, 7), apoptosis (8, 9), development (10, 11), temporal order of gene expression (12–14), and so on, depend on regulatory proteins reaching critical threshold levels. Triggering of these events in single cells is influenced by fluctuations in protein levels that arise naturally due to noise in gene expression (15–18). Increasing evidence shows considerable cell-to-cell variation in timing of intracellular events among isogenic cells (19–21), and it is unclear how noisy expression generates this variation. Characterization of control strategies that buffer stochasticity in event timing are critically needed to understand reliable functioning of diverse intracellular pathways that rely on precision in timing.
Mathematically, noise in the timing of events can be investigated via the first-passage time (FPT) framework, where an event is triggered when a stochastic process (single-cell protein level) crosses a critical threshold for the first time. There is already a rich tradition of using such FPT approaches to study timing of events in biological and physical sciences (22–26). Following this tradition, exact analytical expression for the FPT distribution is computed in experimentally validated and commonly used stochastic models of gene expression. These results provide insights into how expression parameters shape statistical fluctuations in event timing.
To investigate control mechanisms for buffering noise in timing, we consider feedback regulation in protein synthesis, where the transcription rate varies arbitrarily with the protein count. Such feedback can be implemented directly through autoregulation of gene promoter activity by its own protein (27–29) or indirectly via intermediate states (30). It is important to point out that although the effects of such feedback loops on fluctuations in protein copy number are well studied (29, 31–33), their impacts on stochasticity in event timing have been overlooked. We specifically formulate the problem of controlling precision in event timing as follows: What optimal form of feedback regulation ensures a given mean time to an event, while minimizing deviations or noise about the mean? It turns out that for a minimal model of stochastic gene expression, this optimization problem can be solved analytically, providing counterintuitive insights. For example, a negative feedback regulation is found to amplify noise in event timing and the optimal form of feedback is to not have any feedback at all. The robustness of these results is analyzed in the context of different noise mechanisms, such as intrinsic versus extrinsic noise in transcription/translation machinery (34–37). Finally, we discuss in detail how our results explain recent experimental observations of single-cell lysis times in bacteriophage , where precision in timing is obtained without any feedback regulation.
Stochastic Model Formulation
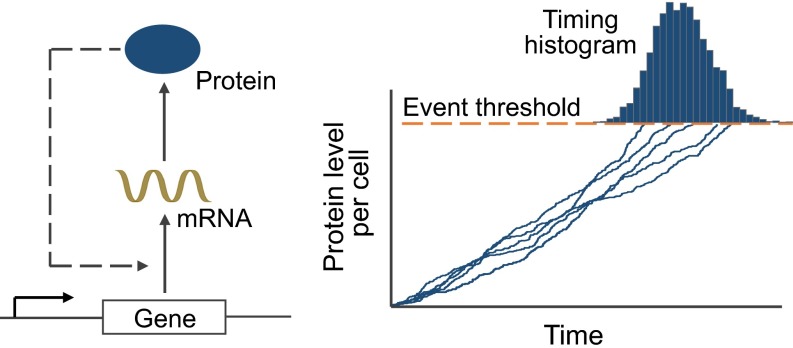
Consider a gene that is switched on at time and begins to express a timekeeper protein. The intracellular event of interest is triggered once the protein reaches a critical level in the cell. We describe a minimal model of gene expression that assumes translation in bursts and incorporates feedback regulation by considering the transcription rate as a function of the protein level (Fig. 1). More precisely, if denotes the level of a protein in a single cell at time , then the gene is transcribed at a Poisson rate when . Any arbitrary form of feedback can be realized by appropriately defining as a function of . For example, increasing (decreasing) ’s correspond to a positive (negative) feedback loop in protein production, and a fixed transcription rate implies no feedback. The translation burst approximation is based on assuming short-lived mRNAs, that is, each mRNA degrades instantaneously after producing a burst of protein molecules. In agreement with experimental and theoretical studies (38–40), is assumed to follow a geometric distribution
| [1] |
where denotes the mean protein burst size and the symbol is the notion for probability. Finally, each protein molecule degrades with a constant rate . The time evolution of is described through the following probabilities of occurrences of burst and decay events in the next infinitesimal time :
| [2a] |
| [2b] |
Note that in this representation of gene expression as a bursty birth–death process, the mRNA transcription rate is the burst arrival rate, whereas the rate at which proteins are translated from an mRNA determines the mean protein burst size . Next, we formulate event timing through the FPT framework.
Fig. 1.
Modeling event timing as an FPT problem. (Left) Schematic depicting a gene transcribing mRNAs, which are further translated into proteins. The transcription rate is assumed to be regulated by the protein level, creating a feedback loop. (Right) The timing of an intracellular event is formulated as the FPT for the protein level to reach a critical threshold. Sample trajectories for the protein level over time obtained via Monte Carlo simulations are shown, and they cross the threshold at different times due to stochasticity in gene expression. The histogram of the event timing is shown on the top.
Computing Event Timing Distribution
The time to an event is the FPT for to reach a threshold starting from a zero initial condition (Fig. 1). It is mathematically described by the following random variable:
| [3] |
and can be interpreted as the time taken by a random walker to first reach a defined point. For the bursty birth–death process in Eq. 2, the probability density function (pdf) of the FPT is given by
| [4] |
where (SI Appendix, section S1).
The FPT pdf in Eq. 4 can be compactly written as product of two vectors:
| [5a] |
| [5b] |
| [5c] |
Here, the dynamics of can be written as a linear system
| [6] |
derived from the chemical master equation corresponding to the bursty birth–death process (SI Appendix, section S1) (23, 41). It turns out that in this case the matrix is a Hessenberg matrix whose ith row and jth column element is given by
| [7] |
. Solving Eq. 6 and using Eq. 5a yields the following pdf for the FPT:
| [8] |
where is vector of probabilities at that follows from . Although this pdf provides complete characterization of the event timing, we are particularly interested in the lower-order statistical moments of FPT. Next, we exploit the structure of matrix to obtain analytical formulas for the first- and second-order moments of FPT.
Moments of the FPT
From Eq. 8, the -order uncentered moment of the FPT is given by
| [9a] |
| [9b] |
Here, in computing the above integral, we used the fact that the matrix is full-rank with negative eigenvalues (SI Appendix, section S2). One can also find explicit formulas for the first two moments as series summations in terms of event threshold , mean burst size , protein decay rate , and transcription rates , (SI Appendix, section S3).
Analysis of the FPT moments in some limiting cases gives important insights (SI Appendix, section S4). For the simplest case of a stable protein () and a constant transcription rate (no feedback; ), the moment expressions simplify to
| [10] |
where represents the noise in FPT as quantified by its coefficient of variation squared (variance/mean2;). The approximate formulas in Eq. 10 are valid for a high event threshold compared with the mean protein burst size (). The mean FPT formula can be interpreted as the time taken to reach with an accumulation rate . Further, represents the average number of burst events required for the protein level to cross the threshold, and increasing leads to noise reduction through more efficient averaging of the bursty process. One can also gain important insights, such as, the noise in FPT is invariant of the transcription rate . Therefore, and can be independently tuned—increasing the event threshold and/or reducing the burst size will lower the noise level. Once is sufficiently reduced, can be altered to obtain a desired mean event timing.
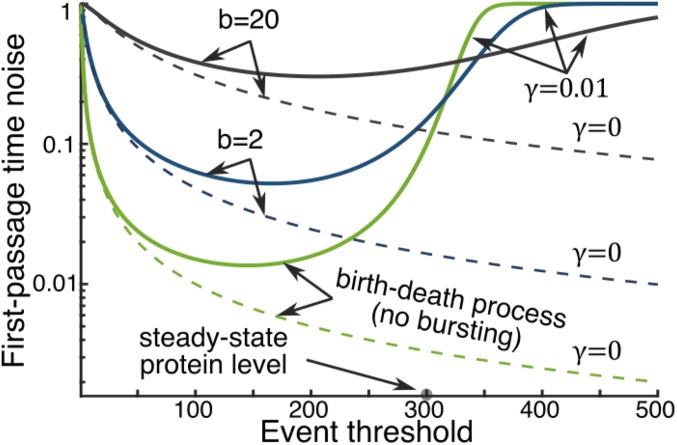
Interesting features of the FPT statistics are revealed when (unstable protein) is considered with a constant transcription rate . In this case, the expressions of FPT moments are quite involved (SI Appendix, section S4), and we investigate the effect of various parameters numerically. It turns out that changing the event threshold leads to a U-shaped profile for , where noise in event timing first decreases and then increases (Fig. 2). Intuitively, when , the protein level approaches a steady-state level . When the event threshold is sufficiently below , reduces with increasing , similar to the case. As approaches , the protein trajectories start saturating and crossing the threshold becomes a noise-driven event. This results in an increase in and ultimately leads to as . Recall that the coefficient of variation of an exponentially distributed random variable is exactly equal to one. Thus, when is much larger than , the timing process becomes memoryless, yielding exponentially distributed FPTs. The minimum value of is achieved at an intermediate threshold level for a birth–death process (), and the dip in the U-shape shifts to the right as the protein expression becomes more bursty (Fig. 2). Another interesting point to note is that whereas increasing increases noise in event timing when , it has a contrasting effect when , where increasing can sometimes reduce . Next, we explore how feedback regulation of the transcription rate affects noise in timing, for a given and .
Fig. 2.
Relative positions of the event threshold and the steady-state protein level determine noise in timing. Noise in the FPT () is plotted as a function of the event threshold () for different mean protein burst sizes and decay rates . For , the noise is high at small values of and decreases with increasing , which is similar to the versus trend when (dashed lines). After attaining a minima at an intermediate value of , increases with further increase in . The minimum value of is achieved at for a birth–death process, and this optimal point shifts to the right as is increased while keeping fixed by commensurate change in . The steady-state protein level and the decay rate are taken as molecules, and per min.
Optimal Feedback Strategy
Having derived the FPT moments, we investigate optimal forms of transcriptional feedback that schedule an event at a given time with the lowest . Because is assumed to be fixed, minimizing is equivalent to minimizing . Thus, the problem mathematically corresponds to a constraint optimization problem: Find transcription rates that minimize for a fixed . We first consider a stable protein whose half-life is much longer than the event timescale, and, hence, degradation can be ignored ().
Optimal Feedback for a Stable Protein.
When the protein of interest does not decay (), the expressions for the FPT moments take much simpler forms:
| [11a] |
| [11b] |
Note that, in Eq. 11a, the contribution of (transcription rate when there is no protein) differs from the other transcription rates , . For instance, when the event threshold is large compared with the mean burst size (), then the term can be ignored and . In contrast, if the burst size is large () then , because a single burst event starting from zero protein molecules is sufficient for threshold crossing. A similar observation for different contributions of can be made about Eq. 11b.
It turns out that, for these simplified formulas, the problem of minimizing given can be solved analytically using the method of Lagrange multipliers (SI Appendix, section S5). The optimal transcription rates are given by
| [12] |
and all rates are equal to each other except for . Intuitively, the difference for comes from the fact that it contributes differently to the FPT moments compared with other rates. Note that for a small mean burst size (), , whereas for a sufficiently large . Despite this slight deviation in , for the purposes of practical implementation, the optimal feedback strategy in this case is to have a constant transcription rate (i.e., no feedback in protein expression).
We tested the above result for a more complex stochastic gene expression model that explicitly includes mRNA dynamics via Monte Carlo simulations (Fig. 3). For ease of implementation, the feedbacks are assumed to be linear:
| [13] |
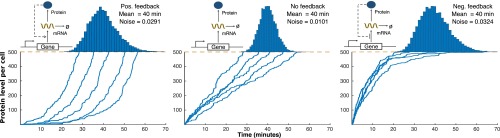
where represents no feedback, and denotes a positive (negative) feedback. In agreement with Eq. 12, a no-feedback strategy outperforms negative/positive feedbacks in terms of minimizing noise in FPT around a given mean event time. The qualitative shape of trajectories in Fig. 3 is determined by the feedback strategy used, with no feedback resulting in linear time evolution of protein levels. This provides an intriguing geometric interpretation of our results—an approximate linear path from zero protein molecules at to molecules at time provides the highest precision in timing. Next, we discuss the optimal feedback strategy when protein degradation is taken into consideration.
Fig. 3.
For a stable protein, no feedback provides the lowest noise in event timing for a fixed mean FPT. Protein trajectories obtained using the stochastic simulation algorithm for a stochastic gene expression model with positive feedback (Left), no feedback (Middle), and negative feedback (Right) (42). The threshold for event timing is assumed to be 500 protein molecules and feedback is implemented by assuming a linear form of transcription rates as . The value of is taken as for positive feedback and for negative feedback. For each feedback, the parameter is taken such that the mean FPT is kept constant (40 min). The mRNA half-life is assumed to be , and proteins are translated from mRNAs at a rate , which corresponds to a mean burst size of . Histograms on the top represent distribution of FPT from 10,000 Monte Carlo simulations.
Optimal Feedback for an Unstable Protein.
Now consider the scenario where protein degradation cannot be ignored over the event timescale (). Unfortunately, the expressions of the FPT moments are too convoluted for the optimization problem to be solved analytically (SI Appendix, section S3, Eq. S3.10), and the effect of different feedbacks is investigated numerically.
We implement the feedbacks using physiologically relevant Hill functions, where the transcription rates for a negative feedback mechanism take the following form:
| [14] |
Here denotes the Hill coefficient, corresponds to the maximum transcription rate, and characterizes the negative feedback strength, with representing no feedback (29, 43). Similarly, a positive feedback is assumed to take the following form:
| [15] |
Note that an additional parameter , referred to as the basal strength, is introduced in Eq. 15. This is to ensure that the transcription rate in protein absence , and this is necessary to prevent protein levels from getting stuck at zero molecules.
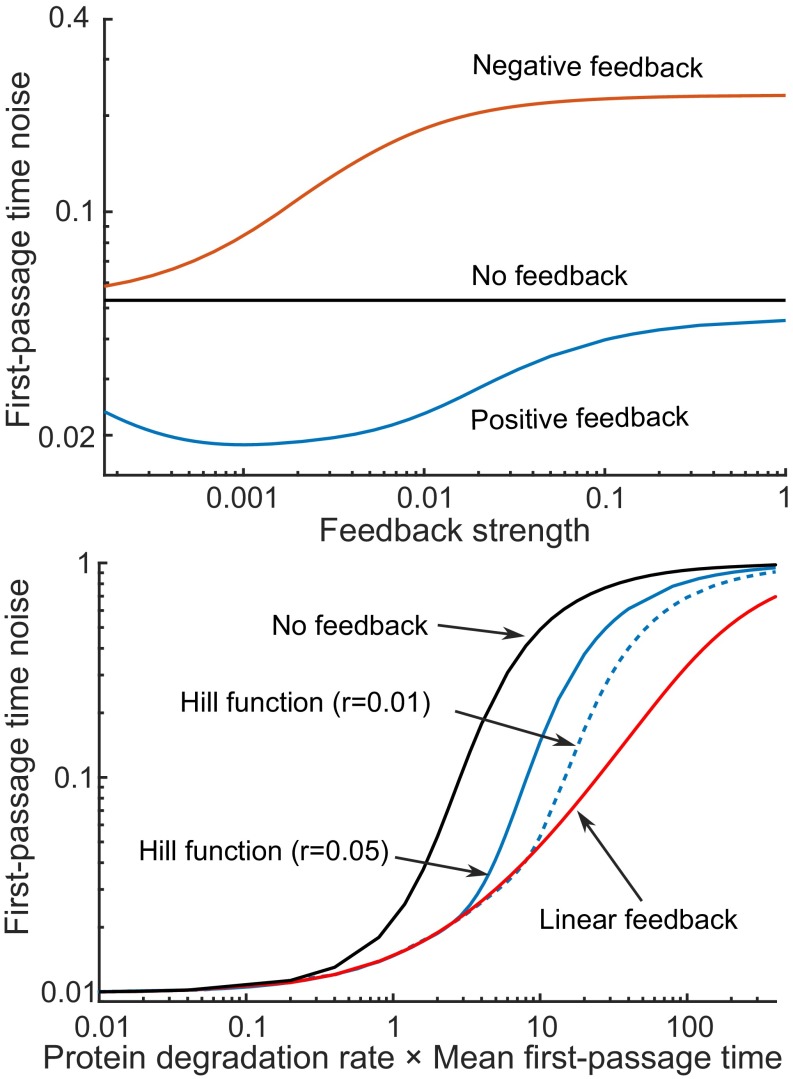
To find the optimal feedback mechanism, our strategy is as follows: For given and , choose a certain feedback strength in Eq. 14/Eq. 15, appropriately tune for the desired mean event timing, and explore the corresponding noise in FPT as measured by its coefficient of variation squared . Counterintuitively, results show that for a given value of , a negative feedback loop in gene expression has the highest , and its performance deteriorates with increasing feedback strength (Fig. 4, Top). In contrast, first decreases with increasing strength of the positive feedback and then increases after an optimal feedback strength is crossed (Fig. 4, Top). Thus, when the protein is not stable, precision in timing is attained by having a positive feedback in protein synthesis with an intermediate strength.
Fig. 4.
For an unstable protein, positive feedback provides the lowest noise in event timing for a fixed mean FPT. (Top) Noise in timing () as a function of the feedback strength for different control strategies. The value of is changed in Eq. 14/Eq. 15 so as to keep fixed. The performance of the negative feedback worsens with increasing feedback strength. In contrast, positive feedback with an optimal value of provides the highest precision in event timing. Other parameters used are , molecules, , , and for positive feedback . (Bottom) The minimum value of obtained via positive feedback increases monotonically with the protein degradation rate. A smaller basal promoter strength in Eq. 15 gives better noise suppression than a larger value . For comparison purposes, obtained without any feedback (), and a linear feedback with and in Eq. 13 chosen to minimize for a given are also shown. The parameter values used are molecules, , and .
We next explore how the minimal achievable noise in event timing, for a fixed , varies with the protein decay rate . Our analysis shows that for a given basal strength , the minimum obtained via positive feedback increases monotonically with , and as becomes large (Fig. 4, Bottom). A couple of interesting observations can be made from Fig. 4, Bottom: (i) The difference in for optimal feedback and no feedback is indistinguishable when the protein is stable () or highly unstable (); (ii) for a range of intermediate protein half-lives the optimal feedback strategy provides better reduction of , as compared with no feedback regulation (which also corresponds to minimum obtained via a negative feedback); (iii) lowering the basal strength results in better performance in terms of noise suppression; and (iv) a linear feedback based on Eq. 13 outperforms feedbacks based on Hill functions and provides significantly lower levels of for high protein decay rates. It is also worth pointing out that the qualitative shape of curves in Fig. 4, Bottom does not change for different values of event threshold or mean burst size (SI Appendix, section S6).
Why is positive feedback the optimal control strategy for ensuring precision in event timing? One way to understand this result is to consider the linear feedback form Eq. 13, in which case the mean protein levels evolve according to the following ordinary differential equation:
| [16] |
Recall the geometric argument presented in Fig. 3, where an approximately linear path for the protein to reach the prescribed threshold in a given time provides the highest precision in event timing. Whereas no feedback () and negative feedback () in Eq. 16 will create nonlinear protein trajectories, choosing a positive value results in linear , and hence minimal noise in event timing. Indeed, our detailed stochastic analysis shows that the optimal feedback strength that minimizes in the stochastic model is qualitatively similar to (SI Appendix, section S6).
Discussion
We have systematically investigated ingredients essential for precision in timing of biochemical events at the level of single cells. Our approach relies on modeling event timing as the FPT for a stochastically expressed protein to cross a threshold level. This framework was used to uncover optimal strategies for synthesizing the protein that ensures a given mean time to event triggering (threshold crossing) with minimal fluctuations around the mean. The main contributions and insights can be summarized as follows: (i) analytical calculations for the FPT in stochastic models of gene expression, with and without feedback regulation are performed; (ii) if the protein half-life is much longer than the timescale of the event, the highest precision in event timing is attained by having no feedback, that is, expressing the protein at a constant rate (Fig. 3); and (iii) if the protein half-life is comparable to or shorter than the timescale of the event, then positive feedback provides the lowest noise in event timing. Moreover, the minimum achievable noise in timing increases with the protein decay rate and approaches as (Fig. 4).
How robust are these findings to alternative noise sources and key modeling assumptions? For example, the model only considers noise from low-copy-number fluctuations in gene product levels and ignores any form of “extrinsic noise” that arises from cell-to-cell differences in gene expression machinery (35, 44). To incorporate such extrinsic noise, we alter the transcription rate to , where is drawn from an a priori probability distribution at the start of gene expression () and remains fixed till the threshold is reached. Interestingly, the optimal feedback derived in Eq. 12 does not change even after adding extrinsic noise to the transcription rate or the protein burst size (SI Appendix, section S7). Another important model aspect is geometrically distributed protein burst size, which results from the assumption of exponentially distributed mRNA lifetimes. We have also explored the scenario of perfect memory in the mRNA degradation process, which results in an mRNA lifetime distribution given by the delta function. In this case, the protein burst size is Poisson and the optimal feedback strategy is fairly close to having no feedback for a stable protein (SI Appendix, section S8). Next, we discuss the biological implications of our findings in the context of phage ’s lysis times (i.e., the time taken by the virus to destroy infected bacterial cells).
Connecting Theoretical Insights to Lysis Times.
Phage has recently emerged as a simple model system for studying event timing at the level of single cells (19, 20). After infecting Escherichia coli, expresses a protein, holin, which accumulates in the inner membrane. When holin reaches a critical threshold concentration, it undergoes a structural transformation, forming holes in the membrane (45). Subsequently the cell lysis and phage progeny are released into the surrounding medium. Because hole formation and cell rupture are nearly simultaneous, lysis timing depends on de novo expression and accumulation of holin in the cell membrane up to a critical threshold (45). Data reveal precision in the timing of lysis—individual cells infected by a single virus lyse on average at 65 min, with an SD of 3.5 min, implying a coefficient of variation of (SI Appendix, section S9). Such precision is expected given the existence of an optimal lysis time (46–49). Intuitively, if lysis is early then there are no viral progeny. In contrast, if lysis is late then the infected cell could die before lysis is effected, trapping the virus with it.
The threshold for lysis is reported to be a few thousand holin molecules (50). Moreover, the holin mean burst size (average number of holins produced in a single mRNA lifetime) is estimated as (50). Based on our FPT moment calculations in Eq. 10, such a small protein burst size relative to the event threshold will yield a tight distribution of lysis times. Interestingly, Eq. 10 provides insights for engineering mutant that lyse, on average, at the same time as the wild type, but with much higher noise. This could be done by lowering the threshold for lysis through mutations in the holin amino acid sequence (20), and also reducing the holin mRNA transcription rate or mean protein burst size by reducing the translation rate so as to keep the same mean lysis time. Notably, the holin proteins are long-lived and do not degrade over relevant timescales (51); therefore, ’s lysis system with no known feedback in holin expression provides better suppression of lysis-time fluctuation compared with any feedback regulated system.
Additional Mechanism for Noise Buffering.
The surprising ineffectiveness of feedback control motivates the need for other mechanisms to buffer noise in event timing. Intriguingly, uses feedforward control to regulate the timing of lysis that is implemented through two proteins with opposing functions: holin and antiholin (52, 53). In the wild-type virus both proteins are expressed in a 2:1 ratio (for every two holins there is one antiholin) from the same mRNA through a dual start motif. Antiholin binds to holin and prevents holin from participating in hole formation, creating an incoherent feedforward circuit. Synthesis of antiholin leads to a lower burst size for active holin molecules and increases the threshold for the total number of holins needed for lysis—both factors functioning to lower the noise in event timing. Consistent with this prediction, variants of lacking antiholin are experimentally observed to exhibit much higher intercellular variation in lysis times compared with the wild-type virus (20, 54) (SI Appendix, section S9). Succinctly put, encodes several regulatory mechanisms (low holin burst size, no feedback regulation, and feedforward control) to ensure that single infected cells lyse at an optimal time, despite the stochastic expression of lysis proteins.
These results illustrate the utility of the FPT framework for characterizing noise in the timing of intracellular events and motivate alternate formulations of the timing problem that might involve additional constraints such as fixing the cost of protein production (SI Appendix, section S10). Exploring these constraints in more detail will be an important avenue for future research. Finally, analytical results and insights obtained here have broader implications for timing phenomenon in chemical kinetics, ecological modeling, and statistical physics.
Supplementary Material
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1609012114/-/DCSupplemental.
References
- 1.Chen KC, et al. Integrative analysis of cell cycle control in budding yeast. Mol Biol Cell. 2004;15:3841–3862. doi: 10.1091/mbc.E03-11-0794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bean JM, Siggia ED, Cross FR. Coherence and timing of cell cycle start examined at single-cell resolution. Mol Cell. 2006;21:3–14. doi: 10.1016/j.molcel.2005.10.035. [DOI] [PubMed] [Google Scholar]
- 3.Liu X, et al. Reliable cell cycle commitment in budding yeast is ensured by signal integration. Elife. 2015;4:e03977. doi: 10.7554/eLife.03977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Champlin DT, Truman JW. Ecdysteroid control of cell proliferation during optic lobe neurogenesis in the moth Manduca sexta. Development. 1998;125:269–277. doi: 10.1242/dev.125.2.269. [DOI] [PubMed] [Google Scholar]
- 5.Koyama T, Iwami M, Sakurai S. Ecdysteroid control of cell cycle and cellular commitment in insect wing imaginal discs. Mol Cell Endocrinol. 2004;213:155–166. doi: 10.1016/j.mce.2003.10.063. [DOI] [PubMed] [Google Scholar]
- 6.Carniol K, Eichenberger P, Losick R. A threshold mechanism governing activation of the developmental regulatory protein sigma F in Bacillus subtilis. J Biol Chem. 2004;279:14860–14870. doi: 10.1074/jbc.M314274200. [DOI] [PubMed] [Google Scholar]
- 7.Piggot PJ, Hilbert DW. Sporulation of Bacillus subtilis. Curr Opin Microbiol. 2004;7:579–586. doi: 10.1016/j.mib.2004.10.001. [DOI] [PubMed] [Google Scholar]
- 8.Spencer SL, Gaudet S, Albeck JG, Burke JM, Sorger PK. Non-genetic origins of cell-to-cell variability in TRAIL-induced apoptosis. Nature. 2009;459:428–432. doi: 10.1038/nature08012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Roux J, et al. Fractional killing arises from cell-to-cell variability in overcoming a caspase activity threshold. Mol Syst Biol. 2015;11:803. doi: 10.15252/msb.20145584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Salz HK. Male or female? The answer depends on when you ask. PLoS Biol. 2007;5:e335. doi: 10.1371/journal.pbio.0050335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Goldschmidt Y, et al. Control of relative timing and stoichiometry by a master regulator. PLoS One. 2015;10:e0127339. doi: 10.1371/journal.pone.0127339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.McAdams HH, Arkin A. Stochastic mechanisms in gene expression. Proc Natl Acad Sci USA. 1997;94:814–819. doi: 10.1073/pnas.94.3.814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nachman I, Regev A, Ramanathan S. Dissecting timing variability in yeast meiosis. Cell. 2007;131:544–556. doi: 10.1016/j.cell.2007.09.044. [DOI] [PubMed] [Google Scholar]
- 14.Pedraza JM, Paulsson J. Random timing in signaling cascades. Mol Syst Biol. 2007;3:81. doi: 10.1038/msb4100121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cai L, Friedman N, Xie XS. Stochastic protein expression in individual cells at the single molecule level. Nature. 2006;440:358–362. doi: 10.1038/nature04599. [DOI] [PubMed] [Google Scholar]
- 16.Raj A, van Oudenaarden A. Nature, nurture, or chance: Stochastic gene expression and its consequences. Cell. 2008;135(2):216–226. doi: 10.1016/j.cell.2008.09.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dar RD, et al. Transcriptional burst frequency and burst size are equally modulated across the human genome. Proc Natl Acad Sci USA. 2012;109:17454–17459. doi: 10.1073/pnas.1213530109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Singh A, Razooky B, Cox CD, Simpson ML, Weinberger LS. Transcriptional bursting from the HIV-1 promoter is a significant source of stochastic noise in HIV-1 gene expression. Biophys J. 2010;98:L32–L34. doi: 10.1016/j.bpj.2010.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Amir A, Kobiler O, Rokney A, Oppenheim AB, Stavans J. Noise in timing and precision of gene activities in a genetic cascade. Mol Syst Biol. 2007;3:71. doi: 10.1038/msb4100113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dennehy JJ, Wang IN. Factors influencing lysis time stochasticity in bacteriophage . BMC Microbiol. 2011;11:174. doi: 10.1186/1471-2180-11-174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yurkovsky E, Nachman I. Event timing at the single-cell level. Brief Funct Genomics. 2013;12:90–98. doi: 10.1093/bfgp/els057. [DOI] [PubMed] [Google Scholar]
- 22.Gardiner CW, et al. Handbook of Stochastic Methods. Vol 4 Springer; Berlin: 1985. [Google Scholar]
- 23.Van Kampen N. Stochastic Processes in Physics and Chemistry. Elsevier; Amsterdam: 2011. [Google Scholar]
- 24.Redner S. A Guide to First-Passage Processes. Cambridge Univ Press; Cambridge, UK: 2001. [Google Scholar]
- 25.Metzler R, Oshanin G, Redner S. First-Passage Phenomena and Their Applications. World Scientific; Singapore: 2014. [Google Scholar]
- 26.Iyer-Biswas S, Zilman A. First-Passage Processes in Cellular Biology. Wiley; New York: 2016. pp. 261–306. [Google Scholar]
- 27.Becskei A, Serrano L. Engineering stability in gene networks by autoregulation. Nature. 2000;405:590–593. doi: 10.1038/35014651. [DOI] [PubMed] [Google Scholar]
- 28.Alon U. Network motifs: Theory and experimental approaches. Nat Rev Genet. 2007;8:450–461. doi: 10.1038/nrg2102. [DOI] [PubMed] [Google Scholar]
- 29.Singh A, Hespanha JP. Optimal feedback strength for noise suppression in autoregulatory gene networks. Biophys J. 2009;96:4013–4023. doi: 10.1016/j.bpj.2009.02.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lestas I, Vinnicombegv G, Paulsson J. Fundamental limits on the suppression of molecular fluctuations. Nature. 2010;467:174–178. doi: 10.1038/nature09333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tao Y, Zheng X, Sun Y. Effect of feedback regulation on stochastic gene expression. J Theor Biol. 2007;247:827–836. doi: 10.1016/j.jtbi.2007.03.024. [DOI] [PubMed] [Google Scholar]
- 32.Hooshangi S, Weiss R. The effect of negative feedback on noise propagation in transcriptional gene networks. Chaos. 2006;16:026108. doi: 10.1063/1.2208927. [DOI] [PubMed] [Google Scholar]
- 33.Voliotis M, Bowsher CG. The magnitude and colour of noise in genetic negative feedback systems. Nucleic Acids Res. 2012;40(15):7084–7095. doi: 10.1093/nar/gks385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Singh A, Soltani M. Quantifying intrinsic and extrinsic variability in stochastic gene expression models. PLoS One. 2013;8:e84301. doi: 10.1371/journal.pone.0084301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shahrezaei V, Ollivier JF, Swain PS. Colored extrinsic fluctuations and stochastic gene expression. Mol Syst Biol. 2008;4:196. doi: 10.1038/msb.2008.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Swain PS, Elowitz MB, Siggia ED. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc Natl Acad Sci USA. 2002;99:12795–12800. doi: 10.1073/pnas.162041399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hilfinger A, Paulsson J. Separating intrinsic from extrinsic fluctuations in dynamic biological systems. Proc Natl Acad Sci USA. 2011;108:12167–12172. doi: 10.1073/pnas.1018832108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Paulsson J. Model of stochastic gene expression. Phys Life Rev. 2005;2:157–175. [Google Scholar]
- 39.Elgart V, Jia T, Fenley AT, Kulkarni R. Connecting protein and mRNA burst distributions for stochastic models of gene expression. Phys Biol. 2011;8:046001. doi: 10.1088/1478-3975/8/4/046001. [DOI] [PubMed] [Google Scholar]
- 40.Shahrezaei V, Swain PS. Analytical distributions for stochastic gene expression. Proc Natl Acad Sci USA. 2008;105:17256–17261. doi: 10.1073/pnas.0803850105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.McQuarrie DA. Stochastic approach to chemical kinetics. J Appl Probab. 1967;4:413–478. [Google Scholar]
- 42.Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81:2340–2361. [Google Scholar]
- 43.Alon U. An Introduction to Systems Biology: Design Principles of Biological Circuits. CRC; Boca Raton, FL: 2011. [Google Scholar]
- 44.Singh A. Transient changes in intercellular protein variability identify sources of noise in gene expression. Biophys J. 2014;107:2214–2220. doi: 10.1016/j.bpj.2014.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.White R, et al. Holin triggering in real time. Proc Natl Acad Sci USA. 2011;108:798–803. doi: 10.1073/pnas.1011921108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wang IN. Lysis timing and bacteriophage fitness. Genetics. 2006;172:17–26. doi: 10.1534/genetics.105.045922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Heineman RH, Bull JJ. Testing optimality with experimental evolution: Lysis time in a bacteriophage. Evolution. 2007;61:1695–1709. doi: 10.1111/j.1558-5646.2007.00132.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Shao Y, Wang IN. Bacteriophage adsorption rate and optimal lysis time. Genetics. 2008;180:471–482. doi: 10.1534/genetics.108.090100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bonachela JA, Levin SA. Evolutionary comparison between viral lysis rate and latent period. J Theor Biol. 2014;345:32–42. doi: 10.1016/j.jtbi.2013.12.006. [DOI] [PubMed] [Google Scholar]
- 50.Chang CY, Nam K, Young R. S gene expression and the timing of lysis by bacteriophage lambda. J Bacteriol. 1995;177:3283–3294. doi: 10.1128/jb.177.11.3283-3294.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shao YP, Wang IN. Effect of late promoter activity on bacteriophage lambda fitness. Genetics. 2009;181:1467–1475. doi: 10.1534/genetics.108.098624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gründling A, Smith DL, Bläsi U, Young R. Dimerization between the holin and holin inhibitor of phage . J Bacteriol. 2000;182:6075–6081. doi: 10.1128/jb.182.21.6075-6081.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bläsi U, Young R. Two beginnings for a single purpose: The dual-start holins in the regulation of phage lysis. Mol Microbiol. 1996;21:675–682. doi: 10.1046/j.1365-2958.1996.331395.x. [DOI] [PubMed] [Google Scholar]
- 54.Singh A, Dennehy JJ. Stochastic holin expression can account for lysis time variation in the bacteriophage . J R Soc Interface. 2014;11:20140140. doi: 10.1098/rsif.2014.0140. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.