Body mass index as a modifiable risk factor for type 2 diabetes: Refining and understanding causal estimates using Mendelian randomisation

Abstract

This study focused on resolving the relationship between body mass index (BMI) and type 2 diabetes. The availability of multiple variants associated with BMI offers a new chance to resolve the true causal effect of BMI on T2D, however the properties of these associations and their validity as genetic instruments need to be considered alongside established and new methods for undertaking Mendelian randomisation. We explore the potential for pleiotropic genetic variants to generate bias, revise existing estimates and illustrate value in new analysis methods. A two-sample Mendelian randomisation (MR) approach with 96 genetic variants was employed using three different analysis methods, two of which (MR-Egger and the weighted median) have been developed specifically to address problems of invalid instrumental variables. We estimate an odds ratio for type 2 diabetes per unit increase in BMI (kg/m²) of between 1.19 and 1.38, with the most stable estimate using all instruments and a weighted median approach (1.26 95%CI (1.17, 1.34)). TCF7L2(rs7903146) was identified as a complex effect or pleiotropic instrument and removal of this variant resulted in convergence of causal effect estimates from different causal analysis methods. This indicated the potential for pleiotropy to affect estimates and differences in performance of alternative analytical methods. In a real type 2 diabetes focused example, this study demonstrates the potential impact of invalid instruments on causal effect estimates and the potential for new approaches to mitigate the bias caused.

Observational studies have shown body mass index (BMI) to be associated with risk of type 2 diabetes as well as with a range of diabetes-related metabolic traits (1; 2). However, it is well known that confounding, reverse causation and biases can generate such associations and that even with careful study design, incorrect inference is possible (3). One approach to circumventing these problems is to use genetic association results within a Mendelian randomization (MR) framework (3; 4). In MR analyses, genetic variants act as proxies for an exposure in a manner independent of confounders. If in addition the variants only affect an outcome of interest through the chosen exposure, then they are said to be valid instrumental variables (IVs). This enables evaluation of the causal effect of the exposure on the outcome, escaping some of the limitations of observational epidemiology; (5).

Following the success of genome-wide association studies (GWASs), the number of MR analyses using large numbers of mostly uncharacterized variants associated with complex health outcomes or intermediates is rapidly increasing (6; 7). In the case of BMI, there are now 97 genetic variants reliably associated and there are examples where multiple variants have been used as a composite IV to estimate the causal impact of BMI on health (8). Although using many IVs can increase the power of MR analyses , it brings with it the concern that enlarged sets of genetic variants are more likely to contain invalid IVs due to violations of the assumptions necessary for valid causal inference using traditional methods (9). In particular, horizontal pleiotropy – where a genetic variant affects the outcome via more than one biological pathway (10) – is a concern. Importantly, the properties of these associations and their validity as genetic instruments need to be considered alongside established and new methods for undertaking Mendelian randomisation.

In response to the general issue of using multiple genetic variants in MR, Bowden et al. (9) propose both MR-Egger regression, an approach developed from the original Egger regression technique for assessing small study bias in meta-analysis and a weighted weighted median approach (11) as alternatives to the standard MR analysis. The MR-Egger and weighted weighted median approaches both operate using distinct, but critically weaker, versions of the IV assumptions, and therefore have the potential to deliver robust causal effect estimates. The MR-Egger method also provides a formal statistical test as to whether or not the average pleiotropic effect of the genetic variants is equal to zero (9).

Research Design and Methods

With increasing evidence for multiple biological pathways underlying type 2 diabetes (12; 13) and increasing numbers of genetic variants available as IVs for BMI, we set out to test the potential for bias in causal estimates from MR using these state-of-the-art approaches. We compared results from MR-Egger regression (9) and weighted weighted median (11) approaches to a traditional inverse-variance weighted (IVW) method (which makes the strong assumption that all variants are valid IVs) (14) in an investigation of the causal relationship between BMI and type 2 diabetes. These methods all undertake two-sample Mendelian randomisation whereby the GWAS results for a disease outcome are unified with those of an exposure of interest and together used to estimate the causal impact of that exposure on disease. We used published data in a two-sample analysis strategy taking SNP-exposure and SNP-outcome associations from different sources (15; 16).

The effect sizes for BMI-associated SNPs with associated standard errors from a mixed-sex cohort of European ancestry were taken from the Genetic Investigation of ANthropometric Traits (GIANT) consortium (17) along with results for type 2 diabetes from the DIAbetes Genetics Replication And Meta-analysis (DIAGRAM) Consortium. To avoid sample overlap, GIANT estimates were recalculated in the absence of DIAGRAM cohorts yielding a maximum sample size at any given locus of 189,079. To aid interpretation of the effects of BMI on type 2 diabetes, effect sizes were transformed to BMI units prior to analysis, assuming one standard deviation (SD) = 4.5kg/m²(17). For the corresponding SNP-outcome association, we took odds ratios (ORs) and confidence intervals from a GWAS meta-analysis conducted by the DIAGRAM Consortium. This genome-wide meta-analysis includes data from 12,171 type 2 diabetes cases and 56,862 controls of mainly European descent imputed at up to 2.5 million autosomal SNPs (DIAGRAMv3) (18). All but one (rs4787491, INO80E) of the BMI-associated SNPs (p<5x10^-8) from GIANT had results listed in the DIAGRAMv3 dataset so 96 SNPs with results in both datasets were taken forward for analysis.

SNP-exposure and SNP-outcome associations were combined using the three different approaches outlined above. All analyses were conducted in R 3.2.0 (19). First, an inverse-variance weighted (IVW) method was implemented to provide a weighted average of the causal effect estimates (14). This method assumes that all genetic variants (i.e. 100%) satisfy the IV assumptions (including zero pleiotropy) and uses weights that assume the gene-exposure association estimates are measured without error (the No Measurement Error (NOME) assumption).

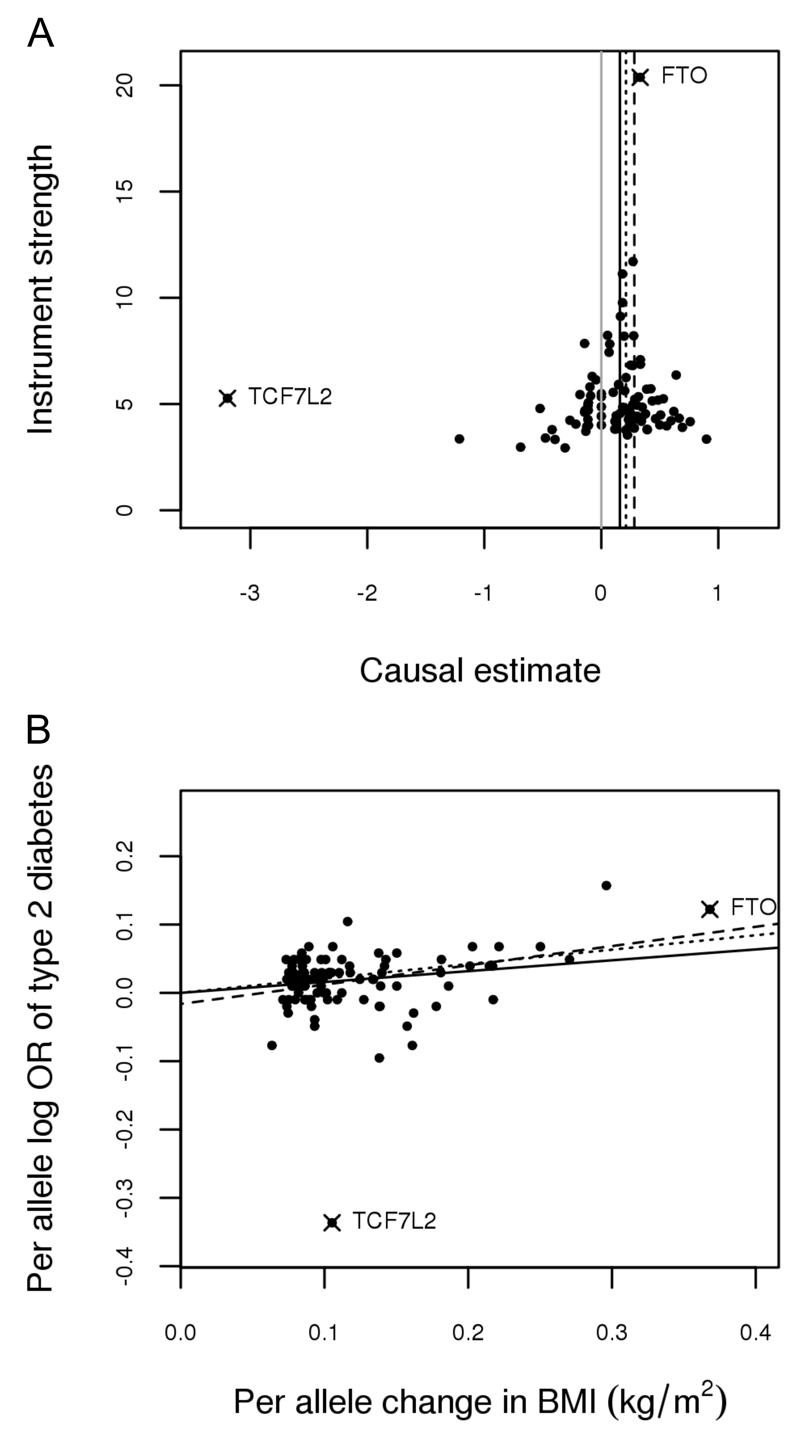
Second, we performed MR-Egger regression (9), which assumes NOME but allows each variant to exhibit pleiotropy. MR-Egger estimates remain consistent only if the magnitude of the gene exposure associations across all variants are independent of their pleiotropic effects (the InSIDE assumption) (9). As recommended by Bowden et al (9), the extent to which pleiotropy was balanced across the set of instruments as a whole was visually assessed by plotting the causal effect estimates against their precision, using a funnel plot and checking for asymmetry (Figure 1A). The NOME assumption was assessed for MR-Egger via an adaptation of the I² statistic $(I_{GX}^2)$ (20) and adjusted for by combining MR-Egger with the method of Simulation Extrapolation (SIMEX) (21). Using SIMEX, new data sets are created by simulating gene-exposure association estimates under increasing violations of NOME and recording the amount of attenuation in the estimate that occurs. The set of attenuated estimates are then used to extrapolate back to the estimate that would have been obtained if NOME had been satisfied.

Figure 1.

Genetic associations with body mass index (BMI) and type 2 diabetes from 96 variants measured in GIANT (17) and DIAGRAM (18), respectively. TCF7L2(rs7903146) and FTO(rs1558902) are marked with a ‘X’ and labelled.

A - funnel plot of minor allele frequency corrected genetic associations with BMI (interpreted as instrument strength) against causal estimates based on each genetic variant individually, where the causal effect is expressed in logs odds ratio of type 2 diabetes for each unit increase in BMI. The overall causal estimates (β coefficients) of BMI on type 2 diabetes estimated by inverse-variance weighted (solid black line), MR-Egger (dashed black line) and weighted median (dotted black line) methods are also shown. Grey solid line represent x=0, that is a causal estimate of zero.

B - scatter plot of genetic associations with type 2 diabetes against associations with BMI, with causal estimates (β coefficients) of BMI on type 2 diabetes estimated by inverse-variance weighted (solid line), MR-Egger (dashed line) and weighted median (dotted line) methods.

Finally, a weighted weighted median estimation method was applied (11). The weighted median provides a consistent estimate of causal effect if at least 50% of the information in the analysis comes from variants that are valid IVs. For a more detailed description of the three methods applied, see Online Appendix (Supplementary methods). A leave-one-out permutation analysis was conducted across all methods to assess the influence of potentially pleiotropic SNPs on the causal estimates (22). In the case of the linear models (IVW and MR-Egger) two additional analyses were conducted (23; 24). Firstly, the extent to which the causal estimate from each SNP in the set could be considered an outlier was assessed using studentized residuals. Secondly, Cook’s distance (25) was used as a measure of the aggregate impact of each SNP on the model.

Results

All three approaches provide evidence of a positive causal relationship between BMI and type 2 diabetes. This is demonstrated in Figure 1B where the slope of the lines show the causal effect estimates as predicted by the IVW, MR-Egger and m weighted median approaches. Estimates correspond to an OR for type 2 diabetes per unit increase in BMI (kg/m²) of 1.19, 1.26 and 1.38 for the IVW, weighted median and MR-Egger analyses, respectively and are in line with a previous MR estimate of 1.27 (95%CI 1.18, 1.36) (2) (Table 1). Assessment of the NOME assumption with respect to the MR-Egger estimate gave $I_{GX}^2=0.83,$ suggesting an approximate 15% attenuation of the causal estimate towards zero. Bias adjustment via SIMEX gave a corrected MR-Egger causal estimate of 1.46 (95%CI 1.16, 1.84) for type 2 diabetes per unit increase in BMI (kg/m²).

Table 1.

Estimates from the application of inverse-variance weighted, MR-Egger and weighted median Mendelian randomisation methodologies. Estimates represent the estimated causal effect of body mass index on type 2 diabetes.

Method	Estimate	95% CI	p-value
Complete variant set (n=96 SNPs)
IVW	1.20	1.09, 1.30	8.00 x 10-05
MR-Egger	1.39	1.14, 1.68	1.53 x 10-03
MR-Egger(α)	-0.019	-0.041, 0.004	0.10
Weighted median	1.26	1.17, 1.34	5.26 x 10-9
TCF7L2(rs7903146) removed from the variant set (n=95 SNPs)
IVW	1.22	1.16, 1.28	1.49 x 10-11
MR-Egger	1.34	1.17, 1.51	9.71 x 10-06
MR-Egger(α)	-0.011	-0.024, -0.024	0.13
Weighted median	1.26	1.19, 1.32	3.29 x 10-10
FTO(rs1558902) removed from the variant set (n=95 SNPs)
IVW	1.16	1.06, 1.27	1.31 x 10-03
MR-Egger	1.30	1.01, 1.65	0.04
MR-Egger(α)	-0.012	-0.038, 0.014	0.34
Weighted median	1.21	1.13, 1.28	6.81 x 10-08

Intercept coefficients MR-Egger^(_α) represent the average pleiotropic effect of a genetic variant on type 2 diabetes risk. “IVW” refers to inverse variance weighted estimates, SNP refers to single nucleotide polymorphism.

Considering the individual SNP-based contributions to MR analysis, there is one clear outlier in the distribution of effects shown in Figure 1 and that is TCF7L2(rs7903146). TCF7L2(rs7903146) shows an association with BMI that is in the opposite direction to the overall trend (and weak relative to its effect on type 2 diabetes), resulting in a large negative causal estimate from this SNP alone. The presence of at least some unbalanced pleiotropy was detected within the set of variants, as reflected by the intercept estimate of -0.019 (p=0.10) in the MR-Egger analysis.

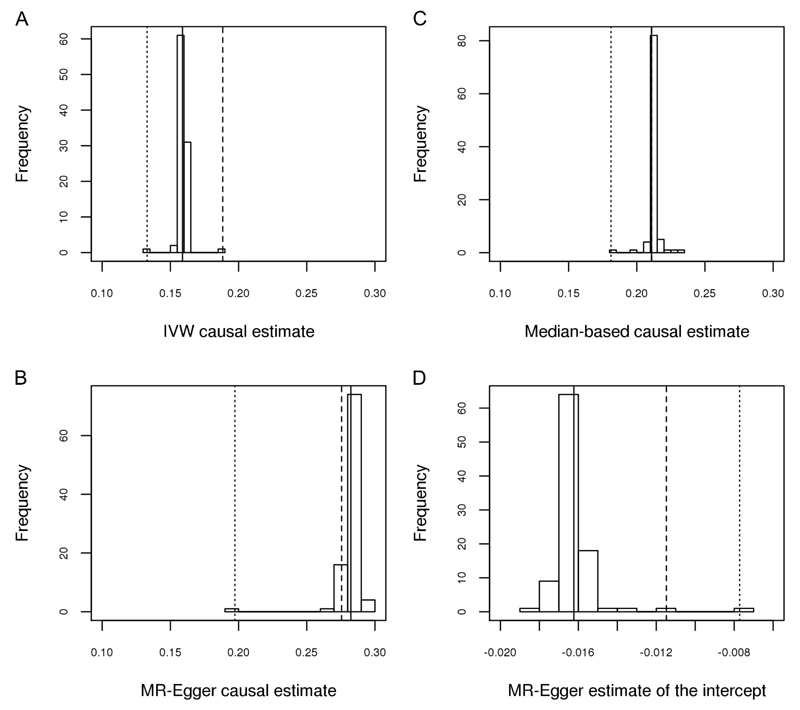
To illustrate the impact of TCF7L2(rs7903146) on causal estimates, we performed a sensitivity analysis in which each SNP in turn was removed from the set in a leave-one-out permutation analysis. We saw a shift in the causal estimates from the IVW (an increase) and MR-Egger (a decrease) as a result of the removal of TCF7L2(rs7903146) but no difference in the estimate from the weighted median approach (Table 1; Figure 2). The results of the leave-one-out permutation analysis showed that the impact of removing TCF7L2(rs7903146) from the variant set on the IVW and MR-Egger estimates was greater than that of removing almost any other variant, with the exception of FTO(rs1558902) (Figure 2A & B). When FTO(rs1558902) was removed, causal estimates from both the IVW and MR-Egger analysis decreased (Table 1; Figure 2). In this instance we also observed movement in the causal effect estimate from the weighted median (Table 1; Figure 2C). The estimate of the intercept from MR-Egger moved closer to zero following both the removal of TCF7L2(rs7903146) and FTO(rs1558902) (Figure 2D). TCF7L2(rs7903146) was also identified as an outlier in both IVW and MR-Egger (studentized residuals, Bonferroni corrected p<1x10^-19) but FTO(rs1558902) was not (Online Appendix (Supplementary Results, Figures S1A/B)). Calculation of Cook’s distance showed both variants to have a disproportionate level of influence on the model compared to other variants in the set (Online Appendix (Supplementary Results, Figures S2A/B)).

Figure 2.

Distributions of regression estimates resulting from leave-one-out permutation analysis. Solid line = estimate from main analysis (n=96 variants); dashed line = estimate with TCF7L2(rs7903146) removed; dotted line = estimate with FTO(rs1558902) removed.

A - Causal estimates (β coefficients) of BMI on type 2 diabetes estimated by an inverse-variance weighted method

B - Causal estimates (β coefficients) of BMI on type 2 diabetes estimated by MR-Egger

C - Causal estimates (β coefficients) of BMI on type 2 diabetes estimated by a weighted median method

D – Estimates of the intercept by MR-Egger

These results suggest TCF7L2(rs7903146) may be pleiotropic with respect to the outcome, i.e. that it influences type 2 diabetes through an alternative pathway (other than BMI). Evidence from existing literature supports this assertion as the type 2 diabetes risk increasing allele at TCF7L2(rs7903146) has been associated with both increased fasting glucose (26) and decreased BMI (17). Under the assumption that TCF7L2(rs7903146) demonstrates horizontal pleiotropy with respect to type 2 diabetes, we would expect its inclusion in the variant set to bias the causal estimate predicted by the IVW approach, but not that predicted by MR-Egger or the weighted median. Removing TCF7L2(rs7903146) from the variant set causes a slight shift in the causal estimates from the IVW and MR-Egger approaches, bringing them more in line with one another and also with the weighted median estimate which remained stable in this instance. Also of note is the reduction in the 95% confidence interval of the MR-Egger estimate following removal of the TCF7L2(rs7903146). This increase in precision following removal of a likely invalid instrument from the set is another potentially favourable quality of this estimator. The relatively small changes observed across all methods as a result of removing TCF7L2(rs7903146) are in line with the relatively weak effect of the SNP as shown in Figure 1B.

In contrast, the effect of removing FTO(rs1558902) is more noticeable. Regardless of the method used, removing this variant results in a lower causal estimate (Table 1; Figure 2). The substantial influence of FTO(rs1558902) was predicable given the strength of its effect relative to the other variants (Figure 1B), though properties of this effect are not in line with other variants used to instrument BMI as reported elsewhere for physical activity (27), thyroid function (28) and depression (29). The concomitant increase in standard error associated with the estimates here point towards increased uncertainty moving the estimates towards the null in the absence of FTO(rs1558902). The weighted median appears robust, even to the removal of FTO(rs1558902), as demonstrated by the relatively tight distribution of estimates returned from the leave-one-out permutation analysis (Figure 2C). This is as expected given the tolerance of weighted median approaches to outliers.

Discussion

By applying new analytical techniques to an old question – the causal relationship between BMI and type 2 diabetes – we have explored the potential for invalid instruments to bias causal estimates in MR. In this case where BMI is the exposure, the opportunity to use a large instrument list in causal analyses presents both opportunity, through variance explained, but also cost, through complications generated by instrument properties or methods employed. Results here suggest that both TCF7L2 and FTO appear to have genetic variation which predicts BMI reliably, but for which associations with type 2 diabetes do not fully align with that for other variants (given BMI effects and assumed causality).

For TCF7L2, only recently suggested to be associated with BMI directly (17), this is not surprising and reinforces the important point that the validity of a specific method’s MR estimate depends on whether the genetic variants collectively satisfy its assumptions. In this case, it is possible that the negative association with BMI observed in GIANT is the product of a form of bias where the risk of type 2 diabetes is leading to effective treatment, health benefit and BMI reduction. This is supported by the apparently causal negative relationship between type 2 diabetes and BMI seen in a reciprocal analysis where BMI is the outcome of interest (Online Appendix (Supplementary Results, Figure S3)), though is likely to be more a comment on study design than biological effect.

In this example, the use of recently derived methods (9; 11) designed to overcome problems caused by directional pleiotropy, yields estimates which are more stable in the presence or absence of potentially invalid instruments and confirm the likely magnitude of the average effect of BMI on type 2 diabetes (i.e. from the most likely and stable estimate, an elevation of odds of disease of ~26% for each additional unit of BMI). The comparison of results from different methods for any set of potential instruments is important when assessing the reliability of causal inferences and important for downstream interpretation. In this case, whilst it is impossible to model precisely, one can estimate the hypothetical impact of an average population level change in lifecourse BMI on type 2 diabetes. Given a population size of 64.1 million in the UK in mid 2013(30) and a modelled prevalence of type 2 diabetes (including non-diagnosed cases) of 7.4%(31; 32), the estimated reduction in odds for a 1kg/m2 reduction would potentially yield a reduction in the number of cases from ~4.7-3.6 million (a shift in prevalence to 5.6%).