High-Resolution Mesoscopic Fluorescence Molecular Tomography Based on Compressive Sensing

Abstract

Mesoscopic fluorescence molecular tomography (MFMT) is new imaging modality aiming at 3-D imaging of molecular probes in a few millimeter thick biological samples with high-spatial resolution. In this paper, we develop a compressive sensing-based reconstruction method with l₁-norm regularization for MFMT with the goal of improving spatial resolution and stability of the optical inverse problem. Three-dimensional numerical simulations of anatomically accurate microvasculature and real data obtained from phantom experiments are employed to evaluate the merits of the proposed method. Experimental results show that the proposed method can achieve 80 μm spatial resolution for a biological sample of 3 mm thickness and more accurate quantifications of concentrations and locations for the fluorophore distribution than those of the conventional methods.

I. Introduction

Mesoscopic fluorescence molecular tomography (MFMT), also known as laminar optical tomography (LOT), has been developed to perform depth-resolved functional and molecular imaging at the spatial junction between microscopic and macroscopic imaging. This novel optical imaging modality that operates in the mesoscopic regime combines the advantages of diffuse optical tomography (DOT) image reconstruction and a microscopy-based setup to allow noncontact imaging of large areas. MFMT (or LOT) is a subsurface imaging technique that relies on an optical inverse problem to generate depth-resolved 3-D images of highly scattering tissues at depths of several millimeters and with high sensitivity [1]–[3]. Although MFMT can achieve reconstructions with higher resolution compared to DOT, it still faces the same challenges as DOT, such as, recovering the depth and size of the biomarkers with accuracy. In MFMT, the number of measurements available is often much smaller than the number of unknown 3-D image elements, which may result in the nonuniqueness of the solution. Moreover, the inverse solution may be more unstable when higher resolution performances are sought (high frequencies in the image space). As in all ill-conditioned diffusion-based inverse problem, the noise in the measurements data may induce large artifacts in the reconstructed image. Furthermore, it becomes harder to obtain accurate reconstructions of fluorophore biodistribution at deeper locations due to exponential decay of light intensities with depth and limited volume probed in reflectance geometry [4].

Recently, the emerging field of compressive sensing (CS) has shown that sparse signals, which have a small number of nonzero entries, can be recovered from far fewer samples or measurements than those required by the traditional Shannon–Nyquist sampling theorem. The CS theory has been generalized to recover sparse signals in general bases from limited number of measurement data. The CS framework has been utilized to solve the inverse problems of optical tomography [5]. For fluorescence tomographic imaging, it has been reported that sparse fluorophore concentration can be reconstructed by solving an l₁-norm constraint optimization problem. Alternative optimization methods proposed in [6] and [7] are shown to offer improved performance relative to l₁-norm. It is demonstrated in these contributions that more accurate signal reconstruction can be achieved by solving an l₁-norm-based minimization problem.

However, reconstruction algorithms selection is highly problem dependent. To our knowledge, CS-based reconstruction methods have not yet been applied to optical tomography in the mesoscopic regime. In this paper, we propose a CS-based reconstruction method to solve the optical inverse problem in MFMT. In such applications, the fluorophore distribution is often concentrated within a small spatial region, where the fluorophore concentrations have large amplitudes, whereas in the background region, the fluorophore concentrations are nonexistent or close to zero. In this case, the objective function is extremely sparse in the imaging domain, and, hence, very amenable to CS methods. Herein, the proposed method introduces an l₁-norm regularization to constrain the solution to a sparsity subspace, suppressing the background noise, and expressing the true distributions of fluorophore concentrations, allowing for an accurate and stable image formation process. We apply this CS-based reconstruction approach to an in silico vascular bed phantom and real multimodal experimental data. In the following section, we describe our MFMT imaging system and image reconstruction algorithm. In the third section, we report our realistic numerical simulation results and physical phantom experiments with microCT coregistration. In the last section, we discuss relevant issues and conclude this paper.

II. Method

A. Imaging Platform

Herein, we employed an MFMT imaging system that has been reported in detail in [3] and used to image bioprinted tissues [8] and to retrieve the 3-D distribution of a photosensitizer in skin cancer prior to PDT treatment [9]. Briefly, the system is an ultrafast multiwavelength MFMT platform using raster scanning of a laser beam and descanned detection of the optical signals by seven offset detectors. The system acquires data over a maximum imaging area of 8 mm × 5.5 mm at 7.5 Hz (<150 ms/frame) in reflectance geometry. The laser beam is raster scanned using a resonant galvo mirror for ultrafast acquisitions. The fluorescence backscattered signal is imaged on a 4 × 8 avalanche photodiode detector array (S8550, Hamamatsu) from which seven elements are employed. The detectors are evenly linearly distributed from 800 to 3900 μm away from the source. The total number of measurements acquired is dependent on the imaged area and is 107 520 measurements (15 360 different positions ×7 detectors measurements for each source position) for the maximum imaging area.

B. Monte Carlo (MC)-Based Inverse Problem

To implement image reconstruction of fluorophore distribution, a numerical model is required to simulate photon propagation in the biological sample. The diffusion approximation (DA) with Robin-type boundary condition [10] is the most widely used as a photon propagation model because of its high computational efficiency. However, it is well established that it only works well in weakly absorbing and highly scattering media and breaks down at near sources and across boundaries. So, the DA model is not suitable to simulate photon propagation in the mesoscopic regime. The MC is the gold standard to simulate light propagation in turbid media as it can accurately simulate photon propagation without the aforementioned limitations of the DA. With the development of a high performance computing technique, MC simulation in a graphics processing unit (GPU) environment can be 1000 times faster than those performed on a single standard central processing unit (CPU) [11], [12], enabling the use of MC techniques for DOT on a personal computer [13], [14]. Herein, a GPU-based MC code has been employed to compute the forward problem using an adjoint formulation for computational efficiency (a few minutes) [15]. This code is also employed to generate the in silico phantom experiments. In all computations herein, 10⁶ photons were employed for good statistical sampling of the volume imaged at all optodes spacing. To simulate fluorescence light emission in diffuse medium using MC, we follow the formulation described in detail in [13]. We provide briefly the main salient points of this formulation later.

The 3-D distribution of the fluorophore’s effective quantum yield η(r) can be obtained by solving an integral equation relating the fluorescence signals at time t and η(r):

$$U_F(r_s,r_d,t)={\int }_{\mathrm{\Omega }}W(r_s,r_d,r,t)\eta (r)dr$$ (1)

where U_F (r_s, r_d, t) is the fluorescence detected by a detector located at r_d at t resulting from an excitation at the source r_s at t₀ = 0, the integration domain Ω is defined as the entire imaging volume, and W (r_s, r_d, r, t), referred to as the weight function or Jacobian, describes how sensitive a change in η(r) will result in a change in U_F (r_s, r_d, t). There are a few MC-based methods to calculate W. Herein, we employed the forward-adjoint MC method to produce Jacobians [15] for computational efficiency. In the method, W is computed by convolving the Green’s functions and the lifetime decay of fluorophore:

$$W(r_s,r_d,r,t)={\int }_0^t{e}^{-\frac{t-t^{\prime }}{\tau }}d{t}^{\prime }\underset{0}{\overset{t^{\prime }}{\int }}{G}^x(r_s,r,t^{\prime }-t^{″})\ast G^m(r,r_d,t^{″})d{t}^{″}$$ (2)

where G^x and G^m are the time-dependent Green’s functions calculated by MC simulations at excitation and emission wavelength, respectively [10], and τ is the lifetime of the fluorophore. As customary done in FMT and MFMT, the optical properties at the excitation and emission wavelengths are considered similar herein. Moreover, as our datasets are time independent, the formulation of (2) is integrated over time to match our data type. The system of linear equations representing the measurements detected at different positions and time can then be solved to obtain η(r).

In practices, (2) should be discretized to perform numerical computation. First, the ROI Ω is discretized into voxels (or tetrahedrons). The size of cubic element is related to the spatial resolution of image reconstruction. Each element e_i is a potential source of fluorescence, which is linearly related to the fluorophore’s effective quantum yield η(r). By tracing excitation and fluorescence photon propagation in the sample using MC, we can compute a system matrix A (also called sensitivity matrix or Jacobian) to describe the relation between the fluorophore effective quantum yield in every 3-D image element (e₁, e₂, …, e_n) and measurement data. The linear equation system describing the relationship between measured photon numbers for each optode combination and the fluorophore bio-distribution is then

$$\mathbf{Y}=\mathbf{AX}+\mathbf{v}$$ (3)

where Y is a vector of the photon fluence rate with noise v measured at each detector element for each scanning position, X a vector of unknown fluorophore concentration at each voxel element, and A is the Jacobian. The task of MFMT consists in reconstructing the unknown fluorophore parameter distribution X based on the linear equation system (3) from the measured data Y.

A is generated for a chosen measurement setup following the formulation provided in [16]. Herein, all parameters, such as assigned optical parameters, the position and separation of light source and detectors, source radius, width of the detector spot detection, mimic our current LOT optical system [3] applied to vascular bioprinted tissue imaging [8]. For our in silico experiments, based on simulated local distribution of fluorophores, we can generate measurement data Y via MC simulations. Noise can be added post hoc to the generated measurements to replicate specific acquisition settings. Herein, we employ a white Gaussian noise and define the signal-to-noise ratio (SNR) as follows:

$$\text{SNR}=\frac{\sqrt{(s_1^2+s_2^2+\dots +s_m^2)/m}}{\sqrt{(n_1^2+n_2^2+\dots +n_m^2)/m}}$$ (4)

where s₁, s₂, …, s_m and n₁, n₂, …, n_m are the entries of measurements matrix and additional noise, respectively. m is the number of measurements.

C. CS-Based Reconstruction

The key concept behind CS-based reconstructions is to exploit the prior knowledge that a large number of the unknown coefficients are close to or equal to zero (sparse and compressible). In optical molecular imaging applications, fluorophore probes are often engineered to specifically target cells/receptors of a preferred type and accumulate locally, forming a focal distribution of fluorophore concentrations. Hence, in such applications in which the image space is populated by relatively few significant pixels with nonzero values in image space, the CS-framework provides enhanced reconstruction performances [17], [18]. Besides sparsity in the image space, it is required that the CS matrix fulfils the incoherence property and that the reconstruction be performed via a solver that enhances sparsity, such as the l₁-norm. To demonstrate the incoherence property of our problem, we employed the same methodology as described in [17].

If the transform point spread function is a natural tool to measure incoherence [19], it is hard to judge the incoherence when most of the inner products are tiny. Here, we employed the cumulative coherence function (CCF) to evaluate coherence between the transformation matrix T and Jacobian matrix A:

$$\mathit{CCF}(m)=max{max}_{\mathrm{\Omega }}\sum _k{A}_k{T}_j$$ (5)

where m denotes the order of the CCF and Ω is the set of all possible subsets of m columns selected from the Jacobian. Furthermore, k ranges over a specific subset of Ω at a given order and j defines columns of the transformation matrix for all possible subsets. It has been shown that a slowly increasing CCF versus order m signifies incoherence [17]. The CCF of the CS matrix (AT) of the Jacobian and transformation basis (Fourier basis) was calculated for an order of up to 16. The slowly increasing trend of CCF curve, shown in Fig. 1, confirms the incoherence property of the CS matrix AT [17].

Fig. 1.

CCF between Jacobian (A) and the discrete Fourier transform (T) for several orders (m = 1 – 16).

For the reconstruction of sparse objective function, CS techniques can achieve high-quality image reconstruction from far fewer measurements than that required by Nyquist sampling. As one type of CS-based reconstruction strategy, the l₀-norm regularization can ensure sparsest image reconstruction. The restricted isometry property can guarantee the equivalence of the solutions from the l₁ and l₀ minimization procedures. However, the l₀-minimization is an NP (non-deterministic polynomial)-hard problem that is almost impossible to solve. Thankfully, the l₁ norm, which is a quantitative index to measure the sparsity of a signal, is a convex function which approximates the l₀ norm well [20]–[24]. Hence, we can formulate the inverse problem as the following linearly constrained minimization:

$$min{\Vert \mathbf{AX}-\mathbf{Y}\Vert }_2^2+\lambda {\Vert \mathbf{X}\Vert }_1$$ (6)

where the variable is X ∈ Rⁿ, A ∈ R^m×n, and Y ∈ R^m, and m and n are the number of measurements and unknowns, respectively. λ is a regularization parameter with the l₁-norm solution giving preference to a sparse spatial distribution. The l₁-regularized problem (6) can be transformed to a convex quadratic program, with linear inequality constraints,

$$\begin{array}{l}min{\Vert \mathbf{AX}-\mathbf{Y}\Vert }_2^2+{\sum }_{i=1}^n\lambda u_i\\ \text{subject}\text{to}-u_i\le x_i\le u_{i}i=1,2,\dots ,n,\end{array}$$ (7)

where the variable u ∈ Rⁿ.

The objective function of optimization (6) is convex but not differentiable. This problem can be transformed to an unconstraint optimization using interior-point methods. The preconditioned conjugate gradients (CG) algorithm is used to compute the search direction for the truncated Newton iterations to solve this optimization problem [25].

D. Objective Quantitative Performance Measure

In this investigation, besides subjective assessment of the performances of the CS approach based on visual inspection, we also employed a quantitative metric for objective evaluation. We first evaluated the mean square error (MSE) between the real fluorophore yield and the reconstructed image over the entire image domain [4]–[6]. Let X_true = {xi_true |i = 1, 2, …, k} and X_recon = {xi_recon|i = 1, 2, …, k} be the original and reconstruction signal, respectively. The proposed quality index is defined as follows:

$$S_{\text{MSE}}={\sum }_{i=1}^k\frac{{\Vert X_{\text{true}}-X_{\text{recon}}\Vert }_2}{\text{total}\text{voxels}\text{of}\text{reconstruction}}.$$ (8)

The dynamic range of S_MSE is [0, +∞). The best value 0 is achieved if and only if X_true = X_recon for all i = 1, 2, …, k, and k is the total number of voxels in fluorophore concentrations. Hence, a smaller S_MSE reflects higher reconstruction fidelity.

E. Experimental Models

In silico models were designed to assess the performances of the proposed method in terms of spatial resolution, depth-dependent performances, and robustness to noise. First, a simple regular model representing a bioprinted vascular tree with main trunk and two off-shoots was employed. The different diameters of the vascular tree components are 400, 300, and 200 μm, as shown in Fig. 2. The fluorophore concentrations are assumed to be homogeneous over the vessel as shown in Fig. 2(a)–(b) with effective quantum yield equal to 1. The simulated imaging domain is a 2 mm × 5 mm surface area with a depth (Fig. 2(c)). We assume a homogeneous scattering coefficient ( ${\mu }_{\mathrm{s}}^{\prime }=5{\text{cm}}^{-1}$) and endogenous absorption coefficient (μ_a = 0.02 cm⁻¹) over the domain. The Henyey–Greenstein phase function was used for all computation herein with g = 0.9. These parameters replicate the optical properties of the collagen scaffold employed in our bioprinting application at collagen density of ~3 mg/mL [3].

Fig. 2.

Vascular tree model. (a) Three-dimensional visualization with maximum projection on the bounding planes. (b) XY view. The dimensions of three components of the vascular tree are 0.4 mm × 2.8 mm × 0.4 mm, 0.7 mm × 0.3 mm × 0.3 mm, and 0.5 mm × 0.2 mm × 0.2 mm, respectively, for the main tree, bigger off shoot, and smaller off shoot. (c) yz-slices of the sensitivity matrix; seven detectors are placed along y-axis on the volume surface.

The vascular tree was placed at six different depths, 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0 mm, to test the impact of depth on reconstruction fidelity. We discretized the imaging domain according to the desired resolution. For example, we discretized the imaging domain into 10 × 25 × 15 voxels when considering a 200 μm discretization, leading to a Jacobian of size 1750 (250 source positions, seven detectors) by 3750. To investigate higher resolutions, we simulated also 100 and 80 μm discretizations. Examples of typical measurements for the 7000 source positions and for individual detectors are provided in Fig. 3.

Fig. 3.

Synthetic measurements for the vascular model of Fig. 2. Each pixel corresponds to a source position for a specific detector offset with the vascular model embedded at depth of (a) 0.5 mm and of (b) 3 mm (SNR of 60). The colorbar represents the spatial contrast distribution acquired by each individual detector (ΔR) normalized to the overall dynamical range of measurements (R).

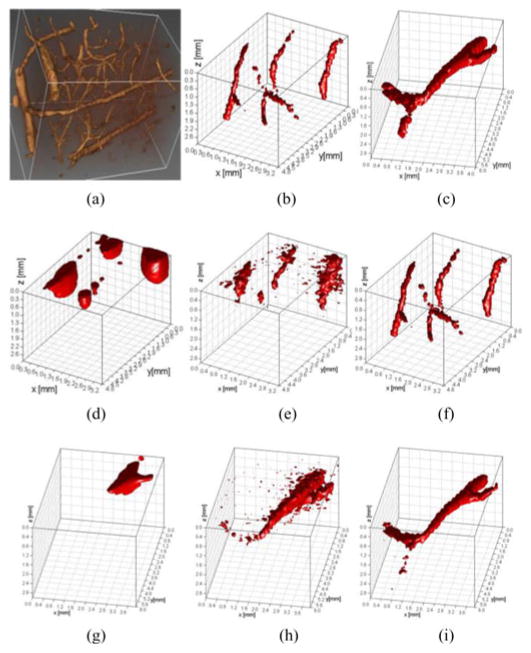
Then, two vasculature networks modeled after in vivo data obtained via two-photon microscopy were employed to simulate more realistic configuration of complex vascular networks in 3-D. To simulate an anatomically accurate vascular bed, we rescaled and cropped part of a microvessel network obtained from two-photon microscopy of a rat somatosensory cortex obtained from [26], as shown in Fig. 7(a). The segmented vessels were simulated to be labeled with fluorophore as reported in [8]. The fluorophore concentrations are assumed to be homogeneous over the vessel as shown in Fig. 7(b) and (c). The size of the image domain and discretization was identical to the previous in silico models.

Fig. 7.

Reconstruction results for complex vasculature by three regularization methods. (a) Raw data were represented in 3-D. (b) and (c) Raw data were segmented for two different sets of vascular channels, T1 and T2. (d)–(f) Segmented vessel, T1, was reconstructed by CG, LSQR, and CS, respectively. (g)–(i) Segmented vessel, T2, reconstructed by CG, LSQR, and CS, respectively (no noise added in the vascular network model).

Finally, the CS method is employed to reconstruct real phantom data and compared to a high-resolution anatomical imaging modality, in this case, microCT (Scanco Medical Viva CT40). Two sealed glass capillaries (d_outer = 1 mm, d_inner = 0.61 mm) containing 5 μM of NIR-664-iodoacetamide (λ_ex = 664 nm, λ_em = 689 nm; Sigma-Aldrich) in methanol were positioned in a 3-mm-thick collagen (9 mg/mL; μ_a = 0.08 cm⁻¹; ${\mu }_s^{\prime }=5{\text{cm}}^{-1}$) scaffold at two different depths in an orthogonal fashion. The phantom was imaged over a 5.5 mm × 8 mm area using our MFMT system (15 360 source positions-7 detectors measurements at each source position: 107 520 total measurements). Under microCT, the collagen phantom with glass capillaries was visualized with a field of view of 32.8 mm² at 16 μm voxel size.

In all cases, both visual results and S_MSE indexes are given to evaluate the performance of the proposed inverse methodology in different scenarios. For the purpose of comparison, we also give the reconstruction results by commonly used iterative regularization methods, least square QR factorization (LSQR) and CG. In order to get optimal results for l₁-norm, LSQR and CG methods, we employ the L-curve method to find the iterative number and regularization parameter when residual norm tends to a least value [7].

III. Result

A. MC Computation and Reconstructions

All computations were carried out to generate the Jacobians and synthetic measurements were performed under less than 5 min in a desktop computer (CPU: Intel Core i7-3820 Quad-Core 3.60 GHz 10 MB Intel Smart Cache, GPU: NVIDIA Kepler K20M). Similarly, reconstructions were performed in a less than 5 min on the aforementioned computer. For instance, reconstructions based on the CS method for a 2 mm × 5 mm × 3 mm volume with 80 μm voxel size were completed in 285 s (4 min 45 s).

B. Different Depths of Fluorophore Concentrations

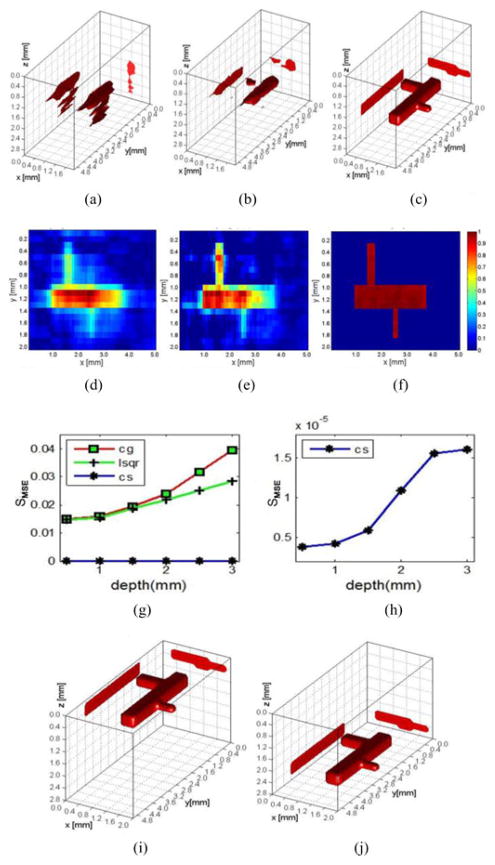
Fig. 4(g) shows the calculated S_MSE from reconstructions performed using the three inverse methods at six different depth locations (from 0.5 to 3 mm with interval 0.5 mm). The CS method far outperforms its counterparts at every depth investigated (four order in magnitude between S_MSE values). For instance, a visual comparison between reconstructions based on the different inversion algorithms employed and for a 2 mm depth location is proposed in Fig. 4(a)–(f). The reconstructed image obtained via CS provides an accurate anatomical description of the simulated vascular tree whereas both CG and LSQR do not recover the three components of the vascular tree distinctly.

Fig. 4.

Reconstruction results at different depths. (a)–(c) Reconstruction results were presented for CG, LSQR, and CS at depth of 2 mm. (d)–(f) Cross section of (a)–(c); colorbars represent the quantum efficiency (η(r)). (g) Reconstruction results of three methods at six different depths. (h) Reconstruction results of CS at six different depths. (i) and (j) Three-dimensional rendering of the reconstructions for CS at 0.5 and 2.8 mm, respectively (voxel size of 100 μm and no noise added in the measurements).

Moreover, the retrieved quantum yield distribution is far more homogeneous with accurate values in the small components of the vascular tree when using the CS method conversely to the two common inverse solvers. As for the CS method, its reconstruction performance also deteriorates with the depth increasing, shown as in Fig. 4(h). However, the reconstruction quality degrades at a slower rate for CS-based reconstructions than the other two methods when depth increases; see Fig. 4(i) and (j).

C. Reconstruction at Different Discretization Levels

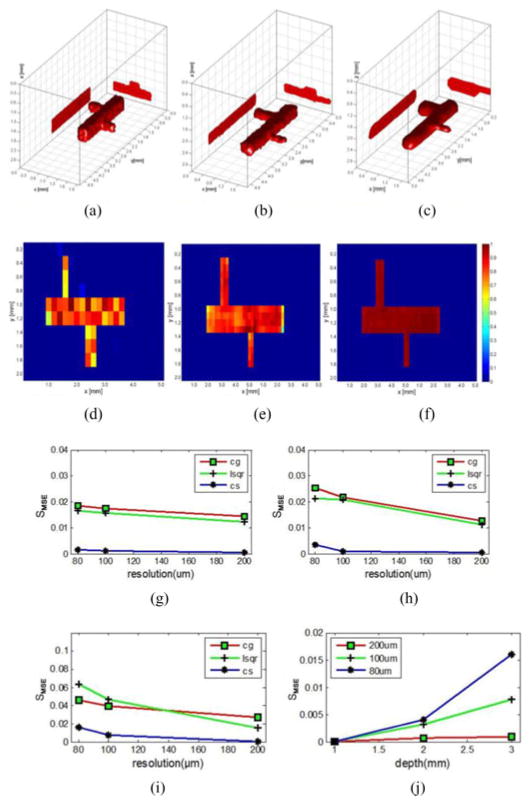
The effect of discretization on performances of CS-based reconstruction for MFMT was investigated by discretizing the imaging domain at three different resolutions: 200, 100, and 80 μm. We tested these three kinds of discretization resolutions for three different depth locations of the vascular tree: 1, 2, and 3 mm deep. Fig. 5(a)–(f) depicts the reconstructions results of CS with different resolutions at the depth of 2 mm (200, 100, and 80 μm, respectively). Fig. 5(g)–(i) shows the S_MSE indexes at different depths for these three different imaging domains (1, 2, and 3 mm, respectively) and the three inversion methods employed. Fig. 5(j) reports the reconstruction quality versus depth for the CS method at the 3 voxel resolutions. In all cases, accurate reconstructions were obtained with reconstructions at 80 μm providing the most homogenous effective quantum yield estimation within the vascular tree.

Fig. 5.

Reconstruction performance for 3 voxel sizes at three different depths: (a)–(c) CS reconstruction results at depth of 2 mm with voxel sizes of 200, 100, and 80 μm, respectively. (d)–(f) Cross section of (a)–(c). Colorbars represent the quantum efficiency (η(r)). (g)–(i) CG, LSQR, and CS reconstruction results of three different resolutions at depth of 1, 2, and 3 mm with different discretization levels. (j) Reconstruction result of CS with 3 voxel sizes.

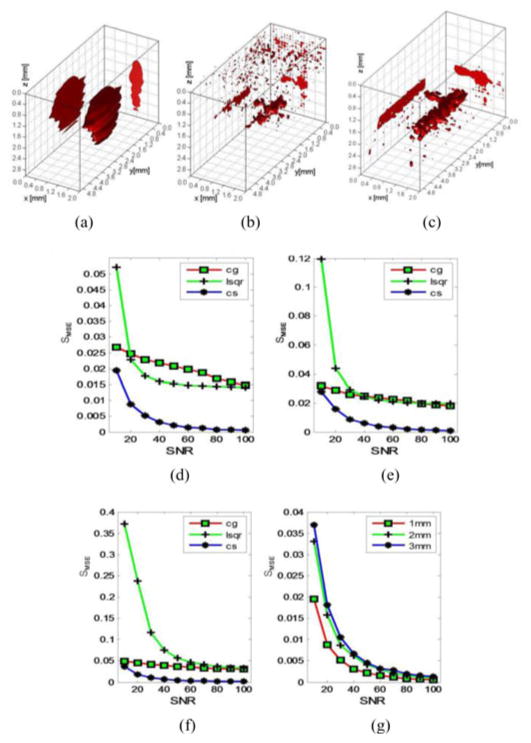
D. Reconstruction of Different Levels of Noise

Ten different levels of Gaussian-distributed electronic noise were added to the synthetic measurements, with SNR ranging from 100 to 10 (evenly spaced), to evaluate the robustness of the proposed reconstruction method. Fig. 6 shows the S_MSE versus SNR for all the ten different levels of noise and at three different depth locations. The S_MSE of CS methods becomes significantly larger when SNR decreases below 40, which indicates that reconstruction performance of the method is also sensitive to noise. Though, despite this decrease in reconstruction quality as the SNR decreases, CS still outperforms CG and LSQR methods for all the levels of noise simulated herein. Moreover, with the depth increasing, the reconstruction quality of CG and LSQR becomes worse drastically.

Fig. 6.

Reconstruction performance for ten levels of additional noise at three different depths. (a)–(c) Reconstruction results of three methods at depth of 1 mm with SNR of 40. (d)–(f) S_MSE of the three methods reconstruction results at depth of 1, 2, and 3 mm with ten levels of noise. (g) S_MSE of CS reconstruction results at depth of 1, 2, and 3 mm with ten levels of noise.

E. Synthetic Model

To mimic more closely real applications, a complex vascular network was simulated based on the segmentation of the real volumetric data depicted in Fig. 7(a). Two vascular beds were simulated, vascular beds with complex 3-D and depth distributions [see Fig. 7(b) and (c)]. Fig. 7(d)–(i) displays the reconstructed images of the vasculature using the different inversion techniques mentioned previously with a discretization of 100 μm. As can be seen from Fig. 7(d) and (g), the results of CG tend to be heavily surface weighted whereas LSQR provides more accurate reconstructions but is able to reconstruct only the lager segment of the vascular bed and failed to recover the most complex distributions, as shown in Fig. 7(e) and (h). Conversely, the CS reconstructions provide accurate rendering of the simulated networks, as shown in Fig. 7(f) and (i). In both cases, the structures of the vascular beds were retrieved with high fidelity at all depths.

F. Vascular Structure Mimicking in a Collagen Scaffold and Validation

The reconstructions employing experimental data are provided in Fig. 8. The experimental data were acquired from a collagen sample, which hosted two orthogonal capillaries. The dye filled capillaries place beneath the surface and ~1 mm apart in depth. Prior to reconstruction, background data were subtracted from fluorescence data similarly to the procedure described in [27]. Examples of fluorescence, background, and subtracted data are provided in Fig. 8(f) and (g). The contrast-to-noise ratio was estimated to be >1000, owing to very small noise standard deviation (~5). Two reconstruction methods, CG [8] and l₁-norm, were used to solve the optical inverse problem using the subtracted dataset and reconstructions are provided in Fig. 8(c) and (b), respectively. Fig. 8(d), (e), (h), and (i) demonstrates the overlaid image of CS and CG reconstructions with microCT. The slices were taken along the y-axis. In both cases, the two capillaries were individually reconstructed at their exact locations. However, the CS-based approach provided more accurate results with better shape over the whole length of the capillaries and more homogenous fluorescence distribution conversely to CG. Also, we defined a coregistration ratio (the number of voxel inside or outside tube reconstructed divided by the total number of voxel in tube) to assess the reconstruction performance of CS for experimental data by counting the total number of voxels in the optical reconstructions that are located inside and outside of the ground-truth location of each tube as estimated by microCT. The values of these coregistration ratios are provided in Table I. The CS method provides better volumetric registration than CG for both tubes with an agreement at least up to 92% between CS-based optical reconstruction and microCT versus only 76% in the best case scenario for CG (see Table I and Fig. 8).

Fig. 8.

Experimental validation of CS reconstruction results in a collagen scaffold compared with microCT and CG methods. (a) Ground truth for localizations of glass wall of two capillaries in the collagen scaffold obtained from a microCT scanner. (b) and (c) Reconstruction results of CS and CG, respectively. (d) and (e) Merged 3-D images of (b) and (c) with (a). (f) Raw data and line profile for fluorescence (blue), background (green), and subtracted (red) data, respectively. (g) Line profiles from two sets of data: left and right profiles. Upper figure shows the left profile for fluorescence (blue square), background (solid green), and subtraction (red circle). Lower figure follows the same convention for right region. (h) and (i) Overlaid reconstruction of CS and CG merged with microCT, respectively, at three different slices along y-axis.

TABLE I.

Quantitative Comparison Between CS and CG Reconstruction Results

Coregistration ratio	CS for upper tube	CG for upper tube	CS for bottom tube	CG for bottom tube
MircoCT (ground truth)	98%	98%	98%	98%
Inside voxels	94%	76%	92%	71%
Outside voxels	16%	22%	19%	30%

IV. Discussion

Herein, we have investigated the performances of CS-based reconstruction versus commonly employed methods (CG and LSQR) when performing mesoscopic fluorescence tomography. In all cases investigated, both in silico and experimental, the CS-based reconstruction outperformed their counterparts both in terms of retrieving the structure of the inclusions with high fidelity but also in recovering quantitatively the biodistribution of the relative quantum yield. The CS approach demonstrated higher resolution performances (as expected), more accurate quantification (homogeneity), and more robust against noise. These results suggest that CS-based reconstruction techniques are very suitable for fluorescence tomographic imaging in the mesoscopic regime as the image domain is generally sparse. As long as optimal regularization parameters are established via techniques such as the L-curve, the l₁-norm is a robust technique that can be implemented easily without much penalty in terms of computation time. Applied to imaging of sparse fluorescence signal, resolution to the scale of the element of volume (voxel) can be attained. This is very significant for numerous applications that require imaging deep thick tissue at a high resolution. However, as one refines the discretization of the image space, the size of the inverse problem becomes the most challenging part due to the sheer size of the matrices/vectors to be manipulated. Massively parallel implementation or matrix reduction based on CS techniques can be employed to solve this issue. This will be investigated in subsequent studies to attempt to identify what the optimal resolution attainable for MFMT is. Note that such resolution is system dependent. In our current implementation, we collect data from only seven detectors. We are currently integrating a new detection module that will allow acquiring 64 × 64 measurements at each source position. Increasing the spatial density of the measurements is also expected to contribute to better reconstructions performances.

V. Conclusion

In this paper, based on the sparsity of the fluorophore distribution in the image domain, we have proposed image reconstruction methods with CS framework to solve the MFMT inverse problem. The proposed method was compared with the conventional method, such as CG and LSQR methods by a synthetic model of microvessel network in different voxel sizes (200, 100, and 80 μm). Simulations and experimental results demonstrate that the CS-based method yields higher fidelity reconstructions of vascular bed with better resolution and improved image reconstruction stability for MFMT. We plan to employ this technique to assess the maturation process of printed vasculature in tissue constructs [8] as well as in vivo imaging during PDT treatments [9].