Evaluating Sequence-Based Genomic Prediction with an Efficient New Simulator

Abstract

The vast amount of sequence data generated to analyze complex traits is posing new challenges in terms of the analysis and interpretation of the results. Although simulation is a fundamental tool to investigate the reliability of genomic analyses and to optimize experimental design, existing software cannot realistically simulate complete genomes. To remedy this, we have developed a new strategy (Sequence-Based Virtual Breeding, SBVB) that uses real sequence data and simulates new offspring genomes and phenotypes in a very efficient and flexible manner. Using this tool, we studied the efficiency of full sequence in genomic prediction compared to SNP arrays. We used real porcine sequences from three breeds as founder genomes of a 2500-animal pedigree and two genetic architectures: “neutral” and “selective.” In the neutral architecture, frequencies and allele effects were sampled independently whereas, in the selective case, SNPs were sites putatively under selection after domestication and a negative correlation between effect and frequency was induced. We compared the effectiveness of different genotyping strategies for genomic selection, including the use of full sequence commercial arrays or randomly chosen SNP sets in both outbred and crossbred experimental designs. We found that accuracy increases using sequence instead of commercial chips but modestly, perhaps by ≤ 4%. This result was robust to extreme genetic architectures. We conclude that full sequence is unlikely to offset commercial arrays for predicting genetic value when the number of loci is relatively large and the prior given to each SNP is uniform. Using sequence to improve selection thus requires optimized prior information and, likely, increased population sizes. The code and manual for SBVB are available at https://github.com/mperezenciso/sbvb0.

ASCERTAINING the genetic basis of complex traits has been a goal of geneticists for decades; however, this endeavor is proving to be more difficult to attain than anticipated, even with current massive data sets. Nevertheless, molecular information can still be used for genetic prediction. Genomic selection (GS) relies on linkage disequilibrium (LD) between markers and the causal mutations, without the need to identify them (Meuwissen et al. 2001). So far, GS and genome-wide association studies (GWAS) have been mainly performed with manufactured genotyping array SNPs, but the current genomics status quo is being challenged by the dramatic improvement in sequencing technologies. Array-based experimental designs are now being superseded by analyses of sequence data at population scale. Similarly, for agriculture, the drop in sequencing costs makes it conceivable that GS programs can routinely employ genome sequencing instead of genotyping arrays in the near future.

Sequence data contains all the information needed (i.e., the causal variants) to make the most accurate prediction of genetic merit possible and its use in GS should, in principle, minimize the need to recalibrate prediction equations (Meuwissen and Goddard 2010). Still, the cost of whole-genome sequencing is currently at least one order of magnitude larger than that of array genotyping, and it is likely that this difference will remain large unless very shallow sequencing is employed. Therefore, it is reasonable to ask under what circumstances the investment in sequencing would pay off, and what outcome can we expect out of large-scale population-scale sequencing studies as compared to high-density genotyping arrays.

This broad question needs to be framed within a specific context, because a variety of factors will influence the response. This is especially pertinent here, as large discrepancies have been found between simulation and empirical results, even if the latter are still scarce (Hayes et al. 2014, 2016; van Binsbergen et al. 2015; Calus et al. 2016; Heidaritabar et al. 2016). The first factor is the genetic architecture of the trait, together with the demographic history of the population. The second one is the design of the breeding scheme. Finally, the statistical method used to derive prediction equations plays a role as well. The genetic determinism of complex traits is not understood in detail and few causal mutations have been identified so far. Yet, a combination of theoretical, simulation, and empirical results has broadened our understanding in recent years. First, the number of causal loci seems to be quite large, at least in the hundreds, and partially population-specific (Hill 2012; Pickrell et al. 2016). The latter can be due to either false discoveries that are not replicated or to low power because of small effects. Also, evolutionary forces such as mutation and drift modify the frequency of potentially causal loci in the populations. Second, the SNPs uncovered by even the largest GWAS usually account for only a modest fraction of total genetic variance. This reinforces the hypothesis of abundant small genetic effects. Third, the distribution of QTN effects is highly leptokurtic and can be reasonably well approximated by a gamma density (Hayes and Goddard 2001; Eyre-Walker and Keightley 2007; Caballero et al. 2015). In addition, a critical parameter determining the distribution of loci variances is the correlation between fitness and the trait studied. Caballero et al. (2015) found by simulation that common (q > 0.05) variants of at least modest effects will be responsible for most of the genetic variance in traits loosely correlated to fitness or neutral traits, whereas rare variants of large effect are relevant for highly selected traits or fitness itself. Furthermore, selection is expected to induce a negative correlation between effect and frequency, simply because large-effect QTNs at intermediate frequencies reach fixation or near fixation quickly, e.g., IGF2 in pigs (Ojeda et al. 2008), and they would contribute very little to total variance. However, sometimes alleles of large effect can have both positive and detrimental effects and they keep segregating by balancing selection, such as DGAT1 in cattle (Grisart et al. 2002) or Socs2 in sheep (Rupp et al. 2015). To our knowledge, no GS simulation study has included all these “subtleties” when modeling the quantitative trait.

Regarding the breeding scheme, thus far, GS simulation and empirical studies have paid special attention to dairy cattle genetic improvement. This was the first species where GS was applied due to its peculiar population structure, since GS can be quite effective in reducing the long generation interval in dairy cattle (García-Ruiz et al. 2016). Currently, GS is being extended to other species. Domestic species are usually structured in populations with limited genetic exchange (breeds). This is important because accuracy depends, among other factors, on the size of the training population and some populations have an upper barrier due to small size. In this scenario, implementing GS is more challenging due to heterogeneous and small populations, and the combination of different breeds to increase training population size has been proposed (de Roos et al. 2009; Zhong et al. 2009). However, the increase in accuracy is not automatic and depends crucially on the existence of shared segregating loci of large effect (Hayes et al. 2009; Karoui et al. 2012). It has been argued that the use of sequence could overcome this problem, allowing accurate predictions across populations (van den Berg et al. 2016).

The choice of GS method to be used for any large p/small n statistical problem requires either shrinkage or variable selection (or a combination of both). This issue is unavoidable with sequence data irrespective of data size; note that p (the number of regressors or SNPs from sequence) will always be much larger than the number of individuals (n), since SNP number increases proportionally to ${\displaystyle \sum }_{\mathit{i}=1}^{2\mathit{n}-1}1/\mathit{i},$ in a neutral model, and this function increases monotonically. Therefore, even with the largest of population sizes, we need to set additional restrictions (priors) on the regressors for the model to be applicable. Note that in a p > n scenario, the influence of prior distribution does not vanish even as n increases (Gianola 2013). In practice, two main strategies are being used for prediction in GS: genomic best linear unbiased prediction (GBLUP) (VanRaden 2008), which employs all markers to build a genomic relationship matrix (GRM) and induces homogeneous shrinkage of their effects, and the family of Bayes methods that select a subset of variables such as Bayes B (Meuwissen et al. 2001) or BayesR (Erbe et al. 2012). From a computational perspective, GBLUP is the method of choice because it naturally accommodates very complex models (e.g., multiple trait and genotype-by-environment interaction) and very efficient algorithms exist (VanRaden 2008; Misztal 2016). Bayesian methods should, in contrast, provide better insight on the true state of nature than GBLUP by identifying neutral and causative SNPs. They also extend very naturally to genome-wide association methods (Moser et al. 2015).

Thus far, there are very few experimental results regarding the use of full sequence in selection. Hayes et al. (2014) reported a minimal increase in accuracy (0–3% depending on trait) when sequencing followed by imputation was compared to SNP array genotyping on real dairy cattle data. In layer chickens, Heidaritabar et al. (2016) also found a low (∼1%) increase in accuracy when imputation to sequence (ca. 4.6 million SNPs) was compared to a 60,000 SNP array. Similarly, neither van Binsbergen et al. (2015) nor Calus et al. (2016) found an advantage of using sequence compared to bovine high-density genotype data in a dairy scheme. In contrast, Macleod et al. (2016) reported a modest increase in the accuracy of genomic prediction for mixed breed populations when different weight priors in coding and regulatory regions were used, compared to high-density SNP genotypes with flat priors. These empirical results contrast with most simulation studies, which were much more optimistic (Meuwissen and Goddard 2010), although broadly agree with our previous simulation study (Pérez-Enciso et al. 2015), where we used a mixed coalescence gene dropping method together with a leptokurtic distribution of gene effects.

Simulation is a fundamental tool to evaluate alternative experimental designs or to interpret the outcome of selection in complex scenarios. Although numerous simulation tools do exist (e.g., Peng et al. 2012; Kessner and Novembre 2013; Messer 2013; Cheng et al. 2015), they suffer from different limitations that may be critical when complete genomes need to be considered. Forqs (Kessner and Novembre 2013) was conceived for population genetic applications rather than plant and animal breeding, and using real sequence data or complicated genetic architectures (e.g., epistasis) is not straightforward. In fact, extant simulation tools such as coalescence and gene dropping, which incorporate mutation, are unable to efficiently simulate complete genomes in a realistic manner. One of their limitations is the impossibility of simulating complete large genomes and retrieving the observed patterns of LD and of variability. This may lead to implausible or biased conclusions: the general overoptimistic predictions reported for sequence-based GS compared to array genotyping suggest that simulations may not be completely accurate.

To remedy this, and improving our previous approach (Pérez-Enciso et al. 2015), we here propose using real complete genome data and simulating new genomes by gene dropping in a very efficient manner: the Sequence-Based Virtual Breeding (SBVB) approach. By using real sequence data, we avoid the computationally intensive, yet likely unrealistic, effort needed to generate full sequence data, and we are able to accurately investigate the performance of actual commercial arrays. Using this tool, we investigate the performance of full sequence for GS in the pig species, compared to alternative strategies. Furthermore, we consider alternative genetic architectures based on the considerations discussed above.

Methods

SBVB algorithm

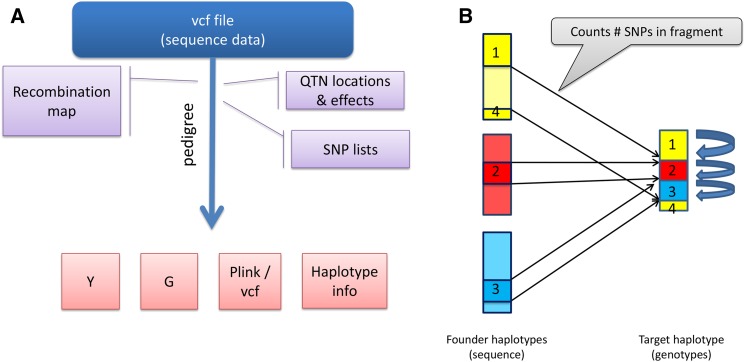
SBVB is a flexible tool for the generation of molecular and phenotypic data using real sequence data, according to specified genetic architectures and pedigrees. Figure 1A shows a graphical representation of the SBVB software. The program requires a parameter file, auxiliary files such as a recombination map, pedigree file to perform gene dropping, causal SNP (QTN) positions, and a file containing all sequence genotypes in standard vcf format (Li et al. 2009). No missing genotypes are allowed, and data must be phased so that SBVB can identify the haplotypes to be transmitted to the offspring. Starting with the haplotypes provided as inputs, which act as “founder,” the algorithm performs gene dropping. The user can specify variable recombination rates along the genome and between sexes as well as sex chromosomes. Importantly, while doing gene dropping, SBVB stores only the recombination breaks and keeps track of the haplotype id from the founder individuals (Figure 1B) (Pérez-Enciso et al. 2000). This results in computer time (CPU) and memory demands that increase linearly with the number of individuals and total genetic map length, but not on the number of markers. This, together with efficient algorithms to recover the marker genotype at desired positions, makes it able to very quickly simulate sequence data for thousands of individuals.

Figure 1.

General outline of SBVB. (A) As input, SBVB reads the vcf file containing all phased SNPs from founder haplotypes. Additional files specify the genetic architecture, the lists of SNPs (each corresponding to one array), and the recombination map for each sex and genome location (optional). SBVB then performs gene dropping following a predetermined pedigree, generating phenotypes (Y), genomic relationship matrices (G, one per SNP list), and molecular genotypes for each individual in a pedigree and for each SNP list in Plink or vcf format, and a file containing haplotype information that allows quick restart of the program. (B) SBVB represents each generated haplotype as a list of only recombination breakpoints and ids of founder haplotypes. In the figure, a hypothetical target haplotype contains four blocks, delimited by the three recombination breakpoints that have been transmitted from three founders, each with a different color. When needed, the genotypes of the target haplotype can be quickly recovered simply by counting how many SNPs are between each recombination event and knowing the founder id of each block. id, identity; QTN, quantitative trait nucleotide; SBVB, sequence-based virtual breeding.

Trait architecture:

SBVB is extremely flexible in terms of genetic architecture, as any number of traits with their own QTNs and allelic effects can be specified. At a minimum, the QTN positions for each trait must be specified, and these must be present in the vcf file or they are otherwise ignored. Additive and dominant effects can either be specified (hard-coded) or sampled from gamma, normal, or uniform distributions. In this latter case, effects are sampled independently of QTN frequencies. This can be appropriate if the trait is neutral, yet it is not expected under selection. To produce more realistic sampling, SBVB allows the generation of correlated additive effects and frequencies. This is done by sorting allele effects and frequencies that correspond to maximum attainable correlation. Next, a dummy variable is generated by adding a random deviate to the allele effects such that the correlation between the dummy variable and the frequency is as expected; finally, true effects are back-sorted according to dummy order. Epistatic action (two loci) can also be specified and each trait can have its own epistatic basis. Environmental variance is determined given desired broad- or narrow-sense heritability.

Genotyping arrays:

SBVB can handle any number of genotyping arrays simultaneously. This means that the program can compute GRMs or print molecular information, e.g., in Plink format (Purcell et al. 2007) obtained with different SNP lists in the same run. Each SNP list needs to be specified in separate files, and the only prerequisite is that SNPs must be present in the vcf file or are ignored. As a future step, we will implement an option to validate imputation.

Recombination:

The recombination map file specifies the cM/Mb rate for each defined segment in the genome, and can be sex-specific. If unspecified, the default cM/Mb = 1 ratio is used, which can be modified by the user. Internally, the program handles heterogeneous recombination rates by drawing nonuniform random numbers, where probabilities are proportional to relative genetic distances between segments. By default, the program generates up to three crossovers per chromosome per generation, as has been experimentally observed in most species (Mercier et al. 2015), although this bound can be modified. The actual number is sampled from a truncated Poisson. No interference is considered, i.e., recombination breakpoints are sampled independently. Sex chromosomes can be modeled.

Any number of SNPs can be handled by saving only the recombination breakpoints and accessing each of the individuals’ nonrecombinant blocks in an efficient manner (Figure 1B). This is done by traversing the nonrecombinant block boundaries only (which is typically orders of magnitude smaller than the number of markers), and keeping track of which genotype corresponds to each marker, given the block and the founder haplotype id. The assignment of genotype to founder haplotypes’ id needs to be done only once, saving CPU time. SBVB saves the haplotype structure, which allows restarting the program with different parameters (e.g., different QTN positions, effects, or h²).

Selection:

SBVB only performs gene dropping following a predefined pedigree, but selection such as in a current breeding program can be implemented easily (Supplemental Material, Figure S5). This is possible since the software can save the haplotype structure of all individuals in the pedigree up to the current generation. Then, individuals can be selected and a new generation can be added to the pedigree. The next run of SBVB reads all current haplotypes and generates the new offspring genomes, conditional on extant ones. Haplotype information contains only recombination breakpoints and haplotype ids, so can be quickly read and written.

SBVB output includes phenotypes, true breeding values, and QTN information (e.g., variance explained and substitution effects). In addition, SBVB can also print individual genotypes and GRMs obtained for each desired genotyping array, including sequence. Source code and examples are at https://github.com/mperezenciso/sbvb0. A manual is also attached in File S1.

Sequence data analysis

We downloaded 107 public pig sequences from the short-read archive, http://www.ncbi.nlm.nih.gov/sra (Groenen et al. 2012; Molnár et al. 2014; Ai et al. 2015; Bianco et al. 2015a; Choi et al. 2015), pertaining to 32 Large White (LW), 19 Landrace (LR), 14 Pietrain (PI), 27 Duroc (DU), and 15 Meishan (MS) pigs. Alignment was carried out with BWA (Li and Durbin 2009), PCR duplicates were removed with samtools, and bam files were then realigned around indels with GATK IndelRealigner tool (McKenna et al. 2010). SNP calling was performed with samtools/bcftools suite v. 1.2.1 (Li et al. 2009) separately for each individual. SNPs were called in positions with read depth bounded between 5 × and twice the average depth plus one. Only autosomal SNPs were considered. We extracted the regions with minimum and maximum depth using samtools depth, further filtering by minimum map and base qualities and then, using bedtools (Quinlan 2014), we intersected these regions with the homozygous blocks provided in the individual gvcf file. This resulted in a modified gvcf file where both SNPs and homozygous blocks had been filtered by the same criteria. Finally, all vcf files were merged in a single file for the 107 individuals. All SNPs found with at least two copies of the nonreference allele and missing rate < 30% were retained, making a total of 28,391,011 SNPs. Finally, missing SNPs and phases were predicted with Beagle 4 (Browning and Browning 2013). Given the weak structure and the closeness between LW, LR, and PI, we merged them into a single LW population, consisting of 65 sequences that we generically called LW.

Population structure

Starting with base population samples (the known sequences), we considered purebred and crossbred pedigrees. For the outbred pedigree, gene dropping was performed along three discrete generations of half and full sibs in LW, and two generations in DU and MS. Within each breed, each sire was mated to two sows and produced six offspring. About 160 (6%) individuals were inbred, and the inbreeding coefficient was > 0.25 in ∼30 of those. The total number of LW, DU, and MS samples was 1829, 291, and 315, respectively, including base animals. The total number of pigs in the pedigree was thus 2435. This was designed to mimic a scenario with a predominant breed and additional breeds of lesser importance, a setting that has been typically advocated as the most favorable for the use of sequence data when compared to SNP arrays (de Roos et al. 2009). In the three-way crossbred pedigree (3WC), the 65 LW pigs were crossed to the 27 DU, and the resulting 300 F1 animals were mated to the 15 MS samples producing a total of 3000 3WC animals. The total pedigree size was 3410. The recombination map in Tortereau et al. (2012) was employed.

Genetic architecture

The precise genetic architecture of complex traits is unknown, but the increasing number of empirical and simulation studies is helping to delineate plausible ranges of parameters. For the distribution of allelic effects, numerous studies (Eyre-Walker and Keightley 2007) confirm that it is highly leptokurtic, with many near-zero effects and a few large effects. This distribution can be approximated by a gamma, and here we used a Γ(shape = 0.2 and scale = 5) based on the simulation study by Caballero et al. (2015); the shape of this distribution is not too different from the review in Hayes and Goddard (2001) and employed previously by us (Pérez-Enciso et al. 2015). Heritability of the simulated phenotype was 0.5.

1. In the neutral architecture, 1000 SNPs were randomly sampled among the 28 million SNPs and Γ-sampled additive effects were randomly assigned. Since Γ always takes positive values, which implies that the alternative allele increases the phenotypic value, 50% of additive effects were randomly assigned a negative sign.

2. In the selective architecture, ca. 1000 SNPs were chosen from those in genes with lowest Tajima’s D in LW and largest Fst between LW and European wild boar. Among those SNPs, we selected as causal QTN those that had a high or moderate effect as inferred from a variant effect predictor tool (McLaren et al. 2010) plus a fraction of SNPs in UTR regions. Again, additive effects were sampled from a Γ (0.2 and 5), but in this case a negative correlation between absolute additive effect and frequency was induced ρ = −0.60, as found empirically (Caballero et al. 2015; Yang et al. 2015).

Note that we used only LW as the breed to model the selective architecture, instead of all breeds, even if QTN effects were constant across breeds. The rationale was that selection usually acts locally, and that breeds are selected for different phenotypes.

Genomic prediction

With GBLUP, we evaluated the predictive performance of alternative GRMs:

1. QTN: all causal variants.

2. GENES: all SNPs within any causal gene. This option was used only in the selective model, the rationale being that the notion of gene is not defined in a pure infinitesimal model, as it assumes that causal variants are distributed uniformly through the genome.

3. SEQ: Sequence, i.e., all 28 million SNPs.

4. 50KI: Illumina’s 60,000 array. It contained about 50,000 informative SNPs in the data set.

5. 700KA: Affymetrix 700,000 array. It contained about 500,000 informative SNPs.

6. 50KR: 50,000 randomly sampled SNPs.

7. 500KR: 500,000 randomly sampled SNPs.

8. MAF01: GRM computed with 1 million random SNPs with minimum allele frequency (MAF) < 0.10.

9. MAF10: GRM computed with 1 million random SNPs with MAF > 0.10.

10. 2MAF: a model comprising MAF01 and MAF10.

For each evaluation model (i.e., each GRM), we considered four cross validation scenarios in the outbred pedigree:

1. 50% of LW phenotypes from the last generation were removed and their breeding values predicted.

2. 50% of DU phenotypes from the last generation were removed and breeding values predicted.

3. 50% of MS phenotypes from the last generation were removed and breeding values predicted.

4. All DU phenotypes were removed and breeding values predicted.

In the 3WC, the strategies compared were:

1. All 3WC pig genetic values were predicted using only pure LW, DU, and MS.

2. 20% of 3WC pig genotypes were predicted using LW, DU, MS, and the rest of 3WC.

3. 20% of 3WC pig genotypes were predicted using LW, DU, MS, F1, and the rest of 3WC.

In all cases, prediction was done using all of the marker information from all animals in the pedigree, except that the phenotypes of the corresponding individuals were removed. The values reported are squared correlations between observed and predicted genetic breeding values obtained with the Bayesian Generalized Linear Regression (BGLR) package (Pérez and de los Campos 2014). BGLR implements various methods for genomic regressions, including the so-called GBLUP model (VanRaden 2008). A principal component analysis (PCA) decomposition of GRM was employed, given its good convergence properties (De los Campos et al. 2010). Default prior parameters and 100,000 iterations plus 2000 burn-in cycles were employed. Results are an average of 10 replicates and, for each replicate, cross-validation was run 10 times. The same pedigree was used across replicates but QTN effects, genotypes, haplotypes, and phenotypes varied.

GBLUP blindly uses all marker genotypes to compute the GRM. This method may not be optimal when variance contribution from each locus is highly heterogeneous (Daetwyler et al. 2010). To compare with GBLUP, we employed BayesR, a hierarchical Bayesian mixture model (Erbe et al. 2012). BayesR samples the SNPs to have an effect in the model and assigns them to discrete classes, according to a prespecified contribution to total genetic variance. By default, SNPs are grouped in four classes that explain 0, 10⁻⁴, 10⁻³, and 10⁻² of total genetic variance, respectively. Although we used the efficient implementation in Moser et al. (2015), BayesR was not feasible in all scenarios, such as with the 28 million sequence SNPs. For that reason, BayesR was run in a limited number of scenarios: QTN, 700KA (Affymetrix array), 500KR, and all 2 million SNPs from MAF01 and MAF10 plus the causal SNPs, as a substitute for using complete sequence. We assessed predictive performance for 10 replicates of the outbred pedigree in which either 50% of LW or 50% of MS from the last generation were removed and predicted, as with GBLUP. For the “sequence” (SEQ) analysis, 100,000 iterates were employed and 50,000 (the default) for the rest of cases. The first 20,000 samples were discarded as burn-in.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.

Results

Genetic architectures

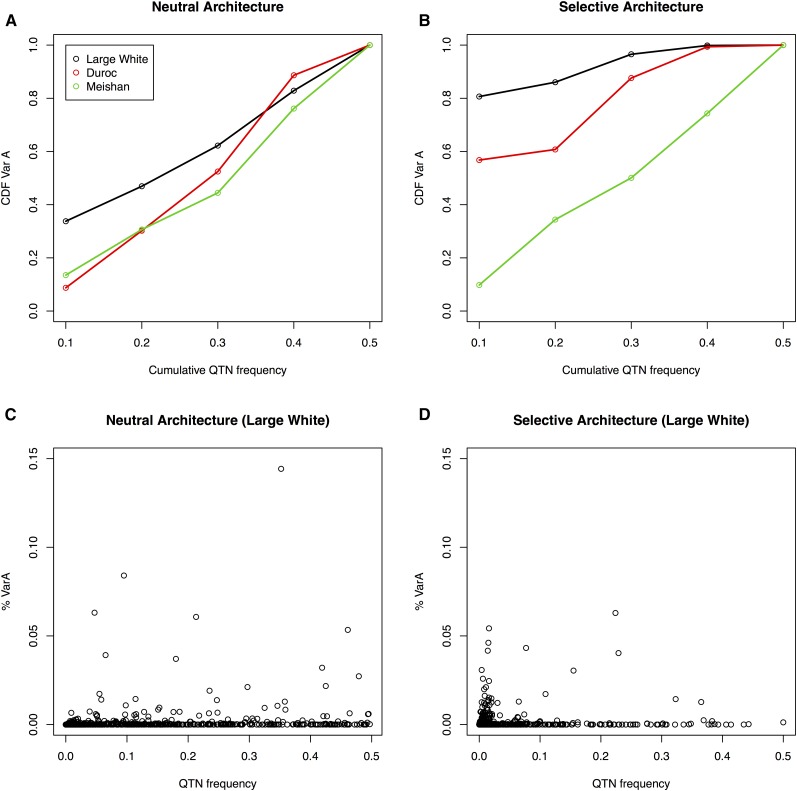
The QTN site frequency spectra (SFS) for both the neutral and selective architecture can be compared in Figure S1 for LW. The selective architecture is enriched in rare variants, compared to the neutral SFS. Then, a priori, the selective scenario should be favorable to the use of sequence compared to SNP arrays, which are biased toward high MAF variants. Importantly, the two genetic architectures result in distinct contributions to total additive variance when QTNs are grouped by MAF. Under a neutral architecture, theory dictates that the fraction of genetic variance explained by SNPs at MAF < q is q%, because variance is proportional to q(1−q) and the folded SFS is proportional to 1/q × (1−q). This is what we observe in our neutral simulations for all three breeds (Figure 2A). The cumulative distribution is, in contrast, highly distorted in the selective architecture (Figure 2B). In this case, up to 80% of genetic variation is due to variants of MAF < 0.10 in LW. In contrast, MS is not affected by a selective architecture in LW, despite identical QTN positions and allele effects, due to the large genetic distance between both breeds (see below). DU architecture is somewhat closer to LW than to MS. Figure 2, C and D plot QTN frequency vs. its contribution to total variance for the LW breed. The figure shows that loci at moderate or high frequency may occasionally explain a large part of h² (≤ 15% in the case shown) in neutral architectures whereas this is much rarer in the selective case. These results are in agreement with empirical results from Yang et al. (2015) (see their Figure 4A), or simulations (Caballero et al. 2015).

Figure 2.

Distribution of genetic variance according to QTN frequency and genetic architecture. (A) Fraction of genetic variance explained by all QTNs at MAF below frequency for the neutral architecture. (B) Idem for the selective architecture. (C) Fraction of genetic variance explained by each QTN vs. its MAF in the neutral architecture for Large White. (D) Idem for the selective architecture. CDF, cumulative density function; MAF, minimum allele frequency; QTN, quantitative trait nucleotide.

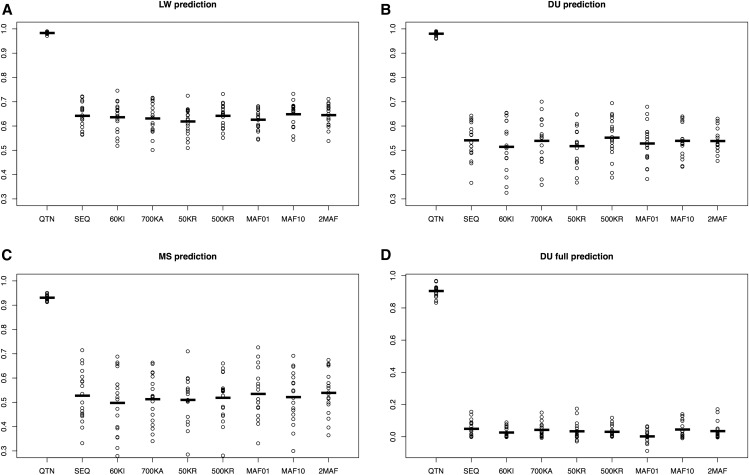
Figure 4.

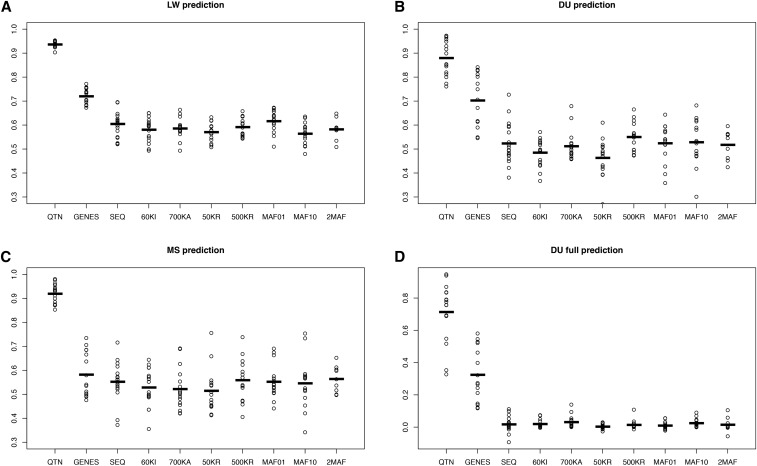
Performance of different models across scenarios for the neutral architecture using GBLUP. (A) 50% of LW from the last generation were removed and predicted. (B) 50% of DU from the last generation removed. (C) 50% MS from the last generation removed. (D) All DU removed. The following models are shown: QTN, GRM computed with all QTNs; SEQ, all SNPs; 60KI, Illumina’s 60k array; 700KA, Affymetrix; 50KR, 50,000 random SNPs; 500KR, 500,000 random SNPs; MAF01, 1 million SNPs with MAF < 0.01; MAF10, 1 million SNPs with MAF > 0.1; and 2MAF, the model uses MAF01 and MAF10. Values reported are accuracies, defined as squared correlation between true and predicted genetic values. Dots correspond to each of the 10 replicates, horizontal bars represent the mean. DU, Duroc; GBLUP, genomic best linear unbiased prediction; GRM, genomic relationship matrix; LW, Large White; MAF, minimum allele frequency; MS, Meishan; QTN, quantitative trait nucleotide.

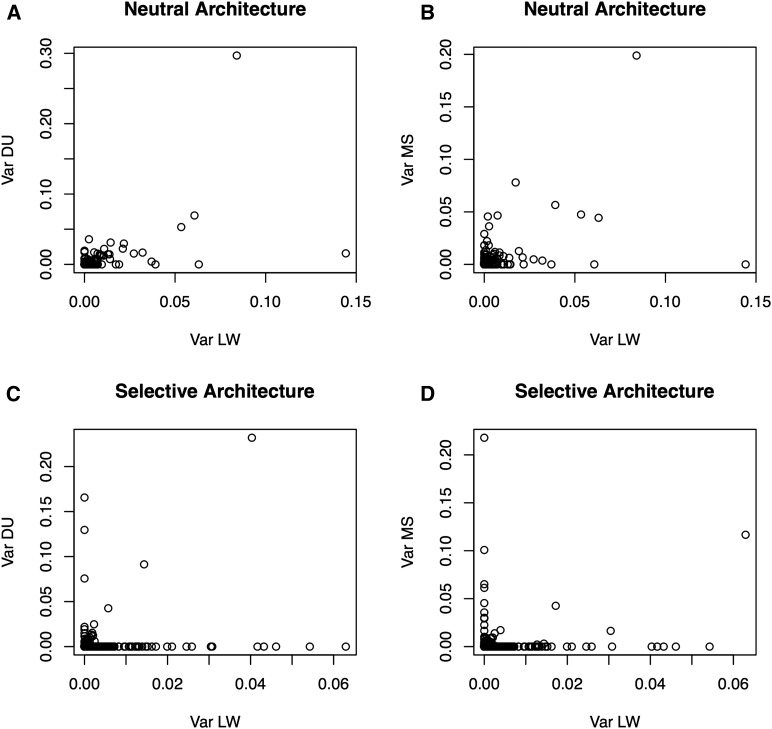
Importantly, differences between breeds regarding the distribution of genetic variances (Figure 2, A and B) are due only to differences in SNP frequencies, since allele effects are constant. Therefore, it is illuminating to consider the joint SFS of QTNs between breeds (Figure S2). The correlations in QTN frequencies between LW and DU were ∼0.74 and 0.80 for the neutral and selective architectures, respectively, but they were much lower, 0.47 and 0.38, between LW and MS, respectively. In the selective architecture, ∼550 out of near 800 segregating QTNs in LW were fixed in the MS breed. Previous genome-wide variability studies have shown that SFS are markedly different between European and Asian breeds (Bianco et al. 2015b), and that this is exacerbated in the case of a selective architecture, as a result of low-frequency variant enrichment. Logically, this has a strong impact on the amount of genetic variance explained by the same QTN in two breeds. The correlation in additive genetic variances explained by each QTN was only ∼0.18 in the selective architecture between LW and MS populations, whereas it was 0.50 for the neutral case. The top 16 QTN that explained 85% of h² in MS only accounted for 12% of h² in LW. Divergence in allele frequencies between breeds is a major issue that has a dramatic impact on genetic correlation, even when causal mutations and effects are the same (Figure 3). Domestic species are highly structured in breeds with limited or no genetic interchange, and we can therefore expect that results similar to those in Figure 3 or Figure S2 will be the rule rather than the exception. This, together with small effects and limited sample size, might also explain the low replication rate that is sometimes observed between GWAS studies; logically, increasing sample size and stringency in declaring an association increases repeatability (Visscher et al. 2012).

Figure 3.

Individual QTN variance contribution across breeds. (A) LW vs. DU, neutral architecture; (B) LW vs. MS, neutral architecture; (C) LW vs. DU, selective architecture; (D) LW vs. MS, selective architecture. Values are percentages of total genetic variance, and are computed assuming linkage equilibrium. DU, Duroc; LW, Large White; QTN, quantitative trait nucleotide.

GBLUP genomic prediction in outbred populations

Next, we investigated the influence of the genetic architecture and the effects of the use of sequence data on prediction accuracy by Monte Carlo simulation in the 2435 pig genome pedigree of LW, DU, and MS breeds, arranged in half- and full-sib families. Molecular data were assumed to be available for all animals in all scenarios. In the current implementation of SBVB and for the data size described, the pig simulation itself consumed negligible amounts of CPU time (< 1 min) in a linux workstation compared to parsing and reading the 28 million polymorphism file (∼20 min), obtaining the GRMs for 500,000 SNPs (∼20 min) or obtaining the GRM with sequence (∼10 hr).

Results of 10 replicates for the neutral architecture are in Figure 4. Values reported are accuracies with GBLUP, defined as squared correlation coefficients between true and predicted genetic values of individuals without phenotypes (ρ²). By populations, the most favorable scenario was prediction within LW (ρ² ∼0.63 on average), while accuracies were similar in either DU (ρ² ∼0.54) or MS (ρ² ∼0.52). This shows that the amount of data has a larger influence on GS performance than genetic distance between populations: there were 1829 LW, 291 DU, and 315 MS in the pedigree. In agreement with this, prediction was impossible when no individuals from the DU breed were phenotyped, unless QTNs were known (Figure 4D).

Figure 4 also shows that differences across SNP sets were minimal except in the unlikely scenario where all causal mutations were known (QTN). All breeds combined (Figure 4, A–C), the average accuracy obtained with sequence was 0.57, i.e., ∼4% larger than with the 60k Illumina array (0.55) and 2% larger than with the higher density 700k Affymetrix array. There were no differences between using complete sequence, 500,000 random SNPs (500KR) or when SNPs were selected among those with MAF > 0.1 (MAF10). A model with two random effects (2MAF) did not provide any substantive improvement either (< 1%).

Figure 5 presents the outcome for the selective architecture. In this case, we considered an additional model where all SNPs located within genes containing any QTN were included in the model (“GENES” model). For the neutral architecture, we assumed that any SNP has the same probability of being causal and therefore the concept of “causal gene” is undefined in this case. The GENES model in fact evaluates how much accuracy is gained had all SNPs in tight disequilibrium with QTNs been identified, which is a priori a less ambitious goal than identifying all causal mutations. The GENES model resulted in an important increase in accuracy (∼20%) compared to SEQ, although it was quite dependent on the actual experimental design; it was associated with larger variances across replicates and the advantage when predicting MS breeding values was minimal (Figure 5C). The GENES model was an improvement compared to SEQ and the rest of the models but still unsatisfactory (ρ² ∼0.30, Figure 5D). Knowing the causal genes may not be enough if the genetic distance between breeds is large.

Figure 5.

Performance of different GBLUP models across scenarios for the selective architecture. (A) 50% of LW from the last generation were removed and predicted. (B) 50% of DU from the last generation removed. (C) 50% MS from the last generation removed. (D) All DU removed. The following models are shown: QTN, GRM computed with all QTNs; SEQ, all SNPs; 60KI, Illumina’s 60k array; 700KA, Affymetrix; 50KR, 50,000 random SNPs; 500KR, 500,000 random SNPs; MAF01, 1 million SNPs with MAF < 0.01; MAF10, 1 million SNPs with MAF > 0.1; and 2MAF, the model uses MAF01 and MAF10. In the GENES model, GRM was obtained with the SNPs segregating in any of the genes containing a QTN. Values reported are accuracies, defined as squared correlation between true and predicted genetic values. Dots correspond to each of the 10 replicates, horizontal bars represent the mean. DU, Duroc; GBLUP, genomic best linear unbiased prediction; GRM, genomic relationship matrix; LW, Large White; MAF, minimum allele frequency; MS, Meishan; QTN, quantitative trait nucleotide.

Overall, results for the neutral and selective architectures were similar (Figure 4 and Figure 5), suggesting that GS performance, at least with GBLUP, is relatively independent of the genetic architectures considered. For the selective architecture and in the LW breed, SEQ resulted in an increase of 3% in accuracy compared to Illumina’s 60k or Affymetrix 700k, and only ∼1.7% higher compared to 500KR. In contrast, using only rare SNPs to build up the GRM (MAF01) resulted in a modest increase in accuracy compared to SEQ (2%). For either DU or MS, this small improvement of MAF01 was not observed, likely because of the low correlation between breeds in terms of their joint SFS (Figure S2).

BayesR performance

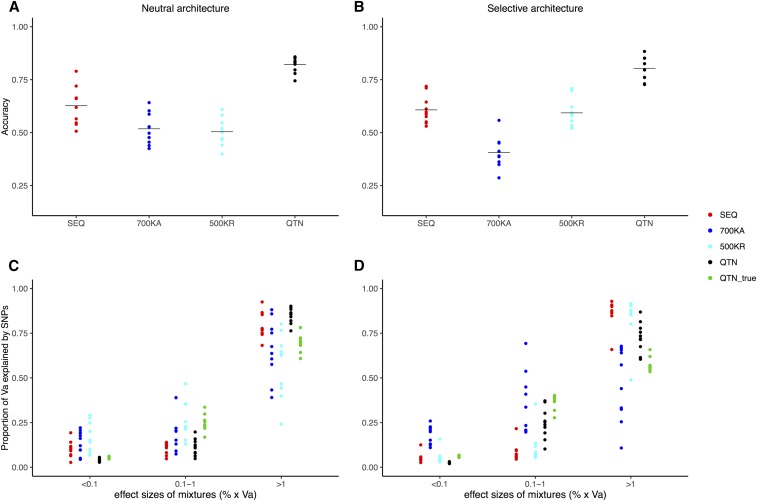
We tested the performance of BayesR in our data but, due to much larger CPU time requirements than GBLUP, we chose a subset of five representative evaluation models only (see Materials and Methods). In agreement with GBLUP, the most favorable scenario was prediction within LW (ρ² ∼0.55 when averaged over SEQ, 700KA, and 500KR models), while accuracies were lower for MS (ρ² ∼0.42), evidencing once again the impact that the amount of data has on GS performance (Figure 6 and Figure S3). Results for LW prediction in Figure 6 show that sequence BayesR outperformed the different chip methods, although it was no better than GBLUP with sequence (Figure 4 and Figure 5). Similar results were found in the MS breed (Figure S3). Overall, BayesR performance was more sensitive to genetic architecture than GBLUP. More interestingly, differences between sequence and commercial arrays were smaller under a neutral than under a selective architecture. BayesR performance exhibited higher variability across replicates with the Affymetrix array (700KA model) than with the other arrays. All this suggests that, depending on the relevance of rare frequency variants, custom arrays where SNPs are discovered in the target sample may be more effective than commercial arrays if BayesR or comparable methods are to be used, and if rare variants are important for the genetic determination of the trait. Otherwise, commercial arrays should suffice.

Figure 6.

Performance of BayesR in LW. (A) Accuracy in predicting genetic merit when 50% of LW from the last generation were removed and predicted with BayesR (neutral architecture). (B) Idem for the selective architecture. (C) Fraction of variance explained by SNPs when classified as 10⁻⁴, 10⁻³, and 10⁻² units of genetic variance, according to different SNP sets (neutral architecture). (D) Idem for the selective architecture. The following models are shown: QTN, GRM computed with all QTNs; SEQ, the two million SNPs from MAF01 and MAF10 plus the QTNs; 700KA, Affymetrix; and 500KR, 500,000 random SNPs. Accuracy is defined as squared correlation between true and predicted genetic values. Dots correspond to each of the five replicates, horizontal bars in (A and B) correspond to the mean. GRM, genomic relationship matrix; LW, Large White; MAF, minimum allele frequency; QTN, quantitative trait nucleotide; Va, additive variance.

An advantage of BayesR over GBLUP is that it provides a classification of SNPs according to their predicted contribution to total genetic variance, facilitating the inference of genetic architecture. By default, BayesR classifies causal SNPs in three classes: those explaining 10⁻⁴, 10⁻³, and 10⁻² units of genetic variance (Erbe et al. 2012). Overall, BayesR was able to detect an increased fraction of variance caused by small-effect QTNs under the selective architecture (Figure 6 and Figure S3) with the Affymetrix array or if QTN were known, although estimates were associated with a large variability. Note in particular that the fraction of medium-effect QTNs was systematically underestimated with sequence data.

Crossed population

In many livestock and plant species, crosses are exploited commercially instead of purebred individuals. A potentially important role of GS would be to predict the performance of commercially crossed animals based on data from purebred individuals. We ran SBVB through a 3WC pedigree that involved the three breeds and comprised a total of 3400 animals (see Materials and Methods). The ideal target would be to predict 3WC performance based solely on purebred performance. We found that accuracy in this case was relatively modest (ρ² ∼0.45 for all models, Figure S4A) but, in practice, the advantage of being able to predict the performance of crosses may overcome this low accuracy. Importantly, even knowing all QTN did not improve accuracy dramatically (ρ² ∼0.53). The next two settings compared whether it is useful to phenotype and genotype F1 individuals, provided that corresponding data from a subset of the 3WC animals are already available (Figure S4, B and C). Interestingly, the simulations show that genotyping, or sequencing, the F1 was not useful, provided data from the 3WC are available; overall accuracies were almost identical (Figure S4B vs. Figure S4C). Again, similar performance between SEQ and the other models was also observed for the crossed individuals.

Discussion

Currently, the availability of genome data at a population level, such as the UK10K project (www.uk10k.org) and comparable initiatives in humans but also in agriculture or model species, pose new challenges for simulation software. Arguably, neither coalescence nor extant forward methods can tackle the realistic simulation of complete large genomes at this scale. Here, as an improvement on Pérez-Enciso et al. (2015), we propose instead the simple, yet powerful, approach of using real data and use efficient forward algorithms to investigate the use of complete sequence at the population scale. We have also proposed new genetic architectures that should be more realistic than those in Pérez-Enciso et al. (2015), and have explored the scenario of crossed populations. Surprisingly, our conclusions are similar.

SBVB is a very flexible tool that implements efficient algorithms. In particular, it keeps track of recombination events instead of storing the full genotypes. This approach was already employed by us (Pérez-Enciso et al. 2000) and has been implemented as well in other recent software such as forqsim (Kessner and Novembre 2013) or XSim (Cheng et al. 2015). Compared to these, SBVB allows much more complex genetic architectures, printing genomic information such as genomic relationships, subsetting SNPs or sex chromosomes, and different recombination rates per sex. In the application presented here, we performed neutral gene dropping. SBVB allows for easy implementation of selection, although the user needs to provide the list of selected individuals each generation and then call SBVB repeatedly (Figure S5 for details). The tool is also able to access any set of SNP genotypes very quickly, allowing us to compare the performance of different genotyping strategies in the same run. In the current implementation, the pig simulation itself consumed negligible amounts of CPU time compared to obtaining the GRMs. Note that computing the GRM is external to the simulation itself and that the current algorithm, although it employed optimized BLAS subroutines (http://www.netlib.org/blas/), can be further improved, e.g., by increasing parallelization. Similarly, reading and writing large files can be sped up if binary instead of text files are managed.

Genomes are extremely complex and the demography of any population under study is typically unknown, obliging us to simplify simulation studies. Using real data circumvents this limitation. A potential problem is that, with this approach, one is sampling a single realization of the coalescence process. Here, for instance, we used most of the main breed sequences that are publicly available, but it was still a modest number. However, from a Bayesian inference perspective, this is no obstacle. More practically, using real data may restrict the generality of the results but, logically, our approach can also be started with simulated data under simplified assumptions. Some errors are incurred in using real sequence with imputed and phased genotypes. Nevertheless, we believe this should have a very mild effect for our purposes, since they would primarily affect rare variants, and simulations are conditional on the data provided. A more serious limitation, in our opinion, is the availability of enough complete sequences for the founder populations. Although this will be of lesser relevance as data accrues, it is a serious hindrance at present. To palliate this as of now, we propose to generate small random dummy pedigrees that, starting with extant real genomes, will result in a new recombinant genome that can be used as additional founders. SBVB has built in this option already, and both the number of generations and the number of founders of the dummy pedigree can be specified. The current algorithm ensures that founders are evenly sampled from the available sequences.

We have applied the SBVB idea to investigate the use of full sequence in practical GS strategies. The potential advantage of sequence data compared to commercial genotyping arrays for GS has attracted the interest of quantitative geneticists and the industry alike, (e.g., Daetwyler et al. 2014; Hayes et al. 2014), but so far simulation studies have been unable to faithfully represent the complexities and sizes of realistic data sets. Here, we investigated a complex scenario where diverse breeds were of interest. In contrast to dairy cattle, where a single breed has a dominant part of the market and where GS has been efficiently implemented, pig breeding depends on a larger number of breeds and the commercial product is a cross between breeds. Under this setting, the usefulness of GS will diminish since predictive accuracy decreases as the training population size decreases, but it is also a scenario where sequence could be most useful. Prediction across breeds is a topic of practical relevance that was also investigated here. Our study shows that there exists an advantage of using sequence over commercial or random SNP arrays, but that the gains in prediction accuracy were modest (< 4% on average), and this result was independent of the genetic architectures considered when GBLUP was employed (but not with BayesR). This seems to be in conflict with simulation studies reporting an influence of genetic architecture performance (Daetwyler et al. 2010). The simulations of Daetwyler et al. (2010) assumed a neutral architecture, and the differences found depended on the number of QTNs, with equal effects sampled from a normal distribution; here we instead assumed leptokurtic distribution for QTN effects and a relatively large number of QTNs, as found in the literature. Nevertheless, we did find an influence of genetic architecture, e.g., accuracy with Illumina’s 60k array was 0.64 and 0.58 in the neutral and selective architectures, respectively, although the relative advantage of SEQ compared to commercial arrays was consistently 2–4%. Other authors have found an important effect of LD or of effective population size (MacLeod et al. 2014), and we should note that we are using species with long-range LD.

It has been found (e.g., Daetwyler et al. 2010) that variable selection methods such as BayesR tend to overperform pure shrinkage methods such as GBLUP when a small number of loci with large effect exist. Such major loci were rare in our simulations; although some QTN could occasionally explain near 15% of total genetic variance in the neutral architecture, their individual effects were often much < 5% (Figure 2). In agreement with this, we did not find a net improvement of BayesR over GBLUP in accuracy (Figure 6 and Figure S3 vs. Figure S4 and Figure S5). BayesR was much more sensitive to genetic architecture and to the SNP set used than GBLUP (Figure 6), as also reported by Daetwyler et al. (2010). Importantly, BayesR performed better with a random set of SNPs than with commercial SNP arrays. It has been proposed that having customized arrays with SNPs segregating in the population of interest can be a good alternative to sequencing (Pérez-Enciso 2014), and our simulations tend to confirm this if BayesR or similar methods are used. BayesR groups SNPs by their fraction of genetic variance explained. Here, we observed an increased shrinkage with sequence and an ensuing overestimated fraction of SNPs of largest effect. Therefore, it seems that the classification provided by BayesR should be treated with caution at very high marker density because of overshrinkage or confounding between SNP estimates.

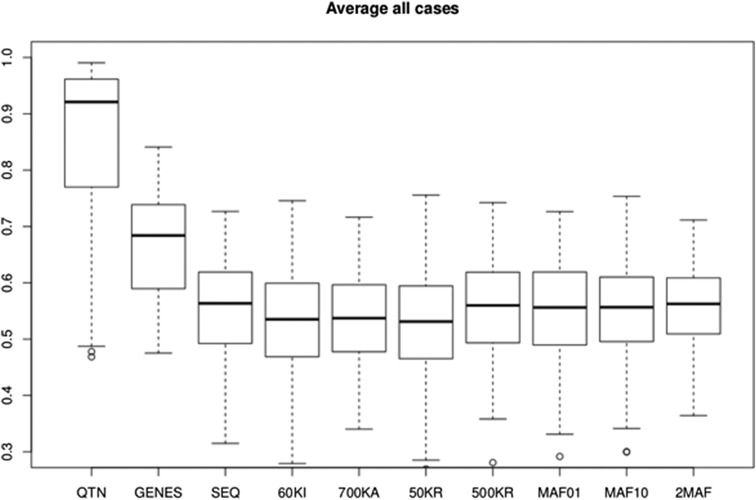
Evidence regarding the use of sequence for GS so far has been conflicting. While earlier simulation studies suggested that response could be boosted by as much as 40% (Meuwissen and Goddard 2010), the very few empirical studies so far have reported either no or a small advantage (Hayes et al. 2014, 2016; Calus et al. 2016; Heidaritabar et al. 2016). As a summary, Figure 7 shows the accuracies obtained with GBLUP by averaging all simulations across architectures and designs, outbred and crossbred combined. Overall, we predict an increase in accuracy of SEQ vs. Illumina’s 60k of ∼3.8% and of 2.8% over Affymetrix’s 700k array. In turn, we found no advantage of sequence over 500KRs, or when GRMs are computed by groups of SNPs according to frequency (MAF01, MAF10, and 2MAF). Yang et al. (2015) proposed partitioning SNPs according to their MAFs and computing separate GRMs, showing that this multi-random model was able to recover all missing heritability in human height and body mass index. Here, we find that using MAF01 or MAF10 can improve accuracy in the selective or neutral architectures, respectively, i.e., when rare or common variants are most relevant, but that the improvement was marginal. Model 2MAF resulted in a minimal increase (0.7%) compared to SEQ. These results suggest that the improvement of sequence vs. commercial arrays for predicting genetic merit is likely to be small even in a multiple breed scenario, at least with GBLUP and flat priors.

Figure 7.

Average performance of different models using GBLUP. Shown are accuracies across all scenarios and genetic architectures considered in this work. Values reported are accuracies, defined as squared correlation between true and predicted genetic values. Models shown are: QTN, GRM computed with all QTNs; SEQ, all SNPs; 60KI, Illumina’s 60k array; 700KA, Affymetrix; 50KR, 50,000 random SNPs; 500KR, 500,000 random SNPs; MAF01, 1 million SNPs with MAF < 0.01; MAF10, 1 million SNPs with MAF > 0.1; 2MAF, the model uses MAF01 and MAF10; and GENES, GRM obtained with the SNPs segregating in any of the genes containing a QTN. GBLUP, genomic best linear unbiased prediction; MAF, minimum allele frequency; QTN, quantitative trait nucleotide.

According to Goddard (2009), prediction accuracy depends on two main factors: (i) the proportion of variance at QTN that can be captured by markers (the so-called “genomic heritability”) (e.g., de los Campos et al. 2015) and (ii) the accuracy of estimated effects. The first factor depends on the extent of disequilibrium between markers and QTN. The second one depends mainly on the ratio between sample size and the number of markers used in the model. However, there are important tradeoffs between these two factors. With sequence data, the genomic heritability can achieve its upper-bound (the trait heritability); yet, the number of effects to be estimated is large and this reduces the accuracy of estimated effects. Therefore, one of the explanations of why models based on SNP arrays perform similarly to models based on full sequence is the relatively small sample size used in most GS studies (small in the sense that n << p). Big data may be needed to obtain the most out of sequence information.

Sample size is not the only limiting step. We argued previously (Pérez-Enciso et al. 2015) that an efficient use of sequence results mainly from the use of accurate priors. In this sense, the identification of causal mutations using sequence can make a big difference, as also shown here. The issue, of course, is that this is an unrealistic goal. In addition to increasing sample size, two additional improvements are nevertheless possible. The first one is to narrow down regions containing QTN using sequence – based large-scale association studies. This kind of work can greatly illuminate the genetic architecture of the trait. For example, recent sequencing work using ∼35,000 diabetics and 110,000 controls revealed that common variants explain most of the genetic determinism for this disease (Morris et al. 2012). The second approach is to give unequal weights to each SNP according to biological knowledge, such as nonsynonymous vs. synonymous variants; recent works suggest that this can enhance the value of sequence as well in practice (MacLeod et al. 2016).

Here, we have applied our tool to study the performance of GS in very large genomic data sets. Certainly, there are other important potential applications of SBVB, in addition to those investigated here, particularly in the evaluating the performance of GWAS full sequence studies or studying the genome dynamics of actual plant or animal breeding schemes. Several ongoing GWAS experiments have produced or have plans to obtain hundreds or thousands of complete genomes. This amount of sequence data has sparked an interest in developing specific tests for “rare” variants (actually the most common set of variants) such as SKAT (Ionita-Laza et al. 2013) or others (Hoffmann and Witte 2015). Our approach makes it possible to test their performance under a variety of genetic architectures in realistic data sets. A reliable assessment of power and false discovery rate seems essential to correctly interpret the results of these studies, and SBVB can be used for this purpose in an efficient and flexible manner.

In conclusion, we propose to use real sequences as initial population genomes for realistic simulation studies in massive genomic data sets. In this way, we ensure faithful representation of the properties of real commercial arrays or of specific SNP positions. With this approach, we have found that sequence-based GS may increase response to GS, but modestly, perhaps by up to 4% in our scenario, and this result is robust to extreme genetic architectures. This applies at least when GBLUP with equal priors given to each SNP is employed and the number of loci is relatively large. Our results are far less optimistic than initial simulations but, importantly, agree with incipient empirical evidence on the use of sequence to predict genetic merit. In our opinion, future efforts should focus on methods to optimize the prior information in prediction tools, including accurate mapping of causal mutations.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.194878/-/DC1.