Gaussian Process Modeling of Protein Turnover

Abstract

We describe a stochastic model to compute in vivo protein turnover rate constants from stable-isotope labeling and high-throughput liquid chromatography–mass spectrometry experiments. We show that the often-used one- and two-compartment nonstochastic models allow explicit solutions from the corresponding stochastic differential equations. The resulting stochastic process is a Gaussian processes with Ornstein–Uhlenbeck covariance matrix. We applied the stochastic model to a large-scale data set from ¹⁵N labeling and compared its performance metrics with those of the nonstochastic curve fitting. The comparison showed that for more than 99% of proteins, the stochastic model produced better fits to the experimental data (based on residual sum of squares). The model was used for extracting protein-decay rate constants from mouse brain (slow turnover) and liver (fast turnover) samples. We found that the most affected (compared to two-exponent curve fitting) results were those for liver proteins. The ratio of the median of degradation rate constants of liver proteins to those of brain proteins increased 4-fold in stochastic modeling compared to the two-exponent fitting. Stochastic modeling predicted stronger differences of protein turnover processes between mouse liver and brain than previously estimated. The model is independent of the labeling isotope. To show this, we also applied the model to protein turnover studied in induced heart failure in rats, in which metabolic labeling was achieved by administering heavy water. No changes in the model were necessary for adapting to heavy-water labeling. The approach has been implemented in a freely available R code.

Graphical Abstract

INTRODUCTION

The continuous degradation and synthesis of proteins plays an important role in maintaining cellular homeostasis.¹ The dynamic equilibrium of cellular protein abundances can change due to, for example, external stimuli, developmental programs, onset of diseases, or aging. The new equilibrium is achieved by balancing between alterations in the rate of synthesis and the rate of degradation. The combined process of synthesis and degradation termed as protein turnover refers to the movement of a protein through its pool and is often expressed as a first-order rate constant.² It is thought that protein degradation is a stochastic process; all proteins (newly synthesized and old) have the same probability of being degraded.²

The labeling of proteins with radioactive amino acids is considered to be a “golden standard” for studying proteome dynamics. In this “pulse-chase” method, proteins of interest are radioactively labeled over a brief period of time (the pulse), and then the decay in radioactivity is measured over time (the chase) and is used to determine the protein half-life.³ This assay is accurate and minimally perturbative but requires a specific antibody for each protein, which makes it difficult for scaling to multiple proteins. Fluorophore tagging of proteins have also been used for proteome dynamics studies.^4,5 Although these methods are real-time, it has been argued that the tagging may affect protein turnover properties, both through changing the protein structure and by altering their abundance and stoichiometry relative to interaction partners.⁶

Mass-spectrometry-based proteomics is a widely used, high-throughput technology to identify and quantify proteins.⁷ Most of the quantitative proteomics applications so far have been used for measuring the net change in protein abundance.⁸ The technology has recently been enhanced and applied⁹ in studies aimed at measuring the rate of protein turnover, both in vivo^10–15 and in vitro.^16–19 Protein turnover studies using metabolic labeling and liquid chromatography–mass spectrometry (LC–MS) analyses have a complex design that includes a critical bioinformatics component to extract protein-decay rate constants.²

The work discussed herein focuses on the application of a stochastic model to extract protein turnover rate constants from in vivo protein turnover studies. Briefly, the metabolic incorporation of stable isotope and LC–MS measurements of time course peptide and protein labeling provide data on protein kinetics. Traditionally, exponential decay curves have been used to fit the experimental data and infer the protein turnover rate constants.^11,18,20,21 Single-compartment (single exponential) and multicompartment (first-order synthesis and multiexponential)^21,22 models have been employed. Time-dependent ordinary differential equations (ODE) have also been used to model the stable isotope incorporation in metabolic labeling.^22,23 However, the general applicability of these models to in vivo studies are limited because they may result in negative decay rates (for multicompartment systems) and are not able to explain fluctuations in the experimental data.²¹

Stochastic models were recently applied to high-throughput time-course data in proteome studies.^24,25 SORAD²⁴ used a Gaussian process (GP) to describe time-course data of phosphor proteins from enzyme-linked immunosorbent assay experiments. Similar models have been used for chromatographic alignment²⁵ and beta-binomial process modeling of high-throughput sequencing.²⁶ The stochastic processes add the flexibility of accounting for fluctuations in the data. Here, we describe a nonparametric, data-driven stochastic approach, GP, for modeling time-course data from metabolic labeling experiments. We show that the GP with the Ornstein–Uhlenbeck (OU) kernel is a natural solution to the protein turnover kinetics in one- or two-compartment models. This approach produces fits that are highly improved compared to the traditional curve-fitting models; it overcomes problems with negative decay rates and random fluctuations in decay rates. Last, the model is isotope-independent (i.e., ¹⁵N or ²H labeling). The R code implementing the model is available at https://ispace.utmb.edu/users/rgsadygo/Proteomics/ProteinKinetics.

METHODS

Protein turnover studies using metabolic labeling, mass spectrometry and bioinformatics have a complex design and comprise multiple stages.²⁷ There are some variations dependent on what type of labeling (e.g., ¹⁵N, ²H, or ¹³C) is used and how a tracer is administered. For, e.g., studies that rely on heavy-water labeling, the animals are provided heavy water using a “primed-infusion” logic. For example, animals are given an initial loading bolus to instantaneously raise the enrichment of body water to a desired level. They are simultaneously given labeled water in the drinking bottles to maintain the enrichment. At predetermined time points, the animals are sacrificed, and the organs or tissues are collected. LC–MS/MS is used to identify proteins and measure the level of incorporation of heavy isotopes.^28–30 The time-course data of the heavy isotope incorporations is then modeled to extract the protein turnover rate constant (Figure 1). The last stage is the focus of this study. In the following text, we will first review the current models and then describe our stochastic model to extract protein turnover rate constants from heavy-isotope labeling data.

Figure 1.

Modeling of protein turnover rate constants from stable-isotope-labeling experiments. The time-course of heavy-isotope labeling, extracted from the full scan spectra of tryptic peptides, is modeled as a GP with OU kernel.

Ordinary differential equations have previously been used to model the incorporation of the heavy-isotope-labeled species in metabolic labeling and LC–MS.^21,23 As a prototypical study, Guan and colleagues²¹ have used one- and two-compartment models to determine protein turnover rate constants from experiments using an ¹⁵N-labeled algae diet (produced from ¹⁵N-enriched NaNO₃) and mass spectrometry. In brief, the one-compartment model assumes that proteins are synthesized at a constant rate, k_syn, and degraded proportional to their abundance levels with the degradation rate constant of k_deg. With the additional assumption of the steady-state for a protein concentration, it was shown that the fraction of the heavy-isotope-labeled proteins, β(t) (characterized by the relative isotope fraction, RIF), is described by a first-order deterministic equation:

$$\stackrel{.}{\beta (\mathrm{t})}=k_{deg}-k_{deg}\beta (t)$$ (1)

where t is the time, and the initial value condition is β(0) = 0(the baseline, before the tracer administration). The solution of this equation is a growth curve with a single exponent:

$$\beta (t)=1-e^{-t{k}_{deg}}$$

The details of all formula derivations are provided in the Supporting Information. We note that under the steady-state assumption (which is used in this work), the protein degradation rate constant is equal to the fractional protein synthesis rate (ratio of the synthesis rate over the protein concentration). Thus, throughout the paper, we refer to the protein turnover rate constant and degradation rate constant interchangeably.

Several other publications^{11,12,18,20,31} modeling protein turnover from stable isotope labeling experiments have used equations similar to eq 1. However, when applied to the data sets from mouse protein turnover studies that used ¹⁵N labeling, the fit to the data was often complicated (in particular, for fast protein turnover).²¹ Better results were achieved by using a two-compartment model. In this model, the first compartment considers the kinetics of amino acids, and the second compartment accounts for the amino acids incorporation into proteins. Protein synthesis is assumed to be a first-order process. It is modeled to depend on the concentrations of heavy-isotope-labeled amino acids (precursor pool). The model leads to a system of equations for the fraction of heavy-isotope-labeled amino acids, α(t) and β(t):

$$\{\begin{array}{l}\stackrel{.}{\alpha (t)}=k_{\text{syn}}-k_{\text{syn}}\alpha (t)\hfill \\ \stackrel{.}{\beta (t)}=k_{deg}\alpha (t)-k_{deg}\beta (t)\hfill \end{array}$$ (2)

where k_syn is the rate constant of protein synthesis from the precursor amino acids. Eq 2 was derived under the assumption of the steady-state for the total (labeled and unlabeled) protein level. The amino acids are synthesized with the constant rate, k₀, and degraded proportional to their abundances with the rate constant, k_syn. Protein degradation is characterized with the rate constant, k_deg. The equation for α(t) is solved first, with the initial value for stable-isotope-labeled amino acids, α(0), set equal to zero:

$$\alpha (t)=1-e^{-t{k}_{\text{syn}}}$$

which leads to the following equation for the β(t):

$$\stackrel{.}{\beta (t)}=k_{deg}(1-e^{-t{k}_{\text{syn}}})-k_{deg}\beta (t)$$ (3)

The solution of eq 3 (β(0) = 0) is the two-exponent growth curve:

$$\beta (t)=1-(k_{\text{syn}}{e}^{-t{k}_{\text{deg}}}-k_{deg}{e}^{-k_{\text{syn}}t})/(k_{\text{syn}}-k_{\text{deg}})$$

The solutions for α(t) and β(t) were obtained with the assumption that the heavy-isotope labeling is asymptotically complete. This assumption, while somewhat reasonable for incorporation of ¹⁵N-labeled amino acids into proteins, will not be generalizable for incorporation of deuteriums during the administration of heavy water. This is because, in contrast to the fully ¹⁵N-labeled diet, the metabolic labeling with heavy water involves administration of only ~5% ²H₂O in the drinking water. Metabolic labeling with 100% ¹⁵N in the diet may lead to the complete labeling of all nitrogen atoms in a protein, but using 5% heavy water will only result in partial labeling of the proteins. The incomplete labeling was also observed⁶ in labeling by SILAC.³² It was observed that unless the cell medium is regularly renewed by labeled amino acids, complete labeling of proteins will not be achieved. In animal experiments, it is not feasible to renew the cellular environment.

To account for the incomplete labeling, we introduced a new parameter, the heavy-isotope-enrichment fraction at the asymptote, λ. With this parameter, the solution for β(t) becomes

$$\beta (t)=\lambda -\lambda (k_{\text{syn}}{e}^{-t{k}_{\text{deg}}}-k_{deg}{e}^{-k_{\text{syn}}t})/(k_{\text{syn}}-k_{\text{deg}})$$ (4)

A more descriptive text on the one- and two-compartment models and their solutions is provided in the Supporting Information. Even though the two-compartment model produced significantly improved fits compared to the experimental data, it was observed that the model was not able to account for the stochastic fluctuations in the experimental data.²¹ It has subsequently lead to high synthesis rate constants in the two-compartment model and negative decay rate constants for the expanded, three-compartment model. Here, we will show that stochastic differential equations based on either eq 1 or eq 2 allow the exact solution in the form of a GP with OU kernel. The stochastic equation uses a model fluctuation parameter that allows one to account for and estimate the effects of stochastic fluctuations in experimental data.

The stochastic analog of eq 3 for β(t) (with the inclusion of the incomplete isotope labeling at the asymptote) is

$$\begin{array}{l}\mathrm{d}X(t)=k_{deg}(\lambda (1-e^{-t{k}_{\text{syn}}})-X(t))\\ \mathrm{d}t+\mathrm{\Gamma }(k_{deg},k_{\text{syn}},t,X,\lambda ,{\sigma }_{\gamma })\mathrm{d}B(t)\mathrm{X}(0)=0\end{array}$$ (5)

where X(t) is a stochastic variable denoting the fraction of the heavy-isotope-enriched protein (β(t) in the deterministic model), Γ(k_deg, k_syn, t, X, λ, and σ_γ) is the volatility, which, in general, is dependent on the model parameters k_syn, k_deg, λ, and X(t), and the variance of the model fluctuations, σ_γ; B(t) is the Brownian motion (white Gaussian noise). If we assume that, in addition to the model fluctuations, there are also measurement errors that are described by a white Gaussian noise, ε (with standard deviation σ_ε), the final model is

$$Y(t)=X(t)+\epsilon \epsilon ~N(0,{\sigma }_{\epsilon }^2)$$

The model depends on the stochastic variable, X(t), which is the solution to eq 5. We assume a homoscedastic variance, which allows for an explicit solution to eq 5. Thus, if the volatility, Γ, depends only on the model fluctuations, σ_γ, then eq 5 becomes

$$\mathrm{d}X(t)=k_{deg}(\lambda (1-e^{-t{k}_{\text{syn}}})-X(t))\mathrm{d}t+{\sigma }_{\gamma }\mathrm{d}B(t)$$ (6)

Eq 6 can be solved (using the assumption of Itô’s process^33,34 for X(t) and the transformation g(X,t) = X(t)*exp(k_degt). The details of the derivation are provided in the Supporting Information). The solution of eq 6 is

$$X(t)=\lambda -\lambda (k_{\text{syn}}{e}^{-t{k}_{deg}}-k_{deg}{e}^{-k_{\text{syn}}t})/(k_{\text{syn}}-k_{deg})+{\sigma }_{\gamma }{\int }_0^t{e}^{-k_{\text{deg}}(t-s)}\mathrm{d}B(s)$$ (7)

Note that the solution, (7), is the OU process^34,35 with a mean value, β(t), in eq 4 and covariance matrix, K(t,s) (also called Gram matrix), expressed as

$$K(s,t)={\sigma }_{\gamma }^2{e}^{(-\mid s-t\mid k_{deg})}/k_{deg}$$

where t and s are time points. The result allows the direct application of the OU process to the proteome turnover dynamics. Because the solution is exact, it is not only methodologically preferable but also offers practical advantages to the Gaussian kernel model that was previously used for the first-order equation;²⁴ this stems from the fact that for the exact solution, there is one less parameter. The scaling factor in the Gaussian kernel is an independent parameter that needs to be estimated from the data. In the exact solution, the scaling parameter in OU kernel is the degradation rate constant, k_deg. In addition, it is natural that for the processes that behave exponentially, eq 7, the covariance terms between the time points will also be exponential (depending on the absolute value of the time difference) rather than Gaussian. Thus, our final model for the heavy-isotope-labeled protein proportions becomes

$$\overrightarrow{Y}~\text{MVN}(\overrightarrow{\mu },\mathrm{\sum })\overrightarrow{Y},\overrightarrow{\mu }\in {\mathrm{R}}^n$$ (8)

where MVN stands for multivariate normal distribution, n is the number of data points (time points at which heavy isotope levels have been measured), μ is equal to β, which is determined in eq 4, and the covariance matrix, Σ is an n by n matrix defined as

$$\sum (s,t)=K(s,t)+{\sigma }_{\epsilon }^2\delta (s,t)$$ (9)

where δ is the Kronecker’s δ. The model (eq 8) with the covariance matrix (eq 9) is a GP with OU kernel, and numerical methods exist^36,37 for its solution to obtain k_deg and k_syn. The approaches to extract the parameters from the data use the posterior distributions or likelihood function and find parameter values that maximize them. In total, there are five hyperparameters in our model, θ = (k_deg, k_syn, σ_γ, σ_ε, λ). The log-likelihood function is

$$\begin{array}{c}log(\mathcal{L}(\theta ))=-0.5log(det(\mathrm{\sum }))-0.5{(\overrightarrow{y}-\overrightarrow{\mu })}^T\\ {\mathrm{\sum }}^{-1}(\overrightarrow{y}-\overrightarrow{\mu })-0.5nlog(2\pi )\end{array}$$ (10)

The posterior distribution, p(θ|y), of the parameters is proportional to the product of the likelihood function and the prior distributions, π(θ). The log of the posterior distribution of the hyperparameters is

$$log(\mathrm{p}(\theta \mid y))\propto log(\mathcal{L}(\theta ))+log(\pi (\theta ))$$

The hyperparameters can be estimated from the data either by maximizing the posterior distribution with respect to the hyperparameters³⁶ or by sampling from the posterior distribution with Markov chain Monte Carlo methods.²⁵ We used a quasi-Newton approach, a Broyden–Fletcher–Gold-farb–Shanno algorithm³⁸ available in R,³⁹ to maximize the posterior distribution function and obtain the hyperparameters. For the prior distributions (except for λ), we chose exponential distributions with the prior decay rates estimated from the nonstochastic model. A uniform prior was chosen for the asymptotic enrichment level, λ. Note that the derivative of the log-likelihood function, eq 10, with respect to the every hyperparameter is in a closed form and is used in the optimizations. The corresponding formulas are shown in the Supporting Information.

The approach is implemented in an R code³⁹ and is available in the Supporting Information.

RESULTS

Performance Metrics Using ¹⁵N Labeling Data

The protein turnover experiments using ¹⁵N labeling were used to test and compare the performance of the stochastic model with the results from exponential curve fitting. The ¹⁵N labeling data is freely available online.²¹ The data consists of two parts, a brain and a liver proteome. For every protein, RIF values of all peptides (for the protein) have been averaged to obtain protein RIF. We used these values to test our model. On average, protein turnover rates in brain are longer than those in the liver. For the nonstochastic model, the fitting of liver data has been more difficult and required three exponential curves, some of which produced negative rate constants.²¹ As a goodness of fit metric, we chose the residual sum of squares (RSS) for each model:

$$\text{RSS}=\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2$$

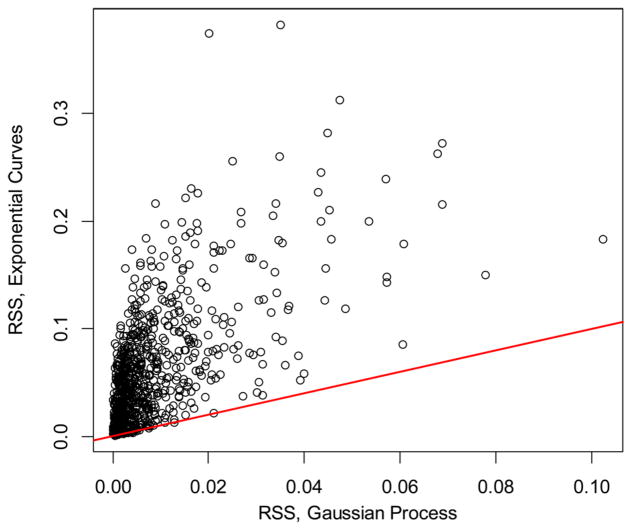
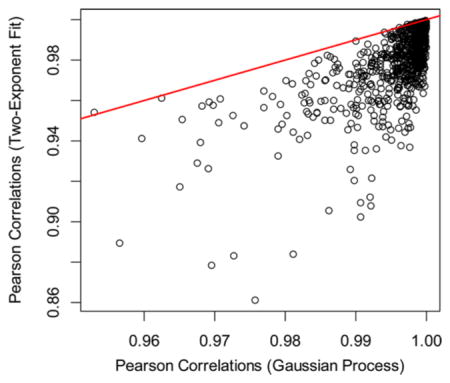
where y_i are the observed values and ŷ_i are the corresponding theoretical predictions. In Figure 2, we show the comparison of the RSS values between the stochastic modeling (x axis) and the two-exponent curve fitting (y-axis) for the mouse liver proteome (the red line is the line of unity). For the data points above the line of unity, the RSSs of the two-exponent curves are larger than the corresponding RSSs from GP. The fits obtained by the GPs resulted in smaller RSS values for 794 out of 797 proteins. Unlike the exponential curve fitting, GP allows for correlations between the measured RIFs in the time-course data. It is a desirable feature because the data points that are nearby in the time domain are expected to be correlated, and ideally, a model will be able to account for the correlation. In the case of the GP, the time correlations are provided in the structure of the Gram matrix. The diagonal elements of the matrix are the sum of the white-noise variance and amplitude of the OU kernel. The nondiagonal elements of the matrix are the covariance between the different time points. The corresponding figure for brain proteome is shown in Figure S1. Another goodness-of-fit measure in time course models is the Pearson correlation between the predicted values and experimental observations along the time axis. In Figure S2 (mouse liver) and Figure S3 (mouse brain), we show the scatter plot of the Pearson correlation coefficients for each protein obtained using predictions from two-exponent fitting and GP modeling. Similar to RSS, GP showed substantially improved correlation coefficients compared to the two-exponent fitting.

Figure 2.

Comparison of the residual sum of squares obtained by using exponential curve fitting⁴⁴ (y-axis) and GP (x-axis). The red line is the line of unity. The shown data is for the liver proteome.

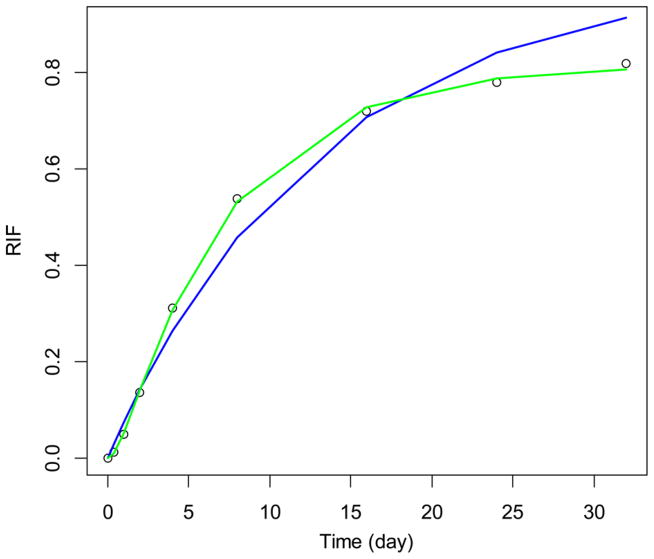
To explicitly compare the fits from the two models, we have chosen a liver mitochondrial protein, trifunctional protein subunit α (Q8BMS1). The experimental data (empty circles) and fits (green line, GP; blue line, exponential curves) are shown in Figure 3. The GP results in a better fit (an approximately 70 times smaller RSS value compared to the two-compartment exponential curve fit). The k_syn rate constant computed in the exponential curve fit is very large, in the order of 10¹² (day⁻¹), and the GP produced 1.4 day⁻¹. The degradation rate constant, k_deg, in GP was 0.15 day⁻¹, which was twice higher than the corresponding value from the two-exponent curve fit. The 95% confidence interval of the GP predicted fit is shown in Figure S4.

Figure 3.

Experimental (empty circles) data and model fits (green line, GP; blue line, exponential curve fitting) for mitochondrial trifunctional protein, subunit α (Q8BMS1). The GP produced a fit with RSS about 70 times smaller than that from the two-exponent fit.

Comparison with the ODE Results Using ¹⁵N Labeling Data

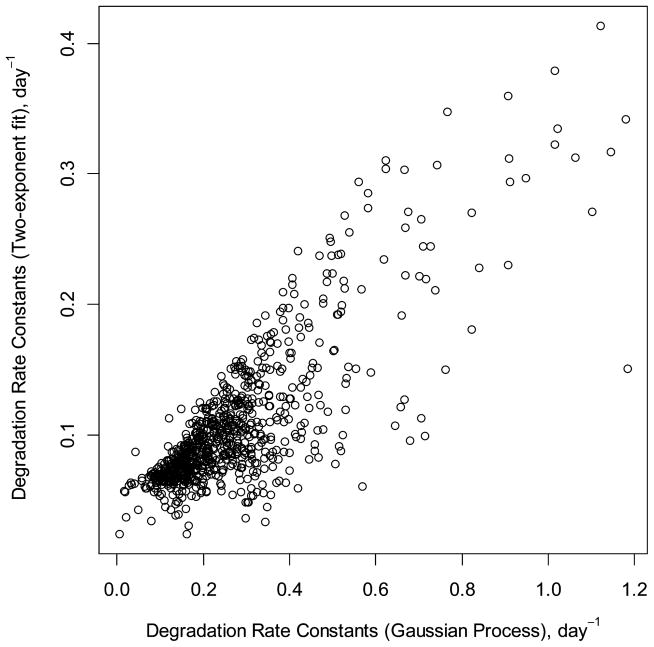
The scatter plot of the computed decay rate constants using a GP model and two-exponent curve fitting for mouse liver proteins is shown in Figure 4. The relevant data for mouse brain are shown in Figure S5. In general, the GP model produced decay rate constants that are larger than those from the two-exponent curve fitting. The correlation between the rate constants was 0.81. The density plot of the differences between k_deg values produced by the GP and two-exponent curve fit are shown in Figure S6. The distribution peaks at about 0.18 day⁻¹ and extends up to 1 day⁻¹. For liver proteins, the median degradation rate constants were 0. 091 and 0.228 day⁻¹ for the two-exponent curve fit and GP, respectively. Thus, GP modeling, on average, predicts more than 2-fold faster degradation rate constants for liver proteins. For the mouse brain proteins, the effects were not so drastic. The median rate constants for brain proteins were 0.040 and 0.054 day⁻¹ in the two-exponent curve fit and GP modeling, respectively. It has been noted previously that the exponent curve-fitting models were less accurate for modeling faster protein turnover (liver proteins).²¹ The ratio of the median turnover rate constants of liver proteins to brain proteins increased from 2.25 in two-exponent fitting to 4.23 in GP modeling. Thus, the GP modeling predicts a larger difference between the protein turnovers in liver and brain. The ratio of the medians of turnover rate constants predicted by the GP modeling compares well to earlier studies that estimated the rate of incorporation of [¹⁴C] tyrosine in mouse liver (2.8% per hour) and brain (0.6% per hour).⁴⁰ Note that in these studies, the calculation of the rate constants are based on the tracer incorporation rate and the steady-state assumption, i.e., the fractional synthesis rate of proteins are equal to the fractional degradation rate. Under the steady-state assumption, the degradation rate constant is linearly dependent on the synthesis rate, as can be seen from the one-compartment model (solution of eq 1b in the Supporting Information). Figure S7 summarizes decay rate constants of brain and liver proteomes computed using two-exponent curve fitting and GP modeling.

Figure 4.

Scatter plot of the decay rates constants as computed by the GP (x-axis) and two-exponent curve fitting (y-axis). In general, the rate constants computed by the GP model were larger (mouse liver proteins).

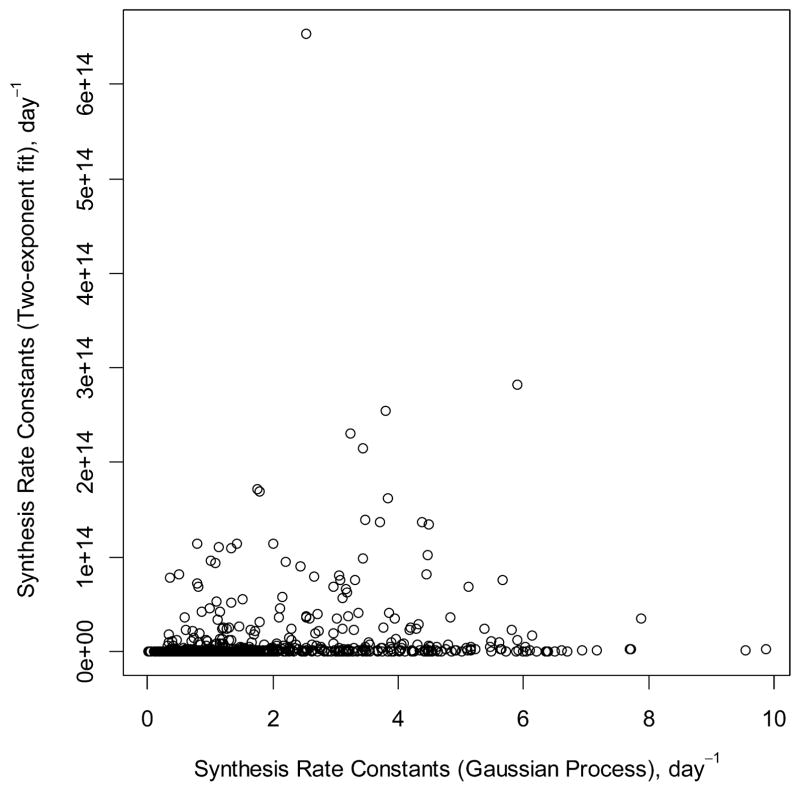
Stronger differences were observed in cases where one estimates the synthesis rate constants, k_syn (Figure 5). Unlike the two-exponent curve fit, there are no k_syn values by the GP that are larger than 10 day⁻¹. For the two-exponent curve fitting k_syn, values as large as 10¹⁴ day⁻¹ have been produced. The median values of k_syn for the two-exponent curve and GP were 9.12 × 10 and 1 day⁻¹, respectively. We note that in the labeling experiments where the first isotope distribution pattern is measured after about 9 h of metabolic labeling, the accurate determination of the rate constants of this much higher magnitude are unrealistic. The GP, however, yielded a maximum synthesis rate constant less than 10 day⁻¹. In addition, as it is shown in Figures 2 and S1–S3, the goodness of fit is substantially improved for the GP. The synthesis and degradation rate constants as computed by GP, and two-exponent curve fittings are provided in Tables S1 and S2 for liver and brain proteins, respectively.

Figure 5.

Synthesis rate constants as computed using two-exponent curves (y-axis) and GP (x-axis) for mouse liver data proteome.²¹

The stochastic model produces a volatility standard deviation, σ_γ, for each protein rate constant estimate. The higher volatility standard deviation means a stronger random fluctuation effects. In Figure S8, we show the distribution of model standard deviations for the liver proteins. The mode of the standard deviation is nonzero at 0.018, and the highest values are at 0.08.

As was mentioned above, one way to improve the model fitting to the data has been to add more compartments. However, we believe that one should consider the development of a rationale solution and interpretation, e.g., make sure the modeling is done properly (as Guan et al.²¹ have shown) but that it is supported by some strong physiological underpinnings. It would appear that the addition of more compartments solved one problem (i.e., gave a better fit of the data) but failed to address what these compartments would represent from a biochemical perspective.

Our approach simply considers another way to align the biology and the modeling. We suspect that the approach described herein provides a better fit than previous ODE methods, in part because of instability in the ¹⁵N-precursor precursor labeling (note that a major assumption is a constant precursor labeling). For example, if the amino-acid enrichment is constant, one would expect that the use of an ODE method should produce a good fit of the apparent protein-decay rate constant. Presumably, the use of ¹⁵N-labeling (via the diet) results in pulsatile (or oscillatory) changes in the ¹⁵N-labeling of proteogenic amino acids. One would expect a maximum ¹⁵N-enrichment immediately following the consumption of the food and a lower degree of labeling at times when food is not consumed (given that during those periods, ¹⁴N would be appearing via endogenous protein degradation). In addition, one needs to consider that there are gradients between plasma amino acid labeling and the labeling of free amino acids in different tissues. Effectively, the “free amino acid” compartment is further compartmentalized, and the “mixing” between different tissues and variable plasma labeling is not necessarily equal across sites. We suspect that this is what led Guan and colleagues²¹ to use models of increasing complexity when they fit the tissue-specific protein labeling. The observations would be expected to play a greater role in cases where protein turnover is faster (e.g., liver versus brain) and therein requires more complex models (e.g., three- versus two-compartment) to get a better fit.

Kinetics of Heart Mitochondrial Carnitine Palmitoyltransferase 1

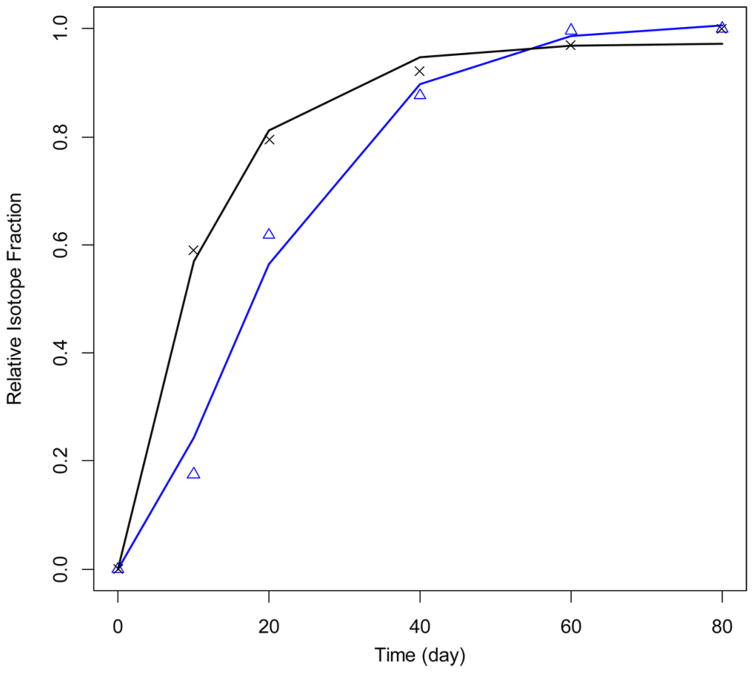
In a recent study,⁴¹ we used heavy-water labeling to determine the changes in half-lives of mitochondrial proteins in cardiomyocytes due to the induced heart failure in rats. One of the proteins that we studied was carnitine palmitoyltransferase (CPT) 1. The experimental data (crosses, normal heart; triangles, induced heart failure) and corresponding GP fits (black line, normal heart; blue line, induced heart failure) are shown in Figure 6 (the data is for the CPT 1 from subsarcolemmal mitochondria (SSM) of cardiomyocytes). The computed turnover rate constants for the normal and induced heart failure samples were practically the same and equal to 0.09 day⁻¹. The result is in agreement with the finding that turnover rates for CPT 1 in SSM were not affected by the induced heart failure. The k_syn rate constant was substantially larger in heart-failure-induced SSM CPT 1 than in the protein of the normal heart: 2.2 versus 0.09 day⁻¹.

Figure 6.

GP modeling of RIF for CPT protein from normal (experimental data is shown with blue triangles and the fit in blue line) and induced heart failure (the experimental data is shown with black crosses and the fit in black line) interfebrullar mitochondria.⁴¹

CONCLUSIONS AND FUTURE WORK

We have applied GP modeling to extract protein turnover rates from the time-course data of isotope incorporation in stable-isotope labeling and LC–MS experiments. It was shown that an exact solution to the stochastic differential equation yields a GP solution with OU kernel. The approach is preferable to the more widely used GP with the Gaussian kernel because the OU solution is exact and the number of parameters is less. We then used this approach to analyze a large-scale data set obtained from mice fed a diet containing ¹⁵N-labeled algae. The results have demonstrated that GP modeling substantially improves the fit to the experimental data, particularly for protein turnover in liver, which in a previous model produced negative rate constants. We also applied the model to the carnitine palmitoyltransferase of SSM of cardiomyocytes that were studied to infer the effects of the induced heart failure. This experiment had used heavy-water labeling.

In future studies, we plan to extend the model to include relative isotope fractions for each peptide of a protein. A similar approach has employed a mixed-effects modeling for growth curves resulting from the Gompertz model.⁴² Using each point of peptide data separately rather than averaging the peptide data will allow us to estimate the variability due to the heavy-isotope labeling of peptides. In addition, we will extend the model to describe the turnover of proteins that are not in a steady-state condition.⁴³

ABBREVIATIONS

GP

Gaussian process

SSM

subsarcolemmal mitochondria

LC–MS

liquid-chromatography–mass spectrometry

ODE

ordinary differential equation

OU

Ornstein–Uhlenbeck