Comparison of two correlated ROC curves at a given specificity or sensitivity level

Abstract

The receiver operating characteristic (ROC) curve is the most popular statistical tool for evaluating the discriminatory capability of a given continuous biomarker. The need to compare two correlated ROC curves arises when individuals are measured with two biomarkers, which induces paired and thus correlated measurements. Many researchers have focused on comparing two correlated ROC curves in terms of the area under the curve (AUC), which summarizes the overall performance of the marker. However, particular values of specificity may be of interest. We focus on comparing two correlated ROC curves at a given specificity level. We propose parametric approaches, transformations to normality, and nonparametric kernel-based approaches. Our methods can be straightforwardly extended for inference in terms of ROC⁻¹(t). This is of particular interest for comparing the accuracy of two correlated biomarkers at a given sensitivity level. Extensions also involve inference for the AUC and accommodating covariates. We evaluate the robustness of our techniques through simulations, compare to other known approaches and present a real data application involving prostate cancer screening.

1. Introduction

The early detection of prostate cancer is primarily based on the serum concentration of prostate-specific antigen (PSA). The use of PSA as a screening biomarker, however, has raised concerns about the potential for overdiagnosis and overtreatment, which results in increased treatment-related morbidity and cost (see [1]). The disadvantage of using PSA as a screening tool is that it is not specific to cancer; other conditions such as prostatitis or urinary tract infections may increase PSA levels (see [2]). That study reported such concerns and the use of a non-coding, large chain RNA known as prostate cancer antigen 3 (PCA3) in prostate cancer screening. They evaluated the incremental value in terms of the diagnostic accuracy of PCA3 compared to that of PSA-based screening. Addressing the concerns of over or underdiagnosis implies that we might need to focus on the performance of the biomarkers at specific false positive rates (or sensitivity levels). Namely in such situations we typically want to force high sensitivity for aggressive cancer while reduce the false positive rate for benign tumors.

The receiver operating characteristic (ROC) curve is a tool for determining the overall effectiveness of a continuous or ordinal biomarker. Assuming continuous measurements for the healthy and diseased individuals, denoted by W_A and W_B respectively, and under the further assumption that higher marker scores are more indicative of the disease (without loss of generality), then sensitivity equals the so-called true positive rate TPR = sens(c) = P(W_B > c) and specificity equals the so-called true negative rate TNR = spec(c) = P(W_A < c), where c is a decision cutoff. For different cutoff values c, we obtain different pairs of sensitivity and specificity. The ROC is the curve obtained by all possible pairs of sensitivity and specificity as c moves through the real line: ROC(c) = {(FPR(c), TPR(c)), c ∈ (−∞, ∞)} where FPR is the false positive rate and is equal to P(W_A > c). It can be shown that if W_A ~ F_A(·) and W_B ~ F_B(·), then the underlying ROC can be written as a function of the corresponding survival functions, S_A(·) = 1 – F_A(·) and S_B = 1 – F_B(·), yielding $\mathit{ROC}(t)=S_B(S_A^{-1}(t))$, t ∈ (0, 1). A summary index for the biomarker’s effectiveness is the area under the curve (AUC) and is simply defined by ${\int }_0^1$ ROC(t)dt. For a detailed overview regarding ROC curves see [3].

In paired studies, where two biomarkers are to be compared, individuals are measured with both biomarkers; hence, their measurements are correlated. Let W_1A be the scores of the healthy individuals when measured with biomarker 1, and W_2A their corresponding scores obtained by biomarker 2 (random variables W_1B and W_2B are similarly defined for the diseased group). For the i–th healthy individual it holds that Corr(W_1Ai, W_2Ai) ≠ 0 and for the j–th diseased individual it holds that Corr(W_1Bj, W_2Bj) ≠ 0. We assume that for a given a marker, whose measurements are denoted with W, a subject’s measurement does not affect another subject’s measurement, regardless the group in which they belong, namely Corr(W_i, W_j) = 0, for ∀i ≠ j. As pointed out by a referee, such an assumption might not always hold. For example if measurements are taken within clustered individuals, e.g. within the same family, same block, or a condition that could hold for multiple subjects (such as hormone replacement use by women) it might be the case that measurements of one subject are correlated with those of another. Covariate adjustments as fixed effects (e.g. hormone replacement therapy) or random effect terms (e.g. family) could be added into a biomarker model to address these issues. However, such settings are beyond the scope of our study. There are three main comparison scenarios on which researchers commonly focus (see also [4, 5]): (1) Testing whether two ROC curves are equal for all FPRs, (2) Testing whether their AUCs (or partial AUCs) are equal, and (3) Testing whether two ROC curves are equal at a particular FPR. In practice, the first comparison scenario is not popular because primary interest lies in specific FPRs and it is rather rare for two biomarkers to perform equally well at all FPR regions. For approaches relevant to this setting, see [6–9]. Most researchers have focused on the AUC. DeLong et al. [10] focused on the nonparametric setting and based their approach on the theory of generalized U-statistics. Metz et al. [11] explored methods based on the maximum likelihood and developed the ROCKIT software. Zhou and Gatsonis [12] considered a nonparametric framework for partially paired designs, and Zou [13] considered a semiparametric approach involving monotone transformations. Molodianovitch et al. [14] investigated the use of the Box-Cox power family of transformations. While two ROCs exhibit the same AUCs, they might differ substantially, i.e. when two ROC curves intersect. In practice, clinicians may need to compare two biomarkers at specific FPRs or even at specific TPRs to avoid overdiagnosis or underdiagnosis. Such issues arise in the aforementioned prostate cancer example. Hence, particular interest lies in scenario (3), on which we focus in this paper. The literature for this scenario is limited. Linnet [15] and Wiend et al. [16] developed nonparametric approaches that refer to the empirical setting. The empirical ROC curve is a step function that exhibits jumps when the number of individuals related to each FPR, TPR, changes, as the cutoff spans the real line. Hence, the crude empirical estimate has the disadvantage of providing the same TPR for different FPRs. This is not the case for the true ROC curve, for which a natural assumption is that it is a smooth curve.

Even though fixing a decision cutoff directly implies a specific FPR level at which to compare the two ROC curves, caution is needed depending on the focus of the study. When the focus is on biomarker discovery then it might be of interest to simply fix directly the FPR level at minimally tolerable levels, for example 5%, in case the clinical interest is to avoid overdiagnosis. If, on the other hand, clinical interest lies in achieving initially a high level of sensitivity then one needs to focus on comparisons where TPR is fixed in high values say 95%. When, however, a biomarker is established and its cutoff (decision threshold) has been validated, then clinical interest may lie in comparing the two ROC curves at that established cutoff so that comparison would also provide the best biomarker in terms of clinical classification.

In this paper, we focus on testing for equality between two correlated ROC curves at a particular t = FPR point. We consider smooth functions for the ROC curve. The paper is organized as follows: In Section 2, we explore the common assumption of normality, in which we assume two bivariate normal distributions that respectively refer to (W_1A, W_2A) and (W_1B, W_2B). We proceed to the construction of a statistic based on the delta method. In Section 3, we extend this delta-based methodology by exploring the Box-Cox transformation to normality, while the variability of the transformation-related parameters is also taken into account. In Section 4, we propose a technique based on a kernel bootstrap as a nonparametric approach. All our approaches are capable of accommodating covariates that might affect the accuracy of the biomarkers under study. In Section 5, we show how our methods can be extended to test the equality of two AUCs. In Section 6, we present a simulation study, showing that all our methods result in tests with satisfactory size and power. For that scenario, we consider comparisons with the most celebrated method, which is presented in [10]. In Section 7, we illustrate our methods on a real data set obtained from patients with prostate cancer and conclude with a discussion.

2. Assuming Bivariate Normality

Here we assume that [W_1AW_2A]′ follows a bivariate normal distribution with corresponding means μ_1A, μ_2A, corresponding variances ${\sigma }_{1A}^2$, ${\sigma }_{2A}^2$ and covariance cov_A. Similarly for [W_1BW_2B]′. Thus, the corresponding likelihood of the data is (see also [14] and [17]).

$$\begin{array}{cc}\hfill L(\mathbf{p})& =\prod _{i=1}^{n_A}\frac{1}{2\pi \sqrt{\mathit{det}({\Sigma }_A)}}\mathit{exp}\left(-\frac{1}{2}(W_{1Ai}-{\mu }_{1A},W_{2Ai}-{\mu }_{2A}){\Sigma }_A^{-1}{(W_{1Ai}-{\mu }_{1A},W_{2Ai}-{\mu }_{2A})}^{\prime }\right)\hfill \\ \hfill & \times \prod _{i=1}^{n_B}\frac{1}{2\pi \sqrt{\mathit{det}({\Sigma }_B)}}\mathit{exp}\left(-\frac{1}{2}(W_{1Bi}-{\mu }_{1B},W_{2Bi}-{\mu }_{2B}){\Sigma }_B^{-1}{(W_{1Bi}-{\mu }_{1B},W_{2Bi}-{\mu }_{2B})}^{\prime }\right)\hfill \end{array}$$ (1)

where p = (μ_1A, σ_1A, μ_2A, σ_2A, μ_1B, σ_1B, μ_2B, σ_2B, cov_A, cov_B) and Σ_A and Σ_B are the corresponding covariance matrices, namely ${\Sigma }_A=\left(\begin{array}{cc}\hfill {\sigma }_{1A}^2\hfill & \hfill {\mathit{cov}}_A\hfill \\ \hfill {\mathit{cov}}_A\hfill & \hfill {\sigma }_{2A}^2\hfill \end{array}\right)$, and ${\Sigma }_B=\left(\begin{array}{cc}\hfill {\sigma }_{1B}^2\hfill & \hfill {\mathit{cov}}_B\hfill \\ \hfill {\mathit{cov}}_B\hfill & \hfill {\sigma }_{2B}^2\hfill \end{array}\right)$.

Maximizing (1) yields the estimate $\widehat{\mathbf{p}}$. From the inverse of the observed Fisher’s information matrix I (which is presented in Web Appendix Part B), we obtain an estimate of the variance covariance matrix V, namely $\widehat{\mathbf{V}}$, of all the parameters in vector $\widehat{\mathbf{p}}$. The two underlying ROC curves under the normality assumptions can be written in closed form as

$${\mathit{ROC}}_1(t)=\Phi \left(\frac{{\mu }_{1B}-{\mu }_{1A}}{{\sigma }_{1B}}+\frac{{\sigma }_{1A}}{{\sigma }_{1B}}{\Phi }^{-1}(t)\right),$$

and similarly for ROC₂(t). Their corresponding estimates are obtained by plugging in the maximum likelihood estimates of the underlying parameters: $R\widehat{O}{C}_1(t)=\Phi \left(\frac{{\widehat{\mu }}_{1B}-{\widehat{\mu }}_{1A}}{{\widehat{\sigma }}_{1B}}+\frac{{\widehat{\sigma }}_{1A}}{{\widehat{\sigma }}_{1B}}{\Phi }^{-1}(t)\right)$. Approximations of their corresponding variances can be obtained on the basis of the delta method. All derivatives of the ROC₁(t) function with respect to its corresponding parameters are tractable in closed form (see Web Appendix B). Hence, based on the delta method we can approximate the variance of $R\widehat{O}{C}_1(t)$:

$$\mathit{Var}(R\widehat{O}{C}_1(t))\approx \left(\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\mu }_{1A}},\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\sigma }_{1A}},\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\mu }_{1B}},\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\sigma }_{1A}}\right){\widehat{\mathbf{V}}}_1{\left(\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\mu }_{1A}},\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\sigma }_{1A}},\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\mu }_{1B}},\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\sigma }_{1B}}\right)}^{\prime }$$ (2)

where ${\widehat{\mathbf{V}}}_1$ is the corresponding estimate of V₁, the covariance matrix of μ_1A, σ_1A, μ_1B, σ_1B, which can be extracted by $\widehat{\mathbf{V}}$. Similarly for $\mathit{Var}(R\widehat{O}{C}_2(t))$ where ${\widehat{\mathbf{V}}}_2$ is also extracted from $\widehat{\mathbf{V}}$ and is the estimated covariance matrix of parameters μ_2A, σ_2A, μ_2B, σ_2B. For their corresponding covariance, we obtain

$$\begin{array}{cc}\hfill \mathit{Cov}(R\widehat{O}{C}_1(t),R\widehat{O}{C}_2(t))\approx & \left(\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\mu }_{1A}},\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\sigma }_{1A}},0,0,\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\mu }_{1B}},\frac{\partial R\widehat{O}{C}_1(t)}{\partial {\sigma }_{1B}},0,0\right){\widehat{\mathbf{V}}}_{12}\hfill \\ \hfill & \times \left(0,0\frac{\partial R\widehat{O}{C}_2(t)}{\partial {\mu }_{2A}},\frac{\partial R\widehat{O}{C}_2(t)}{\partial {\sigma }_{2A}},0,0,\frac{\partial R\widehat{O}{C}_2(t)}{\partial {\mu }_{2B}},\frac{\partial R\widehat{O}{C}_2(t)}{\partial {\sigma }_{2B}}\right)\hfill \end{array}$$ (3)

where ${\widehat{\mathbf{V}}}_{12}$ is the 8 × 8 upper left part of $\widehat{\mathbf{V}}$. Based on the statistic

$$Z=\frac{R\widehat{O}{C}_1(t)-R\widehat{O}{C}_2(t)}{\sqrt{\mathit{Var}(R\widehat{O}{C}_1(t))+\mathit{Var}(R\widehat{O}{C}_2(t))-2\mathit{Cov}(R\widehat{O}{C}_1(t),R\widehat{O}{C}_2(t))}}\underset{~}{H_0}N(0,1),$$ (4)

we may proceed to inference. The simulation studies (see Tables 1 and 2) show overall good performance in terms of the size of this test. However, under the null hypothesis, for highly accurate biomarkers and for large values of the FPR, the size of this test declines, making the test conservative for high FPR regions. This is because the test (4) implies normality of the estimated curves $R\widehat{O}{C}_i(t),i=1,2$ without taking into account the fact that $0\le R\widehat{O}{C}_i(t)\le 1$, i = 1, 2. The same phenomenon appears to hold for the power of the test. An alternative version of the above statistic would involve the comparison of a transformation of ROC₁(t) and ROC₂(t) from [0, 1] to the real line. A convenient transformation under this framework that serves that purpose would be the inverse normal cdf Φ(·) since it would enhance the elegance of all derivatives of the ROC_i(t), i = 1, 2 function with respect to its location and scale parameters. For the required partial derivatives see Web Appendix B. Hence, one can proceed straightforwardly with the delta method since all covariance matrices that are to be extracted from the inverted information matrix remain unchanged under this transformation. We denote the proposed statistic with Z*:

$$Z^{\ast }=\frac{{\Phi }^{-1}(R\widehat{O}{C}_1(t))-{\Phi }^{-1}(R\widehat{O}{C}_2(t))}{\sqrt{\mathit{Var}({\Phi }^{-1}(R\widehat{O}{C}_1(t)))+\mathit{Var}({\Phi }^{-1}(R\widehat{O}{C}_2(t)))-2\mathit{Cov}({\Phi }^{-1}(R\widehat{O}{C}_1(t)),{\Phi }^{-1}(R\widehat{O}{C}_2(t)))}}\underset{\sim }{H_0}N(0,1).$$ (5)

Table 1.

Parameter values used in the simulation studies.

			Size-related scenarios
Distribution	ρ	AUC1 = AUC2	μ 1A	μ 2A	σ 1A	σ 2A	μ 1B	μ 2B	σ 1B	σ 2B
Normals	0.2, 0.4, 0.6	0.6	6.0000	6.0000	1.0000	1.0000	6.3584	6.3584	1.0000	1.0000
		0.7	6.0000	6.0000	1.0000	1.0000	6.7415	6.7415	1.0000	1.0000
		0.8	6.0000	6.0000	1.0000	1.0000	7.1900	7.1900	1.0000	1.0000
Log-Normals	0.2, 0.4, 0.6	0.6	0.0000	0.0000	0.5000	0.5000	0.1978	0.1978	0.6000	0.6000
		0.7	0.0000	0.0000	0.5000	0.5000	0.4096	0.4096	0.6000	0.6000
		0.8	0.0000	0.0000	0.5000	0.5000	0.6573	0.6573	0.6000	0.6000
			α 1A	α 2A	b 1A	b 2A	α 1B	α 2B	b 1B	b 2B
Gammas	0.2, 0.4, 0.6	0.6	3.0000	3.0000	4.0000	4.0000	3.6106	3.6105	4.0000	4.0000
		0.7	3.0000	3.0000	4.0000	4.0000	4.3365	4.3365	4.0000	4.0000
		0.8	3.0000	3.0000	4.0000	4.0000	5.2840	5.2840	4.0000	4.0000
			Power-related scenarios
		(AUC1, AUC2)	μ 1A	μ 2A	σ 1A	σ 2A	μ 1B	μ 2B	σ 1B	σ 2B
Normals	0.2, 0.4, 0.6	(0.6382, 0.8138)	6.0000	6.0000	1.0000	1.0000	6.5000	7.2000	1.0000	0.9000
Log-Normals	0.2, 0.4, 0.6	(0.6957, 0.8472)	0.0000	0.0000	0.5000	0.5000	0.4000	0.8000	0.6000	0.6000
			α 1A	α 2A	b 1A	b 2A	α 1B	α 2B	b 1B	b 2B
Gammas	0.2, 0.4, 0.6	(0.6548, 0.7790)	3.0000	3.0000	3.0000	3.0000	4.0000	3.5000	4.0000	3.5000

Table 2.

Prostate cancer results related to comparisons (one-tailed p-values) using the kernel-based approach (left) and the Box-Cox approach (right). Comparisons for scenario (1) are considered for FPR values of 0.05, 0.10 and 0.20. Comparisons for scenarios (2) and (3) are considered for TPRs=0.80, 0.85 and 0.95.

	Kernel-based				Box-Cox
Scenario (1)	TPRs:	0.80	0.85	0.95	TPRs:	0.80	0.85	0.95
	FPRs (PSA):	0.5895	0.6768	0.8648	FPRs (PSA):	0.6003	0.7072	0.9272
	FPRs (model):	0.4024	0.4749	0.6897	FPRs (model):	0.3697	0.4419	0.6687
	p-values:	< 0.0001	0.0003	0.0003	p-values:	< 0.0001	< 0.0001	< 0.0001
Scenario (2)	TPRs:	0.80	0.85	0.95	TPRs:	0.80	0.85	0.95
	FPRs (PSA):	0.5564	0.6422	0.8324	FPRs (PSA):	0.5513	0.6511	0.8846
	FPRs (model):	0.2836	0.3586	0.5993	FPRs (model):	0.2481	0.3173	0.5654
	p-values:	< 0.0001	< 0.0001	< 0.0001	p – values:	< 0.0001	< 0.0001	< 0.0001
Scenario (3)	FPRs:	0.05	0.10	0.20	FPRs:	0.05	0.10	0.20
	TPRs (PSA):	0.1446	0.2339	0.3930	TPRs (PSA):	0.1780	0.2797	0.4312
	TPRs (model):	0.3837	0.5141	0.6724	TPRs (model):	0.3951	0.5381	0.7031
	p-values:	< 0.0001	< 0.0001	< 0.0001	p-values:	< 0.0001	< 0.0001	< 0.0001

Scenario (1): Diseased defined by Gleason score ≥7. Healthy defined by Gleason score < 7.

Scenario (2): Diseased defined by Gleason score ≥7. Healthy defined by negative biopsy (Gleason score = 0).

Scenario (3): Diseased defined by Gleason score >0. Healthy defined by negative biopsy (Gleason score = 0).

2.1. Accommodating Covariates

Perhaps the accuracy of the biomarkers under study depends on some covariates that (partially) characterize the profile of a subject. Let p be the number of the available covariates as Z₁, Z₂, …, Z_p. Without loss of generality and to keep the notation simple, we consider that p covariates are available for all underlying groups. A common way to incorporate them under an ROC framework is to use the linear regression model. We consider that the covariates may have a different effect with respect to each of the two biomarkers. We consider linear regression models of the following form:

$$W_{1Ai}={\beta }_0^{(1A)}+\sum _{j=1}^p{\beta }_j^{(1A)}{Z}_{\mathit{ji}}^{(1A)}+{ϵ}_{1Ai}$$ (6)

where $Z_{\mathit{ji}}^{(1A)}$ is the value of the j–th covariate for the i–th healthy individual of the first marker (namely for (1A)), and the expressions and notation are analogous for the remaining three regression models. To incorporate the correlation of the two markers, we assume that Cov(ϵ_1Ai, ϵ_2Ai) ≠ 0, Cov(ϵ_1Bi, ϵ_2Bi) ≠ 0, Cov(ϵ_1Ai, ϵ_1Bi) = 0, Cov(ϵ_2Ai, ϵ_2Bi) = 0. Under the further assumptions of zero mean, homoscedasticity and pairwise bivariate normality for the error variances within each regression model (i.e., (1A), (2A), (1B) and (2B)), we have

$$\left(\begin{array}{c}\hfill W_{1A}\hfill \\ \hfill W_{2A}\hfill \end{array}\right)\sim N\left[\left(\begin{array}{c}\hfill {\beta }_0^{(1A)}+\sum _{j=1}^p{\beta }_j^{(1A)}{Z}_{\mathit{ji}}^{(1A)}\hfill \\ \hfill {\beta }_0^{(2A)}+\sum _{j=1}^p{\beta }_j^{(2A)}{Z}_{\mathit{ji}}^{(2A)}\hfill \end{array}\right),\left(\begin{array}{cc}\hfill {\sigma }_{1A}^2\hfill & \hfill {\mathit{cov}}_A\hfill \\ \hfill {\mathit{cov}}_A\hfill & \hfill {\sigma }_{2A}^2\hfill \end{array}\right)\right],$$

and for the joint density function of the data from the diseased individuals the expression is similar. The corresponding likelihood of the data is

$$\begin{array}{cc}\hfill L(\mathbf{p}z)=\prod _{i=1}^{n_A}\frac{1}{2\pi \sqrt{\mathit{det}({\Sigma }_A)}}\mathit{exp}& (-\frac{1}{2}\left(W_{1Ai}-{\beta }_0^{(1A)}-\sum _{j=1}^p{\beta }_j^{(1A)}{Z}_{\mathit{ji}}^{(1A)},W_{2Ai}-{\beta }_0^{(2A)}-\sum _{j=1}^p{\beta }_j^{(2A)}{Z}_{\mathit{ji}}^{(2A)}\right)\phantom{)}{\Sigma }_A^{-1}\hfill \\ \hfill & \phantom{(}{\left(W_{1Ai}-{\beta }_0^{(1A)}-\sum _{j=1}^p{\beta }_j^{(1A)}{Z}_{\mathit{ji}}^{(1A)},W_{2Ai}-{\beta }_0^{(2A)}-\sum _{j=1}^p{\beta }_j^{(2A)}{Z}_{\mathit{ji}}^{(2A)}\right)}^{\prime })\hfill \\ \hfill \times \prod _{i=1}^{n_B}\frac{1}{2\pi \sqrt{\mathit{det}({\Sigma }_B)}}\mathit{exp}& (-\frac{1}{2}\left(w_{1Bi}-{\beta }_0^{(1B)}-\sum _{j=1}^p{\beta }_j^{(1B)}{Z}_{\mathit{ji}}^{(1B)},W_{2Bi}-{\beta }_0^{(2B)}-\sum _{j=1}^p{\beta }_j^{(2B)}{Z}_{\mathit{ji}}^{(2B)}\right){\Sigma }_B^{-1}\phantom{)}\hfill \\ \hfill & \phantom{(}{\left(W_{1Bi}-{\beta }_0^{(1B)}-\sum _{j=1}^p{\beta }_j^{(1B)}{Z}_{\mathit{ji}}^{(1B)},W_{2Bi}-{\beta }_0^{(2B)}-\sum _{j=1}^p{\beta }_j^{(2B)}{Z}_{\mathit{ji}}^{(2B)}\right)}^{\prime })\hfill \end{array}$$ (7)

where p_Z = (β_A, σ_1A, σ_2A, cov_A, β_B, σ_1B, σ_2B, cov_B) with ${\beta }_A=({\beta }_0^{(1A)},{\beta }_1^{(1A)},\dots ,{\beta }_p^{(1A)},\dots ,{\beta }_p^{(2A)})$ and ${\beta }_B=({\beta }_0^{(1B)},{\beta }_1^{(1B)},\dots ,{\beta }_p^{(1B)},\dots ,{\beta }_p^{(2B)})$. Fisher’s information matrix in this setting is given by the block diagonal matrix I_Z = −diag{M_A, M_B} where M_A and M_B contain all second order partial derivatives that refer to vectors (β_A, σ_1A, σ_2A, cov_A) and (β_B, σ_1B, σ_2B, cov_B) respectively. The corresponding derivatives are presented in the Web Appendix (Part B). Similarly, one can derive M_B and hence, by inversion of I_Z, obtain an estimate of the corresponding covariance matrix V_Z, ${\widehat{V}}_Z$. The ROC curves under this setting are

$${\mathit{ROC}}_{k,Z}(t)=\Phi \left(\frac{({\beta }_0^{(1B)}+\sum _{j=1}^p{\beta }_j^{(1B)}{Z}_{\mathit{ji}}^{(1B)})-({\beta }_0^{(1A)}+\sum _{j=1}^p{\beta }_j^{(1A)}{Z}_{\mathit{ji}}^{(1A)})}{{\sigma }_{1B}}+\frac{{\sigma }_{1B}}{{\sigma }_{1A}}{\Phi }^{-1}(t)\right),k=1,2.$$ (8)

where with Z^(1A) and Z^(1B) we denote the given covariate profile for both the healthy and diseased individuals. For the corresponding partial derivatives see Web Appendix B. Approximations of their corresponding variances can be obtained on the basis of the delta method. Specifically, $\mathit{Var}({\Phi }^{-1}\left(R\widehat{O}{C}_{1,Z}(t))\right)$ can be approximated by

$$\begin{array}{cc}\hfill & \left(\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\beta }_0^{(1A)}},\dots ,\frac{{\Phi }^{-1}(\partial R\widehat{O}{C}_1(t))}{\partial {\beta }_p^{(2A)}},\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{1A}},\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{1B}}\right){\widehat{\mathbf{V}}}_{1_Z}\hfill \\ \hfill & \times {\left(\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\beta }_0^{(1A)}},\dots ,\frac{{\Phi }^{-1}(\partial R\widehat{O}{C}_1(t))}{\partial {\beta }_p^{(2A)}},\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{1A}},\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{1B}}\right)}^{\prime }\hfill \end{array}$$

where ${\widehat{\mathbf{V}}}_{1_Z}$ is the corresponding estimate of V_1Z, the variance covariance matrix of (β⁽¹⁾, β⁽²⁾, σ_1A, σ_1B), which can be extracted by ${\widehat{\mathbf{V}}}_Z$. The variance approximation is similar for ${\Phi }^{-1}\left(R\widehat{O}{C}_2(t)\right)$. The covariance $\mathit{Cov}({\Phi }^{-1}\left(R\widehat{O}{C}_{1,Z}(t)\right)$, ${\Phi }^{-1}\left(R\widehat{O}{C}_{2,Z}(t))\right)$ is approximated with a similar fashion by using ${\widehat{\mathbf{V}}}_{{12}_Z}$ which can be constructed on the basis of ${\widehat{\mathbf{V}}}_Z$. Based on the statistic Z*, we may proceed to inference:

$$Z^{\ast }=\frac{{\Phi }^{-1}(R\widehat{O}{C}_{1,Z}(t))-{\Phi }^{-1}(R\widehat{O}{C}_{2,Z}(t))}{\sqrt{\mathit{Var}({\Phi }^{-1}(R\widehat{O}{C}_{1,Z}(t)))+\mathit{Var}({\Phi }^{-1}(R\widehat{O}{C}_{2,Z}(t)))-2\mathit{Cov}({\Phi }^{-1}(R\widehat{O}{C}_{1,Z}(t)),{\Phi }^{-1}(R\widehat{O}{C}_{2,Z}(t)))}}\underset{\sim }{H_0}N(0,1)$$

The partial derivatives involved in the delta method, which are required for the construction of the Z test and Z* test, are given in the Web Appendix (Part B). One might assume that ${\beta }_j^{(1A)}={\beta }_j^{(1B)}$, ${\beta }_j^{(2A)}={\beta }_j^{(2B)}$, σ_1A = σ_1B, σ_2A = σ_2B if such assumptions are justified by the underlying clinical setting. The first two equality assumptions are implying that the covariates have the same effect for both the healthy and the diseased which is often realistic since one may argue that covariates are not to be considered directly as biomarkers themselves. Here we present the more general case for the shake of notation.

3. Box-Cox Transformation

When normality is not justified, it is common practice to use a monotone transformation that will lead to approximate normality. The Box-Cox transformation (see [18]) has been used when the available data do not conform to the binormal assumption (see [4]; [19]). For paired data designs and the corresponding likelihood see under the Box-Cox transformation see [14]. The Box-Cox transformation that would transform a random variable Y to the approximate normal Y^(λ) is defined by $\frac{Y^{\lambda }-1}{\lambda }$, if λ ≠ 0 and as log(Y), if λ = 0. The transformation parameters, λ₁ and λ₂, for each marker, will be estimated by the data and hence their variance must be taken into account. This issue is also addressed in [20] under a different framework. Note that the fact that the underlying densities are marginally transformed to approximate normality is not sufficient to ensure that the underlying bivariate distribution is a bivariate normal distribution. However, in order to take into account the underlying correlation within the healthy and diseased groups, we will assume bivariate normality after the Box-Cox transformation. Hence, we consider $W_{1A}^{({\lambda }_1)}$, $W_{2A}^{({\lambda }_2)}$, $W_{1B}^{({\lambda }_1)}$, $W_{2B}^{({\lambda }_2)}$ as the Box-Cox transformed marker measurements. In this case, the likelihood is of the following form:

$$\begin{array}{cc}\hfill L({\mathbf{p}}^{({\lambda }_{1,2})})& =\prod _{i=1}^{n_A}\frac{1}{2\pi \sqrt{\mathit{det}({\Sigma }_A^{({\lambda }_{1,2})})}}\mathit{exp}\left(-\frac{1}{2}\left(W_{1Ai}^{({\lambda }_1)}-{\mu }_{1A}^{({\lambda }_1)},W_{2Ai}^{({\lambda }_2)}-{\mu }_{2A}^{({\lambda }_2)}\right){\Sigma }_A^{{({\lambda }_{1,2})}^{-1}}{\left(W_{1Ai}^{({\lambda }_1)}-{\mu }_{1A}^{({\lambda }_1)},W_{2Ai}^{({\lambda }_2)}-{\mu }_{2A}^{({\lambda }_2)}\right)}^{\prime }\right)\hfill \\ \hfill & \times \prod _{i=1}^{n_B}\frac{1}{2\pi \sqrt{\mathit{det}({\Sigma }_B^{({\lambda }_{1,2})})}}\mathit{exp}\left(-\frac{1}{2}\left(W_{1Bi}^{({\lambda }_1)}-{\mu }_{1B}^{({\lambda }_1)},W_{2Bi}^{({\lambda }_2)}-{\mu }_{2B}^{({\lambda }_2)}\right){\Sigma }_B^{{({\lambda }_{1,2})}^{-1}}{\left(W_{1Bi}^{({\lambda }_1)}-{\mu }_{1B}^{({\lambda }_1)},W_{2Bi}^{({\lambda }_2)}-{\mu }_{2B}^{({\lambda }_2)}\right)}^{\prime }\right)\hfill \\ \hfill & \times \prod _{i=1}^{n_A}{W}_{1Ai}^{{\lambda }_1-1}\times \prod _{i=1}^{n_A}{W}_{2Ai}^{{\lambda }_2-1}\times \prod _{i=1}^{n_B}{W}_{1Bi}^{{\lambda }_1-1}\times \prod _{i=1}^{n_B}{W}_{2Bi}^{{\lambda }_2-1}\hfill \end{array}$$ (9)

where ${\Sigma }_A^{({\lambda }_{1,2})}=\left(\begin{array}{cc}\hfill {\sigma }_{1A}^{{({\lambda }_1)}^2}\hfill & \hfill {\mathit{cov}}_A^{({\lambda }_{1,2})}\hfill \\ \hfill {\mathit{cov}}_A^{({\lambda }_{1,2})}\hfill & \hfill {\sigma }_{2A}^{{({\lambda }_2)}^2}\hfill \end{array}\right)$, ${\Sigma }_B^{({\lambda }_{1,2})}=\left(\begin{array}{cc}\hfill {\sigma }_{1B}^{{({\lambda }_1)}^2}\hfill & \hfill {\mathit{cov}}_B^{({\lambda }_{1,2})}\hfill \\ \hfill {\mathit{cov}}_B^{({\lambda }_{1,2})}\hfill & \hfill {\sigma }_{2B}^{{({\lambda }_2)}^2}\hfill \end{array}\right)$ and the parameter vector of interest is ${\mathbf{p}}^{({\lambda }_{1,2})}=({\mu }_{1A}^{({\lambda }_1)},{\sigma }_{1A}^{({\lambda }_1)},{\mu }_{2A}^{({\lambda }_2)},{\sigma }_{2A}^{({\lambda }_2)},{\mu }_{1B}^{({\lambda }_1)},{\sigma }_{1B}^{({\lambda }_1)},{\mu }_{2B}^{({\lambda }_2)},{\sigma }_{2B}^{({\lambda }_2)},{\mathit{cov}}_B^{({\lambda }_{1,2})},{\mathit{cov}}_B^{({\lambda }_{1,2})},{\lambda }_1,{\lambda }_2)$.

By maximizing (9), we obtain ${\widehat{\mathbf{p}}}^{({\lambda }_{1,2})}$. By inverting the negative Hessian matrix, we derive an estimate of the covariance matrix of all 12 parameters, denoted as G. The information matrix in this case, denoted as I_(λ1,λ2), is a 12 × 12 matrix and is given in the Web Appendix (Part B). By calculating I_(λ1,λ2) at the maximum likelihood estimates of all parameters followed by inversion, we obtain an estimate of the corresponding covariance matrix, denoted as $\widehat{\mathbf{G}}$. We then obtain the corresponding variances and covariance for the two transformed ROC curves:

$$\begin{array}{cc}\hfill \mathit{Var}({\Phi }^{-1}(R\widehat{O}{C}_1(t)))& \approx \left(\frac{{\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\mu }_{1A}^{({\lambda }_1)}},\frac{{\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{1A}^{({\lambda }_1)}},\frac{{\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\mu }_{1B}^{({\lambda }_1)}},\frac{{\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{1A}^{({\lambda }_1)}}\right){\widehat{\mathbf{G}}}_1^{({\lambda }_1)}\hfill \\ \hfill & \times {\left(\frac{{\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\mu }_{1A}^{({\lambda }_1)}},\frac{{\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{1A}^{({\lambda }_1)}},\frac{{\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\mu }_{1B}^{({\lambda }_1)}},\frac{{\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{1A}^{({\lambda }_1)}}\right)}^{\prime }\hfill \end{array}$$ (10)

where ${\widehat{\mathbf{G}}}_1^{({\lambda }_1)}$ is the corresponding estimate of ${\mathbf{G}}_1^{({\lambda }_1)}$, the variance covariance matrix of ${\mu }_{1A}^{({\lambda }_1)}$, ${\sigma }_{1A}^{({\lambda }_1)}$, ${\mu }_{1B}^{({\lambda }_1)}$, ${\sigma }_{1B}^{({\lambda }_1)}$, which can be extracted by $\widehat{\mathbf{G}}$. Similarly for $\mathit{Var}({\Phi }^{-1}(R\widehat{O}{C}_2(t)))$ where ${\widehat{\mathbf{G}}}_2^{({\lambda }_2)}$ is also extracted from $\widehat{\mathbf{G}}$. The covariance $\mathit{Cov}({\Phi }^{-1}(R\widehat{O}{C}_1(t)),{\Phi }^{-1}(R\widehat{O}{C}_2(t)))$, can be approximated by

$$\begin{array}{cc}\hfill \mathit{Cov}({\Phi }^{-1}(R\widehat{O}{C}_1(t)),{\Phi }^{-1}(R\widehat{O}{C}_2(t)))& \approx \left(\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\mu }_{1A}^{({\lambda }_1)}},\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{1A}^{({\lambda }_1)}},0,0,\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\mu }_{1B}^{({\lambda }_1)}},\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{1B}^{({\lambda }_1)}},0,0\right){\widehat{\mathbf{G}}}_{12}\hfill \\ \hfill & \times \left(0,0,\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_2(t))}{\partial {\mu }_{2A}^{({\lambda }_2)}},\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_1(t))}{\partial {\sigma }_{2A}^{({\lambda }_1)}},0,0,\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_2(t))}{\partial {\mu }_{2B}^{({\lambda }_1)}},\frac{\partial {\Phi }^{-1}(R\widehat{O}{C}_2(t))}{\partial {\sigma }_{2B}^{({\lambda }_1)}}\right)\hfill \end{array}$$ (11)

where ${\widehat{\mathbf{G}}}_{12}$ is the 8 × 8 upper left part of $\widehat{\mathbf{G}}$. The variability of the transformation parameters has been taken into account at this stage and, based on statistic Z or the proposed statistic Z*, we can proceed to inference.

3.1. Accommodating Covariates

Consider models (6). A more robust approach is to assume that instead of direct normality for the response, normality is achieved by the Box-Cox transformation. The likelihood of the data in this case is of the following form:

$$\begin{array}{cc}\hfill L({\mathbf{p}}_Z^{({\lambda }_{1,2})})& =\prod _{i=1}^{n_A}\frac{1}{2\pi \sqrt{\mathit{det}({\Sigma }_A^{({\lambda }_{1,2})})}}\mathit{exp}\left(-\frac{1}{2}\left(W_{1Ai}^{({\lambda }_1)}-{\mu }_{1Ai}^{({\lambda }_1)},W_{2Ai}^{({\lambda }_2)}-{\mu }_{2Ai}^{({\lambda }_2)}\right){\Sigma }_A^{{({\lambda }_{1,2})}^{-1}}{\left(W_{1Ai}^{({\lambda }_1)}-{\mu }_{1Ai}^{({\lambda }_1)},W_{2Ai}^{({\lambda }_2)}-{\mu }_{2Ai}^{({\lambda }_2)}\right)}^{\prime }\right)\hfill \\ \hfill & \times \prod _{i=1}^{n_B}\frac{1}{2\pi \sqrt{\mathit{det}({\Sigma }_B^{({\lambda }_{1,2})})}}\mathit{exp}\left(-\frac{1}{2}\left(W_{1Bi}^{({\lambda }_1)}-{\mu }_{1Bi}^{({\lambda }_1)},W_{2Bi}^{({\lambda }_2)}-{\mu }_{2Bi}^{({\lambda }_2)}\right){\Sigma }_B^{{({\lambda }_{1,2})}^{-1}}{\left(W_{1Bi}^{({\lambda }_1)}-{\mu }_{1Bi}^{({\lambda }_1)},W_{2Bi}^{({\lambda }_2)}-{\mu }_{2Bi}^{({\lambda }_2)}\right)}^{\prime }\right)\hfill \\ \hfill & \times \prod _{i=1}^{n_A}{W}_{1Ai}^{{\lambda }_1-1}\times \prod _{i=1}^{n_A}{W}_{2Ai}^{{\lambda }_2-1}\times \prod _{i=1}^{n_B}{W}_{1Bi}^{{\lambda }_1-1}\times \prod _{i=1}^{n_B}{W}_{2Bi}^{{\lambda }_2-1}\hfill \end{array}$$ (12)

where ${\mu }_{1Ai}^{({\lambda }_1)}={\beta }_0^{(1A)}+{\sum }_{j=1}^p{\beta }_1^{(1A)}{Z}_{\mathit{ji}}$ and similarly for ${\mu }_{2Ai}^{({\lambda }_2)}$, ${\mu }_{1Bi}^{({\lambda }_1)}$, ${\mu }_{2Bi}^{({\lambda }_2)}$. By maximizing (12), we obtain an estimate of ${\mathbf{p}}_Z^{({\lambda }_{1,2})}$, ${\widehat{\mathbf{p}}}_Z^{({\lambda }_{1,2})}$. Obtaining and inverting the corresponding Fisher’s information matrix (see the Web Appendix B for its derivation) allows us to proceed to the delta method. The partial derivatives of ROC₁(t) and ROC₂(t) with respect to all regression coefficients and corresponding variances are presented in the Web Appendix (Part B).

4. Kernel-based Approach

In scenarios in which the Box-Cox transformation is not sufficient, a nonparametric approach is preferable. We explore a kernel-based approach. We consider two bivariate kernel density estimates, one for W_A and one for W_B. The simplest bivariate or multivariate kernel estimator is obtained through the product kernel form, also known as the multiplicative kernel. This form has the appealing property that marginally the densities have the same form as in the univariate setting, which reduces the computational burden of the numerical integration. Kernel based ROC curves have also been discussed in [21]. For an overview of kernel density estimation and multivariate kernel estimators, see [22–24]. Using the bivariate kernel product, the bivariate kernel density for the data from the healthy individuals is of the following form:

$${\widehat{f}}_A(w_{1A},w_{2A})=\frac{1}{n_A{h}_{1A}{h}_{2A}}\sum _{i=1}^{n_A}K\left(\frac{w_{1A}-W_{1Aj}}{h_{1A}}\right)K\left(\frac{w_{2A}-W_{2Aj}}{h_{2A}}\right),$$ (13)

and the expression similar for the data from the diseased individuals, where $K(t)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{t^2}{2}}$, h_1A and h_2A are bandwidths for the healthy individuals and h_1B and h_2B are the bandwidths for the diseased individuals. Scott [22] presented bandwidths that are optimal in terms of the asymptotic integrated mean squared error (AMISE) when normal kernels are employed. Here, we explore the use of normal kernels and such bandwidths that are of the form $h_{1A}=\mathit{std}(W_{1A}){(1-\mathit{Corr}{(W_{1A},W_{2A})}^2)}^{5∕12}{(1+\mathit{Corr}{(W_{1A},W_{2A})}^2∕2)}^{-1∕6}{n}_A^{-1∕6}$, where std(W_1A), std(W_2A), and ρ_A refer to the standard deviations, and correlation of the corresponding samples and their estimates can be directly plugged in to obtain the corresponding estimated bandwidths. The expressions for h_1B, h_1B, h_2B are similar. Based on (13), we can derive the marginal distributions and hence the two correlated kernel-based estimates $R\widehat{O}{C}_1(t)$ and $R\widehat{O}{C}_2(t):R\widehat{O}{C}_k(t)={\widehat{S}}_{W_{kB}}\left({\widehat{S}}_{W_{kA}}^{-1}(t)\right)$, k = 1, 2, where $S_W(x)={\int }_x^{\infty }{f}_W(t)\mathit{dt}$ is the survival function related to a random variable W. By performing the bootstrap in which the kernels are refitted for each bootstrap sample (sampled in pairs), we can obtain the needed estimates of $\mathit{Var}(R\widehat{O}{C}_1(t))$, $\mathit{Var}(R\widehat{O}{C}_2(t))$, $\mathit{Cov}(R\widehat{O}{C}_1(t),R\widehat{O}{C}_2(t))$ and proceed to inference using the statistic Z*, as stated in the previous sections. Performing the bootstrap takes into account both the correlation within the healthy and diseased individuals as well as the variability of the bandwidths. The proposed approach is summarized by the following algorithm:

• Step 1: Sample with replacement n_A pairs of (W_1Ai,W_2Ai), i = 1, 2, … , n_A and n_B pairs of (W_1Bj,W_2Bj) j = 1, 2, … , n_B and obtain the bootstrap-based data set: $(W_{1A}^{(b)},W_{2A}^{(b)})$ and $(W_{1B}^{(b)},W_{2B}^{(b)})$.

• Step 2: Based on $(W_{1A}^{(b)},W_{2A}^{(b)})$ and $(W_{1B}^{(b)},W_{2B}^{(b)})$, estimate the corresponding kernel survival functions and obtain the transformed kernel-based ROC estimates: ${\Phi }^{-1}\left(R\widehat{O}{C}_k^{(b)}(t)\right)={\Phi }^{-1}\left({\widehat{S}}_{W_{kB}}^{(b)}\left({\widehat{S}}_{W_{kA}}^{-1(b)}(t)\right)\right)$, k = 1, 2.

• Step 3: Repeat Steps 1-2 m times and based on these m bootstrap estimates of Φ⁻¹(ROC_k(t)), obtain $\widehat{V}ar({\Phi }^{-1}(R\widehat{O}{C}_1(t)))$, $\widehat{V}ar({\Phi }^{-1}(R\widehat{O}{C}_2(t)))$, $\widehat{C}ov({\Phi }^{-1}(R\widehat{O}{C}_1(t),R\widehat{O}{C}_1(t)))$. and proceed to inference based on Z*.

4.1. Accommodating Covariates

We consider two multivariate normal kernel densities:

$$\begin{array}{cc}\hfill \widehat{f}(w_{1A},w_{2A},Z_1,Z_2,\dots ,Z_p)& =\frac{1}{n_A{h}_{1A}{h}_{2A}{h}_{Z_1}{h}_{Z_2}\times \dots \times h_{Z_p}}\hfill \\ \hfill & \times \sum _{i=1}^{n_A}K\left(\frac{w_{1A}-W_{1Ai}}{h_{1A}}\right)K\left(\frac{w_{2A}-W_{2Ai}}{h_{2A}}\right)K\left(\frac{z_1-Z_{1i}}{h_{Z_1}}\right)\times \cdots \times K\left(\frac{z_p-Z_{\mathit{pi}}}{h_{Z_p}}\right)\hfill \end{array}$$ (14)

and similarly for $\widehat{f}(w_{1B},w_{2B},Z_1,Z_2,\dots ,Z_p)$, where K(·) refers to the normal kernel and the bandwidth related to the healthy group (A) of the first marker is $h_{1A}=\mathit{std}(W_{1A}){(1-\mathit{Corr}{(W_{1A},W_{2A})}^2)}^{5∕12}{(1+\mathit{Corr}{(W_{1A},W_{2A})}^2∕2)}^{-1∕6}{n}_A^{-1∕6}$. Similarly for h_2A, h_1B, h_2B. For the bandwidths of the covariates one could assume simple plug in bandwidths of the form $h_X=0.9\times \mathit{min}(\mathit{std}(X),\mathit{IQR}∕1.34)\times n_X^{-0.2}$ since the correlation is taken into account by the product of the kernels. However, more sophisticated bandwidth techniques could be employed that involve bandwidth matrices (see [23, 24] among others). By appropriate integration one can derive kernel based estimates of the conditional densities of the scores given the covariates fW_ij|Z₁,Z₂,…,Z_p where i = 1, 2 and j = A,B. The construction of the underlying kernel based ROC estimate is then straightforward. The proposed bootstrap based approach in this setting involves resampling with replacement and deriving the necessary conditional density estimates. Based on these densities we can construct the corresponding ROC curves for each bootstrap sample. We repeat m times, and based on these m bootstrap ROC estimates, we can calculate the necessary variances and covariances involved in statistic Z*. A further advantage of this non-parametric technique is that the assumption of an underlying linear model is relaxed.

5. Comparing Areas under the ROC Curve

In the previous section, we focused on comparing two correlated ROC curves at a specific FPR. Even though the AUC suffers from the drawbacks stated in the Introduction, its use is celebrated. Our methods can be straightforwardly expanded for AUC comparison. Under the assumption that the measurements of the healthy and diseased individuals follow two bivariate normal distributions, the AUC for the first biomarker can be written in closed form (see also [3], for an overview regarding the AUC estimation): ${\mathit{AUC}}_1=\Phi \left(\frac{({\mu }_{1B}-{\mu }_{1A})∕{\sigma }_{1B}}{\sqrt{1+{({\sigma }_{1A}∕{\sigma }_{1B})}^2}}\right)$, and similarly for biomarker 2. The transformation Φ(·) convenient in terms of ROC(t) since it will reduce all partial derivatives to simpler expressions. In addition, it circumvents the fact that inference of AUC is based on approximate normality (and hence the underlying implied support lies on the real line) of the corresponding estimate $A\widehat{U}C$. By definition, 0 < AUC < 1 (even though clinically we can assume that 0.5 < AUC < 1) and hence a transformation to the real line might be useful, especially in settings where we are dealing with biomarkers for which there is a threshold that corresponds to a sensitivity or specificity near 1. In this setting, the partial derivatives involved in the delta method are persented in Web Appendix B.

One can proceed straightforwardly to the delta method by using the variance matrix V₁ that refers to all the parameters involved. The corresponding partial derivatives for AUC₂ are analogous, and one can proceed to the delta method for the approximation of $\mathit{Var}(A\widehat{U}{C}_2)$ by using the variance matrix V₂. The covariance $\mathit{Cov}(A\widehat{U}{C}_1,A\widehat{U}{C}_2)$ can be approximated by the delta method using V₁₂. The assumption of normality in terms of the AUC has been used before ( [14]). In their case, the corresponding test statistic was constructed directly in terms of the AUC. They also investigated the use of the Box-Cox transformation and presented a large simulation study that indicated that the Box-Cox approach is preferred over the standard empirical-based method presented in [10]. The Box-Cox approach in our context will be constructed in an analogous way, as presented in Section 3. We also take into account the variability of the transformation parameters. An alternative approach might involve considering the transformation parameters as fixed, as indicated in [14]. The Box-Cox approach, although robust, may not be appropriate when multimodal densities are involved in the cases and/or controls. When normality (or bivariate normality) is not justified after the transformation, then a nonparametric approach would be preferable. Our kernel-based approach can be straightforwardly extended in terms of the AUC by replacing $R\widehat{O}{C}_k(t)$ with $A\widehat{U}{C}_k(t)$ throughout the algorithm presented in Section 4, by using the following statistic.

$$Z^{\ast }=\frac{{\Phi }^{-1}(A\widehat{U}{C}_1)-{\Phi }^{-1}(A\widehat{U}{C}_2)}{\sqrt{\mathit{Var}({\Phi }^{-1}(A\widehat{U}{C}_1))+\mathit{Var}({\Phi }^{-1}(A\widehat{U}{C}_2))-2\mathit{Cov}({\Phi }^{-1}(A\widehat{U}{C}_1),{\Phi }^{-1}(A\widehat{U}{C}_2))}}\underset{\sim }{H_0}N(0,1)$$

In cases where covariates are present, the proposed approach in terms of the AUC is analogous to the one presented in Section 4.1 and is obtained by substituting ROC_k,Z(t) with the AUC for a specific covariate profile, AUC_k,Z(t) throughout. The necessary partial derivatives are presented in Web Appendix B. The involved covariance matrices remain the same as in the settings in which comparisons in terms of ROC(t) were explored. The proposed kernel-based approach in terms of the AUC is completely analogous to that described in the previous section. Note that when covariates are present, the expression ROC(t)_k,Z, k = 1, 2 is replaced by AUC_k,Z, k = 1, 2 throughout.

6. Simulation Studies

Here, we evaluate our approaches through a simulation study in terms of size and power. All the parameter values we considered for every scenario (data generated from bivariate normals, gammas, and lognormals) are presented in Table 1. For the simulations related to statistical power, we considered points on the ROC curves such that theoretical differences of ROC₂(t) – ROC₁(t) = 0.05, 0.10, 0.15, and 0.20 are obtained. All simulation results are presented in the Web Appendix (Part A).

We first explore the known maximum likelihood approach. The results are presented in Table 1 of the Web Appendix (Part A). In terms of the size, we compare both tests presented in this study, namely Z and Z*. We observe that in most settings, both tests provide a size close to the nominal level. An essential difference in the performance of the two tests arises for higher t values, as expected. We observe that the Z test has unacceptably low values of size. This is somewhat corrected as the sample size increases, but even for sample sizes of (200,200) we observe a size equal to 0.032 (in the setting of ρ = 0.6, and AUC₁ = AUC₂ = 0.8), while for the same scenario, when the sample sizes are equal to (100, 100) the corresponding size equals 0.01. We note that this problem appears to be more vivid as t and/or as the AUC increases. This is expected since the more accurate the marker, the closer is the ROC curve to the TPR = 1 line, and normality of the $R\widehat{O}{C}_k$, k = 1, 2 might not be justified due to the bound. The merit of using the Φ⁻¹(·) is clear based on the results shown in Tables 1 and 2 in the Web Appendix (Part A). Z* provides a value close to the nominal level of size in all cases. It is also robust in settings of larger t values, as well as for large AUC values for all sample sizes. We note that, for example, in the setting of ρ = 0.6, AUC₁ = AUC₂ = 0.8, (n_A, n_B) = 100, 100 its size equals 0.0450. In Web Appendix (Part A) Table 2, we present the corresponding simulation results for the power of the tests. We observe that the Z test is outperformed by the Z* test in all scenarios in which the two tests do not yield the same power. For large sample sizes (200,200), both tests achieve a power equal to one and generally exhibit the same performance. For smaller sample sizes, the differences in terms of power are impressive. For example, for sample sizes of (50,50), correlation ρ = 0.6 and d = ROC₂(t) – ROC₁(t) = 0.05, the Z test achieves a power equal to 0.245; whereas the Z* test achieves a power of 0.839. We observe in all scenarios that power increases as correlation increases, as expected.

For the Box-Cox approach, we consider data generated from both normal and non-normal distributions. We first discuss the former. We observe that in terms of size, the Z* test based on the Box-Cox approach yields size results close to the nominal level in all settings, in contrast to the Z test based on the same approach (Web Appendix A, Table 3). As in the setting in which the likelihood-based tests were used, we observe the same pattern. The Z test fails to provide reasonable size values for higher t values and/or higher AUC values for the reason stated before. This is remedied by the Z* test. The results are also analogous in terms of power (Web Appendix A, Table 4). As an example, we mention that for (n_A, n_B) = (50, 50) and d = 0.05, the Z test yields power no larger than 0.223; whereas the power achieved by the Z* test reaches up to 0.696. For large sample sizes, both tests exhibit power > 0.990 in all scenarios. For this setting (i.e., when data are generated from multivariate normal distributions), we also consider the bootstrap approach under the empirical estimate. These results are not presented for brevity. We mention one observation: for such a technique and true correlation set to 0.8, FPR set to 0.8, AUC₁ = AUC₂ = 0.8, and sample sizes (100, 100), (200, 200), (100, 200), we obtain size values of 0.0150, 0.0200, and 0.0200, respectively, which indicates inferior performance compared to the Box-Cox approach.

To evaluate the robustness of the Box-Cox approach, we consider generating data from two bivariate gamma distributions (see [26]) as well as two bivariate lognormal distributions. The simulation results for these scenarios are presented in Web Appendix A, Table 4. We examine the performance of only the Z* test for reasons stated before. We observe that the Z* test provides size values close to the nominal level in all scenarios and results are better for larger sample sizes, as expected. We note that in some settings, the results appear to be somewhat more conservative for data generated under the gamma distribution compared to the lognormal distribution. This might be true since the lognormal distribution lies in the Box-Cox family whereas the gamma distribution does not. In terms of power, we obtain satisfactory results that reach levels of approximately 1 for larger sample sizes and higher correlation values (Web Appendix A, Table 5). Smaller values are achieved for smaller sample sizes and small values of correlation, especially for d = 0.05, as expected. The simulation results are essentially better with respect to power in almost all settings when the data are generated with bivariate lognormal distributions compared to gamma distributions.

For the kernel-based Z* test, we consider the same scenarios. In terms of size, we obtain satisfactory results in almost all settings, and in terms of power, we see reduced levels compared to those of the Box-Cox approach, as expected (Web Appendix A, Table 6). This is the price to pay for not making any parametric assumptions. Nevertheless, we observe that the kernel-based Z* test achieves high power values for larger sample sizes, and even for small values of d.

We also explore the extension of our approaches for testing the hypothesis AUC₁ = AUC₂ against the alternative hypothesis AUC₁ ≠ AUC₂. We consider exploring the Box-Cox and kernel-based Z* tests along with the commonly used approach presented in [10]. In terms of size, we observe results close to the nominal level in all scenarios (Web Appendix A, Table 7). In terms of power, we observe that the Box-Cox approach yields better results compared to those achieved by DeLong’s method in almost all scenarios, although the differences are not remarkable (Web Appendix A, Table 8). In terms of power, the results from comparing the kernel-based approach to DeLong’s method are somewhat inconclusive, yielding only minor differences between the two methods in almost all scenarios.

In summary, based on our simulations the use of the statistic Z* is generally to be preferred over Z. For high FPR and TPR values the use of statistic Z* performs essentially better in terms of both coverage and power when comparing two correlated ROC curves. Both the Box-Cox and the kernel based approach provide coverage close to the nominal level. The Box-Cox approach provides higher power compared to the kernel approach when the underlying model lies in the Box-Cox family, as expected. The Box-Cox approach seems to be robust from deviations to the underlying family, when for example the gamma distribution is the true underlying model, and still outperforms the kernel based approach in terms of power. This is the price one has to pay for not making any distributional assumptions when using the kernel based technique. However, it can be argued that the kernel based approach is a safe alternative when the Box-Cox transformation cannot be justified by the given data. In addition to the previously discussed simulations we also considered comparisons with the non-parametric bootstrap based methods BTI and BTII presented in [27]. The results of the simulations that refer to the size and power for all normal and gamma related scenarios previously considered, are presented in Web Appendix C (Tables 9-11). We observe that both the Box-Cox and and the kernel based approach outperform the BTII in terms of size in almost all cases. When compared to the BTI method we observe approximately similar results in terms of size, however the performance of BTI is outperformed when we focus on high FPR values and this is due to the transformation Φ⁻¹(·) which is crucial for that region as we have previously stated. In terms of power, both the Box-Cox based approach and the kernel based approach outperform BTI and BTII in all cases.

7. Application

We explore our approaches using the data from a prospective multicenter study. The study was designed to evaluate RNA assays for T2: ERG fusion and PCA3 for prostate cancer diagnosis. The clinical study was conducted from 2009 to 2011 at 11 U.S. centers. An objective was to examine whether the combination of biomarkers would improve specificity for the detection of aggressive prostate cancer (Gleason score > 7) (personal communication with Drs. John Wei and Scott Tomlins, University of Michigan). The study population was 859 men who had undergone a prostate biopsy for possible diagnosis of prostate cancer. In this context, we focus on a subgroup of participants who presented for their initial biopsy and for whom the scores of T2:ERG, PCA3, and PSA are available (n=561). For the cases and the controls, we considered three scenarios: (1) The diseased men are those who had Gleason scores ≥ 7 (n_B = 148), and the healthy controls are defined by Gleason scores < 7 (n_A = 413). (2) The diseased men are those who had Gleason scores ≥ 7 (n_B = 148), and the controls (n_A = 297) are those who had a negative biopsy (Gleason score =0). (3) The diseased men are those who had a positive biopsy (Gleason score >0) (n_B = 264), and the controls (n_A = 297) are those who had a negative biopsy (Gleason score =0).

The following logistic regression model was developed (personal communication with Dr. Scott Tomlins, University of Michigan) in order to combine all three available biomarkers: logit(p) = −5.8588 + 0.59038log₂(1 + PSA) + 0.55316log₂(1 + PCA3) + 0.14371log₂(T2 : ERG). The scores generated by the aforementioned model can be considered as a new score (marker) that combines the information from all three available scores. We are only applying a developed model that was obtained by a different data set (personal communication with Drs. John Wei and Scott Tomlins, University of Michigan) and consider its coefficients fixed and known to evaluate its performance in different subgroups of the study we explore. As pointed out by a referee, in case the coefficients were not considered fixed and known, then there is an extra source of variation that needs to be taken into account that refers to the estimated coefficients, but this problem is beyond the scope of this paper. A critical objective of the study we explore, was to validate the performance of the combined biomarkers, with the aim of reducing unnecessary prostate biopsy and overdetection of potential cancer that may result from relying on PSA concentrations alone. We examine scenarios (1) and (2) at thresholds that correspond to high sensitivity values, namely 0.80, 0.90, and 0.95. The rationale for using high sensitivity is that the diseased group for these two scenarios have aggressive prostate cancer; therefore, it is crucial to identify them so that they can quickly begin treatment. For scenario (3), it is of interest to focus on low FPRs. The rationale for this focus is that the diseased group in this scenario has an indolent form of prostate cancer, so the aim is to avoid overtreatment. The nominal level used throughout this application is α = 0.05.

Note that for scenario (2), all individuals that have a Gleason score = 6 are removed from the analysis. Apart from the analysis presented in Table 2, for this scenario, we report the positivity of the analysis on the basis of the cutoff/threshold that corresponds to a sensitivity of 0.95. Using the kernel-based approach, the positivity equals 0.8899 and 0.8989 for the PSA and the combined marker, respectively. The corresponding values under the Box-Cox approach are 0.9933 and 0.9618.

For the kernel-based approach, we first test for equality in terms of the AUC. The corresponding empirical-based and kernel-based ROC curves are presented in Figure 1. The kernel-based estimates for AUC_PSA and AUC_C are 0.6962 (SE=0.0227) and 0.7789 (SE=0.0196), respectively. The p-value we obtain based on our kernel-based methodology equals 5.8740 × 10⁻⁴; whereas DeLong’s approach yields p-value = 0.0048. Thus, both methods indicate a significant difference in favor of the combined marker in terms of the overall discriminatory capability of the markers.

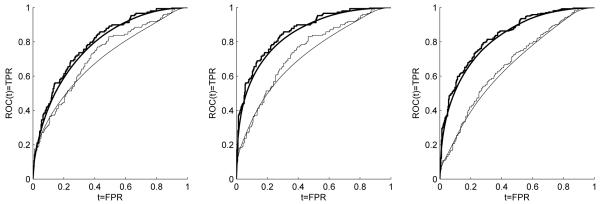
Figure 1.

Empirical-based and kernel-based ROC estimates for PSA alone (thin line) and the combined biomarker values (thick line). Left to right (i.e., scenarios (1) to (3)) for the empirical-based estimates: (AUC_PSA = 0.7185, AUC_C = 0.7933), (AUC_PSA = 0.7347, AUC_C = 0.8620), (AUC_PSA = 0.6682, AUC_C = 0.8342). Left to right (i.e., scenarios (1) to (3)) for the kernel-based estimates: (AUC_PSA = 0.6962, AUC_C = 0.7789), (AUC_PSA = 0.7096, AUC_C = 0.8456), (AUC_PSA = 0.6537, AUC_C = 0.8203).

In terms of the ROC curve, we explore comparisons at FPR = 0.05, 0.10, and 0.20 for scenario (3) for the reason explained above. The corresponding p-values obtained are all < 0.0001. This is also visually justified by the corresponding graph, which shows that for small FPR values, the two ROC curves exhibit essential differences. For scenarios (1) and (2), we compare the biomarkers in terms of fixed TPRs of 0.80, 0.85 and 0.95. For the kernel-smoothed ROC estimates (scenario (1)), we derive $R\widehat{O}{C}_{\mathit{PSA}}(0.8648)=R\widehat{O}{C}_{\mathit{PSA}}(\mathit{spec}=0.1351)=0.95$, and for the combined biomarker we have $R\widehat{O}{C}_C(0.6897)=R\widehat{O}{C}_C(\mathit{spec}=0.3103)=0.95$. For the values of sensitivity 0.80 and 0.90, see Table 2. We are interested in testing for the equality of $F\widehat{P}{R}_{\mathit{PSA}}(\mathit{TPR}=0.95)=F\widehat{P}{R}_C(\mathit{TPR}=0.95)$. This in turn can be written as $R\widehat{O}{C}_{\mathit{PSA}}^{-1}(0.95)=R\widehat{O}{C}_C^{-1}(0.95)$, and the corresponding test statistic we use is

$$Z_{{\mathit{ROC}}^{-1}}^{\ast }=\frac{{\Phi }^{-1}(R\widehat{O}{C}_C^{-1}(t))-{\Phi }^{-1}(R\widehat{O}{C}_{\mathit{PSA}}^{-1}(t))}{\sqrt{\mathit{Var}({\Phi }^{-1}(R\widehat{O}{C}_C^{-1}(t))-({\Phi }^{-1}(R\widehat{O}{C}_{\mathit{PSA}}^{-1}(t)))}}\underset{\sim }{H_0}N(0,1).$$

Using the kernel-based approach, we obtain a p-value < 0.0001, which indicates that the combined biomarker exhibits significantly greater specificity compared to using the PSA alone, at TPR = 0.95. This is also true when sensitivity is fixed at 0.80 or 0.85. The conclusions for scenario (2) are similar, since all p-values < 0.0001.

Since the data are not normally distributed (Shapiro-Wilk test rejects normality in all cases), we also explore the Box-Cox approach in order to validate our findings obtained by the kernel-based method. After applying the Box-Cox transformation, we re-perform the Shapiro Wilk test and determine that normality is rejected for the transformed samples except for the combined biomarker measurement among the healthy group in both scenario (2) and scenario (3). Hence, there is indication that even after the Box-Cox transformation, the normality assumption is not justified by the data. Possible ways to check normality are the Kolmogorov Smirnov (KS) test, in which however one has to set the mean and variance of the underlying normal, the Lilliefors test, which is equivalent to KS and can accommodate estimated parameters. The Shapiro Wilk test for which the parameters are left unspecified has greater power and is considered as a better alternative. We recommend the use of the kernel based approach when marginal normality is not achieved by the transformed scores. Here we also proceed to the Box-Cox based the analysis for illustration purposes. Using the Box-Cox transformation, the AUC estimates for the combined biomarker and the PSA alone are equal to 0.7946 and 0.7118, respectively, which again indicates the overall superiority of the combined biomarker over the PSA. In terms of comparing the two underlying AUCs, the Box-Cox approach yields a p-value equal to 2.9732 × 10⁻⁴. In terms of comparing the two ROC curves, we investigate comparisons similar to those considered for the kernel-based approach. The results are presented in Table 2. For comparisons involving scenario (1) and scenario (2), we observe statistically significant differences (for fixed TPRs). This is in line with what we observe in the kernel-based analysis. For scenario (3), we observe that for FPRs of 0.05 and 0.10, the difference in terms of TPR = ROC(t) is not statistically significant, and this is also visualized by the corresponding graph (see Figure 1 in the Web Appendix B). In scenario (2) we observe differences between the Box-Cox analysis and the kernel based one. We can rely on the kernel based analysis since as stated the marginal normality of the transformed scores is rejected.

8. Discussion

Medical decision making should employ statistical methods to properly compare the performance of two competing tests or biomarkers at specific false positive and true positive rates that are set by clinicians with the appropriate expertise. Such situations are of great importance when designing a biomarker study. These issues are addressed in detail in [25] who set the guidelines for the appropriate design of a biomarker study and stress that this is a crucial issue. A biomarker that results in overdiagnosis or underdiagnosis might have a severe impact on how a patient is clinically treated. Healthy subjects need to be spared from aggressive and invasive follow up techniques, and hence comparisons should be applied at minimally acceptable FPRs. It might as well be the case that a marker needs to be very sensitive so as to avoid underdiagnosis, and hence focusing on high values of TPRs might also be appropriate. In cases where established and validated markers are considered, it might be of clinical interest to compare them at their established cutoff value. Our methods can be used in these cases in order to make inference regarding their performance at the decision threshold. It is important to highlight the difference between fixed threshold and fixed FPR. Based on our experience in the Early Detection Research Network as well as other projects related to continuous biomarkers, the fixed threshold does not occur until a very late stage, e.g. FDA registry trial, due to two reasons: First, early stage biomarker evaluations usually do not have large enough sample size for a threshold to be established. The second reason is that a clinical test for FDA approval requires industry to develop clinical grade assay, which is an expensive step. The biomarker evaluation, selection, and comparison (before a clinical grade assay is available) are done by research assays used in academics. A threshold chosen by a research assay will not be applicable for a clinical grade assay developed later. Therefore, in academic settings, most continuous diagnostic biomarker comparisons, should be on either AUC, or more clinically relevant criteria such as the sensitivity at a fixed FPR level (or FPR at a fixed sensitivity level), depending on the clinical context. Therefore, efficient methodology to facilitate these kind of comparisons is needed. .

In this study, we develop parametric, as well as power transformation and kernel-based methods to address such comparisons. Many authors have focused on comparisons based on the AUC. However, clinicians are often interested in making comparisons between diagnostic tests or biomarkers, as seen in the present application, thereby exploring the incremental value of biomarkers at a specific and tolerable FPR (or at a specific tolerable sensitivity rate). Our approaches perform satisfactorily in terms of size and power. The Box-Cox approach seems to perform well even in scenarios outside the Box-Cox family. The kernel-based approach provides an even more robust alternative. Qin et al. [27] consider only resampling based approaches for such a problem and the issue of covariates is not addressed. This is also the case considered in [29] in which the authors consider density ratio models. A Box-Cox based approach is also presented in [28] in which however the variability of the transformation parameters is not taken into account. Our approaches can be extended to comparisons in terms of the AUC or in terms of ROC⁻¹(t) and also incorporate a transformation that conforms with the support of the asymptotic normality of the corresponding statistic, which is necessary in many cases as shown in our simulations. Our approaches can also be employed in a time-dependent setting (see [30,31]). Along the same line, an even more interesting setting, in which our methods are directly applicable, is an assessment of a single biomarker at two different time points given the desired FPR. There are other issues that need to be explored. For example, the use of more sophisticated bandwidths for the kernel-based method might improve the power of the underlying statistic. Such bandwidths may involve computationally intensive cross-validation techniques (see [24] for an overview on that subject). Another possible approach to improve the kernel-based technique would be to first apply the Box-Cox transformation and then perform kernel smoothing on the transformed data. Such an approach might make the computationally simple plugin bandwidths we employ even more appropriate. All these issues deserve further study. Other approaches (see [32]) are available for comparing two correlated pAUCs under the notion of generalized pivotal quantities. Such an approach could be modified to address comparisons of two sensitivities given a specificity level. However, even under the normality assumption their approach involves resampling while we offer asymptotic delta based approximate formulas. Furthermore, their Box-Cox version does not take into account the variability of the transformation parameter. For our non-parametric counterparts, we provide a smooth version of the ROC curve which a natural assumption for the true underlying ROC curve. Such smoothness naturally allows a distinct TPR estimate for any given FPR (and vice versa). In addition, the involved transformation Φ⁻¹(·) in the numerator of our proposed statistic seems to be essential so as to assume approximate normality for the sensitivity/specificity estimates. This is not addressed in the literature (already referred in our study) that involves inference in terms of AUC, pAUC, or ROC(t). A generalized pivotal based approach that addresses these issues and can also accommodate covariates would be interesting for further research.