Direct measurement of sequence-dependent transition path times and conformational diffusion in DNA duplex formation

Significance

The transition path time in folding reactions—the time required to cross through the high-energy transition states—offers a powerful tool for studying folding mechanisms because it is uniquely sensitive to the microscopic motions along the transition paths that dominate the folding dynamics. We used transition path times to probe helix formation in nucleic acids and elucidate differences between the formation of canonical G:C and A:T base pairs. Stem-loop hairpins of the same size but increased G:C content had faster transition path times, revealing that the conformational diffusion coefficient determining the timescale for molecular dynamics was higher for formation of G:C base pairs than A:T base pairs. Such sequence dependence, not previously observed, reflects differences in the internal friction for reconfiguring the bases.

Abstract

The conformational diffusion coefficient, D, sets the timescale for microscopic structural changes during folding transitions in biomolecules like nucleic acids and proteins. D encodes significant information about the folding dynamics such as the roughness of the energy landscape governing the folding and the level of internal friction in the molecule, but it is challenging to measure. The most sensitive measure of D is the time required to cross the energy barrier that dominates folding kinetics, known as the transition path time. To investigate the sequence dependence of D in DNA duplex formation, we measured individual transition paths from equilibrium folding trajectories of single DNA hairpins held under tension in high-resolution optical tweezers. Studying hairpins with the same helix length but with G:C base-pair content varying from 0 to 100%, we determined both the average time to cross the transition paths, τ_tp, and the distribution of individual transit times, P_TP(t). We then estimated D from both τ_tp and P_TP(t) from theories assuming one-dimensional diffusive motion over a harmonic barrier. τ_tp decreased roughly linearly with the G:C content of the hairpin helix, being 50% longer for hairpins with only A:T base pairs than for those with only G:C base pairs. Conversely, D increased linearly with helix G:C content, roughly doubling as the G:C content increased from 0 to 100%. These results reveal that G:C base pairs form faster than A:T base pairs because of faster conformational diffusion, possibly reflecting lower torsional barriers, and demonstrate the power of transition path measurements for elucidating the microscopic determinants of folding.

Structure formation in biological macromolecules like proteins and nucleic acids is a complex, dynamic process. Physically, it is described in the context of energy landscape theory as a diffusive search in conformational space for the minimum-energy structure (1–3). The speed at which this search takes place at the microscopic level is set by the conformational diffusion coefficient, D. Because D plays a key role in determining the kinetics of the folding, as encapsulated in the well-known expression for rates derived by Kramers (4), it is one of the fundamental physical determinants of folding phenomena: it connects the thermodynamics encoded in the energy landscape to the dynamics of conformational changes. The properties of D relate to such key issues as internal friction in the polymer chain (5–8), roughness in the energy landscape (9–12), projection of the full phase-space for conformational dynamics onto experimental reaction coordinates (13), and “speed limits” for folding transitions (14).

Despite its importance, D remains challenging to determine experimentally. Several studies have found D from the reconfiguration times for unfolded proteins or polypeptides (15–19), using fluorescence probes to measure interactions between specific locations on the polymer chain. However, few studies have measured D across the energy barrier separating the folded and unfolded states (12, 20–22), which is not necessarily the same as the value within the unfolded state because D can be position dependent (13, 23). It is the value of D within the barrier region that is most relevant for describing the kinetics of folding. Unfortunately, standard approaches for determining D from the folding rates, such as via Kramers’ kinetic theory (4), tend to suffer from high experimental uncertainty: rates are very sensitive to barrier heights, but errors in barrier height measurements can be quite large (24).

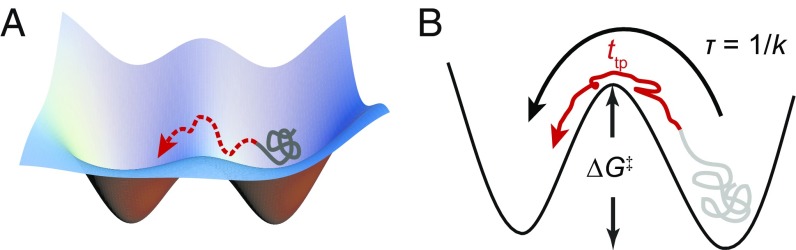
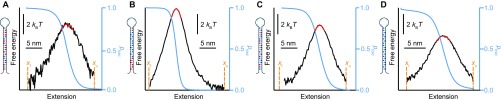
Recently, an alternate approach for determining D based on measurements of the duration of transition paths has been developed (24, 25). Transition paths are the brief portions of a folding trajectory during which the molecule passes through the transition states and undergoes the most significant parts of the structural changes (Fig. 1). In contrast to the situation with folding rates—which are exponentially more sensitive to the barrier height, ΔG^‡, than to D (4)—the average transition path time, τ_tp, is far more sensitive to D than to ΔG^‡. For a harmonic barrier in a 1D energy landscape, τ_tp is given in the high-barrier limit (ΔG^‡ > 2k_BT) by the following:

$${\tau }_{\text{tp}}\approx \frac{\ln \left(2e^{\mathrm{\gamma }}\beta \mathrm{\Delta }{G}^{\mathrm{‡}}\right)}{\beta D{\kappa }_{\text{b}}},$$ [1]

where κ_b is the barrier stiffness, β is the inverse thermal energy, and γ is Euler’s constant (26, 27). As a result, τ_tp provides a much more sensitive measure of D than does the folding rate (8, 24, 28). Moreover, if the individual transit times (t_tp) can themselves be measured, in addition to the average transition path time, then D can also be found independently from the distribution of t_tp, P_TP(t): in the same limit as above, P_TP(t) decays exponentially at long times as follows:

$$P_{\text{TP}}\left(t\right)\approx 2{\omega }_{\text{K}}\beta \mathrm{\Delta }{G}^{\mathrm{‡}}\exp \left(-{\omega }_{\text{K}}t\right),$$ [2]

where ω_K = βDκ_b (27).

Fig. 1.

Folding transition paths. (A) Transition paths represent the brief portion of folding trajectories (red) where the energy barrier is crossed. (B) Whereas the mean first-passage time (τ) across the barrier is mostly spent waiting for a sufficiently large thermal fluctuation to overcome the barrier height, ΔG^‡, the time to cross the transition path (t_tp) is much shorter than τ and depends primarily on the rate of diffusion over the landscape, D, rather than ΔG^‡.

Advances in single-molecule methods now allow transition times to be measured directly, opening up more detailed and direct studies of conformational diffusion. Fluorescence spectroscopy studies have measured τ_tp for both proteins (8, 29) and nucleic acids (30), permitting questions such as the origin of internal friction to be investigated in greater detail (28). More recently, force spectroscopy experiments using optical tweezers (31) have measured both τ_tp (22) and the information-rich distribution P_TP(t) (25), as well as other transition path properties such as occupancy statistics (32, 33). Here, we investigate the sequence dependence of conformational diffusion in nucleic acid duplex formation by measuring transition paths in DNA hairpins held under tension in optical tweezers. Nucleic acid hairpins provide a powerful model system for studying folding phenomena because they have been studied extensively at the single-molecule level by experiment (34–39), theoretical and computational models have described experimental results quantitatively (38, 40–42), and hairpin folding can be manipulated predictably through sequence changes (43). We used measurements of τ_tp and P_TP(t) from the folding of hairpins having different stem sequences to determine whether the two canonical Watson–Crick base pairs, A:T (containing two hydrogen bonds) and G:C (containing three), give rise to sequence dependence in D. By applying Eq. 1 to measurements of τ_tp and fitting P_TP(t) to Eq. 2, we found that the conformational diffusion during A:T formation was in fact distinctly slower than for G:C formation.

Results

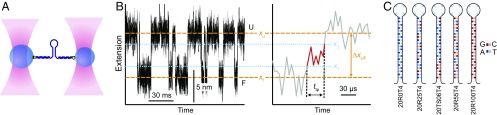
Single DNA hairpins that fold as two-state systems (37, 43) were attached to polystyrene beads via kilobase-long DNA handles as described previously (37), and their extension was measured while held under tension in high-resolution dual-beam optical traps at constant trap separation (Fig. 2A). We kept the stiffness of each trap high (0.56–0.63 for one trap and 0.75–1.1 pN/nm for the other) to obtain maximal time resolution as measured from the instrument response time (25), 6–9 μs (Fig. S1 and Methods). The applied load was such that the hairpins fluctuated rapidly in equilibrium between folded and unfolded states around the force where each state was occupied equally, F_1/2, allowing transition paths across the barrier to be observed directly (Fig. 2B) similar to previous work (25). We measured five different hairpins having G:C content ranging from 0 to 100% but identical stem length: hairpins 20R0/T4, 20R25/T4, 20R55/T4, 20R100/T4, and 20TS06/T4 from refs. 37 and 43. These hairpins have been well characterized previously (37, 43) and have important differences, such as an energy barrier in hairpin 20TS06/T4 that is both higher and stiffer than in the other hairpins. The hairpin sequences are listed in Table S1 and illustrated in Fig. 2C.

Fig. 2.

Force spectroscopy measurements of transition paths in DNA hairpin folding. (A) Schematic of assay: a single DNA hairpin is attached at each end via double-stranded handles to beads held in optical traps. (B, Left) Segment of extension trajectory for hairpin 20R100/T4, showing repeated transitions between the folded state (F) at extension x_f and the unfolded state (U) at x_u (dashed lines). (Right) Single transition from the trajectory, revealing the transition path across the barrier region (red). The transition time, t_tp, is measured between boundaries x₁ and x₂ bracketing the barrier region (dotted lines). (C) Sequences of hairpins studied with varying G:C content.

Fig. S1.

Instrumental response time. (A) The response time of the optical tweezers to changes in extension, t_c, was measured using a reference construct consisting of DNA handles only. The construct was held at about 10, 14, and 19 pN, and one trap was jumped abruptly back and forth to cause the extension to change by an amount equivalent to the extension change in the folding of the hairpins. (B) Extension trajectories of the handle-only reference construct (black) were analyzed in the same way as the folding/unfolding transitions, measuring t_c from individual transitions (red) as the time required to move between the boundaries x₁ and x₂ (dotted lines). Back-and-forth motion in the trajectories reflects the diffusive motion of the bead. (C) The distribution of response times was peaked near 4–6 μs for the different forces, with an average of 6 ± 1 (20 pN) to 9 ± 1 (10 pN) μs.

Table S1.

DNA hairpins

Hairpin name	Sequence	G:C, %	No. transitions
			U	R
20R100T4	CGCCGCGGGCCGGCGCGCGG–(T)4–CCGCGCGCCGGCCCGCGGCG	100	20,700	20,705
20R55T4	GAGTCAACGTCTGGATCCTG–(T)4–CAGGATCCAGACGTTGACTC	55	18,262	18,292
30R50T4	GAGTCAACGTACTGATCACGCTGGATCCTA–(T)4–TAGGATCCAGCGTGATCAGTACGTTGACTC	50	24,591	24,600
20TS06T4	GCCGGCTATTATTTATATTC–(T)4–GAATATAAATAATAGCCGGC	35	6,816	6,824
20R25T4	AAGTTAACATCTAGATTCTA–(T)4–TAGAATCTAGATGTTAACTT	25	26,702	26,719
20R0T4	TATTATATATTAATATATAA–(T)4–TTATATATTAATATATAATA	0	24,811	24,949

The sequence of the DNA hairpins and their GC content. Number of transitions shown for unfolding (U) and refolding (R).

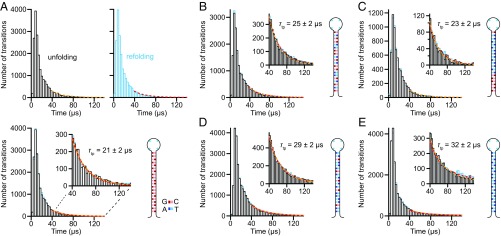
We identified individual transition paths from the extension trajectories as those parts of the trajectory crossing between the boundaries x₁ and x₂ bracketing the barrier region. For consistency when comparing the different hairpins, x₁ and x₂ were defined based on the extension change between the folded and unfolded states, Δx_FU, being located at 1/4Δx_FU above the folded state and 1/4Δx_FU below the unfolded state, respectively (Fig. 2B, dotted lines). We then measured individual transit times (t_tp) directly from the trajectory as the time required to pass between x₁ and x₂, or vice versa (25). The hairpin stem lengths were all equal, to ensure that Δx_FU was similar for all hairpins and hence that artifactual differences in t_tp owing to travel over different distances were minimized. The transit time distributions P_TP(t) for unfolding and refolding (Fig. 3, unfolding, black; refolding, cyan) were the same within error for each hairpin, as expected from time-reversal symmetry (27).

Fig. 3.

Distribution of individual transit times. (A) Distributions for the time to cross the barrier region during transition paths for unfolding (black) and refolding (cyan) of hairpin 20R100/T4. The exponential tails of the distributions are fit to Eq. 2 (unfolding, yellow; refolding, red). (Lower) The two distributions are virtually identical; (Inset) exponential tails. (B–E) Unfolding (black) and refolding (cyan) distributions, with fits to exponential tails (Insets; unfolding, yellow; refolding, red), for hairpins (B) 20R55/T4, (C) 20TS06/T4, (D) 20R25/T4, and (E) 20R0/T4.

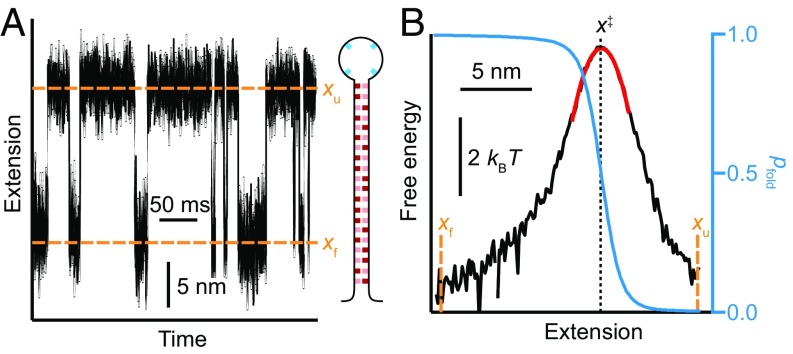
We next reconstructed the shape of the energy barrier to determine the barrier height and stiffness, which are needed to find D from Eqs. 1 and 2. The barriers were reconstructed from equilibrium trajectories of the molecular extension using a method based on the committor statistics (44); as we showed previously using DNA hairpins, this method allows barrier shapes to be determined without the need to deconvolve instrumental compliance effects (24, 43, 45–47). We measured the extension at F_1/2 (Fig. 4A), but this time at constant force, using a passive force clamp (48) to avoid feedback loop artifacts (49). We calculated the splitting probability, p_fold (Fig. 4B, blue), as described in Methods and then used Eq. 3 to reconstruct the barrier profile (Fig. 4B, black). The barrier height was found directly from this reconstructed landscape, and the curvature was measured from a harmonic fit to the barrier top (Fig. 4B, red). Repeating these calculations for each hairpin sequence (Fig. S2), we found that ΔG^‡ varied a few k_BT with changing sequence but κ_b was roughly constant, with the exception of hairpin 20TS06/T4, which had a barrier that was noticeably sharper (Table S2).

Fig. 4.

Landscape reconstruction. (A) Extension trajectory at constant force for hairpin 20R100/T4. (B) Energy landscape profile of the barrier between the folded and unfolded states (black) reconstructed from the empirical splitting probability, p_fold (blue), showing a harmonic fit to the barrier top (red).

Fig. S2.

Energy landscape reconstructions from p_fold. Energy landscapes (black) reconstructed from p_fold (blue) using Eq. 3, with harmonic fit to the barrier peak (red) to determine curvature, for hairpins (A) 20R55/T4, (B) 20TS06/T4, (C) 20R25/T4, and (D) 20R0/T4.

Table S2.

Energy landscape parameters from p_fold analysis

Hairpin	ΔG‡, kBT	κb, kBT/nm2	ΔG′‡tp, kBT
20R100T4	5.0 ± 0.2	0.27 ± 0.03	2.7 ± 0.1
20R55T4	4.4 ± 0.2	0.25 ± 0.04	2.5 ± 0.1
30R50T4	9.1 ± 0.1	0.29 ± 0.02	4.3 ± 0.2
20TS06T4	6.4 ± 0.2	0.4 ± 0.1	4.1 ± 0.2
20R25T4	4.8 ± 0.2	0.29 ± 0.03	2.3 ± 0.1
20R0T4	3.8 ± 0.2	0.24 ± 0.02	2.0 ± 0.1

Errors represent SEM.

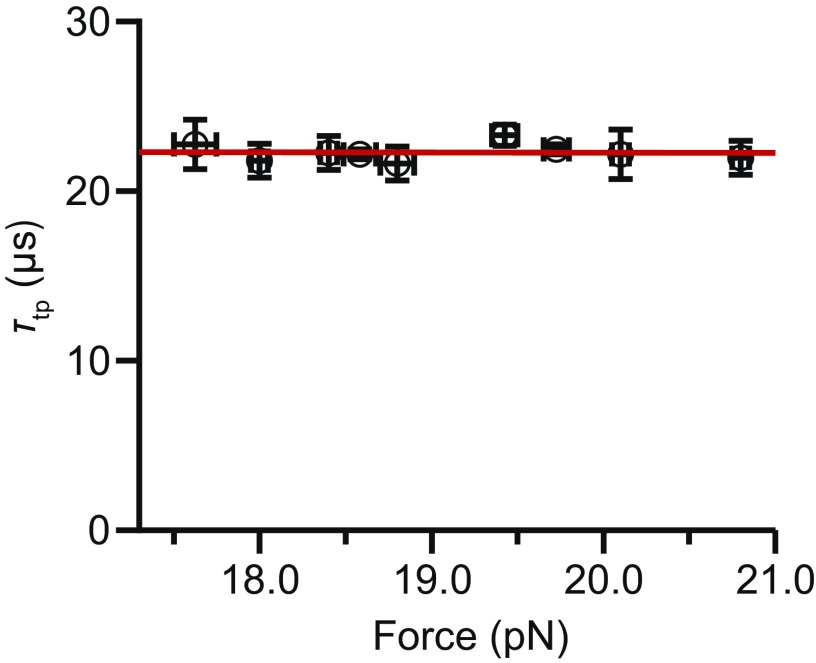
Finally, we found D for each of the hairpins studied by combining the individual transit time measurements with the landscape analysis. We calculated D in two independent ways for each hairpin: via Eq. 1 using τ_tp, averaging over all transitions (Fig. 5A), and by fitting the exponential tail of P_TP(t) to Eq. 2 (Fig. 3, Insets). For these calculations, we used the height of the barrier measured with respect to the barrier region boundaries x₁ and x₂, rather than the full activation barrier, as argued recently (50). The results, based on 13,000–53,000 transitions for each of the five hairpins studied, show a linear rise of D with G:C content (Fig. 5B). Numerical values for all results are listed in Table S3. Note that hairpin unfolding force also correlates linearly with G:C content (37), hence the diffusion coefficient might be varying with force instead of G:C content. We verified that D did not have any appreciable force dependence by measuring transition paths for hairpin 20R100/T4 at difference forces, over the range of forces (∼3 pN) within which sufficient transitions could be detected to calculate τ_tp reliably (Fig. S3). Determining D from Eq. 1, we found that force had little, if any, effect on D—less than 10% of the effect observed from changing the sequence—confirming that the differences in D did indeed arise primarily from sequence differences.

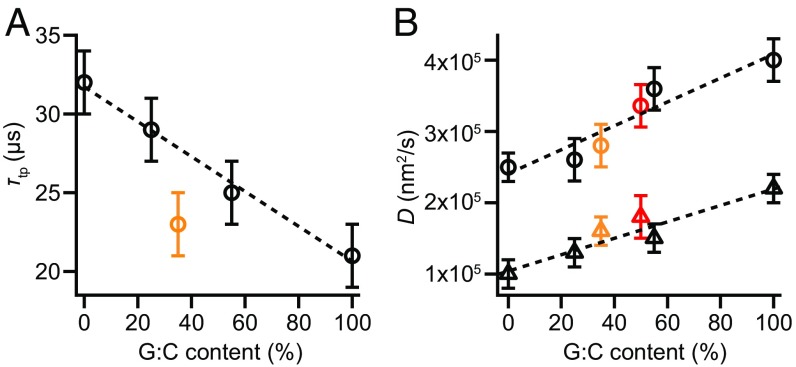
Fig. 5.

G:C dependence of τ_tp and D. (A) The average transition path time decreases linearly with increasing G:C content, with the exception of hairpin 20TS06/T4 (orange). (B) D increases linearly with G:C content for all hairpins, including hairpin 20TS06/T4 (orange), as determined from τ_tp (circles) and from fitting the exponential tail of P_TP(t) (triangles). Error bars represent SEM, averaging over both folding and unfolding data for all molecules measured. Data points in red represent values for hairpin 30R50/T4 derived from measurements in ref. 25.

Table S3.

Numerical results for each hairpin

Hairpin name	τtp, μs			D from τtp, ×105 nm2/s			D from PTP(t), ×105 nm2/s
	U	R	Avg	U	R	Avg	U	R	Avg
20R100T4	21 ± 2	21 ± 2	21 ± 2	4.1 ± 0.3	4.1 ± 0.3	4.1 ± 0.3	2.2 ± 0.2	2.1 ± 0.2	2.2 ± 0.2
20R55T4	24 ± 1	25 ± 1	25 ± 2	3.5 ± 0.3	3.6 ± 0.3	3.6 ± 0.3	1.5 ± 0.2	1.4 ± 0.2	1.5 ± 0.2
30R50T4	27 ± 2	28 ± 2	28 ± 2	3.5 ± 0.3	3.4 ± 0.3	3.5 ± 0.3	1.8 ± 0.3	1.8 ± 0.3	1.8 ± 0.2
20TS06T4	23 ± 2	22 ± 2	23 ± 2	3.1 ± 0.3	3.1 ± 0.3	3.1 ± 0.3	1.5 ± 0.2	1.6 ± 0.2	1.6 ± 0.2
20R25T4	29 ± 1	29 ± 1	29 ± 2	2.5 ± 0.3	2.6 ± 0.3	2.6 ± 0.3	1.3 ± 0.2	1.3 ± 0.2	1.3 ± 0.2
20R0T4	31 ± 2	32 ± 2	32 ± 2	2.5 ± 0.2	2.5 ± 0.2	2.5 ± 0.2	1.0 ± 0.1	1.0 ± 0.2	1.0 ± 0.2

Results for unfolding transitions (U), refolding transition (R), and the average (Avg). Errors represent SEM.

Fig. S3.

Force dependence of τ_tp. τ_tp for the hairpin 20TS06T4 over a force range of 3 pN, in which the hairpin changed from mostly folded to mostly unfolded. Transition path time varied very little with the force for the hairpin (slope, 0.02 ± 0.02 μs/pN), indicating little to no change in D with force.

Discussion

For all hairpins but one, τ_tp decreased linearly with increasing G:C content, being 50% longer for hairpins with only A:T base pairs compared with hairpins with only G:C base pairs. The exception, hairpin TS06/T4, had a shorter transition time than expected based on the G:C content and was almost as fast as hairpin 20R100/T4. However, this hairpin was designed to have a different barrier than the others: the barrier is both higher and stiffer. The stiffer barrier increases the speed for crossing the transition paths much more than the higher barrier height reduces it (Eq. 1). Indeed, when we look at D for this hairpin instead of τ_tp (Fig. 5B), we find that it lies on the same linear curve as for the other hairpins—the effect of the stiffer barrier is no longer apparent. This result shows that analyzing the average transition time alone, without also characterizing D, may sometimes be misleading: it is D that is the more fundamental descriptor of the folding, because τ_tp is affected by factors like the shape of the barrier.

From Fig. 5, we see that there are distinct differences between the diffusion coefficients for A:T and G:C base-pair formation during folding. G:C base pairs are thus not only more stable, because of their extra hydrogen bond, but they also undergo conformational fluctuations faster. To confirm that the sequence-dependent values for D obtained from these five hairpins represent a basic property of the base pairs, we performed the same analysis on previous measurements of a hairpin with a stem that is 50% longer, hairpin 30R50/T4 (25). Notably, the values for D calculated from Eqs. 1 and 2 (Fig. 5B, red) matched very well the results expected based on the G:C content of the hairpin, given the G:C dependence of D found from the shorter hairpins.

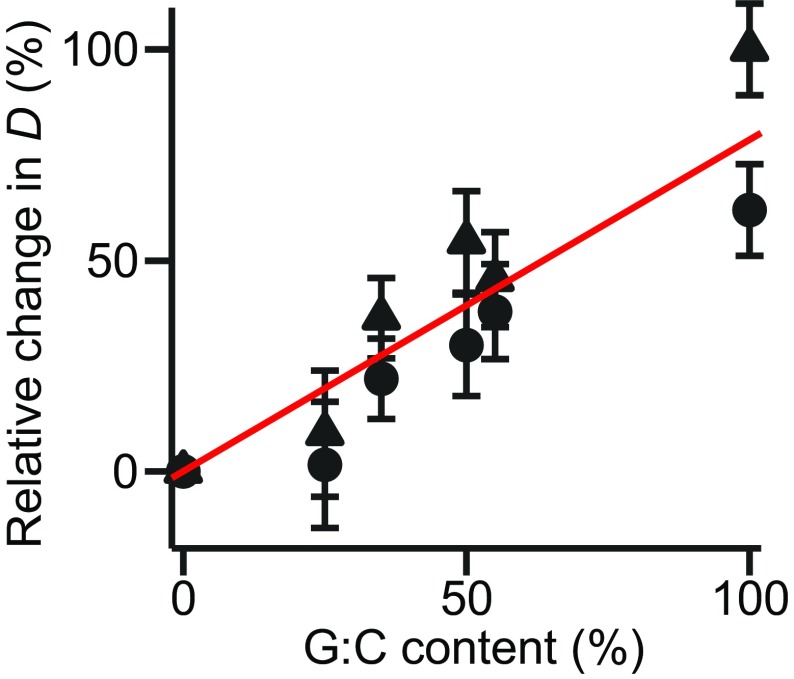
The qualitative trend in D (i.e., a linear increase in D with G:C content) is the same whether D is found from τ_tp via Eq. 1 (Fig. 5B, circles) or the fit to the exponential tail via Eq. 2 (Fig. 5B, triangles), as shown by replotting the results in terms of relative changes (Fig. S4). However, the quantitative results differ: the values found from τ_tp are consistently about twofold higher. One possible source of this discrepancy is that the assumptions used in the analyses—that the folding involves simple 1D diffusion over a harmonic barrier—are not completely correct. The barriers do differ significantly from a purely harmonic profile: whereas the very tops of the barriers are well approximated as harmonic, regions further away are not (Fig. 4B, black). Such anharmonicity can alter the properties of the transition paths (51), with flatter energy profiles (as in the regions away from the barrier top) yielding longer transit times (27), consistent with a longer tail in P_TP(t) suggesting slower diffusion. Brownian dynamics simulations of motions transitions across an anharmonic barrier like that in Fig. 4B did indeed find that all transitions were slower than for a harmonic barrier with the same height and curvature (Fig. S5), but D implied by the exponential tail of the distribution decreased about 35% more than did D implied by τ_tp. These simulations thus suggest that barrier anharmonicity accounts for up to one-half of the observed discrepancy between the two estimates of D. The rest of the discrepancy presumably arises from contributions from other factors, such as deviations from 1D behavior that distort P_TP(t) from expectations, or the mechanical coupling of the hairpins to the linkers and beads, which can alter kinetic properties (24, 52–55) including transition times (24, 55). Such effects are expected to be relatively small, however: previous analysis of some of the same DNA hairpins found that the conditional transition path probability matched expectations for 1D diffusion over the measured landscapes quite well (32), and our measurements are done in a limit where the mechanical coupling artifacts are small (56).

Fig. S4.

Relative change in D with G:C content. The change in D relative to the result at 0 G:C content, based on Eq. 1 (circles) or Eq. 2 (triangles).

Fig. S5.

Transit time distributions from Brownian dynamics simulations. The transit times observed in simulations of diffusive motion over a 1D anharmonic energy profile similar to that in Fig. 4B (red) are longer than those (black) found for a harmonic energy profile having the same barrier height and curvature. The timescale for the exponential decay of the distribution for the anharmonic barrier increased 35% more than did the average transition path time, compared with the results for the harmonic barrier, leading to a discrepancy between D calculated from Eq. 1 versus Eq. 2 for the anharmonic barrier.

What might account for the difference in diffusion coefficient between A:T and G:C base pairs? Because D is inversely proportional to the friction coefficient, one possible explanation is that the internal friction during base-pair formation is different for the different base pairs. We speculate that the sequence dependence of D may result from sequence-dependent differences in the torsion angle dynamics during folding, motivated by recent computational simulations indicating that torsion angle isomerization effects are a key source of internal friction in proteins (57, 58) and earlier work on RNA hairpins showing that torsion angle isomerization can cause dramatic changes in rates (41). It is known, for example, that G can adopt the syn conformation of the glycosidic bond between the base and the backbone more readily than other nucleotides, such as in Z-DNA (59). The energy barrier for syn/anti isomerization is predicted to be lower for purines than pyrimidines (60), and the isomerization rate was observed to be faster for G than A (61). Calculations of dinucleoside energies in torsion angle hyperspace also found generally broader energy minima for G:C-paired dinucleosides than A:T-paired ones (62). Such results suggest that G may be more dynamic in torsion angle space, allowing it to find the right torsion angle faster and hence raising the diffusion coefficient for G:C formation compared with A:T formation. If this picture is correct, we can estimate the difference in the torsion angle energy barriers using the theory of Zwanzig (9), treating the problem as diffusion over a set of periodic “microbarriers” between each base pair, each of which is too small and too close together to resolve on its own. The factor of ∼2 difference for D between A:T and G:C would then reflect a torsional barrier that is just marginally higher for A:T, by about 1 k_BT.

This work provides a first look at the sequence dependence of conformational diffusion, showing how measurements of individual transit times can be used to probe the fundamental properties that govern folding dynamics. Our results suggest that the kinetic models widely used to describe nucleic acid duplex formation (35, 38, 40) can now be refined, replacing the constant microscopic rates typically assumed with rates that are sequence dependent, so as to reflect the twofold difference in D between G:C and A:T base-pair formation. An interesting implication of the sequence dependence of D is that D should be position dependent along the duplex, leading to changes in the shape of the transition paths (51). Such position dependence has been previously sought but not reliably observed (44, 63); it may soon be detectable through analysis of transition path shapes.

Methods

Samples and Measurements.

DNA hairpin constructs containing hairpins of the desired sequence connected at each terminus to double-stranded DNA handles were prepared as described previously (25). Hairpin constructs were attached to avidin- and anti-digoxigenin–labeled polystyrene beads, respectively, via biotin and digoxigenin labels at the ends of the handles to create dumbbells (Fig. 2A). For measurement, dumbbells were put in 50 mM Mops, pH 7.5, 200 mM KCl, with an oxygen-scavenging system [8 mU/μL glucose oxidase, 20 mU/μL catalase, 0.01% (wt/vol) d-glucose] to prevent oxidative damage. Constant-force measurements were made using a passive force clamp (48), measuring in the linear-stiffness region of one trap (stiffness, 0.3 pN/nm) and the zero-stiffness region of the other trap, sampling at 20–50 kHz and filtering on-line at the Nyquist frequency. Constant-position measurements were made with stiffness 0.56–0.63 pN/nm in one trap and 0.75–1.1 pN/nm in the other, sampling data at 124–400 kHz and again filtering on-line at the Nyquist frequency. Additional details about the properties of the hairpins (unfolding forces, rates, barrier location, etc.) may be found in previous work (37, 43). Owing to the effect of compliance (48), the extension change observed during unfolding/refolding transitions in measurements at constant trap position was shorter than that in experiments at constant force.

Energy Barrier Reconstructions.

The shape of the energy barrier for each hairpin was reconstructed from the extension trajectories using the committor, p_fold, as described previously (44). Briefly, p_fold(x) was calculated empirically from the trajectory at each value of the extension, and then the landscape was reconstructed using the following:

$$G\left(x\right)={\beta }^{-1}\ln \left(-\frac{d{p}_{\mathrm{fold}}}{dx}\right).$$ [3]

This method recovers the shape of the landscape in the region between the folded and unfolded states, allowing the barrier height and stiffness to be measured directly from the reconstruction. Note that Eq. 3 assumes that the diffusion coefficient is constant along the reaction coordinate, and the method depends on extension being a good reaction coordinate (else the barrier height and curvature will appear to be broader than they actually are). Previous work on some of the same hairpins discussed here, however, showed that extension was a good reaction coordinate (32). Furthermore, landscapes reconstructed by Eq. 3 were found to agree well with those reconstructed from the inverse Boltzmann transform (which makes no assumptions about D), suggesting not only that the correct barrier height and curvature are being reliably recovered (within experimental error) but also that any effects from the small sequence dependence of D do not noticeably alter the landscape reconstruction (44). To reduce noise in the numerical differentiation, p_fold(x) was first smoothed in a 1-nm window with a boxcar filter. The barrier height within just the barrier region (used for calculating D from Eq. 1), ΔG^‡_tp (values listed in Table S2), was found by averaging the energy difference between the top of the barrier and the energy at the two boundaries defining the barrier region, x₁ and x₂.

Instrument Response Time.

The instrument response time was measured over the range of forces studied here (10–20 pN) similarly to previous work (25), using constructs that were the same as those for the hairpin measurements but without any hairpin between the handles. The traps were moved apart suddenly to cause a change in the extension (Fig. S1) equivalent to the extension change seen in the hairpin measurements, and the resulting motion of the beads was measured. Individual response trajectories were analyzed in a similar way as the folding/unfolding transitions (Fig. S1B), obtaining the distribution of times required to cross between boundaries x₁ and x₂ separated by the same distance as in the hairpin trajectories. The average relaxation time varied from 6 ± 1 μs at 20 pN to 9 ± 1 μs at 10 pN.

Transition Time and Diffusion Coefficient Analysis.

Transitions were identified as those parts of the trajectories traversing between the boundaries x₁ and x₂ separating the folded and unfolded states, respectively, from the transition region, as described previously (25). Briefly, the boundaries were chosen to bracket the middle half of the distance between the folded and unfolded states (Δx_UF), so that x₁ = x_f + 1/4Δx_UF and x₂ = x_u − 1/4Δx_UF, where x_f and x_u are the positions of the folded and unfolded states, respectively (Fig. 2B, Inset). An adaptive smoothing algorithm was used to mitigate the effects of noise in the data. First, an initial estimate of the transit time for a given transition, t_tp, was found by fitting the transition path trajectory to a logistic function. The trajectory was then median-filtered in a window equal to one-half this initial estimate, and t_tp was measured directly from the smoothed trajectory as the time required to move between x₁ and x₂, interpolating linearly between the sampled points where necessary to obtain the best estimate of the crossing time at each boundary (25).

The instrument response time was roughly one-third to one-quarter the average transition time for each hairpin. The finite response time would be expected to alter the observed transition times only for the most rapid transitions, those having transit times close to the response time limit. To avoid any distortion of the shape of the transit time distribution P_TP(t) at small times arising from effects of the finite response time, when fitting P_TP(t) to Eq. 2 to determine D, we used only the long-duration tail of the distribution, involving transit times 40 μs or longer (severalfold larger than the instrument response time). We verified that the fitting results did not depend on the precise choice of the fitting bound, being the same (within error) for choices between 30 and 50 μs, suggesting that the finite time response does not distort the exponential tail of P_TP(t).

We note that care must be taken when calculating D from constant-position measurements to account for compliance corrections to the distance changes that are measured, corrections that arise from the changes in the force during the trajectory (48). Although the time taken to cross the barrier region is not affected by compliance corrections, the apparent distance traversed (i.e., the width of the barrier) is reduced, because the beads move less than the ends of the hairpin. The curvature of the barrier thus appears larger than it truly is, and D is artificially lowered. We account for the compliance correction when calculating D by using the barrier curvature obtained from constant-force measurements, where there is no compliance correction and the motions of the beads match the motions of the hairpin.

Brownian Dynamics Simulations.

Simulations of transition paths arising from diffusive motion over a 1D potential surface were performed following a procedure described previously (64). Briefly, simulations were based on a rescaled, discretized Langevin equation with a random Gaussian force of mean 0. Simulations were run for an anharmonic potential similar to the energy profile in Fig. 4B, rescaled proportionately in energy and distance to reduce the simulation time, and for a harmonic potential with the same barrier height and curvature as the anharmonic potential.