How Native and Alien Metal Cations Bind ATP: Implications for Lithium as a Therapeutic Agent

Abstract

Adenosine triphosphate (ATP), the major energy currency of the cell, exists in solution mostly as ATP-Mg. Recent experiments suggest that Mg²⁺ interacts with the highly charged ATP triphosphate group and Li⁺ can co-bind with the native Mg²⁺ to form ATP-Mg-Li and modulate the neuronal purine receptor response. However, it is unclear how the negatively charged ATP triphosphate group binds Mg²⁺ and Li⁺ (i.e. which phosphate group(s) bind Mg²⁺/Li⁺) and how the ATP solution conformation depends on the type of metal cation and the metal-binding mode. Here, we reveal the preferred ATP-binding mode of Mg²⁺/Li⁺ alone and combined: Mg²⁺ prefers to bind ATP tridentately to each of the three phosphate groups, but Li⁺ prefers to bind bidentately to the terminal two phosphates. We show that the solution ATP conformation depends on the cation and its binding site/mode, but it does not change significantly when Li⁺ binds to Mg²⁺-loaded ATP. Hence, ATP-Mg-Li, like Mg²⁺-ATP, can fit in the ATP-binding site of the host enzyme/receptor, activating specific signaling pathways.

Lithium (Li⁺), a non-biogenic cation not known to have essential biological functions in mammals, is used (in the form of soluble salts) as a first-line medication for psychiatric diseases, in particular bipolar disorder¹. It has been considered as a possible treatment for chronic neurodegenerative diseases such as Alzheimer’s, Parkinson’s, and Huntington’s¹,². Although the beneficial effects of Li⁺ therapy have been known for decades, the mechanism of Li⁺ action remains largely enigmatic. Several hypotheses have been put forth which, taken together, suggest that Li⁺ may exert its therapeutic effect via diverse, multifaceted pathways:

1. Li⁺ competes with Na⁺ in the cytosol. Li⁺ enters the intracellular space via sodium channels or transporters and accumulates, thus competing with Na⁺. In the cytosol, elevated Li⁺ concentration decreases the Na⁺ level, which in turn reduces the Ca²⁺ concentration³. Lowering both cytosolic Na⁺ and Ca²⁺ concentrations decreases the cell excitability and eventually normalizes the neuron activity in bipolar disorder patients whose intracellular Na⁺ concentration is abnormally high³,⁴.

2. Li⁺ modulates neurotransmitter signaling. Lithium may interact with cellular receptors that regulate the synthesis, release, turnover and reuptake of neurotransmitters such as dopamine and serotonin. Thus, lithium’s therapeutic effect has been postulated to be related to its ability to modulate neurotransmitter signaling in the central nervous system⁵.

3. Li⁺ competes with Mg²⁺ for specific protein binding sites. This hypothesis posits that Li⁺, by replacing the native Mg²⁺ cofactor, inhibits key metalloenzymes (G-proteins, GSK-3β, inositol monophosphatase, inositol polyphosphate phosphatase) involved in specific neurotransmission pathways in the brain⁶,⁷,⁸.

4. Li⁺ affects signaling pathways involving Mg²⁺-loaded nucleotide cofactors. Li⁺ has been hypothesized to co-bind with Mg-bound adenosine triphosphate (ATP) forming a ATP-Mg-Li complex which, when protein-bound, may elicit different responses from key ATP-dependent enzymes/receptors involved in cell signaling⁹.

The last hypothesis is supported by recent experiments showing that the ATP-Mg-Li complex can indeed modulate the neuronal purine receptor response¹⁰. The P2X receptor, a ligand-gated ion channel that mediates the influx of extracellular Ca²⁺ into the cytoplasm, exhibited prolonged activation when stimulated by ATP-Mg-Li. Solution ⁷Li and ³¹P NMR experiments show that upon the metal–ATP complexation, Mg²⁺ and Li⁺ interact with the highly charged triphosphate group and do not bind the adenine and ribose moieties. Notably, Li⁺ does not compete with Mg²⁺ for the ATP-binding site(s); instead it binds to the Mg²⁺-loaded ATP forming a ternary ATP-Mg-Li complex. The interactions between the metal cation and ATP are thought to be mostly electrostatic, guided by the cation’s coordination preference.

Although ATP is known to exist as [ATP-Mg]²⁻ in neutral solution¹¹,¹², a solution structure of Mg²⁺-bound ATP has remained elusive. There is also no solution structure of Li⁺ bound to free or Mg²⁺-bound ATP. Thus, the most stable binding mode of Mg²⁺/Li⁺ to ATP or Li⁺ to [ATP-Mg]²⁻ in solution remains unclear, raising several intriguing and quite fundamental questions:

1. Which of the three ATP phosphate sites (labeled α, β, and γ in order of increasing distance from the ribose) does Mg²⁺ prefer and does it prefer to bind to one (monodentate) phosphate O or simultaneously to two (bidentate) or three (tridentate) phosphate O atoms?

2. Does Li⁺ show the same ATP-binding mode preference as Mg²⁺?

3. When Mg²⁺ is already bound to ATP, which phosphate(s) best accommodate Li⁺ binding?

4. How is the ATP solution conformation affected by metal ion binding? Is the native ATP-Mg conformation altered by Li⁺ binding, thus affecting enzyme/receptor recognition?

To address these questions, we modeled Li⁺/Mg²⁺-ATP complexes with different metal composition, coordination sites, and metal-binding modes (mono/bi/tridentate), and evaluated their thermodynamic characteristics using density functional theory combined with a polarizable continuum model (see Methods). First, the calculations were calibrated with respect to available experimental data. They reveal the relative stabilities of Li⁺/Mg²⁺-ATP complexes that differ in metal-binding mode and how the ATP conformation differs depending on the cation type (Mg²⁺/Li⁺) and the metal-binding mode. Importantly, the results show that when Li⁺ co-binds with Mg²⁺ to the ATP triphosphate group, the native ATP-Mg conformation remains virtually unchanged. Thus, like native ATP-Mg, the ATP-Mg-Li complex may also be bound by cellular receptors or ATP-dependent enzymes and activate specific signaling pathways.

Results

Effect of Mg²⁺-Binding Mode on the ATP Conformation

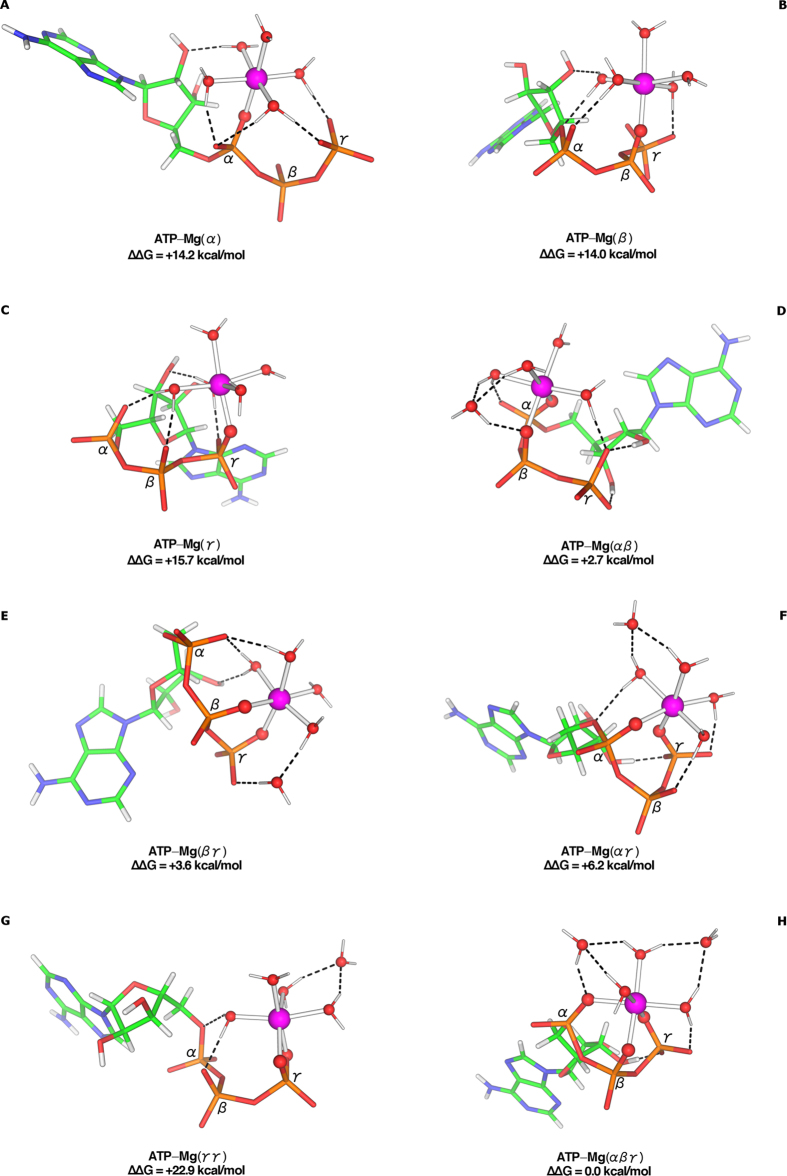
Each of the ATP phosphate groups (α, β, and γ) was probed for its ability to bind Mg²⁺ by itself or in combination with its neighbor(s). The fully optimized structures of Mg²⁺ bound (i) monodentately to the α/β/γ phosphate (Fig. 1A–C), (ii) bidentately to the αβ, βγ, αγ, and γγ phosphates (Fig. 1D–G), and (iii) tridentately to αβγ phosphates (Fig. 1H) are stabilized by favorable metal–O(phosphate) charge–charge interactions and water···O(ribose/phosphate) hydrogen bonds. They reveal that ATP, when allowed to freely optimize its geometry in water, adopts distinct conformations depending on the metal-binding mode/site. The mean root-mean-square deviation (RMSD) between the ATP heavy atoms of any two superimposed structures in Fig. 1 is 1.9 Å with the largest RMSD (3.4 Å) between the βγ and α structures, and the next largest RMSD (3.1 Å) between the βγ and γγ structures (Supplementary Table S1a). This underscores the importance of the metal-binding mode and site on the nucleotide conformation.

Figure 1. M062X/6-311++G(d,p) optimized structures of [ATP-Mg]²⁻ complexes and relative free energies, ∆∆G (kcal/mol), of complex formation in water.

The dashed lines indicate hydrogen bonds, defined by a hydrogen-acceptor distance <1.4 Å and a D–H…A angle >130°. The structures were oriented to give the clearest view of the metal-binding site.

Mg²⁺ Prefers to Bind Tridentately to all 3 ATP Phosphates

The free energy of ATP-Mg complex formation relative to the free energy of the αβγ tridentate complex show that Mg²⁺ prefers multidentate to monodentate binding: Compared to the αβγ tridentate complex, the complexation free energies are less favorable by 3, 4, and 6 kcal/mol for the αβ, βγ, and αγ bidentate structures, respectively and by 14–16 kcal/mol for the monodentate complexes (see Fig. 1). The least preferred metal-binding mode corresponds to Mg²⁺ bound to two O atoms from the same (γ) phosphate (Fig. 1g). This is likely due to the unfavorable coordination geometry imposed on Mg²⁺ in this binding mode: the O^P–Mg–O^P angle (72°) is more acute than the mean O^P–Mg–O^P angle (~91°) in the other polydentate structures, which corresponds to the preferred coordination geometry of Mg^2+ 13. For the same reason, a ATP–Mg(βγγ) tridentate structure (see Supplementary Figure S1), which had been used to study ATP hydrolysis¹⁴, was disfavored (by 11 kcal/mol) compared to the ATP–Mg(αβγ) tridentate structure (Fig. 1H). Thus, Mg²⁺ favors binding all three ATP phosphate groups forming two six-membered rings, thus stabilizing the ATP–Mg(αβγ) tridentate structure.

Effect of Li⁺-Binding Mode on the ATP Conformation

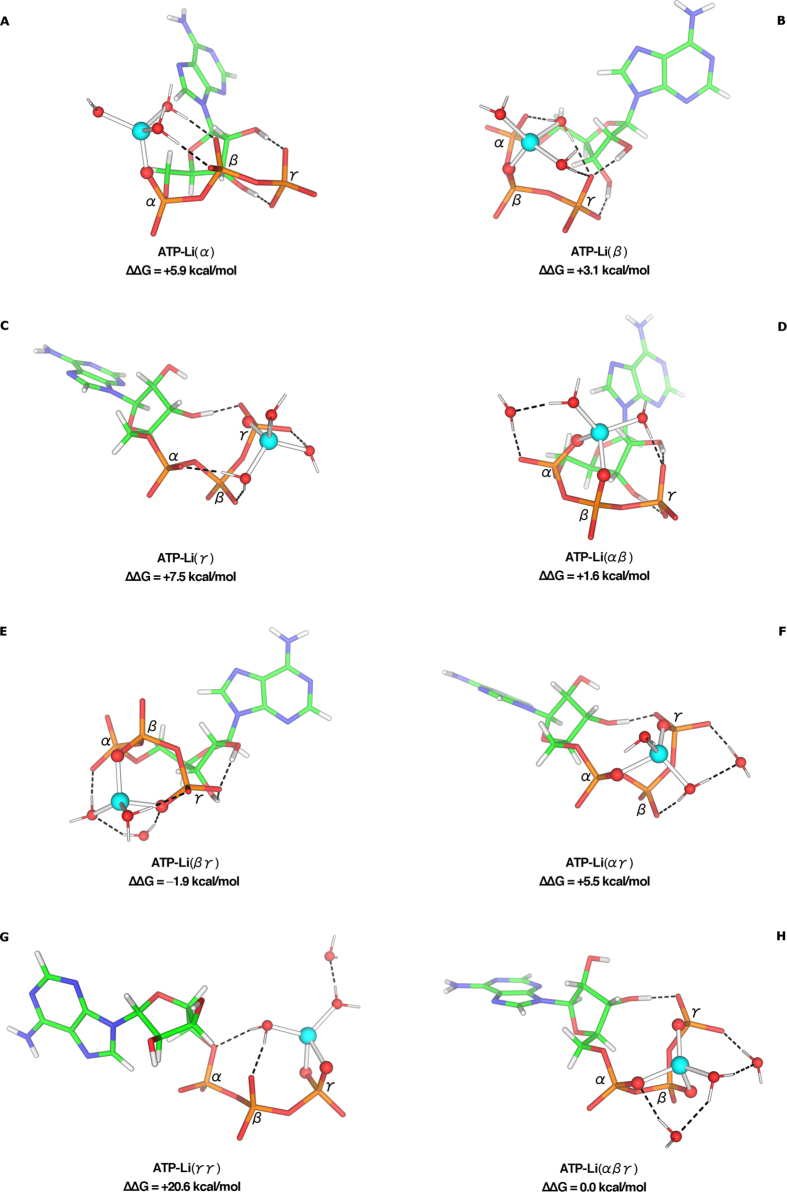
To examine if ATP binds Li⁺ in the same way as Mg²⁺ and how its conformation depends on the Li⁺-binding mode, we fully optimized Li⁺ counterparts of the Mg-ATP complexes (Fig. 2A–H). Compared to Mg²⁺, the weaker coordination strength of Li⁺ induces smaller conformational changes: only two pairs of ATP-Li structures exhibit RMSD ≥2 Å, compared with ten pairs of ATP-Mg structures (Supplementary Table S1b). Depending on the ATP-binding mode, Li⁺ and Mg²⁺ induce different changes in the nucleotide conformation: The RMSDs between the ATP heavy atoms of superimposed [ATP-Mg]²⁻ and [ATP-Li]³⁻ α, γ, β, and βγ structures are respectively 1.7, 1.8, 2.0, and 2.6 Å, but are ≤0.6 Å for the other bi/tridentate-binding modes.

Figure 2. M062X/6-311++G(d,p) optimized structures of [ATP-Li]³⁻ complexes and relative free energies, ∆∆G (kcal/mol), of complex formation in water.

Li⁺ Prefers to Bind Bidentately to the ATP βγ Phosphates

Whereas the tridentate ATP-Mg structure (Fig. 1H) is the most stable, upon Li⁺ binding to ATP, the bidentate βγ complex (Fig. 2E) is slightly more stable than the tridentate complex (Fig. 2H), which is more stable than the other bidentate or monodentate structures. Like Mg²⁺, Li⁺ bound to two O atoms from the same phosphate group (Fig. 2G) is energetically unfavorable, as this binding mode creates coordination geometry strain with a O^P–Li–O^P angle (78°) much smaller than the mean O^P–Li–O^P angle (~105°) in the other bi/tridentate structures. Whereas divalent Mg²⁺ exhibits distinct preference towards the ATP-binding sites, monovalent Li⁺ appears less discriminative: Excluding the high-energy γγ configuration (Figs 1G and 2G), the ΔΔG range for the ATP-Mg complexes (~16 kcal/mol) is greater that for the ATP-Li structures (~10 kcal/mol).

Li⁺ Binds Mg-bound ATP Forming a OH-Bridged Binuclear Complex

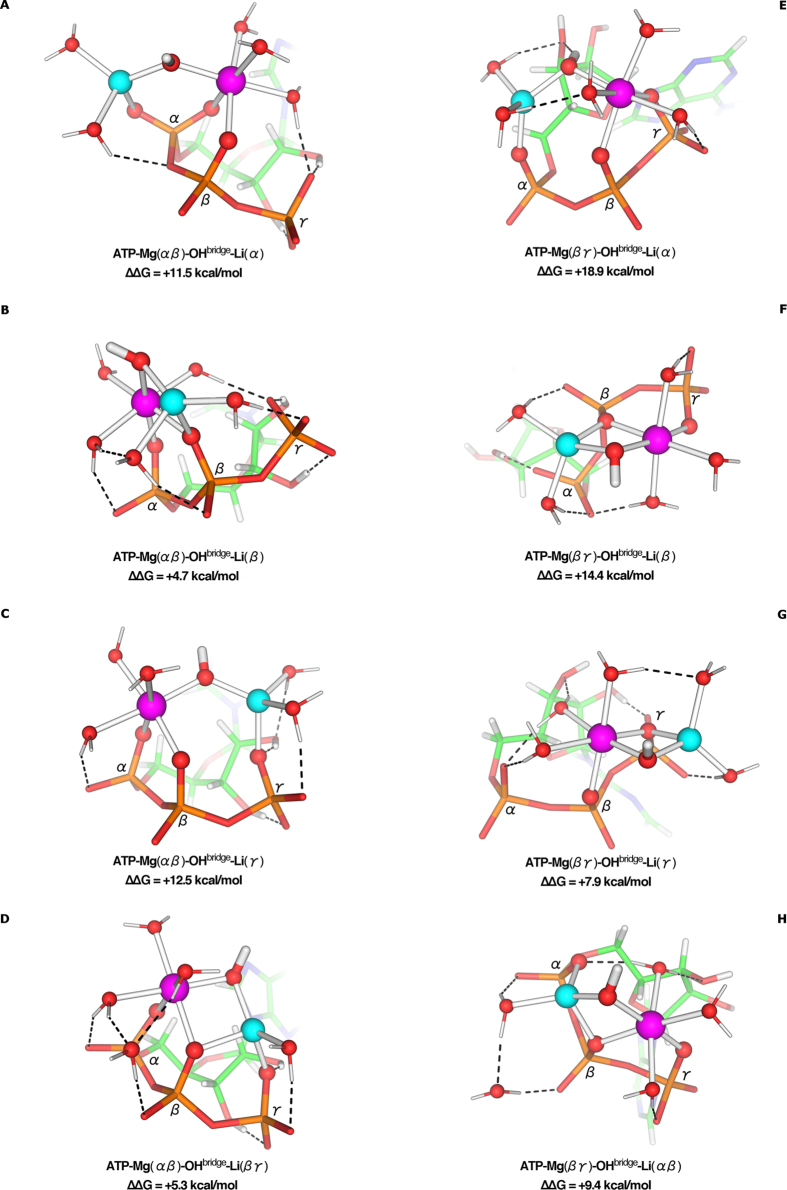
The most stable and hence most populated [ATP-Mg]²⁻ complex in solution with Mg²⁺ bound to ATP tridentately (Fig. 1H) was used to derive bimetallic [ATP-Mg-Li]⁻ complexes where different available sites were systematically probed for their varying Li⁺ affinities (Fig. 3). Due to the structural constraints imposed by Mg²⁺ binding to all three ATP phosphates and because the γγ mode (Fig. 2G) is a high-energy configuration, we modeled Li⁺ binding mono/bidentately to the ATP triphosphate group, yielding a mono or binuclear site with a water molecule bridging the two cations. As shown in our previous work¹⁵, the bridging water molecule may be deprotonated; hence, its protonation state was determined by computing the ∆G^deprot free energy for ATP-Mg(αβγ)-H₂O^bridge-Li + OH⁻ → ATP-Mg(αβγ)-OH^bridge-Li + H₂O in solution. Regardless of the coordination mode, the resulting ∆G^deprot is negative (−16 to −20 kcal/mol). Even though the hydroxide concentration is minute (10⁻⁷ M) at physiological pH of 7, a hydroxide bridge is still favored over a water bridge; e.g., the ∆G^deprot for ATP-Mg(αβγ)-H₂O^bridge-Li(βγ) + OH⁻ → ATP-Mg(αβγ)-OH^bridge-Li(βγ) + H₂O of −16 kcal/mol yields a concentration of the OH^bridge complex that is ~1,000 greater than that of the H₂O^bridge counterpart. Furthermore, the OH^bridge structures in Fig. 3 were more stable than their non-bridged counterparts (Supplementary Figure S2).

Figure 3. M062X/6-311++G(d,p) optimized structures of Li⁺ bound to ATP-Mg(αβγ), and relative free energies, ∆∆G (kcal/mol), of complex formation in water.

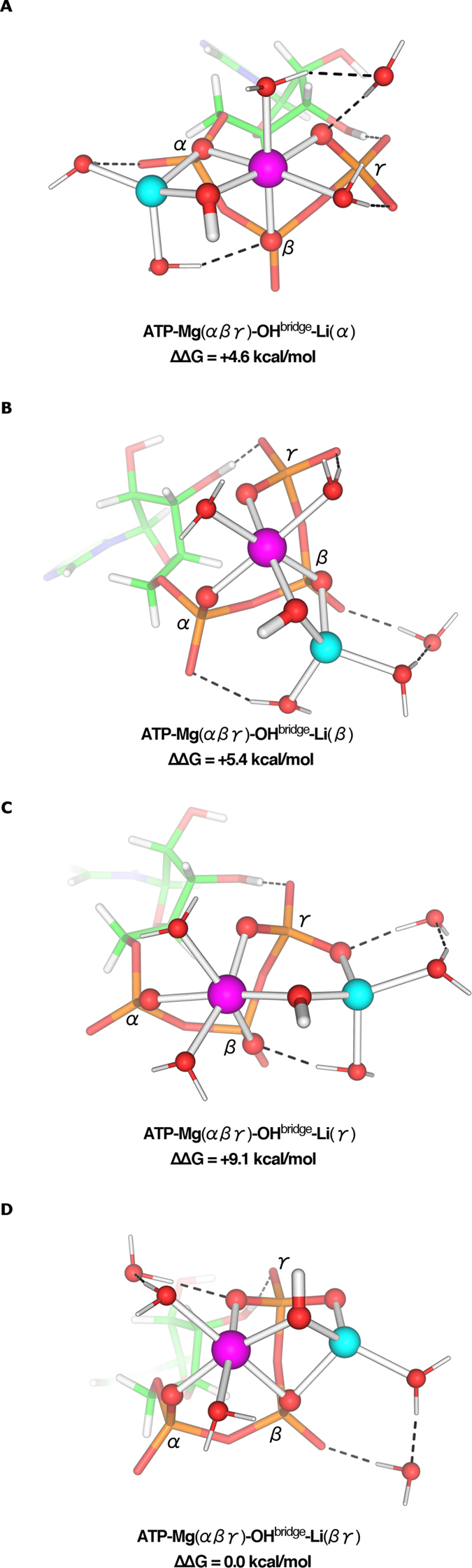
Li⁺ Prefers to Bind Bidentately to Mg-Bound ATP

Among the complexes formed by Li⁺ binding to the tridentate ATP-Mg(αβγ) structure, the most stable one corresponds to Li⁺ bidentately bound to the β and γ phosphates (Fig. 3D), as found for Li⁺ binding to free ATP. In this ATP-Mg(αβγ)-OH^bridge-Li(βγ) structure, the two metal ions and the bridging hydroxide form a four-membered ring with the β phosphate and a six-membered ring with the γ phosphate. Such a bicyclic structure cannot be formed when Li⁺ is monodentately bound to the ATP: Li⁺ forms a four or six-membered ring in the monodentate structures (Fig. 3A–C), which are less stable than the ATP-Mg(αβγ)-OH^bridge-Li(βγ) bidentate structure (by ~5–9 kcal/mol).

Since ATP-Mg-αβ and ATP-Mg-βγ (Fig. 1D,E) have comparable stabilities and are the next most stable (populated) [ATP-Mg]²⁻ conformers in solution, they were also used to derive bimetallic [ATP-Mg-Li]⁻ complexes. The fully optimized solution structures of the [ATP-Mg-Li]⁻ complexes with a bridging hydroxide (Fig. 4) are far more stable than the corresponding structures without a bridging hydroxide (Supplementary Figure S3). Relative to the free energy of the ATP-Mg(αβγ)-OH^bridge-Li(βγ) structure (Fig. 3D), the complexes formed by Li⁺ binding to the bidentate ATP-Mg(αβ) or ATP-Mg(βγ) structure are all less stable (by 5–19 kcal/mol, Fig. 4) probably because they cannot form a bicyclic structure as for the ATP-Mg(αβγ)-OH^bridge-Li(βγ) complex.

Figure 4. M062X/6-311++G(d,p) optimized structures of Li⁺ bound to ATP-Mg(αβ) (left) or ATP-Mg(βγ) (right) and relative free energies, ∆∆G (kcal/mol), of complex formation in water.

Li⁺ Does Not Significantly Alter the Mg-Bound ATP Conformation

As the triphosphate moiety conformation has been firmly locked by bi/tridentate coordination of Mg²⁺, the ATP overall conformation remains virtually unchanged upon Li⁺ binding, regardless of its coordination mode/site. The RMSD of the ATP heavy atoms in the [ATP-Mg-Li]⁻ structures (Figs 3 and 4) from those in the [ATP-Mg]²⁻ counterparts are generally ≤0.6 Å (see Supplementary Table S2), which is within the RMSD resulting from thermal fluctuations.

Discussion

Despite ATP’s importance as the major energy currency of the cell and its known existence in solution mostly as [ATP-Mg]²⁻, how its triphosphate group binds the native Mg²⁺ ion or alien cations such as Li⁺ and how its solution conformation depends on the metal ion type and metal-binding mode was not known. By computing the solution structures and free energies of various [ATP-Mg]²⁻, [ATP-Li]³⁻, and [ATP-Mg-Li]⁻ complexes differing in metal-binding mode, as summarized in Fig. 5, we have delineated the most thermodynamically preferred structures, which result mainly from a balance between “intramolecular” phosphate–metal/water interactions and “intermolecular” phosphate–solvent interactions. We show that in solution, ATP prefers to bind Mg²⁺ via all three αβγ phosphates, but it prefers to bind Li⁺ via its terminal βγ phosphates. We also show that in solution, Mg-bound ATP binds Li⁺ bidentately to form a OH-bridged ATP-Mg(αβγ)-OH^bridge-Li(βγ) complex (Fig. 3D).

Figure 5.

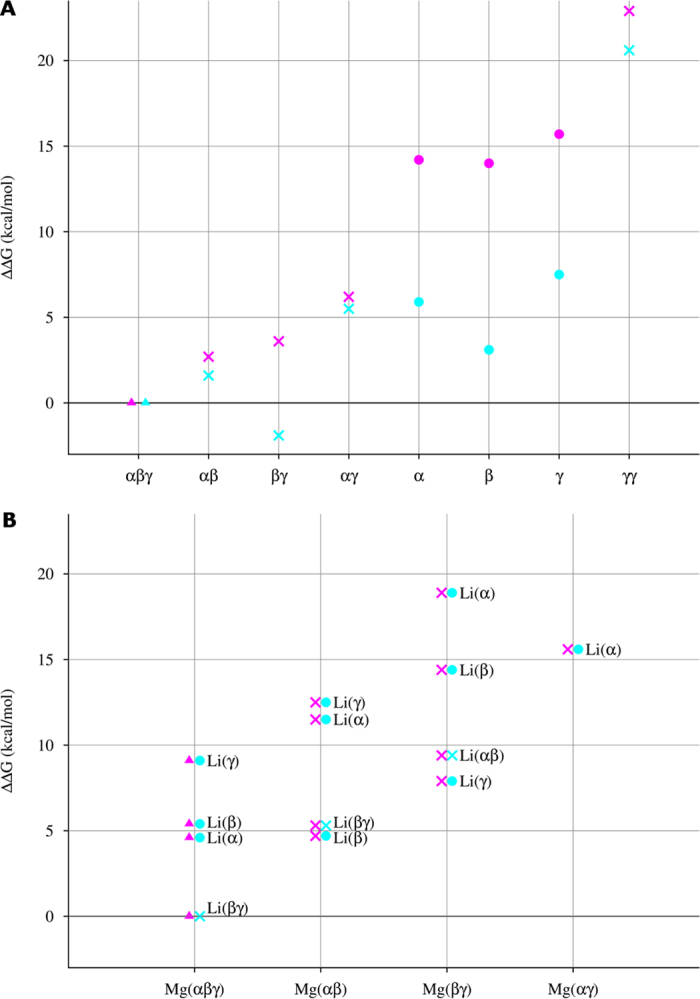
Relative solution free energies, ∆∆G (kcal/mol), of (A) [ATP-Mg]²⁻ (magenta) and [ATP-Li]³⁻ (turquoise) complexes from Figs 1 and 2, respectively, and (B) [ATP-Mg-Li]⁻ complexes from Figs 3 and 4 with the Mg- and Li-binding modes in magenta and turquoise, respectively. The filled circles, crosses and triangles denote mono, bi and tridentate binding, respectively.

The lowest free-energy solution structures of ATP-Mg (Fig. 1H) and ATP-Li (Fig. 2E) complexes yielded a free energy for [Mg(H₂O)₆]²⁺ + [Li (H₂O)₃ ATP]³⁻ → [Mg (H₂O)₅ ATP]²⁻ + [Li(H₂O)₄]⁺ (−4.2 kcal/mol, see Methods) in agreement with the corresponding experimental value (−3.5 kcal/mol¹²), thus lending support to the preferred binding modes found herein. Our finding that tridentate coordination of Mg²⁺ to ATP is slightly favored over αβ bidentate coordination is consistent with experimental estimates of ~60% tridentate coordination for [ATP-Mg]²⁻ in solution¹⁶. That Li⁺ and Mg²⁺ prefers to ligate to two and three phosphate O atoms, respectively, is in line with earlier work showing that the maximum number of metal-bound anionic O-containing ligands is two for a monocation, but three for a dication¹⁷. Notably, in a previous study¹⁰, a ATP-Mg(βγ)-H₂O^bridge-Li(γ) structure was proposed for the [ATP-Mg-Li]⁻ complex. This structure was found herein to be high-energy one: It is less stable than the corresponding hydroxide-bridged structure (Fig. 4G), which in turn is less stable than the ATP-Mg(αβγ)-OH^bridge-Li(βγ) structure by ~8 kcal/mol.

We also reveal how the metal cation type and its binding mode affect the ATP conformation. Li⁺ binding to Mg²⁺-loaded ATP did not significantly alter the ATP conformation or the properties of the P^γ–O(–P^β) bond that is hydrolyzed: The P–O bond lengths in the Mg-ATP and Mg-Li-ATP complexes are identical (1.693 Å), while the bond polarities, estimated by the difference between the P and O Hirschfeld charges, are 0.81e and 0.83e, respectively. These findings have important consequences for [ATP-Mg]²⁻ and [ATP-Mg-Li]⁻ recognition by cellular receptors/ATP-dependent enzymes. Since these two types of metal complexes have similar overall ATP conformation and P^γ–O(–P^β) bond properties, the [ATP-Mg-Li]⁻ complex might fit in the host receptor/enzyme binding site and trigger cellular response. Indeed, experiments show that [ATP-Mg-Li]⁻, like the native [ATP-Mg]²⁻ complex, is recognized by purinergic receptors and can activate subsequent signaling pathways¹⁰. Hence, Li⁺ binding to Mg²⁺-loaded ATP may permit recognition of the [ATP-Mg-Li]⁻ complex by certain host enzymes/receptors and activate specific signaling pathways. These findings thus help elucidate the mechanism of lithium’s therapeutic action.

Methods

Modeling ATP Complexes

As the pK_a of ATP ranges from 6.5–6.95¹⁸,¹⁹, its dominant form at physiological pH is ATP⁴⁻. Furthermore, ATP exists mostly as [ATP-Mg]²⁻ in neutral solution¹¹. Since Mg²⁺ is mostly hexacoordinated in complexes with organic ligands and proteins²⁰,²¹, as in aqueous solution²², hexacoordinated [Mg(H₂O)₅.ATP]²⁻ complexes were modeled. In contrast to Mg²⁺, Li⁺ is found mostly tetracoordinated²¹,²³, hence its complexes with ATP were modeled as [Li(H₂O)₃.ATP]³⁻ or [Mg(H₂O)₅.ATP.Li(H₂O)₃]⁻. Regardless of the metal-binding mode, the number of water molecules (five for Mg²⁺ and three for Li⁺ complexes) was kept the same: all water molecules were bound directly to the cation in monodentate complexes, but one and two water molecules were transferred to the second shell in bidentate and tridentate complexes, respectively. All the structures were built using GaussView version 3.09²⁴.

Geometry Optimization

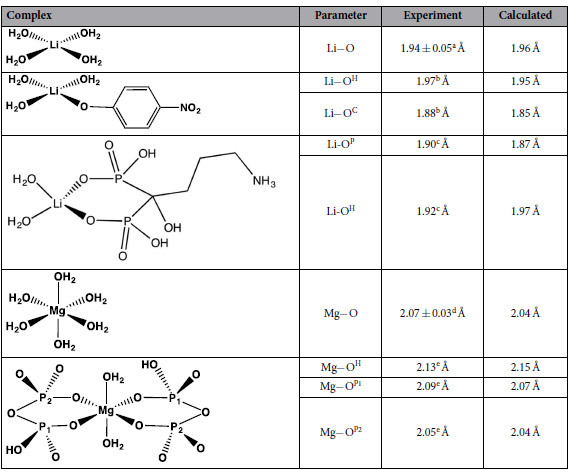
High-resolution structures of pertinent Mg²⁺ and Li⁺ complexes from the Cambridge Structural Database²⁵ (see Table 1) were used to determine an optimal method for optimizing the geometries of Mg²⁺ and Li⁺ complexes. Among the various combinations of different density functionals (B3LYP, SVWN, M062X, M06HF and BMK) and basis sets (6-31 + G(d), 6-31 + G(d,p), 6-31 + G(2d,2p), 6-31 + G(3d,p), 6-31 + G(3d,2p), 6-311++G(d,p), 6-311++G(2d,2p)) tested, the M062X/6-311++G(d,p) method was found to be the most efficient in yielding structural parameters of Mg²⁺ and Li⁺ complexes that are closest to the respective experimental values (see Table 1 and Supplementary Tables S3a–e).

Table 1. Comparison Between Computed and Experimental Average Metal−O Distances of M062X/6-311++G(d,p)-Optimized Mg²⁺ and Li⁺ Complexes.

^aFrom Dudev & Lim, 2006¹⁷. ^bCambridge Structural Database entry, FECWIT. ^cCambridge Structural Database entry, EJEZUP. ^dFrom Dudev & Lim, 2005³⁰. ^fCambridge Structural Database entry, GEQBIO.

Hence, the M062X/6-311++G(d,p) method was used to optimize the geometry of each ATP-Mg²⁺/Li⁺ complex in water employing the polarizable continuum model implemented in Gaussian 09²⁶ and to compute the respective vibrational frequencies. For each metal-binding mode/site, we modeled many structures, trying to maximize the number of water–phosphate and water–ribose/water hydrogen-bonding interactions. The optimized complex with the lowest energy was chosen for further evaluations (see below) – no imaginary frequency was found in the chosen complexes.

Solution Free Energy Calculation

The electronic energies in solution, E_el, were corrected by single-point energy calculations implementing the SMD solvation model²⁷. The thermal energies (E_th) and entropies (S) were computed from standard statistical mechanical formulas²⁸ using frequencies scaled by an empirical factor of 0.979²⁹. The differences ∆∆E_el, ∆∆E_th, and ∆∆S between the respective metal complexes were used to calculate the relative formation free energies, Δ∆G, at T = 298.15 K according to

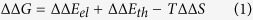The experimental binding constants of ATP-Mg (9554 M⁻¹) and ATP-Li (25 M⁻¹) complexes¹² were used to determine an optimal method for the single-point energy calculations. Since it is unclear if one or two Li⁺ ions are bound to ATP, both [Li(H₂O)₃ATP]³⁻ and [Li₂(H₂O)₆ATP]²⁻ were modelled. The lowest free-energy structures of ATP-Mg (Fig. 1), ATP-Li (Fig. 2), and Li₂ATP (Supplementary Figure S4) complexes were used to compute the solution free energy for replacing Li⁺ bound to ATP with Mg²⁺. Using single-point M062X/6-311++G(d,p) calculations, the solution free energy for [Li₂(H₂O)₆ATP]²⁻ + [Mg(H₂O)₆]²⁺ + H₂O → [Mg(H₂O)₅ATP]²⁻+2[Li(H₂O)₄]⁺ was computed to be 18.5 kcal/mol for a hydroxide molecule bridging the two Li⁺ ions. It remained positive (7.3 kcal/mol) even if a water molecule replaced the bridging hydroxide. On the other hand, the solution free energy for [Li(H₂O)₃ATP]³⁻ + [Mg(H₂O)₆]²⁺ → [Mg(H₂O)₅ATP]²⁻ + [Li(H₂O)₄]⁺ (−5.5 kcal/mol) is close to the respective experimental free energy (−3.5 kcal/mol), indicating that only one Li⁺ is likely bound to ATP.

As the M062X/6-311++G(d,p) energies overestimated the experimental free energy, single-point calculations were performed using M062X with increasing basis sets (6-311++G(2d,2p) 6-31 + G(3d,p), 6-311++G(3d,p) as well as B3-LYP with D3 dispersion correction (B3LYP-D3). With increasing basis set, the solution free energy for [Li(H₂O)₃ATP]³⁻ + [Mg(H₂O)₆]²⁺ → [Mg(H₂O)₅ATP]²⁻ + [Li(H₂O)₄]⁺ converged to a value roughly twice the experimental number using M062X, but to within 1.5 kcal/mol of the experimental free energy using B3LYP-D3 (Table 2). Since the B3LYP-D3/6-311++G(d,p) method could reproduce the experimental Li⁺ → Mg²⁺ exchange free energy in solution to within a kcal/mol, it was chosen for all single-point energy calculations.

Table 2. Computed Solution Free Energies for [Li(H₂O)₃ATP]³⁻+[Mg(H₂O)₆]²⁺ → [Mg(H₂O)₅ATP]²⁻+[Li(H₂O)₄]⁺ using Different Methods^a.

Basis Set	6-311 + G(d)	6-311++G(d)	6-311++G(d,p)	6-311++ G(2d,2p)	6-31 + G(3d,p)	6-311++G(3d,p)
# of functions	848	866	920	1149	1187	1270
M062X	−3.7	−3.6	−5.5	−6.4	−6.7	−6.9
B3LYP-D3	−2.6	−2.4	−4.2	−4.6	−5.0	−5.1

^aExperimental value of −3.5 kcal/mol is determined from the binding constants of ATP-Mg (9554 M⁻¹) and ATP-Li (25 M⁻¹) complexes from Wilson and Chin, 1991¹².

Additional Information

How to cite this article: Dudev, T. et al. How Native and Alien Metal Cations Bind ATP: Implications for Lithium as a Therapeutic Agent. Sci. Rep. 7, 42377; doi: 10.1038/srep42377 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.