Diagnostics for confounding of time-varying and other joint exposures

Abstract

The effects of joint exposures (or exposure regimes) include those of adhering to assigned treatment vs. placebo in a randomized controlled trial, duration of exposure in a cohort study, interactions between exposures, and direct effects of exposure, among others. Unlike the setting of a single point exposure (e.g. propensity score matching), there are few tools to describe confounding for joint exposures or how well a method resolves it. Investigators need tools that describe confounding in ways that are conceptually grounded and intuitive for those who read, review, and use applied research to guide policy.

We revisit the implications of exchangeability conditions that hold in sequentially randomized trials, and the bias structure that motivates the use of g-methods such as marginal structural models. From these we develop covariate balance diagnostics for joint exposures that can (1) describe time-varying confounding (2) assess whether covariates are predicted by prior exposures given their past, the indication for g-methods (3) describe residual confounding after inverse probability weighting. For each diagnostic we present time-specific metrics that encompass a wide class of joint exposures, including regimes of multivariate time-varying exposures in censored data, with multivariate point exposures as a special case. We outline how to estimate these directly or with regression and how to average them over person-time. Using a simulated example, we show how these metrics can be presented graphically.

This conceptually grounded framework can potentially aid the transparent design, analysis, and reporting of studies that examine joint exposures. We provide easy-to-use tools to implement it.

INTRODUCTION

The effects of joint exposures (or exposure regimes) are of wide interest. These include the effect of adhering to treatment vs. placebo in a randomized controlled trial, duration of exposure in a cohort study, interactions between exposures, and direct effects of exposure, among others. Rarely are they pursued with designs that conditionally randomize each exposure given exposure history, so most studies suffer time-varying confounding. To control for this, investigators measure and adjust for time-varying covariates that predict exposures and the outcome.

When covariates are affected by exposure or its unmeasured cause—we call this exposure-covariate feedback—conventional adjustments may yield bias.^1–3 Other approaches known as g-methods avoid this bias.⁴ These include g-estimation of structural nested models,⁵ the parametric g-formula,⁶ and inverse probability weighted estimation of marginal structural models.⁷ This last method is by far the most popular and appears in substantive journals.^8–10

Unfortunately, there are few tools to describe how exposure regimes are confounded. First, some studies report how time-varying covariates distribute over person-time without accounting for exposure history. Second, there are few tools to inform whether g-methods are needed to adjust for confounding. Many investigators justify their choice to use g-methods (or not) on substantive grounds alone. Even those who do use g-methods could obtain more efficient estimates if they knew which covariates they could stratify on without inducing bias. Third, implementing g-methods involves layers of modeling decisions and their impact on residual confounding is usually expressed (if at all) in opaque summary statistics. These summaries may not be intuitive for those who read, review, and use research to guide policy. This paper aims to provide a conceptually-grounded framework to describe confounding of time-varying exposures and other joint exposures, assess whether g-methods are indicated to adjust for it, and evaluate how well certain g-methods resolve it.

DIAGNOSTIC FRAMEWORK

Overview

Our framework contains three diagnostics for confounding. Each involves some form of covariate balance. Diagnostic 1 describes how exposures relate to prior covariates within levels of exposure history (for time-varying confounding). Diagnostic 2 describes how covariates relate to prior exposures given the exposures’ past (for exposure-covariate feedback). Diagnostic 3 is a weighted analogue of Diagnostic 1 for residual time-varying confounding in marginal structural models (see eAppendix for the parametric g-formula). These are summarized in Table 1 for a single time-varying exposure, our focus here. In the eAppendix we extend these to multivariate time-varying exposures, of which multivariate point exposures are a special case. We begin with diagnostics for uncensored data, and then address interpretations and adaptations for right-censored data. Afterwards we outline how to estimate these time-specific metrics and their averages over person-time.

Table 1.

Time-specific balance metrics for confounding of a time-varying exposure A(t) by time-varying covariates C(t) in the presence of censoring S(t)

Diagnostic 1: Time-varying confounding i.e. C(t − k) across levels of A(t) (for all t ∈ {0, …, t} and chosen k ∈ {0, …, t} where 0 ≤ k ≤ t′)
Balance metrica	Definitions
E[C(t − k)|A(t) = a′,Ā(t − 1),S̄(t) = 0] − E[C(t − k)|A(t) = a″,Ā(t − 1),S(t) = 0]	N/A
Diagnostic 2: Exposure-covariate feedback i.e. C(t) across levels of A(t − k) (for all t ∈ {0, …, t} and all k ∈ {1, …, t} where 1 ≤ k ≤ t′)
Balance metrica
a. by inverse probability weighting	Weight Was(t−k) = Wa(t−k) × Ws(t)
E[Wa′s(t−k) × I(A(t−k) = a′)×C(t)|Ā(t − k − 1), S̄(t) = 0] − E[Wa″s(t−k) × C(t)|Ā(t − k − 1), S̄(t) = 0]	$W_{a(t-k)}=\frac{P[A(t-k)=a\mid \overline{A}(t-k-1),\overline{S}(t-k)=0]}{P[A(t-k)=a\mid \overline{A}(t-k-1),\overline{C}(t-k),\overline{S}(t-k)=0]}$ $W_{s(t)}={\prod }_{k=0}^{k=t}\frac{P[S(t-k)=0\mid \overline{S}(t-k-1)=0]}{P[S(t-k)=0\mid \overline{S}(t-k-1)=0,\overline{A}(t-k-1),\overline{C}(t-k-1)]}$
b. by propensity score stratificationb	Propensity score ea(t−k) and weight Ws(t)
E[Ws(t − k) × I(A(t − k) = a′ × C(t)|ea′(t − k),S̄(t) = 0] − E[Ws(t − k) × I(A(t − k) = a″ × C(t)|ea′(t − k),S̄(t) = 0]	ea(t −k) = P[A(t − k) = a′|Ā(t − k − 1), S̄(t − k) = 0 $W_{s(t)}={\prod }_{k=0}^{k=t}\frac{P[S(t-k)=0\mid \overline{S}(t-k-1)=0]}{P[S(t-k)=0\mid \overline{S}(t-k-1)=0,\overline{A}(t-k-1),\overline{C}(t-k-1)]}$
Diagnostic 3: Residual time-varying confounding i.e. C(t − k) across levels of A(t) (for all t ∈ {0, …, t} and chosen k ∈ {0, …, t} where 0 ≤ k ≤ t′)
Balance metrica	Weight Wa(t)
E[Wa′(t) × I(A(t) = a′) × C(t − k)|Ā(t − 1),S̄(t) = 0] − E[Wa″(t) × I(A(t) = a″) × C(t − k)|Ā(t − 1), S̄(t) = 0]	$W_{a(t)}={\prod }_{k=0}^{k=t}\frac{P[A(t-k)=a\mid \overline{A}(t-k-1),\overline{S}(t-k)=0]}{P[A(t-k)=a\mid \overline{A}(t-k-1),\overline{C}(t-k),\overline{S}(t-k)=0]}$

^aThese balance metrics are on the mean difference scale. They can be reported on the standardized mean difference scale by dividing by the (unweighted) pooled standard deviation conditional on exposure history (for Diagnostics 1, 2a and 3) or propensity-score strata (for Diagnostic 2b). Doing so places metrics for binary and continuous covariates on the same scale.

^bFor categorical exposures one needs to jointly condition on the predicted probabilities for each non-referent exposure level

We measure covariate balance using the mean difference between any arbitrary level of exposure a′ and a common referent a″. This difference contributes to bias expressions for confounding of the average exposure effect in the entire population, and also among the exposed.¹¹ Other measures could be used, however, including novel bias metrics that incorporate empirical data on the covariate-outcome relationship (see eAppendix). We argue that, for causal inference, these diagnostics are best applied to specific regimes of interest as they evolve. For simplicity we reserve this detail for the Discussion and eAppendix.

We now structurally define our use of the terms time-varying confounding and exposure-covariate feedback. On a causal directed acyclic graph (DAG),¹² time-varying confounding occurs when, for any exposure in a regime, conditioning on its exposure history does not block all backdoor paths linking it to the outcome.¹³ Exposure-covariate feedback occurs when any measured covariate (used to block a backdoor path) is affected by exposure or an unmeasured cause of prior exposure.³ Note that Hernán and Robins have coined this latter phenomenon treatment-confounder feedback.¹⁴ The literature lacks standard nomenclatures for these phenomena.

SIMULATED EXAMPLE AND NOTATION

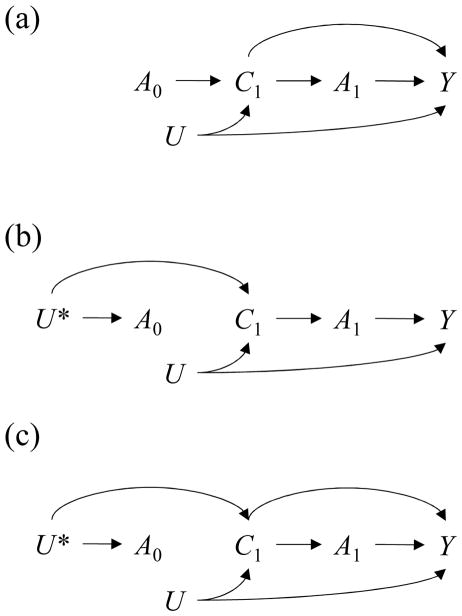
To illustrate how to report the diagnostics succinctly, we simulated data on a time-varying binary exposure A(t) randomized at baseline, a vector of five binary covariates C(t) = L(t), M(t), N(t), O(t), P(t) that vary over time (some affected by exposure), an unmeasured variable U, and censoring indicators S(t) where 1=censored and 0=otherwise. These data were generated according to the structure shown in Figure 1a (without censoring) and also Figure 1c (with censoring). Our analyses did not require data on the outcome Y so we did not simulate it. Had we done so, it would have been affected by all prior variables. Data were generated for times t = 0,1,2 with S(t), C(t), and A(t) occurring in that order. See the eAppendix ‘Details of Example Simulations’ for details.

Figure 1.

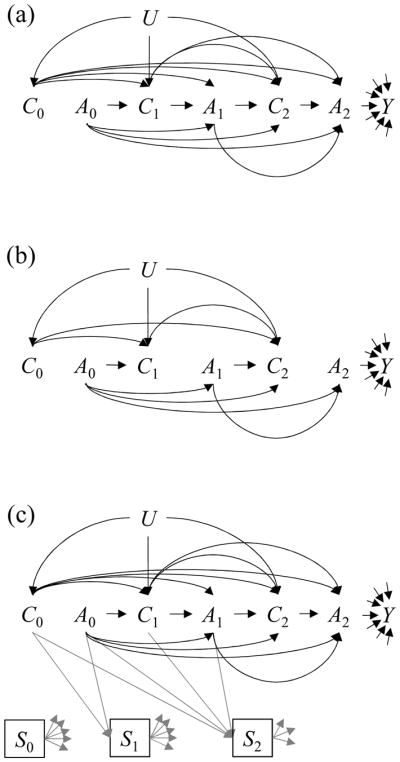
Causal Directed Acyclic Graphs describing unmeasured covariate U, measured covariates C(t), exposures A(t), and outcome Y for a hypothetical trial where exposure is randomized (a) at baseline only (b) at each time within levels of past exposure (c) at baseline only, with continuing data collection among the uncensored at time t i.e. S(t) = 0.

For notation, let V̄(t) be a historical vector of random variable V through time t i.e. V(0), …, V(t). Let k index the amount of time by which a variable precedes time t. Let V_x̄ represent the counterfactual value that V would have realized had the sequence of X̄ been set to regime x̄. In our simulation an example regime ā might be “always exposed” (A(0) = 1, A(1) = 1, A(2) = 1). Let the expression V ∐ A | C represent statistical independence between V and A conditional on C. The indicator function I(·) equals one if true and zero otherwise.

Diagnostics for a Time-Varying Exposure without Censoring

Diagnostic 1: time-varying confounding in the study population

The exchangeability assumptions used to estimate causal effects of exposure regimes imply certain data patterns under confounding vs. no confounding. Consider the DAG in Figure 1a where exposure is randomly assigned at baseline but not during follow-up. There is confounding because, for some exposures A(t), conditioning on exposure history Ā(t − 1) does not block all backdoor paths linking them to the outcome Y. Conditioning on exposure history in a longitudinal study of this kind would not render each exposure independent of prior covariates that predict the outcome.

When we assume exchangeability given exposure and covariate history Y_ā∐A(t)|Ā(t − 1), C̄(t), we imply that exposure and covariate histories can be used to block the backdoor paths. But in Figure 1b where each exposure is conditionally randomized given exposure history, the only backdoor paths are through prior exposures. A stronger form of exchangeability Y_ā∐A(t)|Ā(t − 1) holds and exposure regimes are not confounded.¹³ As a result, each exposure is independent of prior covariates given its own history C̄(t)∐A(t)|Ā(t − 1).^13,15 This testable property—statistical exogeneity—speaks to measured confounding.

Investigators address confounding by adjusting for covariates or their surrogates. While there are many ways to select variables for this purpose,^16,17 drawing causal inference presumes that the ones chosen can grant exchangeability Y_ā∐A(t)|Ā(t − 1), C̄(t). In this setting, every departure from statistical exogeneity is of concern.

Having selected covariates to satisfy exchangeability Y_ā∐A(t)|Ā(t − 1), C̄(t), one can describe confounding by evaluating, for each exposure measurement, the balance of prior covariates within levels of exposure history (Diagnostic 1):

$$E[C(t-k)\mid A(t)=a^{\prime },\overline{A}(t-1)]-E[C(t-k)\mid A(t)=a^{″},\overline{A}(t-1)]$$

where 0 ≤ k ≤ t. These time-specific metrics could be reported on a trellised plot,¹⁸ as shown in Figure 2. With many measurements one can report metrics for selected times or, as we later describe, averages over person-time. Note that the diagnostic adjusts for exposure history (eFigure 1a). Otherwise it could mislead by capturing imbalance for covariates that do not confound current exposure but are affected by prior exposure (e.g. in Figure 1b there is an association between A(1) and C(1) but it is completely through prior exposure A(0)).

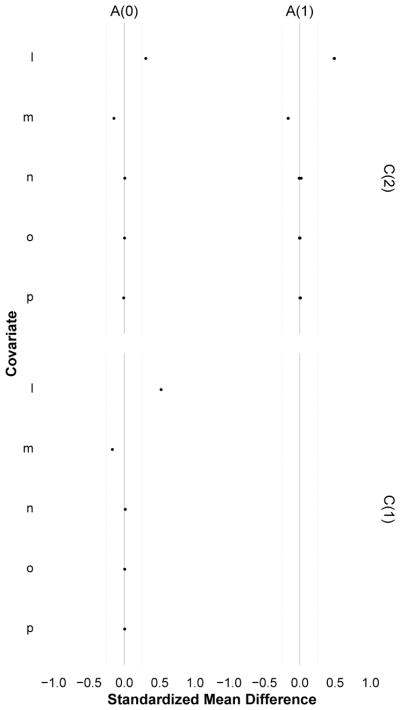
Figure 2.

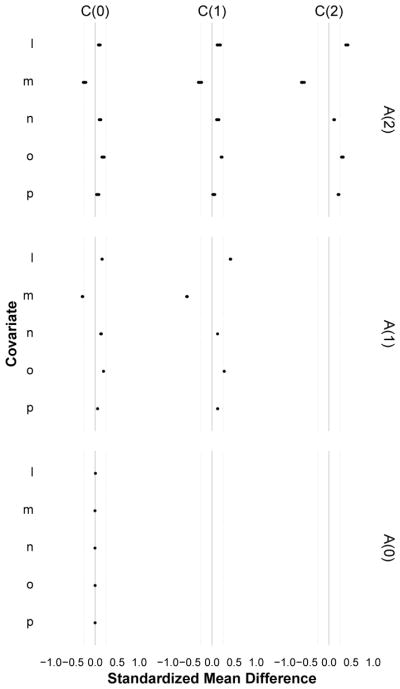
A trellised covariate balance plot for Diagnostic 1 (time varying confounding), indexed by measurement times for exposure (rows) and covariates (columns). Each subplot evaluates the balance of covariates C (i.e. L,M,N,O,P) at time t − k across levels of exposure A = 1 versus A = 0 at time t, for each pattern of exposure history through time t − 1 (dots). When every dot in a horizontal plane aligns at zero, that exposure measurement is not confounded by that covariate. When this holds for all exposure measurements (across all covariates), the exposure is statistically exogenous and there is no measured time-varying confounding. In the simulated data example shown here, imbalance was largest for the most recent covariates and decayed with increasing distance between exposure and covariate times; there was no confounding at t = 0 but the pattern of confounding was the same for t = 1 and t = 2; the least balanced covariates were L (higher among the exposed) and M (higher among the unexposed), and N was the least imbalanced. Note that here, all observed exposure regimes were examined.

Diagnostic 2: exposure-covariate feedback in the study population

Having described the chosen covariate history’s departure from statistical exogeneity, the next step is to assess whether covariates are predicted by any prior exposure given its past, to determine whether g-methods are needed to adjust for them. Any estimator that merely stratifies on covariates involved in feedback with exposure could block exposure effects or suffer selection bias, while g-methods avoid these problems.⁴ The selection bias would arise when the association between the covariate and a prior exposure is causal (Figure 3a) or through a shared but unmeasured cause (Figure 3b).³ Any metric of exposure-covariate feedback should capture both sources of association by adjusting for covariates that precede the exposure.

Figure 3.

Causal Directed Acyclic Graphs describing a hypothetical study with exposures A(t), measured covariates C(t), and unmeasured variables U^* and U, and also outcome Y. Each scenario represents a different structure of bias due to exposure-covariate feedback. In scenario (a) stratifying on C(1) will block the effect of A(0) and Y and open the non-causal path 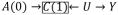. In scenarios (b) and (c) stratifying on C(1) opens the non-causal pathway 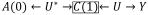. In all scenarios, adjusting for C(1) by stratification leads to bias. Adjusting by a g-method e.g. removing the arrow from C(1) to A(1) does not induce bias. Note that in (c) there is unmeasured confounding by U^* from the path A(0) ← U^* → C(1) → Y and g-methods will not remove it. Because Diagnostic 2 would pick up this unmeasured confounding as an imbalance e.g. A(0) ← U^* → C(1), it is most interpretable when investigators are diagnosing covariate history sufficient enough to support exchangeability assumptions (i.e. no unmeasured confounding).

One could test for exposure-covariate feedback by regressing covariate measurements on prior exposures and covariates (the test is whether all exposure parameters equal zero).¹⁹ But such models must be correctly specified. An alternative is to examine associations between covariates and prior exposures that are statistically exogenous i.e. independent of prior covariates given exposure history (after inverse probability weighting or propensity score stratification). One could evaluate the weighted balance of every covariate measurement across each prior exposure, within levels of exposure history preceding that exposure (Diagnostic 2a):

$$E\left[W_{a^{\prime }(t-k)}\times I(A(t-k)=a^{\prime })\times C(t)\mid \overline{A}(t-k-1)\right]-E\left[W_{a^{″}(t-k)}\times I(A(t-k)=a^{″})\times C(t)\mid \overline{A}(t-k-1)\right]$$

where 1 ≤ k ≤ t and the weight is the stabilized inverse probability of the prior exposure at time t − k:

$$W_{a(t-k)}=\frac{P[A(t-k)=a\mid \overline{A}(t-k-1)]}{P[A(t-k)=a\mid \overline{A}(t-k-1),\overline{C}(t-k)]}$$

Estimating these weights requires correctly specified models for each exposure measurement given prior exposure and covariate histories (that block all backdoor paths linking that exposure to the outcome). This yields weighted populations where the exposure is statistically exogenous.²⁰ Any imbalance will reflect the association from that exposureds causal and confounded relationships with the covariate (see eFigure 1b).

The same goal can be achieved through propensity-score stratification. For binary exposures, one could diagnose exposure-covariate feedback by evaluating the balance of every covariate measurement across each prior exposure within levels of its propensity-score (Diagnostic 2b):

$$E\left[C(t)\mid A(t-k)=a^{\prime },e_{a^{\prime }(t-k)}\right]-E\left[C(t)\mid A(t-k)=a^{″},e_{a^{\prime }(t-k)}\right]$$

where 1 ≤ k ≤ t and the propensity score is the probability that the prior exposure equals the non-referent value given the past:

$$e_{a^{\prime }(t-k)}=P[A(t-k)=a^{\prime }\mid \overline{A}(t-k-1),\overline{C}(t-k)]$$

For categorical exposures one must jointly condition on the estimated probability of each non-referent exposure value given the past. Provided correctly specified models for these quantities, exposures will be statistically exogenous among those with the same propensity score²¹ or, more generally, the propensity score function²² (as shown in eFigure 1c). Any imbalance will reflect the association from that exposure’s causal and confounded relationships with the covariate. Propensity score values are usually coarsened into strata that retain statistical exogeneity. For a categorical exposure with n levels, predicted values for each level are coarsened into j classes, so that the final strata are locations on a jⁿ⁻¹ dimensional grid formed by crossing the classes for all but one exposure level. As shown in Figure 4, metrics from Diagnostic 2a could be reported as a trellised plot and, as with Diagnostic 1, for specific times or as averages over person-time.

Figure 4.

A trellised covariate balance plot for Diagnostic 2a (exposure-covariate feedback), indexed by measurement times for covariates (rows) and exposure (columns). Each subplot evaluates the balance of covariates C (i.e. L,M,N,O,P) at time t across levels of exposure A = 1 versus A = 0 at time t − k, for each pattern of exposure history through time t − k − 1 (dots). For Diagnostic 2b, the plot would pertain to a specific propensity score stratum and unlike Diagnostic 2a, the dots would not represent a specific exposure history. When all the dots in a horizontal plane align at zero, the covariate measurement is independent of every prior exposure and does not contribute to exposure-covariate feedback. When this holds for every covariate measurement, there is no exposure-covariate feedback. In the simulated data example, covariate measurements for L and M were associated with previous exposures: for L the associations were strong and positive; for M they were weaker and negative. In this simulated data, any causal analysis of exposure regimes would want to consider adjusting for L and M using g-methods. Note that here, all observed exposure regimes were examined.

Diagnostic 3: residual time-varying confounding in the weighted population

Many investigators fit marginal structural models via inverse probability weights to estimate the average causal effect of an exposure regime. Given enough covariate history to grant exchangeability Y_ā∐A(t)|Ā(t − 1), C̄(t), one could fit a marginal structural model by applying a cumulative inverse probability weight for each exposure measurement, formed from models for each exposure A(t) given covariate history C̄(t) and exposure history Ā(t − 1).^7,23 Hernán and Robins²⁰ proved that if the models for exposure are correctly specified and positivity holds, each exposure in the weighted population would be statistically exogenous. A departure from statistical exogeneity would reflect residual confounding and can result from positivity violations, finite sample bias, or when the models or weights are misspecified (e.g. by truncating their values).

The current standard for diagnosing residual confounding in the weighted population is to examine whether, for all exposure times, the mean of the stabilized weights diverges from one.²³ The rationale is that, for each covariate stratum, weights that create equally sized exposure groups will average to one. So this practice can alert us to residual confounding, but it will not tell us which covariates to suspect, because it only assesses departures from statistical exogeneity in aggregate. And, although the mean of correctly specified weights must equal one, the mean of misspecified weights could still approach one (when the weights’ mean do not equal one for some covariate strata but cancel out across strata). Because this standard can understate residual confounding, it would be better used in concert with other diagnostics.

To further investigate residual confounding, we can examine, for each exposure measurement, the weighted balance of prior covariates within levels of exposure history (Diagnostic 3):

$$E\left[W_{a^{\prime }(t)}\times I(A(t)=a^{\prime })\times C(t-k)\mid \overline{A}(t-1)\right]-E\left[W_{a^{″}(t)}\times I(A(t)=a^{″})\times C(t-k)\mid \overline{A}(t-1)\right]$$

where 0 ≤ k ≤ t and the weight is a stabilized cumulative inverse probability weight for current exposure at time t, perhaps

$$W_{a(t)}={\prod }_{k=0}^{k=t}\frac{P[A(t-k)=a\mid \overline{A}(t-k-1)]}{P[A(t-k)=a\mid \overline{A}(t-k-1),\overline{C}(t-k)]}$$

to target the average causal effect. This diagnostic appropriately adjusts for exposure history (eFigure 1d) and can summarize residual imbalance in any weighted population, even for covariates that the weights ignore. It can be estimated within levels of baseline covariates that appear in both the weight numerator and denominator (that a marginal structural model would also condition on) by using regression models that we later describe. These metrics could be plotted in the same manner as those from Diagnostic 1 (see eFigure 2). An important use of Diagnostic 3 will be to examine residual imbalance under post-hoc model and weight specifications, as we demonstrate in Figure 5.

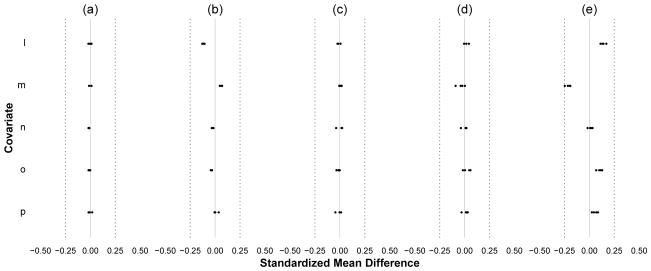
Figure 5.

Demonstration of Diagnostic 3 (residual imbalance in the weighted population) under various sources of residual confounding. Here, we present the balance for covariates and exposures measured at time t = 2. Scenario (a) correct specification of the exposure model. Scenario (b) mis-specification of the exposure model for A(t) by only including recent covariates C(t) and omitting covariate-covariate interactions. Scenarios (c) through (e) have correct specification of the exposure model but with random positivity violations built into the data-generating model for A(t) such that P[A(t)|Ā(t − 1), C̄(t)] = 1/10,000,000 when L(t) = 0 and O(t) = 1. In Scenario (c) the weights are not truncated. In (d) they are truncated to the 1st and 99th percentiles. In (e) they are truncated to the 10th and 90th percentiles. Scenarios (b) through (d) all contained residual confounding which appeared as imbalances for Diagnostic 3.

Diagnostics for a Time-Varying Exposure with Censoring

Until now we have assumed complete follow-up for all subjects. But study-dropout and competing events can affect whether data at time t are observed. In this section we describe how to interpret and adapt the diagnostics under right censoring. In Table 1 we present formulae for diagnostics of a single time-varying exposure that accommodate censoring (see eAppendix Table 1 for multivariate time-varying exposures).

Diagnostics 1 and 3 for Censored Data

Diagnostic 1 can capture selection-bias in censored data. As an example, consider the DAG in Figure 1c where exposure A(2) and outcome Y are linked through censoring S(2), a collider that has been conditioned on³ e.g. 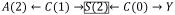. Diagnostic 1 would reflect this selection-bias as an imbalance of C(0) across A(2). Diagnostic 3 can also capture residual selection-bias to the degree that the cumulative inverse probability weights fail to produce statistical exogeneity in the weighted population, leaving paths like 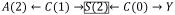possibly attenuated but nonetheless intact. Note that Diagnostics 1 and 3, as specified in Table 1, only capture selection-bias through censoring up to time t, but not after that point.

It is important to also examine statistical exogeneity for censoring. Some tools to address censoring view it as another treatment,⁷ such that the underlying causal question concerns a joint intervention on exposure and censoring. Assumptions of exchangeability, positivity, and consistency apply for both, even if the implications for bias are somewhat subtle.²⁴ One can examine statistical exogeneity for exposures A(t) first, and then censoring S(t) second, conditional on uncensored exposure history, both in the actual study population and after applying joint inverse probability weights for exposure and censoring.⁷ This is a special case of Diagnostics 1 and 3 for multivariate time-varying exposures (see eAppendix).

Diagnostic 2 for Censored Data

When censoring is associated with exposure and covariates, it can bias assessments of exposure-covariate feedback, even when the query concerns a randomized exposure’s effect on a covariate (consider the open path in Figure 1c). Whenever the exposure’s association with censoring is not through measured covariates on backdoor paths, our original proposal for Diagnostic 2 will pick up the selection-bias as an imbalance. But this source of imbalance does not motivate the use of g-methods. To see this, consider Figure 1c again. If we studied the effect of a regime involving A(0), A(1) and A(2) on Y while stratifying on C(0), C(1) and C(2), the path 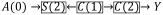would be blocked. The joint effect of A(0), A(1) and A(2) on Y would still suffer selection bias e.g. 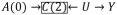, but this involves A(0)’s causal relationship with C(2). Their association through censoring is irrelevant.

Under strong assumptions, we can modify Diagnostic 2 to recover associations between covariates and prior exposures that do motivate g-methods: ones that are causal or through unmeasured common causes. To do so we must measure the variables needed to block all backdoor paths linking censoring to future covariates. With these we fit models for remaining uncensored at each time t − k, e.g.:

$$\text{logit}P[S(t-k)=0\mid \overline{A}(t-k-1),\overline{C}(t-k-1),\overline{S}(t-k-1)=0]={\gamma }_0+{\gamma }_1^{\prime }\overline{A}(t-k-1)+{\gamma }_2^{\prime }\overline{C}(t-k-1)$$

were 0 ≤ k ≤ t. The predicted probabilities from these models become the denominator of time-specific inverse probability weights, one for each time t − k. The weight numerators are the probability of remaining uncensored at time t − k among those present at time t − k − 1. Taking the product of these weights from baseline through time t gives the time-specific cumulative inverse probability weights for each uncensored observation:

$$W_{s(t)}={\prod }_{k=0}^{k=t}\frac{P[S(t-k)=0\mid \overline{S}(t-k-1)=0]}{P[S(t-k)=0\mid \overline{S}(t-k-1)=0,\overline{A}(t-k-1),\overline{C}(t-k-1)]}$$

Diagnostic 2 is then estimated in the weighted population (for Diagnostic 2a the final weight is the product between this cumulative censoring weight and the time-specific exposure weight). Provided that the weights and models are specified correctly, and no strata are deterministically censored,²⁵ the selection-bias will be purged from the weighted data where censoring is a random process (see eFigures 3b and 3c). When these conditions are not met there will be residual bias in Diagnostic 2.

Estimating Diagnostic 2 in censored data requires care. While the final metric only uses data from the uncensored at time t, the model for the exposure is fit among the uncensored at time t − k. If the cumulative censoring weight is incorporated, models for remaining uncensored at each time t − k are fit among those present at time t − k − 1. (Note that while the censoring weight denominators condition on prior exposure, the numerators do not because doing so could reintroduce selection-bias via paths like 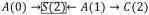in Figure 1c). The cumulative censoring weight can be omitted when investigators artificially censor observations based on their exposure history before time t − k to focus Diagnostic 2 on specific regimes (when that is the only censoring mechanism). For reasons elaborated elsewhere,^26,27 it seems prudent to incorporate it whenever censoring is informative of future covariates.

ESTIMATING TIME-SPECIFIC AND SUMMARY DIAGNOSTICS

Each diagnostic can be estimated using a special data structure. With a slight shift in notation, they can all be expressed as weighted measures of covariate balance Q_x(τ) contrasting covariate means measured at time τ_c, across exposure values a′ versus a″ measured at time τ, within strata X(τ) defined by exposure history H(τ) (i.e. Ā(τ − 1)) or the propensity score e(τ). The distance between exposure and covariate times can be represented as k (which equals |τ − τ_c|). To estimate Q_x(τ), one could first structure the data so that each row is a person-time observation classified by the exposure value, its measurement time and history; the covariate name, its value and measurement time; and finally a weight that equals one for unweighted diagnostics. Data scientists would call this format “tidy” because the key observation of interest is the pairing of exposure-covariate measurements.²⁸ For a given covariate, one would take weighted means within joint levels of the exposure value, timing of the exposure and covariate measurements, and strata X(τ). The results could be used to directly estimate any of the metrics.

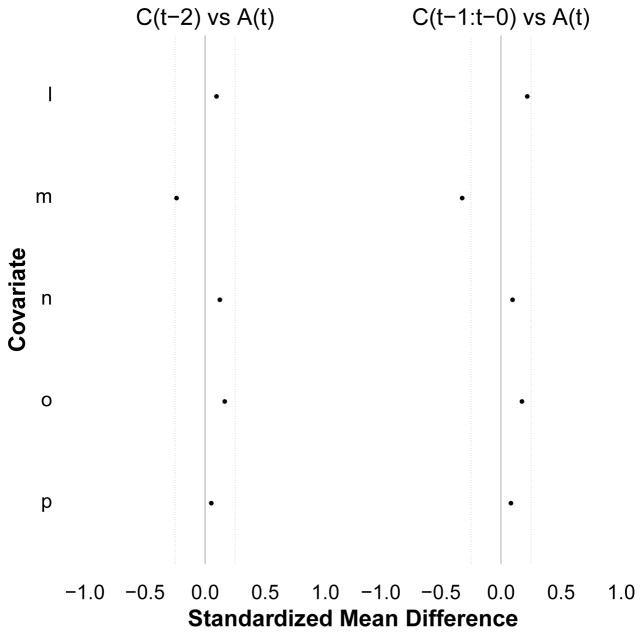
The metrics can be averaged over the person-time distribution up to a desired level. For example, when regimes of interest incorporate values from categorical exposures one could begin by standardizing over the non-referent values within levels of history, time, and distance. Going on to standardize over exposure history yields the average balance for each time and distance pair τ, k. Standardizing further over time yields the average balance for each distance k (an analogous plot appears in eFigure 4). One could finally standardize over distance, across all k or among partitions of k (an example plot appears in Figure 6). These summary metrics and their interpretations, which are formally presented in Table 2, will be most useful in longitudinal studies with many measurement times.

Figure 6.

A trellised plot for Diagnostic 1 among the uncensored, after averaging over exposure history, time, and segments of distance. The panels are indexed by segments of distance between exposure and covariate measurement times (columns). The right panel reports the summary metrics that assess the average balance (adjusting for exposure history) between exposures and proximal covariates at one unit of distance or less: A(1) vs. C(0), A(2) vs. C(1), A(0) vs C(0), A(1) vs C(1), A(2) vs. C(2). The left panel reports the analogous balance metric at two units of distance: A(2) vs. C(0). The average balance across these pools of person-time appear similar, and reflect the same patterns described in Figure 2. Note that here, all observed exposure regimes among the uncensored were examined. Note also that, because censoring is present, this diagnostic should be repeated to assess statistical exogeneity for censoring at time t within levels of uncensored exposure history through time t − 1 (e.g. eFigure 5).

Table 2.

Summary balance metrics averaged over person-time by standardization

Time-specific metrics for Diagnostics 1, 2a, and 3 have the general forma,b: $$Q_{H(\tau ),\tau ,k}=E[W(\tau )\times I(A(\tau )=a^{\prime })\times C({\tau }_c)\mid H(\tau ),\tau ,k]-E[W(\tau )\times I(A(\tau )=a^{″})\times C({\tau }_c)\mid H(\tau ),\tau ,k]$$ Where k is the distance between the covariate time τc and the exposure time τ i.e. k = |τ − τc|. H(τ) is the exposure history at time τ i.e. A(τ − 1); W(τ) is equal to one or an inverse probability weight, and follows the exposure time τ except for Diagnostic 2 under censoring where it follows covariate time τc. Each diagnostic QH(τ),τ,k is estimated from weighted person-timec: $$N_{H(\tau ),\tau ,k}=\sum W(\tau )\times I(A(\tau )=a^{\prime })\mid H(\tau ),\tau ,k+\sum W(\tau )\times I(A(\tau )=a^{″})\mid H(\tau ),\tau ,k$$
Summary metric	Example Interpretation for Diagnostic 1
Average over exposure history H(τ)c
${\overline{Q}}_{\tau ,k}={\displaystyle \sum _{H(\tau )}}(Q_{H(\tau ),\tau ,k}\times N_{H(\tau ),\tau ,k})/{\displaystyle \sum _{H(\tau )}}{N}_{H(\tau ),\tau ,k}$	The average balance for exposure A assessed at time 2 and covariate C assessed at time 1 is…
Average over exposure history H(τ) and time τ
${\overline{Q}}_k={\displaystyle \sum _{H(\tau ),\tau }}(Q_{H(\tau ),\tau ,k}\times N_{H(\tau ),\tau ,k})/{\displaystyle \sum _{H(\tau ),\tau }}{N}_{H(\tau ),\tau ,k}$	The average balance for exposure A at any given time τ and covariate C assessed at time τ − 1 is…
Average over exposure history H(τ), time τ, and distance kd
$\overline{Q}={\displaystyle \sum _{H(\tau ),\tau ,k}}(Q_{H(\tau ),\tau ,k}\times N_{H(\tau ),\tau ,k})/{\displaystyle \sum _{H(\tau ),\tau ,k}}{N}_{H(\tau ),\tau ,k}$	The average balance for exposure A assessed at any given time and covariate C assessed at any prior time is…

^aFor Diagnostic 2b replace exposure history H(τ) with propensity score strata e(τ). The standardization over person-time defined by e(τ) gives the average balance for an exposure assessed at a specific time τ and a covariate assessed at a specific time τ_c

^bWe omitted censoring here to simplify the expressions but this can be incorporated as in Table 1 or eAppendix Table 1

^cThe time-specific metrics are implicitly indexed by their non-referent value a′. When there are many such values, one can first average metrics over the non-referent person-time distribution within levels of exposure history H(τ), time τ, distance k. The person-time contributing to this metric is the sum over all exposure levels. This metric can then be averaged over exposure history, time, and distance.

^dOne can first define disjoint ranges of distance p, and then average over distance k for each range p. An example interpretation for Diagnostic 1 would be “the average balance for exposure A assessed at time τ and covariate C assessed anywhere between time τ − 1 and τ − 10.”

Alternatively, one could use models to estimate Q_x(τ) and summary metrics from this same person-time dataset. Take Diagnostic 1 or 3 with a binary exposure, for example. For each covariate name, one could subset to where covariates precede exposure (τ_c ≤ τ) and regress the covariate value C(τ_c) on the exposure value A(τ), exposure history H(τ), exposure time τ, and covariate distance k e.g. a linear model for E[C(τ_c)|A(τ), H(τ), τ, k], possibly weighted by the inverse probability of exposure and/or censoring. If this model were saturated, parameter combinations involving A(τ) would yield the same estimates as the formulae in Table 1. This model would be hard to fit, so one might specify a simpler model with just main effects and first-order interactions with exposure A(τ):

$$E[C({\tau }_c)\mid A(\tau ),H(\tau ),\tau ,k]={\beta }_0+{\beta }_{1}A(\tau )+{\beta }_{2}H(\tau )+{\beta }_3\tau +{\beta }_{4}k+A(\tau )\times ({\beta }_{5}H(\tau )+{\beta }_6\tau +{\beta }_{7}k)$$

where τ_c ≤ τ. In this model, the balance metric is allowed to vary by exposure history, time, and distance. If β₅ = 0 then the diagnostic parameter is constant over exposure history H(τ); if also β₆ = 0 it is constant over time τ; and if also β₇ = 0, it is constant over distance k. One could assume these constraints and omit the corresponding parameters. But the summary estimates would be biased if the assumptions made were false. In contrast, pooling estimates by standardization does not require that the diagnostic parameter be constant over any partition of person-time. Nor does it require a correctly specified model for covariate measurements. Although pooling estimates by regression might handle values from continuous exposures and yield summaries for sparse data, these may rely on extrapolations that are hard to justify. The regression approach may be favored when investigators need to condition metrics on baseline covariates. These arguments also apply to models for Diagnostic 2 i.e. models for E[C(τ_c)|A(τ), H(τ), τ, k] where τ < τ_c.

DISCUSSION

We have outlined a framework to assess confounding for one or more point exposures or time-varying exposures by examining: (1) departures from statistical exogeneity in the study population (2) whether covariates associate with prior exposures, causally or through unmeasured causes (3) departures from statistical exogeneity in a weighted or stratified population (see eAppendix). Diagnostics 1 and 2 can be used to understand confounding regardless of how investigators choose to control for it. Diagnostic 3 applies after particular methods are chosen. They can be used for regimes involving one or more binary, categorical, or continuous exposures. Importantly, the metrics map to exchangeability conditions that define confounding for joint exposures (Diagnostics 1 and 3), and to the bias that motivates g-methods (Diagnostic 2). We have outlined ways to estimate them directly or with regression models and summarize them over person-time. The results can be reported as trellised plots that portray a wealth of substantive information.

To implement this framework, one can articulate precise contrasts between two or more specific exposure regimes and artificially censor observations once their exposure history becomes incompatible with them (see eAppendix). Diagnostics need only be estimated at times when there is exposure variation given exposure history. When no one follows a regime of interest, though, this represents a fundamental positivity violation. Problems will also arise under left-censoring or when the start of exposure regimes is unclear. In these situations, one might pursue better data for the causal contrast at hand. Future work could explore alternative implementations for sparse data that leverage functions of exposure history through modeling.

Selecting covariates for causal inference should be deeply guided by subject matter knowledge. Several strategies have been discussed elsewhere^16,17 and they all caution against choosing instruments. Such variables do not predict the outcome, can bias point estimates, and inflate standard errors.^29,30 In longitudinal settings an instrument could be a fixed or relative phenomenon, depending on the outcome. For time-to-event and repeated measures outcomes an early covariate might predict them initially but less so as follow-up accrues. Investigators ultimately choose some set of covariate history for confounding control, and the diagnostics may help illuminate implicit assumptions (see, for example, eFigure 6).

The diagnostics should be applied after choosing covariates to control for confounding. Each imbalance for Diagnostics 1 and 3 is to be addressed unless one’s assumptions involve a series of bias cancellations. Any imbalance for Diagnostic 2 would call for using g-methods to adjust for confounding. Some g-methods can segregate covariates into separate groups, one to stratify the analysis, and the other to weight or standardize by; the choice may affect bias and precision. For marginal structural models, weights that adjust for too many covariates may explode. For the parametric g-formula, correct models for each covariate are required. One might choose to weight or standardize only with covariates that show imbalances for Diagnostic 2 and stratify on the rest. Different strategies might be pursued for structural nested models which are less sensitive to positivity violations and do not require models for covariates. These issues deserve further study as conditioning on covariates that precede exposure can induce selection-bias in some cases³¹ and this may compound or cancel over time.

Using covariate balance to diagnose confounding has its limits. It does not measure bias at the covariate level or in aggregate. The magnitude and direction of bias depends on the covariate-outcome association and Diagnostics 1 and 3 can be modified to incorporate empirical data on this relationship (see eAppendix). Our proposal does not account for covariate-covariate correlations, though. And the joint distribution of measured covariates can still suffer imbalance even though the marginal means are balanced.³² This issue can be ameliorated by adapting stricter definitions of balance.³³ But potential bias from unmeasured confounding, unmeasured selection-bias, and also measurement error may still go undetected. Nevertheless, the proposed diagnostics could support design-based analyses that avoid outcome data until the final stage.³⁴

We have outlined a framework for diagnosing confounding of exposure regimes. In an era of “Big Data” and significant advances in causal modeling, epidemiologists must remain intimate with data, using diagnostics grounded in the causal theory we rely on. This intimacy can inform our statistical analyses, and can help communicate our methods and their performance to stakeholders. We developed diagnostics and plots that we hope enable these aspirations and provide easy-to-use R functions (Austria, Vienna) to implement them. SAS macros (Cary, NC) are forthcoming.