Fluctuations in population fecundity drive variation in demographic connectivity and metapopulation dynamics

Abstract

Demographic connectivity is vital to sustaining metapopulations yet often changes dramatically through time due to variation in the production and dispersal of offspring. However, the relative importance of variation in fecundity and dispersal in determining the connectivity and dynamics of metapopulations is poorly understood due to the paucity of comprehensive spatio-temporal data on these processes for most species. We quantified connectivity in metapopulations of a marine foundation species (giant kelp Macrocystis pyrifera) across 11 years and approximately 900 km of coastline by estimating population fecundity with satellite imagery and propagule dispersal using a high-resolution ocean circulation model. By varying the temporal complexity of different connectivity measures and comparing their ability to explain observed extinction–colonization dynamics, we discovered that fluctuations in population fecundity, rather than fluctuations in dispersal, are the dominant driver of variation in connectivity and contribute substantially to metapopulation recovery and persistence. Thus, for species with high variability in reproductive output and modest variability in dispersal (most plants, many animals), connectivity measures ignoring fluctuations in fecundity may overestimate connectivity and likelihoods of persistence, limiting their value for understanding and conserving metapopulations. However, we demonstrate how connectivity measures can be simplified while retaining utility, validating a practical solution for data-limited systems.

1. Introduction

The dynamics of spatially structured metapopulations are fundamentally governed by the degree to which local populations are demographically connected through migration [1]. Therefore, understanding why demographic connectivity varies over space and time, and how this variation affects population dynamics are central goals in ecology and its applications in conservation, ecosystem management and epidemiology [1–5]. Great progress has been made in understanding the role of spatial variation in metapopulations (e.g. the influence of landscape features), but much less is known about the causes and consequences of temporal variation in connectivity [2,6,7], despite theoretical predictions that time-averaged connectivity patterns may be insufficient for understanding metapopulation dynamics [8–10].

Demographic connectivity may fluctuate due to variation in several processes, including the production of offspring and their dispersal (net movement from a natal location; [11]). This is entirely true for metapopulations of sessile and sedentary species (e.g. plants and many animals) whose dispersal is restricted to propagules (e.g. eggs, larvae, seeds, spores). For these species, connectivity can be structured by changes in the production of propagules [7,12] and variation in abiotic and biotic transport processes that influence propagule dispersal, such as the movement of water, wind or animal vectors [12,13]. However, while both the production and dispersal of propagules among local populations can fluctuate dramatically, there is limited empirical evidence demonstrating the relative importance of these two processes in structuring demographic connectivity and local dynamics in metapopulations. Recently, there has been debate over the drivers and importance of connectivity fluctuations in marine metapopulations, where planktonic propagules can be subject to large temporal variability in stochastic oceanographic dispersal [7,9,13–20].

The paucity of spatially and temporally comprehensive data on offspring production and dispersal has led most metapopulation studies to rely on simplifying assumptions about how connectivity varies over time [1,2,21–23]. Early investigations of terrestrial and marine metapopulations typically assumed temporally constant quantities of emigrants (e.g. using patch area as a proxy for reproductive output) and dispersal probabilities (e.g. Euclidean distances between patches). Where these assumptions proved unreliable (reviewed in [21,22]), time-series data of patch occupancy have been used as simple time-varying scalars of emigrant abundance [1,24]. However, empirical evaluations of the assumptions underlying these widespread models are scarce due to the difficulties of exhaustively measuring emigrant abundance and dispersal [25]. Understanding the causes and significance of fluctuations in connectivity is especially valuable for plants, which despite having large influences on biodiversity and ecosystem function remain understudied as metapopulations [26–28].

In light of these gaps in knowledge, we developed a framework to evaluate how temporal variation in propagule production and dispersal determine demographic connectivity and structure metapopulation dynamics. We applied this framework to the giant kelp Macrocystis pyrifera, a marine plant (sensu [29]) that forms the foundation of diverse and productive subtidal forests in temperate coastal ecosystems worldwide [30]. Giant kelp is ideal for plant metapopulation studies because populations are patchy [30–33]; linked by the passive dispersal of spores through ocean currents, analogous to wind dispersal of seeds [31,32,34–36]; spatially asynchronous [37]; and experience frequent local extinctions and colonizations [31,32], facilitating the application of patch-occupancy metapopulation models [1]. Giant kelp has a short generation time (approximately 1 or more per year), high population turnover, and undergoes rapid population growth during suitable conditions [30]. Moreover, because giant kelp forms a canopy that floats at the ocean's surface, aerial and satellite imagery can be used to estimate spatially comprehensive, long-term population dynamics [31,32,38–40]. We quantified demographic connectivity in a large and environmentally heterogeneous [32,39,41] metapopulation system of 469 giant kelp patches spanning nearly 900 km of coastline in southern California, USA (figure 1), by combining 11 years of population fecundity estimates from satellite-based, diver-calibrated giant kelp surveys and propagule dispersal estimates from a high-resolution, spatio-temporally explicit ocean circulation model. We used these data to calculate a series of connectivity measures that differed in the temporal complexity of fecundity and dispersal estimates (e.g. time-varying versus time-averaged; table 1). We determined how fluctuations in fecundity and dispersal affect variation in connectivity and influence metapopulation dynamics by comparing the ability of different connectivity measures to explain observed local extinctions and colonizations. Using the same approach, we assessed the degree to which connectivity measures can be simplified while retaining practical utility in basic and applied metapopulation research.

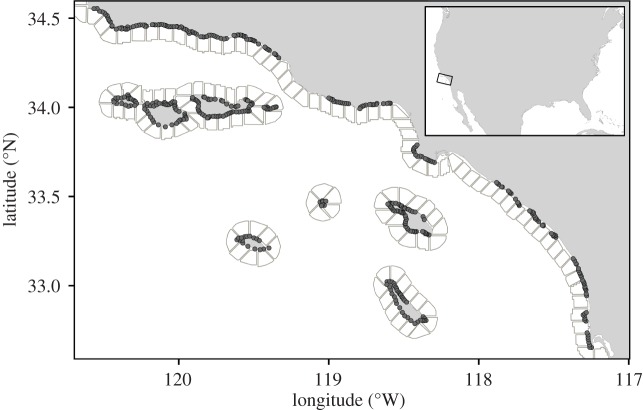
Figure 1.

Map of the study domain in southern California, USA. Points indicate the centroids of giant kelp patches (n = 469; not to scale). Polygons depict boundaries of cells in the ocean circulation model used to estimate the dispersal of giant kelp spores among patches.

Table 1.

Summary of connectivity measures and results of model comparisons (see Methods for detailed descriptions). AIC model comparisons are described by the number of model parameters (k) and AIC values, and ranked by AIC differences (Δ_i).

model	description of connectivity measure			AIC model comparison
	fecundity estimation	dispersal estimation	formula	k	AIC	Δi	rank
0	—	—	—	5	7187.7	93.5	7
1	time-averaged without occupancy data	time-averaged		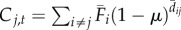6	7177.3	83.0	6
2	time-averaged without occupancy data	time-varying		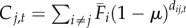6	7175.0	80.8	5
3	time-averaged with occupancy data	time-averaged		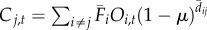6	7143.0	48.7	4
4	time-averaged with occupancy data	time-varying		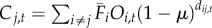6	7130.9	36.6	3
5	time-varying	time-averaged		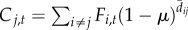6	7107.9	13.6	2
6	time-varying	time-varying		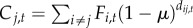6	7094.3	0	1

2. Methods

(a). Study system

The giant kelp Macrocystis pyrifera is a fast-growing marine alga that forms dense, highly productive forests on shallow subtidal reefs in temperate seas worldwide [30]. Giant kelp sporophytes (the large, habitat-forming stage) consist of a holdfast anchored to the seafloor, a bundle of buoyant vegetative fronds extending to the ocean's surface, and spore-producing reproductive blades (sporophylls) near the base. We focused on giant kelp populations across approximately 880 km of coastline in southern California, USA, encompassing the mainland (Point Purisima to San Diego) and eight Channel Islands (figure 1). Giant kelp populations in this region are restricted by the availability of shallow (5–30 m) subtidal hard substrata (i.e. rocky reefs) that are patchily distributed along the coastline within a larger matrix of unsuitable sandy habitat [30–33,40]. Local populations of giant kelp are demographically linked by microscopic spores that are produced and released throughout the year by mature sporophytes and passively dispersed by ocean currents [31,34–36,42]. Demographic connectivity is typically limited to several kilometres due to relatively short durations of spore dispersal (hours to days) and high spore densities required for post-settlement fertilization (greater than 1 spore mm⁻²; [31,34–36,43]). Owing to environmental and demographic stochasticity, local abundances of giant kelp are highly dynamic [30,39,44] with frequent extinctions and colonizations [31,32]. However, probabilities of giant kelp colonization and persistence are mediated by patch size and connectivity [31,32].

(b). Estimations of abundance, patch dynamics and fecundity

The floating surface canopy formed by giant kelp can be measured by satellite-based remote sensing [38]. Therefore, we estimated the biomass density (kg wet mass m⁻²) of the surface canopy across the region using 30-m resolution multispectral Landsat 5 Thematic Mapper and Landsat 7 Enhanced Thematic Mapper Plus satellite imagery taken at least every 16 days from 1984 to 2015 (details in [38]). Briefly, we estimated giant kelp canopy cover from atmospherically corrected, radiometrically standardized Landsat reflectance data using multiple end-member spectral mixture analysis and correlated canopy cover estimates with diver measurements of canopy biomass. Landsat estimates of canopy biomass density were used as a proxy for population size because they are highly correlated with the density of mature giant kelp sporophytes (p < 0.001, r² = 0.85; [37]).

Defining patches of local populations is pivotal to the construction of spatially realistic metapopulation models, but is often based on arbitrary rules that can agglomerate distinct adjacent subpopulations into ‘megapatches’ [1,33]. Instead of using traditional approaches (e.g. habitat contiguity) that inadequately characterize giant kelp patches and population dynamics in southern California [33], we delineated giant kelp patches using a method that avoids the consolidation of adjacent, independently fluctuating local populations into megapatches and accounts for the fact that giant kelp is patchily distributed across a range of depths irrespective of underlying patchiness in reef habitat. Briefly, we used a network theory modularity approach to optimally cluster Landsat pixels into patches based on suitable habitat area (defined as the composite area of all pixels containing giant kelp at least five times from 1984 to 2011) and the spatial synchrony of canopy biomass (1984–2011; details in [33]). Using this technique, we delineated 469 patches in the study region (figure 1) ranging in size from 0.09–402.93 ha (median = 14.13 ha). The average distance between a patch and its nearest neighbouring patch was 1.1 km (range = 0.06–4.3 km; centroid-to-centroid over-water distance).

Although each Landsat sensor captures an image of a given area at least every 16 days, cloud cover creates unequal numbers of canopy observations over time and space. To standardize sampling, we calculated mean canopy biomass within each patch for two semesters each year (January–June and July–December; mean number of measurements per semester = 7.3 ± 3.1 [s.d.]; range = 1–15). To characterize patch dynamics, we determined giant kelp occupancy (canopy biomass > 0) for each semester and classified a patch as extinct when canopy biomass was undetected for at least one semester because plants typically grow to the surface within six months [44]. We classified a patch as persistent when it was occupied for two or more successive semesters. We restricted our analysis of patch dynamics to an 11-year (22-semester) period from 1996 to 2007 during which we could estimate giant kelp spore dispersal (see below).

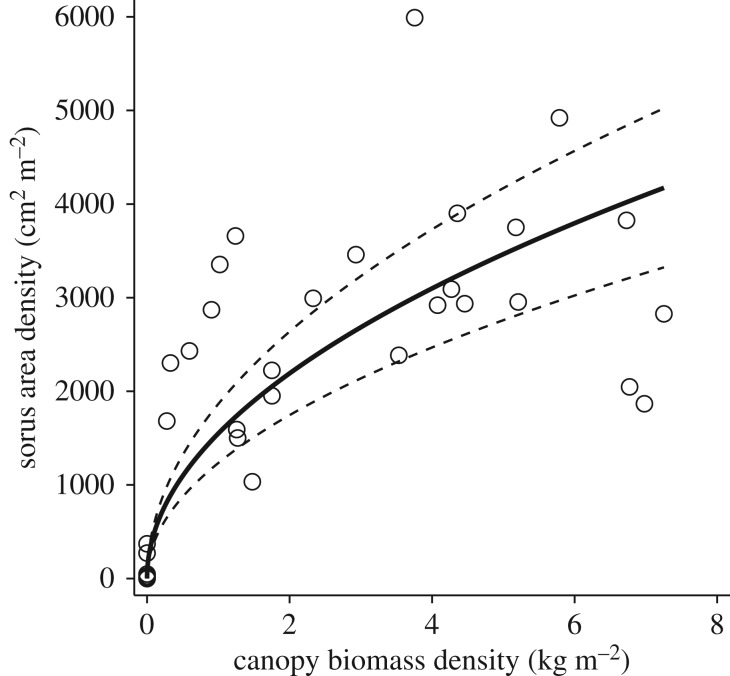
We estimated patch fecundity from canopy biomass by developing a relationship between the diver-measured density of giant kelp spore-bearing tissue (i.e. sorus area per reef area) and the Landsat estimate of canopy biomass density using data collected across 5 years at the San Clemente Artificial Reef, located offshore of San Clemente, California, USA (figure 2; see details in electronic supplementary material, appendix S1; [45]). We fit this relationship using a zero-intercept regression that assumed no fecundity in extinct patches, as well as a non-zero-intercept regression to accommodate the possibility of spore production by subsurface adult kelp in patches classified as extinct due to a lack of kelp canopy (see electronic supplementary material, appendix S1). All of our results were extremely robust to differences in these assumptions (see electronic supplementary material, appendix S2 and table S1) and hence we assumed no fecundity in extinct patches for our analyses. We adjusted fecundity to account for seasonal variation in biomass-specific fecundity (i.e. fecundity per frond; see electronic supplementary material, appendix S1, and [42]). Using the 95% confidence interval (CI) of the estimated fit (figure 2), we found that our results were highly robust to uncertainty in the fecundity–canopy biomass relationship (see electronic supplementary material, appendix S2).

Figure 2.

Relationship between giant kelp canopy biomass density and fecundity (i.e. the density of spore-bearing sorus tissue) in January–June. Equation for solid fit line is sorus area density = 1463 × √canopy biomass density. Dashed lines show 95% confidence intervals.

(c). Estimation of spore dispersal

To estimate dynamic, asymmetrical dispersal of giant kelp spores among patches, we employed Lagrangian particle simulations using solutions from a high-resolution (1 km horizontal), three-dimensional, spatio-temporally explicit ocean circulation model (Regional Oceanic Modeling System, ROMS; see model construction in [46–48] and validation in [48–50]). ROMS solutions for the Southern California Bight are available from 1996 to 2007, which restricted the time period of our analysis. Briefly, we released 63 000 particles every 12 h at 5–30 m depth from 135 near-shore ROMS connectivity cells (figure 1) and used the resulting trajectories to estimate monthly water-parcel connectivity as the minimum mean transit time connecting source and destination ROMS cells (details in [41,51]). To match the temporal resolution of giant kelp patch dynamics, we averaged monthly water-parcel connectivity estimates for each semester. Because the giant kelp patches in the study region are smaller than the ROMS connectivity cells (nominal alongshore distance = 8 km; figure 1), minimum transport times between any two giant kelp patches cannot not be calculated without making assumptions. Thus, we assumed minimum transport times between giant kelp patches are proportional to minimum transport times between ROMS cells and the alongshore distance between giant kelp patches (see electronic supplementary material, appendix S1).

The ROMS calculated transport times do not account for the loss of giant kelp spores occurring during dispersal due to mortality or settlement in areas between source and recipient patches. Laboratory experiments suggest that giant kelp spores have limited periods of effective settlement competency (less than approx. 5 days; [52]). We assumed a proportional spore loss rate of 0.9 d^–1; however, we found that our results were highly robust to uncertainty in this parameter for a wide range of tested spore loss rates (0.5 to 0.99 d^–1; electronic supplementary material, appendix S2 and figures S1 and S2). Our modelled distances of spore dispersal probabilities (electronic supplementary material, figures S3 and S4) were consistent with in situ dispersal measurements [31,35], population genetic estimates [43] and earlier hydrodynamic and oceanographic models of giant kelp spore dispersal [32,34–36].

(d). Measures of demographic connectivity

We varied the temporal complexity of source patch fecundity (three levels) and dispersal (two levels) in a factorial design to calculate six distinct measures of connectivity (table 1). In general, we estimated the demographic connectivity of a population at patch j during semester t (C_j,t) as

where F_i,t is the estimated fecundity of the population at patch i during semester t and μ is the daily proportional spore loss rate, which is compounded according to d_ij,t, the modelled transport time for spores dispersing from patch i to patch j in semester t (for n total patches in which i ≠ j). We approximated the relative quantity of spores for patch i using three levels of increasing complexity: time-averaged (over all semesters from 1996 to 2007) fecundity of patch i (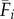), in which there is no information about whether patch i is occupied (and thus a potential source of spores) in a given semester; time-averaged fecundity of patch i scaled using occupancy time series data to exclude extinct patches that cannot be sources of spores (i.e. the product of 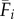and O_i,t, the occupancy [0 or 1] of patch i in semester t); and time-varying patch fecundity (F_i,t) using all available data (i.e. explicit patch fecundity estimates for each semester from 1996 to 2007). Similarly, the dispersal from patch i to patch j was either time-averaged (1996–2007; 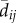) or time-varying (d_ij,t).

(e). Model specification, validation and evaluation

We specified a series of regression models to quantify the influence of each connectivity measure on probabilities of patch extinction and colonization. Response data were binomial (patch occupancy = 0 or 1), clustered due to repeated measurements from each patch (intraclass correlation = 0.2), temporally autocorrelated between successive semesters (i.e. first-order autoregressive; electronic supplementary material, figure S5), and spatially autocorrelated among patches (electronic supplementary material, figure S6). Therefore, we used binomial generalized linear mixed-effects models (GLMMs; logit link function) with random intercepts conditional on each semester and patch [53–56], which eliminated problems of spatio-temporal autocorrelation and satisfied the assumption of independent model residuals (electronic supplementary material, figures S5 and S6).

For each connectivity measure, we specified a separate GLMM to predict patch occupancy as a function of that connectivity measure, occupancy in the prior semester [54–56], and patch size (natural log of patch area; [1]), because larger patches are less likely to go extinct and more likely to be colonized [32]. We log-transformed (ln[x + 1]) all connectivity measures to satisfy linearity with the log odds of patch occupancy [56,57], a procedure typical in metapopulation models [1]. Because giant kelp sporophytes generally take six to nine months to mature to canopy-forming sporophytes following spore settlement [44], we predicted patch occupancy based on a one-semester lag in connectivity (models based on longer lags were less predictive). We also specified a null GLMM predicting patch occupancy based only on occupancy in the prior semester and patch size (model 0; table 1). Prior to all analyses, we standardized predictors to allow for direct comparisons of effect sizes and ensured that data conformed to all model assumptions (electronic supplementary material, appendix S1). In addition to modelling metapopulation dynamics over the full time series (1996–2007), we fit models to subsets of the data focused on the highly destructive 1997–1998 El Niño and the subsequent recovery from this regional disturbance (1998–2000; [32]).

We evaluated connectivity measures based on comparisons of model goodness-of-fit and standardized regression coefficients. We analysed GLMMs in R 3.2.5 [58] using the package ‘lme4’ 1.1–12 [59] with maximum-likelihood estimation by the Laplace approximation [57]. For each model, we performed model-based parametric bootstraps (n = 1000 randomizations) to estimate 95% CIs around coefficient estimates and determined the significance of fixed predictors by the Wald likelihood-ratio (LR) χ²-test [54,57]. We assessed model fit using Akaike's information criterion (AIC) and ranked models based on AIC differences (Δ_i; for model i versus the best model, Δ_i = AIC_i − AIC_min; [54,57]).

3. Results

(a). Patch dynamics

Over the 11-year (22-semester) time series, we observed 5903 extinction or persistence events (in 441 of 469 total patches) of which 893 were extinctions (relative frequency = 0.15). Likewise, we observed 3946 colonization/failure-of-colonization events (in 430 patches) of which 891 were colonizations (relative frequency = 0.23). In total, 39 patches (8.3%) were highly persistent and failed to go extinct, 26 patches (5.5%) were unoccupied and failed to be colonized, and the remaining 404 patches (86.1%) went extinct or were colonized at least once over the duration of the study.

(b). Metapopulation processes structuring patch dynamics

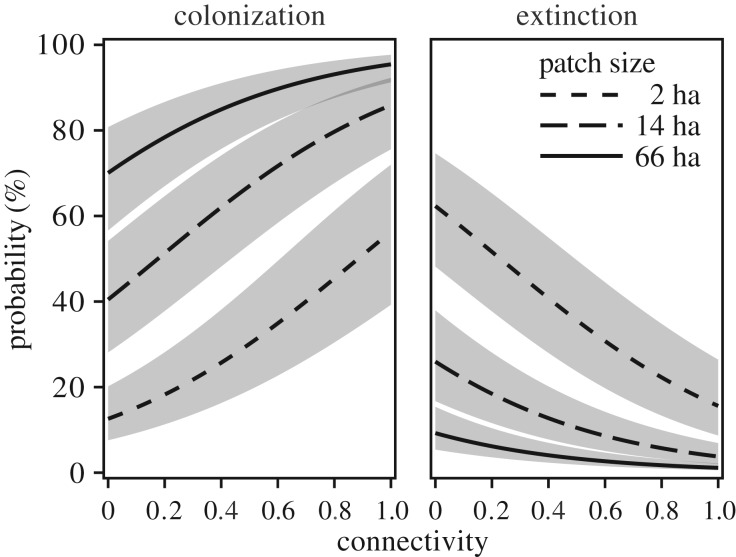
For all models, increases in connectivity increased the probability of patch colonization and decreased the probability of local extinction (p < 0.001; figure 3; electronic supplementary material, table S2). Consistent with theory [1] and prior studies of giant kelp [32,39,40], patch size and occupancy in the prior six-month period (i.e. semester) were positively associated with likelihoods of colonization and persistence (p < 0.001; figure 3; electronic supplementary material, table S2).

Figure 3.

Predicted probabilities of patch colonization and extinction as a function of patch size (line type) and demographic connectivity based on the best model (no. 6; time-varying fecundity and dispersal; see table 1 and Methods). Lines and shaded areas represent marginal model predictions and 95% confidence intervals, respectively. Patch sizes represent median values between 33% quantiles of patch area.

(c). Comparisons of connectivity measures

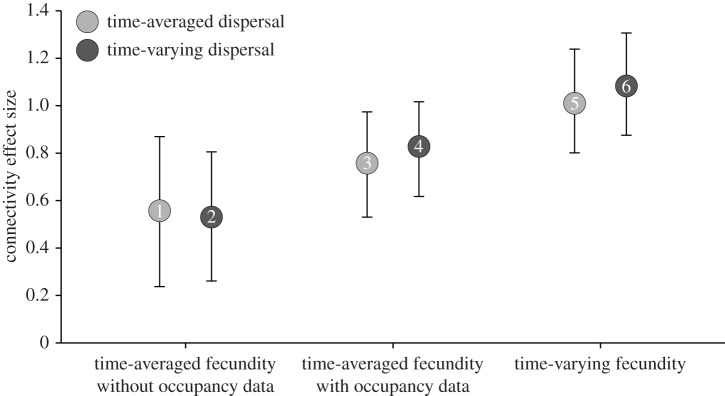
Increases in the temporal complexity of fecundity and dispersal estimates were associated with improvements to model fit (table 1) and increases in the standardized effect of connectivity on patch occupancy (figure 4; electronic supplementary material, table S2). However, the temporal complexity of fecundity was more important than that of dispersal. When holding the method of dispersal estimation constant, models with time-varying fecundity estimates fit the data much better (table 1) and had 31–104% larger connectivity effect sizes than models with time-averaged fecundity estimates with or without occupancy data (compare models 5–6 versus 1–4 in figure 4). On the other hand, when holding the method of fecundity estimation constant, models with time-varying dispersal estimates saw relatively modest improvements to fit (table 1) and slight changes in connectivity effect sizes (–5% to +9%) compared with models with time-averaged dispersal estimates (compare models 1 versus 2, 3 versus 4, and 5 versus 6 in figure 4). Adding patch-occupancy data to time-averaged fecundity estimates greatly improved model fit (table 1) and increased connectivity effect sizes by 36–56% (compare models 1 versus 3 and 2 versus 4 in figure 4). The best model used a connectivity measure with time-varying fecundity and dispersal (model 6; figures 3 and 4 and table 1; electronic supplementary material, table S2). Results of analyses using data restricted to the 1997–1998 El Niño and its subsequent recovery (1998–2000) were similar to those using the full time series (1996–2007) in that models with time-varying fecundity estimates fit the data better (Δ_i = 2.6–9.9) and had larger connectivity effect sizes (+6% to +20%) than those with time-averaged fecundity estimates, and models with time-varying dispersal differed only slightly from their time-averaged counterparts (Δ_i = 0.4–4.7; effect size differences = 1–8%).

Figure 4.

Standardized effect (±95% confidence intervals) of demographic connectivity on local population dynamics for six measures of connectivity that differ in the temporal complexity of population fecundity and propagule dispersal estimations (see table 1 and Methods). Numbers within points correspond to model numbers in table 1.

4. Discussion

Recent interest in the temporal dynamics of metapopulations has sparked debate about the causes of fluctuations in demographic connectivity and the consequences for metapopulation dynamics [7,9,13–20]. Concurrently, the search for practical measures of demographic connectivity to understand and conserve metapopulations has led to disagreement about the degree to which temporal dynamics should be simplified [21–25]. Using estimates of population fecundity and propagule dispersal over an unprecedented range in space (two to three orders of magnitude larger than typical dispersal distances; [31,34–36]) and time (approx. 11 generations; [30]), we found that variation in demographic connectivity among local populations of giant kelp in southern California was governed primarily by fluctuations in source population fecundity and to a lesser degree by fluctuations in propagule dispersal (figure 4 and table 1). Increasing demographic connectivity diminished the risk of local extinction and improved the likelihood of subsequent patch colonization (figure 3). Given the robustness of our findings across a large and environmentally heterogeneous region [32,39,41], our conclusions likely apply broadly to metapopulations of giant kelp elsewhere and may extend to other species with similar demographic and dispersal traits.

Our results clarify the mechanisms structuring giant kelp metapopulation dynamics and offer three general conclusions: (i) for metapopulations of species with highly variable population fecundity and relatively modest variation in dispersal (e.g. most vascular and non-vascular plants, many animals; [12,13]), changes in the reproductive output of local populations may be the dominant driver of demographic connectivity and contribute substantially to the recovery and persistence of local populations. (ii) Connectivity measures that ignore fluctuations in reproductive output (e.g. using habitat area as a proxy for time-averaged fecundity) may have limited utility for understanding metapopulation dynamics in many species, especially short-dispersing plants and sedentary animals. (iii) Combining time-averaged metrics of reproductive output with patch-occupancy time-series data produces a measure of demographic connectivity that can greatly improve the performance of metapopulation models (see models 3–4; table 1 and figure 4) and may be more feasible to measure in many systems. This latter result bolsters the typically untested assumptions underlying many empirical metapopulation studies [1,21–25] and validates a practical solution for approximating demographic connectivity where it is impractical to accurately estimate the fecundity of each local population through time.

(a). Causes and consequences of variation in demographic connectivity

Temporal variability in dispersal appears to play a lesser role in structuring variation in demographic connectivity and metapopulation dynamics of giant kelp than suggested by studies of species with longer dispersal durations [6–10,14,18]. The relatively limited dispersal duration of giant kelp spores (hours to a few days; [31,34–36]) reduced the influence of temporal variation in oceanographic transport, resulting in relatively small fluctuations in spore dispersal distances (mean temporal coefficient of variation, CV_t = 0.15 ± 0.05 [s.d.]) but very large fluctuations in patch-scale spore production (CV_t = 0.95 ± 0.38) over the spatio-temporal scales relevant to metapopulation dynamics. This finding reinforces prior work suggesting that the dynamics and fecundity of source populations are important to connectivity in metapopulations [16,19,60] and bolsters earlier giant kelp metapopulation studies that assumed time-averaged dispersal patterns [32,40].

Our findings for giant kelp likely apply broadly to plant metapopulations in terrestrial, freshwater and marine ecosystems because fluctuations in the population fecundity of many plants are large relative to temporal variation in the vectors that disperse their propagules [12,61,62]. For example, demographic connectivity in metapopulations of species with wind-dispersed seeds may be controlled by fecundity and post-dispersal processes because fluctuations in wind primarily regulate rare, long-distance dispersal and have little influence on the shorter distances over which the vast majority of seeds disperse [12,63]. By contrast, metapopulations of species with relatively long dispersal durations [17,20], high survival of dispersing offspring, strong seasonality in reproductive output [7,16,18] or multiple important mechanisms of dispersal may be very sensitive to the temporal dynamics of dispersal vectors. While giant kelp has the potential for long-distance dispersal through fecund sporophytes that are dislodged and set adrift [64], this vector likely does not play a dominant role in demographic connectivity and metapopulation dynamics because drifting plants contain a relatively small spore source and are highly transitory over suitable habitat [31]. Thus, patch recovery by this method would most likely occur gradually over time as populations expand from a relatively small number of initial colonists, which contrasts starkly with the rapid and widespread recovery of patches observed in our time series [32]. Long-distance dispersal via giant kelp drifters may play a more prominent role in genetic connectivity and biogeographic expansion.

Post-settlement processes also likely structure temporal variation in demographic connectivity. For example, density-dependent mortality (e.g. due to competition or predation) likely dampen the effect of fluctuations in dispersal and fecundity on demographic connectivity in giant kelp [65,66] and many other plant species [12] by constraining recruitment. Year-round reproduction [42] may further diminish the importance of dispersal fluctuations to giant kelp metapopulation dynamics. Similarly, persistent latent stages (e.g. dormant seeds) can effectively average connectivity patterns over time and thereby reduce the demographic importance of variation in dispersal and fecundity [12,27,28]. This is unlikely in giant kelp, however, because its early life-history stages suffer high mortality rates [66–68] and the vast majority of recruitment results from recently settled spores [69]. However, additional research is needed to evaluate the importance of latent early life-history stages on giant kelp metapopulation dynamics.

In addition to considering post-settlement processes, estimates of demographic connectivity and predictions of metapopulation dynamics may be improved by incorporating information on environmental and genetic factors that influence survival, fecundity, dispersal and recruitment. As in many terrestrial plants [12], the production, recruitment and survival of giant kelp propagules are mediated by the availability of resources (i.e. nutrients and light; [30,42,67]) and the degree of inbreeding [70]. We found that our results were consistent among periods of typical environmental conditions, widespread catastrophic loss (i.e. the 1997–1998 El Niño), and subsequent recovery (i.e. 1998–2000). Future studies may help resolve disagreements about the relative importance of environmental variation, survival, fecundity, dispersal and post-settlement processes in metapopulations by systematic consideration of the intrinsic and extrinsic processes influencing connectivity from adult reproduction through recruitment [20].

Temporally explicit data on population fecundity are often impractical to obtain and thus rarely incorporated into connectivity estimates in metapopulation studies [1,2]. However, our findings indicate that a simplified connectivity measure that combines information about the typical number of offspring produced by a local population (e.g. time-averaged patch fecundity) with time series of patch occupancy can greatly improve the fit of metapopulation models. This result complements and extends the conclusion shared by several recent studies that patch-occupancy information is key to improving the performance of connectivity measures for metapopulations of epiphytic lichens [71] and mosses [72], terrestrial invertebrates [22,23], amphibians and reptiles [22]. Fortunately, our findings suggest a practical and relatively efficient solution similar to stochastic patch-occupancy models that are already in use for some metapopulations [1,21–25]. To our knowledge, our study is among the first to empirically confirm these theoretical predictions, strengthening the assumptions underlying many earlier empirical studies [1,24]. However, these conclusions need to be validated in other systems and in plants in particular [26–28]. The flexible framework that we developed for this study can be readily adapted to address basic and applied challenges in other metapopulation systems with different species traits and data availability.

(b). Implications for conservation

Our results indicate that ignoring fluctuations in fecundity can over- or underestimate demographic connectivity and the likelihoods of population recovery and persistence in metapopulations. This finding highlights the need for conservation and ecosystem management efforts to consider the importance of variation in connectivity and the factors that underlie it. For example, the potential for protected area networks to fulfil design objectives may depend greatly on temporal variation in population fecundity, dispersal, recruitment and survival of target species [2]. Similarly, optimal control of biological invasions [3], containment of infectious diseases [4] or facilitation of species range shifts under climate change [5] may differ if spread rates are dominated by variation in reproductive output as opposed to dispersal. In fragmented landscapes, determining the causes and consequences of variation in connectivity will help identify local populations that contribute disproportionately to metapopulation dynamics, such as those that are highly resilient to extinction, frequently rescue or recolonize other populations, form critical demographic or genetic links, or harbour high genetic diversity. For metapopulations of plants and sedentary animals, efforts focused on increasing the size, persistence and reproductive success of source populations are likely to have the greatest impact on enhancing connectivity and improving population recovery and persistence. Such efforts directed towards metapopulations of foundation species that underpin entire ecosystems, such as giant kelp, are likely to pay great dividends for the conservation of biodiversity and the management of ecosystem structure and function.

Data accessibility

Datasets supporting this article can be accessed through the Long Term Ecological Research Network: kelp metapopulations: semi-annual time series of giant kelp patch area, biomass and fecundity in southern California, 1996–2006. See http://dx.doi.org/10.6073/pasta/448cc3e3d4d32dd5ad616e066a78bace. Kelp metapopulations: semi-annual time series of spore dispersal times among giant kelp patches in southern California, 1996–2006. See http://dx.doi.org/10.6073/pasta/14a2849b021ced9a7510d375bed25cd9.

Authors' contributions

M.C.N.C. conceived of and designed the study with contributions from D.C.R., P.T.R., F.A. and D.A.S.; T.W.B., R.D.S., K.C.C. and D.A.S. collected, formatted and analysed data streams; M.C.N.C. compiled the data, conducted the analyses and drafted the manuscript; all authors contributed to interpreting the results and revising the manuscript.

Competing interests

We declare we have no competing interests.

Funding

A National Science Foundation (NSF) grant (OCE-1233839) to P.T.R., F.A. and D.C.R. funded this project and supported M.C.N.C. An NSF grant (OCE-1155813) supported R.D.S. and D.A.S. A National Aeronautics and Space Administration Earth System Science Fellowship supported T.W.B. NSF provided additional support through the Santa Barbara Coastal Long Term Ecological Research project (OCE-1232779).