Abstract
Most bacterial habitats are topographically complex in the micro scale. Important examples include the gastrointestinal and tracheal tracts, and the soil. Although there are myriad theoretical studies that explore the role of spatial structures on antagonistic interactions (predation, competition) among animals, there are many fewer experimental studies that have explored, validated and quantified their predictions. In this study, we experimentally monitored the temporal dynamic of the predatory bacterium Bdellovibrio bacteriovorus, and its prey, the bacterium Burkholderia stabilis in a structured habitat consisting of sand under various regimes of wetness. We constructed a dynamic model, and estimated its parameters by further developing the direct integral method, a novel estimation procedure that exploits the separability of the states and parameters in the model. We also verified that one of our parameter estimates was consistent with its known, directly measured value from the literature. The ability of the model to fit the data combined with realistic parameter estimates indicate that bacterial predation in the sand can be described by a relatively simple model, and stress the importance of prey refuge on predation dynamics in heterogeneous environments.
Keywords: estimation, heterogeneous environments, optimization, predator–prey model
1. Introduction
The topography of most bacterial habitats is complex in the micro scale. The gastrointestinal, tracheal tracts and the soil are important examples. Previous studies showed that heterogeneous habitat may alter the interaction between bacteria and their prey and promote coexistence, mainly due to prey refuge [1–3]. Prey refuge may occur due to the existence of bacterial post-predation debris [1], the existence of habitat fixed structures (soil particles, [2]), or self-organized ones, such as variable prey and predator densities and biofilms [2–4]). Thus, exploring the role of spatial structures in the interaction between sympatric microorganisms such as bacteria and their predators/parasites can be of fundamental importance to microbial ecology, epidemiology and agronomy [5,6].
Although there are a myriad of theoretical (mathematical modelling) works that explore the role of complex spatial structures on antagonistic interaction among animals (e.g. competition, predation and parasitism), there are many fewer experimental studies that explore, validate and quantify their predictions [7–9]. For example, most evidence of the effect of prey refuge on the temporal dynamics of predator–prey systems are based on theoretical works and simulations [1,2,7,8], while only few experimental set-ups have found evidence that refuge indeed promotes coexistence [3,4]. One of the main reasons for this mismatch is the practical difficulty in terms of resources and time needed to manipulate natural habitats into experimental set-ups, which enable quantification and hypothesis testing. In this context, microbial habitats can be much easier to control compared with macro ecological systems due to their smaller size and the shorter generation time of microorganisms [10].
In this study, we quantify the dynamics of the predatory bacterium Bdellovibrio bacteriovorus and its prey, Burkholderia stabilis st.2 in soil. Bdellovibrio bacteriovorus belongs to the Bdellovibrio and like organisms (BALOs), a group of bacterial predators that prey upon Gram-negative bacteria and can be found in various environments like soil, fresh and marine water, and animal guts [11]. The life cycle of BALOs includes a highly motile free-living phase that searches for an appropriate prey. Upon encounter, the predator penetrates the prey periplasm and converts it into a bdelloplast that provides nutrient and shelter to the predator during its growth and division to progeny cells, that finally burst out to start a new cycle. Predation by BALO has a lot in common with bacteriophage parasitism: in both cases, infectious particles invade a host cell, which finally dies while emitting more infectious particles into the environment. However, unlike BALOs, which typically kill and consume their victims, phages can either engage in a lytic cycle or stay inactive for a long period.
During the past decades, several mathematical methodologies have proposed ways to incorporate spatial heterogeneities into population dynamics models. The most important ones include the use of partial differential equations (e.g. reaction–diffusion models), coupled map lattices, spatial moments and metapopulation models [7,12–15]. These models are usually difficult to analyse and parametrize, and it is difficult to draw general conclusions. Consequently, attempts have been made to formulate simpler frameworks, also known as ‘strategic models’ [16] which use low dimensional ordinary differential equations (ODEs) that have fewer parameters, and are thus easier to analyse and interpret. These models capture some features regarding the complex role of space in population dynamics by using implicit spatial parameters [17]. In addition, the limited number of parameters in strategic models facilitates their estimation even in cases of a limited amount of data.
Fitting models to time-series data has become standard practice in epidemiology [18–26], while in ecology it is much less used, due mainly to the lack of sufficient data. Nevertheless, some important theoretical and practical contributions include [27–30]. Fitting a differential equation model to empirical data is usually done by maximum-likelihood, nonlinear least-squares or Bayesian methods. Although maximum-likelihood estimation has desirable statistical properties, currently, there is no method (either numerical or analytical) which can assure optimal parameter estimates. The likelihood function is often multivariable, and may have complicated surfaces with several local minima, maxima and saddle points, all of which (provided that they are interior points) may lead to local convergence by the optimization algorithms. Finding the maximum-likelihood estimators can therefore be highly dependent on the chosen initial values used in the optimization algorithm, thus making the search for acceptable optimum computationally demanding and complex.
To quantify the dynamics of the predatory bacteria B. bacteriovorus and its prey, Bu. stabilis st.2 in soil, we constructed a ‘strategic’ dynamic model, fitted it to data in order to study its dynamical behaviour in different soil humidity and estimated its parameters. The model describes the predation between a predator and a bacterial prey strain, and more generally, explores the role of complex spatial structures on predator–prey interaction in a microbial system. The model is relatively simple, and captures the effect of spatial structures implicitly via a special refuge parameter (see model description for further information). The model was fitted to the experimental data by further developing and optimizing a novel statistical procedure; specifically, we used a direct integral approach that exploits the separability of state equations and parameters, thus overcoming the difficulty of exploring complex likelihood parameter space. Model validation was done by fitting the model to data and contrasting some of our estimated parameters with their known values from the literature, thus providing additional confidence to both model representative and statistical methodology abilities.
2. Data and experimental design
Soil microcosm experiments: 10 g of fine sand was used to construct microcosms in flasks. Each flask was inoculated with a suspension of the B. bacteriovorus 109 J predator (2 × 106 plaque forming units, PFU × ml−1) and of the Bu. stabilis st.2 prey (1 × 108 colony forming unit, CFU × ml−1) and water to create microcosms with different water contents (WC, w/w) ranging from 100% (fully saturated) to 20%. Treatments were in triplicate. The vials were sealed and incubated at 28°C. At selected time points (8, 12, 24, 36, 48, 96 and 168 h), the total volume of water in each flask was adjusted with HEPES buffer by weight, to reach 100% WC, mixed and the liquid was removed from the flask to a sterile test-tube. In total, 50 µl from this was taken for dilution plating to measure the concentration of the predator and of the prey in each sample.
3. Model description
As noted earlier, the interaction between the BALO and its prey resembles the dynamics of phage–bacteria. We therefore adopted a designated modelling framework developed previously for this type of system [31–34], and further developed it to fit the above experimental set-up. In this framework, ODEs are used to model the dynamics of the system which includes free predators, P, prey, N, and predator–prey complexes (the bdelloplast), C. In ours and similar systems (like phage–bacteria), the time it takes the predator to handle its prey (i.e. searching and invading it to form bdelloplast) is of the same order as the time it takes for the consumed prey items to be converted into new predators (i.e. reproduction). To account for this dynamics, we explicitly modelled them in a separate compartment.
The separate complex compartment therefore models the delay between the predator invasion and the burst of the bdelloplast (which releases the predator progeny) as was proposed in some earlier models [31,33,34]. The dynamics of these compartments are described by
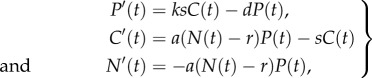 |
3.1 |
where the notation P′(t) stands for dP/dt, and the same for C and N. In equation (3.1), the predators are produced at the rate ksC (first equation in (3.1)), where k is the number of predatory bacteria emitted by one bdelloplast (multiplication factor) and s is the bdelloplast decay rate. We assume for simplicity that the predator has a density-independent death rate, d, and the complex formation rate can be approximated using the classical mean field assumption, i.e. it is equal to aNP [35]. To account for the prey refuge dynamics, we add an additional new parameter, r, denoting refuge prey density, which is not available to the predator. Prey refuge may occur in our set-up due to habitat spatial heterogeneity consisting of soil grains [1,2]. The formation rate of bdelloplast complexes is therefore updated here to be a(N − r)P, where a is the interaction (contact) rate. Because in our system the prey is not supplied with nutritional substrate, it neither reproduces nor dies (its death rate is too low to be accounted for in our experimental timescale). Thus, the only prey loss in the model is due to predation, i.e. a(N – r)P.
In order to assess whether the model can capture the predator–prey dynamics in a heterogeneous environment and to estimate the model parameters, we further develop the direct integral approach [36,37]. Indeed, testing the model both qualitatively and quantitatively (i.e. estimating the parameters based on experimental data) is of interest to several disciplines, including microbial ecology, theoretical ecology (modelling) and statistics. Furthermore, in our case, the conversion ratio k, has been previously measured directly and independently in designated experiments. Our estimations can therefore be contrasted with a ‘gold standard’ value, thus enabling the validation of the model and its proper interpretation (i.e. that the model parameters indeed represent what is commonly believed).
4. Estimating model parameters using the direct integral method
4.1. Background
We denote a system of ODEs by
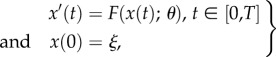 |
4.1 |
where x(t) takes values in  in
in 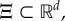 and
and 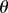 in
in 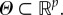 Given known values of ξ and θ the solution of (4.1) is denoted by
Given known values of ξ and θ the solution of (4.1) is denoted by
The common statistical model assumes that measurements are collected at a series of time points t1, … ,tn, each of them includes a signal and an additive error term,
| 4.2 |
where the random variables 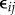 are independent measurement errors (not necessarily Gaussian) with zero mean and finite variance. As is the case with the experimental study considered in this work, we allow the system to be only partially measured and thus r ≤ d. Based on the observation Yj(ti), i = 1, … ,n, j = 1, … ,r one could estimate the parameters θ. In cases where the initial values ξ are not known, one would also like to estimate them. However, here the initial values are known and therefore are not discussed further in this paper.
are independent measurement errors (not necessarily Gaussian) with zero mean and finite variance. As is the case with the experimental study considered in this work, we allow the system to be only partially measured and thus r ≤ d. Based on the observation Yj(ti), i = 1, … ,n, j = 1, … ,r one could estimate the parameters θ. In cases where the initial values ξ are not known, one would also like to estimate them. However, here the initial values are known and therefore are not discussed further in this paper.
As in most biological models, the ODEs (4.1) are nonlinear and therefore numerical integration techniques are required in the estimation process. For instance, the nonlinear least-squares estimator of θ is defined as a minimizer of the least-squares criterion function
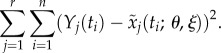 |
Here, 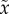 is a numerical solution (e.g. using Runge–Kutta) of the ODEs equation (4.1) for a given parameter and initial values. Thus, estimation methods such as nonlinear least-squares or maximum-likelihood require the system to be solved numerically for a large set of potential parameters values, and then choosing an optimal parameter using some nonlinear optimization technique. However, the combination of sparse and noisy data, nonlinear optimization and the need for numerical integration makes the parameter estimation a complex task (even for systems of low dimensions, e.g. [38]), and in many instances requires heavy computation. In recent years, the inverse problem of parameter estimation for ODEs has received growing attention in the statistical literature. In particular, much focus has been given to developing estimation methods that bypass the need for numerical integration (see [39] and the discussion therein; [40–44], and more recently [36,37,45,46]).
is a numerical solution (e.g. using Runge–Kutta) of the ODEs equation (4.1) for a given parameter and initial values. Thus, estimation methods such as nonlinear least-squares or maximum-likelihood require the system to be solved numerically for a large set of potential parameters values, and then choosing an optimal parameter using some nonlinear optimization technique. However, the combination of sparse and noisy data, nonlinear optimization and the need for numerical integration makes the parameter estimation a complex task (even for systems of low dimensions, e.g. [38]), and in many instances requires heavy computation. In recent years, the inverse problem of parameter estimation for ODEs has received growing attention in the statistical literature. In particular, much focus has been given to developing estimation methods that bypass the need for numerical integration (see [39] and the discussion therein; [40–44], and more recently [36,37,45,46]).
4.2. The direct integral approach
Below, we further develop the direct integral approach. The method is an extension of ‘two-step’ approaches [47,48] that include step (i): bypassing numerical integration by using non-parametric smoothing of the data, and step (ii): estimating the parameters by fitting the ODEs model to the estimated functions, as explained below. Let 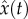 , and
, and 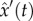 stand for non-parametric estimators (e.g. smoothing the data using splines or local polynomials) of the solution x of the ODEs equation (4.1), and its derivative x′, respectively. The criterion function of the two-step approach for a fully observed system of ODEs takes the form
stand for non-parametric estimators (e.g. smoothing the data using splines or local polynomials) of the solution x of the ODEs equation (4.1), and its derivative x′, respectively. The criterion function of the two-step approach for a fully observed system of ODEs takes the form
| 4.3 |
where w is an appropriate weight function and  denotes the standard Euclidean norm. The estimator of the parameter will be the minimizer of the criterion function (4.3), with respect to θ. The direct integral approach takes advantage of linear feature of the ODEs system as explained now. Consider the Lotka–Volterra system of ODEs [49], a classical population dynamics model that describes evolution over time of the populations of two species, predator and its prey. The system takes the form
denotes the standard Euclidean norm. The estimator of the parameter will be the minimizer of the criterion function (4.3), with respect to θ. The direct integral approach takes advantage of linear feature of the ODEs system as explained now. Consider the Lotka–Volterra system of ODEs [49], a classical population dynamics model that describes evolution over time of the populations of two species, predator and its prey. The system takes the form
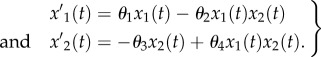 |
4.4 |
Here, x1 and x2 represent the prey and predator population, respectively. One can view (4.4) as a regression where the ‘covariates’ variables are the solutions of the ODEs on the right-hand side of the equations, while the ‘response’ variables are the derivatives x′(t) on the left-hand side. We refer to such systems as ‘linear in the parameter’ 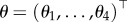 (as in a linear regression model), where
(as in a linear regression model), where  stands for the matrix transpose. Thus, when using the criterion equation (4.3), the parameter θ can be estimated in an ordinary least-squares fashion where nonlinear optimization is not required. More generally, consider the case where the model is linear in the parameters, namely, that
stands for the matrix transpose. Thus, when using the criterion equation (4.3), the parameter θ can be estimated in an ordinary least-squares fashion where nonlinear optimization is not required. More generally, consider the case where the model is linear in the parameters, namely, that
| 4.5 |
where the measurable function 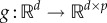 maps the d-dimensional column vector x into a d × p matrix (typically d ≤ p). For instance, model (4.4) has d = 2 equations and p = 4 parameters and the 2 × 4 matrix g(x(t)) from (4.5) is given by
maps the d-dimensional column vector x into a d × p matrix (typically d ≤ p). For instance, model (4.4) has d = 2 equations and p = 4 parameters and the 2 × 4 matrix g(x(t)) from (4.5) is given by
Further, note that by integration, (4.1) and (4.5) yield the system of integral equations
| 4.6 |
Here, 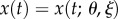 is the true solution of the ODE. Let
is the true solution of the ODE. Let 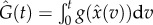 . Motivated by (4.6), one can consider minimizing with respect to θ the criterion function
. Motivated by (4.6), one can consider minimizing with respect to θ the criterion function
| 4.7 |
Let 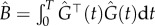 . Minimizing the criterion function (4.7) with respect to θ yields the direct integral estimator
. Minimizing the criterion function (4.7) with respect to θ yields the direct integral estimator
| 4.8 |
Necessary and sufficient conditions for 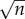 -consistency of the direct integral estimator (4.8) are provided in [36]. Furthermore, the extensive simulation study in the aforementioned paper has demonstrated that using integrals as in (4.8) instead of derivatives as in (4.3) yields more accurate estimates. Indeed, it is well known (see [50] and [51]) that estimating derivatives from noisy and sparse data may be rather inaccurate. An application of the direct integral method to a variety of synthetic and real data was shown to yield accurate and stable results in [45] and [46].
-consistency of the direct integral estimator (4.8) are provided in [36]. Furthermore, the extensive simulation study in the aforementioned paper has demonstrated that using integrals as in (4.8) instead of derivatives as in (4.3) yields more accurate estimates. Indeed, it is well known (see [50] and [51]) that estimating derivatives from noisy and sparse data may be rather inaccurate. An application of the direct integral method to a variety of synthetic and real data was shown to yield accurate and stable results in [45] and [46].
The methodology discussed so far is aimed at cases where all the equations of the ODEs can be measured. Recall that in our experiment x = (P, C, N), and one variable (the complex C) is unobserved. The direct integral methodology for dealing with partially observed systems linear in the parameters was proposed in [37] and its consistency was proven in [52]. However, in the case of equation (3.1) there are two main challenges (i) the system is partially unobserved, and (ii) equation (3.1) is not fully linear in all the parameters. Thus, below we further develop the direct integral method to enable parameter estimation in such a case. Note that our notation in the sequel resembles the specific case where only one equation of the system is unmeasured; however, the method can be used for more general cases. We first describe the model we have in mind
| 4.9 |
where 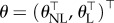 . Here, θNL stands for the ‘nonlinear’ parameters that cannot be separated from the equations, while θL are the ‘linear’ parameters, as above in equation (4.5). More details regarding the above abstract form equation (4.9) are given in the electronic supplementary material. Now, denote the measured equations of x by m and the unmeasured ones by u. Using the observations we have for m, we first generate an estimator using non-parametric smoothing, denoted by
. Here, θNL stands for the ‘nonlinear’ parameters that cannot be separated from the equations, while θL are the ‘linear’ parameters, as above in equation (4.5). More details regarding the above abstract form equation (4.9) are given in the electronic supplementary material. Now, denote the measured equations of x by m and the unmeasured ones by u. Using the observations we have for m, we first generate an estimator using non-parametric smoothing, denoted by 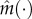 . In order to deal with the unmeasured states, we continue as follows. Define for some function
. In order to deal with the unmeasured states, we continue as follows. Define for some function 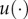 the quantity
the quantity 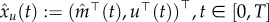 (the vector x is assumed to be arranged such that its first equation is the measured one m). Let
(the vector x is assumed to be arranged such that its first equation is the measured one m). Let
Motivated by equation (4.7), we define the criterion function
| 4.10 |
Minimizing 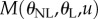 with respect to θL yields
with respect to θL yields
where
Plugging back 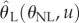 into equation (4.10) results with
into equation (4.10) results with
Finally, let 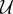 be some appropriate space of functions on [0,T] and define
be some appropriate space of functions on [0,T] and define
Then the estimator for θ is given by
| 4.11 |
4.3. Smoothing
In order to estimate the solutions of the ODEs model (3.1), we use cubic B-splines. In particular, it is assumed that the ODE solutions can be approximated for any 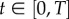 by a linear combination of cubic B-spline functions denoted by ϕk(t), k = 1, … ,Kℓ,
by a linear combination of cubic B-spline functions denoted by ϕk(t), k = 1, … ,Kℓ, 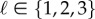 , namely,
, namely,
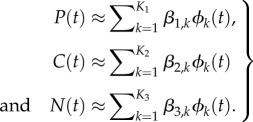 |
The choice of number of bases. As the regularity of the solutions of the ODEs model (3.1) might be different, we allow the number of bases K1, K2, K3 to be (potentially) different. Choosing the number of cubic spline bases is crucial [53] and is known to affect the accuracy of the final estimates. Let K = {K1, K2, K3} stand for the number of bases used for the first, second and third equations of the system (3.1), respectively. Denote by 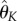 the vector of parameter estimators
the vector of parameter estimators 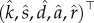 calculated using the direct integral method (4.11) for a given number of bases K = {K1, K2, K3}. For each
calculated using the direct integral method (4.11) for a given number of bases K = {K1, K2, K3}. For each 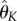 , we solve the system of ODEs (using numerical integration) to obtain
, we solve the system of ODEs (using numerical integration) to obtain 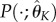 ,
, 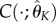 and
and 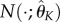 . We then choose the combination
. We then choose the combination 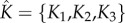 that minimizes the squared distance between the observations (recall that C is unobserved), denoted by
that minimizes the squared distance between the observations (recall that C is unobserved), denoted by 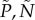 , and the solutions of the system
, and the solutions of the system
| 4.12 |
The final estimator is given by 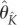 . Here, we consider variety of combinations of triplets K = {K1, K2, K3}. Extensive simulation studies suggest (see §5, electronic supplementary material) that the regularization (4.12) leads to accurate and stable estimation results.
. Here, we consider variety of combinations of triplets K = {K1, K2, K3}. Extensive simulation studies suggest (see §5, electronic supplementary material) that the regularization (4.12) leads to accurate and stable estimation results.
In the following section, we study some finite sample properties of the methodology described above.
5. Finite sample properties of the estimation method
In order to test the finite sample performance of the direct integral method developed above, we conducted a large Monte Carlo experiment. We solve model (3.1) with initial conditions given by 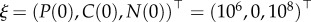 , similar to the experimental design, and the ‘true’ parameters given by
, similar to the experimental design, and the ‘true’ parameters given by 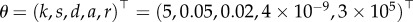 (for values that are in the vicinity of those estimated from the real data, see table 2). Recall that the statistical model we consider is additive as in equation (4.2). Here, we add Gaussian measurement errors to the deterministic system equations so that the measurements of the predator will be given by
(for values that are in the vicinity of those estimated from the real data, see table 2). Recall that the statistical model we consider is additive as in equation (4.2). Here, we add Gaussian measurement errors to the deterministic system equations so that the measurements of the predator will be given by 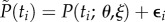 , and those of the prey are given by
, and those of the prey are given by 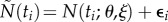 , i = 1, … ,n, where P(ti; θ, ξ) and N(ti; θ, ξ) are the deterministic solutions of (3.1) at point ti with respect to initial values ξ and parameter θ. The measurement error
, i = 1, … ,n, where P(ti; θ, ξ) and N(ti; θ, ξ) are the deterministic solutions of (3.1) at point ti with respect to initial values ξ and parameter θ. The measurement error 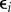 follows a Gaussian distribution with zero expectation and a standard deviation that is proportional to both P and N:
follows a Gaussian distribution with zero expectation and a standard deviation that is proportional to both P and N: 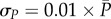 , and
, and 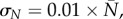 where
where 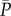 , and
, and 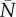 are the means of
are the means of 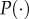 , and
, and 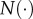 over the time interval of the experiment, respectively.
over the time interval of the experiment, respectively.
Table 2.
Parameter estimation results for the predator–prey–bdelloplast system for a gradient (20–100%) of water content.
| water content (%) | k | s | d | a | r |
|---|---|---|---|---|---|
| 20 | 2.5356 | 0.0300 | 0.0269 | 3.2456×10−8 | 33 800 |
| 50 | 2.3034 | 0.0400 | 0.0184 | 2.0321×10−8 | 55 500 |
| 70 | 4.4985 | 0.0410 | 0.0269 | 6.8059×10−9 | 46 000 |
| 80 | 1.4898 | 0.0480 | 0.0073 | 1.5646×10−8 | 62 500 |
| 100 | 3.5618 | 0.0300 | 0.0269 | 1.9331×10−8 | 34 650 |
In the Monte Carlo experiment, 400 different random samples were generated. We consider two experimental set-ups, in the first we sample the model using the exact sampling times as done in the experimental set-up [0, 8, 16, 24, 36, 48, 96, 168], hence, n = 8. In the second set-up, we consider n = 16 time points [0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 72, 96, 168]. Next, we estimate the model parameters using the direct integral method. Table 1 summarizes the estimation from the simulations with the additive noise, note the ability of the direct integral method to obtain good estimates (especially given a small sample of size n = 8).
Table 1.
Monte Carlo study. The table presents the mean estimate, the square root of the empirical mean square error, empirical absolute bias and empirical standard deviation, based on 400 simulations for each of the sample sizes. The first block of the table is for n = 8 while the second is for n = 16.
| parameter | value | estimate | sqrtMSE | absBIAS | s.d. |
|---|---|---|---|---|---|
| k | 5 | 4.7876 | 0.2440 | 0.2121 | 0.1207 |
| s | 0.05 | 0.0574 | 0.0076 | 0.0073 | 0.0020 |
| d | 0.02 | 0.0195 | 0.0011 | 0.0004 | 0.0010 |
| a | 4×10−9 | 3.3609×10−9 | 6.9739×10−10 | 6.3405×10−10 | 2.9039×10−10 |
| r | 3×105 | 298 637 | 214 233 | 108 | 214 230 |
| k | 5 | 5.1958 | 0.3656 | 0.1895 | 0.3127 |
| s | 0.05 | 0.0487 | 0.0045 | 0.0011 | 0.0044 |
| d | 0.02 | 0.0210 | 0.0019 | 0.0010 | 0.0016 |
| a | 4×10−9 | 3.9405×10−9 | 1.7755×10−10 | 6.2554×10−11 | 1.6617×10−10 |
| r | 3×105 | 294 503 | 99 494 | 6786 | 99 262 |
In section 1.5 of the electronic supplementary material, a comparison between the direct integral method and nonlinear least-squares was conducted for various noise levels. The findings suggest that for small number of points, the performance of the direct integral method as applied here, in terms of residual sum of squares, is comparable to that of the nonlinear least-squares.
6. Estimating parameters of the predator–prey–bdelloplast system
We fitted model (3.1) to five different environmental conditions (various different water contents). Thus, we estimated the five parameters of each configuration using its corresponding data (table 2).
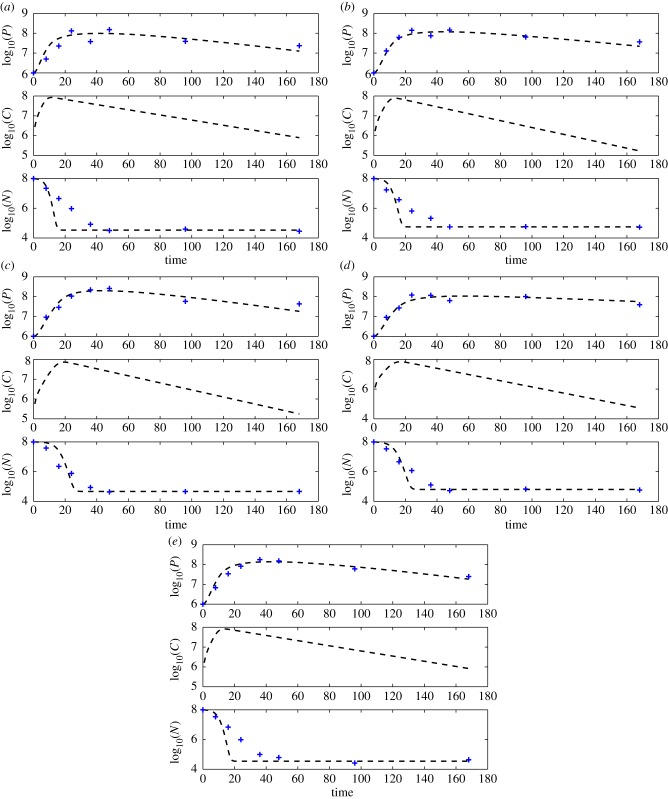
Figure 1 demonstrates the ability of our simple ‘strategic’ model to capture both qualitatively and quantitatively the dynamics of predation in a heterogeneous environment.
Figure 1.
Model fits. Observations are displayed with the plus sign. Numerical solution of model (1) given the estimated parameters using the direct integral method (see Table 2) with a dashed line. Note the ability of the simple model to capture the predation dynamics. Water content: (a) 20%, (b) 50%, (c) 70%, (d) 80% and (e) 100%. (Online version in colour.)
To the best of our knowledge, in previous studies only the progeny size (parameter k) was directly measured. The estimated k's in our case fall within the range of 1–9, known values from the literature, see, e.g. fig. 1a in [54]. The estimation results of the other four parameters seem to be stable over the water content gradient.
In order to provide further information regarding the estimation process, and to show the strength of the direct integral method, we present two additional plots. The spline estimators used in the estimation procedure are displayed in electronic supplementary material, figure S1. One can see that the splines are able to capture the dynamics of the predator–prey interactions and specifically, to recover the unmeasured complex C. The loss function given in equation (4.7) of electronic supplementary material, used to choose the optimal s (i.e. the bdelloplast decay rate) is displayed in electronic supplementary material, figure S2 for the five experimental set-ups. One can see there a clear minimum, which is an indication of the ability of the method to estimate the parameter s.
7. Discussion
To the best of our knowledge, this is the first attempt to fit a BALO–prey model to experimental data using a statistical procedure. The model we have developed can both qualitatively and quantitatively describe the temporal dynamics of a predator–prey system in the heterogeneous soil environment. The fact that the model can be fitted to the experimental data indicates that although the soil is a spatially complex environment at the microbial scale, predation dynamics can be captured by a relatively simple dynamical system of ODEs with prey refuge and separated complex compartment denoting the time delay between predator invasion and progeny emergence. This is a relatively rare and encouraging result; mean field approximation of interacting species in a spatially complex environment usually gives poor results [55]. To obtain reasonable results under such circumstances, dynamical models usually include spatial structures by various techniques (e.g. metapopulation, spatial moment equations, coupled map lattice, etc.) [55].
According to our model, not all the prey is available to the predator (i.e. some of it has a refuge); the prey population density decreases due to predation, and approaches r, the refuge parameter, asymptotically. When the refuge parameter was absent from the model equations (i.e. r = 0), fitting results were poor (data not shown) and the prey gradually approached zero (i.e. become extinct) and not a positive value. In our experimental set-up, the prey cannot coexist with its predator, because it does not reproduce due to the lack of nutritional substrate, yet, our model indicates the role of the complex spatial structure in protecting the prey and thus may contribute to coexistence, as indicated by previous theoretical and laboratory studies [1–4,56].
In this paper, we demonstrated the application of the direct integral approach to a challenging experimental set-up. The observations were collected for only eight time points, and only for part of the system, namely, for predator and prey; the ‘complex’ was not observed. By exploiting linear features of the dynamics system and using non-parametric smoothing, the direct integral approach enabled us to reduce the complex nonlinear optimization to a simple search over a grid of values of a single parameter s (see details in electronic supplementary material, and also figure S2 there). That resulted in a reasonable parameter estimates as well as important insights. For instance, we note that information about the parameter r can be recovered mostly from the tail of the experiment, where we have only two observations (this can be easily seen from model (3.1), where N′ = 0 when N = r). This fact made the estimation task a very challenging one. Thus, one concludes that measuring the process in its ‘tail’ is also important, a fact that should be taken into account in future experimental design. Our analysis was broken into steps (see the detailed analysis in the electronic supplementary material), an approach that resulted in improved stability of the parameter estimation (see, e.g. [38]). Finally, our analysis is based on a small number of observations, so the conclusions should be viewed as encouragement for further research using more data points, which will allow better inference. Indeed, in order to move from point to interval estimation, future work should combine improved data collection and further theoretical studies, which will enable the calculation of reliable confidence intervals (see the electronic supplementary material for details).
Supplementary Material
Acknowledgements
We thank the editor and two anonymous reviewers for their constructive comments, which helped us to improve the manuscript.
Data accessibility
The Matlab code used to generate the results of this paper will be provided by the first author upon request.
Authors' contributions
I.D. developed the statistical methodology, carried out the simulations, analysed the data and drafted the manuscript; E.M. developed the mathematical model, participated in data analysis and helped draft the manuscript; M.P. carried out the laboratory work; D.E.K. is DARPA programme's principle investigator and project coordinator; E.J. designed the laboratory work, and helped draft the manuscript; A.H. conceived the study, coordinated the study and helped draft the manuscript. All authors gave final approval for publication.
Competing interests
We declare we have no competing interests.
Funding
This research was sponsored by the U.S. Army Research Office and the Defense Advanced Research Projects Agency (DARPA) was accomplished under Cooperative Agreement Number W911NF-15-2-0036. In addition, this research was supported by the Israeli Science Foundation grants nos. 1583/12 and 387/15, and by a Grant from the GIF, the German-Israeli Foundation for Scientific Research and Development number I-2390-304.6/2015.
Disclaimer
The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office, DARPA, or the US Government. The US Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation hereon.
References
- 1.Aviram I, Rabinovitch A. 2008. Dynamical types of bacteria and bacteriophages interaction: shielding by debris. J. Theor. Biol. 251, 121–136. ( 10.1016/j.jtbi.2007.11.003) [DOI] [PubMed] [Google Scholar]
- 2.Heilmann S, Sneppen K, Krishna S. 2012. Coexistence of phage and bacteria on the boundary of self-organized refuges. Proc. Natl Acad. Sci. USA 109, 12 828–12 833. ( 10.1073/pnas.1200771109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schrag S, Mittler J. 1996. Host–parasite coexistence: the role of spatial refuges in stabilizing bacteria–phage interactions. Am. Nat. 148, 348–377. ( 10.1086/285929) [DOI] [Google Scholar]
- 4.Brockhurst M, Buckling A, Rainey P. 2006. Spatial heterogeneity and the stability of host–parasite coexistence. J. Evolut. Biol. 19, 374–379. ( 10.1111/j.1420-9101.2005.01026.x) [DOI] [PubMed] [Google Scholar]
- 5.Kimura M, Jia ZJ, Nakayama N, Asakawa S. 2008. Ecology of viruses in soils: past, present and future perspectives. Soil Sci. Plant Nutr. 54, 1–32. ( 10.1111/j.1747-0765.2007.00197.x) [DOI] [Google Scholar]
- 6.Hol FJ, Rotem O, Jurkevitch E, Dekker C, Koster DA. 2016. Bacterial predator–prey dynamics in microscale patchy landscapes. Proc. R. Soc. B. 283, 20152154 ( 10.1098/rspb.2015.2154) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kareiva P, Mullen A, Southwood R. 1990. Population dynamics in spatially complex environments: theory and data [and discussion]. Phil. Trans. R. Soc. Lond. B 330, 175–190. ( 10.1098/rstb.1990.0191) [DOI] [Google Scholar]
- 8.Comins HN, Blatt DW. 1974. Prey–predator models in spatially heterogeneous environments. J. Theor. Biol. 48, 75–83. ( 10.1016/0022-5193(74)90180-5) [DOI] [PubMed] [Google Scholar]
- 9.Burroughs N, Marsh P, Wellington E. 2000. Mathematical analysis of growth and interaction dynamics of streptomycetes and a bacteriophage in soil. Appl. Environ. Microbiol. 66, 3868–3877. ( 10.1128/AEM.66.9.3868-3877.2000) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jessup CM, Kassen R, Forde SE, Kerr B, Buckling A, Rainey PB, Bohannan BJM. 2004. Big questions, small worlds: microbial model systems in ecology. Trends Ecol. Evol. 19, 189–197. ( 10.1016/j.tree.2004.01.008) [DOI] [PubMed] [Google Scholar]
- 11.Sockett RE. 2009. Predatory lifestyle of Bdellovibrio bacteriovorus. Annu. Rev. Microbiol. 63, 523–539. ( 10.1146/annurev.micro.091208.073346) [DOI] [PubMed] [Google Scholar]
- 12.Blasius B, Huppert A, Stone L. 1999. Complex dynamics and phase synchronization in spatially extended ecological systems. Nature 399, 354–359. ( 10.1038/20676) [DOI] [PubMed] [Google Scholar]
- 13.Hanski I. 1999. Metapopulation ecology. Oxford, UK: Oxford University Press. [Google Scholar]
- 14.Brännström Å, Sumpter DJ. 2005. Coupled map lattice approximations for spatially explicit individual-based models of ecology. Bull. Math. Biol. 67, 663–682. ( 10.1016/j.bulm.2004.09.006) [DOI] [PubMed] [Google Scholar]
- 15.Barraquand F, Murrell DJ. 2013. Scaling up predator–prey dynamics using spatial moment equations. Methods Ecol. Evol. 4, 276–289. ( 10.1111/2041-210X.12014) [DOI] [Google Scholar]
- 16.May RM. 1973. Stability and complexity in model ecosystems, vol. 6 Princeton, NJ: Princeton University Press. [Google Scholar]
- 17.May RM. 2004. Uses and abuses of mathematics in biology. Science 303, 790–793. ( 10.1126/science.1094442) [DOI] [PubMed] [Google Scholar]
- 18.Yaari R, et al. 2016. Modeling the spread of polio in an IPV-vaccinated population: lessons learned from the 2013 silent outbreak in southern Israel. BMC Med. 14, 1–12. ( 10.1186/s12916-015-0545-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yaari R, Katriel G, Stone L, Mendelson E, Mandelboim M, Huppert A. 2016. Model based reconstruction of an epidemic using multiple datasets: understanding influenza A/H1N1 pandemic dynamics in Israel. J. R. Soc. Interface 13, 20160099 ( 10.1098/rsif.2016.0099) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yaari R, Katriel G, Huppert A, Axelsen J, Stone L. 2013. Modelling seasonal influenza: the role of weather and punctuated antigenic drift. J. R. Soc. Interface 10, 20130298 ( 10.1098/rsif.2013.0298) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huppert A, Barnea O, Katriel G, Yaari R, Roll U, Stone L. 2012. Modeling and statistical analysis of the spatio-temporal patterns of seasonal influenza in Israel. PLoS ONE 7, e45107 ( 10.1371/journal.pone.0045107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hooker G, Ellner SP, Roditi LDV, Earn DJ. 2011. Parameterizing state–space models for infectious disease dynamics by generalized profiling: measles in Ontario. J. R. Soc. Interface 8, 961–974. ( 10.1098/rsif.2010.0412) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ionides EL, Bhadra A, Atchadé Y, King A. 2011. Iterated filtering. Ann. Stat. 39, 1776–1802. ( 10.1214/11-AOS886) [DOI] [Google Scholar]
- 24.Bretó C, He D, Ionides EL, King AA. 2009. Time series analysis via mechanistic models. Ann. Appl. Stat. 3, 319–348. ( 10.1214/08-AOAS201) [DOI] [Google Scholar]
- 25.He D, Ionides EL, King AA. 2009. Plug-and-play inference for disease dynamics: measles in large and small populations as a case study. J. R. Soc. Interface 7, 271–283. ( 10.1098/rsif.2009.0151) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ionides E, Bretó C, King A. 2006. Inference for nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 103, 18 438–18 443. ( 10.1073/pnas.0603181103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.de Valpine P, Hastings A. 2002. Fitting population models incorporating process noise and observation error. Ecol. Monogr. 72, 57–76. ( 10.1890/0012-9615(2002)072%5B0057:FPMIPN%5E2.0.CO;2) [DOI] [Google Scholar]
- 28.Lele SR, Dennis B, Lutscher F. 2007. Data cloning: easy maximum likelihood estimation for complex ecological models using Bayesian Markov chain Monte Carlo methods. Ecol. Lett. 10, 551–563. ( 10.1111/j.1461-0248.2007.01047.x) [DOI] [PubMed] [Google Scholar]
- 29.Brunel NJ, Clairon Q, dAlché Buc F. 2014. Parametric estimation of ordinary differential equations with orthogonality conditions. J. Am. Stat. Assoc. 109, 173–185. ( 10.1080/01621459.2013.841583) [DOI] [Google Scholar]
- 30.Hooker G, Ellner SP. 2015. Goodness of fit in nonlinear dynamics: misspecified rates or misspecified states? Ann. Appl. Stat. 9, 754–776. ( 10.1214/15-AOAS828) [DOI] [Google Scholar]
- 31.Levin BR, Stewart FM, Chao L. 1977. Resource-limited growth, competition, and predation: a model and experimental studies with bacteria and bacteriophage. Am. Nat. 111, 3–24. ( 10.1086/283134) [DOI] [Google Scholar]
- 32.Payne RJ, Jansen VA. 2001. Understanding bacteriophage therapy as a density-dependent kinetic process. J. Theor. Biol. 208, 37–48. ( 10.1006/jtbi.2000.2198) [DOI] [PubMed] [Google Scholar]
- 33.Weld RJ, Butts C, Heinemann JA. 2004. Models of phage growth and their applicability to phage therapy. J. Theor. Biol. 227, 1–11. ( 10.1016/S0022-5193(03)00262-5) [DOI] [PubMed] [Google Scholar]
- 34.Wilkinson MH. 2016. Mathematical modelling of predatory prokaryotes. In Predatory prokaryotes, pp. 93–130. Berlin, Germany: Springer. [Google Scholar]
- 35.Huppert A, Blasius B, Stone L. 2002. A model of phytoplankton blooms. Am. Nat. 159, 156–171. ( 10.1086/324789) [DOI] [PubMed] [Google Scholar]
- 36.Dattner I, Klaassen CAJ. 2015. Optimal rate of direct estimators in systems of ordinary differential equations linear in functions of the parameters. Electronic J. Stat. 9, 1939–1973. ( 10.1214/15-EJS1053) [DOI] [Google Scholar]
- 37.Dattner I. 2015. A model-based initial guess for estimating parameters in systems of ordinary differential equations. Biometrics 71, 1176–1184. ( 10.1111/biom.12348) [DOI] [PubMed] [Google Scholar]
- 38.Voit EO, Almeida J. 2004. Decoupling dynamical systems for pathway identification from metabolic profiles. Bioinformatics 20, 1670–1681. ( 10.1093/bioinformatics/bth140) [DOI] [PubMed] [Google Scholar]
- 39.Ramsay JO, Hooker G, Campbell D, Cao J. 2007. Parameter estimation for differential equations: a generalized smoothing approach. J. R. Stat. Soc. Series B (Stat. Methodol.) 69, 741–796. ( 10.1111/j.1467-9868.2007.00610.x) [DOI] [Google Scholar]
- 40.Brunel NJB. 2008. Parameter estimation of ODE's via nonparametric estimators. Electronic J. Stat. 2, 1242–1267. ( 10.1214/07-EJS132) [DOI] [Google Scholar]
- 41.Liang H, Wu H. 2008. Parameter estimation for differential equation models using a framework of measurement error in regression models. J. Am. Stat. Assoc. 103, 1570–1583. ( 10.1198/016214508000000797) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hooker G. 2009. Forcing function diagnostics for nonlinear dynamics. Biometrics 65, 928–936. ( 10.1111/j.1541-0420.2008.01172.x) [DOI] [PubMed] [Google Scholar]
- 43.Fang Y, Wu H, Zhu LX. 2011. A two-stage estimation method for random coefficient differential equation models with application to longitudinal HIV dynamic data. Statistica Sinica 21, 1145–1170. ( 10.5705/ss.2009.156) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gugushvili S, Klaassen CAJ. 2012. √n-Consistent parameter estimation for systems of ordinary differential equations: bypassing numerical integration via smoothing. Bernoulli 18, 1061–1098. ( 10.3150/11-BEJ362) [DOI] [Google Scholar]
- 45.Vujačić I, Dattner I, González J, Wit E. 2014. Time-course window estimator for ordinary differential equations linear in the parameters. Stat. Comput. 25, 1057–1070. ( 10.1007/s11222-014-9486-9) [DOI] [Google Scholar]
- 46.Dattner I, Gugushvili S. 2015. Accelerated least squares estimation for systems of ordinary differential equations. (http://arxiv.org/abs/1503.07973) [Google Scholar]
- 47.Bellman R, Roth RS. 1971. The use of splines with unknown end points in the identification of systems. J. Math. Anal. Appl. 34, 26–33. ( 10.1016/0022-247X(71)90154-5) [DOI] [Google Scholar]
- 48.Varah J. 1982. A spline least squares method for numerical parameter estimation in differential equations. SIAM J. Sci. Stat. Comput. 3, 28–46. ( 10.1137/0903003) [DOI] [Google Scholar]
- 49.Edelstein-Keshet L. 2005. Mathematical models in biology. Classics in applied mathematics, vol. 46 Philadelphia, PA: Society for Industrial and Applied Mathematics. [Google Scholar]
- 50.Voit EO. 2000. Computational analysis of biochemical systems: a practical guide for biochemists and molecular biologists. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 51.Chou IC, Voit EO. 2009. Recent developments in parameter estimation and structure identification of biochemical and genomic systems. Math. Biosci. 219, 57–83. ( 10.1016/j.mbs.2009.03.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Vujačić I, Dattner I. 2016. Consistency of direct integral estimator for partially observed systems of ordinary differential equations linear in the parameters. (http://arxiv.org/abs/1602.05761) [Google Scholar]
- 53.Ramsay JO. 2006. Functional data analysis. Hoboken, NJ: Wiley Online Library. [Google Scholar]
- 54.Fenton A, Kanna M, Woods R, Aizawa SI, Sockett R. 2010. Shadowing the actions of a predator: backlit fluorescent microscopy reveals synchronous nonbinary septation of predatory Bdellovibrio inside prey and exit through discrete bdelloplast pores. J. Bacteriol. 192, 6329–6335. ( 10.1128/JB.00914-10) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Morozov A, Poggiale JC. 2012. From spatially explicit ecological models to mean-field dynamics: the state of the art and perspectives. Ecol. Complexity 10, 1–11. ( 10.1016/j.ecocom.2012.04.001) [DOI] [Google Scholar]
- 56.Cuddington K, Yodzis P. 2002. Predator–prey dynamics and movement in fractal environments. Am. Nat. 160, 119–134. ( 10.1086/340611) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The Matlab code used to generate the results of this paper will be provided by the first author upon request.