A mathematical model of tumour angiogenesis: growth, regression and regrowth

Abstract

Cancerous tumours have the ability to recruit new blood vessels through a process called angiogenesis. By stimulating vascular growth, tumours get connected to the circulatory system, receive nutrients and open a way to colonize distant organs. Tumour-induced vascular networks become unstable in the absence of tumour angiogenic factors (TAFs). They may undergo alternating stages of growth, regression and regrowth. Following a phase-field methodology, we propose a model of tumour angiogenesis that reproduces the aforementioned features and highlights the importance of vascular regression and regrowth. In contrast with previous theories which focus on vessel remodelling due to the absence of flow, we model an alternative regression mechanism based on the dependency of tumour-induced vascular networks on TAFs. The model captures capillaries at full scale, the plastic dynamics of tumour-induced vessel networks at long time scales, and shows the key role played by filopodia during angiogenesis. The predictions of our model are in agreement with in vivo experiments and may prove useful for the design of antiangiogenic therapies.

1. Introduction

Angiogenesis is the growth of new capillaries from preexisting blood vessels. The growth process is usually triggered by cells whose oxygen or nutrient requirements are not satisfied by the current vasculature and it can happen both in physiological and pathological conditions [1]. Notably, angiogenesis plays a pivotal role in tumour development because it is a necessary step for a solid tumour to grow beyond a certain size and become malignant [2].

In cancer, tumour cells proliferate abnormally quickly consuming the oxygen and nutrient released by preexisting blood vessels. As a consequence, they generate hypoxic regions within the tumour. Hypoxic cancerous cells may release tumour angiogenic factors (TAFs) [3], such as vascular endothelial growth factor (VEGF) or basic fibroblast growth factor (bFGF) [4,5], that unbalance the equilibrium between pro- and anti-angiogenic substances in their microenvironment. Endothelial cells (those that line the interior surface of blood vessels) are able to sense this change through their surface receptors. This activates the angiogenic response, a complex process that includes: selection of tip endothelial cells (TECs, those that will lead capillary growth); degradation of the basement membrane; sprout initiation; TEC migration towards the hypoxic region; proliferation of the capillary stalk to elongate the vessel; formation of the lumen that allows blood flow; and anastomoses between capillaries to form loops [6]. Angiogenesis peaks with the formation of a new vascular network. The newly developed network provides cancerous cells with virtually limitless oxygen and nutrients, as well as a way to escape the primary tumour and potentially metastasize.

Tumours give rise to dense, tortuous and defective capillary networks (figure 1a), which are significantly different from those formed in physiological conditions [7]. Arguably, the most characteristic feature of tumour-induced capillaries is that they are TAF-dependent as suggested by experiments [8–11]. Specifically, in [10], Mancuso and co-workers performed in vivo experiments where newly formed capillaries regressed after chemically inhibiting VEGF receptor signalling of endothelial cells (figure 1b). Perhaps more importantly, the experiment showed that tumour-induced capillaries regrew when VEGF receptors were made functional again (figure 1c–d). Owing to this evidence, it is currently believed that vascular regression can also happen locally and spontaneously in areas which are temporarily well oxygenated. After local regression, nearby tumour cells become hypoxic again, activating back the angiogenesis cascade. Mancuso et al. also observed in their work that regressing capillaries leave (temporarily) behind the vascular membrane that enveloped them. When new capillaries regrew afterwards, these vascular membranes were used by TECs as a scaffold that facilitated their migration: by going through these empty sleeves of basement membrane, TECs avoid or at least minimize the effort of degrading the extracellular matrix. As a consequence, the authors also observed that the regrowth was faster than the normal growth. Notably, the role of detecting the basement membranes relies on filopodia. Filopodia are receptor-rich, slender cytoplasmatic protrusions that TECs extend to enhance their sensitivity, to prove their microenvironment and to respond to it. In particular, when filopodia sense the remnants of basement membrane, TECs alter their direction towards them to use them as the path of minimum resistance in their migration.

Figure 1.

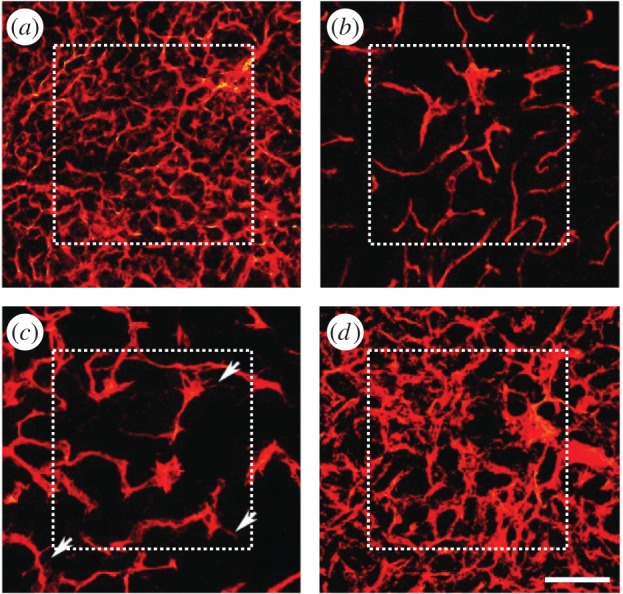
Tumour angiogenesis in vivo. (a) Growth of capillaries in a Rip-Tag2 tumour; (b) regressed capillaries after a 2-day inhibition of VEGF receptors; (c) regrowth of first sprouts (arrows) 2 days after inhibition removal; and (d) regrown capillaries 7 days after removal. Scale bar, 115 μm (adapted from [10]). (Online version in colour.)

There is an emerging view that regression and regrowth may play a significant role in the long-term dynamics of tumour angiogenesis and cancer development [12,13]. Numerous investigations have shed light on the intricate growth of capillaries through mathematical models (see [14–16] for extensive reviews). In the literature, we found different strategies to model capillaries. Some approaches use fully continuous theories that represent capillaries as averaged endothelial cell concentrations [17–21]. Although they set the basis for angiogenesis modelling, either they are fundamentally unable to capture the structure of capillaries or they only model the onset of angiogenesis. Using a different approach, several authors developed models such as [22–29] based on one-dimensional discrete theories for the description of TECs. In these models, capillaries are defined as the trail of TECs, capturing thus the medial line of the capillaries, but not their width. Continuing with discrete theories, another common approach is to model every endothelial cell using full-scale agent-based theories, as in [30–32]. These theories are able to define the faulty structure of capillaries, but are, in turn, computationally demanding. Lately, the phase field theory [33,34] has been used to model angiogenesis [35–39]. This theory is based on the definition of an order parameter that typically takes two values, each one representing a ‘phase’. The intermediate region between these two phases is a thin, smooth transition which in the limit becomes a sharp interface. The order parameter is interpreted in angiogenesis as a marker of the location of the endothelial cells, such that one phase represents the capillaries, the other the extravascular region, and the interface the capillary wall. The dynamics of the capillaries is governed by a partial differential equation that minimizes an energy functional. The phase field model allows one to resolve capillaries at full scale and to represent their structure. Furthermore, because it is not computationally expensive, the theory can capture the long-term dynamics of angiogenesis, or can be coupled with tumour growth models [37,40]. We also envision phase-field theories of angiogenesis being coupled with three-dimensional fluid dynamics simulations to compute blood flow [41].

In the last few years, new or augmented mathematical models of tumour-induced angiogenesis have been developed to include more biological phenomena, such as vascular adaptation, vessel remodelling, blood flow and capillary collapse [16,42,43]. In these theories, neo-vessels are no longer viewed as static, but they adapt to the changes of their environment. One of the first works on this topic was pioneered by Secomb & Pries [44], in which vessels changed their radius as a function of wall shear stress, intravascular pressure, and short- and long-range metabolic stimuli. This one-dimensional theory for blood flow has also been used in two- and three-dimensional models of angiogenesis such as [45–52], which also include phenomena such as varying vessel radii, haematocrit, non-Newtonian effects or subcellular dynamics. The interested reader is referred to the above-mentioned reviews for further works on this topic. In these theories, capillary remodelling depends upon blood flow. However, its dependency on TAF and the long-term dynamics of regression and regrowth has received little attention. In this work, we present a model for tumour angiogenesis that includes not only growth of new capillaries, but their natural regression and regrowth subject to TAF availability. The model, based on the phase field theory, resolves capillaries at full scale, allowing a description of their structure. We analyse the long-term dependency of this structure upon external stimuli. Our results achieve good agreement with in vivo experiments and suggest that our model could be a useful tool for the design of antiangiogenic therapies, which are emerging as a promising treatment for cancer [53].

2. Mathematical model

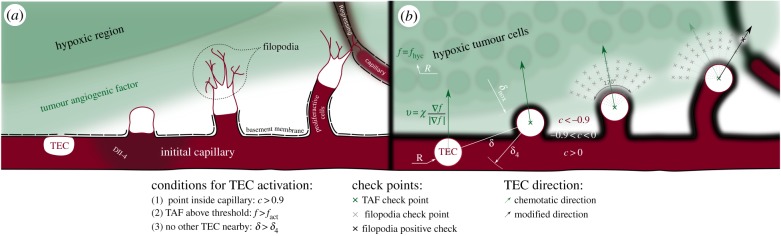
Our formulation accounts for three essential ingredients of angiogenesis, namely, TAF, capillaries and TECs, as shown in figure 2. In our theory, TAF is interpreted as one general and potent angiogenic factor, for instance VEGF, for the wide variety and functions of TAFs makes it effectively impossible to account for everyone. We model TAF as a normalized continuous variable f ε [0,f_hyc] representing the concentration of the factor. Capillaries are modelled using an order parameter c ε [−1,1], such that the areas where c ≥ 0 are identified with the endothelial cells that form capillaries and those where c < 0 represent the extravascular tissue. Furthermore, as capillaries are enveloped by a basement membrane and occasionally by a thin cell coverage (pericytes and smooth muscle cells), we extend the definition of c to include them: the extravascular tissue is compartmentalized into the capillary coverage, −0.9 < c <0, and the extracellular matrix, c < −0.9. Finally, TECs are modelled as discrete agents which follow chemical cues and sense nearby capillaries or empty basement membranes left by regressed capillaries.

Figure 2.

Conceptualization of tip endothelial cells. (a) Tumour angiogenic factor (TAF) activates tip endothelial cells (TECs) that extend filopodia to survey their environment. (b) In the model, discrete circular agents are activated and migrate following TAF gradients. Each agent evaluates conditions at filopodia check points. A positive check (c > −0.9) alters the (otherwise chemotactic) migration direction.

2.1. Tumour angiogenic factor

TAF is produced by tumour cells when they enter a hypoxic state. Tumour cells are located at fixed points and are assumed to be hypoxic when they do not have a capillary closer than the oxygen diffusion length, δ_nox (figure 2). TAF diffuses from the hypoxic cells (HYCs) and throughout the tissue, decays naturally, is consumed by endothelial cells, and eventually triggers angiogenesis. Its dynamics is supposed to be governed by the reaction–diffusion equation

2.1

where D is the diffusion coefficient and f_hyc is a constant representing the maximum TAF concentration in the tissue. 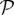is defined as

2.2

Here, P is the production rate, d is the distance to the closest hypoxic tumour cell and R is an average cell radius. The term 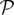(d)(f_hyc −f) in equation (2.1) limits the concentration of TAF within a hypoxic cell to f_hyc. The uptake function 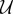is defined as

2.3

where U_u is the endothelial cell uptake rate, and U_d combines the TAF decay rate and the uptake rate by other cells. The uptake function acts such that deep inside the capillaries where c = 1 the uptake term −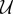(c)f of equation (2.1) reduces to −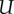_uf, that is, the endothelial cell uptake. On the other hand, when c = −1, the term reduces to −U_df which accounts for natural decay. Note that natural decay is neglected inside capillaries, as the uptake by endothelial cells is two orders of magnitude higher than natural decay, i.e. 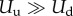. In the intermediate region, the uptake function creates a transition between the endothelial cell uptake and the natural decay.

2.2. Capillaries

The dynamics of capillaries is modelled using the phase field theory. While at tissue scales averaged descriptions of the capillaries may be enough, at the scale at which we study angiogenesis, that is cellular to tissue scale, the morphology of the new vascular networks plays an important role. For instance, the location of new sprouts alters the distribution of TAF, oxygen and hypoxic regions and the width and connections of capillaries influence blood flow. The phase field model allows one to describe this morphology without tracking the evolution of the capillary walls. Following this theory, the evolution of the order parameter c that represents a marker of the location of endothelial cells is such that it tends to adopt the configuration of minimum energy given by the energy functional

2.4

where Ψ_s and Ψ_c are the so-called surface free energy and chemical free energy, respectively. The surface free energy is defined as

2.5

where λ is a constant proportional to the width of the capillary wall. This term accounts for the required energy to create and maintain the capillary wall. The chemical free energy, defined as

2.6

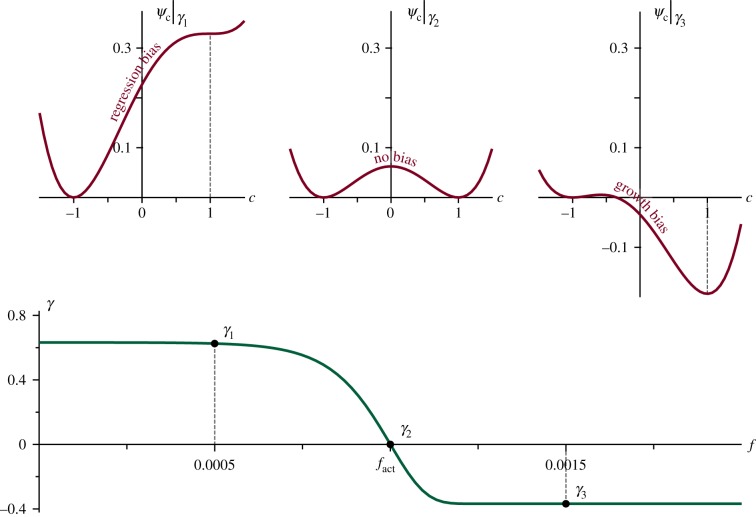
is a double-well, non-convex function with two local minima (as shown on the top row of figure 3) where α is a parameter and γ(f) is a tilting function. Each local minimum represents a phase. The first one is at c = 1, where the concentration of endothelial cells is maximum, while the other is at c = −1, where there are no endothelial cells; that is, the extravascular tissue. Between them there is a local maximum such that the energy contribution Ψ_c leads to the separation of the phases. Furthermore, the second term on the right-hand side of equation (2.6), by means of the function γ(f), tilts the double well favouring one phase over the other. This term captures the following proliferative to apoptotic phenotype switch. Endothelial cell receptors stimulated by TAF activate molecular pathways that change the cell phenotype either to a migratory (TECs, modelled separately) or to a proliferative one. In the absence of stimuli, endothelial cells lining immature, tumour-induced capillaries become apoptotic, which eventually leads to vascular regression [13]. Hence, we define γ(f) as

2.7

where β is a constant. As shown in figure 3, this function tilts the double well in such a way that capillary growth (proliferative phenotypes) is favoured when f > f_act and capillary regression (apoptotic phenotypes) is promoted otherwise. In equation (2.6), the parameter α is set to guarantee the existence of two local minima in Ψ_c for all γ.

Figure 3.

Chemical energy and tilting function. The chemical free energy Ψ_c (in red), is a double-well potential tilted by the TAF value through the function γ(f) (in green). Low values of TAF bias the evolution of c towards regression (top-left graph), while high values of TAF promote growth (top-right graph).

The key idea to successfully model this phenotype switch is to make use of non-conserved phase-field dynamics rather than previously used conserved models [36]. In the latter, the energy structure of the phase-field would be broken down by the incorporation of a reactive term. This new approach, however, allows a seamless integration of proliferation and apoptosis of endothelial cells in the energy functional. Thus, our phase-field equation is

2.8

where M is the mobility, a positive time-scale parameter, and

2.9

is the variational derivative of the energy 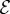. In equation (2.9),

2.10

is the derivative of Ψ_c with respect to the order parameter. Finally, we end the derivation of the phase field equation gathering equations (2.8) and (2.9), which leads to the following reaction–diffusion partial differential equation:

2.11

The reader is referred to [54–57] for detailed descriptions of this kind of phase-field models often used in dendritic solidification, but also in biological problems [58].

2.3. Tip endothelial cells

When capillaries receive TAF signals, some privileged cells (TECs) acquire a migratory phenotype and lead the growth of new sprouts [59]. This phenotype was not included in equations (2.7), (2.10) and (2.11). When an endothelial cell becomes a TEC, it expresses Delta-like ligand 4 (Dll-4). Dll-4 binds to Notch receptors of nearby endothelial cells preventing them from becoming also TECs [60,61]. This mechanism is known as lateral inhibition. TECs migrate following cues that guide the new capillaries towards nutrient-demanding cells. These cues may be, for example, chemical or mechanical. TECs are especially sensitive to such cues because they extend highly dynamic, receptor-rich protrusions called filopodia [62,63] towards the angiogenic stimuli (figure 2a). Furthermore, as filopodia probe the cell's microenvironment, they may detect nearby endothelial cells. In this event, the TEC anastomoses with the identified endothelial cell forming a loop between the growing sprout and the detected capillary. Note that this mechanism increases the vascular network connectivity. Perhaps, more surprisingly, filopodia may even sense basement membranes left behind by regressed capillaries and use them to improve their migratory capacity (see [64] and the supporting information therein for examples of in vitro experiments). The fact that no other cell will become migratory in the vicinity of a TEC through the lateral inhibition mechanism makes TECs ideally suited for a discrete description. A prime example is the work by Bentley et al. [65,66] which predicts TEC selection combined with migration and fusion using a cell-scale agent-based model.

Thus, TECs are discrete agents in our formulation, as shown in figure 2b. They are modelled using ideas from the literature [35], but further extended to include filopodia, to detect nearby capillaries, and to migrate not only following chemotactic cues (figure 2b, green arrows) but also using the empty sleeves of basement membrane left in the extracellular matrix (figure 2b, black arrow) by regressed capillaries. Following [35], we use discrete agents that are characterized by their centre and their radius R. TEC activation, that is, the phenotype switch from quiescent or proliferative to migratory, is performed according to the following deterministic rules: a point of the domain is the centre of a new TEC if

• (1) it is inside a capillary (c > c_act), to guarantee that it is an endothelial cell;

• (2) the TAF is greater than a threshold (f > f_act), to ensure that the stimulus is potent; and

• (3) there is no other TEC in the vicinity (distance to every TEC greater than δ₄), to account for the Delta-Notch selection.

Activated cells, unless they detect a nearby basement membrane or a capillary, migrate through the extracellular matrix following chemotactic cues with a velocity proportional to the TAF gradient, given by

2.12

where χ is the chemotactic constant and | · | denotes the Euclidean norm.

In our model, TECs also develop filopodia, which we model as a set of check points that mimic their high concentration of receptors (figure 2b, grey crosses). Because TAFs polarize tip cells such that they spread filopodia towards their front [59], we evenly place the check points into an annular sector of angle θ = 2π/3 centred around the chemotactic direction, as shown in figure 2b. The internal and external radii of the annular sector are set to ℓ_int = 2R and ℓ_ext = 4R, respectively, which is within the range of filopodia length [62]. Filopodia do not develop immediately after TEC activation, thus, in the model, the check points are not tested until the sprout has been initiated, that is, until the TEC has migrated a diameter from its activation point and it is outside its parent vessel. A positive check (figure 2b, black cross), defined as c > −0.9, means that the TEC has detected a basement membrane or a capillary through filopodia. Under this circumstance, the (chemotactic) direction of migration is altered towards the check point. Furthermore, the velocity magnitude is doubled when tip cells move using the vascular membrane scaffold to account for the easier migration through the already-degraded extracellular matrix. In the event of several positive checks, the check point where the value of c is higher is selected.

There are two ways by which a TEC can be deactivated, that is, the endothelial cell loses its migratory phenotype. The first one occurs when the TEC anastomoses with another TEC or capillary. Anastomosis is modelled in a similar way to filopodia: TECs test the value of c in a 2π/3-radians arc with radius R centred around the direction of migration. If any of these values is greater that 0.9, that is, the TEC is already touching the capillary, then there is an anastomosis event and the TEC gets deactivated. The second deactivating circumstance happens when the stimulus ceases (failure to meet condition 2). In both cases, the discrete agent is removed.

Finally, to close the model, we need to couple the discrete agents and the continuous variables. The connection between these two parts of the model is that both the TECs and the continuous variable c describe endothelial cells. Thus, we include TECs in the phase-field variable using a straightforward approach: c is updated to c = 1 in those regions of the computational domain occupied by TECs. Further elaborated strategies could be used to conciliate the discrete agents with the phase-field theory at the expense of a greater complexity. In addition, other discrete models for TECs that also operate at the cellular scale such as [66] could be easily coupled with this model using the proposed approach.

2.4. Numerical methods

Our theory is composed of two continuum variables and a set of discrete agents. Thus, we develop numerical methods for the partial differential equations, for the discrete agents and for coupling both of them. First, we derive the weak form of the continuous partial differential equations (2.11) and we discretize them in space and time using the Galerkin method and the generalized-α method [67,68], respectively (electronic supplementary material, text T1). Isogeometric analysis [69,70] permits us to use globally smooth functions on the domain and a means of accurately solving the equations. Additionally, we implement a time-step correction algorithm similar to those in [71–73]. Then, we develop an algorithm that handles TEC activation, filopodia probing, migration and deactivation. Note that the migration of TECs is meshless, meaning that it is independent of the spatial discretization of the continuum variables. This fact hinders the coupling between the discrete agents and the continuum variables, which we perform by updating the value of the order parameter c at the locations of TECs every time step using the concept of templates presented in [36]. Thus, each time step t_n before solving the continuous partial differential equations, we replace the phase field c with

2.13

for all j = 1, … ,N_tec, where N_tec is the number of active TECs, Ω^j_tec is the domain of the jth TEC, and the template function g^j_c is a multidimensional generalization of an exact one-dimensional solution to the phase-field equation on an infinite domain (see details in [36]). Note that the implemented adaptive time-step scheme could yield a large time step, which in turn could create a gap between capillaries and TECs. Hence, the continuous/discrete coupling limits the maximum time step size so that each time step a TEC is moved a maximum of 10% of its radius.

The parameter values in dimensionless units used in the computations are summarized in table 1. The physical quantities of these parameters may be retrieved by using the length and time scales L₀ = 1.25 μm and T₀ = 5460 s, respectively. Some of them are taken from in vivo observations, while others have been used in previous models of tumour angiogenesis.

Table 1.

Parameters of the model in dimensionless units.

parameter	description	in-text reference	value
D	tumour angiogenic factor diffusion coefficient	equation (2.1)	350.0
fhyc	maximum tumour angiogenic factor concentration in the tissue	equation (2.1)	1.0
P	tumour angiogenic factor production by HYCs	equation (2.2)	350.0
R	average cell radius	equation (2.2)	4.0
Uu	tumour angiogenic factor endothelial cell uptake	equation (2.3)	21.875
Ud	tumour angiogenic factor natural decay	equation (2.3)	0.35
λ	interface width	equation (2.5)	1.0
α	phenotype switch	equation (2.6)	0.525
β	phenotype switch	equation (2.7)	104
M	mobility	equation (2.8)	0.0875
χ	chemotatic constant of tip endothelial cells	equation (2.12)	25.48
cact	condition for TEC activation	condition 1	0.9
fact	condition for TEC activation	condition 2	0.001
δ4	Dll-4 radius of action	condition 3	32.0
δnox	nutrient and oxygen diffusion length		20.0

The diffusion coefficient of the TAF, following [35,74], has been set to D = 8.64 × 10⁻⁹ cm² s⁻¹. In the model, the radius of the TECs is 5 μm, which is within its measured 5–10 μm range [75]. We define the endothelial cell uptake as U_u =D/R² = 14.42 h⁻¹ so that the TAF cannot penetrate inside a capillary farther than the radius of a TEC. The value of the natural decay rate, U_d = 0.230 h⁻¹, is set so that its half-life is 3 h, an averaged value between TAFs [76,77]. P controls the production of TAF within a hypoxic cell. In the model, it acts as a penalty parameter that needs to be sufficiently large, without compromising the stability of the numerical scheme; thus, we have set its value to 350. As shown in the electronic supplementary material, the solution has proved to be fairly insensitive to variations of this parameter. The TAF condition for TEC activation f_act is set to 0.001 so that for f_hyc = 1 hypoxic cells located farther than 200 μm away from a capillary can activate TECs within the time scale of angiogenesis (electronic supplementary material, text T1). Furthermore, we have set δ₄ to 8R so that TECs impede the activation of other TECs in their neighbourhood.

The migration of TECs is controlled by the chemotactic constant χ which is set to 0.504 mm d⁻¹, which is within the range of velocities observed in the mouse cornea micropocket angiogenesis assays [78]. On the other hand, proliferation and apoptosis of stalk cells is controlled by the phase field equation, in particular by the velocity of the interface. For a straight interface it can be proved [79] that this velocity is V =3Mλαγ(f). Here, α and λ are computational parameters which do not directly relate with physical measures. The reader can find in the electronic supplementary material a parametric study of these quantities. As shown in [79], the condition 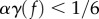is necessary to guarantee the existence of two minima in the energy functional and recalling that λ is a fixed length scale that defines the capillary wall thickness, we can assume that the proliferation/apoptosis velocity is controlled by the mobility M. Because the diffusion of TAF is much faster than cell dynamics, we have set the ratio between the diffusion coefficient and the mobility to 4000. In addition, the definition of γ is such that the velocity of capillary regression through apoptosis is 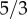times slower than its proliferation, to maintain the integrity of growing capillaries. β is a computational parameter that has been set to 10⁴ to produce a smooth transition in γ around f_act. Finally, under physiological conditions, every cell is at a maximum of 100–200 μm from a blood vessel. Because of the faulty structure of tumour-induced capillaries and the high nutrient uptake of cancer cells, we have reduced this distance to δ_nox = 25 μm. In this respect, the model could be improved by adding nutrient and flow compartments so that δ_nox would not need to be estimated.

3. Results

We open this section with a simple simulation whose aim is to give insight and study the proposed mathematical model. The study is continued with an analysis of the parameters that control filopodia extension. Then, we show how the theory is able to capture the growth patterns in configurations that resemble in vivo experimental setups, in particular, in a two-dimensional simulation of the mouse corneal micropocket angiogenesis assay. Finally, we present the full potential of this new theory in a simulation that replicates the experiment shown in figure 1.

3.1. Basic features of the model

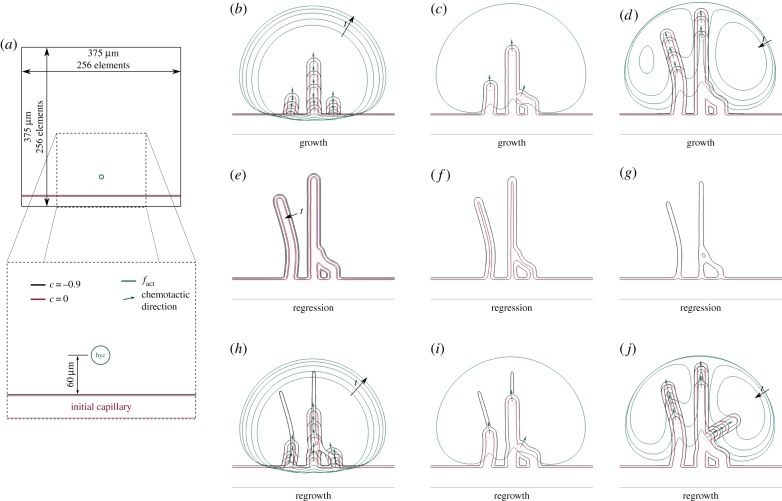
In order to study how the model works, we perform a simple simulation on a square domain (figure 4; electronic supplementary material, video V1). The simulation is performed on a 375 × 375 μm square domain using a mesh composed by 256² quadratic elements (figure 4a), a configuration that has already proved to accurately capture the phase-field interface [36,80]. The boundary conditions for this and every other simulation hereafter are zero-flux conditions. We consider this set-up simply because, contrary to the following simulations in this paper, it only has an initial straight capillary and one HYC located close to it—approximately 60 μm away. Furthermore, for the sake of simplicity, we have set f_hyc to 0.1 to reduce the potential number of new capillaries.

Figure 4.

Basic features of the model. Simulation of the mathematical model in a simplistic setup (a) that shows the process of growth (b–d), regression (e–g) and regrowth (h–j). Each snapshot corresponds to the following times: (a) t = 0, (b) t = 1.60, 2.23, 2.86, 3.49, 4.12, (c) t = 4.76, (d) t = 5.39, 6.02, 6.65, 7.28, (e) t = 9.18, 12.95, (f) t = 16.85, (g) t = 20.55, (h) t = 22.45, 23.06, 23.72, 24.33, 24.95, (i) t = 25.60 and (j) t = 26.23, 26.85, 27.48, 28.36.

Figure 4b–j shows the time evolution of this simulation by means of zoomed snapshots. The simulation starts with TAF being produced at the HYC which diffuses throughout the domain. The first activation of a TEC (dotted, red circumferences in figure 4) occurs when enough TAF infiltrates the initial capillary, that is, when the amount of TAF is greater than f_act (green lines in figure 4) inside the capillary. Several time steps afterwards, two other TECs get activated on both sides of the first one. Note that all TECs are separated from each other as dictated by the lateral inhibition mechanism. As shown in figure 4b, the three TECs initially migrate following the chemotactic direction, marked with green arrows. Figure 4c reveals, however, that the chemotactic direction may be altered. There, the filopodia of the rightmost TEC detect the presence of a capillary located on its left-hand side. Consequently, the chemotactic direction is overridden and, even though the green arrow points to the top-right corner, the TEC moves towards the detected capillary, anastomoses with it and gets immediately deactivated. This event highlights that anastomosis is driven by filopodia contact sensing rather than through chemotaxis in our model, which is in agreement with recent in vivo observations [63]. Meanwhile, the two other TECs, that have already promoted the deactivation of the HYC, continue their migration through the extracellular matrix still following chemotactic cues. Proliferative cells keep widening and elongating the capillaries. And, as shown in figure 4d, the growth process evolves unaltered until all TAF gets consumed.

At this point, in the absence of TAF, the endothelial cells of the tumour-induced vasculature, which are highly TAF-dependent, change their phenotype to an apoptotic one and regression starts. Figure 4e–g shows how this process, although slower than the initial growth (note the time steps in the caption and its duration in the video), promotes the gradual disappearance of the capillaries. The vascular basement membrane that was enveloping the capillaries, however, remains after the capillaries have regressed forming the already mentioned empty sleeves, through which future TECs can migrate easily. And, indeed, after the HYC gets activated again the new TECs that orchestrate the regrowth, aided by their filopodia, use these remnants of basement membrane to direct the formation of new capillaries (figure 4h–j). Note that, given enough time, the basement membranes would eventually regress. As shown in figure 4j, the regrowth and the growth pattern are not equal, even in this simple setup. The source of this difference is that TECs migrate faster through the empty sleeves than through the extracellular matrix, thus, their velocities are higher with respect to TAF consumption. In particular, in the regrowth process shown in that figure a new TEC gets activated soon after the anastomosis event between the rightmost TEC and the middle capillary, creating a new sprout that grows towards the top-right corner.

3.2. Parametric study of filopodia

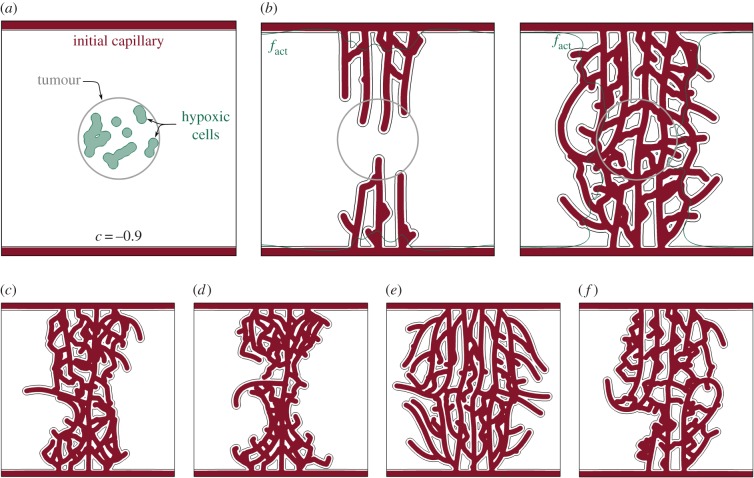
In the previous example, we observe how filopodia play a pivotal role in creating anastomoses between capillaries. The parameters that define filopodia probing, that is θ, ℓ_int and ℓ_ext, were estimated from observations [64]. Note that the parameter ℓ_int measures the minimum distance at which filopodia start to sense. Its value has been set to a minimum 2R so that TECs do not sense themselves. There is no biological reason to increase this parameter, either. Therefore, we perform here a study of the value of the other parameters. As shown in figure 5a, for this study we make use of a more realistic, although still academic configuration of the computational domain. Initially, we place two capillaries along opposite edges of the square domain and an aggregate of hypoxic cells at its centre. These HYCs represent hypoxic regions of a 112.5 μm diameter tumour. The size of the domain and mesh used for this simulation are the same as in the previous example (figure 4a).

Figure 5.

Parametric study of filopodia. (a) Initial conditions: tumour angiogenesis is induced by the TAF released by hypoxic cells aggregated in a tumour-like circular region. (b–f) Simulations showing the comparison of the vascular patterns generated with different parameters of the model. (b) Two snapshots (t = 20, 30, respectively) of the formation of a vascular network using the estimated parameters θ = 2π/3 and ℓ_ext = 4R. (c–f) Resulting vascular patterns at time t = 30 with the following variations of the estimated parameters: (c) ℓ_ext = 8R, (d) ℓ_ext = 12R, (e) θ = 5π/12 and (f) θ = 11π/12. In (b), the resulting pattern is more connected and regular than in the remaining cases.

First, we present in figure 5b two snapshots of the evolution of the vascular network for θ = 2π/3 and ℓ_ext = 4R, that is, the estimated values. In the first snapshot, we observe that the longest capillaries, those created first, grow parallel to each other separated by a distance close to δ₄. However, as more capillaries grow behind, the distance between TECs and capillaries falls within the extension range of filopodia, which triggers the creation of anastomoses. The network starts to form loops until a lattice-like pattern that spans and oxygenates the tumour gets generated at time t = 30. In the remaining subfigures, we show the vascular patterns at that time generated under the same initial conditions and parameters, except for one. In figure 5c,d we have altered the maximum extension of the filopodia twice and thrice, respectively. As the detection range of TECs has been increased, tip cells detect nearby capillaries easily. Indeed, the scope of filopodia is now greater or equal to δ₄, meaning that TECs sense other capillaries as soon as they initiate the formation of a new sprout. The resulting networks create an hourglass-like shape with the thinnest part over the tumour. This shape is more pronounced in figure 5d, where a higher value of ℓ_ext favours the creation of aberrant capillary clusters. In the simulation shown in figure 5e, we have decreased the spread angle of filopodia θ to 5π/12, and in figure 5f we have increased it to 11π/12. In the former case, the highly reduced detection by filopodia promotes a vascular network of capillaries that run parallel and only get occasionally connected by short vessels. In the latter, we observe a small number of top-to-bottom capillaries from which many short sprouts emerge. These sprouts get rapidly connected (in many instances even with its parent capillary) due to the large value of θ, creating capillary masses and saccular regions.

In this parametric study, we have shown that the vascular patterns for the altered parameters are more defective either by forming clusters of capillaries or by creating parallel, poorly interconnected ones. Note, however, that in experimental observations the direction and extent of filopodia is not constant, but varies widely. In the absence of data, we have estimated these parameters as constants for the sake of simplicity, although a more complicated stochastic model could be easily incorporated.

3.3. Vascular growth

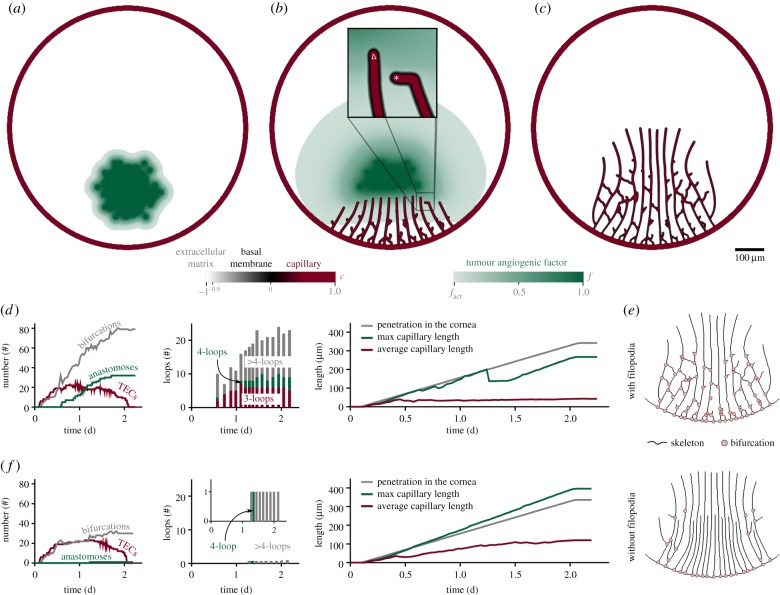
As a first illustration of the capabilities of our model in an experimental-like set-up, we show in figure 6 a computation in a configuration that resembles the mouse cornea micropocket angiogenesis assay [81]. The cornea is an avascular tissue surrounded by a region called limbus formed by capillaries. Tumour cells in the cornea may promote the creation of new capillaries from the limbus. Thus, in our simulation, the entire system is initially avascular (figure 6a), except for a circular capillary (red) that mimics the limbal vessels. We include a cluster of hypoxic tumour cells that release a generic TAF (green) that triggers angiogenesis. Figure 6b shows a snapshot of the growing capillaries that are pervading the cornea and forming a new vessel network. As this network grows, endothelial cells consume angiogenic factor and tumour cells that are close to capillaries become normoxic and stop releasing TAF. Capillaries grow led by TECs. TECs follow gradients of TAF (triangle-labelled discrete agent of the inset), unless they sense nearby capillaries through filopodia (star-labelled agent of the same inset) and anastomose with them. The pattern obtained in this numerical simulation immediately after capillary growth has ceased (figure 6c) is similar to those observed in vivo [81–83] and in silico [24,26,84].

Figure 6.

Corneal neovascularization. (a) Circular initial capillary (red) and cluster of tumour cells that release TAF (green). (b) Tip endothelial cells (TECs) lead the growth of the new capillaries; (c) vascular pattern after growth; (d) neovasculature quantification; (e) skeletons of the final patterns of the simulations with and without filopodia extension; (f) quantification of the simulation without filopodia.

We performed a quantification of the neovasculature over time (figure 6d). The vasculature starts as a tree-like network (no loops) driven by an increasing number of TECs that create new branches and bifurcations. However, as their filopodia detect nearby capillaries, the number of anastomosis events grows rapidly. Consequently, the tree-like network gradually evolves to a mesh-like one with loops that facilitate blood flow. By the end of the simulation approximately 30 anastomoses have shaped the vasculature into a highly interconnected network with more than 20 loops. Note that by the end of the simulation more than 50% of the loops involve four capillary branches or more (‘>4-loops’ in figure 6). These long-range connections favour the oxygenation of tumour cells. The pace at which the vasculature penetrates the cornea (measured as the distance from the limbus to the innermost TEC using the shortest path) is linear, as reported in [82,83]. We also measured the maximum and average capillary length (distance between bifurcations) and observed that anastomoses reduce the maximum length compared with the penetration distance and maintain the average length almost constant.

With the aim of evaluating the role of filopodia, we repeated the same simulation disabling the extension of filopodia in each tip cell. Electronic supplementary material, video V2 presents the side-by-side vascular network evolution of both simulations and figure 6e shows a comparison of the resulting medial lines or skeleton of the final patterns. Visual observation reveals two marked differences between them. The first one is that in the absence of functional filopodia, chemotactically driven TECs chiefly migrate in the same direction creating almost parallel capillaries. The second one is that the number of bifurcations, represented as grey dots in the figure, is drastically reduced from one simulation to the other. These facts are supported by the quantitation of the last simulation shown in figure 6f. There, we observe that, although the number of TECs created during angiogenesis is almost the same, the number of bifurcations is reduced by a factor of two. Not only that, but the majority of these bifurcations are a consequence of the initiation of angiogenesis from the limbus and not due to anastomoses. The absence of filopodia prevents TECs from sensing nearby vessels and the only anastomosis event is the result of a tip cell that runs close to a capillary. As a consequence, the new vasculature presents a single loop and is mainly formed by dead-end capillaries that prevent blood flow. Note also that the duration of both simulations is equal and that both networks penetrate approximately the same distance into the cornea.

3.4. Regression and regrowth

The result in figure 6 illustrates the capabilities of the model to predict vascular growth patterns, but a major goal of this work was to develop a model that naturally leads to regression and regrowth. We study this phenomenon motivated by the in vivo experiment shown in figure 1. To replicate the experiment, we need first to simulate the growth process. To this end, we chose as our computational domain the area enclosed by the dotted lines in figure 1. In the simulation, the system is initially avascular, except for a capillary placed on the boundary which serves as a precursor to the neo-vasculature (figure 7a). Randomly distributed hypoxic cells (that resemble the Rip-Tag2 tumour in the experiment) release angiogenic factor that activates TECs. Initially, capillaries grow inwards, forming a new vasculature (figure 7b). Then, the vasculature regresses due to the absence of TAF (figure 7c) and the system enters a transient behaviour with local regressions and regrowths (electronic supplementary material, video V3) similar to those observed in experiments. Figure 7d–h shows snapshots of different patterns that highlight the dynamism and adaptation of the vasculature when regression and regrowth are considered. Note that in figure 7h the initial capillary has completely regressed. We assume that this configuration is analogous to the starting point of the experiment (figure 1a).

Figure 7.

Tumour angiogenesis simulation: growth, regression and regrowth. (a–h) Snapshots of the growth phase of angiogenesis. (i–l) The chemical inhibition of TAF receptors promotes capillary regression during 7 days. (m–p) When the inhibition is removed, new TECs get activated and start the regrowth process. The vasculature recovers its original density 7 days after the inhibition removal. This simulation replicates the experiment of figure 1 and both are compared in figure 8. Colour legend in figure 6.

The experimental procedure of Mancuso et al. is continued by chemically inhibiting the VEGF receptors of endothelial cells, so that capillaries are unable to detect the presence of TAF and eventually regress (figure 1b). The receptors are kept blocked for 7 days and the capillaries regrow afterwards (figure 1c,d). Our simulation proceeds along the same lines. We model the receptor inhibition by blocking the activation of new TECs. Those that were active will eventually get deactivated in the absence of TAF. During the inhibition, most capillaries regress, as shown in figure 7i–l. Note that regressed capillaries leave behind a trail (grey colours representing low values of c in figure 7) which we identify with the basement membrane. If the treatment were prolonged, all the capillaries and basement membranes will eventually disappear. However, as in the experiment, we remove the inhibition after approximately 7 days (figure 7m) and the regrowth process starts (figure 7n–p). The high availability of TAF due to the treatment promotes an almost instant activation of TECs after its removal.

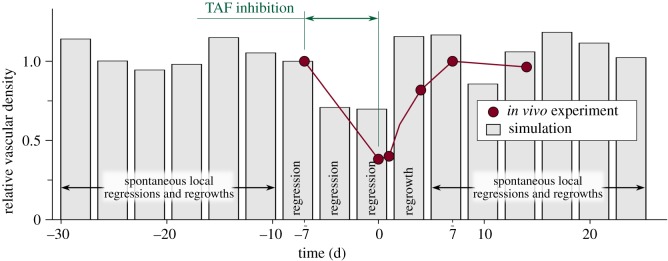
Visual inspection shows that the in vivo experiment and the numerical simulation compare well. In both cases, the network is composed of tortuous, highly interconnected vessels that oxygenate the tissue unevenly. Also, as the new vasculature is particularly dependent on TAF, the inhibition acts successfully, leaving in both cases few, barely functional capillaries in the region. The dependency on TAF also implies that the vasculature recovers rapidly after the treatment, a finding that may be useful in the design of antiangiogenic therapies. Adding to the visual inspection, we performed a quantitative comparison between the simulation and the experiment. Figure 8 shows the vascular density of the former in grey and of the latter (data taken from [10]) in red. Vascular density suffers a drastic drop due to the inhibition. Then, the regrowth process starts and the vascular density eventually recovers its original value. After the regrowth, our model predicts mild oscillations of the vascular density due to spontaneous local regressions and regrowths. To some extent, this can also be inferred in the experiment, but there is insufficient data to be conclusive. In addition, in order to pose the mathematical model we had to make several assumptions. One of the strongest ones is that we neglect the proliferation and death of cancerous cells and assume fixed hypoxic regions, as the time scale of angiogenesis is smaller than that of tumour growth. In this experiment, in particular, we presume that the tumour is not aggressive and remains constant and occupying the whole domain throughout the duration of the simulation. This assumption hinders the quantitative comparison with assays. In summary, although precise agreement with in vivo experiments is a daunting task, the simulation captures the trend of the experiment.

Figure 8.

Evolution of the relative vascular density (current vascular density over a reference vascular density). Both the experiment (red, figure 1) and the simulation (grey, figure 7) show regression promoted by TAF inhibition, followed by regrowth after the inhibition is over.

4. Conclusion

In this work, we have presented a new model for tumour-induced angiogenesis growth, regression and regrowth. The model is based in a non-conservative phase-field theory which, opposite to previous models that include vessel remodelling, allows one to resolve capillaries at full scale and to simulate long-term dynamics of angiogenesis. Existing models consider vessel regression and remodelling mainly based on one-dimensional theories of blood flow [44,45]. Here, we model an alternative regression mechanism which emanates from the fact that tumour-induced capillaries are TAF dependent. In addition, we have included a discrete conceptualization of filopodia that endows TECs with the ability to sense their microenvironment.

Even assuming a fixed tumour and neglecting blood flow, our model predicts the plasticity and dynamic evolution of capillaries at long time spans. In particular, the simulations are in agreement with in vivo experiments and capture capillary regression induced by TAF inhibition and their subsequent regrowth after inhibition removal. Our simulations reinforced the view that filopodia-based sensing plays a major role in anastomosis and loop formation and that chemotaxis itself is not enough to create connected networks that favour blood flow and oxygenation. Furthermore, filopodia have proved to facilitate regrowth, as they enhance TEC exploration of the least resistant path for migration, which is formed by the left-behind basement membranes. In this respect, the model could be augmented by explicitly considering extracellular matrix degradation during migration and making TEC velocity a function of this new variable. Also, the directional switch of TEC migration between the chemotactic and vessel detection by filopodia could be improved by incorporating a smooth transition based on experimental data.

In conclusion, our model reinforces the view that tumours need to be analysed as a complex system which interacts dynamically with its microenvironment. In this context, our study highlights the importance of regression and regrowth of tumour vasculature. The proposed model may be a useful tool not only to predict capillary growth patterns, but also for the design of antiangiogenic therapies, which are currently considered the fourth pillar of cancer treatment after surgery, chemotherapy and radiation.

Authors' contributions

G.V. and H.G. conceived and designed the research. G.V. ran the simulations. G.V., H.G. and I.C. analysed the data. G.V., H.G. and I.C. participated in the preparation and editing of the manuscript.

Funding

G.V. and H.G. were partially supported by the European Research Council (contract no. 307201), Xunta de Galicia, and by Ministerio de Economía y Competitividad (contract no. DPI-2013-44406-R, cofinanced with FEDER funds). I.C. was partially supported by Consellería de Cultura, Educación e Ordenación Universitaria of the Xunta de Galicia (grant no. GRC2014/039).