Measurement of DNA translocation dynamics in a solid-state nanopore at 100-ns temporal resolution

Abstract

Despite the potential for nanopores to be a platform for high-bandwidth study of single-molecule systems, ionic current measurements through nanopores have been limited in their temporal resolution by noise arising from poorly optimized measurement electronics and large parasitic capacitances in the nanopore membranes. Here, we present a complementary metal-oxide-semiconductor (CMOS) nanopore (CNP) amplifier capable of low noise recordings at an unprecedented 10 MHz bandwidth. When integrated with state-of-the-art solid-state nanopores in silicon nitride membranes, we achieve an SNR of greater than 10 for ssDNA translocations at a measurement bandwidth of 5 MHz, which represents the fastest ion current recordings through nanopores reported to date. We observe transient features in ssDNA translocation events that are as short as 200 ns, which are hidden even at bandwidths as high as 1 MHz. These features offer further insights into the translocation kinetics of molecules entering and exiting the pore. This platform highlights the advantages of high-bandwidth translocation measurements made possible by integrating nanopores and custom-designed electronics.

Nanopore-based sensors are one of the few transducers capable of electronic label-free, single-molecule detection and analysis. In experiments using solid-state nanopores, an ion current flows through a molecular-scale-size hole in a thin dielectric membrane immersed in electrolyte under the influence of a driving transmembrane voltage. When a molecule is driven into the nanopore, its presence gates this current, and the magnitude of this gating can be correlated to the molecule’s physical properties, such as its volume and charge. Similar systems can be constructed with biological components using protein channels, such as α-hemolysin, in lipid bilayer membranes.^1,2 Solid-state nanopores can now be fabricated with pore sizes comparable to protein pores but with signal levels that are at least one order of magnitude higher due to the thinner extent of the solid-state pores (sometimes down to the single nanometer range) and due to the higher transmembrane voltages that can be supported across solid-state membranes.³

One of the advantages of electronic approaches to single-molecule detection over fluorescence-based approaches generally is the higher signal levels. The current measured in solid-state nanopores can be as large as 30 nA, as in this study. In contrast, typical organic fluorophores under laser pump powers on the order of 50 mW⁴ deliver photon fluxes on the order of 3000 photons/s,⁵ which amounts to a current of only 0.2 fA in an imager with a quantum efficiency of ~40%. These signal levels limit single-molecule fluorescence experiments to temporal resolutions that are typically on the scale of 50 ms.⁶ In contrast, the approximately 10⁶ times higher signal levels from nanopores should translate into temporal resolutions on the scale of 100 ns (or better) at the same noise levels. Despite this potential, achieved temporal resolutions have been at best 1 µs,⁷ using integrated complementary metal-oxide-semiconductor (CMOS) amplifiers, and more typically 10–100 µs with discrete voltage-clamp amplifiers, such as the Axopatch 200B.^8–12 The inherently transient nature of DNA translocation through nanopores – which can occur at rates higher than 10 bp/µs – reinforces the need for improved temporal resolution in these measurements.¹³ For pores less than 5 nm in diameter, pore-molecule interaction serves to reduce the average translocation rate to ~1–2 bases/µs for ssDNA,³ but these rates are still very fast relative to achieved temporal resolution in measurement systems to-date. For proteins translocating through nanopores with diameters greater than 10 nm, over 90% of all events go undetected because of inadequate temporal resolution in the detection electronics.¹⁴

Because of the poor temporal resolution of typical nanopore instrumentation, a range of “slowing-down” approaches have focused specifically on reducing the translocation speed: by ratcheting the molecules using an enzyme,¹⁵ by using temperature gradients⁸ and viscosity gradients,^12,13,16 and by using different salt solutions.^9,17 While these techniques manage to reduce the average translocation rate, this is achieved at the expense of either increased sample preparation or reduced signal levels. In addition, for techniques that slow down translocation using enzyme dynamics, there are Poisson statistics at work in the ratcheting dynamics. High instrumentation bandwidth improves error rates, because of one’s ability to “see” all events, including the rare ones that may be significantly faster than the mean.

It is noise that limits temporal resolution in nanopore measurements. A typical nanopore noise spectrum is as shown in Figure 1a.^18,19 At low frequencies, noise is determined by the flicker noise through the pore (with a 1/f characteristic in the noise power spectrum), at moderate frequencies by white noise from the resistance of the pore itself and the feedback resistance of the amplifier, and at high frequency by amplifier input-referred voltage noise interacting with the total capacitance at the input of the amplifier (with an f²-characteristic in the noise power spectrum). Over a frequency window, an f-dependent section of the characteristic is sometimes observed (as shown in Figure 1a), which has been attributed to interaction of the amplifier’s thermal noise with losses in the membrane dielectric^19,20 but may also be caused by interaction of the amplifier’s flicker noise with the capacitance at its input. Advances in nanopore treatment protocols have minimized flicker noise from the pores. As such, integrated noise in high bandwidth nanopore measurements are dominated by the contributions of the amplifier.²¹ Several efforts have focused on improving these amplifiers either through adjustments to off-the-shelf amplifiers, such as the Axopatch 200B,^22–24 or more recently, through custom-designed amplifiers.^7,25–27 Most custom amplifiers have exploited CMOS technology and have the additional advantage of allowing arrays of amplifiers to be supported on the same chip. These approaches have been able to extend measurement bandwidths, as limited by signal-to-noise ratios (SNRs), up to 1 MHz,⁷ offering microsecond temporal resolution.

Figure 1.

Small-diameter nanopores and amplifier design. (a) Typical input-referred current noise spectrum for a nanopore measurement. The axes are plotted in log-log scale. Low frequency noise is primarily governed by flicker and thermal contributions whereas high frequency noise is dominated by the voltage noise of the amplifier interacting with the capacitance at the amplifier’s input. (b) Schematic of the cross-section of the nanopore chip including the silicone passivation on the top. (c) Bright-field TEM image of nanopores made in STEM-thinned membranes.²⁹ Circles indicating diameters of 1.7 nm, 2.0 nm, and 2.6 nm are shown in overlay with corresponding nanopores. (d) Simplified electrical schematic illustrating the various capacitances and noise sources that determine high-frequency noise behavior. Input current signals are converted to a voltage with a gain set by R_F. The net capacitance that determines the noise is C_amp + C_pore. (e) Die micrograph of the 5 mm × 5 mm amplifier chip with a zoomed-in micrograph of a single channel. The chip has 25 amplifiers, each of which implement the schematic illustrated in (c) and which can be operated independently of each other. Each channel has an Al electrode that is converted to an Ag/AgCl electrode through postprocessing.

In this Letter, we report the fastest ion current measurements through nanopores to-date with temporal resolutions approaching 100 ns (with an SNR of better than 10). This high measurement bandwidth is achieved through the use of ultra-thin solid-state nanopores that offer signal levels as large as 30 nA measured using a custom CMOS-integrated nanopore (CNP) amplifier. Recording at such high bandwidths enables us to detect transient features within translocation events that are related to the translocation dynamics of ssDNA that are otherwise undetectable at lower bandwidths.

Several important parameters determine the SNR in nanopore measurements. For a given blockade current ΔI, with a root-mean-squared (RMS) noise level of I_RMS, the signal-to-noise ratio is defined as $SNR=\frac{\mathrm{\Delta }I}{I_{RMS}}$. At high frequency, the noise is dominated by the f² part of the characteristics shown in Figure 1a. As such, the SNR-constrained bandwidth (B_MAX) obeys the equation $B_{\mathit{\text{MAX}}}\propto {\left(\frac{\mathrm{\Delta }I}{{\nu }_n\sum C_i}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$, where ν_n is the voltage thermal noise floor of the amplifier and ∑ C_i is the net capacitance at the input of the amplifier, composed of contributions from the pore (C_pore) (Figure 1b), and the measurement electronics (C_amp) (Figure 1d).¹⁹ To further increase B_MAX, ΔI must be increased, while simultaneously lowering ν_n and ∑ C_i. ΔI can be increased by increasing the conductivity of the salt solution or by reducing the nanopore thickness.²⁸ While some commercial amplifiers can offer lower ν_n than their integrated CMOS counterparts, this comes at the expense of higher ∑ C_i.²¹ Although some new discrete amplifiers have managed to reduce C_amp to as little as 20 pF, this value can still dominate ∑ C_i in optimized nanopore structures, in which C_pore can be less than 5 pF.²¹ Achieving the full temporal benefit afforded by a given ΔI involves careful reduction of ν_n, C_amp and C_pore.

Reduction of ν_n and C_amp is achieved in the CNP amplifier with a custom-designed integrated circuit (IC) designed in a 0.18-µm CMOS technology. The IC contains 25 independent low-noise, high-bandwidth transimpedance amplifiers, each occupying 0.16 mm² in a 5 mm × 5 mm chip. Figure 1e shows a die micrograph of the IC. The design of the amplifier (see Supplementary Information) follows from our earlier design⁷ but has been further optimized for lower ν_n. The feedback networks (shown as the parallel combination of R_F and C_F in Figure 1d) in these amplifiers often differ in their implementation from their discrete counterparts. Since realizing large valued resistors is difficult in CMOS processes and would add too much capacitance at the input, the feedback resistance R_F, is realized using an active current-divider circuit.²⁵ R_F is tunable and is set to either 7.5 MΩ (low gain) or 45 MΩ (high gain). While these relatively low R_F values will reduce the SNR slightly at frequencies below ~100 kHz, where the integrated noise is dominated by the white noise of R_F (Figure 1a), this is not a concern at MHz bandwidths where the integrated noise is dominated by the interaction of the amplifier thermal noise with the input capacitance^18,19 (see Supplementary Information). Furthermore, the lower R_F values yield a larger dynamic range with the amplifier being capable of tolerating baseline currents as large as V_DD/2R_F = 120 nA (20 nA) in the low (high) gain setting, where V_DD = 1.8 V is the supply voltage for the IC.

The feedback capacitance, required to ensure amplifier stability, is programmable and set to C_F = 0.9 pF (0.15 pF) in the low (high) gain setting. The combination of C_F and R_F limits the 3-dB bandwidth of the amplifier to approximately 1/(2πR_F (C_F/8)) (see Supplementary Information), which is set to ≈ 200 kHz for both gain settings. The output of the amplifier is then subjected to additional off-chip filtering to restore flat response up to 10 MHz (see Supplementary Information). C_F directly contributes to C_amp. However, C_F also introduces an additional pole in the amplifier’s response at a frequency proportional to $\frac{C_F}{\sum C_i}$ (see Supplementary Information) which we can effectively push beyond 10 MHz for $\frac{C_F}{\sum C_i}>0.1$ for this amplifier design.

The CNP design allows the tight integration of the nanopore and the measurement electronics. Rather than having wires connecting nanopore electrodes to the input of the headstage, as is the case in most commercial systems, the nanopore is mounted directly on the amplifier chip (see Supplementary Information). Connectivity between the amplifier input and the trans-chamber is achieved by realizing an Ag/AgCl electrode on the surface of the chip (Figure 1e) through post-processing of the integrated circuit after fabrication in a CMOS foundry (see Supplementary Information). This electrode contributes a series resistance of approximately 200 Ω, but the associated interconnection capacitance (C_W) is less than 2 pF. The input transistors of the amplifier present a capacitance C_I ≈ 1 pF. Thus, the net input capacitance presented by the amplifier becomes C_amp = C_W + C_I + C_F ≈ 4 pF, significantly lower than the ≈ 20 pF seen in most discrete systems.

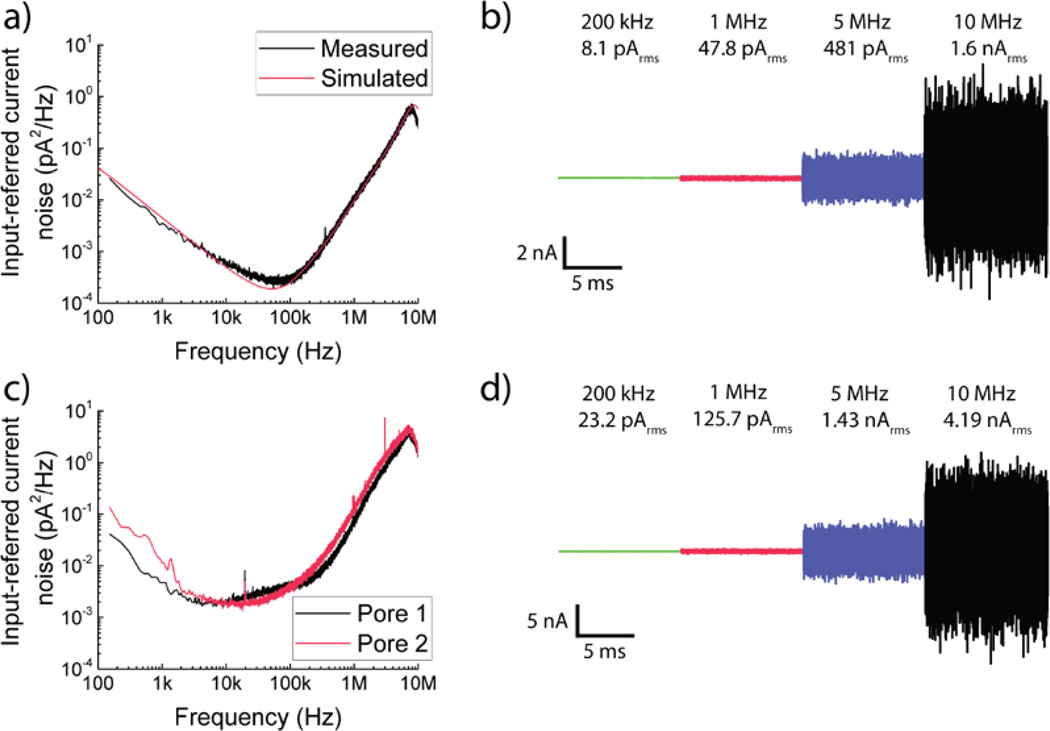
The amplifier is designed to have an thermal voltage noise floor of ν_n,amp = 2.6 nV/√Hz. The resistance of the on-chip Ag/AgCl electrodes generates an additional thermal voltage noise ${\nu }_{n,R_s}=\sqrt{4kT{R}_s}=1.8\mathrm{n}\mathrm{V}/\surd \mathrm{H}\mathrm{z}$, which is uncorrelated with the amplifier’s thermal noise. The net thermal noise floor of the setup in ionic measurements is thus ${\nu }_n=\sqrt{{{\nu }_{n,\mathit{\text{amp}}}}^2+{{\nu }_{n,R_s}}^2}=3.15\mathrm{n}\mathrm{V}/\surd \mathrm{H}\mathrm{z}$. Figure 2a shows the simulated and measured power spectral density (PSD) of the input-referred current noise in open headstage configuration. We note that the flicker noise at low frequencies, which contributes negligibly to the integrated noise at bandwidths greater than 1 MHz, is dominated by that contributed by off-chip amplifiers used to extend the bandwidth (see Supplementary Information). The CNP amplifier has an integrated input-referred open-headstage noise level of 8.1 pA_RMS at 200 kHz, 47.8 pA_RMS at 1 MHz, 481 pA_RMS at 5 MHz and 1.62 nA_RMS at the full 10 MHz measurement bandwidth (Figure 2b). Table S3 in the Supplementary Information provides a detailed comparison of our measurement electronics with prior work.

Figure 2.

Noise performance of the high-bandwidth CNP amplifier. (a) Input-referred current noise PSD for the open-headstage configuration of the CNP amplifier. Measurement results agree with the predictions of transistor-level simulations of the amplifier. (b) Concatenated time trace of a 10 ms long open-headstage measurement. Each section corresponds to the same trace filtered using a digital four-pole Bessel filter to cutoff frequencies of 200 kHz, 1 MHz and 5 MHz respectively. The 10 MHz trace already includes the effect of an analog four-pole Bessel filter and is not filtered further. I_RMS values are indicated. (c, d) Noise performance of the CNP amplifier with two different pores. Pore 1 has C_pore ≈ 10 pF while Pore 2 has C_pore ≈ 13 pF. Concatenated time trace is for data from Pore 1.

Silicon nitride nanopores in this work were thinned to an absolute thickness of less than 4 nm,²⁹ allowing for blockade current signals ΔI, as high as 30 nA in 3M KCl at 900 mV bias. The ΔI of a nanopore is maximized for small nanopore thickness, and can be estimated by the equation,

$$\mathrm{\Delta }I=\sigma V_{\mathit{\text{bias}}}({[\frac{4h_{\mathit{\text{eff}}}}{\pi d^2}+\frac{1}{d}]}^{-1}-{[\frac{4h_{\mathit{\text{eff}}}}{\pi d_{\mathit{\text{eff}}}^2}+\frac{1}{d_{\mathit{\text{eff}}}}]}^{-1})$$

where V_bias is the applied transmembrane voltage, σ is the solution conductivity, h_eff is the effective membrane thickness, d is the nanopore diameter, and d_eff is a reduced effective diameter of the nanopores in the presence of DNA defined as $d_{\mathit{\text{eff}}}=\sqrt{d^2-d_{dna}^2}$, where d_dna is the cross-sectional width of ssDNA.³⁰

Nanometer thicknesses are achieved using a scanning transmission electron microscope (STEM) based ablation technique that enabled precise thinning to near the theoretical limit (~1 nm).²⁹ STEM thinning uses electron irradiation with rastering of the electron probe of a JEOL 2010F S/TEM over a defined area of silicon nitride. This causes the sputtering of silicon and nitrogen atoms³¹ with the final membrane consisting of amorphous silicon, due to the higher rate of sputtering of nitrogen.²⁹ A two-step process is used, with an initial thinning of a 65 nm × 65 nm region of 50-nm thick freestanding silicon nitride membrane to 10 nm amorphous silicon by using a 2.5 nm probe size, with membrane thickness controlled by quantifying the mass loss using electron-energy loss spectroscopy (EELS) (see Supplementary Information). A second thinning in a smaller 25 nm × 25 nm region is made using a 0.5-nm spot size, bringing the membrane thickness down from 10 nm to less than 4 nm.

We tested several nanopores with different diameters (all less than 2.5 nm) (Figure 1c) and recorded translocation characteristics using them. C_pore is a major factor that determines the SNR-limited bandwidth in nanopore recordings. Previous efforts have suggested different techniques to minimize this capacitance.^20,21,32 For our experiments, the membrane capacitance is reduced by using window sizes smaller than 25 µm × 25 µm for the membrane openings while augmenting a passivating oxide layer outside this window with an additional layer of silicone. C_pore varies between pores, with some chips giving C_pore as low as 6 pF. Figure 2c shows the power spectral density (PSD) of the output noise spectrum for Pore 1 (C_pore = 10 pF, d = 1.3 nm, h_eff = 1.4 nm) and Pore 2 (C_pore = 13 pF, d = 1.7 nm, h_eff = 1.2 nm) that were among the ones used for the experimental results presented here. We also perform some translocation experiments with a third pore, Pore 3 (C_pore = 15 pF, d = 1.9 nm, h_eff = 3.3 nm). As a representative example, the integrated input-referred noise for Pore 1 at 200 kHz is 23.2 pA_RMS, at 1 MHz is 125.7 pA_RMS, at 5 MHz is 1.43 nA_RMS, and at 10 MHz is 4.19 nA_RMS (Figure 2d).

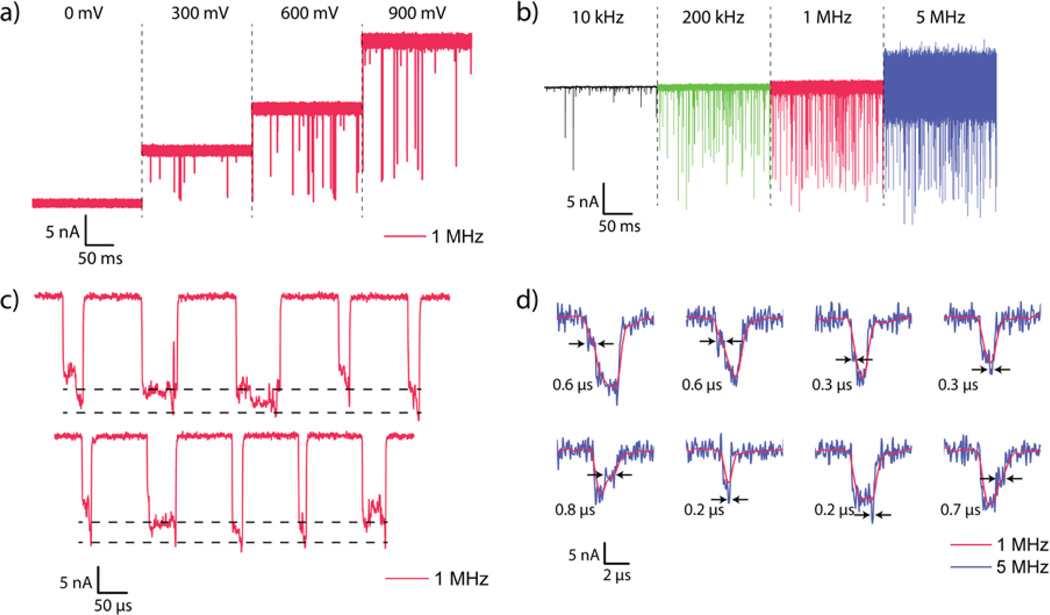
We performed measurements with ssDNA samples that were either 40 or 100 nucleotides (nt) long and prepared in aliquots of 200 nM in 3 M KCl. Since ΔI plays a significant role in improving the measurement bandwidth, a 3-M KCl concentration is used. Increasing molarity increases ΔI, but does not affect the relative blockade ΔI/I, where I is the baseline current level. The nanopore is biased at voltages ranging from 300 mV to 900 mV. Given the small diameter of the nanopores, voltage biases lower than 300 mV frequently cause blockage of the pore. The data are recorded using a custom-designed data acquisition board and software at 40 million samples per second (MSPS) and subsequently filtered to the bandwidths presented here using a digital approximation of a four-pole low-pass Bessel filter. The post-filtered data is then resampled such that the new sampling rate is four times the filter cutoff frequency. Figures 3a,b show translocation data for 100-nt ssDNA through Pore 3 and Pore 1, respectively, at different voltage biases and cutoff frequencies. In our experiments, the conductance of the nanopores stayed within 10% of its initial value for at least 20 minutes. We did not further test the long-term stability of these nanopores.

Figure 3.

Nanopore signal variation with applied bias and frequency cutoffs. (a) Concatenated time trace of 100-nt ssDNA translocation recordings through Pore 3 at biases of 0 mV, 300 mV, 600 mV and 900 mV. Each trace is 0.2 s long and filtered using a 4-pole Bessel filter with a cutoff frequency of 1 MHz. (b) Concatenated time trace of a 0.2 s long recording of 100-nt ssDNA translocation through Pore 1 at 900 mV bias. The traces are filtered using a 4-pole Bessel filter to 10 kHz, 200 kHz, 1 MHz and 5 MHz bandwidths. Low cutoff frequencies show severe degradation of signal amplitudes. All data recorded at 40 MSPS and then resampled to 4× the cutoff frequency. (c) Concatenated events from 100-nt ssDNA translocation through Pore 3 at 900 mV bias padded with baseline points for reference. The dashed black lines indicate the shallow level corresponding to the molecule being in the access region and the deep level corresponding to the actual translocation. The standard deviation of the current in the shallow region is significantly higher than even that of the baseline. (d) Example events from 100-nt ssDNA translocation through Pore 1 at 900 mV bias showing features visible at 5 MHz bandwidth (blue) that are invisible at 1 MHz bandwidth (red). Feature durations are indicated.

Several previous studies^7,29,33 have reported two-level translocation current waveforms as are observed in Figure 3c. Because the diameters of the nanopores used in these experiments are smaller than in any of these previous studies, the access resistance R_A now starts to play a more important role in determining the overall ionic current. In particular, modulation of R_A by a molecule in the vicinity of the nanopore can be significant. The two-level behavior observed is attributed to a molecule that gets trapped as it enters or exits the pore. Such an explanation in our case is further bolstered by the fact that the standard deviation of the shallow levels observed (σ = 834 pA_RMS − 1.81 nA_RMS for the data of Figure 3c) is significantly higher than that of the baseline current itself (σ = 281 pA_RMS). If a molecule in the vicinity of the pore is indeed the cause of the shallow level, then Brownian motion of the molecule could explain the increased standard deviation in the current. A shallow level is not always present at the onset of a translocation event, which is also consistent with previous results²⁹ (see Supplementary Information).

The need for a high-bandwidth measurement platform is best demonstrated by its ability to resolve and detect events and features that were undetectable previously. Figure 3d shows examples of 100-nt ssDNA translocation events through Pore 1 filtered to 5 MHz and 1 MHz bandwidths. The four-pole Bessel filter used for filtering down to lower bandwidths has a rise time of ≈ 0.5 µs and 0.1 µs at 1 and 5 MHz cutoff frequencies respectively. Consequently, events with durations less than twice these times will have their amplitudes significantly attenuated. Figure 3d shows examples of features that are visible only at bandwidths made possible by this work, some with durations of less than 200 ns; all labeled features exceed the 3σ noise levels of the baseline. We believe that some of these events reveal extremely brief interactions of the molecule with the pore as it enters and exits. Some of the features, however, correspond to a deeper event within another relatively shallow level. These features are likely to be true translocation events. In these cases, events are likely to be fast even at 1 MHz bandwidths, leading to distortion of event depth and duration.

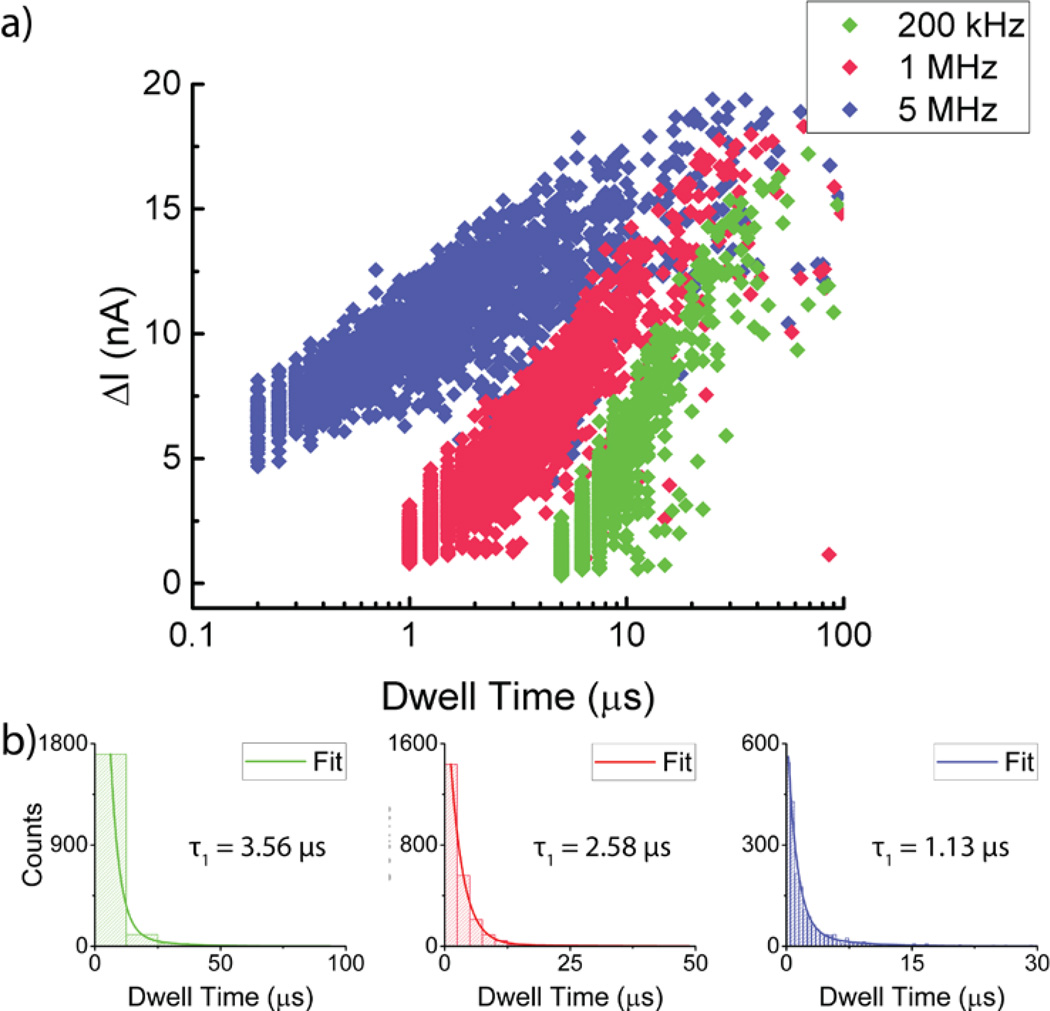
Figure 4a shows a scatter plot of average current blockade values as a function of dwell time for a 4-s trace recorded for 100-nt ssDNA at 900 mV bias. Event detection is determined by setting a threshold that is 6σ away from the baseline. The large spread in the average ΔI values is due to the variance in the dwell time in the access region during a translocation event. A long dwell in the access region corresponds to a relatively shallow average ΔI. Larger average ΔI values are associated with short dwell times in the access region. As the filtering cutoff frequency is reduced, σ decreases, but so does the amplitude of short events which means that some events fail to get detected at lower bandwidths. Conversely, shallow and long events are more likely to be seen at lower bandwidths. Figure 4b also shows fits of the dwell times to A₁e^−t/τ₁ + A₂e^−t/τ₂ where τ₁ < τ₂, τ₁ is attributed to full translocation events while τ₂ is attributed to collision events.⁸ More aggressive filtering increases τ₁ indicating that the increased bandwidth results presented here are more accurate in capturing the average translocation rate.

Figure 4.

Fast ssDNA translocation statistics. (a) Mean current blockage vs dwell time scatter plot for n = 2008 100-nt ssDNA translocation events through Pore 1 at 5 MHz, 1 MHz and 200 kHz filtering bandwidths (n indicated for the 5 MHz filtering bandwidth). Filtering to lower frequencies clearly indicates increased attenuation especially for events close to the inverse of the filter’s cutoff frequency. (b) Histogram plot of counts vs dwell time for the data presented in (a). Each of the plots are fitted to A₁e^−t/τ₁ + A₂e^−t/τ₂ and τ₁ is indicated for each of the fits where τ₁ < τ₂. Increasing the filtering bandwidth indicates a reduction in the characteristic dwell time for the event suggesting that even at bandwidths as high as 1 MHz, translocation events were distorted.

In conclusion, we have presented a nanopore sensing platform that leverages the integration of small-diameter ultra-thin nanopores with custom-designed low-noise electronics to enable the highest bandwidth recordings of DNA translocation yet achieved, demonstrating the potential for nanopores as a single-molecule detection platform capable of temporal resolutions down to 100 ns. Additional improvements may be possible with further reductions in C_pore.²¹ These may enable new applications for nanopores that rely on the ability to resolve single-molecule transient events on heretofore unachievable timescales.