Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Jan 17;13(2):451–459. doi: 10.1021/acs.jctc.6b00778

Multireference Perturbation Theory with Cholesky Decomposition for the Density Matrix Renormalization Group

Leon Freitag †,*, Stefan Knecht †,*, Celestino Angeli ‡,*, Markus Reiher †,*
PMCID: PMC5312874  PMID: 28094988

Abstract

graphic file with name ct-2016-00778r_0005.jpg

We present a second-order N-electron valence state perturbation theory (NEVPT2) based on a density matrix renormalization group (DMRG) reference wave function that exploits a Cholesky decomposition of the two-electron repulsion integrals (CD-DMRG-NEVPT2). With a parameter-free multireference perturbation theory approach at hand, the latter allows us to efficiently describe static and dynamic correlation in large molecular systems. We demonstrate the applicability of CD-DMRG-NEVPT2 for spin-state energetics of spin-crossover complexes involving calculations with more than 1000 atomic basis functions. We first assess, in a study of a heme model, the accuracy of the strongly and partially contracted variant of CD-DMRG-NEVPT2 before embarking on resolving a controversy about the spin ground state of a cobalt tropocoronand complex.

1. Introduction

An electronic structure that is governed by strong electron correlation effects is a commonly encountered phenomenon in molecules that are, for example, (i) in a nonequilibrium structure, (ii) in an electronically excited state, and/or (iii) contain transition metal center(s). Multiconfigurational methods, which have been very successful in describing strongly correlated systems,1,2 typically feature a separation of the electron correlation into a static and a dynamic contribution.3−5 Static correlation is often described by a complete active space self-consistent field (CASSCF) ansatz,6,7 which requires a careful selection of a limited number of (partially occupied) active orbitals that may be automated.8,9 As the computational cost for CASSCF scales exponentially with the number of active orbitals, CASSCF calculations (on traditional computer architectures) are limited to about 18 electrons in 18 orbitals.10 In contrast, the density matrix renormalization group11−13 (DMRG) approach in quantum chemistry14−23 in combination with a self-consistent-field orbital optimization ansatz (DMRG-SCF) is capable of approximating CASSCF wave functions to arbitrary accuracy with a polynomial rather than an exponential scaling. DMRG-SCF therefore provides access to much larger active orbital spaces than those that are in reach for standard CASSCF.

For a quantitative description of electron correlation, a subsequent step must account also for dynamic correlation. In this context, multireference perturbation theories such as the second-order complete active space perturbation theory (CASPT2)24,25 or N-electron valence state perturbation theory (NEVPT2)26 have been successfully employed to obtain energies, properties, and approximate wave functions for a variety of strongly correlated systems.2,27−29

Both CASPT224 and NEVPT230 require the evaluation of higher-order reduced density matrices (RDMs) in the active space. The salient properties of NEVPT2 (see below) require the four-body RDM, which scales as L8 where L is the number of active orbitals. This L8 scaling, although subexponential, still puts a constraint on the active orbital space size tractable by multireference perturbation theory, in particular in combination with a DMRG reference wave function. Therefore, in addition to straightforward implementations such as DMRG-CASPT231 or strongly contracted (SC)-DMRG-NEVPT2,32,33 several approaches have been proposed to tackle the scaling problem of the higher-order RDMs. The CASPT2 implementation of Kurashige et al.34 and the NEVPT2 implementation of Zgid et al.35 employ cumulant-type expansions to approximate the three- and four-body RDMs which, however, may entail N-representability problems of the approximated higher-order RDMs and/or lead to numerical instabilities in the perturbation summations. Very promising alternative formulations such as matrix product state perturbation theory (MPS-PT),36,37 a time-dependent formulation,38 or the projected approximation to SC-NEVPT239 avoid the construction of higher-order RDMs altogether. Besides multireference perturbation theory, DMRG-SCF has been successfully combined with other methods such as multireference configuration interaction (MRCI),40 canonical transformation theory,41−43 coupled cluster (CC) theory,44 and short-range density functional theory45 to describe dynamic correlation.

In this work, we present a full-fledged NEVPT2 for a DMRG reference function that exploits density fitting for the two-electron integrals in order to make large molecules more accessible to this methodology. We apply our implementation to a prototypical problem in transition metal chemistry, namely, the spin-state energetics problem.46 In computational transition metal and bioinorganic chemistry, gaining insight into the electronic structure, spin-state energetics and reactivity of (polynuclear) transition metal complexes with extensive ligands are key components for the understanding of the chemistry of metalloproteins.47 Albeit being in many cases unreliable and/or heavily dependent on the choice of the density functional, density functional theory (DFT) is the standard approach to study such systems,48,49 mainly because of its affordable computational cost. Thermal spin crossover (SCO) complexes constitute prime examples for the difficulty of DFT with present-day functionals. On the one hand, this may be due to static correlation abundant in many transition metal systems50 which none of the currently available standard density functionals can describe properly. On the other hand, the prediction of the correct ground state in SCO complexes is often a matter of a few kJ/mol, an accuracy which DFT does not always offer.51 To this end, multiconfigurational studies on SCO complexes have become increasingly popular.52

In the quest for making multiconfigurational methods capable of treating larger molecular systems of arbitrary complexity (and therefore establishing them as a part of the standard toolbox in theoretical transition metal and bioinorganic chemistry), providing access to larger active orbital spaces only partly solves the problem as the convergence of the results can be slow with respect to the size of the atomic basis set. For large atomic basis sets, the transformation of the two-electron repulsion integrals from an atomic orbital (AO) to a molecular orbital (MO) basis required for the subsequent perturbation theory step will become a (second) bottleneck. In this context, a promising ansatz has been recently proposed by Neese and co-workers,53 who have developed a domain-based pair local natural orbital NEVPT2 (DLPNO-NEVPT2) formulation. Very recently, Evangelista and co-workers54,55 put forward a novel second-order multireference perturbation theory based on the driven similarity renormalization group which exploits factorized two-electron integrals to enable an on-the-fly generation of the two-electron repulsion integrals in the MO basis while avoiding any explicit storage of the latter.

In this work, we will take advantage of a Cholesky decomposition (CD) of the two-electron integral matrix.56,57 Although the idea of CD for two-electron integrals dates back to 1977,56 the approach has been only recently fully explored and elaborated by Aquilante et al.58 They also implemented CD for traditional multiconfigurational electronic structure methods such as CASSCF59,60 and CASPT2.2,61,62 While these developments have significantly spurred various applications of CASPT2 in theoretical inorganic and bioinorganic chemistry,2 CASPT2 in its most successful formulation contains a parameter (the so-called IPEA shift) with a default value of 0.25 au introduced by Ghigo et al.63 to match a set of experimental dissociation energies of main group diatomics. The default value of the IPEA shift has sparked a controversy among researchers employing CASPT2 for problems other than dissociation energies, such as excited states,64 magnetic coupling constants, and spin-state energetics of SCO complexes65−68 which still remains unsettled. Moreover, CASPT2 shows in some cases unstable results due to the so-called “intruder-state problem” due to the appearance of very small denominators in the perturbation expansion. This problem has been counteracted with a level-shift technique,69,70 but the final CASPT2 energies depend on the value of the level shift. In contrast, NEVPT2, which is parameter-free and has the noteworthy property of avoiding the intruder state problem (owing to the sophistication of its zero order Hamiltonian), not only avoids any IPEA shift controversy but also has shown promising results for spin-state energetics in model compounds and SCO complexes.28,65,68

We here present a DMRG-NEVPT2 implementation employing CD that is capable of treating both large active orbital spaces and large AO basis sets which allows for multireference calculations on large transition metal complexes that are typically encountered in bioinorganic chemistry. To demonstrate its capabilities, we examine the spin-state energetics of two SCO complexes.

2. Theory and Computational Methodology

As details of the NEVPT2 approach, quantum-chemical DMRG, and its combination to DMRG-NEVPT2 have been discussed elsewhere,11−13,15,16,19,22,23,26,30,32,35,71,72 we only outline briefly the Cholesky decomposition and show how it is employed in the context of CD-DMRG-NEVPT2.

2.1. Cholesky Decomposition

Mathematically, CD73 is a special case of a LU decomposition of a positive semidefinite symmetric matrix M into a product of a triangular matrix L and its transpose,

2.1. 1

M now contains two-electron integrals (ij|kl) (with indices ij and kl combined to row and column indices of M). Of particular interest is the incomplete CD, where M may be approximated to an arbitrary accuracy with Cholesky vectorsL⃗J, which constitute the columns of the matrix L,58

2.1. 2

where M is typically significantly smaller than the full dimension of M. One important advantage of CD is that the Cholesky vectors can be computed without evaluating the full matrix M,58 resulting in large disk space savings. Two-electron integrals may then be reconstructed from the corresponding Cholesky vector elements,

2.1. 3

CD also proves particularly useful in integral transformations: instead of a full-fledged integral transformation, we only need to transform Cholesky vectors,

2.1. 4

where i, j and μ, ν refer to indices in the AO and MO basis, respectively. The cost of such a transformation is K3M in contrast to a formal K5 scaling for the full integral transformation. In NEVPT2, two-electron integrals with up to two inactive and two virtual orbital indices must be transformed from AO to the MO basis, which is typically the most time-consuming step following the calculation of four-body RDMs. Additionally, in a multistate calculation, integrals with inactive/virtual indices must be transformed to a state-specific representation. In our implementation of CD-DMRG-NEVPT2, the integral transformation based on Cholesky vectors yielded by far the largest computational savings. Additionally, we implemented the construction of the Fock matrix directly from the Cholesky vectors (albeit without employing the local K screening by Aquilante et al.74 for the exchange contributions); however, the computational advantage arising from this step is negligible compared to the integral transformation.

2.2. Selected Spin-Crossover Complexes

The first complex studied in this work, [Fe(C3N2H5)2(OH2)] (Figure 1a), is a heme model employed by Strickland and Harvey75 (named model 2 in their paper). We employ the model 2 complex as a benchmark system and assess the performance of the CD-DMRG-NEVPT2 method for spin-state energetics by comparing the relative energies of the lowest singlet, triplet, and quintet states of the model 2 with previous accurate CCSD(T) calculations.

Figure 1.

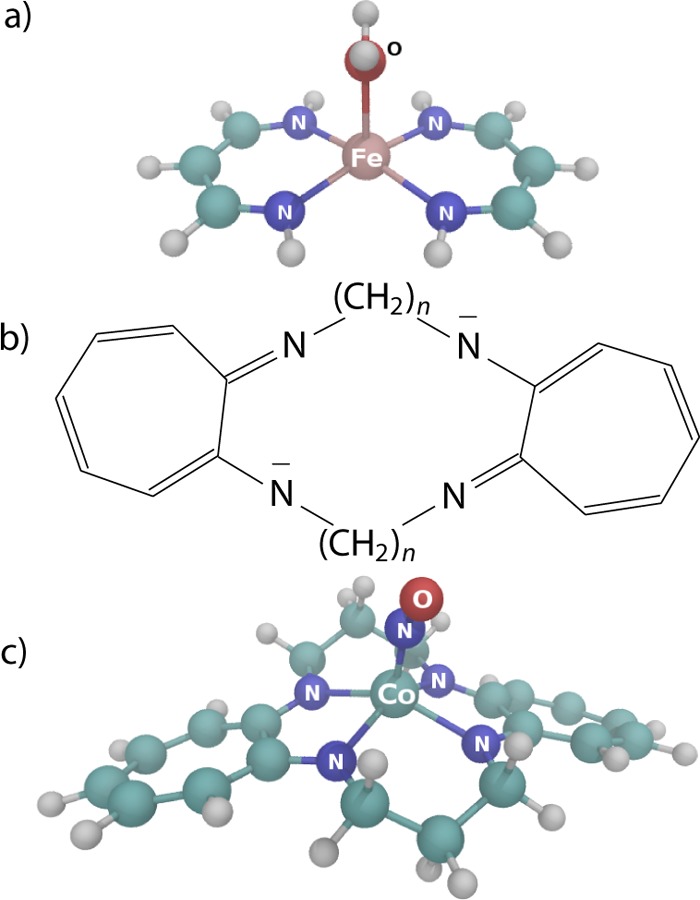
Figure 1

Open in a new tab

Structures of the compounds used in this work: (a) [Fe(C3N2H5)2(OH2)] (model 2), (b) the TC(n,n) ligand, and (c) [Co(TC-3,3)(NO)].

The second compound investigated is a cobalt tropocoronand nitrosyl complex, [Co(TC-3,3)(NO)] (Figure 1c). In a series of homologous tropocoronand complexes with an increasing methylene chain length n, initially [Co(TC-3,3)(NO)] with n = 3 was previously found to be paramagnetic unlike its homologues with larger n.76−78 However, a recent DFT and experimental study79 showed the opposite. Nitrous oxide (NO) is a well-known noninnocent ligand,80,81 and therefore, transition metal nitrosyl complexes are known to have an intricate and challenging electronic structure, described best with multiconfigurational methods.82−86 Here, we employ CD-DMRG-NEVPT2 to contribute to the discussion of spin-state energetics of [Co(TC-3,3)(NO)].

2.3. Computational Details

The structures of both complexes studied in this work were taken from previous publications: the model 2 structures were optimized by Strickland and Harvey75 for each individual spin state with the B3LYP87,88 density functional, a Los Alamos effective core potential, and LACV3P basis set for Fe and the 6-311G* basis set for other atoms with a C2v symmetry constraint. The [Co(TC-3,3)(NO)] structures were taken from ref (79), where they were optimized with the PW9189 density functional and 6-311G** basis set.

Subsequently, DMRG-SCF calculations employing a 14 electrons in 18 spatial orbitals, i.e., (14,18), active space for the model 2 complex and a (22,22) active space for [Co(TC-3,3)(NO)] have been performed. A procedure following our automated active space selection8 delivered the choice of the active spaces (more details on the active spaces and the selection procedure can be found in the Supporting Information). To study the effect of the number of renormalized block states m on the results and the errors arising from the CD approximation, different approaches to prepare the DMRG wave function were investigated for the model 2 complex: (i) DMRG-SCF calculations with m values of 256, 512, 1024, and 2048; (ii) DMRG-SCF calculations with m = 256 followed by a DMRG-CI calculation with m = 512 and m = 1024 (denoted as 512/256 and 1024/256, respectively, in the following); (iii) DMRG-SCF calculations with m = 256 but without employing the Cholesky decomposition, denoted as 256* in the following. For the [Co(TC-3,3)(NO)] complex, DMRG-SCF calculations with m = 512 and 1024 were carried out. NEVPT2 calculations with DMRG-SCF reference wave functions with m = 1024 and 2048 for the model 2 complex and m = 1024 for the [Co(TC-3,3)(NO)] complex were performed omitting energy contributions which require the four-body RDM (i.e., those in Sr(−1) and Si subspaces in the notation of ref (30)): due to the missing contributions, these calculations were not used for the evaluation of spin-state energetics but rather for the estimation of errors of the full-fledged calculations with smaller m values.

We have implemented the CD-DMRG-NEVPT2 approach in a modularized version of the original QDNEVPT2 program by Angeli et al.90 for both the strongly contracted (SC) and partially contracted (PC) variant of NEVPT2.30 SC- and PC-NEVPT2 calculations were performed with all DMRG-SCF and DMRG-CI reference wave functions. The ANO-RCC91 basis set was chosen for all calculations: in the model 2 complex, a moderately sized double-ζ (VDZP) contraction on all atoms was employed to facilitate the comparison with a conventional integral calculation (yielding 248 basis functions in total), whereas for [Co(TC-3,3)(NO)], a larger triple-ζ (VTZP) contraction on all atoms, totaling 1147 basis functions, was used.

Additionally, CCSD(T) calculations were performed on the model 2 complex employing the same ANO-RCC-VDZP basis set for comparison. For the open-shell species, restricted open-shell reference wave functions and the triples contributions according to Watts et al.92 were calculated.

Cholesky vectors in the AO basis were generated on the basis of the atomic compact Cholesky decomposition (acCD) approach93 with a decomposition threshold of 10–4 a.u. as implemented in the MOLCAS 8.0 program.10 All DMRG reference wave functions and three- and four-body RDMs were calculated with the QCMaquis33,94−96 program with its MOLCAS interface.97 Additional CCSD(T) calculations with conventional integrals were carried out with MOLCAS 8.0.

3. Results and Discussion

3.1. Harvey’s Model 2 Complex

The model 2 complex is one of the three heme models employed by Strickland and Harvey75 in their ab initio and DFT study of ligand binding to heme and the largest model treated with the CCSD(T) method in their work. Given its small size, which still allows one to employ the conventional integral implementation for comparison with the CD approach, an electronic structure typical for SCO complexes, and the availability of CCSD(T) reference data, we chose the model 2 complex to study the performance and the accuracy of CD-DMRG-NEVPT2 for spin-state energetics.

3.1.1. Spin-State Energy Differences

Table 1 lists electronic energies of the lowest singlet (1A1) and triplet (3B1) states of the model 2 relative to the lowest quintet state (5B2) calculated with the strongly contracted (SC-NEVPT2) and the partially contracted (PC-NEVPT2) approach for different values of the number of renormalized block states m. CCSD(T) data are presented from both our calculations and ref (75).

Table 1. Electronic Energies of the Singlet and Triplet States of the Model 2 Complexa.
  m
  256* 256 512 512/256 1024/256
  DMRG-SC-NEVPT2
3B1 3.4 3.4 3.1 2.6 1.9
1A1 32.8 33.1 33.8 32.8 31.8
  DMRG-PC-NEVPT2
3B1 6.5 –34.1 4.1 –1.3 0.5
1A1 –6.0 3.3 31.8 28.7 31.0
           
  CCSD(T)    
  b c d    
3B1 3.1 3.7 –2.0    
1A1 31.5 25.9 19.6    
Open in a new tab
a

In kcal/mol, relative to the quintet 5B2 state.

b

This work, ANO-RCC-VDZP basis set.

c

cc-pVTZ/cc-pVDZ basis set for Fe/other atoms (see Ref. (75)).

d

cc-pV∞Z extrapolation/cc-pVDZ basis set for Fe/other atoms (see Ref. (75)).

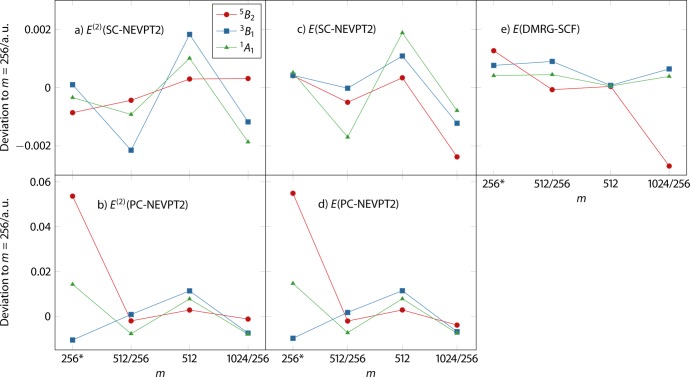
The relative energies computed with SC-NEVPT2 agree well with the CCSD(T) results obtained with the same (ANO-RCC-VDZP) basis set: the largest deviation from the CCSD(T) results is 1.3 kcal/mol. Moreover, the variation of the relative energies with m is even smaller (with the largest deviation being below the chemical-accuracy threshold of 1 kcal/mol), providing further evidence that one may save computational time by using relatively low m values (evaluation of 4-RDM scales as m3)32 without significant loss of accuracy. The difference of the SC-NEVPT2 relative energies obtained with and without CD is less than 0.1 kcal/mol for the quintet–triplet gap and about 0.3 kcal/mol for the quintet–singlet gap and therefore comparable to the variation of the gaps with m.

Unlike SC-NEVPT2, the PC-NEVPT2 relative energies are highly dependent on m. At m = 256, PC-NEVPT2 predicts a qualitatively wrong spin-state ordering with the triplet state 34.1 kcal/mol below the quintet state. Only at m = 512, PC-NEVPT2 yields the same spin-state ordering as CCSD(T) and SC-NEVPT2. The faulty energies arise due to small denominators in the PC-NEVPT2 energy expressions for different subspaces, which is reflected by the norm of the PC-NEVPT2 first-order wave function shown in Figure 2. The norm for all states decrease by several orders of magnitude with increasing m, reaching from values up to 2230 (m = 256, 5B2 state) down to 5 (m = 1024/256, 1A1). For comparison, SC-NEVPT2 norms are in the range of 0.5–0.6, regardless of the m value, which is comparable with wave function norms in non-DMRG NEVPT2 calculations.28 Although calculations without CD (m = 256* in Figure 2) show lower norms than those with CD, the ordering of spin states and the relative energies are still flawed. Hence, numerical errors leading to small denominators are partially to blame on the Cholesky decomposition but to a larger extent on the small m values. DMRG-PC-NEVPT2 therefore shows the problem of “false intruder states” similar to that observed in NEVPT2 with cumulant approximations to RDMs described by Zgid et al.35

Figure 2.

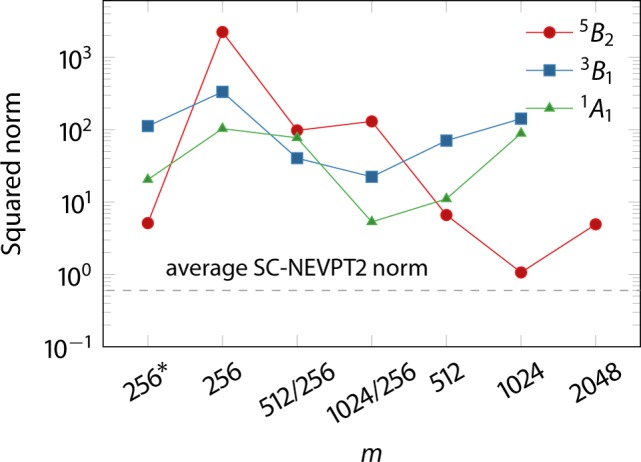
Figure 2

Open in a new tab

Squared norms of first-order wave functions of the model 2 complex calculated with DMRG-PC-NEVPT2 for different values of m. Calculations for m = 1024 and 2048 were performed without the contributions of Sr(−1) and Si subspaces in the notation of ref (30).

In order to assess the behavior of the PC norms with increasing m, we performed calculations with m = 1024 and in case of the 1A1 state also for m = 2048 omitting the contributions of Sr(−1) and Si subspaces, requiring only the three-body RDM. Despite the missing contributions, the norms for m = 1024 do not improve compared to m = 512 except for the 1A1 state. In contrast, at m = 2048, the calculation shows a norm similar to that for m = 512, revealing that the apparent convergence of the norm at m = 1024 is accidental rather than systematic. Hence, we do not observe the convergence of the PC norms to the values similar to the SC ones.

Concerning the dependence of PC- and SC-NEVPT2 on the computational parameters, we recall that the speed-up of the approach introduced in ref (71) and fully formalized in ref (30) is a consequence of the choice of the CI solution within the CAS space as the zeroth-order wave function. This allows one to greatly simplify the formalism and to use the four-body RDMs only (otherwise, also the five-body RDMs would be required). Even at m = 2048, the maximum m value used in this work, the zeroth-order DMRG wave function is far from numerical convergence to the full CI wave function, as can, for example, be seen on inspection of the absolute electronic energy in Table S9, and therefore can produce numerical problems with a formulation assuming an exact full CI reference wave function. We expect the situation to improve with even larger m values where the zeroth-order wave function becomes a better approximation to the full CI wave function. In those cases, however, the three- and four-body RDM calculations become computationally unfeasible. Furthermore, it is important to stress that the “false intruder states” are related to this inconsistency; i.e., they originate from the approximations in the zeroth-order wave function and are unrelated to the “standard” intruder states found, e.g., in the CASPT2 approach which have their origin in the nature of the zeroth-order Hamiltonian.

By considering that each denominator of SC is obtained by a weighted average of a set of denominators in PC (the weights being related to the interactions of the PC perturbers with the zeroth-order wave function), it can be easily understood that the PC approach is much more dependent on the quality of the zeroth-order wave function (for instance, on the degree of CI convergence), whereas SC is more robust and yields more stable results for a lower-quality zeroth-order wave function. Hence, large variations of the PC denominators for perturbers with a small interaction with the zeroth-order wave function (which can have important effects on the PC energy if the denominators approach zero) have almost no effects on SC.

The discrepancy of our CCSD(T)/ANO-RCC-VDZP results with the CCSD(T) results of Strickland and Harvey75 (Table 1) might point to a large basis set effect at first glance. However, the discrepancy may also arise due to the convergence of the single-reference wave function to a different state. In our calculations, the guess orbitals for the reference ROHF wave function for the quintet and triplet CCSD(T) calculation were generated from state-averaged CASSCF calculations for three quintet states and triplet states to ensure the correct state character (and similarly for the NEVPT2 calculations). The CASSCF calculations show gaps of 2–6 kcal/mol between the lowest quintet or triplet states. A black-box single-reference calculation may therefore well converge to an adjacent state, which will affect the spin-state energetics. This emphasizes the need for multireference methods even in cases where single-reference methods appear to perform well, as judged by multireference criteria such as the T1 norm in the CC theory.

3.1.2. CD Accuracy: Absolute Energies

Figure 3 shows deviations of the second-order energy corrections and the total electronic CD-DMRG-SC-NEVPT2 and CD-DMRG-PC-NEVPT2 energies calculated with different m values. Deviations of the corresponding DMRG-SCF energies are also shown for comparison. (The total electronic NEVPT2 and DMRG-SCF energies are provided in Table S1.) The first point (m = 256*) in each subplot is simply the difference between CD and non-CD energies for m = 256. For SC-NEVPT2, the errors in the second-order energy arising due to Cholesky decomposition are on the order of 10–3 atomic units and are comparable to those (and even slightly smaller) of DMRG-SCF. The total NEVPT2 energies show even smaller errors on average due to the cancellation of DMRG-SCF and second-order energy errors. In all cases, errors arising due to CD are smaller than errors due to smaller m values in SC-NEVPT2, which justifies CD as an approximation for (DMRG)-SC-NEVPT2 calculations. We note that errors in both absolute and relative energies due to CD are similar to those in the CD-CASPT2 method,61 and we would expect a similar increase of accuracy with decreasing CD threshold. For PC-NEVPT2, the CD errors are much larger and reach 0.05 atomic units for the quintet state, because of the numerical errors leading to “false intruder states” mentioned earlier. However, errors associated with different m values are also larger than for SC-NEVPT2, likely for the same reason. Therefore, we conclude that PC-NEVPT2 is much more prone to numerical problems arising from both Cholesky decomposition and a DMRG-SCF reference wave function.

Figure 3.

Figure 3

Open in a new tab

Differences of second-order energy corrections (a, b) and total electronic energies (c, d) obtained with DMRG-SC-NEVPT2 and DMRG-PC-NEVPT2 for various states for the model 2 complex for varying values of the number of renormalized block states m compared to the results obtained with m = 256. DMRG-SCF energy differences are shown in (e).

3.2. Cobalt Tropocoronand Complex

Tropocoronand ligands (Figure 1b) with different lengths of the alkylidene chain n provide a fine-tuned constrained coordination environment that varies with n, yielding metal complexes with interesting geometric and electronic structures, especially if coordinated with a noninnocent ligand80,81 such as NO. [Co(TC-3,3)(NO)], the smallest member of a homologous series of cobalt complexes with n = 3 to 5, was previously reported to be paramagnetic, unlike its higher homologues and other cobalt nitrosyl complexes,76,78 which contradicts a recent DFT and experimental study.79 Metal-nitrosyl bonds are known to show a large amount of static correlation (see, e.g., ref (86)), which cannot be reliably described by single-reference methods such as DFT. Due to this fact and the controversy on the spin state, we study with DMRG-SCF and CD-DMRG-NEVPT2 the electronic structure and spin-state energetics of [Co(TC-3,3)(NO)].

3.2.1. Electronic Structure of the Complex

In metal nitrosyl complexes, it is usually not trivial to unambiguously describe the electronic structure of the metal and the NO ligand separately by assigning them distinct electronic occupations: hence, it is common to use the Enemark-Feltham notation98 to describe their electronic structure. [Co(TC-3,3)(NO)] is a {CoNO}8 complex, according to the notation, where 8 is the total number of electrons in the metal d and NO π* orbitals.

To gain insights into the electronic structure of the complex, we analyzed the DMRG-SCF wave functions of the spin states, in particular the natural orbital occupation numbers of metal d and NO π* orbitals, which are essential for the Co–NO bond description. Since DFT results from ref (79) are ambiguous about predicting the character of the lowest triplet state of the complex and the DMRG-SCF optimization of an excited state in QCMaquis may occasionally converge to a higher-lying state due to the nature of the excited state optimization algorithm,95 we have calculated the two lowest triplet states. All results are compiled in Figure 4.

Figure 4.

Figure 4

Open in a new tab

Natural orbital occupation numbers for orbitals participating in the Co-nitrosyl bond in [Co(TC-3,3)(NO)] in different spin states.

Although the orbitals are delocalized and several occupation numbers severely deviate from 2 or 0 (which is a sign of a multireference character and significant static correlation typical for metal nitrosyl complexes),86 we may approximately assign electronic occupations to both metal and NO. The occupation numbers in the lowest singlet state S0 most closely resemble the following occupation pattern:

3.2.1.

This may be interpreted as a d8 Co coupled to a NO+ cation, although the occupation numbers of the 3dz2 and πNO,y* show a significant admixture of a neutral NO and d7 Co. Analogously, the T2 state may be characterized as d7 Co and neutral NO. However, the T1 state shows occupation numbers of 3dyz and πNO,y orbitals close to 1.5 and 0.5, which represents a situation exactly between Co d7 and d8 and neutral and cationic NO. The state characters are in contrast to those found in the DFT study by Hopmann et al.,79 where the T1 and T2 states are characterized as d7 Co and neutral NO and as d6 Co and anionic NO–, respectively. However, such discrepancies are not surprising as the single-configuration nature of standard Kohn–Sham DFT does not allow for an accurate description of states with multireference character. It is well-known that spin densities in metal nitrosyl complexes obtained with DFT and multiconfigurational methods may differ significantly.83−85

3.2.2. Singlet–Triplet Gap

Having characterized the electronic structure of [Co(TC-3,3)(NO)] with DMRG-SCF, we calculated the singlet–triplet energy gap with CD-DMRG-SC-NEVPT2, listed in Table 2. CD-DMRG-SC-NEVPT2 predicts S0 as the ground state of [Co(TC-3,3)(NO)], just as DMRG-SCF and all DFT functionals do, which is consistent with the diamagnetism of its ground state recently confirmed in ref (79). However, the gap predicted by NEVPT2 is by at least 10 kcal/mol larger than those calculated with DFT. Notably, CD-DMRG-SC-NEVPT2 predicts that T1 and T2 are close-lying, with an energy gap of only 1.1 kcal/mol; a similar result (a difference of 0.6 kcal/mol) is obtained with the PW91 functional in ref (79), although, as mentioned before, the characters of the triplet states are different from those described in this work.

Table 2. Singlet–Triplet Energy Gap (in kcal/mol) of [Co(TC-3,3)(NO)] Calculated with CD-DMRG-SC-NEVPT2 (Abbreviated as “SC-NEVPT2”) and Other Methodsa.
  SC-NEVPT2 DMRG-SCF OLYP79 PW9179 B3LYP-D379
T1 35.0 38.6      
T2 36.1 29.6 23.8 25.1 10.4
Open in a new tab
a

DFT results from ref (79) are provided for the state of an equivalent character.

In order to assess the error arising from the choice of the m value (which was set to 512), similarly to the model 2 complex, the singlet–triplet gaps were also calculated with a larger m value of 1024 but excluding the contributions of Sr(−1) and Si subspaces. Table 3 collects these singlet–triplet gaps along with analogous values for m = 512. The deviations of 1.1 and 0.4 kcal/mol for T1 and T2, respectively, are comparable with those in model 2 calculations, indicating that m = 512 essentially offers results of chemical accuracy, although the absolute electronic energies (cf. Table S8) are still far from being converged.

Table 3. Singlet–Triplet Energy Gap (in kcal/mol) of [Co(TC-3,3)(NO)] Calculated with CD-DMRG-SC-NEVPT2 Excluding Contributions of the Sr(−1) and Si Subspaces for m = 512 and 1024.
  m
  512 1024
T1 32.7 33.8
T2 40.5 40.9
Open in a new tab

3.3. A Note on Computing Resources

Table 4 lists computing time (CPU time) and hard disk usage for the integral transformation step, which yielded by far the largest computational savings in our calculations. Cholesky decomposition speeds up the integral transformation by over 40 times and requires more than 10 times less disk space for the integral transformation in model 2 calculations. However, we should note that in all cases the majority of the CPU time is spent calculating the four-body RDM, where we currently resort to a massively parallel implementation, which takes up to several days on 800–1000 Intel(R) Xeon(R) E5-2697 v2 CPU cores (independent of whether or not the Cholesky decomposition was exploited). Hence, for the model 2 calculation, the total speedup due to Cholesky decomposition is still very small.

Table 4. CPU Time and Disk Usage for the Integral Transformation in Calculations with and without Cholesky Decomposition.

  CPU time/s
 disk usage/GByte
# bf CD no CD CD no CD
248 (model 2) 15 620 0.77 10
1147 (CoTC) 9251 ≈1 310 000a 83 25 880b
Open in a new tab
a

Estimated value from perfect K5 scaling.

b

Estimated value, without taking prescreening into account

Turning, however, to the larger CoTC calculation with 1147 basis functions, we estimate that such a calculation becomes barely feasible if one employs conventional integrals. We did not attempt to perform such a calculation, but even an optimistic runtime estimation based on current runtimes, assuming perfect K5 scaling, yields about 1 310 000 s or 15 days of CPU time, not even counting the time required for input and output operations (which will be ample, as a similar estimation for the total disk space required for both AO and MO integral storage yields approximately 25 TByte without any prescreening and would remain on the order of TBytes even if integrals below a certain threshold are not stored on disk). For comparison, the MO transformation for CoTC employing CD requires “modest” 83 GByte of space and approximately 2.5 h of CPU time. Although the four-body RDM calculation remains a bottleneck, the integral transformation bottleneck is eliminated by CD.

4. Conclusions

In this work, we have presented an implementation of the second-order N-electron valence state perturbation theory (NEVPT2) employing a density-matrix renormalization group (DMRG) reference wave function and Cholesky decomposition (CD) for the two-electron repulsion integrals dubbed as CD-DMRG-NEVPT2 which is a parameter-free multireference perturbation theory applicable to large systems.

A multireference perturbation theory faces two challenges when applied to large systems. These are the calculation of the higher-order reduced density matrix and the calculation of a large number of integrals. In this work, we have considered a solution to the second one, yielding a method that is capable of dealing with systems containing more than 1000 basis functions. We demonstrated the application of the method on two examples of SCO complexes: a smaller heme model (model 2) and a larger cobalt nitrosyl tropocoronand complex. The strongly contracted (SC) variant of CD-DMRG-NEVPT2 describes the spin-state energetics with a similar accuracy as CCSD(T) in the heme model and is very insensitive to the number of renormalized block states m. The approximations introduced by CD turn out to be negligible. Unlike the SC variant, the partially contracted CD-DMRG-NEVPT2 is prone to “false intruder states”35 due to numerical approximations introduced by the DMRG and Cholesky decomposition.

Subsequently, we employed a large-scale DMRG-SCF and a strongly contracted CD-DMRG-NEVPT2 calculation to describe the electronic structure of a cobalt nitrosyl tropocoronand complex. The electronic structure of the lowest singlet and triplet states calculated with DMRG-SCF showed significant static correlation. The NEVPT2 calculation confirmed the singlet ground state and with it the diamagnetism of the complex shown experimentally in a recent study. Combined with the recent advances to overcome the bottleneck of the higher-order RDM evaluation35−39 (loc. cit.), we believe that CD-DMRG-NEVPT2 will be a valuable tool in transition metal, bioinorganic, and f-element99 chemistry for calculating energies and properties of large molecular systems that are governed by static electron correlation.

Acknowledgments

We gratefully acknowledge the team of the ETH Zurich Euler high-performance computing cluster for providing generous access and resources for the RDM calculations reported in this work.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.6b00778.

  • Details on the active space selection procedure, absolute electronic energies, and DMRG-SCF relative spin-state energies for the model 2 complex (PDF)

L.F. acknowledges the Austrian Science Fund FWF for a Schrödinger fellowship (Project No. J 3935). This work was also supported by the Swiss National Science Foundation SNF (Project No. 200020_169120).

The authors declare no competing financial interest.

Supplementary Material

ct6b00778_si_001.pdf (2.1MB, pdf)

References

  1. Szalay P. G.; Müller T.; Gidofalvi G.; Lischka H.; Shepard R. Chem. Rev. 2012, 112, 108–181. 10.1021/cr200137a. [DOI] [PubMed] [Google Scholar]
  2. Roca-Sanjuán D.; Aquilante F.; Lindh R. WIREs Comput. Mol. Sci. 2012, 2, 585–603. 10.1002/wcms.97. [DOI] [Google Scholar]
  3. Bartlett R. J.; Stanton J. F. In Reviews in Computational Chemistry; Lipkowitz K. B., Boyd D. B., Eds.; John Wiley & Sons, Inc.: New York, 1994; pp 65–169. [Google Scholar]
  4. Sinanoğlu O.; Tuan D. F. J. Chem. Phys. 1963, 38, 1740–1748. 10.1063/1.1776948. [DOI] [Google Scholar]
  5. Boguslawski K.; Tecmer P.; Legeza Ö.; Reiher M. J. Phys. Chem. Lett. 2012, 3, 3129–3135. 10.1021/jz301319v. [DOI] [PubMed] [Google Scholar]
  6. Roos B. O.; Taylor P. R.; Siegbahn P. E. Chem. Phys. 1980, 48, 157–173. 10.1016/0301-0104(80)80045-0. [DOI] [Google Scholar]
  7. Olsen J. Int. J. Quantum Chem. 2011, 111, 3267–3272. 10.1002/qua.23107. [DOI] [Google Scholar]
  8. Stein C. J.; Reiher M. J. Chem. Theory Comput. 2016, 12, 1760–1771. 10.1021/acs.jctc.6b00156. [DOI] [PubMed] [Google Scholar]
  9. Stein C. J.; von Burg V.; Reiher M. J. Chem. Theory Comput. 2016, 12, 3764–3773. 10.1021/acs.jctc.6b00528. [DOI] [PubMed] [Google Scholar]
  10. Aquilante F.; et al. J. Comput. Chem. 2016, 37, 506–541. 10.1002/jcc.24221. [DOI] [PubMed] [Google Scholar]
  11. White S. R. Phys. Rev. Lett. 1992, 69, 2863–2866. 10.1103/PhysRevLett.69.2863. [DOI] [PubMed] [Google Scholar]
  12. White S. R. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 48, 10345–10356. 10.1103/PhysRevB.48.10345. [DOI] [PubMed] [Google Scholar]
  13. Schollwöck U. Ann. Phys. 2011, 326, 96–192. 10.1016/j.aop.2010.09.012. [DOI] [Google Scholar]
  14. Legeza Ö.; Noack R. M.; Sólyom J.; Tincani L. In Computational Many-Particle Physics; Fehske H., Schneider R., Weiße A., Eds.; Lecture Notes in Physics 739; Springer: Berlin, Heidelberg, 2008; pp 653–664. [Google Scholar]
  15. Chan G. K.-L.; Dorando J. J.; Ghosh D.; Hachmann J.; Neuscamman E.; Wang H.; Yanai T. In Frontiers in Quantum Systems in Chemistry and Physics; Wilson S., Grout P. J., Maruani J., Delgado-Barrio G., Piecuch P., Eds.; Progress in Theoretical Chemistry and Physics 18; Springer: Netherlands, 2008; pp 49–65. [Google Scholar]
  16. Marti K. H.; Reiher M. Z. Phys. Chem. 2010, 224, 583–599. 10.1524/zpch.2010.6125. [DOI] [Google Scholar]
  17. Marti K. H.; Reiher M. Phys. Chem. Chem. Phys. 2011, 13, 6750–6759. 10.1039/c0cp01883j. [DOI] [PubMed] [Google Scholar]
  18. Chan G. K.-L.; Sharma S. Annu. Rev. Phys. Chem. 2011, 62, 465–481. 10.1146/annurev-physchem-032210-103338. [DOI] [PubMed] [Google Scholar]
  19. Wouters S.; van Neck D. Eur. Phys. J. D 2014, 68, 272. 10.1140/epjd/e2014-50500-1. [DOI] [Google Scholar]
  20. Kurashige Y. Mol. Phys. 2014, 112, 1485–1494. 10.1080/00268976.2013.843730. [DOI] [Google Scholar]
  21. Yanai T.; Kurashige Y.; Mizukami W.; Chalupský J.; Lan T. N.; Saitow M. Int. J. Quantum Chem. 2015, 115, 283–299. 10.1002/qua.24808. [DOI] [Google Scholar]
  22. Szalay S.; Pfeffer M.; Murg V.; Barcza G.; Verstraete F.; Schneider R.; Legeza Ö. Int. J. Quantum Chem. 2015, 115, 1342–1391. 10.1002/qua.24898. [DOI] [Google Scholar]
  23. Chan G. K.-L.; Keselman A.; Nakatani N.; Li Z.; White S. R. J. Chem. Phys. 2016, 145, 014102. 10.1063/1.4955108. [DOI] [PubMed] [Google Scholar]
  24. Andersson K.; Malmqvist P. A.; Roos B. O.; Sadlej A. J.; Wolinski K. J. Phys. Chem. 1990, 94, 5483–5488. 10.1021/j100377a012. [DOI] [Google Scholar]
  25. Andersson K.; Malmqvist P.-A.; Roos B. O. J. Chem. Phys. 1992, 96, 1218–1226. 10.1063/1.462209. [DOI] [Google Scholar]
  26. Angeli C.; Cimiraglia R.; Evangelisti S.; Leininger T.; Malrieu J.-P. J. Chem. Phys. 2001, 114, 10252. 10.1063/1.1361246. [DOI] [PubMed] [Google Scholar]
  27. Pierloot K. Mol. Phys. 2003, 101, 2083–2094. 10.1080/0026897031000109356. [DOI] [Google Scholar]
  28. Havenith R. W. A.; Taylor P. R.; Angeli C.; Cimiraglia R.; Ruud K. J. Chem. Phys. 2004, 120, 4619–4625. 10.1063/1.1645243. [DOI] [PubMed] [Google Scholar]
  29. Pulay P. Int. J. Quantum Chem. 2011, 111, 3273–3279. 10.1002/qua.23052. [DOI] [Google Scholar]
  30. Angeli C.; Cimiraglia R.; Malrieu J.-P. J. Chem. Phys. 2002, 117, 9138–9153. 10.1063/1.1515317. [DOI] [Google Scholar]
  31. Kurashige Y.; Yanai T. J. Chem. Phys. 2011, 135, 094104. 10.1063/1.3629454. [DOI] [PubMed] [Google Scholar]
  32. Guo S.; Watson M. A.; Hu W.; Sun Q.; Chan G. K.-L. J. Chem. Theory Comput. 2016, 12, 1583–1591. 10.1021/acs.jctc.5b01225. [DOI] [PubMed] [Google Scholar]
  33. Knecht S.; Hedegård E. D.; Keller S.; Kovyrshin A.; Ma Y.; Muolo A.; Stein C. J.; Reiher M. Chimia 2016, 70, 244–251. 10.2533/chimia.2016.244. [DOI] [PubMed] [Google Scholar]
  34. Kurashige Y.; Chalupský J.; Lan T. N.; Yanai T. J. Chem. Phys. 2014, 141, 174111. 10.1063/1.4900878. [DOI] [PubMed] [Google Scholar]
  35. Zgid D.; Ghosh D.; Neuscamman E.; Chan G. K.-L. J. Chem. Phys. 2009, 130, 194107. 10.1063/1.3132922. [DOI] [PubMed] [Google Scholar]
  36. Sharma S.; Chan G. K.-L. J. Chem. Phys. 2014, 141, 111101. 10.1063/1.4895977. [DOI] [PubMed] [Google Scholar]
  37. Sharma S.; Jeanmairet G.; Alavi A. J. Chem. Phys. 2016, 144, 034103. 10.1063/1.4939752. [DOI] [PubMed] [Google Scholar]
  38. Sokolov A. Y.; Chan G. K.-L. J. Chem. Phys. 2016, 144, 064102. 10.1063/1.4941606. [DOI] [PubMed] [Google Scholar]
  39. Roemelt M.; Guo S.; Chan G. K.-L. J. Chem. Phys. 2016, 144, 204113. 10.1063/1.4950757. [DOI] [PubMed] [Google Scholar]
  40. Saitow M.; Kurashige Y.; Yanai T. J. Chem. Phys. 2013, 139, 044118. 10.1063/1.4816627. [DOI] [PubMed] [Google Scholar]
  41. Yanai T.; Kurashige Y.; Neuscamman E.; Chan G. K.-L. J. Chem. Phys. 2010, 132, 024105. 10.1063/1.3275806. [DOI] [PubMed] [Google Scholar]
  42. Neuscamman E.; Yanai T.; Chan G. K.-L. J. Chem. Phys. 2010, 132, 024106. 10.1063/1.3274822. [DOI] [PubMed] [Google Scholar]
  43. Yanai T.; Kurashige Y.; Neuscamman E.; Chan G. K.-L. Phys. Chem. Chem. Phys. 2012, 14, 7809–7820. 10.1039/c2cp23767a. [DOI] [PubMed] [Google Scholar]
  44. Veis L.; Antalík A.; Brabec J.; Neese F.; Legeza Ö.; Pittner J. J. Phys. Chem. Lett. 2016, 7, 4072–4078. 10.1021/acs.jpclett.6b01908. [DOI] [PubMed] [Google Scholar]
  45. Hedegård E. D.; Knecht S.; Kielberg J. S.; Jensen H. J. A.; Reiher M. J. Chem. Phys. 2015, 142, 224108. 10.1063/1.4922295. [DOI] [PubMed] [Google Scholar]
  46. Costas M.; Harvey J. N. Nat. Chem. 2013, 5, 7–9. 10.1038/nchem.1533. [DOI] [PubMed] [Google Scholar]
  47. Swart M.; Costas M.. Spin States in Biochemistry and Inorganic Chemistry: Influence on Structure and Reactivity; John Wiley & Sons, Ltd.: New York, 2015. [Google Scholar]
  48. Cramer C. J.; Truhlar D. G. Phys. Chem. Chem. Phys. 2009, 11, 10757–10816. 10.1039/b907148b. [DOI] [PubMed] [Google Scholar]
  49. Tsipis A. C. Coord. Chem. Rev. 2014, 272, 1–29. 10.1016/j.ccr.2014.02.023. [DOI] [Google Scholar]
  50. Harvey J. N. Annu. Rep. Prog. Chem., Sect. C: Phys. Chem. 2006, 102, 203–226. 10.1039/b419105f. [DOI] [Google Scholar]
  51. Swart M.; Güell M.; Solà M. In Quantum Biochemistry; Matta C. F., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, 2010; pp 551–583. [Google Scholar]
  52. Sousa C.; de Graaf C. In Spin States in Biochemistry and Inorganic Chemistry; Swart M., Costas M., Eds.; John Wiley & Sons, Ltd.: New York, 2015; pp 35–57. [Google Scholar]
  53. Guo Y.; Sivalingam K.; Valeev E. F.; Neese F. J. Chem. Phys. 2016, 144, 094111. 10.1063/1.4942769. [DOI] [PubMed] [Google Scholar]
  54. Li C.; Evangelista F. A. J. Chem. Theory Comput. 2015, 11, 2097–2108. 10.1021/acs.jctc.5b00134. [DOI] [PubMed] [Google Scholar]
  55. Hannon K. P.; Li C.; Evangelista F. A. J. Chem. Phys. 2016, 144, 204111. 10.1063/1.4951684. [DOI] [PubMed] [Google Scholar]
  56. Beebe N. H. F.; Linderberg J. Int. J. Quantum Chem. 1977, 12, 683–705. 10.1002/qua.560120408. [DOI] [Google Scholar]
  57. Koch H.; de Merás A. S.; Pedersen T. B. J. Chem. Phys. 2003, 118, 9481–9484. 10.1063/1.1578621. [DOI] [Google Scholar]
  58. Aquilante F.; Boman L.; Boström J.; Koch H.; Lindh R.; de Merás A. S.; Pedersen T. B. In Linear-Scaling Techniques in Computational Chemistry and Physics; Zalesny R., Papadopoulos M. G., Mezey P. G., Leszczynski J., Eds.; Challenges and Advances in Computational Chemistry and Physics 13; Springer: Netherlands, 2011; pp 301–343. [Google Scholar]
  59. Aquilante F.; Pedersen T. B.; Lindh R.; Roos B. O.; de Merás A. S.; Koch H. J. Chem. Phys. 2008, 129, 024113. 10.1063/1.2953696. [DOI] [PubMed] [Google Scholar]
  60. Delcey M. G.; Freitag L.; Pedersen T. B.; Aquilante F.; Lindh R.; González L. J. Chem. Phys. 2014, 140, 174103. 10.1063/1.4873349. [DOI] [PubMed] [Google Scholar]
  61. Aquilante F.; Malmqvist P.-A.; Pedersen T. B.; Ghosh A.; Roos B. O. J. Chem. Theory Comput. 2008, 4, 694–702. 10.1021/ct700263h. [DOI] [PubMed] [Google Scholar]
  62. Aquilante F.; Todorova T. K.; Gagliardi L.; Pedersen T. B.; Roos B. O. J. Chem. Phys. 2009, 131, 034113. 10.1063/1.3157463. [DOI] [PubMed] [Google Scholar]
  63. Ghigo G.; Roos B. O.; Malmqvist P.-A. Chem. Phys. Lett. 2004, 396, 142–149. 10.1016/j.cplett.2004.08.032. [DOI] [Google Scholar]
  64. Zobel J. P.; Nogueira J. J.; González L. Chem. Sci. 2017, 10.1039/C6SC03759C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Queralt N.; Taratiel D.; de Graaf C.; Caballol R.; Cimiraglia R.; Angeli C. J. Comput. Chem. 2008, 29, 994–1003. 10.1002/jcc.20859. [DOI] [PubMed] [Google Scholar]
  66. Kepenekian M.; Robert V.; Guennic B. L. J. Chem. Phys. 2009, 131, 114702. 10.1063/1.3211020. [DOI] [PubMed] [Google Scholar]
  67. Lawson Daku L. M.; Aquilante F.; Robinson T. W.; Hauser A. J. Chem. Theory Comput. 2012, 8, 4216–4231. 10.1021/ct300592w. [DOI] [PubMed] [Google Scholar]
  68. Vela S.; Fumanal M.; Ribas-Ariño J.; Robert V. J. Comput. Chem. 2016, 37, 947–953. 10.1002/jcc.24283. [DOI] [PubMed] [Google Scholar]
  69. Roos B. O.; Andersson K. Chem. Phys. Lett. 1995, 245, 215–223. 10.1016/0009-2614(95)01010-7. [DOI] [Google Scholar]
  70. Forsberg N.; Malmqvist P.-A. Chem. Phys. Lett. 1997, 274, 196–204. 10.1016/S0009-2614(97)00669-6. [DOI] [Google Scholar]
  71. Angeli C.; Cimiraglia R.; Malrieu J.-P. Chem. Phys. Lett. 2001, 350, 297–305. 10.1016/S0009-2614(01)01303-3. [DOI] [Google Scholar]
  72. White S. R.; Martin R. L. J. Chem. Phys. 1999, 110, 4127–4130. 10.1063/1.478295. [DOI] [Google Scholar]
  73. Benoît C. Bull. Géodésique 1924, 2, 67–77. [Google Scholar]
  74. Aquilante F.; Pedersen T. B.; Lindh R. J. Chem. Phys. 2007, 126, 194106. 10.1063/1.2736701. [DOI] [PubMed] [Google Scholar]
  75. Strickland N.; Harvey J. N. J. Phys. Chem. B 2007, 111, 841–852. 10.1021/jp064091j. [DOI] [PubMed] [Google Scholar]
  76. Ellison M. K.; Scheidt W. R. Inorg. Chem. 1998, 37, 382–383. 10.1021/ic971109j. [DOI] [PubMed] [Google Scholar]
  77. Franz K. J.; Doerrer L. H.; Spingler B.; Lippard S. J. Inorg. Chem. 2001, 40, 3774–3780. 10.1021/ic010181l. [DOI] [PubMed] [Google Scholar]
  78. Jaworska M. Chem. Phys. 2007, 332, 203–210. 10.1016/j.chemphys.2006.11.036. [DOI] [Google Scholar]
  79. Hopmann K. H.; Conradie J.; Tangen E.; Tonzetich Z. J.; Lippard S. J.; Ghosh A. Inorg. Chem. 2015, 54, 7362–7367. 10.1021/acs.inorgchem.5b00901. [DOI] [PubMed] [Google Scholar]
  80. Jørgensen C. K. Coord. Chem. Rev. 1966, 1, 164–178. 10.1016/S0010-8545(00)80170-8. [DOI] [Google Scholar]
  81. Kaim W. Eur. J. Inorg. Chem. 2012, 2012, 343–348. 10.1002/ejic.201101359. [DOI] [Google Scholar]
  82. Radoń M.; Pierloot K. J. Phys. Chem. A 2008, 112, 11824–11832. 10.1021/jp806075b. [DOI] [PubMed] [Google Scholar]
  83. Radoń M.; Broclawik E.; Pierloot K. J. Phys. Chem. B 2010, 114, 1518–1528. 10.1021/jp910220r. [DOI] [PubMed] [Google Scholar]
  84. Boguslawski K.; Jacob C. R.; Reiher M. J. Chem. Theory Comput. 2011, 7, 2740–2752. 10.1021/ct1006218. [DOI] [PubMed] [Google Scholar]
  85. Boguslawski K.; Marti K. H.; Legeza Ö; Reiher M. J. Chem. Theory Comput. 2012, 8, 1970–1982. 10.1021/ct300211j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  86. Freitag L.; Knecht S.; Keller S. F.; Delcey M. G.; Aquilante F.; Pedersen T. B.; Lindh R.; Reiher M.; González L. Phys. Chem. Chem. Phys. 2015, 17, 14383–14392. 10.1039/C4CP05278A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  87. Becke A. D. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  88. Lee C.; Yang W.; Parr R. G. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  89. Perdew J. P.; Chevary J. A.; Vosko S. H.; Jackson K. A.; Pederson M. R.; Singh D. J.; Fiolhais C. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 46, 6671–6687. 10.1103/PhysRevB.46.6671. [DOI] [PubMed] [Google Scholar]
  90. Angeli C.; Borini S.; Cestari M.; Cimiraglia R. J. Chem. Phys. 2004, 121, 4043–4049. 10.1063/1.1778711. [DOI] [PubMed] [Google Scholar]
  91. Roos B. O.; Lindh R.; Malmqvist P.-A.; Veryazov V.; Widmark P.-O. J. Phys. Chem. A 2005, 109, 6575–6579. 10.1021/jp0581126. [DOI] [PubMed] [Google Scholar]
  92. Watts J. D.; Gauss J.; Bartlett R. J. J. Chem. Phys. 1993, 98, 8718–8733. 10.1063/1.464480. [DOI] [Google Scholar]
  93. Aquilante F.; Gagliardi L.; Pedersen T. B.; Lindh R. J. Chem. Phys. 2009, 130, 154107. 10.1063/1.3116784. [DOI] [PubMed] [Google Scholar]
  94. Dolfi M.; Bauer B.; Keller S.; Kosenkov A.; Ewart T.; Kantian A.; Giamarchi T.; Troyer M. Comput. Phys. Commun. 2014, 185, 3430–3440. 10.1016/j.cpc.2014.08.019. [DOI] [Google Scholar]
  95. Keller S.; Dolfi M.; Troyer M.; Reiher M. J. Chem. Phys. 2015, 143, 244118. 10.1063/1.4939000. [DOI] [PubMed] [Google Scholar]
  96. Keller S.; Reiher M. J. Chem. Phys. 2016, 144, 134101. 10.1063/1.4944921. [DOI] [PubMed] [Google Scholar]
  97. Ma Y.; Keller S.; Stein C.; Knecht S.; Lindh R.; Reiher M.. 2016, in preparation.
  98. Enemark J. H.; Feltham R. D. J. Am. Chem. Soc. 1974, 96, 5002–5004. 10.1021/ja00822a057. [DOI] [Google Scholar]
  99. Knecht S.; Keller S.; Autschbach J.; Reiher M. J. Chem. Theory Comput. 2016, 12, 5881. 10.1021/acs.jctc.6b00889. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct6b00778_si_001.pdf (2.1MB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES