Abstract
Stochastic processes can play an important role in microbial community assembly. Dispersal limitation is one process that can increase stochasticity and obscure relationships between environmental variables and microbial community composition, but the relationship between dispersal, selection and stochasticity has not been described in a comprehensive way. We examine how dispersal and its interactions with drift and selection alter the consistency with which microbial communities assemble using a realistic, individual-based model of microbial decomposers. Communities were assembled under different environmental conditions and dispersal rates in repeated simulations, and we examined the compositional difference among replicate communities colonizing the same type of leaf litter (‘within-group distance'), as well as between-group deterministic selection. Dispersal rates below 25% turnover per year resulted in high within-group distance among communities and no significant environmental effects. As dispersal limitation was alleviated, both within- and between-group distance decreased, but despite this homogenization, deterministic environmental effects remained significant. In addition to direct effects of dispersal rate, stochasticity of community composition was influenced by an interaction between dispersal and selection strength. Specifically, communities experiencing stronger selection (less favorable litter chemistries) were more stochastic, possibly because lower biomass and richness intensified drift or priority effects. Overall, we show that dispersal rate can significantly alter patterns of community composition. Partitioning the effects of dispersal, selection and drift based on static patterns of microbial composition will be difficult, if not impossible. Experiments will be required to tease apart these complex interactions between assembly processes shaping microbial communities.
Introduction
A common framework to understand community assembly is the distinction between deterministic, or niche-driven, processes and those that are stochastic or neutral (Hubbel, 2001; Vellend et al., 2014). Because microbes have high dispersal rates, large population sizes, fast growth rates and a propensity for dormancy, communities were traditionally thought to assemble deterministically. However, recent characterizations of microbial communities provide evidence that in addition to environmental selection, stochastic processes can be important drivers of microbial community assembly (Ferrenberg et al., 2013; Nemergut et al., 2013; Zhou et al., 2013; Fukami, 2015).
Here, we define stochastic processes as those that are probabilistic in relation to species identity (Vellend et al., 2014). Some mechanisms of microbial community assembly (Vellend, 2010) map easily onto the stochastic–deterministic framework: demographic drift, or fluctuation in population size due to random birth and death events, is a stochastic process, whereas selection, equivalent to environmental filtering or species sorting, can be considered deterministic. In contrast, dispersal can be deterministic—when certain species are better dispersers than others—or stochastic, occurring through passive processes like wind (Nemergut et al., 2013; Lowe and McPeek, 2014). Low or limited dispersal can also introduce stochasticity in microbial communities (Martiny et al., 2006; Bell, 2010; Lindström and Östman, 2011), potentially through increased drift (Hanson et al., 2012; Stegen et al., 2013), whereas high rates of dispersal can induce mass effects. Through mass effects, high dispersal rates can swamp selection, making microbial communities more similar to a regional species pool than expected by chance and less predictable from environmental variables (Leibold et al., 2004).
In this study, we examine how dispersal and its interactions with drift and selection alter the consistency with which microbial communities assemble. If communities are only influenced by deterministic processes, repeated assembly under identical conditions will yield identical communities. Conversely, variation in the composition of communities under the same conditions could be introduced by stochastic processes. In a multivariate framework, in which community differences are represented by multidimensional distance, this variation is quantified by within-group dissimilarity or distance (used synonymously here). At the same time, the mean difference between communities in different environments, or between-group distance, is driven by deterministic selection. Using this variance-partitioning framework, we ask:
How does dispersal rate affect within- and between-group differences in community composition?
How does selection strength interact with dispersal to alter within-group distance in community composition?
Empirical studies face several challenges when assessing stochastic effects on microbial community assembly. First, calculations of within-group distance include variance generated by error and unmeasured environmental factors, inflating estimates of stochasticity. In addition, it is often not possible to manipulate—or measure—microbial dispersal (but see, for example, Bell, 2010; Peay et al., 2010; Lindström and Östman, 2011), making it challenging to isolate its influence on patterns or describe generalities across studies. The individual-based Decomposition Model of Enzymatic Traits (DEMENT) (Allison, 2012) is well suited to fill gaps in our theoretical understanding of microbial community assembly. DEMENT not only retains the complexity of a realistic microbial system by using empirically determined physiological, community and environmental parameters, but also allows us to manipulate dispersal and quantify within- and between-group distance without confounding variables. Using DEMENT, we can subject randomly assembled, replicated communities of taxa to different dispersal rates and environments (here, substrate chemistries). Taxa with different suites of traits assemble through stochastic and deterministic processes. In the end, we can quantify variation in community composition between environments and within replicate communities as we would in an experiment, but without confounding factors.
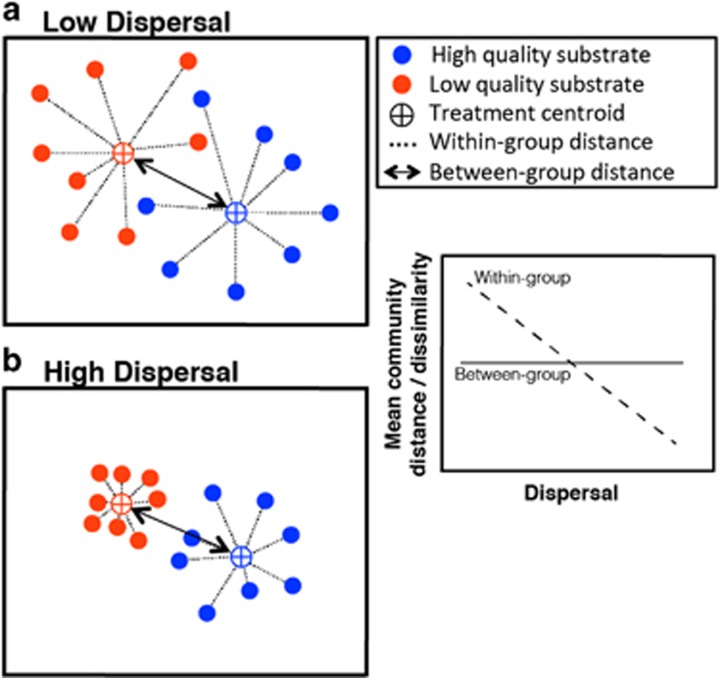
Although little is known about the relationship between dispersal and microbial community composition, we can form general hypotheses for how dispersal alters within- and between-group distances of microbial communities (Figure 1). We first hypothesize that low dispersal rates cause increases in within-group distance as a result of demographic drift (Hanson et al., 2012), whereas higher dispersal rates result in decreases in within-group distance (Figure 1, compare panels a and b). High dispersal can also ‘swamp' the variation caused by local environmental factors through mass effects, but this may be minimal in microbial communities because of fast turnover and selection (Lindström and Östman, 2011). Thus, we expect between-group distance to remain high even at high dispersal. Second, niche selection can be stronger when environmental conditions are suboptimal (Chase, 2007; Vellend, 2010). Assembly under strong selective conditions would result in lower within-group distance among communities provided dispersal is sufficient enough to support larger populations and overcome ecological drift (Hubbel, 2001; Vellend, 2010). Therefore, we hypothesize that strong selection, (here, low-quality substrates and high dispersal will result in lower within-group dissimilarity, such that stochastic effects are less apparent (low- and high-quality substrates in Figure 1b).
Figure 1.
Conceptual illustration of hypothesized patterns of microbial communities under low (a) and high (b) dispersal rates, assembled under two environments (symbol colors). Selection strength differs by environment, with low quality litter substrates (orange) exerting a stronger selection pressure on microbial communities than those that are high quality (blue) and easier to degrade. We hypothesize that within- and between-group distance among microbial communities will be influenced by dispersal rate (comparing a and b) and selection strength (comparing colors in b).
Materials and methods
Model core structure
In the DEMENT model, litter decomposes through the microbial production of extracellular enzymes on a spatially explicit grid analogous to a leaf. Fungal and bacterial taxa are assigned values of several enzymatic traits, drawn from empirically derived trait distributions and constrained by tradeoffs (Supplementary Figure S1) (Allison, 2012). As a result, taxa have unique resource assimilation strategies and competitive abilities that determine community filtering and biogeochemical dynamics across the grid. At initialization of the model, a senesced leaf supplies a source of substrate, and microbial cells are randomly assigned to grid boxes, colonizing the leaf. Leaf substrate chemistry varies by user input (see ‘Selection by leaf chemistry' section below). On the first day of each subsequent model year (365 days), a new leaf falls, corresponding to senescence. Taxa from the previous year's leaf colonize the new leaf, along with a pool of immigrant taxa, the size of which is determined by dispersal rate (see ‘Dispersal' section below). Sampling of taxa from the prior year's leaf as well as cell death are random processes weighted according to taxa abundances. These processes contribute to demographic drift in the model. Model parameters are similar to Allison (2012), and those important or unique to this study are reported in Table 1. For a more detailed description of the model, including dynamics of growth and mortality, see Supplementary Figure S1 and Allison (2012, 2014).
Table 1. Model parametersa.
| Parameter | Value |
|---|---|
| Initial number of local taxa | 100 |
| Number of taxa in regional pool | 1102 |
| Dispersal rateb | 0–60% |
| Substrate lignin/N | 3.9–48.1 |
| Grid size (number of grid cells) | 100 × 100 |
| Number of substrates | 12 |
| Probability taxa occupies grid cellc | 0.01 |
| Days per year | 365 |
| Years | 6 |
Parameters not listed follow those in Table 1 of Allison (2012).
Number of immigrants (dispersal rate) per year are expressed as percent of starting community.
With 10 000 (100 × 100) grid cells, and 100 taxa at the start of each year, an occupancy probability of 0.01 produces an average of 1 microbial cell per grid cell, or initial density of 1 mg cm−3.
Dispersal
We simulate dispersal in the model by introducing a new immigrant community at the beginning of each year, ranging in biomass from 10 to 6000 mg C m−2 and 1 to 600 taxa. We express dispersal rate as a percentage of initial microbial biomass of all communities each year that equaled 10 000 mg C m−2 (summed over all grid cells). Thus, a 1% dispersal rate signifies that immigrant biomass is 1% of 10 000 mg C m−2 or 100 mg C m−2. In this case, the other 99% of biomass would comprise colonizers from the previous year, a proportion that would decrease with increasing dispersal levels. Within a community, the population size of each immigrant is held constant at 10 mg C m−2. The regional pool in the model consisted of 1102 taxa, and local communities each began with 100 taxa. The size of the local and regional species pools was based on data from an experiment at Loma Ridge, CA, USA (Matulich et al., 2015). In this previous study, the total number of operational taxonomic units at 97% sequence similarity across all plots (regional pool) equaled 2199 and the median observed on each sample of leaf litter (local community) was 211. However, including these many taxa was not feasible in our model. We adjusted the size of the regional pool to 1102 taxa, and the size of local communities to 100 taxa, so that we achieved a similar ratio of local to regional richness (100:1102 compared with 211:2199 in the field study) as this ratio can influence within- and between-group distance through sampling effects (Chase and Myers, 2011).
Immigrant communities were randomly drawn from the regional pool (with replacement) and introduced on day 1 of each year together with other taxa colonizing the new leaf from the previous year (Supplementary Figure S1). The total colonizer biomass at the beginning of each year (immigrants and colonizers from the previous year) was kept constant across dispersal treatments, such that a larger immigrant community (under high dispersal rates) decreases the likelihood that low-abundance residents in the previous year's community would colonize the new leaf. In this way, as dispersal rate increased, emigration rate of resident taxa also increased, making dispersal rates more similar to an estimate of community turnover.
We subjected communities in our model to dispersal rates of 0%, 0.5%, 2.5%, 5%, 50% and 60%. We chose these levels a priori because they resembled the range of dispersal rates experimentally induced in other studies (Van der Gucht et al., 2007; Lindström and Östman, 2011), and allowed us to more closely examine low rates of dispersal that are likely to limit sorting in nature. To provide additional perspective on the extent that communities in each of these dispersal levels were dispersal limited, Supplementary Table S1 shows the probability that a taxon was never introduced over all years, and the probability that a taxon is introduced at least once. Probability of dispersing is not linked to other traits in the model (for example, competitive ability), and did not vary among taxa in any deterministic way. Although studies have found that some microbial life forms are more easily dispersed than others (for example, spores), most microorganisms are likely to disperse passively over large areas (Martiny et al., 2006; Nemergut et al., 2013).
Selection by leaf chemistry
We limited the potential deterministic drivers of community composition to one, known environmental factor: leaf substrate chemistry. We varied leaf chemistry by altering the lignin to nitrogen (N) ratio. We chose this metric because it is a well-established control on microbial activity and litter decomposition (Parton et al., 1987), and because we know that the ability of microbes to degrade different substrate lignin/N varies depending on specific traits they posses (Paul and Clark, 1997). Lignin/N ranged from 3.9 to 48.6 (see Supplementary Table S2 for complete chemical composition), representing the breadth of litter chemistries across diverse environments (Adair et al., 2008). We used this environmental gradient in two ways in our study. First, we used lignin/N as an environmental variable over which we expected community composition to vary in a deterministic way. Specifically, when examining the effect of dispersal on community composition, average distance between centroids of lignin/N treatments, as well as the overall correlation of lignin/N to community composition, provided a measure of deterministic variation under different dispersal rates, contextualizing our comparison of within-group distance across dispersal rates. Second, we took advantage of the varying selection pressure introduced by high and low lignin/N. We define a strongly selecting environment as one in which fewer taxa are able to survive and grow optimally, and that consistently favor specialist taxa that are able to survive the harshness of the environment. Substrates with high lignin:N are a strongly selective habitat for microorganisms because they are nutrient-poor and difficult for taxa lacking specialized enzymes to degrade. In contrast, low lignin:N substrates exert milder selection pressure because they provide conditions more favorable for the growth of most taxa (Chapin et al., 2002; Allison et al., 2014; Allison, 2012).
Model scenarios and statistical analyses
We examined stochasticity that resulted from variation in dispersal and lignin/N by performing repeated (N=6) simulations of each combination of the two factors. The replicate assembly simulations were initiated with 100 taxa (10 000 mg C m−2 biomass) that were randomly chosen from the regional pool, and run for six simulation years to allow sufficient time for filtering but still maintain computational feasibility. Annual taxon abundance was calculated by summing biomass over the entire grid and integrating over a year, and at time 0, abundance was calculated on the first day of year 1. To examine differences in community properties (biomass, species richness, Shannon's diversity index and community evenness) we first log-transformed response variables that did not fit a normal distribution. We used a two-factor analysis of variance to test for an overall effect of lignin/N and when a significant interaction was observed, we examined lignin/N within dispersal levels.
To examine community similarity, we first standardized abundance by the total biomass of each sample, calculated Bray–Curtis similarity between all samples, converting it to dissimilarity or distance (1−similarity). Mean and s.e. of within-group distance (differences in communities in the same lignin/N and dispersal treatments) and between-group distance (average differences among communities in different lignin/N treatments) were calculated from this distance matrix. We also calculated within-group distance as a proportion of total variance as a relative measure of stochasticity that is analogous to residuals often reported in empirical studies. In addition, many studies test for significant effects of environmental factors as an indicator of whether stochasticity obscures detectable relationships between community composition and environmental factors. Thus, we also tested the null hypothesis that there was no effect of leaf chemistry within each dispersal level using PerMANOVA (permutational multivariate analysis of variance; Anderson, 2001) that calculates a pseudo F-statistic by comparing the total variance explained by sample identities with variance explained by random permutations of sample identities. We tested for significant differences in within-group variation among the selection strengths of different lignin/N levels using the test of β-dispersion homogeneity (Anderson, 2006) that is analogous to Levene's test for homogeneity of variance (Levene, 1960). All analyses were performed in R (R Core Team, 2013) using package vegan (Okanen et al., 2013).
To examine how dispersal influences the within-group dissimilarity of microbial communities (question 1), we examined the within-group distances (averaged over lignin/N levels) as well as the average distance between groups of lignin/N under each dispersal rate. To assess how selection strength interacted with dispersal (question 2), we also compared within-group distances of communities in strongly selecting environments (high lignin/N) with those under weak selection (low lignin/N).
Results
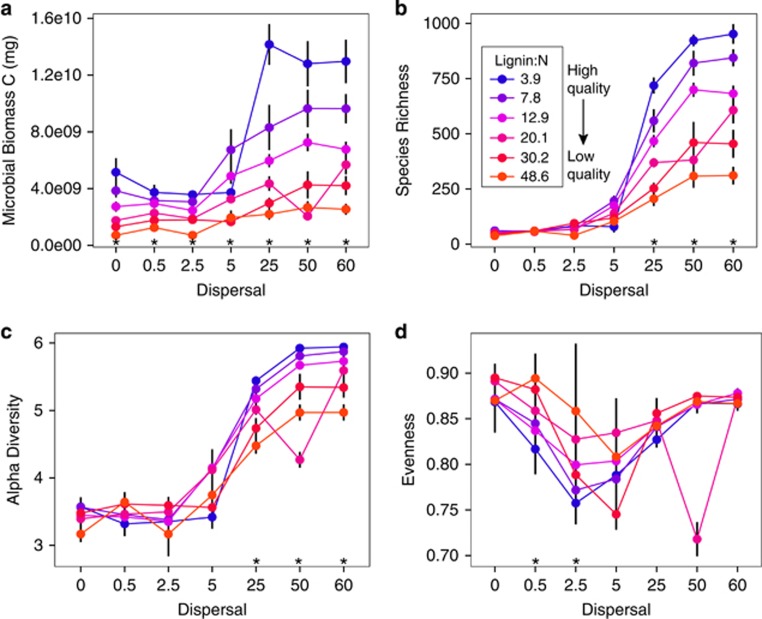
We simulated community assembly of microbial taxa on leaves with varying substrate chemistry and under different dispersal rates in the DEMENT model. Under 6 years of assembly, both leaf chemistry (lignin/N) and dispersal influenced microbial biomass, species richness and Shannon's index of α-diversity (that incorporates richness and evenness) in local communities (Figures 2a–c), but had a weaker effects on community evenness (Figure 2d). Higher dispersal rates resulted in significantly greater microbial biomass carbon, species richness and diversity, particularly in communities under weak selection (low lignin/N).
Figure 2.
Microbial community biomass (a), richness (b), diversity (c), and evenness (d) after communities assembled under different dispersal levels (x-axis) and litter chemistries (lignin:N, symbols and colored lines) for six years. Species richness is the number of species present, while alpha diversity (measured by Shannon's diversity index) incorporates both richness and evenness. Taxa abundances were integrated over 365 days in year six and summed over the entire grid. Asterisks indicate a significant effect (P<0.01) of lignin:N, and error bars show standard error around the mean (N=6).
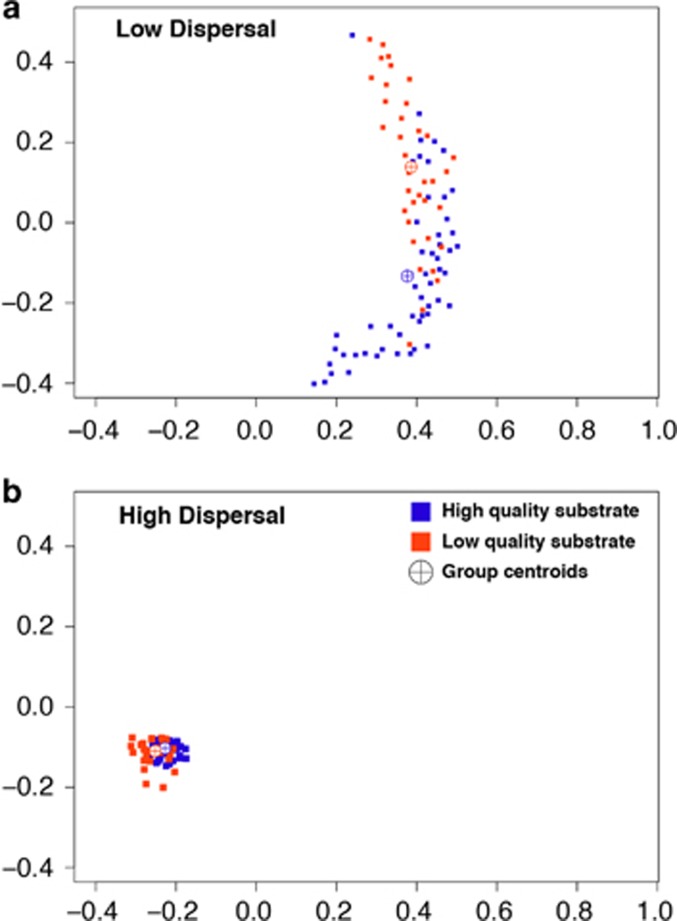
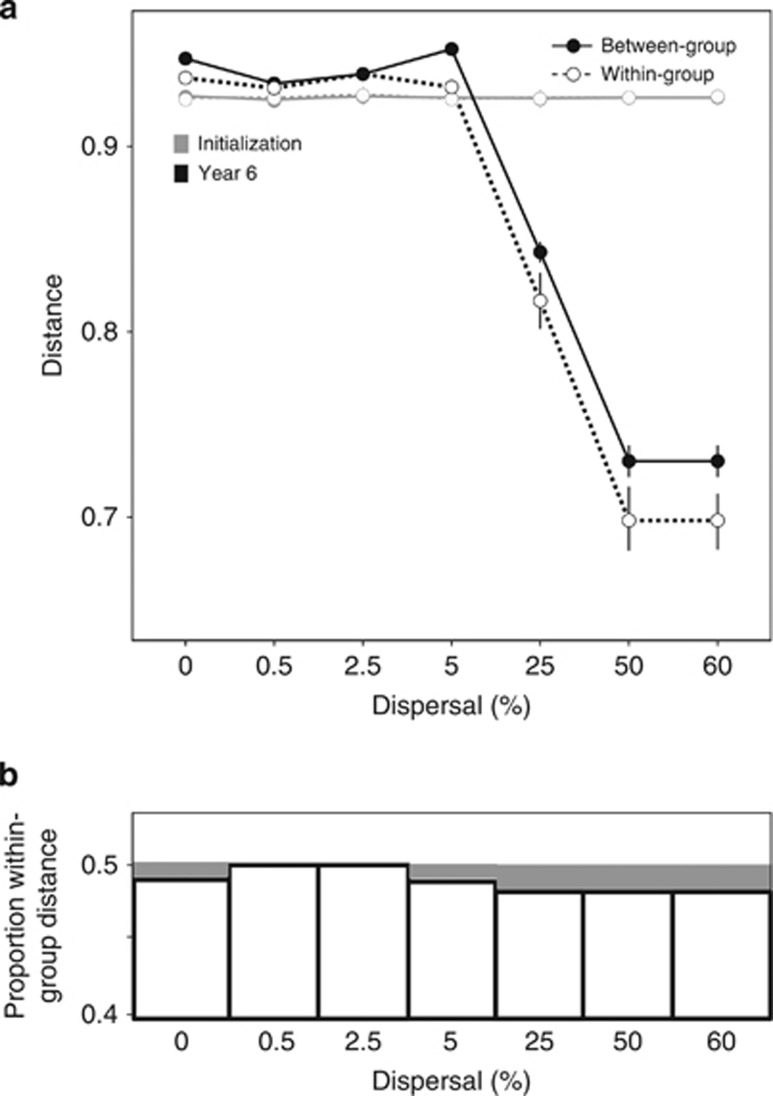
We examined how dispersal affected the relative influence of stochastic and deterministic assembly processes by calculating the average within- and between-group distance across all lignin/N treatments. Within-group distance of replicate communities under low dispersal (0–5% biomass/year) remained high or increased throughout the 6-year simulation (Figures 3a and 4 and Supplementary Figure S2). In contrast, high dispersal rates coincided with a large decrease in within-group distance (Figures 3b and 4), a trend that was already apparent by year 2 (Supplementary Figure S3).
Figure 3.
Nonmetric multidimensional scaling ordinations showing simulated communities after 6 years of sorting on substrates with low lignin/N (orange, lignin/N=20.1, 30.2, 48.6) that are low in quality and induce strong selection, or substrate with low lignin/N (blue, lignin/N=3.9, 7.8, 12.9) that are high in quality and induce weaker selection. Low dispersal (a) includes dispersal rates 0%, 0.5% and 2.5%. High dispersal (b) includes dispersal rates 25%, 50% and 60%. The x and y axes are NMDS axes 1 and 2, respectively. See Supplementary Figure S2 for ordinations of all dispersals and lignin/N levels, and all communities and their similarities at initialization of the model.
Figure 4.
(a) Mean within- and between-group distances (1−Bray–Curtis Similarity) of communities in a given dispersal level at the initialization of the model (time 0) and after 6 years of exposure to different lignin/N treatments. Error bars represent s.e.m. (N=6). See Results for significance of lignin/N treatment for a given dispersal level. (b) Within-group distance as a proportion of the sum of within- and between-group distances, referred to as ‘relative stochasticity' in the text (compared with stochasticity measured by within-group distance in (a)).
The average between-group distance among communities on different substrates (representing deterministic selection) followed the same trend as within-group distance, decreasing with increasing dispersal. At lower dispersal rates, both within-group and between-group distance remained high (Figure 4a). However, as dispersal increased, within-group distance decreased more than between-group distance, causing within-group distance to decline as a proportion of total variation (Figure 4b), although overall differences were relatively minor.
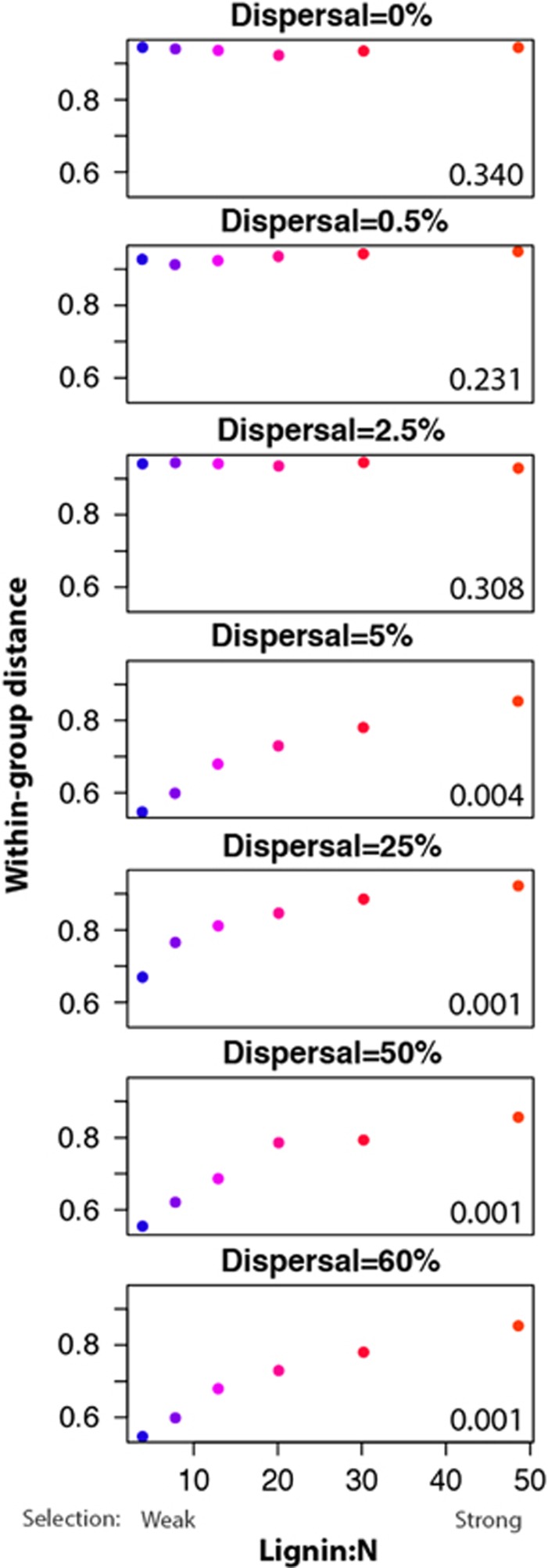
We assessed the null hypothesis that there is no difference between lignin/N levels within each dispersal rate using PerMANOVA (N=6). Leaf chemistry was a significant predictor of community composition above 5% dispersal (P-values <0.01 for dispersal levels 5%, 25%, 50% and 60%), but not significant or only marginally significant at low dispersals (PerMANOVA P-values >0.01 for dispersal levels 0%, 0.5% and 2.5%). Although leaf chemistry weakly affected community composition without any dispersal (P=0.04, Figure 4), trends without dispersal were similar to those with low dispersal (little decrease in within- or between-group distance over time, Supplementary Figure S3, and no effect of selection strength on within-group distance, Figure 5), and hence we did not interpret this to mean that fundamentally different dynamics occur at zero dispersal compared with low dispersal levels.
Figure 5.
Within-group distance (1−Bray–Curtis similarity) of replicate communities within lignin/N treatments (x axis) that were exposed to different dispersal rates for 6 years (panels). Lignin/N levels are shaded from blue (lowest) to orange (highest), corresponding to previous color codes. The bottom right of each panel shows P-values for the null hypothesis that within-group distances across lignin/N treatments are equal in a single dispersal level. Note the x axis is across lignin/N, not over time or dispersal level (but see Supplementary Figure S3), and that low lignin/N corresponds to high substrate quality and weaker selection.
We also tested whether the strength of selection—defined by the lignin/N content of the leaves—affected within-group distance. We found that selection strength interacted with dispersal to affect within-group distance (Figure 5). At low dispersal (0–2.5%), within-group distance did not vary with selection strength (Figure 5, rows 1–3), as induced by variation in lignin/N (Figure 5, x axis). Under higher levels of dispersal, selection strength influenced within-group distance, but in the opposite direction that we predicted. As selection intensified under higher lignin/N, conditions in which fewer taxa can thrive, within-group distance increased (Figure 5, rows 4–7, and Supplementary Figure S2).
Discussion
In this study, we describe specific relationships between dispersal rates and microbial community composition (within- and between-group distance) using an individual-based model parameterized with realistic microbial traits and environmental conditions. Taken together, our results show that dispersal limitation introduces significant stochasticity in microbial community assembly (Figures 3 and 4), but stochasticity is also high under high dispersal in strongly selecting conditions (Figure 5). This is possibly because these conditions foster communities with smaller populations and/or lower diversity (Figure 2) in which drift is more prominent (Vellend, 2010). This work suggests that complex interactions between microbial dispersal, drift and selection are likely to alter or obscure relationships between environmental variables and microbial community composition.
Dispersal alters the relative contribution of stochastic and deterministic processes
In answer to our first question, dispersal rate altered both within- and between-group distances. Stochastic effects—measured as within-group distance of replicate communities—decreased with increasing dispersal rate, consistent with our hypothesis. However, different mechanisms contributed to this pattern at low and high dispersal.
At low dispersal, within-group distance slowly and consistently increased over time (Supplementary Figure S3). This trend is characteristic of stochasticity introduced by drift that can increase in importance under low dispersal rates (Vellend, 2010; Hanson et al., 2012), although we cannot rule out that priority effects also contributed to this pattern. Between-group distance also increased slightly at low dispersal rates, relative to that of communities randomly assembled at initialization, suggesting that some selection occurred. However, our deterministic factor, leaf chemistry (lignin/N), was relatively unimportant for community composition with the number of statistical replicates examined here (Figure 4). Thus, we find that low dispersal rates in natural decomposer communities might result in apparently weak deterministic effects (low significance of environmental effect) that would have been apparent with higher dispersal rates. Supporting this idea, Lindström and Östman (2011) also found that deterministic effects in lakes only become apparent when bacterial dispersal reached intermediate rates (but see Declerck et al., 2013, where this occurs at a much lower dispersal rate). Notably, when we grouped taxa into functional groups according to their traits and performed the same community analyses, communities grouped more strongly by their local environment (data not shown), suggesting in these conditions, function would be affected to a lesser extent by dispersal limitation.
At high dispersal, within-group distance decreased. High dispersal rates are thought to lead to communities overwhelmed by mass effects that can alter the importance of stochasticity on microbial community composition (Ofiteru et al., 2010; Adams et al., 2014). Our model allows us to distinguish between two possible outcomes of mass effects. On the one hand, mass effects can increase within-group distance of community composition by introducing maladapted taxa. If dispersal is random with respect to species identity, this would increase within-group distances of microbial communities and potentially overwhelm species sorting. We did not find evidence of this: within-group distance among replicate communities was reduced at high dispersal rates (Figures 3 and 4 and Supplementary Figures S2 and S3).
On the other hand, mass effects can homogenize local communities, decreasing between-group distance and making them more similar to one another and to the regional species pool (Leibold et al., 2004; Stegen et al., 2013). We did find evidence for this type of mass effect: between-group distance decreased at high dispersal rates. However, microbial communities under very high dispersal rates were still strongly influenced by selection, as indicated by a significant relationship with the environment, and a low proportional contribution of stochastic processes (Figure 4, bars). Thus, mass effects induced by high dispersal rates may not increase microbial community stochasticity as measured by within-group distance, but can homogenize communities across environments. This was only revealed by a consideration of within-group distance relative to between-group distance (what we call relative stochasticity), rather than within-group alone distance serving as an indicator of stochasticity. Stegen et al. (2015) developed a simpler model in which communities assembled according to species' evolutionary optima to a predetermined community size, yet found remarkably similar outcomes under varying selection and dispersal. This may be related to the fact that the emergent community size in DEMENT (and starting regional pool) was similar to richness and number of individuals used in this study.
Some empirical studies, often in aquatic systems, have detected mass effects in microbial communities under high dispersal, but the ultimate influence it has on selection can vary. For example, Ofiteru et al. (2010) studied communities in wastewater treatment plants that are subject to high dispersal rates, and found that deterministic selection had little influence on microbial community composition, and was instead driven by neutral dynamics (drift and random immigration). In lakes, high immigration rates rarely overwhelm local selection (Jones and McMahon, 2009; Logue and Lindström, 2010) but can cause local communities to become more similar to the composition of communities immigrating (for example, from a stream inlet) (Lindström et al., 2006; Crump et al., 2007; Adams et al., 2014). Our results suggest that microbial growth rates are fast enough to observe strong deterministic effects in leaf litter communities even under extremely high dispersal rates. High dispersal may be more likely to swamp local deterministic effects on shorter timescales, after a sudden influx of microorganisms (Adams et al., 2014; Symons and Arnott, 2014).
Although we focused on effects of dispersal on β-diversity, it is notable that α-diversity increased with dispersal rate in our model. This deviates from predictions in simpler theoretical models that local diversity begins to decline at intermediate dispersal levels (Loreau and Mouquet, 1999; Mouquet and Loreau, 2002). This could be a result of the initial ratio of local to regional species richness used in our model, or the fact that initial biomass in our model was far below carrying capacity of the simulated environment (as indicated by steadily increasing biomass and richness over time). Evenness tended to be lower at intermediate dispersals, suggesting that more competitive colonizers were able to dominate at these levels, but mass effects increased both richness and evenness at high dispersal rates. In addition, increases in α-diversity likely contributed to decreases in β-diversity (Chase and Myers, 2011). When comparing across metacommunities that may differ in size or source pool, removing this effect can be important (for example, through statistical methods such as Raup-Crick distance; Chase et al., 2011). However, we aimed to compare local diversity within a single metacommunity, and hence changes in β-diversity were important to capture even if influenced by α-diversity. Local species richness relative to that of the regional pool will also alter the extent that community homogenization is observed under high dispersal. Thus, when possible, studies should measure and report these community properties.
The effect of dispersal on community composition depends on environment
In answer to our second question, dispersal interacted with selection to influence stochastic community assembly in our model communities. However, this interaction was only apparent at high dispersal rates (Figure 5, rows 4–7). At low dispersal rates (below 5%), within-group distance was invariant across lignin/N (Figure 5, rows 1–3). At higher dispersal rates, assembly of replicate communities was more consistent under weak selection than strong selection induced by high lignin/N. In contrast, Chase (2007) found that drought led to a decrease in stochastic assembly in pond communities, presumably because drought amplified niche selection.
The most parsimonious explanation for the observed effect of selection strength on within-group distance is that biomass and population size also changed with shifts in selection strength. Communities under strong selection (high lignin/N) had the fewest species and lowest biomass (Figure 2). The smaller sizes of these communities (number of individuals summed over species) may have made them more susceptible to demographic drift (Vellend et al., 2014). In addition, the low total biomass in these treatments likely lessened the intensity of competitive interactions, essentially weakening density-dependent selection despite (apparently) strong abiotic selection. This could be tested by examining diversity of microbial functional groups, but overall this finding highlights the importance of community size in understanding outcomes of assembly processes.
We also cannot rule out priority effects as a generator of stochasticity in community composition, although to our knowledge, priority effects are not necessarily more prominent under strong selection. We tested for priority effects in all levels of selection by examining the relationship between a taxon's final abundance and its starting abundance or year of introduction, but they were not significantly correlated in any scenario (P>0.05, data not shown). A positive correlation might provide evidence for a ‘niche preemption' priority effect (sensu Fukami, 2015), whereby earlier colonizers fill niche space from which later colonizers are excluded, but the test could miss ‘environmental modification' priority effects that occur as early colonizers modify the environment in a way that favors certain taxa. The latter type of priority effect could have occurred in DEMENT; in the model, a microbial cell's effect on grid cell substrate chemistry lingers until a new leaf is introduced (annually). Despite this possibility, there is no support that this priority effect would be stronger under suboptimal conditions or strong environmental selection (here, higher lignin/N). In general, priority effects are stronger in communities with high productivity or turnover (Fukami, 2015), or after experiencing a disturbance or environmental shift (Mergeay et al., 2011), none of which describe high lignin/N scenarios.
Caveats and recommendations for future work
The patterns we observed in this theoretical model provide new testable hypotheses about how dispersal and selection influence microbial community assembly. However, future research might address some of our model's omissions. For instance, we treated dispersal as a one-time, yearly event, but assembly patterns can be sensitive to whether an immigration event is sequential or simultaneous (Steiner, 2014), or whether colonizers are primary (the first to arrive in an area) or secondary (colonizing an area with a pre-existing community) (Vellend et al., 2014). We also did not include variation in dispersal ability among taxa. Although passive dispersal is prominent in microbial communities, dispersal ability and mode can vary among taxa that would add a deterministic driver of community assembly (Vanette et al., 2014). Finally, we did not include reciprocal effects between regional and local species pools, but several studies have found that community and evolutionary dynamics in local assemblages (sorting, speciation) influence immigration and mass effects (Leibold et al., 2004; Venail et al., 2008; Mittelbach and Schemske, 2015). Inclusion of feedbacks between regional and local pools might have resulted in greater homogenization of community composition across treatments in our model, or increased within-group distance by reinforcing priority effects (Fukami, 2015).
Environmental factors explain a significant portion of variation in microbial community composition, but just as often, large residuals are left unexplained, with little knowledge of why. Our results indicate that partitioning the effects of dispersal, selection and drift based on static patterns of microbial composition will be difficult, if not impossible. Thus, teasing apart the complex interactions between assembly processes will require more direct assays. For instance, greater efforts should be placed on the quantification and manipulation of microbial dispersal rates across microbial communities. Although several studies have tackled this challenge (Bruns, 1995; Bell, 2010; Lindström and Östman, 2011; Peay et al., 2012; Martiny, 2015), we need to pay careful attention to the methods (and units) for characterizing dispersal rate in order to generalize across studies and scales. A second key measurement in future studies should be microbial biomass and/or absolute abundance. We found community size (number of individuals summed over all species) and biomass were major drivers of the compositional outcome of shifts in dispersal and selection. Such measures are often omitted from studies assessing community composition with high-throughput sequencing, but are directly related to the importance of stochastic effects on microbial community assembly.
Acknowledgments
This manuscript is dedicated to the memory of Diana R Nemergut. This work was funded by the National Science Foundation Postdoctoral Research Fellowship in Biology (NSF DEB 1202882) to SE and the US Department of Energy, Office of Science, Office of Biological and Environmental Research (BER), under Award Number DE-PS02-09ER09-25 to SDA and JBHM. This is Kellogg Biological Station Contribution no. 1912. We also thank the Allison and Martiny labs at UC Irvine for helpful feedback, and Dylan Fitzpatrick for help with analysis. Finally, we thank Jenny Rocca, Gary Mittelbach, James Stegen, and one anonymous reviewer whose comments greatly improved the quality of this paper.
Footnotes
Supplementary Information accompanies this paper on The ISME Journal website (http://www.nature.com/ismej)
The authors declare no conflict of interest.
Supplementary Material
References
- Adair EC, Parton WJ, Del Grosso SJ, Silver WL, Harmon ME, Hall SA et al. (2008). Simple three-pool model accurately describes patterns of long-term litter decomposition in diverse climates. Glob Chang Biol 14: 2636–2660. [Google Scholar]
- Adams HE, Crump BC, Kling GW. (2014). Metacommunity dynamics of bacteria in an arctic lake: the impact of species sorting and mass effects on bacterial production and biogeography. Front Microbiol 5: 82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allison SD. (2012). A trait-based approach for modelling microbial litter decomposition. Ecol Lett 15: 1058–1070. [DOI] [PubMed] [Google Scholar]
- Allison SD. (2014). Modeling adaptation of carbon use efficiency in microbial communities. Front Microbiol 5: 571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allison SD, Chacon SS, German DP. (2014). Substrate concentration constraints on microbial decomposition. Soil Biol Biochem 79: 43–49. [Google Scholar]
- Anderson MJ. (2001). Permutation tests for univariate or multivariate analysis of variance and regression. Can J Fish Aquat Sci 58: 626–639. [Google Scholar]
- Anderson MJ. (2006). Distance-based tests for homogeneity of multivariate dispersions. Biometrics 62: 245–253. [DOI] [PubMed] [Google Scholar]
- Bell T. (2010). Experimental tests of the bacterial distance-decay relationship. ISME J 4: 1357–1365. [DOI] [PubMed] [Google Scholar]
- Bruns TD. (1995). Thoughts on the processes that maintain local species diversity of ectomycorrhizal fungi. Plant Soil 170: 63–73. [Google Scholar]
- Chapin FS, Matson PA, Mooney HA. (2002) Principles of Terrestrial Ecosystem Ecology. Springer: New York, NY, USA.
- Chase JM. (2007). Drought mediates the importance of stochastic community assembly. Proc Natl Acad Sci USA 104: 17430–17434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chase JM, Kraft NJB, Smith KG, Vellend M, Inouye BD. (2011). Using null models to disentangle variation in community dissimilarity from variation in α-diversity. Ecosphere 2: art24. [Google Scholar]
- Chase JM, Myers JA. (2011). Disentangling the importance of ecological niches from stochastic processes across scales. Philos Trans R Soc Lond B Biol Sci 366: 2351–2363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crump BC, Adams HE, Hobbie JE, Kling GW. (2007). Biogeography of bacterioplankton in lakes and streams of an arctic tundra catchment. Ecology 88: 1365–1378. [DOI] [PubMed] [Google Scholar]
- Declerck SAJ, Winter C, Shurin JB, Suttle CA, Matthews B. (2013). Effects of patch connectivity and heterogeneity on metacommunity structure of planktonic bacteria and viruses. ISME J 7: 533–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrenberg S, O'Neill SP, Knelman JE, Todd B, Duggan S, Bradley D et al. (2013). Changes in assembly processes in soil bacterial communities following a wildfire disturbance. ISME J 7: 1102–1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukami T. (2015). Historical contingency in community assembly: integrating niches, species pools, and priority effects. Annu Rev Ecol Evol Syst 46: 1–23. [Google Scholar]
- Hanson CA, Fuhrman JA, Horner-Devine MC, Martiny JBH. (2012). Beyond biogeographic patterns: processes shaping the microbial landscape. Nat Rev Microbiol 10: 497–506. [DOI] [PubMed] [Google Scholar]
- Hubbel SP. (2001) The Unified Neutral Theory of Biodiversity and Biogeography. Princeton University Press: Princeton, NJ, USA.
- Jones SE, McMahon KD. (2009). Species-sorting may explain an apparent minimal effect of immigration on freshwater bacterial community dynamics. Environ Microbiol 11: 905–913. [DOI] [PubMed] [Google Scholar]
- Leibold MA, Holyoak M, Mouquet N, Amarasekare P, Chase JM, Hoopes MF et al. (2004). The metacommunity concept: a framework for multi-scale community ecology. Ecol Lett 7: 601–613. [Google Scholar]
- Levene H. (1960). Robust tests for equality of variances. In: Olkin I, Ghurye SG, Hoeffding W, Madow WG, Mann HB (eds), Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling. Stanford University Press: Palo Alto, CA, USA, pp 278–292. [Google Scholar]
- Lindström ES, Forslund M, Algesten G, Bergström A-K. (2006). External control of bacterial community structure in lakes. Limnol Oceanogr 51: 339–342. [Google Scholar]
- Lindström ES, Östman Ö. (2011). The importance of dispersal for bacterial community composition and functioning. PLoS One 6: e25883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logue JB, Lindström ES. (2010). Species sorting affects bacterioplankton community composition as determined by 16S rDNA and 16S rRNA fingerprints. ISME J 4: 729–738. [DOI] [PubMed] [Google Scholar]
- Loreau M, Mouquet N. (1999). Immigration and the maintenance of local species diversity. Am Nat 154: 427–440. [DOI] [PubMed] [Google Scholar]
- Lowe WH, McPeek MA. (2014). Is dispersal neutral? Trends Ecol Evol 29: 444–450. [DOI] [PubMed] [Google Scholar]
- Martiny JBH. (2015). Dispersal and the microbiome. Microbe Mag 10: 191–196. [Google Scholar]
- Martiny JBH, Bohannan BJM, Brown JH, Colwell RK, Fuhrman JA, Green JL et al. (2006). Microbial biogeography: putting microorganisms on the map. Nat Rev Microbiol 4: 102–112. [DOI] [PubMed] [Google Scholar]
- Matulich KL, Weihe C, Allison SD, Amend AS, Berlemont R, Goulden ML et al. (2015). Temporal variation overshadows the response of leaf litter microbial communities to simulated global change. ISME J 9: 2477–2489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mergeay J, De Meester L, Eggermont H, Verschuren D. (2011). Priority effects and species sorting in a long paleoecological record of repeated community assembly through time. Ecology 92: 2267–2275. [DOI] [PubMed] [Google Scholar]
- Mittelbach GG, Schemske DW. (2015). Ecological and evolutionary perspectives on community assembly. Trends Ecol Evol. 30: 241–247. [DOI] [PubMed] [Google Scholar]
- Mouquet N, Loreau M. (2002). Coexistence in metacommunities: the regional similarity hypothesis. Am Nat 159: 420–426. [DOI] [PubMed] [Google Scholar]
- Nemergut DR, Schmidt SK, Fukami T, O'Neill SP, Bilinski TM, Stanish LF et al. (2013). Patterns and processes of microbial community assembly. Microbiol Mol Biol Rev 77: 342–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ofiteru ID, Lunn M, Curtis TP, Wells GF, Criddle CS, Francis CA et al. (2010). Combined niche and neutral effects in a microbial wastewater treatment community. Proc Natl Acad Sci USA 107: 15345–15350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oksanen J, Blanchett FG, Kindt R, Legendre P, Minchin PR, O'Hara RB et al. (2013). Vegan: Community Ecology Package. R package version 2.0-10.
- Parton WJ, Schimel DS, Cole C V, Ojima DS. (1987). Analysis of factors controlling soil organic matter levels in great plains grasslands. Soil Sci Soc Am J 51: 1173–1179. [Google Scholar]
- Paul EA, Clark F. (1997) Soil Microbiology and Biochemistry. Academic Press. [Google Scholar]
- Peay KG, Garbelotto M, Bruns TD. (2010). Evidence of dispersal limitation in soil microorganisms: isolation reduces species richness on mycorrhizal tree islands. Ecology 91: 3631–3640. [DOI] [PubMed] [Google Scholar]
- Peay KG, Schubert MG, Nguyen NH, Bruns TD. (2012). Measuring ectomycorrhizal fungal dispersal: Macroecological patterns driven by microscopic propagules. Mol Ecol 21: 4122–4136. [DOI] [PubMed] [Google Scholar]
- R Core Team. (2013) R: a Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria.
- Stegen JC, Lin X, Fredrickson JK, Chen X, Kennedy DW, Murray CJ et al. (2013). Quantifying community assembly processes and identifying features that impose them. ISME J 7: 2069–2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stegen JC, Lin X, Fredrickson JK, Konopka AE. (2015). Estimating and mapping ecological processes influencing microbial community assembly. Front Microbiol 6: 370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steiner CF. (2014). Stochastic sequential dispersal and nutrient enrichment drive beta diversity in space and time. Ecology 95: 2603–2612. [Google Scholar]
- Symons CC, Arnott SE. (2014). Timing is everything: priority effects alter community invasibility after disturbance. Ecol Evol 4: 397–407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Gucht K, Cottenie K, Muylaert K, Vloemans N, Cousin S, Declerck S et al. (2007). The power of species sorting: local factors drive bacterial community composition over a wide range of spatial scales. Proc Natl Acad Sci USA 104: 20404–20409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanette RL, Marie-Pierre LG, Fukami T. (2014). Microbial community structure and function in floral nectar are shaped by variation in dispersalIn: Ecological Society of America Annual Meeting.
- Vellend M. (2010). Conceptual synthesis in community ecology. Q Rev Biol 85: 183–206. [DOI] [PubMed] [Google Scholar]
- Vellend M, Srivastava DS, Anderson KM, Brown CD, Jankowski JE, Kleynhans EJ et al. (2014). Assessing the relative importance of neutral stochasticity in ecological communities. Oikos 123: 1420–1430. [Google Scholar]
- Venail PA, MacLean RC, Bouvier T, Brockhurst MA, Hochberg ME, Mouquet N. (2008). Diversity and productivity peak at intermediate dispersal rate in evolving metacommunities. Nature 452: 210–214. [DOI] [PubMed] [Google Scholar]
- Zhou J, Liu W, Deng Y, Jiang YH, Xue K, He Z et al. (2013). Stochastic assembly leads to alternative communities with distinct functions in a bioreactor microbial community. MBio; e-pub ahead of print 5 March 2013; doi:10.1128/mBio.00584-12. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.