Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2016 Sep 21;118(3):211–220. doi: 10.1038/hdy.2016.72

Importance of incomplete lineage sorting and introgression in the origin of shared genetic variation between two closely related pines with overlapping distributions

Y Zhou 1,2,3,6, L Duvaux 4,6, G Ren 1, L Zhang 1, O Savolainen 2,5, J Liu 1,*
PMCID: PMC5315522  PMID: 27649619

Abstract

Genetic variation shared between closely related species may be due to retention of ancestral polymorphisms because of incomplete lineage sorting (ILS) and/or introgression following secondary contact. It is challenging to distinguish ILS and introgression because they generate similar patterns of shared genetic diversity, but this is nonetheless essential for inferring accurately the history of species with overlapping distributions. To address this issue, we sequenced 33 independent intron loci across the genome of two closely related pine species (Pinus massoniana Lamb. and Pinus hwangshanensis Hisa) from Southeast China. Population structure analyses revealed that the species showed slightly more admixture in parapatric populations than in allopatric populations. Levels of interspecific differentiation were lower in parapatry than in allopatry. Approximate Bayesian computation suggested that the most likely speciation scenario explaining this pattern was a long period of isolation followed by a secondary contact. Ecological niche modeling suggested that a gradual range expansion of P. hwangshanensis during the Pleistocene climatic oscillations could have been the cause of the overlap. Our study therefore suggests that secondary introgression, rather than ILS, explains most of the shared nuclear genomic variation between these two species and demonstrates the complementarity of population genetics and ecological niche modeling in understanding gene flow history. Finally, we discuss the importance of contrasting results from markers with different dynamics of migration, namely nuclear, chloroplast and mitochondrial DNA.

Introduction

Understanding speciation has been a long-standing interest since the publication of ‘On the Origin of Species' (Darwin, 1859). The allopatric speciation model was considered as the null hypothesis for decades (Mayr, 1963; Coyne and Orr, 2004). However, recent investigations have suggested that speciation in the face of gene flow has been more common (Nosil, 2008), especially in plants where gene exchange among closely related species is estimated to occur in at least 25% of species (Mallet, 2005). Scenarios of speciation with gene flow are not all equivalent though. On one hand, gene flow can be continuous from an early phase of speciation to completion of reproductive isolation (sympatric or parapatric speciation), in which case divergent selection is thought to play the major role in promoting reproductive isolation between incipient species (Coyne and Orr, 2004; Feder et al., 2013). On the other hand, current sympatric or parapatric species distributions may result from secondary contacts occurring during late phases of speciation. This may occur when an allopatric period was not long enough for species to evolve complete reproductive isolation, for example, when they come into secondary contact during climatic cycle oscillations (Barton and Hewitt, 1985; Melo-Ferreira et al., 2005; Rieseberg et al., 2007). Introgression following such secondary contact may introduce foreign alleles and reduce the differentiation between species gene pools at loci unlinked to speciation genes (Coyne and Orr, 2004; Petit and Excoffier, 2009).

Patterns of genetic diversity within and among populations carry much information about population demographic history and therefore have been widely used to infer speciation history (Hey and Nielsen, 2004; Won and Hey, 2005; Duvaux et al., 2011; Roux et al., 2013; Butlin et al., 2014). However, retention of ancestral polymorphism because of incomplete lineage sorting (ILS) and secondary gene flow produce very similar patterns of shared genetic diversity, making the investigation of speciation history difficult (Rieseberg et al., 1999; Charlesworth et al., 2005; Sousa and Hey, 2013; Huerta-Sánchez et al., 2014). Indeed, ILS can be the cause of shared genetic diversity a long time after species divergence. Under a simple allopatric speciation model, drift alone requires 9–12 Ne (effective population size) generations to make incipient species reciprocally monophyletic at more than 95% of loci (Hudson and Coyne, 2002). Therefore, species with long generation times, such as coniferous trees, or recently isolated populations, often share genetic variation (see, for example, Du et al., 2009; Wang et al., 2011; Li et al., 2012; Sun et al., 2015).

The recent availability of new tools in population genetics now allows us to discriminate better between gene flow and ILS. The development of coalescent-based frameworks, for example, isolation with migration (IM) model-based programs (Wakeley and Hey, 1998; Nielsen and Wakeley, 2001; Hey, 2010) and approximate Bayesian computation (ABC) frameworks using coalescent genealogy samplers (Beaumont et al., 2002; Kuhner, 2009; Csilléry et al., 2010; Sunnåker et al., 2013), has allowed direct comparison of different scenarios of population divergence. For example, Qu et al. (2012) found, using the program IMa (Hey, 2010), that alleles shared between eastern and western lineages of the parrotbill Paradoxornis webbianus might have resulted from both ILS and secondary gene flow. Ecological niche modeling based on present distribution data can also be applied to infer demographic dynamics and historical variation of species ranges (Elith et al., 2011). Used jointly with coalescent-based frameworks, this method allows refined interpretations about possible secondary contacts between closely related species during past climate oscillations (see, for example, Levsen et al., 2012; Sun et al., 2015).

When geographic distribution information is available, ILS and secondary gene flow can also be distinguished by comparing patterns of genetic diversity between pairs of neighboring and distantly located populations of the different species (Muir and Schlötterer, 2005). Gene flow is expected to happen preferentially among neighboring populations that therefore results in higher levels of intraspecific genetic diversity and lower levels of interspecific genetic differentiation than between distantly located populations (Petit and Excoffier, 2009). In contrast, under the ILS scenario, shared polymorphism is expected to be distributed evenly in all populations. Using this approach, Muir and Schlötterer (2005) showed that FCT between two closely related oak species was randomly distributed across distant and nearby populations, suggesting a major role for ILS. However, Lexer et al. (2006) showed that FCT was unevenly distributed across the genome and that a limited number of loci showed significantly increased FCT, a pattern they argued was more likely because of recurrent gene flow and selection at differentiated loci.

Closely related coniferous tree species often share genetic variation (Ma et al., 2006; Li et al., 2010a; Wachowiak et al., 2011; Ren et al., 2012). One possible reason lies in their long generation times (>20 years in average) and large Ne. This means that most coniferous species have probably experienced climatic oscillations as rapid successions, in terms of drift units (Tgen/Ne, where Tgen is speciation time in generations), of isolation periods and expansion intervals with secondary contacts. Using this rationale, most coniferous species diverged relatively recently (∼0.1–0.2 million generations, that is, 2–3 Ne generations ago; Leslie et al., 2012; Mao et al., 2012), leading them to maintain a high proportion of ancestral diversity. Moreover, interspecific gene exchange promoted by frequent secondary contacts during climate cycle turnover may have contributed to maintaining weak reproductive barriers between closely related species (see, for example, Ma et al., 2006; Li et al., 2010a).

Pinus massoniana and P. hwangshanensis are two closely related pines occurring in Southeast China with overlapping distributions. They have a different preference for altitude as populations are usually found at low (below 900 m) and high altitudes (above 700 m) for P. massoniana and P. hwangshanensis, respectively (Fu et al., 1999). The species can occur on the same mountains but at different (partially overlapping) altitudes (parapatric populations) or occur on different mountains (allopatric populations) (Zhou et al., 2010, 2014; Li et al., 2010b, 2012). Analysis of cytoplasmic genetic variation revealed that mitochondrial diversity was extensively shared and randomly distributed across populations of the two species (Zhou et al., 2010), whereas chloroplast variation was clearly species specific. In coniferous trees, chloroplast, mitochondrial and nuclear genomes are paternally, maternally and biparentally inherited respectively (Wagner et al., 1987; Neale and Sederoff, 1988; Mogensen, 1996). These two pines therefore offer a great opportunity to test for the preponderance of ILS and introgression during speciation and to compare results from markers with differential inheritance.

Here, we analyzed noncoding genetic variation at 33 intron loci across the genome for both parapatric and allopatric populations of the two species. First, we compared patterns of genetic diversity and population admixture between parapatric and allopatric populations of both species. We then conducted an ABC analysis to infer the demography and speciation scenario of both species. Along with the demographic modeling, we used ecological niche modeling to track distribution changes of the two species during the Pleistocene climate changes. Our results suggest that secondary contact(s) rather than ILS explains shared nuclear genetic variation between the two pine species, in contrast to the earlier conclusions based on cytoplasmic markers alone.

Materials and methods

Sampling, sequencing and analyses of genetic diversity

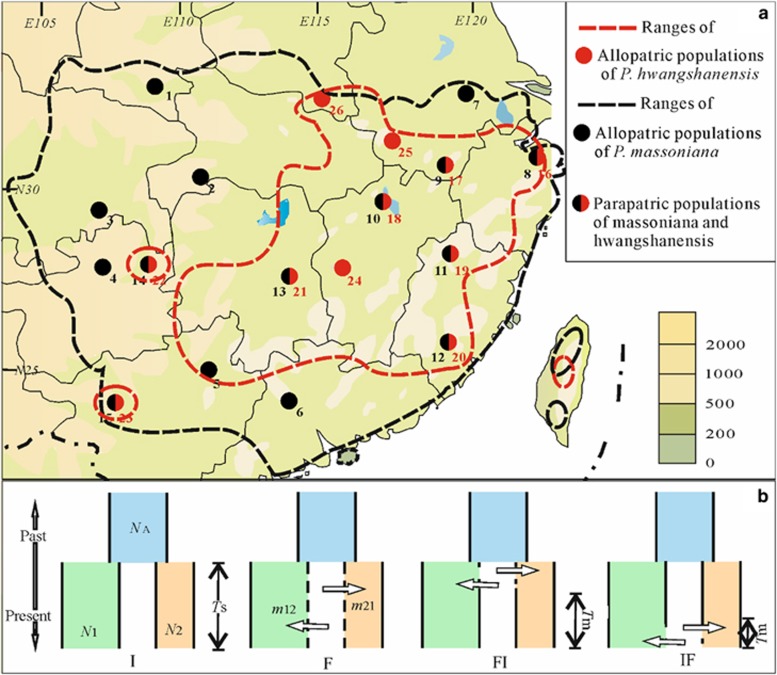
We used a range-wide sample of individuals from eight parapatric as well as seven and three allopatric populations of P. massoniana and P. hwangshanensis, respectively (Figure 1a). In order to reduce the probability of sampling hybrids in parapatric populations, we sampled trees at altitudes at least 100 m lower or higher than the margins of the contact zones, that is, at 600 and 1000 m, respectively. Basic passport information of the sampled populations can be found in Supplementary Table S1, and geographic information is presented in Figure 1a. Two individuals of Pinus koraiensis belonging to subgenus Strobus (Wang et al., 1999; Gernandt et al., 2005) from Northeast China were used as outgroup.

Figure 1.

Figure 1

Open in a new tab

(a) Ranges and sampled populations for P. massoniana and P. hwangshanensis. (b) Speciation models tested in the ABC analysis.

We amplified and Sanger sequenced a set of 37 loci distributed across the genome. Genomic DNA was extracted from haploid megagametophytes of germinated seeds using the QIAGEN DNeasy Plant Mini Kit (QIAGEN, Inc., Valencia, CA, USA). The primers were designed based on previous published sequences of closely related pines (Zhou et al., 2014). PCR and sequencing information have been described in detail in Zhou et al. (2014). We only used intron sequences in order to reduce the confounding effect of natural selection. Despite this, four outlier loci showed Tajima's D strongly deviating from our sample mean, suggesting a close genetic proximity with selected sites. As a precaution, we therefore excluded these loci from analyses. The remaining 33 loci were aligned using MUSCLE (Edgar, 2004) as implemented in Mega 5 (Tamura et al., 2011).

In order to compare genetic diversity and differentiation in parapatric and allopatric populations of both species, we computed the following statistics for each locus: nucleotide diversity (πs, Nei, 1987; θs, Watterson, 1975), the number of haplotypes (K), Tajima's D (Tajima, 1989), average number of nucleotide substitutions (Dxy, Nei and Kumar, 2000), average number of net nucleotide substitutions (Da, Nei and Kumar, 2000), differentiation among populations within species (FST) and differentiation between the two species (FCT). All the summary statistics (Supplementary Table S2) were computed using DnaSP v 5.10 (Librado and Rozas, 2009).

Bayesian admixture analysis

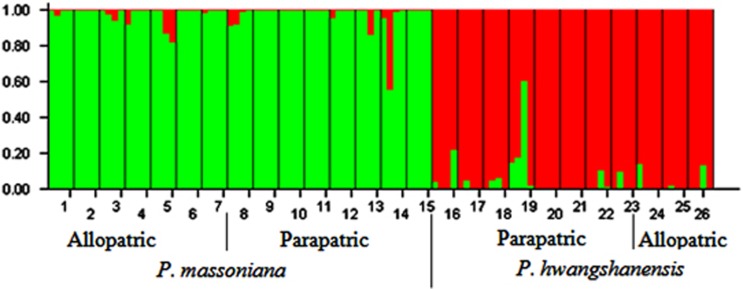
To examine genetic structure in each species and to compare genetic admixture between parapatric and allopatric groups, we used the Bayesian clustering approach using the software STRUCTURE v.2.3.3 (Hubisz et al., 2009). We ran 6 replicates for each value of K from 1 to 8 (100 000 burn-in cycles followed by 1 000 000 cycles of data collection, admixture allowed) and identified the best K for our data set according to the statistic ΔK (Evanno et al., 2005). Clustering analyses were first conducted for each species to examine intraspecific population structure. As within-species population structure was weak (Figure 2), we merged populations into allopatric and parapatric groups for each species to compare levels of admixture at different biogeographic settings.

Figure 2.

Figure 2

Open in a new tab

Population structure and admixture in parapatric and allopatric populations of the two species (STRUCTURE results).

Approximate Bayesian computation

ABC allows inference on complex models by using data simulated under a model to replace its intractable likelihood function (Csilléry et al., 2010).

ABC data set

In order to reproduce the structure of the observed data set closely during simulations, we used msnsam, a modified version of the program ms, allowing different sample sizes across loci (Hudson, 2002; Ross-Ibarra et al., 2008). Each simulated data set consisted of 33 loci with 48–60 and 40–44 individuals for P. massoniana and P. hwangshanensis, respectively. As ms uses an infinite site model and only simulates ancestral-derived states, we removed all positions with indels, missing data and triallelic single-nucleotide polymorphisms before computing statistics.

Model description

We inferred the best speciation scenario among four models (Figure 1b), all derived from the ‘classical' IM model (Nielsen and Wakeley, 2001). In these models, an ancestral population of size Na split at time Ts in the past to form two populations of size N1 (P. massoniana) and N2 (P. hwangshanensis). These models are mainly characterized by the following features: in model I (for Isolation, Figure 1b), there is no gene flow between species; in model F (for gene Flow, Figure 1b), there is continuous gene flow (potentially at asymmetrical rates m12 and m21); in model FI, gene flow ceases at time Tm; and in model IF, gene flow starts at time Tm (Figure 1b).

Priors on demographic parameters

All demographic parameters had uniform prior distributions and some were scaled by a factor N0=100 000 for convenience. Prior ranges were defined by trial and error to fully cover the posterior distribution ranges of each parameter for each model, thereby allowing us to properly estimate model posterior probabilities and parameter posterior distributions. Prior distributions of population parameters N1/N0, N2/N0 and NA/N0 ranged over 0.001–6. Prior distributions of migration parameters 4N0m12 and 4N0m21 ranged over 0.0001–8 and those of time parameters Tm/Ts and Ts/4N0 over 0.0001–1 and 0.0001–20, respectively.

Priors on locus-specific parameters

In order to account for heterogeneity in local mutation and recombination rates (μ and r respectively), we computed per generation θi (4N0μili, where li is the locus length) and ρi (4N0rili) for each locus i using outgroup sequence information. We first estimated μi as μi=Di/2T, where Di is the mean of the DAs (net substitution rates per site, equation 12.67 in Nei and Kumar, 2000) between P. massoniana or P. hwangshanensis and the outgroup and T is the divergence time with the outgroup in generations (that is, 2.25–4.25 M generations assuming a generation time of 20 years; Willyard et al., 2007). Second, we estimated ri/μi by calculating the average of γi/πi across species where γi is an estimator of ρi (Hey and Wakeley, 1997). Because the divergence time T is a range estimate rather than a point estimate, we obtained two estimates of μi and ri corresponding to bounding values of T. In order to account for this uncertainty, we used log-normal distributions as hyperpriors for each θi and ρi. For any θi or ρi distribution, the log mean and log s.d. were set equal to the mean and variance computed from the corresponding two estimates of μi or ri. Although simple, this approach is conservative to estimate θi and ρi uncertainties. For loci with no outgroup sequences available, we used the mean and s.d. of μ and r across loci instead. Computation of population genetics estimators were made using SITES (Hey and Wakeley, 1997; https://bio.cst.temple.edu/~hey/software/software.htm#SITES).

Summary statistics for ABC analysis

We used the means and s.d. values across loci of the following statistics: per population π and Tajima's D, the number of sites with fixed derived alleles in one population yet polymorphic in the other (sxjfi and sxifj, where i and j refer to P. massoniana and P. hwangshanensis, respectively), the number of sites with a derived allele fixed in one population and the ancestral allele fixed in the other (sfi and sfj) and the number of sites with a shared derived allele (ss), FST, DA and DXY (Nei and Kumar, 2000, equations 12.66 and 12.67). Although this set of 24 summary statistics is probably not optimal, it is only slightly different from the one Duvaux et al. (2011) have shown to be informative enough to distinguish between speciation models. We therefore chose not to implement recent methods optimizing the choice of summary statistics (Aeschbacher et al., 2012; Fearnhead and Prangle, 2012) in order to keep the same pipeline during the whole study. Summary statistics were computed using a modified version of the program used in Roux et al. (2013) (http://www.abcgwh.sitew.ch).

Model selections and parameter estimations

We used tools from the ‘abc' R package (Csilléry et al., 2012; cran.r-project.org/web/packages/abc/vignettes/abcvignette.pdf). We first determined the best model with the function ‘postpr'. We set the number of units in the hidden layer to 9, and loaded 2.5 million simulations per model. We retained the best 5000 simulations during the rejection step and fitted a neural network regression on them (100 neural networks). The false positive rate for model selection was estimated by using 500 pseudo-observed data sets from the second best model and by performing model choice using each pseudo-observed data set in turn in place of the real data set. The false discovery rate is thus the proportion of times we observe a posterior probability equal or superior to the real posterior probability of the best model. To do so, we used a modified version of the function ‘cv4postpr' that uses as pseudo-observed data sets simulations retained by the rejection step only (that is, not drawn from the whole parameter space as in the original function). We used the function ‘abc' with the best 5000 simulations to estimate the posterior distributions of the model parameters. Statistics were log transformed for the regression step and simulations with parameter values outside the prior ranges were removed before estimation of the posterior distributions (Duvaux et al., 2011).

Goodness of fit (GoF) of the best model

To assess the GoF of the best model, we used posterior predictive simulations (Gelman, 2003). We ran 10 000 simulations for the 33 loci using parameter values sampled from the joint posterior distribution and computed the resulting summary statistics. We used two sets of statistics for the GoF: those used to perform the ABC analysis and, in order to avoid overestimation of the fit, a set of new statistics. 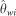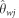The second set was made of 10 statistics including mean and variance across loci for S the expected number of segregating sites across both species, an estimator of θw for each species (Inline graphic and Inline graphic) and the number of sites polymorphic in one population yet fixed for the ancestral allele in the other (sxi and sxj). For both data sets, an initial check of the fit was obtained by performing principal component analysis on a subset of 2000 posterior predictive simulations along with 2000 prior (original) simulations and the observed data set. Finally, using posterior predictive distributions, we computed a two-sided P-value for each statistic (that is, two times the probability of obtaining the observed statistic or a more extreme value under the estimated model).

The full ms command lines for model simulations and other R code developed (R Core Team, 2013) for the ABC analysis are available in Dryad.

Species distribution modeling

Along with ABC inferences of species demography, we modeled the dynamic changes in species distributions during the Pleistocene climatic oscillations (for example, the Last Glacial Maximum (LGM; ~21 000 years before present) and the Last Inter-Glacial (LIG; ~120 000–140 000 years before present)). The knowledge of current species geographical distribution along with series of historical climate data allow ecological niche modeling that can also be used to track down the distribution changes of closely related species that can potentially be used to indicate the possibility of gene flow during speciation (Elith et al., 2011). We used geographical information system-based methods with layers of historical and current environmental variables under the maximum entropy model implemented in the program MaxEnt 3.3.3k (Phillips et al., 2006; Phillips and Dudík, 2008). GPS data from 123 and 109 localities (our sampling sites and museum records, Supplementary Table S1) were used to generate species distribution models for P. massoniana and P. hwangshanensis, respectively. We used 19 environmental variables (Supplementary Table S4) from the WorldClim database (Hijmans et al., 2005) with spatial resolution of 2.5′ (arc-minutes) and 30′ as environment layers. The methods assume that the probability of occurrence of a species has a uniform probability distribution considering present distributional data (that is, maximum entropy; Phillips et al., 2006; Phillips and Dudík, 2008). Assuming niche conservation over time (Wiens and Graham, 2005), we applied this model to LGM and LIG climatic layers to predict historical species distributions. Both the CCSM (community climate system model) (Collins et al., 2006) and MIROC (model for interdisciplinary research on climate) (Hasumi and Emori, 2004) were used to predict species distributions during the LGM. We generated 10 jackknife replicates with deletion of 20% of species occurrence localities for each analysis to account for error in the predictive modeling. Replicate was run for 500 interactions with a convergence threshold 10−5. We configured the machine-learning algorithm to use 75% of species records for training and 25% for testing the model. The program DIVA-GIS v7.5 (Hijmans et al., 2005) was used to create the graphics of species distributional ranges based on raster cells from original species distribution modeling with a logistic probability of presence >0.1.

To measure the levels of climate niche overlap between P. massoniana and P. hwangshanensis, we calculated the niche overlap statistic Schoener's D (Schoener, 1968) for the two species using the program ENMTools 1.3 (Warren et al., 2010). We also computed the overlap between species ranges at LGM and present with a threshold 0.5 in the ENMTools.

Results

Comparisons of genetic diversity and differentiation between parapatric and allopatric populations

In total, we aligned 11 588 bp noncoding nuclear sequences. Summary statistics on genetic diversity and divergence at each locus are listed in Supplementary Table S2. As interspecific gene flow should bring foreign genetic diversity and reduce genetic differentiation, we expected to observe higher levels of genetic diversity and lower differentiation in parapatric populations than in allopatric populations. Genetic diversity was found to be similar in allopatric and parapatric populations of both species (θallo=0.0053±0.0044, θpara=0.0056±0.0050 for P. massoniana and θallo=0.0083±0.0064, θpara=0.0090±0.0061 for P. hwangshanensis). Although 24 out of the 33 examined loci had higher FCT values in allopatric than parapatric populations (Supplementary Table S1), the average interspecific differentiation was not significantly different between allopatric and parapatric populations (0.41±0.26 and 0.37±0.26, respectively; Supplementary Table S2).

Genetic structure and admixture

STRUCTURE (Hubisz et al., 2009) analyses showed that our data were best described by K=2 genetic clusters. The inferred ancestry of each of the 104 pine samples was calculated and reported as the fraction assigned to each of the two clusters (Figure 2). We observed that each species was made up of one specific cluster with some individuals showing admixed patterns. These individuals were slightly more frequent in parapatric groups (2.9% and 4.9% for P. massoniana and P. hwangshanensis, respectively) than in allopatric groups (2.0 and 2.6% for P. massoniana and P. hwangshanensis, respectively; Figure 2).

Demographic histories and speciation models

In order to infer the speciation history of the two species, we performed an ABC analysis (Beaumont et al., 2002; Csilléry et al., 2010) on the set of 33 noncoding loci. Among our four speciation scenarios, those that did not incorporate any current gene exchange, namely scenarios I and FI, had posterior probability equal to zero, consistent with the present distribution of the two species (see Table 1). Furthermore, the secondary contact scenario was the most compatible with observed data (posterior probability=0.79). The false discovery rate, computed by including the F and IF models only, was very low (0.015), meaning that the model selection was robust to our choice of statistics (Csilléry et al., 2010). The GoF further demonstrates the relatively good ability of the IF scenario to generate data close to the observed data, highlighting its overall appropriateness to model the speciation history of our two species. Apart from the second axis of the first principal component analysis (statistics of the ABC analysis, Supplementary Figure S1), the observed data always lie in regions of the principal component analysis showing a reasonable density of prior and posterior predictive simulations (Supplementary Figures S1 and S2). The P-values of most summary statistics, including those not used for the ABC, were usually far above 0.05 (Supplementary Figure S3 and Supplementary Table S2). Where not, the posterior predictive simulations show better P-values than the prior simulations (for example, FST). The only aspect of the data poorly predicted by our model was the variation of genetic diversity among loci that was overestimated in the simulations (see θi_std, πi_std and DA_std in Supplementary Figure S3 and Supplementary Table S3, and the Discussion section).

Table 1. Results of ABC model selection.

Model I F FI IF
PP 0 0.2066 0.0003 0.7932
Open in a new tab

Abbreviations: ABC, approximate Bayesian computation; F, there is continuous gene flow; FI, gene flow ceases at time Tm; I, isolation model; IF, gene flow starts at time Tm; PP, posterior probability.

One striking result of the IF scenario was the length of the isolation period between the two species, estimated to have lasted 90% of the divergence time (with Ts=591 605 and Tm=45 984 generations (11.83 and 0.92 Mya, respectively), Table 2 and Supplementary Figure S4 modal values). The effective population size of P. hwangshanensis (N2) was estimated to be ∼3 times larger than that of P. massoniana (N1) (253 000 (167 000–351 044) and 80 000 (48 712–143 850) respectively, Table 2) and this difference was significant (P=0.003 estimated from the posterior distribution of the difference), in line with higher genetic diversity found in P. hwangshanensis. However, this did not seem to have a strong impact on the direction of migration as there was no significant gene flow asymmetry between species (2N1m12=1.05, 2N2m21=1.44, P=0.32, Table 2).

Table 2. Parameters estimates and 90% higher probability density (HPD) intervals under the IF (secondary contact) models, with times in generations (generation of 20 years).

Parameter Mode Median HPD90low HPD90High
N1 79 737 86 639 48 712 143 850
N2 253 189 253 281 167 302 351 044
Na 352 588 393 784 69 280 801 875
m12 4.31E−06 5.92E−06 1.65E−06 1.53E−05
2N1m12 0.871 1.008 0.367 2.26
m21 1.80E−06 2.95E−06 6.26E−07 9.76E−06
2N2m21 1.015 1.452 0.34 4.339
Tm 45 985 79 159 6630 369 906
Ts 591 605 1 033 626 202 235 2 315 909
(Ts−Tm)/Ts 0.94 0.91 0.76 0.98
Open in a new tab

Ni and 2Nimij parameters are expressed as number of individuals and mij are migration rates. Population 1 and 2 refers to P. massoniana and P. hwangshanensis, respectively. Abbreviation: IF, gene flow starts at time Tm.

Species distribution change

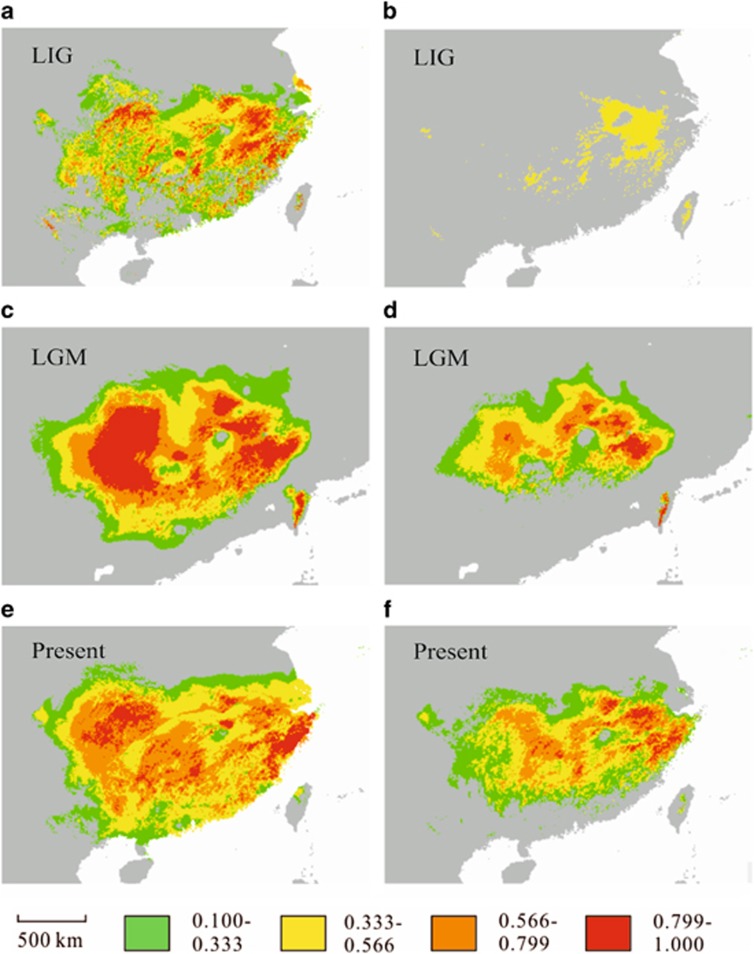
In order to track historical distribution changes of both species, we modeled the potential distribution for the LIG, the LGM and present (Figure 3). The accuracy of species distribution modeling was relatively high for both species (area under the curve=0.972 and s.d.=0.022 for P. massoniana; area under the curve=0.952 and s.d.=0.039 for P. hwangshanensis). The simulated distributions (Figures 3e and f) based on present climate data were mostly congruent with current ranges (Figure 1) of the two species. The climate variables that contributed the most percentage in predictions of species distributions were the precipitation of warmest quarter (56%) and the minimum temperature of coldest month (38%) for P. massoniana and P. hwangshanensis, respectively.

Figure 3.

Figure 3

Open in a new tab

Species distribution modeling for P. massoniana (a, c and e) and P. hwangshanensis (b, d and f) from the last inter-glacial to present. The different colors represent the probabilities of occurrence of the species.

Paleodistribution models suggested that P. massioniana had a nearly constant distributional range but P. hwangshanensis experienced a gradual expansion during the Pleistocene climatic oscillations (Figure 3). We compared the modeled distributions at the LGM and the present using ENMTools with a threshold 0.5. The two species showed moderate reduction of ranges sizes at LGM (0.81 and 0.79 for P. massoniana and P. hwangshanensis respectively). The two closely related species showed overall overlapping distributions since the LGM (21 Kya) (Figures 3c and d). The current range overlap (0.69, threshold 0.5) between the two species was similar with the overlap at the LGM (0.46, threshold 0.5).

Discussion

We investigated two alternative hypotheses to explain the extent of shared genetic diversity between two closely related pine species with overlapping distributions, namely (1) retention of ancestral polymorphisms because of ILS and (2) introgression through secondary contact. By contrasting genetic variation of allopatric and parapatric populations, we observed that patterns of between-species genetic differentiation and admixed ancestries, although not significant, were more compatible with the introgression hypothesis. Comparison of speciation scenarios using ABC also favored the secondary contact hypothesis (Figure 1b). Species distribution modeling supported a gradual expansion of P. hwangshanensis during the Pleistocene climatic oscillations leading to the current distribution overlap with P. massoniana. In contrast, results of a previous study showed that mitotypes were commonly shared and randomly distributed across allopatric and parapatric populations (Zhou et al., 2010). We discuss how these apparently contradictory results can be synthesized. We argue that the discordant information observed from the chloroplast DNA (cpDNA), mitochondrial DNA (mtDNA) and nuclear DNA (nuDNA) genomes actually reflects the differential dynamics in conifers of their main dispersal vectors, that is, seeds or pollen.

Successes and limitations of the ABC approach

As shown by the GoF analysis, the secondary contact (IF) model simulates data reasonably well, although there is still room for improvement. First, the results of the ecological niche modeling suggest that incorporating an exponential expansion for P. hwangshanensis could have improved the model fit. However, we do not expect such improvements to change our main result, namely the secondary contact scenario being largely favored. Indeed, the absence of real expansions from models is expected to have little effect on gene flow estimations (see, for example, table 6 in Strasburg and Rieseberg, 2010). The poorest predicted aspect of the data is the variance of diversity and the distribution of fixed alleles among loci that was over- and under-estimated by the posterior predictive simulations, respectively (for example, θi_std, πi_std and DA_std, sfX in Supplementary Figure S3, where std stands for s.d.). A supplementary analysis based on the IF model (not shown) indicated that the genetic variance among loci within a population/species is positively correlated with the effective population size Ne, meaning that if Ne was overestimated by the ABC analysis, so was the variance in the posterior predictive simulations. A well-known cause of Ne overestimation is the exclusion of population structure from models where some actually does exist in reality (Chikhi et al., 2010; Strasburg and Rieseberg, 2010). Including structure into models of speciation with gene flow is not trivial, however, as it is difficult to implement and, most importantly, increase the ‘curse of dimensionality' (Sunnåker et al., 2013). Because our data showed only moderate within-species structure (Supplementary Figure S2), we decided to include none in our models. As another possible explanation, Roux et al. (2013) showed that modeling the heterogeneity of migration rates across loci considerably improves the fit of speciation models to the data in the context of ancient divergence. Because the divergence history of our pine species appears ancient, it seems likely that modeling the heterogeneity of gene flow across loci would improve the inference of the parameter posterior distributions (for example, by inferring smaller effective population sizes) and thus the quality of posterior predictive simulation (especially for the sfX statistics). It is important to note though that properly fitting the hyperparameters of the β-distribution used to model heterogeneity of gene flow requires a huge amount of data (for example, Roux et al., 2013 used 852 loci for a total alignment length of 270 kb) that are not yet available for these two pine species. We therefore restrain ourselves to investigate basic but essential models of divergence. Finally, although 33 loci may appear to be a very small sample for ABC analyses, our false discovery rate analysis showed that this number of loci was sufficient to distinguish among models of speciation with gene flow.

Both ILS and secondary contact contributed to current shared genetic diversity between species

Shared polymorphisms across closely related species might play very important roles in processes of adaptation and speciation. They can be generated in various ways, including hybridization (Rieseberg, 2009; Abbott et al., 2013), adaptive introgression (Song et al., 2011; Jones et al., 2012; Pardo-Diaz et al., 2012; Staubach et al., 2012; Hedrick, 2013; Huerta-Sánchez et al., 2014), balancing selection favoring specific ancestral alleles (Leffer et al., 2013) and incomplete lineage sorting (Hobolth et al., 2011). In this study, using a pair of closely related parapatric pine species, we assessed the importance of ILS and secondary introgression in explaining shared polymorphisms. We estimated the species divergence time for nuclear loci to be 2.62 Ne generations (Table 2) corresponding to an early stage of divergence. As the divergence date is much lower than 9 Ne (Hudson and Coyne, 2002), we expect that lineage sorting should be limited, meaning that the two species still share much of their ancestral polymorphism.

Although ILS cannot be ignored in our case, climate oscillations strongly influence species distributions and thus the possibility of secondary contacts (Hewitt, 1996, 2000; Taberlet and Cheddadi, 2002). If the duration of an allopatric episode is not long enough to build complete reproductive isolation between two incipient species, secondary contacts may promote interspecific gene flow resulting in shared genetic polymorphism (Melo-Ferreira et al., 2005; Rieseberg et al., 2007). For these two pine species, we showed that our results were more compatible with a secondary introgression scenario rather than with a strict isolation model. Our STRUCTURE analysis suggested the presence of admixture in parapatric populations and the ABC analysis showed that this may be due to an ancient secondary contact dating back to 920 Kya (Table 2). This value is unlikely to be strongly inflated as the modal estimation of the divergence time (~12 Mya) falls within the range of a conservative estimation based on observed Ks (9.17–17.33 Mya—calibrated using the divergence time between Pinus and Strobus and 20 years per generation; Willyard et al., 2007). Accordingly, our ecological niche modeling suggested that the two species probably had overlapping distribution during the LIG (~140 KYA; Figure 3). Most importantly, it also showed that the range of P. hwangshanensis was more sensitive to climatic oscillations (Figure 3). Together, the ABC and niche modeling therefore suggest that the species demographic history has been complex and probably involves multiple range contractions and expansions leading to successive periods of gene flow that were initiated before the LIG. The possibility of current and past secondary gene flow is also supported by recent studies showing, along elevation gradients, that the two species still hybridize at a low rate in intermediate altitude contact zones (Luo and Zou, 2001; Zhang et al., 2014). This low introgression rate is more likely to be associated with postzygotic rather than prezygotic isolation. First, the long period of initial isolation (~550 000 generations) should have permitted fixation, through selection or drift, of many new mutations in both species and therefore generation of Bateson–Dobzhansky–Muller incompatibilities before any secondary contact (Orr and Turelli, 2001). Second, field observations suggest that postzygotic barriers may be more prevalent than prezygotic ones. Indeed, seeds from hybrid zones have been shown to have lower germination rate than other seeds, suggesting hybrids may carry Bateson–Dobzhansky–Muller incompatibilities (Li et al., 2010b). In parallel, prezygotic isolation appears relatively weak as the two species still share a synchronous flowering period in April–May (Fu et al., 1999).

The differential evolutionary dynamics of mtDNA, cpDNA and nuDNA reveal different aspect of conifer histories

In a previous study, we investigated cytoplasmic genetic differentiation between the two pine species and found that chlorotypes were highly species specific, whereas mitotypes were extensively shared and were randomly distributed among parapatric and allopatric populations. The cause of shared mtDNA variation was thought to be the retention of ancestral polymorphism rather than recurrent interspecific gene flow (Zhou et al., 2010). In contrast, we show here that the nuDNA diversity presents a different picture, that is, 0.6% of fixed and 38% of shared polymorphism sites between species, respectively (Supplementary Table S2). Such conflicting results from markers transmitted differentially through males and females have been observed in other species (Petit et al., 2005; Petit and Excoffier, 2009; Toews and Brelsford, 2012; Poznik et al., 2013). Most of them have been explained by sex-specific introgression patterns resulting from the interaction of two distinct effects (Petit and Excoffier, 2009; Toews and Brelsford, 2012). First, loci associated with different sex-specific dispersal vectors have different rates of gene flow, pollen being more efficient to disperse than seeds (Liepelt et al., 2002). Second, interspecific introgression is negatively correlated with intraspecific gene flow (Currat et al., 2008). Indeed, high level of intraspecific gene flow efficiently homogenizes within species gene pools. Coupled with partial reproductive isolation (that is, low interspecific introgression rates), this leads to reduce the probability of fixation of locally introgressed alleles. Inversely, low intraspecific gene flow increases the probability of local fixation of introgressed alleles (Rieseberg et al., 2006; Petit and Excoffier, 2009; Zhou et al., 2010). In conifers interestingly, mitochondrial, chloroplast and nuclear genomes are maternally, paternally or biparentally inherited through seeds, pollen or both, respectively (Wagner et al., 1987; Neale and Sederoff, 1988; Mogensen, 1996). In agreement with the above expectations, cpDNA, which is always efficiently dispersed by pollen, shows weak within-species structure and high between-species differentiation, whereas mtDNA, which is only dispersed locally by seeds, shows high intraspecific structure and more commonly shared polymorphisms between species (Du et al., 2009; Zhou et al., 2010; Jiang et al., 2011). Finally, we showed in this study that nuDNA, which is dispersed both by pollen and seeds, shows intermediate patterns.

The occurrence of gene flow is also strongly consistent with cpDNA and mtDNA having an expected effective population size four times smaller than nuDNA (Ne equal to N and 2N, respectively). Given our ABC results, this implies that the cpDNA and mtDNA lineages should have diverged ∼10.5 Ne generations ago and would have a very high probability to be reciprocally monophyletic currently. Only long-lasting or recurrent period gene flow seems to be able to explain why it is clearly not the case for mtDNA. In addition, it is worth noting that the nucleotide substitution rate varies greatly among seed plants genomes, with the mtDNA and nuDNA having the lowest and highest rates of nucleotide substitution, respectively (Wolfe et al., 1987). In practice, mitochondrial genetic variation has been used very efficiently to infer population structure and has been found to be shared between closely related coniferous species, whereas chloroplast markers have shown weak population structure but clear species boundaries (Petit et al., 2005; Du et al., 2009; Zhou et al., 2010). By reflecting evolutionary dynamics at different timescales and in different sexes, the three kinds of coniferous DNAs provide complementary views of the evolutionary processes.

Data archiving

The sequences of each locus reported in this study were deposited in GenBank under accession numbers: KJ921127–KJ921496.

Acknowledgments

We are grateful to Dr Remy Petit for useful discussions and to Professor Roger Butlin for comments on the manuscript. We thank Dr Bin Tian and Xingmin Tian for their help in collecting samples. This research was supported by grants from the National Key Project for Basic Research (2014CB954100 and 2012CB114504), the National Natural Science Foundation of China (30725004) and the ‘111' collaboration Program. Data analyses were partly conducted on computer clusters in the Finnish IT Center for Science (CSC) and on the Iceberg cluster at the University of Sheffield. YZ was supported by the International Postdoctoral Exchange Fellowship Program 2015 by the Office of China Postdoctoral Council, the funding from the Center for International Mobility (CIMO, Finland) and Biocenter Oulu (to OS). LD was supported by the Natural Environment Research Council (Grant Number NE/J021660/1) and the Leverhulme trust (Grant Number RPG-2013-198).

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

The authors declare no conflict of interest.

Supplementary Material

Supplementary Information
Click here for additional data file. (87.5KB, docx)
Supplementary Figure S1
Click here for additional data file. (460.3KB, pdf)
Supplementary Figure S2
Click here for additional data file. (310.3KB, pdf)
Supplementary Figure S3
Click here for additional data file. (293KB, pdf)
Supplementary Figure S4
Click here for additional data file. (40.1KB, pdf)

References

  1. Abbott R, Albach D, Ansell S, Arntzen JW, Baird SJ, Bierne N et al. (2013). Hybridization and speciation. J Evol Biol 26: 229–246. [DOI] [PubMed] [Google Scholar]
  2. Aeschbacher S, Beaumont MA, Futschik A. (2012). A novel approach for choosing summary statistics in approximate Bayesian computation. Genetics 192: 1027–1047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Barton NH, Hewitt GM. (1985). Analysis of hybrid zones. Annu Rev Ecol Evol Syst 16: 113–148. [Google Scholar]
  4. Beaumont MA, Zhang W, Balding DJ. (2002). Approximate Bayesian computation in population genetics. Genetics 162: 2025–2035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Butlin RK, Saura M, Charrier G, Jackson B, André C, Caballero A et al. (2014). Parallel evolution of local adaptation and reproductive isolation in the face of gene flow. Evolution 68: 935–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Charlesworth B, Bartolome C, Noel V. (2005). The detection of shared and ancestral polymorphisms. Genet Res 86: 149–157. [DOI] [PubMed] [Google Scholar]
  7. Chikhi L, Sousa VC, Luisi P, Goossens B, Beaumont MA. (2010). The confounding effects of population structure, genetic diversity and the sampling scheme on the detection and quantification of population size changes. Genetics 186: 983–995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Collins WD, Bitz CM, Blackmon ML, Bonan GB, Bretherton CS, Carton JA et al. (2006). The community climate system model version 3 (CCSM3). J Clim 19: 2122–2143. [Google Scholar]
  9. Coyne JA, Orr HA. (2004) Speciation. Sinauer & Associates: Sunderland, MA. [Google Scholar]
  10. Csilléry K, Blum MGB, Gaggiotti OE, François O. (2010). Approximate Bayesian computation (ABC) in practice. Trends Ecol Evol 25: 410–418. [DOI] [PubMed] [Google Scholar]
  11. Csilléry K, François O, Blum MGB. (2012). abc: an R package for approximate Bayesian computation. Methods Ecol Evol 3: 475–479. [Google Scholar]
  12. Currat M, Ruedi M, Petit RJ, Excoffier L. (2008). The hidden side of invasions, massive introgression by local genes. Evolution 62: 1908–1920. [DOI] [PubMed] [Google Scholar]
  13. Darwin C. (1859) On the Origin of Species by Natural Selection. Murray: London. [Google Scholar]
  14. Du FK, Petit RJ, Liu JQ. (2009). More introgression with less gene flow: chloroplast vs mitochondrial DNA in the Picea asperata complex in China, and comparison with other conifers. Mol Ecol 18: 1396–1407. [DOI] [PubMed] [Google Scholar]
  15. Duvaux L, Belkhir K, Boulesteix M, Boursot P. (2011). Isolation and gene flow: inferring the speciation history of European house mice. Mol Ecol 20: 5248–5264. [DOI] [PubMed] [Google Scholar]
  16. Edgar RC. (2004). MUSCLE, multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res 32: 1792–1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Elith J, Phillips SJ, Hastie T, Dudík M, Chee YE, Yates CJ. (2011). A statistical explanation of MaxEnt for ecologists. Divers Distrib 17: 43–57. [Google Scholar]
  18. Evanno G, Regnaut S, Goudet J. (2005). Detecting the number of clusters of individuals using the software STRUCTURE, a simulation study. Mol Ecol 14: 2611–2620. [DOI] [PubMed] [Google Scholar]
  19. Fearnhead P, Prangle D. (2012). Constructing summary statistics for approximate Bayesian computation: semi-automatic approximate Bayesian computation. J R Stat Soc Series B Stat Methodol 74: 419–474. [Google Scholar]
  20. Feder JL, Flaxman SM, Egan SP, Comeault AA, Nosil P. (2013). Geographic mode of speciation and genomic divergence. Annu Rev Ecol Evol Syst 44: 73–97. [Google Scholar]
  21. Fu LG, Li N, Elias TS, Mill RR (1999). Pinaceae. In: Wu Z, Raven PH (eds). Flora of China Vol. 4, Science Press: Beijing. pp 15–90. [Google Scholar]
  22. Gelman A. (2003). A Bayesian formulation of exploratory data analysis and goodness-of-fit testing. Int Stat Rev 71: 369–382. [Google Scholar]
  23. Gernandt DS, Lopez GG, Garcia SO, Liston A. (2005). Phylogeny and classification of Pinus. Taxon 54: 29–42. [Google Scholar]
  24. Hasumi H, Emori S. (2004) K-1 Coupled GCM (MIROC) Description. Center for Climate System Research, University of Tokyo, National Institute for Environmental Studies, Frontier Research Center for Global Change: Tokyo. [Google Scholar]
  25. Hedrick PW. (2013). Adaptive introgression in animals: examples and comparison to new mutation and standing variation as sources of adaptive variation. Mol Ecol 22: 4606–4618. [DOI] [PubMed] [Google Scholar]
  26. Hey J, Wakeley J. (1997). A coalescent estimator of the population recombination rate. Genetics 145: 833–846. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hey J. (2010). Isolation with migration models for more than two populations. Mol Biol Evol 27: 905–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hey J, Nielsen R. (2004). Multilocus methods for estimating population sizes, migration rates and divergence time, with applications to the divergence of Drosophila pseudoobscura and D. persimilis. Genetics 167: 747–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hewitt GM. (1996). Some genetic consequences of ice ages and their role in divergence and speciation. Biol J Linn Soc Lond 58: 247–276. [Google Scholar]
  30. Hewitt GM. (2000). The genetic legacy of the Quaternary ice ages. Nature 405: 907–913. [DOI] [PubMed] [Google Scholar]
  31. Hijmans RJ, Cameron SE, Parra JL, Jones PG, Jarvis A. (2005). Very high resolution interpolated climate surfaces for global land areas. Int J Climatol 25: 1965–1978. [Google Scholar]
  32. Hobolth A, Dutheil JY, Hawks J, Schierup MH, Mailund T. (2011). Incomplete lineage sorting patterns among human, chimpanzee, and orangutan suggest recent orangutan speciation and widespread selection. Genome Res 21: 349–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Hudson RR. (2002). Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinform 18: 337–338. [DOI] [PubMed] [Google Scholar]
  34. Hudson RR, Coyne J. (2002). Mathematical consequences of the genealogical species concept. Evolution 56: 1557–1565. [DOI] [PubMed] [Google Scholar]
  35. Hubisz MJ, Falush D, Stephens M, Pritchard JK. (2009). Inferring weak population structure with the assistance of sample group information. Mol Ecol Resour 9: 1322–1332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Huerta-Sánchez E, Jin X, Asan, Bianba Z, Peter BM, Vinckenbosch N et al. (2014). Altitude adaptation in Tibetans caused by introgression of Denisovan-like DNA. Nature 512: 194–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Jiang ZY, Peng YL, Hu XX, Zhou YF, Liu JQ. (2011). Cytoplasmic DNA variation in and genetic delimitation of Abies nephrolepis and Abies holophylla in northeastern China. Can J For Res 41: 1555–1561. [Google Scholar]
  38. Jones FC, Grabherr MG, Chan YF, Russell P, Mauceli E, Johnson J et al. (2012). The genomic basis of adaptive evolution in three spine sticklebacks. Nature 484: 55–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Kuhner MK. (2009). Coalescent genealogy samplers: windows into population history. Trends Ecol Evol 24: 86–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Leffer EM, Gao Z, Pfeifer S, Segurel L, Auton A, Venn O et al. (2013). Multiple instances of ancient balancing selection shared between humans and chimpanzees. Science 339: 1578–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Leslie AB, Beaulieu JM, Rai HS, Crane PR, Donoghue MJ, Mathews S. (2012). Hemisphere-scale differences in conifer evolutionary dynamics. Proc Natl Acad Sci USA 109: 6217–16221. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Levsen ND, Tiffin P, Olson MS. (2012). Pleistocene speciation in the genus Populus (Salicaceae). Syst Biol 61: 401–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Lexer C, Kremer A, Petit RJ. (2006). Shared alleles in sympatric oaks: recurrent gene flow is a more parsimonious explanation than ancestral polymorphism. Mol Ecol 15: 2007–2012. [DOI] [PubMed] [Google Scholar]
  44. Li Y, Stocks M, Hemmila S, Kallman T, Zhu H, Zhou Y et al. (2010. a). Demographic histories of four spruce (Picea species of the Qinghai-Tibetan Plateau and neighboring areas inferred from multiple nuclear loci. Mol Biol Evol 27: 1001–1014. [DOI] [PubMed] [Google Scholar]
  45. Li Z, Zou J, Mao K, Lin K, Li H, Liu J et al. (2012). Population genetic evidence for complex evolutionary histories of four high altitude juniper species in the Qinghai-Tibetan plateau. Evolution 66: 831–845. [DOI] [PubMed] [Google Scholar]
  46. Li SX, Chen Y, Gao HD, Yin TM. (2010. b). Potential chromosomal introgression barriers revealed by linkage analysis in a hybrid of Pinus massoniana and P. hwangshanensisBMC. Plant Biol 10: 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Li SX, Tang ZX, Zhang DF, Ye N, Xu CX, Ying TM. (2012). Genome-wide detection of genetic loci triggering uneven descending of gametes from a natural hybrid pine. Tree Genet Genomes 8: 1371–1377. [Google Scholar]
  48. Librado P, Rozas J. (2009). DnaSP v5, a software for comprehensive analysis of DNA polymorphism data. Bioinform 25: 1451–1452. [DOI] [PubMed] [Google Scholar]
  49. Liepelt S, Bialozyt R, Ziegenhagen B. (2002). Wind-dispersed pollen mediates post-glacial gene flow among refugia. Proc Natl Acad Sci USA 99: 14590–14594. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Luo SJ, Zou HY. (2001). Study on the introgressive hybridization between Pinus hwangshanensis and P. massoniana. Sci Silvae Sin 37: 118–122. [Google Scholar]
  51. Ma XF, Szmidt AE, Wang XR. (2006). Genetic structure and evolutionary history of a diploid hybrid pine Pinus densata inferred from the nucleotide variation at seven gene loci. Mol Biol Evol 23: 807–816. [DOI] [PubMed] [Google Scholar]
  52. Mao KS, Milne RI, Zhang LB, Peng Y, Liu J, Thomas P et al. (2012). Distribution of living Cupressaceae reflects the breakup of Pangea. Proc Natl Acad Sci USA 109: 7793–7798. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Mallet J. (2005). Hybridization as an invasion of the genome. Trends Ecol Evol 20: 229–237. [DOI] [PubMed] [Google Scholar]
  54. Mayr E. (1963) Animal Species and Evolution. Belknap: Cambridge, MA. [Google Scholar]
  55. Melo-Ferreira J, Boursot P, Suchentrunk F, Ferrand N, Alves PC. (2005). Invasion from the cold past: extensive introgression of mountain hare (Lepus timidus mitochondrial DNA into three other hare species in northern Iberia. Mol Ecol 14: 2459–2464. [DOI] [PubMed] [Google Scholar]
  56. Muir G, Schlötterer C. (2005). Evidence for shared ancestral polymorphism rather than recurrent gene flow at microsatellite loci differentiating two hybridizing oaks (Quercus spp.). Mol Ecol 14: 549–561. [DOI] [PubMed] [Google Scholar]
  57. Mogensen HL. (1996). The hows and whys of cytoplasmic inheritance in seed plants. Am J Bot 83: 383–404. [Google Scholar]
  58. Neale DB, Sederoff RR (1988). Inheritance and evolution of conifer organelle genomes. In: Hanover JW, Keathley DE (eds). Genetic Manipulation of Woody Plants. Plenum Press: New York, NY, USA. pp 251–264. [Google Scholar]
  59. Nei M. (1987) Molecular Evolutionary Genetics. Columbia University Press: New York. [Google Scholar]
  60. Nei M, Kumar S. (2000) Molecular Evolution and Phylogenetics. Oxford University Press: New York. [Google Scholar]
  61. Nielsen R, Wakeley J. (2001). Distinguishing migration from isolation. A Markov chain Monte Carlo approach. Genetics 158: 885–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Nosil P. (2008). Speciation with gene flow may be common. Mol Ecol 17: 2103–2106. [DOI] [PubMed] [Google Scholar]
  63. Orr AH, Turelli M. (2001). The evolution of postzygotic isolation: accumulating Dobzhansky-Muller incompatibilities. Evolution 55: 1085–1094. [DOI] [PubMed] [Google Scholar]
  64. Pardo-Diaz C, Salzar C, Baxter SW, Merot C, Figueiredo-Ready W, Joron M et al. (2012). Adaptive introgression across species boundaries in Heliconius butterflies. PLoS Genet 8: e1002752. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Petit RJ, Excoffier L. (2009). Gene flow and species delimitation. Trends Ecol Evol 24: 386–393. [DOI] [PubMed] [Google Scholar]
  66. Petit RJ, Duminil J, Fineschi S, Hampe A, Salvini D, Vendramin GG. (2005). Comparative organization of chloroplast, mitochondrial and nuclear diversity in plant populations. Mol Ecol 14: 689–701. [DOI] [PubMed] [Google Scholar]
  67. Phillips SJ, Anderson RP, Schapire RE. (2006). Maximum entropy modeling of species geographic distributions. Ecol Modell 190: 231–259. [Google Scholar]
  68. Phillips SJ, Dudík M. (2008). Modeling of species distributions with Maxent: new extensions and a comprehensive evaluation. Ecography 31: 161–175. [Google Scholar]
  69. Poznik GD, Henn BM, Yee MC, Sliwerska E, Euskirchen GM, Lin AA et al. (2013). Sequencing Y chromosomes resolves discrepancy in time to common ancestor of males versus females. Science 341: 562–565. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Qu YH, Zhang RY, Quan Q, Song G, Li SH, Lei F. (2012). Incomplete lineage sorting or secondary admixture: Disentangling historical divergence from recent gene flow in the vinous-throated parrotbill Paradoxornis webbianus. Mol Ecol 21: 6117–6133. [DOI] [PubMed] [Google Scholar]
  71. R Core Team. (2013) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria. Available at: http://www.R-project.org/. [Google Scholar]
  72. Ren GP, Abbott RJ, Zhou YF, Zhang LR, Peng YL, Liu JQ. (2012). Genetic divergence, range expansion and possible homoploid hybrid speciation among pine species in Northeast China. Heredity 108: 552–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Rieseberg LH, Whitton J, Gardner K. (1999). Hybrid zones and the genetic architecture of a barrier to gene flow between two sunflower species. Genetics 152: 713–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Rieseberg LH, Wood TE, Baack EJ. (2006). The nature of plant species. Nature 440: 524–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Rieseberg LH, Kim SC, Randell RA, Whitney KD, Gross BL, Lexer C et al. (2007). Hybridization and the colonization of novel habitats by annual sunflowers. Genetica 129: 149–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Rieseberg LH. (2009). Evolution: replacing genes and traits through hybridization. Curr Biol 19: R119–R122. [DOI] [PubMed] [Google Scholar]
  77. Roux C, Tsagkogeorga G, Bierne N, Galtier N. (2013). Crossing the species barrier: genomic hotspots of introgression between two highly divergent Ciona intestinalis species. Mol Biol Evol 30: 1574–1587. [DOI] [PubMed] [Google Scholar]
  78. Ross-Ibarra J, Wright SI, Foxe JP, Kawabe A, DeRose-Wilson L, Gos G et al. (2008). Patterns of polymorphism and demographic history in natural populations of Arabidopsis lyrata. PLoS One 3: e2411. [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Schoener TW. (1968). The Anolis lizards of Bimini: resource partitioning in a complex fauna. Ecology 49: 704–726. [Google Scholar]
  80. Sousa V, Hey J. (2013). Understanding the origin of species with genome-scale data: modeling gene flow. Nat Rev Genet 14: 404–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Song Y, Endeplos S, Klemann N, Richter D, Matuschka FR, Shih CH et al. (2011). Adaptive introgression of anticoagulant rodent poison resistance by hybridization between old world mice. Curr Biol 21: 1296–1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  82. Staubach F, Lorenc A, Messer PW, Tang K, Petrov DA, Tautz D. (2012). Genome patterns of selection and introgression of haplotypes in natural populations of the house mouse (Mus musculus. PLoS Genet 8: e1002891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  83. Strasburg JL, Rieseberg LH. (2010). How robust are ‘isolation with migration' analyses to violations of the IM model? A simulation study. Mol Biol Evol 27: 297–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
  84. Sun Y, Li L, Li L, Zou J, Liu J. (2015). Distributional dynamics and interspecific gene flow in Picea likiangensis and P. wilsonii triggered by climate change on the Qinghai-Tibet Plateau. J Biogeogr 42: 475–484. [Google Scholar]
  85. Sunnåker M, Busetto AG, Numminen E, Corander J, Foll M, Dessimoz C. (2013). Approximate Bayesian computation. PLoS Comput Biol 9: e1002803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  86. Tamura K, Peterson D, Peterson N, Stecher G, Nei M, Kumar S. (2011). MEGA5, molecular evolutionary genetics analysis using maximum likelihood, evolutionary distance, maximum parsimony methods. Mol Biol Evol 28: 2731–2739. [DOI] [PMC free article] [PubMed] [Google Scholar]
  87. Taberlet P, Cheddadi R. (2002). Quaternary refugia and persistence of biodiversity. Science 297: 2009–2010. [DOI] [PubMed] [Google Scholar]
  88. Tajima F. (1989). Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123: 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  89. Toews DPL, Brelsford A. (2012). The biogeography of mitochondrial and nuclear discordance in animals. Mol Ecol 21: 3907–3930. [DOI] [PubMed] [Google Scholar]
  90. Wakeley J, Hey J (1998). Testing speciation models with DNA sequence data. In: DeSalle R, Schierwater B (eds). Molecular Approaches to Ecology and Evolution. Birkhauser Verlag: Basel. pp 157–175. [Google Scholar]
  91. Wang J, Abbott RJ, Peng YL, Du FK, Liu JQ. (2011). Species delimitation and biogeography of two fir species (Abies in central China, cytoplasmic DNA variation. Heredity 107: 362–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  92. Wang XR, Tsumura Y, Yoshimaru H, Nagasaka K, Szmidt AE. (1999). Phylogenetic relationships of Eurasian pines (Pinus, Pinaceae) based on chloroplast rbcLmatKrpl20-rps18 spacer, and trnV intron sequences. Am J Bot 86: 1742–1753. [PubMed] [Google Scholar]
  93. Wagner DB, Furnier GR, Saghai-Maroof MA, Williams SM, Dancik BP, Allard RW. (1987). Chloroplast DNA polymorphisms in lodgepole and jack pines and their hybrids. Proc Natl Acad Sci USA 84: 2097–2100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  94. Wachowiak W, Palmé AE, Savolainen O. (2011). Speciation history of three closely related pines Pinus mugo (T.). P. uliginosa (N.) and P. sylvestris (L.). Mol Ecol 20: 1729–1743. [DOI] [PubMed] [Google Scholar]
  95. Warren DL, Glor RE, Turelli M. (2010). ENMTools: a toolbox for comparative studies of environmental niche models. Ecography 33: 607–611. [Google Scholar]
  96. Watterson GA. (1975). On the number of segregating sites in genetical models without recombination. Theor Popul Biol 7: 256–275. [DOI] [PubMed] [Google Scholar]
  97. Wiens JJ, Graham CH. (2005). Niche conservatism: integrating evolution, ecology, and conservation biology. Annu Rev Ecol Evol Syst 36: 519–539. [Google Scholar]
  98. Willyard A, Syring J, Gernandt DS, Liston A, Cronn R. (2007). Fossil calibration of molecular divergence infers a moderate mutation rate, recent radiations for Pinus. Mol Biol Evol 24: 90–101. [DOI] [PubMed] [Google Scholar]
  99. Wolfe KH, Li WH, Sharp PM. (1987). Rates of nucleotide substitution vary greatly among plant mitochondrial, chloroplast, and nuclear DNAs. Proc Natl Acad Sci USA 84: 9054–9058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  100. Won YJ, Hey J. (2005). Divergence population genetics of chimpanzees. Mol Biol Evol 22: 297–307. [DOI] [PubMed] [Google Scholar]
  101. Zhang D, Xia T, Yan M, Dai X, Xu J, Li S et al. (2014). Genetic introgression and species boundary of two geographically overlapping pine species revealed by molecular markers. PLoS One 9: e101106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  102. Zhou YF, Abbott RJ, Jiang ZY, Du FK, Milne RI, Liu JQ. (2010). Gene flow and species delimitation: a case study of two pine species with overlapping distributions in southeast china. Evolution 64: 2342–2352. [DOI] [PubMed] [Google Scholar]
  103. Zhou YF, Zhang LR, Liu JQ, Wu GL, Savolainen O. (2014). Climatic adaptation and ecological divergence between two closely related pine species in Southeast China. Mol Ecol 23: 3504–3522. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (87.5KB, docx)
Supplementary Figure S1
Click here for additional data file. (460.3KB, pdf)
Supplementary Figure S2
Click here for additional data file. (310.3KB, pdf)
Supplementary Figure S3
Click here for additional data file. (293KB, pdf)
Supplementary Figure S4
Click here for additional data file. (40.1KB, pdf)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES