Feature Fusion via Hierarchical Supervised Local CCA for Diagnosis of Autism Spectrum Disorder

Abstract

Early diagnosis of autism spectrum disorder (ASD) is critical for timely medical intervention, for improving patient quality of life, and for reducing the financial burden borne by the society. A key issue in neuroimaging-based ASD diagnosis is the identification of discriminating features and then fusing them to produce accurate diagnosis. In this paper, we propose a novel framework for fusing complementary and discriminating features from different imaging modalities. Specifically, we integrate the Fisher discriminant criterion and local correlation information into the canonical correlation analysis (CCA) framework, giving a new feature fusion method, called Supervised Local CCA (SL-CCA), which caters specifically to local and global multimodal features. To alleviate the neighborhood selection problem associated with SL-CCA, we further propose a hierarchical SL-CCA (HSL-CCA), by performing SL-CCA with the gradually varying neighborhood sizes. Extensive experiments on the multimodal ABIDE database show that the proposed method achieves superior performance. In addition, based on feature weight analysis, we found that only a few specific brain regions play active roles in ASD diagnosis. These brain regions include the putamen, precuneus, and orbitofrontal cortex, which are highly associated with human emotional modulation and memory formation. These finding are consistent with the behavioral phenotype of ASD.

Introduction

Autism spectrum disorder (ASD) is a prevalent and highly heterogeneous childhood neurodevelopmental disorder, which is characterized in varying degrees by impairment in social interaction, behavior, communication, and cognitive functions [1, 2]. According to the 2014 community report released by the Centers for Disease Control and Prevention¹, 1 in 68 American children was identified with ASD, an increase of 78% compared to the past decade, with boys outnumbering girls by a ratio of 5:1. Some children with ASD may suffer from depression or experience behavioral problems during adolescence, and usually require continual support as they get older, thus often resulting in immense suffering to the individuals and their families. So early diagnosis and medical intervention are tremendously important for improving the life quality of patients and their families, as well as for reducing the financial burden borne by the society.

Currently, the diagnosis of ASD relies mainly on a series of behavioral-based clinical tests that seek to quantify the severity of the disorder. However, a main drawback of these tests is that many behavioral phenotypes are associated with numerous other psychological and psychiatric disorders [3–5]. Additionally, ASD is in essence a complex disorder and is highly heterogeneous, affecting patients in different ways with mild to severe symptoms. Therefore, behavioral-based tests can be highly variable when used for diagnosis and prognosis.

In fact, some related studies have verified that ASD is highly associated with several neuroanatomical abnormalities [3, 6–8]. For example, structural magnetic resonance imaging (MRI) based neuroimaging studies show that abnormal structural changes exist in ASD patients compared to normal controls [2, 7]. A study found that cortical thickness was thinner in the left temporal and parietal regions in adolescents with ASD [9]. Another study reported a thicker cortex in the temporal and parietal lobes in younger subjects with autism [10]. Also, a plethora of functional MRI (fMRI) studies reveal that ASD is associated with functional connectivity changes. For example, some connections are weaker while others are stronger in individuals with ASD, compared to typically developing controls [11]. Therefore, combining biological information with behavioral examination could assist physicians with ASD diagnosis.

A significant amount of effort has been dedicated to investigating the underlying biological or neurological mechanisms associated with ASD so that biomarkers can be identified for early diagnosis or prognosis of ASD [11–15]. Especially, in recent years, different imaging modalities, including MRI [3], fMRI [16, 17], electrophysiology techniques [18], and diffusion-weighted MRI [19, 20], have been utilized for ASD diagnosis with relatively high accuracy. In fact, various imaging modalities usually afford complementary information for diagnosis. For example, MRI provides information on different types of tissues in the brain, while FDG-PET captures cerebral metabolic rate for glucose. Fusing information from these multiple modalities may yield better performance compared with any single modality, which has been verified in various studies [3, 21].

As an effective feature fusion technique, canonical correlation analysis (CCA) has been widely applied in many fields, including face recognition [22], multi-dimension signal processing [23], image pose estimation [24], and neurodegenerative disease identification [4, 25]. Mathematically, CCA aims to find a set of basis vector pairs that maximize the correlation between two different sample sets obtained from two different modalities of the same information source. However, CCA can only capture the linear correlation between sample pairs in a global manner and hence tends to under-fit the data in the complex nonlinear scenarios. Moreover, CCA, as an unsupervised method, does not take advantage of the label information, resulting in limited classification performance.

To address these limitations, many variants of CCA have been proposed in the past decades. Kernel CCA (K-CCA), a popular nonlinear extension of CCA, maps all the samples into a higher (even infinite) dimensional space (referred to as feature space) and then performs traditional CCA in the feature spaces based on the so-called “kernel trick” [24, 26]. Thus, a nonlinear problem in the original space is transformed to a simple linear counterpart in the feature space for discovering the complex correlation inherent in the data. Another example is locality-preserving CCA (LP-CCA), which decomposes the global problem into many locally linear ones and investigates correlations in small neighborhoods [27]. LP-CCA and K-CCA can reveal the nonlinear relationship between data, but both of them do not utilize supervised information, which is essential for improving classification. In order to tailor the extracted features for classification tasks, Peng et al. [28] proposed the locally discriminant CCA (LD-CCA) to simultaneously maximize local within-class correlations and also minimize local between-class correlations. Compared with K-CCA and LP-CCA, LD-CCA yields better classification performance due to the simultaneous consideration of local properties and class discrimination. However, LD-CCA can only capture local discrimination based on the local correlation between samples sets, but ignores the global discriminating information in data. Besides, it is generally challenging to determine an appropriate neighbor size in LD-CCA, just as in many locality-based methods.

To overcome these problems, in this paper we propose a novel feature fusion method, called hierarchical supervised local CCA (HSL-CCA), to capture the effective discriminating information from different modalities and to alleviate the difficulty of neighbor size selection. First, we develop a new supervised local CCA (SL-CCA) model by incorporating the Fisher discriminant criterion and LD-CCA into the CCA framework. SL-CCA takes into account not only nonlinear information like LD-CCA, but also global discriminant information given the Fisher criterion. Second, in order to reduce the influence of the neighbor size used to define a local neighborhood, we propose a hierarchical version of SL-CCA, where SL-CCA is performed using the gradually decreasing neighborhood sizes.

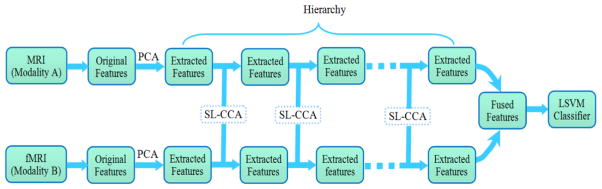
Fig. 1 shows the pipeline of the proposed classification framework. We first obtain the original features by preprocessing of two image modalities (i.e., MRI and fMRI), followed by PCA to remove the redundant information. Then, we hierarchically perform SL-CCA for fusing features from two modalities. Finally, the fused features are used to train a linear SVM (LSVM) classifier. The experimental results demonstrate that SL-CCA tends to capture more discriminating features. Note that this hierarchical scheme effectively reduces sensitivity to neighborhood size and also greatly improves diagnosis performance.

Fig. 1.

Overview of the proposed classification framework.

The rest of the paper is organized as follows. In the “Materials and Preprocessing” section, we describe the data acquisition and preprocessing pipeline. In the “Methods” section, we introduce SL-CCA and its hierarchical version, HSL-CCA. In the “Experiments” section, we demonstrate the effectiveness of the proposed method for ASD patient identification via comparison with the related methods, and then analyze the importance of different regions-of-interest (ROIs) for ASD diagnosis. Finally, we conclude this paper and discuss some possible future directions.

Materials and Preprocessing

Subjects

Data used in this study are obtained from an online public Autism Brain Imaging Data Exchange (ABIDE) database[29], which was created as a data repository for facilitating collaboration across laboratories to help accelerate scientific discovery in autism research. ABIDE database consists of various imaging modalities, such as structural magnetic resonance imaging (MRI), resting-state functional magnetic resonance imaging (fMRI), diffusion tensor imaging (DTI), and so on. In this paper, we use MRI and fMRI data from 54 ASD patients and 57 normal controls under 15 years of age, scanned at New York University (NYU) Langone Medical Center. Mean group ages, in years, were 10.8±2.2 for ASD patients and 11.3±2.3 for controls. The sex ratio (male: female) is 47:7 in ASD and 40:17 in controls. The details on data collection, exclusion criteria, and scan parameters are available on the ABIDE website².

Data acquisition and preprocessing

For MRI, we used the Freesurfer software suite (version 4.5.0)³ to automatically extract the regional morphological features. Skull stripping[30], cerebellum removal, and tissue segmentation [31] were performed for each image. The entire brain was parcellated into 94 ROIs by registering the Desikan-Killiany cortical atlas[32]. Similarly, the subcortical structures were parcellated into 37 ROIs by using the subcortical structural atlas[33]. Then, we computed the regional mean cortical thickness, the cortical GM and WM volumes, and the subcortical structural volumes in the corresponding ROIs as the MRI features.

For fMRI, slice timing correction, motion correction, and global signal regression were performed using the Data Processing Assistant for fMRI (DPARSF) software [34]. We then parcellated the brain space into 116 ROIs by warping the automatic anatomical labeling (AAL) atlas [35] to each image using a deformable registration method, called HAMMER [36]. For each ROI, we computed its mean time series and performed the band-pass filtering (0.01–0.08Hz), for trading-off between avoiding the physiological noise [37], the measurement error [38], and the magnetic field drifts of the scanner [39]. Finally, we computed Pearson correlation between the mean time series and obtained a 116×116 correlation coefficient matrix for each subject as the fMRI features.

Methods

In this section, we briefly introduce two related methods, CCA and LD-CCA. Then, we describe our proposed method SL-CCA and its extension HSL-CCA.

Canonical correlation analysis (CCA)

Assume ${\{x_i\}}_{i=1}^n\subset R^p$ and ${\{y_i\}}_{i=1}^n\subset R^q$ are two mean-normalized sample sets from two different modalities of the same subject, p and q denote the dimensions of the corresponding sample space, and n denotes sample size. The aim of CCA is to find two projection directions, w_x ∈ R^p and w_y ∈ R^q, that maximize the correlation between $w_x^{T}X$ and $w_y^{T}Y$, where X = [x₁, x₂, ···, x_n] and Y = [y₁, y₂, ···, y_n] denote the sample matrices, respectively. Formally, in CCA we solve

$$\mathrm{\rho }=\underset{w_x,w_y}{max}\frac{w_x^T{C}_{xy}{w}_y}{\sqrt{(w_x^T{C}_{xx}{w}_x)(w_y^T{C}_{yy}{w}_y)}}$$ (1)

where C_xy = XY^T denotes the between-set covariance matrix, and C_xx = XX^T and C_yy = YY^T denote two within-set covariance matrices.

When the within-set covariance matrices C_xx and C_yy are non-singular, the solution of CCA can be obtained by computing the following generalized eigen-problem.

$$\left(\begin{array}{cc}{C}_{xy}{C}_{yy}^{-1}{C}_{yx}& 0\\ 0& C_{yx}{C}_{xx}^{-1}{C}_{xy}\end{array}\right)\left(\begin{array}{c}{w}_x\\ w_y\end{array}\right)=\mathrm{\lambda }\left(\begin{array}{c}{w}_x\\ w_y\end{array}\right)$$ (2)

Let W_x = [w_x1, w_x2, …, w_xd] and W_y = [w_y1, w_y2, …, w_yd] denote two projection direction matrices, where the vector pairs ${(w_{xi},w_{yi})}_{i=1}^d$ correspond to the first d largest generalized eigenvalues in Eq. (2). For any sample pair (x, y) from the two modalities, we can obtain the fused feature as follows:

$$z=\left(\begin{array}{c}{W}_x^{T}x\\ W_y^{T}y\end{array}\right)$$ (3)

More details about the derivation and solution of CCA can be found in [22, 40].

In practice, we often need to deal with the small sample problems where the dimensionality of features is larger than the sample size, as in ASD diagnosis. In this case, the within-set covariance matrix C_xx or C_yy is singular. We therefore need to apply PCA to reduce the dimension of the original samples and then perform CCA in the PCA-transformed space [22]. It can be theoretically verified that the loss of discriminating information is minimal if the transformed space preserves sufficient information, as given by a high eigenvalue ratio. This strategy is also suitable for some variants of CCA, including SL-CCA and HSL-CCA, which will be introduced below.

Although CCA has been widely used as an important feature fusion technique, it uses only the linear correlation between two different modalities and does not use data label information, which result in limited recognition performance of CCA.

Locally discriminant CCA (LD-CCA)

In order to improve the performance of CCA in classification tasks, LD-CCA incorporates local discriminative analysis into CCA. Specifically, the between-set covariance matrix C_xy in Eq. (1) is replaced by C̃_xy which is defined as the sum of local within-class covariance matrices penalized by the sum of local between-class covariance matrices. LD-CCA aims to find two sets of projection directions w_x ∈ R^p and w_y ∈ R^q that maximizes the correlation of within-class k-NN samples and minimizes the correlation of between-class k-NN samples. Mathematically, the objective function can be written as follows:

$$\mathrm{\rho }=\underset{w_x,w_y}{max}\frac{w_x^T{\stackrel{\sim }{C}}_{xy}{w}_y}{\sqrt{(w_x^T{C}_{xx}{w}_x)(w_y^T{C}_{yy}{w}_y)}}$$ (4)

where C̃_xy = C_w − ηC_b. C_w denotes the sum of local within-class covariance matrices, while C_b denotes the sum of local between-class covariance matrices, and η is a balancing factor between C_w and C_b. C_w and C_b are defined as follows:

$$\{\begin{array}{l}{C}_w=\sum _{i=1}^n\sum _{x_k\in N^I(x_i),y_k\in N^I(y_i)}{x}_i{y}_k^T+x_k{y}_i^T\hfill \\ C_b=\sum _{i=1}^n\sum _{x_k\in N^E(x_i),y_k\in N^E(y_i)}{x}_i{y}_k^T+x_k{y}_i^T\hfill \end{array}$$ (5)

where N^I(x_i) and N^E(x_i) denote the within-class and between-class k nearest neighborhoods of x_i, respectively. For example, N^I(x_i) is the set of samples which are the most similar to x_i within the same class, while N^E(x_i) is the set of samples which are the most similar to x_i in a different class. N^I(y_i) and N^E(y_i) are similarly defined.

Compared with CCA, LD-CCA affords two advantages: (1) it can deal with the nonlinearity due to locality modeling; (2) it encodes class information. Nevertheless, LD-CCA has also some limitations: (1) it only utilizes the local correlation to indirectly reflect the local class difference, but ignores the global discriminating information; (2) its performance is influenced by the neighbor size. However, it is still a challenging problem to determine an appropriate neighbor size in most locality-based methods [27, 28].

Hierarchical supervised local CCA (HSL-CCA)

In this section, we present a hierarchical variant of CCA, called HSL-CCA, to improve LD-CCA in two aspects. First, we propose a new feature fusion method, called supervised local CCA (SL-CCA), by incorporating the local correlation information and the Fisher discrimination information into the CCA framework. Its model can be formalized as follows:

$$\rho =\underset{w_x,w_y}{max}\frac{w_x^T{\stackrel{\sim }{C}}_{xy}{w}_y+w_x^T{S}_b^x{w}_x+w_y^T{S}_b^y{w}_y}{\sqrt{(w_x^T{C}_{xx}{w}_x)(w_y^T{C}_{yy}{w}_y)}}$$ (6)

where $S_b^x$ and $S_b^y$ respectively denote the between-class scatter matrices of the sample sets X and Y, which are defined as in [41].

$$S_b^x={\mathit{XUX}}^T,S_b^y={\mathit{YUY}}^T$$ (7)

where U = [U_ij]_n×n and U_ij = 1/n_c if x_i and x_j belong to the c-th class (c=1,2); U_ij = 0, otherwise. n_c denotes the size of the c-th class.

The objective function in Eq. (6) comprises two parts. One part is the same as LD-CCA, where the local within-class correlation is maximized and the local between-class correlation is minimized. By doing this, we can extract the nonlinear discrimination features as LD-CCA. The other part is similar to Fisher criterion that maximizes the global between-class scatter matrix and minimizes the global within-class scatter matrix. As a consequence, the extracted features are very compact for the same class and also well-separated for different class. In other words, the features extracted by SL-CCA may capture more discriminative information due to the simultaneous consideration of local and global supervising information.

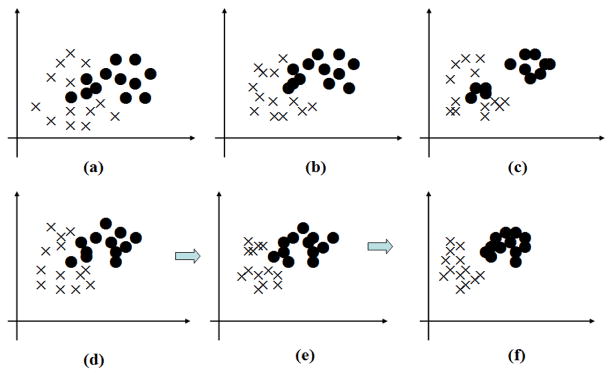
However, as a locality-based method, the performance of SL-CCA is significantly affected by the neighborhood size k. With a large k, the neighborhood covers a large number of samples, resulting in a loss of local information. With a small k, samples from a single class may be falsely separated into multiple clusters.

Fig. 2 shows that the effect of the value of k on SL-CCA. On one hand, when the value of k is very large (Fig. 2 (b)), although the data in the same class is more compact and the data in the different class is more scatter to some degree, it is still not enough to distinguish the two classes very well. The reason is that the neighbors of each point almost include the whole sample set, which causes the local preserving very weak. On the other hand, when the value of k is very small (Fig. 2 (c)), the local preserving is enhanced, which means the data in the local neighbor is very compact. However, from a global view, all the data in the same class may not be compact very well.

Fig. 2.

Diagram of the data distribution under different k. (a) the original distribution. (b) the distribution with a large k. (c) the distribution with a small k. (d~f) the distribution when k gradually decreases from large to small.

In order to reduce the influence of the neighborhood size and further improve diagnosis, we adopt a hierarchical version of SL-CCA, called hierarchical supervised local CCA (HSL-CCA), by sequentially performing SL-CCA and gradually decreasing the neighborhood size. In this processing, the samples from the same class will become more concentrated and also the samples from different classes will become better separated with the neighborhood size k gradually reducing from a large value to a small one. Fig. 2 (e–f) intuitively shows the process of HSL-CCA. We can see from Fig. 2 (e–f) that the data in the same class gradually become compact with the value of k gradually reducing from a large value to a small one. The reason is that the global effect of the same class gradually becomes weak in the process, while it is opposite of the local effect of the same class, which cause the data in the same class gradually getting together and the data in the different class gradually scatter.

Experiments

In this section, we evaluate the proposed method based on data scanned at NYU Langone Medical Center. We employ six different metrics to evaluate its diagnostic power for ASD. Next, the influences of the neighborhood size k and the number of hierarchical layers are investigated. Finally, we perform feature weight analysis to understand the importance of each ROI in ASD diagnosis.

Comparison for ASD diagnosis using different feature fusion methods

We perform extensive experiments on ASD diagnosis and compare HSL-CCA with several related methods, including SVM, PCA-1, PCA-2, CCA, K-CCA, LD-CCA and SL-CCA. For SVM, we combine MRI and fMRI for the subsequent classification. For PCA-1, we firstly use PCA on the combined MRI and fMRI features, and then use Linear SVM to classification. For PCA-2, we perform PCA based on the two sets of original features respectively, and then concatenate them for the subsequent classification [42]. For K-CCA, we map all the original features into a high-dimensional space and then perform conventional CCA. The other methods have been described in the “Methods” section. Features extracted by each method are concatenated into a vector. Finally, linear SVM (LSVM) based on the LIBSVM toolbox⁴ with default parameters was used for classification. Three layers were used for HSL-CCA, where the number of the layers is determined by searching in the range from two layers to eight layers.

For comprehensive evaluation, we adopt seven different statistical measures, namely classification accuracy (ACC), standard deviation of ACC (STD), sensitivity or true positive rate (TPR), specificity or true negative rate (TNR), precision or positive predictive value (PPV), negative predictive value (NPV), and F1 score (F1)⁵. High values for these scores reflect good performance. 10-fold Cross Validation (CV), repeated 100 times, was used during evaluation. To be specific, all subject samples are partitioned into 10 subsets (each subset with a roughly equal size), and each times all samples within one subset are successively selected as the testing data, while the remaining samples in the other nine subsets are combined together as the training data to perform feature selection and classification. Finally, we repeated the process 100 times and reported the average values. Here, it is worth noting that PCA was performed before the cross-validation among CCA, LD-CCA, SL-CCA and HSL-CCA and determined dimensions based on the cumulative contribution rate (in our experience, the cumulative contribution rate is 0.98). Table 1 shows the performance of different methods, where MRI and fMRI indicate that only the corresponding single modality was used. In addition, the classification accuracy of train data, denoted using ACC(T) in the second column of Table 1, is also listed for analyzing the overfitting issue.

Table 1.

Performance statistics

Method	ACC(T)	ACC	STD	TPR	TNR	PPV	NPV	F1
MRI	0.768	0.708	0.037	0.677	0.736	0.706	0.711	0.691
fMRI	0.791	0.748	0.052	0.671	0.820	0.777	0.729	0.720
SVM	0.824	0.751	0.043	0.721	0.772	0.786	0.705	0.758
PCA-1	0.819	0.726	0.056	0.721	0.737	0.778	0.674	0.748
PCA-2	0.835	0.744	0.069	0.661	0.820	0.774	0.723	0.713
CCA	0.818	0.755	0.058	0.697	0.808	0.773	0.742	0.733
K-CCA	0.917	0.773	0.084	0.792	0.754	0.778	0.796	0.785
LD-CCA	0.841	0.782	0.031	0.736	0.825	0.796	0.771	0.765
SL-CCA	0.857	0.791	0.028	0.811	0.772	0.782	0.800	0.789
HSL-CCA	0.862	0.816	0.014	0.813	0.825	0.815	0.823	0.814

From the results shown in Table 1, we have the following conclusions: (1) among all the competing methods, K-CCA has the serious overfitting issue while HSL-CCA is affected in a very less degree; (2) among all the compared methods, HSL-CCA has the lowest value of STD, which means HSL-CCA is very steady; (3) compared with the single modality methods (MRI or fMRI) and PCA, both CCA and its variants achieve better diagnostic accuracy due to multimodal feature fusion; (4) SL-CCA performs better than LD-CCA by incorporating the Fisher discrimination criterion; (5) HSL-CCA achieves the best performance for all diagnostic metrics, such as ACC, TPR and so on. The reason is that it not only inherits the advantages of SL-CCA but also reduces the sensitivity to the parameter k by using the hierarchical strategy.

Effect of parameter k

To our best knowledge, the performance of many locality-preserving methods is sensitive to the neighborhood size k. Also, determining the optimal k is a challenging problem.

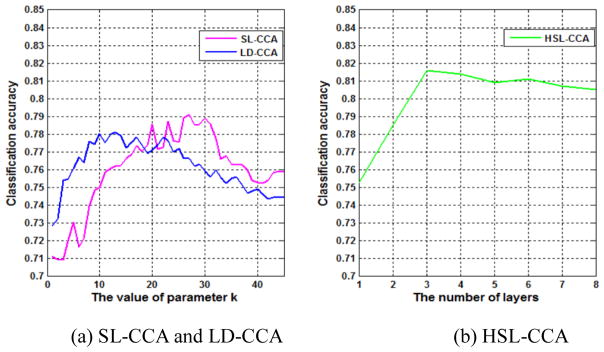
Fig. 3 (a) shows the influence of k on the classification accuracy of LD-CCA and SL-CCA. We can observe that both curves fluctuate significantly, implying that these methods are sensitive to k. Therefore, we have to determine a proper k using grid search at the cost of tremendous computational load.

Fig. 3.

Classification accuracy with respect to (a) parameter k in SL-CCA and LD-CCA (b) the number of layers in HSL-CCA.

Fig. 3 (b) shows the performance variation of HSL-CCA with respect to the number of layers. The parameter k is set as 40 in the first layer and reduces by 5 for each successive layer. As can be seen, HSL-CCA not only reduces parameter sensitivity, but also improves accuracy.

The most discriminative features for ASD diagnosis

We analyze the weight of each feature to determine features that are important to classification. Given that w_i (i = 1,2, ···, r) denotes the projection matrix (or weight matrix) of the i-th layer, the weighting vector v = (v₁, v₂, ···, v_p)^T is defined as

$$\{\begin{array}{c}v=\raisebox{1ex}{$\stackrel{\sim }{w}$}\!\left/ \!\raisebox{-1ex}{$\Vert \stackrel{\sim }{w}\Vert $}\right.\\ \stackrel{\sim }{w}=\text{abs}(w_1{w}_2\cdots w_r)·\mathbf{1}\end{array}$$ (8)

where p denotes the number of the features, and v_j (j = 1,2, ···, p) is the weighting value of the j-th feature, reflecting its contribution on classification. A larger v_j indicates a larger contribution of the j-th feature, and vice versa. The operator abs (·) denotes the absolute value. Column vector 1 consists of unit elements, and its dimension is equal to the row size of w₁.

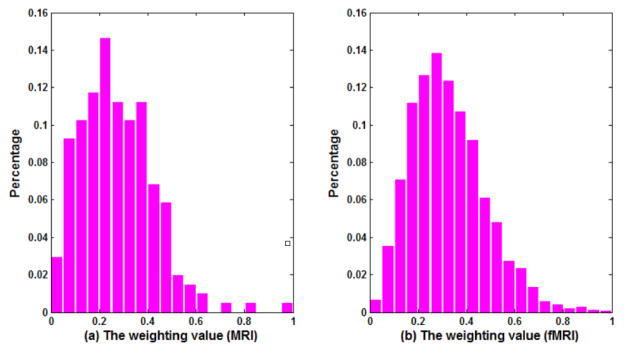
To HSL-CCA, we computer the weight value of each feature according to Eq.(8) in each experience and get the average weight distribution from all 100 times runs. Fig. 4(a) and (b) show the average weight distribution of single-modality feature from MRI and fMRI, respectively, where the horizontal axis denotes the weights and the vertical axis denotes the corresponding percentage values. From the figure, we can see that the percentages of features with large weights are low for both MRI and fMRI. In other words, only limited features capture strong discriminating information for ASD diagnosis. For example, we find that all the weight values corresponding to the features from cortical GM volumes are small, implying that the features from cortical GM volumes contain weak discriminating information. In addition, most inter-regional connections seem unimportant for ASD classification.

Fig. 4.

The distribution of the weighting factor of each feature.

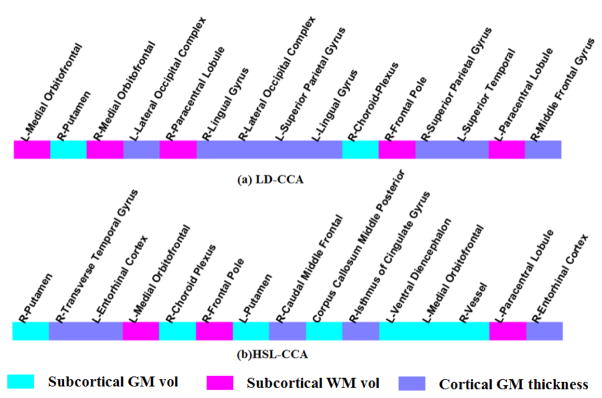
We list in Fig. 5 the top 15 regional features with the higher selection frequency based on their weight values. Specifically, for each run, we got the top 15 regional features with the large weight values. Then, we counted the frequency of these selected regional features from all 100 runs. Finally, the top 15 regional features with the higher frequency are selected. Fig. 5 (a) and (b) shows the result of LD-CCA and HSL-CCA respectively. As can be seen from Fig. 5, the selected features, no matter using LD-CCA or HSL-CCA, include the regional subcortical GM volume, the regional subcortical WM volume, and cortical thickness, indicating the spread of morphological abnormalities over the whole brain in ASD patients. In addition, most of the selected regions, such as Putamen, Entorhinal cortex, Medial orbitofrontal, Caudal middle frontal, and Frontal pole, are associated with episodic memory, social cognition and emotion processing. These findings are in agreement with the fact that ASD is a behavioral- and language-related neurodevelopmental disorder. The features selected by HSL-CCA can potentially be used as biomarkers to aid ASD clinical diagnosis.

Fig. 5.

Top 15 regional features with largest weight values in (a) LD-CCA and (b) HSL-CCA

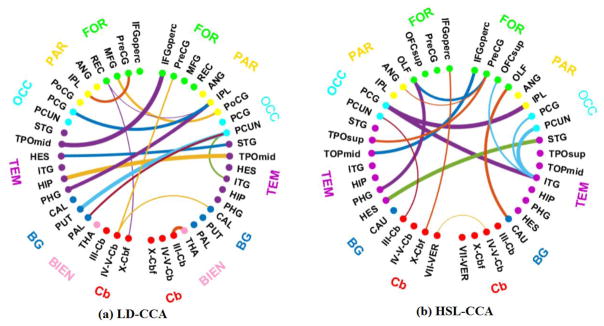
Similar to the process we do in Fig. 5, we also graphically show in Fig. 6 the connectogram of the most discriminating connections involving the top 15 selected interregional features, where the same colored points denote neighboring regions and each connection denotes the correlation relationship between two regions [43]. These connections are selected based on the classification results, thus implying they are discriminative. The edges in this figure indicate the importance of this edge. A thicker line indicates the higher frequency and the larger weight. To be specific, we got the top 15 interregional features with the larger weight values in each experiment. Then, we counted the frequency of these selected interregional features from all runs and got the top 15 interregional features according to the higher frequency. Because the weight value reflects the contribution for accurate classification, a thicker line indicates the higher frequency and a greater contribution to the discriminative. Fig. 6 (a) and (b) shows the result of LD-CCA and HSL-CCA respectively. For the abbreviations of the regions in Fig. 6, please refer to Table 2.

Fig. 6.

Connectogram of the most discriminating connections in (a) LD-CCA and (b) HSL-CCA

Table 2.

Abbreviations of the regions

FRO: frontal	IFGoperc: Inferior frontal gyrus (opercular) OFCsup: Orbitofrontal cortex (superior) MFG: Middle frontal gyrus	PreCG: Precentral gyrus OLF: Olfactory REC: Gyrus rectus
PAR: Parietal	ANG: Angular gyrus PoCG: Postcentral gyrus	IPL: Inferior parietal lobule
OCC: Occipital	PCG: Posterior cingulate gyrus	PCUN: Precuneus
TEM: temporal	STG: Superior temporal gyrus TPOmid: Temporal pole (middle) ITG: Inferior temporal PHG: ParaHippocampal gyrus	TPOsup: Temporal pole (superior) HES: Heshl gyrus l HIP: Hippocampus HES: Heschl gyrus
BG: basal ganglia	CAU: Caudate PUT: Putamen	CAL: Calcarine fissure and surrounding cortex PAL: Pallidum
DIEN: Diencephalon	THA: Thalamus
CER: cerebellum	III-Cb:Lobule III of cerebellar hemisphere X-Cbf: lobule X of cerebellar hemisphere (flocculus)	IV–V-Cb: lobule IV, V of cerebellar hemisphere VII-VER: Lobule VII of vermis

It can be clearly observed in Fig. 6 that pairs of regions (i.e., links in the connectogram) that contribute to accurate ASD classification are not restricted to the same hemisphere or lobe, but also across hemispheres and all lobes, indicating the spread of morphological abnormalities over the whole brain in ASD patients. On the other hand, we can see that most regions with the strong connections locate in the front part of the brain, such as frontal lobes, parietal lobes, occipital lobes and temporal lobes, most of which are highly correlated with the perception of emotion, the interpretation of sensory information, language performance and sports coordination. Contrarily, the regions located in the posterior of the brain, such as basal ganglia and cerebellum lobes, have sparse and weak connections, and most of them are highly correlated with exercise, smell, and hearing. These findings are also in agreement with the behavioral phenotype of ASD.

Based on the above analysis, we obtain the following conclusions: (1) There indeed exists some biomarkers which exhibit remarkable differences between ASD patients and normal controls; (2) Although the spread of morphological abnormalities covers whole brain in ASD patients, only a small part of morphological measures carry strongly discriminative information for ASD diagnosis; (3) The regions that enormously contribute to accurate ASD classification usually have close relationships with human emotional modulation and memory formation, which are in good agreement with the behavioral phenotype of ASD. Furthermore, we found most of the above findings are reported in the existing literatures and relevant to ASD. For example, it is reported that structural or histological abnormalities of the putamen may underlie the pathologies of ASD [44]. This is highly consistent with our findings.

Conclusion

We have proposed a novel feature weighting and fusion method, called HSL-CCA, to effectively identify ASD patients from healthy controls. Compared with CCA and its existing variants, the difference of HSL-CCA lies in two aspects: (1) a new feature fusion model, called SL-CCA, is designed to simultaneously model the correlations between sample pairs, local neighborhoods, and between-class discrimination information; this improves the discriminative power of the extracted features; (2) a hierarchical strategy is adapted to reduce the sensitivity of SL-CCA to the neighbor parameter. Hierarchical strategy is another important innovation in this work. Locality has significant influence on the proposed method. However, it is difficult to find a proper parameter for k nearest neighbor-based in original high-dimensional space through just one step. Therefore, we propose this hierarchical strategy which tries to find effective parameter by multiple steps. After each step was finished, the inherent data structure can be well discovered as shown in Fig. 2. In such a way, this parameter can be continuously optimized such that a better performance can be achieved. The experimental results demonstrate that the proposed method can significantly improve diagnostic performance.

Furthermore, we find that the regions, which are selected for accurate classification, have a close relationship with episodic memory, social cognition and emotion processing. The conclusion is in line with the behavioral phenotype of ASD, which is associated with several impairments of interaction, language, behavior, and cognitive functions. Our analysis also reveals the percentage of the selected regions is much lower in the whole brain, hinting that physicians only need to pay attention to some special regions in ASD diagnosis.

Lastly, note that HSL-CCA can be easily extended for diagnosis of other highly heterogeneous neurodevelopmental disorders, such as Alzheimer’s disease, Parkinson disease, depressive illness, and so on. Of course, findings in this study are still preliminary and require further study in the future. In our next work, we plan to extend HSL-CCA to more than two modalities.