Sources of cosmic dust in the Earth's atmosphere

Abstract

There are four known sources of dust in the inner solar system: Jupiter Family comets, asteroids, Halley Type comets, and Oort Cloud comets. Here we combine the mass, velocity, and radiant distributions of these cosmic dust populations from an astronomical model with a chemical ablation model to estimate the injection rates of Na and Fe into the Earth's upper atmosphere, as well as the flux of cosmic spherules to the surface. Comparing these parameters to lidar observations of the vertical Na and Fe fluxes above 87.5 km, and the measured cosmic spherule accretion rate at South Pole, shows that Jupiter Family Comets contribute (80 ± 17)% of the total input mass (43 ± 14 t d⁻¹), in good accord with Cosmic Background Explorer and Planck observations of the zodiacal cloud.

Key Points

• Solar system dust sources are fitted to the cosmic spherule accretion rate and the Na and Fe fluxes in the mesosphere

• Jupiter Family Comets provide ~80% of the cosmic dust entering the atmosphere, with 12% from long‐period comets and 8% from asteroids

• The resulting differential ablation of Ca and Fe relative to Na explains the relative abundances of these metal layers in the mesosphere

1. Introduction

Estimates of the mass influx of cosmic dust entering the Earth's atmosphere vary over a wide range from 5 to 270 tons per day (t d⁻¹), depending on the method used to make the estimate [Plane, 2012]. These dust particles are present in the zodiacal cloud (ZC), which is a circumsolar disk of small debris particles produced by sublimating comets and collisions between asteroids. The principal sources to the ZC are short‐period Jupiter Family Comets (JFCs); particles from the asteroid belt (ASTs); longer‐period Halley Type Comets (HTCs); and Oort Cloud Comets (OCCs) [Nesvorný et al., 2011, 2010; Pokorný et al., 2014]. In the 1990s, it was assumed that gravitational focusing of relatively slow‐moving AST particles would enhance their contribution to the ZC and the terrestrial input [Durda and Dermott, 1997; Flynn, 1989]. However, Nesvorný et al. [2010] used numerical modeling of dust ejected from these different sources, together with observations of infrared emission from the ZC made by the InfraRed Astronomy Satellite (IRAS), to show that JFCs are the dominant source (85–95%) of the dust. This is because the profile of IR emission across the plane of the ecliptic matches that expected from JFC particles, whereas HTC particles should have a broader profile and the AST profile should be narrower (Huang et al. [2015] showed that the relatively large Na ablation flux compared to Fe in the upper mesosphere was consistent with the dominant JFC particle model). Subsequently, Rowan‐Robinson and May [2013] modeled IRAS and Cosmic Background Explorer (COBE) observations, concluding that the cometary contribution was 70% with a 22% AST contribution. Most recently, Yang and Ishiguro [2015] combined observations of the albedo and spectral gradient of the ZC to show that cometary dust contributes ~94% of the ZC, with the remaining ~6% from asteroidal particles.

The present study will employ a completely different approach to this problem. We will use the cosmic spherule accretion rate at the bottom of an ice chamber at the Amundsen‐Scott base at South Pole [Taylor et al., 1998], together with recent measurements of the vertical fluxes of Na and Fe atoms above 87.5 km in the atmosphere [Gardner et al., 2016, 2014; Huang et al., 2015], to determine the absolute contributions of each of these dust sources to the global input of cosmic dust.

2. Mass and Velocity Distributions of Dust From Different Sources

For the present study, the size distribution of cosmic dust particles was assumed to be represented by a broken power law with a differential index −2 to −3 below the break diameter D _break and a differential index −4 to −5 above D _break. COBE observations indicate that D _break lies between 30 µm and 60 µm [Fixsen and Dwek, 2002], which is supported by measurements of weak ZC emission at submillimeter wavelengths by the Planck telescope launched in 2009 [Ade et al., 2014]. Here we assume D _break = 36 µm, which corresponds to a dust composition in between amorphous carbon (D _break ~ 28 µm) and silicate (D _break ~ 64 µm) [Fixsen and Dwek, 2002]. The cumulative size distribution is shown in Figure S1 in the supporting information. The IRAS observations suggested D _break ~ 100 µm [Nesvorný et al., 2010], compared in Figure S1.

In the Zodiacal Cloud Model (ZCM) [Nesvorný et al., 2011, 2010], particles of different sizes were launched from the four sources (JFCs, ASTs, etc.) and their orbits were tracked with an N‐body code. These integrations accounted for the gravity of all planets, solar pressure, and Poynting‐Robertson drag. A collisional model is used where particles are assumed to experience an erosive collision with another particle in the ZC after a characteristic time, τ, which is a function of the particle size and orbit; the particles then undergo a collisional cascade, with smaller fragments being progressively more affected by Poynting‐Robertson drag [Nesvorný et al., 2011]. For example, 50 µm and 500 µm radius particles in a circular orbit at 1 AU have collisional lifetimes of 1.5 × 10⁵ and 7.3 × 10³ years, respectively [Grün et al., 1985]. The accretion probability of particles on planets was computed with the standard Öpik code [Greenberg, 1982]. The thermal infrared emission from these modeled particle distributions was then compared iteratively with the emission measured by Planck (or IRAS).

Figures 1a and 1b are histograms of the particle mass distributions for the four cosmic dust sources accreted at the Earth derived from the Planck and IRAS observations, respectively. These distributions are shown as mass flux per decade over the mass range 10⁻⁹ to 10⁻² g, i.e., with a radius between 5 µm and 1 mm, assuming a particle density of 2.2 g cm⁻³ [Consolmagno et al., 2008]. The mass influx of each source has been weighted according to the fitting procedure in section 4. As discussed above, the JFCs were modeled using either the Planck or IRAS distributions—these are termed JFC‐IRAS and JFC‐Planck particles, respectively. Figures 1a and 1b show that the JFCs‐Planck mass distribution peaks around 0.01 µg, whereas the largest mass contribution of accreted JFC‐IRAS, HTC, and OCC particles is from particles of ~1 µg, and the AST peak is ~10 µg. Following from the conclusion that most of the ZC emission is from JFC particles, the IRAS and Planck observations indicate a global input of 34 ± 17 t d⁻¹ of JFC‐IRAS particles [Carrillo‐Sánchez et al., 2015; Nesvorný et al., 2011] or 30 ± 15 t d⁻¹ of JFC‐Planck particles [Janches et al., 2015] into the atmosphere. Meanwhile, the total mass input rates of the AST, HTC, and OCC sources are arbitrarily set to 10 t d⁻¹ in the ZCM, because the ZC observations cannot be used to calibrate these mass distributions. In section 4 the absolute magnitudes of all four dust sources are optimized to get an estimate of the total input mass (TIM).

Figure 1.

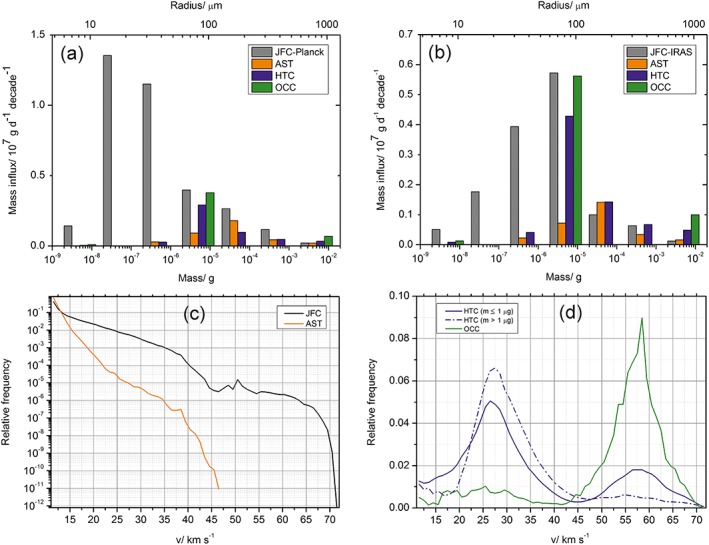
(a and b) Histograms illustrating the mass input rate into the atmosphere as a function of particle mass or size, for the four dust sources; (c and d) entry velocity distributions for the JFC (black), AST (orange), HTC (blue), and OCC (green) particles.

Figures 1c and 1d show the entry velocity distributions of the different populations, modeled by the ZCM. The slowest particles tend to be JFC and AST particles, and the fastest particles are HTC and OCC particles from long‐period comets. The average entry velocity of the JFCs and the ASTs is 14.5 km s⁻¹ and 12.0 km s⁻¹, respectively, which means that most of these particles are in prograde orbits originating from the helion and antihelion sporadic sources [Nesvorný et al., 2011, 2010].

The velocity distribution for the HTC and OCC particles is shown in Figure 1d. The HTC distribution depends on the mass range: for masses < 1 µg, the distribution follows a bimodal trend with a dominant peak at 26 km s⁻¹ and a second maximum at 57 km s⁻¹. For masses > 1 µg there is a single peak at 26 km s⁻¹. The OCC distribution exhibits a single peak at 58 km s⁻¹. Most of these particles are in a retrograde orbit, and they are likely released from the north and south apex sources.

3. Meteoric Ablation Modeling

The Chemical ABlation MODel (CABMOD) solves the momentum and energy balance for a cosmic dust particle of a particular mass entering the atmosphere with a defined velocity and entry angle [Vondrak et al., 2008]. The ablation of individual elements occurs both through sputtering (i.e., collisions with air molecules causing the ejection of surface atoms, which is important before the particle melts) and the much more rapid evaporation of metal atoms and oxides after melting. CABMOD has recently been tested using the Meteoric Ablation SImulator [Bones et al., 2016], commissioned in our laboratory to test the predicted evaporation of Na, Fe, and Ca from meteoritic particles under realistic heating conditions. These tests have enabled the evaporation kinetics of a particle around its melting point to be better described using a sigmoidal function for the uptake coefficient describing Langmuir evaporation from the melt [Vondrak et al., 2008]. For the present study we use a sigmoidal function which best describes the ablation of a carbonaceous chondrite (Allende, CV3) [Macke et al., 2011], with a melting point of 1800 K and a density of 2.2 g cm⁻³ [Consolmagno et al., 2008].

Owing to the large number of particles from each cosmic dust source that are produced by the ZCM (6.7 × 10⁶ for JFC‐IRAS, 9.3 × 10⁶ for JFC‐Planck, 1.5 × 10⁶ for AST, 3.3 × 10⁶ for HTC, and 1.9 × 10⁵ for OCC), we use a Monte Carlo procedure to sample the particle velocity and entry angle distributions in each mass interval [Carrillo‐Sanchez et al., 2015]. Only particles smaller than 500 µm in radius (<10³ µg) are sampled, in order to ensure isothermal heating of the particles which is a requirement of CABMOD [Vondrak et al., 2008]. This size limitation is a reasonable approximation because the very large particles do not represent a significant share of the total input (Figures 1a and 1b). Each mass decade is divided into five bins, and the velocity and zenith angle distributions are Monte Carlo selected. The resulting atmospheric ablation profiles are then coadded. Finally, the results for each mass bin are summed to obtain the integrated injection rates profiles for each metallic element [Carrillo‐Sanchez et al., 2015]. The total number of sampled particles is 15,500 for each dust source, assuming a sample size of 500 particles per mass and 5 bins per decade in the mass range between 10⁻³ and 10³ µg.

The injection rate profiles for individual elements from the different sources are shown in Figure 2. Note that these ablation profiles have been weighted following the fitting procedure in section 4, in order to show their absolute contributions to the total input of each element. Figure 2 (top row) illustrates the contributions of JFC‐Planck, AST, and HTC particles. Figure 2 (bottom left) shows the elemental ablation rate profiles for JFC‐IRAS, and Figure 2 (bottom middle and bottom right) shows the total inputs for IRAS and Planck. In all cases, the most volatile elements (Na and K) ablate 10–15 km higher than the main constituent elements (Fe, Mg, and Si), which in turn ablate higher than the most refractory elements (Ca, Al, and Ti). As expected, the ablation profiles for the AST are about 10–20 km below that the corresponding profiles for the JFCs and HTCs. This is caused by their slower velocity distribution (Figure 1) and the larger particles in the AST population taking longer than the JFCs to reach the melting point. The ablation profiles for the HTCs represent the opposite extreme. The ablation profiles for the OCCs are very similar to the HTCs and so are not shown in Figure 2.

Figure 2.

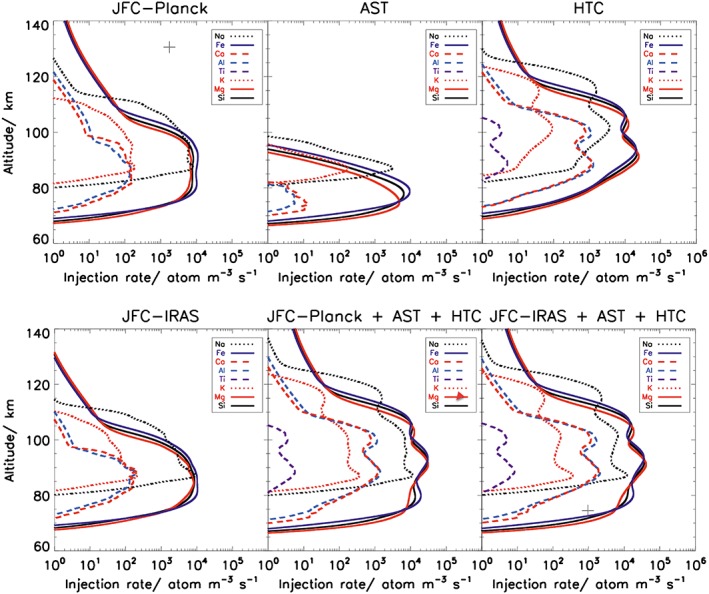
Ablation rate profiles for individual elements integrated for the JFC (constrained with the Planck and IRAS observations), AST, and HTC particle populations. The final two plots show the overall injection rates.

Meteoroids that melt but do not ablate completely become cosmic spherules. When the size of these particles is recorded in the CABMOD output, they are assumed to have a higher density (3.2 g cm⁻³ [Kohout et al., 2014]) than the initially more porous meteoroids.

4. Determining the Contribution of Each Cosmic Dust Source

We now use three observations to constrain the relative contributions of each of these dust sources. First, the analysis of cosmic spherules at South Pole indicates a global accretion rate of 4.4 ± 0.8 t d⁻¹, for spherules with diameters between 50 and 700 µm [Taylor et al., 1998]. Second, the global input rate of Na atoms from meteoric ablation above 87.5 km is estimated to be 0.30 ± 0.06 t d⁻¹, by taking the annual mean vertical flux of Na atoms at 87.5 km (16700 ± 1800 atoms cm⁻² s⁻¹) measured at the Starfire Optical Range (35°N) [Gardner et al., 2014], assuming that this can be extrapolated globally [Gardner et al., 2016], though we (arbitrarily) double the error to allow for uncertainty in this extrapolation, and multiplying the flux by a factor of 1.03 to obtain the total Na input by including the other forms of Na modeled to be present at 87.5 km [Marsh et al., 2013]. Third, the global input rate of Fe atoms above 87.5 km is estimated to be 2.29 ± 1.05 t d⁻¹, by taking the ratio of the Fe to Na atom fluxes measured at the Table Mountain Lidar Facility (40°N) to be 2.36 at 87.5 km [Huang et al., 2015, Figure 1] and multiplying by a factor of 1.38 [Feng et al., 2013] to obtain the total Fe input.

The ablation profiles of Na and Fe from each cosmic dust source (Figure 2) can now be integrated above 87.5 km to produce an ablation flux, which is then multiplied by the global surface area of the atmosphere at 87.5 km to produce a global input rate. This assumes that the flux is globally isentropic, which should be the case when integrated over a year [Feng et al., 2013]. The cosmic spherule flux predicted by CABMOD for each dust source can similarly be converted into a global accretion rate.

We now have three simultaneous equations of the form in equation (1):

$${\psi }_{\text{Total}}=\alpha {\psi }_{\mathrm{J}\mathrm{F}C}+\beta {\psi }_{\mathrm{A}\mathrm{S}\mathrm{T}}+\gamma {\psi }_{\mathrm{L}\mathrm{P}\mathrm{C}}$$ (1)

where ψ _Total is the global mass accretion rate of Na atoms, Fe atoms, or cosmic spherules, ψ _JFC, ψ _AST, and ψ _LPC are the global mass accretion rates of Na, Fe, or spherules from the different sources, and α, β, and γ are the coefficients which weight the contribution from each source. LPC in equation (1) refers to Long‐Period Cometary particles. This covers both HTCs and OCCs, which cannot be distinguished using our three criteria (see below). In the following discussion, the LPC particles are treated as HTCs unless otherwise stated.

Since there are three simultaneous equations and three unknowns (α, β, and γ), the solution is, in principle, unambiguous. However, one constraint on the solution is the elemental abundance ratio of Na to Fe in the cosmic dust particles. The measured Fe and Na atom fluxes above 87.5 km [Huang et al., 2015] correspond to a Fe:Na ratio of ~3.16. However, if the Fe:Na ratio in the cometary particles is the Carbonaceous Ivuna (CI) ratio of 15.5 [Asplund et al., 2009], then CABMOD predicts that the Fe:Na ablation flux above 87.5 km would be 3.4, 13.2, or 14.6 for the JFC, HTC, and OCC sources, respectively. Thus, even if LPC particles make up a small proportion of the total input, because they ablate relatively efficiently, this implies that the cometary particles must be enriched in Na. There is in fact strong evidence for Na overabundance compared to Fe: a measured enrichment factor of 2.0 from the Stardust mission to comet 81P/Wild 2 [Gainsforth et al., 2015], ~2 from meteor spectroscopic analysis during the Perseid and Leonid showers [Trigo‐Rodriguez and Llorca, 2007], 3.2 from the VEGA‐1 mission to comet 1P/Halley [Jessberger et al., 1988], and most recently, 4.8 ± 3.7 from the Rosetta mission to 67P/Churyumov‐Gerasimenko [Hilchenbach et al., 2016].

The optimal fits using the JFC‐Planck particles—termed the ZCM‐Planck model—are Na enrichment factor = 2.5, α = 1.17 ± 0.47, β = (3.46 ± 1.96) × 10⁻², and γ = (4.99 ± 2.72) × 10⁻². These values and their stated uncertainties were estimated by using Monte Carlo selection (assuming a top‐hat distribution) to choose the cosmic spherule, Na and Fe fluxes within their quoted uncertainties, and then solving the simultaneous equations for new values of α, β, and γ. Trials which generated negative values of any of these parameters were rejected. A Na enrichment factor of 2.5 gave a high number of successful trials (71%) and is well within the observed range (see above). The values and their uncertainties are then the mean and standard deviations of 10⁵ trials. In terms of the global mass input rate, the contributions of the JFC, AST, and LPC particles are 34.6 ± 13.8 t d⁻¹ (80%), 3.7 ± 2.1 t d⁻¹ (8%), and 5.0 ± 2.7 t d⁻¹ (12%), respectively. The corresponding results for the JFC‐IRAS distribution (termed the ZCM‐IRAS model) are shown in the supporting information.

5. Discussion

Table 1 (first to third rows) illustrates the partitioning of the accreted mass between unmelted micrometeorites, cosmic spherules, and ablated atoms, for the JFC‐Planck, AST, and LPC (= HTC) dust sources. Table 1 (fifth column) shows the total from the three sources. The bottom part of Table 1 shows the ablated mass of each element for each of the dust sources. Table 1 (sixth column) shows the fate of the OCC particle population, which was calculated by setting LPC = OCC instead of HTC in the fitting procedure (minor changes to the JFC and AST outcomes are not shown in the table). Because the HTCs and OCCs are relatively fast particles (Figure 1), Table 1 shows that 88% of the HTC mass input, or 98% of the OCC mass input, ablates. As a consequence, these dust populations make an insignificant (6% and 1% for HTC and OCC, respectively) contribution to the cosmic spherule flux. They also produce very similar Fe:Na ablation ratios (5.7 and 5.9, respectively, with a Na enrichment factor of 2.5). This explains why solving equation (1) does not distinguish between HTCs and OCCs.

Table 1.

Global Mass Input From the Four Cosmic Dust Sources for the JFC‐Planck Fit^a

Mass Flux	JFC (t d−1)	AST (t d−1)	LPC = HTC (t d−1)	Total (t d−1)	LPC = OCC (t d−1)
Unmelted micrometeorites	27.4	1.2	0.3	28.9	0.04
Cosmic spherules	4.4	1.8	0.3	6.5	0.06
Ablated atoms	2.8	0.7	4.4	7.9	4.4
Cosmic spherules b	2.4	1.7	0.3	4.4	0.05
Unmelted (∅ > 50 µm)	3.0	1.1	0.2	4.3	0.03
Na	0.2 (28%)	0.02 (75%)	0.09 (99%)	0.3 (40%)	0.09 (100%)
K	7.7 × 10−3 (27%)	2.2 × 10−3 (74%)	4.0 × 10−3 (97%)	0.01 (28%)	3.8 × 10−3 (100%)
Fe	1.0 (10%)	0.3 (28%)	1.3 (90%)	2.6 (21%)	1.2 (98%)
Si	0.4 (6%)	0.1 (17%)	0.7 (87%)	1.2 (17%)	0.7 (97%)
Mg	0.3 (5%)	0.06 (11%)	0.6 (85%)	1.0 (16%)	0.6 (97%)
Ca	7.0 × 10−3 (1%)	1.8 × 10−4 (0.4%)	0.05 (70%)	0.06 (10%)	0.06 (93%)
Al	3.7 × 10−3 (0.8%)	5.5 × 10−5 (0.1%)	0.04 (59%)	0.04 (7%)	0.05 (88%)
Ti	3.6 × 10−5 (2%)	1.7 × 10−6 (0.8%)	2.5 × 10−4 (84%)	2.9 × 10−4 (11%)	3.0 × 10−4 (100%)
O	0.9 (7%)	0.2 (18%)	1.6 (90%)	2.7 (17%)	1.7 (100%)
Total	34.6	3.7	5.0	43.3	4.5
% Na|87.5 km c	86%	46%	99%	87%	100%
% Fe|87.5 km c	52%	0.9%	92%	65%	98%

^aElemental ablation inputs are italicized; the percentages in parentheses show the fraction of each element that ablates from its total atmospheric input from each source.

^bSpherules in the size range 50  µm ≤ ∅ ≤ 700 µm corresponding to measurements at South Pole [Taylor et al., 1998].

^cFraction of Na and Fe ablated above 87.5 km.

We now consider why the fitting procedure yields such a high relative input of JFCs. The ratio of the Na mass input measured by lidar above 87.5 km [Gardner et al., 2016, 2014; Huang et al., 2015] to the cosmic spherule flux [Taylor et al., 1998] is Na|_87.5 km : ψ _sp = 0.07. For Fe, the corresponding ratio is Fe|_87.5 km : ψ _sp = 0.52. These ratios can be compared with the corresponding ratios for the different sources in Table 1. The JFCs produce the closest ratios to the measurements with Na|_87.5 km : ψ _sp = 0.08 and Fe|_87.5 km : ψ _sp = 0.42. In contrast, the ASTs and LPCs represent lower and upper limits, since these sources are at the opposite extreme in the production of ablated atoms and spherules. For the ASTs, where there is a low average velocity, there is a significant production of spherules compared to ablated atoms, so that Na|_87.5 km : ψ _sp = 0.01 and Fe|_87.5 km : ψ _sp = 0.18. For the LPCs, where there is a high average velocity, the situation is reversed: Na|_87.5 km : ψ _sp = 0.30 and Fe|_87.5 km : ψ _sp = 4.33. Consequently, the fitting procedure determines a minor contribution from both ASTs and LPCs.

A significant result of the present study is that the JFC particles contribute (80 ± 17)% of the mass input to the terrestrial atmosphere. This is consistent with the conclusions of Nesvorný et al. [2010], Yang and Ishiguro [2015], and Rowan‐Robinson and May [2013] (see section 1). It should be noted, as pointed out by Yang and Ishiguro [2015], that the analysis of Antarctic micrometeorites and cosmic dust particles collected in the stratosphere has found that less than 50% are “chondritic porous” particles, which are taken to be of cometary origin [Noguchi et al., 2015]. In contrast, the present study indicates that 63% of unmelted micrometeorites and cosmic spherules with diameters > 50 µm (the lower limit for measurements) should be cometary. This may indicate that some of the “chondritic smooth” particles, assumed to be asteroidal, are wrongly assigned. Because the JFC‐Planck particle mass distribution peaks around 0.01 µg (Figure 1), there is only significant ablation of the high‐mass tail of the distribution, so that 67% of the TIM does not melt during entry.

Table 1 shows that there are striking differences in the ablation efficiencies of individual elements for the different dust sources (see Table S1 in the supporting information for the corresponding data from the ZCM‐IRAS model). In the case of Na, the ablation efficiency from JFC‐Planck particles is 28%, compared with 99% for LPC particles. For the highly refractory elements, the differences are even more extreme: for Ca, the ablation efficiency is 1%, compared with 70% for the LPCs. Note that even though the average velocity of ASTs is lower than JFCs (Figure 1), the ablation efficiencies are higher for all the elements apart from the most refractory (Ca, Al, and Ti) because the particle mass distribution is shifted to larger particles which tend to reach higher temperatures during atmospheric entry.

Figure 3 correlates the ablation efficiencies of Fe, Mg, and Ca relative to Na (data taken from Table 1) against the relative ablation rates of these elements required to produce good agreement between the Whole Atmosphere Climate Model (WACCM) and lidar and satellite observations of the mesospheric metal atom layers [Carrillo‐Sanchez et al., 2015]. The black circles show the CI chondritic ratios [Asplund et al., 2009], and the red circles are the CI ratios but with a Na enrichment factor of 2.5. The red points represent the case where there is no differential ablation, i.e., complete ablation of all elements, and are well above the line of 1:1 correspondence. However, when differential ablation is included, ZCM‐Planck (orange diamonds) produces much improved correlation with the modeled observations. Figure 3 also shows the differential ablation ratios for the JFC, AST, and HTC particles in the ZCM‐Planck model, where the HTCs essentially ablate in their chondritic ratios for all metals. In contrast, the ASTs exhibit such a high degree of differential ablation for the refractory elements that the Ca:Na ratio is well below the line of 1:1 correspondence.

Figure 3.

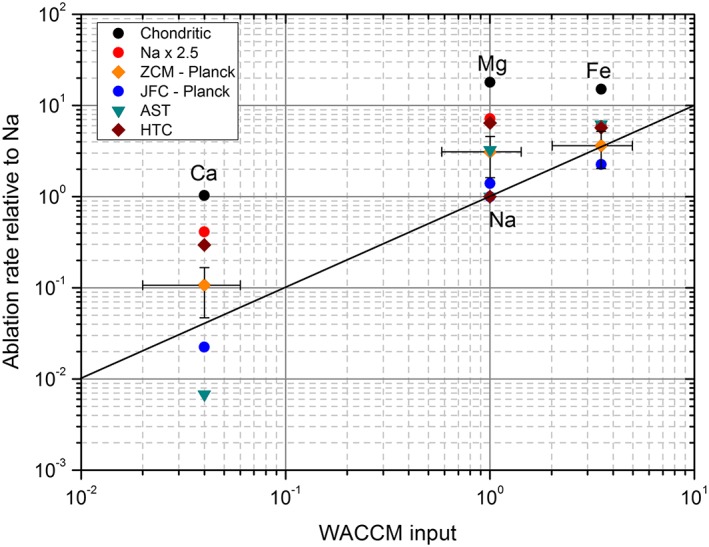
Ablation rates for Ca, Fe, and Mg relative to Na, plotted against the relative input rates required to model the global metal atom layers in the MLT using WACCM [Carrillo‐Sanchez et al., 2015]. The solid line is the 1:1 correlation line. The black points show the relative CI chondritic compositions, and the red points are the CI compositions with a Na enrichment factor of 2.5. The predicted ratios for the JFC‐Planck, AST, and LPC sources are also shown (see legend). For the overall ZCM‐Planck prediction (orange diamonds), the horizontal error bars indicate the uncertainties in the WACCM ratios, and the vertical error bars show the uncertainties in the relative ablation rates derived from the Monte Carlo analysis (see text).

6. Conclusions

In this study the absolute inputs of cosmic dust particles from four different sources—JFCs, ASTs, HTCs, and OCCs—to the Earth's atmosphere were constrained using the measured vertical Na and Fe fluxes above 87.5 km and the accretion rate of cosmic spherules at South Pole. Because HTCs and OCCs are characterized by high entry velocities, it is not possible to distinguish between them in terms of these constraints. Taking a JFC mass distribution determined recently from observations of the zodiacal cloud by the Planck satellite, JFCs are shown to contribute (80 ± 17)% of the total input mass of 43 ± 14 t d⁻¹, assuming a Na to Fe enrichment of 2.5 which is close to the average enrichment measured in cometary particles. Finally, the differential ablation of Ca and Fe, with respect to Na, is now large enough to model the respective metal atom layers in the upper mesosphere.

Supporting information

Supporting Information S1

Carrillo‐Sánchez, J. D. , Nesvorný D., Pokorný P., Janches D., and Plane J. M. C. (2016), Sources of cosmic dust in the Earth's atmosphere, Geophys. Res. Lett., 43, 11,979–11,986, doi:10.1002/2016GL071697.